Известия РАН. Теория и системы управления, 2019, № 3, стр. 24-33

Введение. Важным классом технических систем, моделируемых совокупностью твердых тел, являются колесные транспортные средства, в частности автомобили [1, 2]. Критическими моментами в управлении автомобилями служат динамические режимы изменения их движения (начало движения, торможение, изменение направления). Ключевую роль здесь играют силы взаимодействия колес с дорогой, в особенности сила трения. В связи с этим актуальной представляется проблема расчета и оптимизации режимов управления автомобилями с учетом моделей сухого трения. В последнее время появились работы, значительно уточняющие модели сил сухого трения и пригодные для расчета движения колесных транспортных средств и анализа нежелательных колебаний колес [3, 4].

Для уменьшения негативного влияния трения на колеса переднеприводного автомобиля, а именно для уменьшения их износа и улучшения управляемости, используется межколесный дифференциал, уравнивающий крутящие моменты на ведущих колесах и позволяющий им вращаться с разной угловой скоростью. Однако если система блокировки дифференциала отсутствует, то возникает серьезный недостаток, который проявляется в существенной потере тяги в различных стандартных ситуациях при наличии несимметрии в условиях движения: при резком повороте или повороте на большой скорости; при движении с большим креном вдоль линий уровня кюветов, склонов, оврагов, гор; при проскальзывании одного из колес в колее с водой летом или в углублении со льдом зимой; при подвисании одного из колес в воздухе на неровной дороге и т.д.

В данной статье исследован еще один подобный эффект, но возникающий в почти идеальных условиях при прямолинейном движении по горизонтальной плоскости. При быстром разгоне транспортного средства из-за проскальзывания ведущих колес возможен нежелательный эффект, связанный с нарастанием колебаний колес в вертикальной плоскости и их последующим незатуханием. Как показано далее, наличие межколесного дифференциала приводит к тому, что колеса взаимодействуют с дорогой так, что автомобиль практически не в состоянии двигаться вперед. Решение этой проблемы важно для обеспечения безопасности движения обычных автомобилей, управляемых водителями, и, в особенности, беспилотных автомобилей, разработка которых интенсивно ведется во многих промышленно развитых странах.

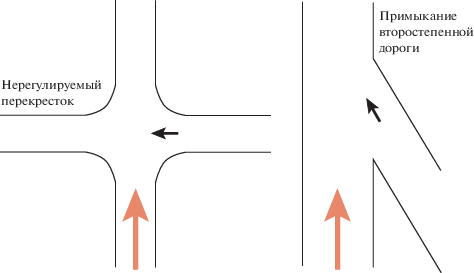
1. Оптимальный разгон с проскальзыванием. Постановка задачи управления. Рассмотрим ради определенности переднеприводное транспортное средство, имеющее неблокируемый межколесный дифференциал и не снабженное какими-либо электронно-механическими средствами, которые предотвращают пробуксовку (нем. Antriebsschlupfregelung, ASR; англ. Traction Control System, TCS; Dynamic Traction Control, DTC). Предполагаем, что происходит интенсивный разгон с места по ровному сухому асфальту. Так обычно выглядит ситуация, когда требуется быстро пересечь нерегулируемый перекресток или быстро выехать на главную дорогу с примыкающей (второстепенной) перед другим быстро приближающимся транспортным средством, которое представляет опасность (см. рис. 1, где рассматриваемое резко ускоряющееся транспортное средство обозначено короткой стрелкой, а другое быстро приближающееся транспортное средство – длинной стрелкой).

Далее, в следующих двух разделах, рассмотрим только несколько режимов интенсивного старта с проскальзыванием ведущих колес: первый – без колебаний колес в вертикальной плоскости, остальные три – с колебаниями, причем вид этих колебаний постепенно усложняется по мере их рассмотрения. Предполагаем, что возникающие колебания периодические и установившиеся, хотя, на самом деле, на коротких интервалах времени их амплитуда, очевидно, нарастает из-за накачки энергией. Иными словами, короткие переходные процессы не рассматриваем.

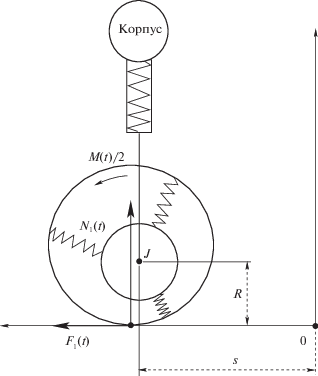
Отметим, что плоские колебания колес хорошо описываются упрощенной двухмассовой моделью передней стойки [5]. Предполагаем, что продольные колебания оси колеса относительно корпуса полностью отсутствуют из-за большой жесткости соответствующих элементов подвески (см. рис. 2). Дополнительно предполагаем, что момент инерции колес относительно мал, а шины невесомы. Это означает, что действие крутящих моментов с полуосей колес мгновенно передается на создание тяги в случае контакта колеса с дорогой, причем крутильная упругость шин на это не влияет. Аналогичные допущения и допущения о невесомости колес иногда используются при анализе движения автомобилей с учетом трения, например устойчивости и неустойчивости режимов с прямолинейным движением [6, 7]. Наконец, предполагаем, что в процессе разгона управляющий крутящий момент не влияет на силы нормальной реакции дороги, действующие на колеса. Здесь можно провести аналогию с решением полуобратной задачи динамики в работах [8, 9], где часть обобщенных координат, а именно переменные длины звеньев экзоскелета, задавалась в виде функций времени на основании эмпирических данных.

Сформулируем задачу оптимального управления.

Во-первых, в каждом из указанных режимов требуется определить максимально возможную в некотором смысле интенсивность разгона (ускорения автомобиля) при условии, что сила нормальной реакции для каждого колеса задана в виде кусочно-гладкой функции времени. В качестве управления выступает приходящий на дифференциал крутящий момент M, который определяется степенью открытия дроссельной заслонки и другими факторами. В значительной степени $M(t)$ зависит от манеры управления конкретного водителя. Назовем управление допустимым, если оно является неотрицательной кусочно-непрерывной функцией времени. Цель управления – максимизация суммарной средней тяги в процессе всего разгона:

где ${{F}_{1}}(t)$ и ${{F}_{2}}(t)$ – силы тяги первого и второго ведущего колеса соответственно, черта сверху означает усреднение на некотором достаточно большом заданном интервале времени, который намного больше периода колебаний колес.

Во-вторых, требуется определить кинематику движения автомобиля и его мощность в частном случае, когда расходуемая энергия минимальна. Горизонтальная скорость движения корпуса в начальный момент времени задана:

Горизонтальную координату корпуса без ограничения общности считаем нулевой:

2. Движение с симметричными силами нормальной реакции. Обозначим через ${{N}_{1}}(t) \geqslant 0$ и ${{N}_{2}}(t) \geqslant 0$ зависимости сил нормальной реакции от времени, где цифровой индекс указывает номер колеса. Получим предварительные соотношения для движения, когда эти функции одинаковы:

Максимальная сила тяги ведущих колес ($F_{1}^{{\max }}$ – первого, $F_{2}^{{\max }}$ – второго) определяется из закона Амонтона–Кулона:

где f – коэффициент трения, который считаем постоянным. Здесь и далее все равенства выполнены с некоторой точностью.

Известно, что при проскальзывании колес оптимальное управление, обеспечивающее максимальное ускорение, может быть выбрано неоднозначно. Например, в задаче 35.5 о качении отдельного колеса со скольжением по горизонтальной прямой из сборника задач И.В. Мещерского [10] движение центра масс колеса не зависит от приложенного к нему вращающего момента. Можно показать, что и в рассматриваемой задаче об автомобиле оптимальное управление неединственно:

где $J$ – момент инерции колеса, $R$ – радиус колеса, который считается постоянным. Неравенство (2.2) следует из доказанной ниже формулы (2.11). Частный случай – движение на грани проскальзывания обоих ведущих колес – может возникать только в случае выполнения равенства в (2.2). При этом энергозатраты минимальны.

В случае отрыва колес от дороги оптимальное управление, обеспечивающее максимальное ускорение, тоже может быть выбрано неоднозначно:

однако энергозатраты минимальны только при выполнении равенства

Как показано далее, при бесконечно малых значениях момента инерции в пределе имеет место равенство

так как в противном случае возникают бесконечно большие скорости вращения колес при наличии трения скольжения или развивается бесконечно большая кинетическая энергия вращения колес при отрыве от дороги, что невозможно при ограниченной мощности двигателя (см. замечания 1–3, приведенные ниже). Иными словами, нестрогие неравенства (2.2) и (2.3) трансформируются в соответствующие равенства, из которых в результате получается (2.4).

Проиллюстрируем вышесказанное на примере движения с N > 0. Составим уравнения движения первого колеса автомобиля:

где ${{\omega }_{1}}$ – угловая скорость вращения колеса, $m$ – половина массы автомобиля, $v$ – скорость автомобиля. Для второго колеса уравнения аналогичны в силу симметрии. Вращением задних колес и другими второстепенными эффектами пренебрегаем.

Кинетическая энергия складывается из энергии поступательного движения той половины автомобиля, которую тянет первое колесо, и энергии вращения первого колеса:

Первое слагаемое не зависит явно от управления при движении с проскальзыванием или на грани проскальзывания. Мощность, расходуемая на диссипацию, равна ${{F}_{1}}({{\omega }_{1}}R - v)$ и неотрицательна. Таким образом, энергозатраты минимальны, если движение происходит на грани проскальзывания. В этом случае второе слагаемое в (2.7) минимально в каждый момент времени, а диссипация отсутствует:

где ${{N}_{1}}(t)$ – произвольная положительная сила нормальной реакции. Подставляя (2.8) в (2.5), (2.6), получим

Из (2.10) следует

где $v(t')$ – скорость автомобиля в начале рассматриваемого процесса. Исключая ${{\dot {\omega }}_{1}}$ из (2.9) и (2.10), находим

В результате получаем мощность, подаваемую на первое колесо:

Если момент инерции J относительно мал:

то равенства (2.11), (2.12) трансформируются в

Видно, что мощность расходуется в основном на увеличение кинетической энергии поступательного движения автомобиля.

З а м е ч а н и е 1. Отметим, что допущение (2.13) обычно выполняется, так как масса автомобиля намного превосходит массу колеса.

З а м е ч а н и е 2. В случае проскальзывания при ограниченной мощности и при малых значениях момента инерции крутящий момент представим в виде (ср. с формулой (2.11))

где $\mu (t) > 0$ – ограниченная сверху функция. После подстановки (2.14) в (2.9) находим ограниченную на конечном интервале времени угловую скорость вращения и мощность, расходуемую на диссипацию в точке контакта первого колеса с дорогой:

Данный режим не обеспечивает минимум энергопотребления.

З а м е ч а н и е 3. В случае отрыва колеса от дороги

При ограниченной мощности и при малых значениях момента инерции крутящий момент представим в виде

где ${{\mu }_{0}}(t) \geqslant 0$ – ограниченная сверху функция, так что выполнены равенства

Расходуемая мощность подсчитывается по формуле

В пределе получим ограниченную на конечном интервале времени величину мощности

Данный режим обеспечивает минимум энергопотребления только при ${{\mu }_{0}}(t) \equiv 0.$

Рассмотрим подробнее две ситуации, когда в равенствах (2.1) $N$ – либо постоянная, либо периодическая по времени функция.

2.1. Отсутствие колебаний ведущих колес. Средняя максимальная сила тяги ведущих колес ($\overline {F_{1}^{{\max }}} $ – первого, $\overline {F_{2}^{{\max }}} $ – второго) совпадает с максимальной силой тяги ведущих колес:

где $\varkappa $ – постоянный коэффициент, N – постоянная сила нормальной реакции, в данном случае совпадающая по величине с весом машины $\varkappa mg$, приходящимся на одно колесо.

Оптимальное решение (2.4) оказывается постоянным. Ему соответствует наискорейшее равноускоренное движение с минимально возможной мощностью

причем с совпадающими угловыми скоростями вращения колес: ${{\omega }_{1}} = {{\omega }_{2}} = v{\text{/}}R$. Здесь максимально возможная в каждый момент скорость $v$ определяется соотношениями

2.2. Синхронные колебания всех ведущих колес. Проскальзывание может вызывать колебания колес в вертикальной плоскости (см., например, видео на интернет-портале YouTube: https://www.youtube.com/watch?v=_dYmhHOfLW8). На рис. 3 изображен трактор К-701 “Кировец” из этого видео. Из-за того, что колеса большие, их колебания имеют достаточно низкую частоту и большую амплитуду, а следовательно, отчетливо видны. Было проведено два пробных старта и видно, что в обоих случаях колебания устойчиво развиваются. Это говорит о том, что нежелательный резонанс изначально заложен в конструкцию этой машины. При этом возможен отрыв колес от поверхности дороги, так что время контакта намного меньше периода колебаний. Аналогичные колебания с частотой порядка 10 Гц могут наблюдаться и у автомобилей.

В случае колебаний двух ведущих колес переднеприводного транспортного средства их средняя максимальная сила тяги остается практически неизменной, т.е. такой же, как и в (2.15) при отсутствии колебаний:

где T – период колебаний силы нормальной реакции N(t), которая для обоих колес предполагается одинаковой и периодической (см. рис. 4).

Оптимальное решение (2.4) оказывается периодичным. Ему соответствует движение с минимальной мощностью

где $v(t)$ – максимально возможная в каждый момент скорость, определяемая соотношением

Угловые скорости вращения ведущих колес совпадают: ${{\omega }_{1}} = {{\omega }_{2}} = v{\text{/}}R$.

3. Движение с несимметричными силами нормальной реакции. Получим предварительные соотношения для случая, когда функции, задающие силы нормальной реакции, различны. Рассмотрим ради определенности интервал времени, когда сила нормальной реакции для первого колеса строго больше силы нормальной реакции для второго колеса:

Если разгон оптимальный, то сила тяги второго колеса достигает своего максимально возможного значения:

Из уравнений движения

следует, что в пределе при малых $J$ и ограниченной мощности должно выполняться условие

В этом случае первое колесо не проскальзывает, так что

Условие непроскальзывания первого колеса выполнено:

Из уравнения (3.4) получаем

Из соотношений (3.2), (3.5), (3.6) находим более точное выражение

Подставим его в уравнение (3.3). Учитывая (3.1), получим

Таким образом, с точностью до членов более высокого порядка малости угловые ускорения совпадают:

Интегрируя равенство (3.7), определяем, что

в случае, когда второе колесо крутится на грани проскальзывания без диссипации энергии в точке контакта с дорогой.

3.1. Колебания одного ведущего колеса. Проблемы со средней тягой возникают в случае колебаний только одного колеса. Пусть колеблется только второе колесо:

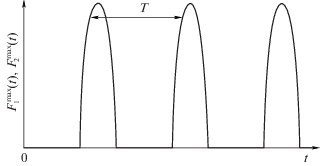
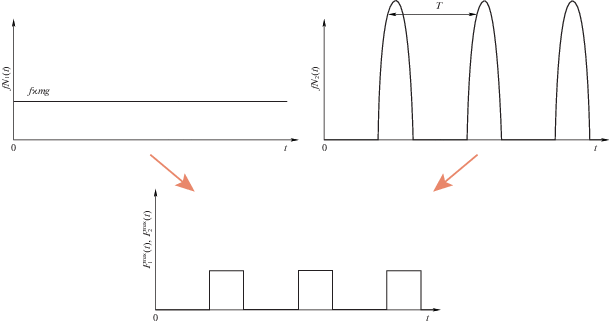
Соответствующая максимальная сила трения, которая теоретически могла бы реализоваться в пятне контакта соответствующего колеса, показана на двух верхних графиках на рис. 5.

Как и ранее, считаем, что момент инерции колес J относительно мал, а мощность ограничена. Тогда моменты, передаваемые с дифференциала на колеса, идут в основном на создание тяги, которая в свою очередь равна действию сил трения. Кроме того, эти моменты должны быть одинаковы согласно основному свойству межколесного дифференциала [11] (трением внутри дифференциала пренебрегаем). Таким образом, ради простоты предполагаем, что

и приходим к следующей задаче оптимизации:

Ее решение сводится к соотношениям

из которых при условии (3.9) следует значительное уменьшение средней тяги по сравнению с двумя рассмотренными выше случаями (2.15) и (2.16): (см. нижний график на рис. 5). Действительно, нижний график получен из правого верхнего путем срезки всех пиков до величины $f\varkappa mg$, из-за чего площадь под графиком значительно уменьшилась. Так как развитие подобных колебаний происходит достаточно быстро, то это приводит к резкой потере средней тяги. При этом сама тяга как функция времени создается рывками с периодом $T$. Оптимальное управление может быть выбрано в виде

Минимально возможная мощность равна

где ${{\omega }_{1}}(t)$ определяется по формуле, аналогичной (3.8): причем ${{\omega }_{1}}(t) = {{\omega }_{2}}(t)$, $v(t) = {{\omega }_{1}}(t)R$.

3.2. Колебания двух ведущих колес в противофазе. Рассмотрим теперь периодические колебания обоих колес, такие, что соответствующие силы нормальной реакции сдвинуты по фазе на половину периода $T$:

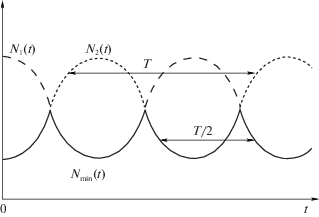
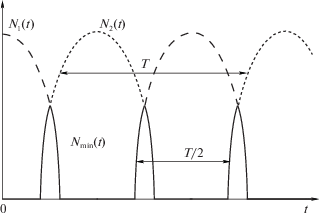
причем ${{N}_{2}}(t)$ имеет вид, аналогичный тому, который рассматривался ранее (см. рис. 5). Если ширина оснований пиков графиков ${{N}_{1}}(t)$ и ${{N}_{2}}(t)$, построенных в общих осях, достаточно мала и они не перекрываются, то, применяя формулу (3.10), справедливую и в этом случае, получим нулевую тягу. В результате транспортное средство будет практически стоять на месте. При этом ведущие колеса будут интенсивно колебаться в вертикальной плоскости и вращаться. Для дальнейшего движения потребуется остановить процесс вращения колес, дождаться затухания колебаний и снова начать старт. Это приведет к потере нескольких секунд и может привести к аварии в ситуациях, требующих наискорейшего разгона (рис. 1).

Для примера на рис. 6 показана другая ситуация, когда основания пиков графиков сил нормальной реакции ${{N}_{1}}(t)$, ${{N}_{2}}(t)$ частично перекрываются. При этом тяга как функция времени создается рывками с периодом T/2. Более простая ситуация, когда отрывов колеса от дороги нет, а рассинхронизация колебаний колес есть, проиллюстрирована на рис. 7. В обоих случаях средняя тяга значительно теряется.

Заключение. Исследованы режимы движения транспортного средства с проскальзыванием и колебаниями ведущих колес во время интенсивного старта. Объяснен физический механизм возможного резкого и значительного уменьшения среднего ускорения. Отмечена серьезная опасность этого редко возникающего эффекта, так как реальная тяга может оказаться намного меньше ожидаемой. Иными словами, автомобили без блокировки межколесного дифференциала и антипробуксовочных устройств ведущих колес являются не просто плохо адаптированными к эксплуатации в РФ, но еще и опасны – водитель неожиданно может оказаться в тяжелой ситуации.

Эффекты, рассмотренные в разд. 2.2, известны и неопасны, так как средняя тяга не теряется по сравнению с обычным режимом без проскальзывания и колебаний колес, описанным в разд. 2.1. Феномен, приведенный в разд. 3.1, 3.2, либо неизвестен, либо мало известен из-за малой вероятности его возникновения. Причем режим разд. 3.1 с частичной потерей средней тяги, отмеченный также в [12], скорее всего, является переходным, и в результате реализуется режим разд. 3.2 с полным отсутствием тяги, краткий качественный анализ которого дан также в [13]. Этот вопрос, связанный с устойчивостью режимов, подлежит дополнительному изучению.