Известия РАН. Теория и системы управления, 2019, № 4, стр. 166-173

Введение. В настоящее время наблюдается бурный рост объема решаемых с применением беспилотных летательных аппаратов (БЛА) задач. При этом большинство используемых в коммерческих целях БЛА имеет взлетную массу не более 500 кг. Для обеспечения надежности таких БЛА применяют дублирование датчиков следящих систем (резервирование с одним резервным каналом), составляющих основу бортовой системы управления БЛА [1–3]. Примером следящей системы может служить система автоматического управления скоростью полета БЛА, в которой требуемая скорость движения передается с наземного пункта дистанционного управления и заранее неизвестна, а результаты управления оцениваются бортовыми датчиками. Дублирование обладает преимуществами по массогабаритным показателям перед другими видами резервирования, в то же время для обнаружения отказавшего канала необходима дополнительная информация о виде, типе отказа или возможных диапазонах значений выходных сигналов (параметров) каналов в исправном и отказавшем состояниях.

Известны алгоритмы обнаружения отказов в дублированных системах, основанные на контроле выходных сигналов с помощью моделей систем или устройств, контроле по пороговой величине, контроле с использованием тестовых сигналов и нечеткой логики [4–7]. В этих работах алгоритмы обнаружения отказов разработаны для случая, когда на систему действуют отказы одного типа – либо внезапные, такие, как “обрыв цепи” или “короткое замыкание”, либо постепенные. Также не оценены возможности алгоритмов [4–7] по обнаружению такого типа внезапного отказа, как “заклинивание”, которое для ряда систем БЛА может составлять от 10 до 15% от общего числа отказов.

1. Постановка задачи. Рассмотрим следящую систему с дублированием датчиков в условиях воздействия на нее шумов и отказов. Отказы воздействуют только на датчики, при этом одновременный отказ двух датчиков – невозможное событие. До наступления отказов датчики идентичны. В качестве возникающих в системе отказов рассмотрим внезапные отказы типа “короткое замыкание”, “обрыв цепи”, “заклинивание” и постепенные отказы. Устройства обнаружения отказов, реализующие алгоритмы обнаружения, абсолютно надежны. Воздействующий на следящую систему шум и шумы датчиков дельта-коррелированные.

Такая следящая система описывается следующим векторно-матричным дифференциальным уравнением:

где X – вектор состояния (фазовых координат) системы размерности m; ${{U}^{l}}$ – вектор входных воздействий размерности $p \leqslant m$, представляющий собой сумму входных сигналов следящей системы ${{U}_{{в х }}}$ и приведенных к ее входу шумов следящей системы ${{\xi }_{{с с }}}$ и шумов датчиков ${{\xi }_{{д 1}}}$, ${{\xi }_{{д 2}}}$; ${{A}^{l}}$, B – стационарные матрицы состояния и входных воздействий системы соответствующей размерности ($m \times m,{\text{ }}m \times p$); $l = \overline {1,S} $ – номер состояния системы с учетом решения о наличии в ней отказа.

Полагаем, что в устройствах обнаружения отказов уровень шумов много меньше, чем в датчиках, а инерционность практически отсутствует, тогда вектор измерения (наблюдения) системы Z размерности $k \leqslant m$, используемый для оценки состояния системы, представим в виде

где C – стационарная матрица наблюдения системы размерности $k \times m$.

Процесс обнаружения отказов в рассматриваемой системе (1.1) по наблюдениям (1.2) носит случайный характер. При этом принимаемые решения о состоянии датчиков системы (1.1) характеризуются следующими вероятностями:

при отсутствии отказа – вероятностями правильного решения об исправности первого (${{P}_{{П Р И 1}}}$) и второго (${{P}_{{П Р И 2}}}$) датчиков и ложного решения об отказе первого (${{P}_{{Л Р О 1}}}$) или второго (${{P}_{{Л Р О 2}}}$) датчиков;

в случае наличия отказа – вероятностями правильного решения об отказе первого (${{P}_{{П Р О 1}}}$) или второго (${{P}_{{П Р О 2}}}$) датчиков, ложного решения об исправности первого (${{P}_{{Л Р И 1}}}$) и второго (${{P}_{{Л Р И 2}}}$) датчиков, ложного решения об отказе первого датчика (${{P}_{{Л Р О 1}}}$) при отказе второго или второго датчика (${{P}_{{Л Р О 2}}}$) при отказе первого.

Случай принятия решения об отказе двух датчиков одновременно не рассматриваем, сохраняя состояние системы неизменным (оба датчика остаются подключенными к системе).

В зависимости от наличия или отсутствия в системе отказа возможен только один из трех исходов: оба датчика исправны; отказал первый датчик, второй датчик исправен; отказал второй датчик, первый датчик исправен. Принимая во внимание эти исходы и решение о наличии или отсутствии отказа, введем следующие состояния системы:

l = 1 – отказа в системе нет, принято правильное решение о его отсутствии;

l = 2 – отказал один из датчиков, принято правильное решение о его отказе;

l = 3 – отказа в системе нет, принято ложное решение об отказе одного из датчиков;

l = 4 – отказал один из датчиков, принято ложное решение о его исправности;

l = 5 – отказал один из датчиков, принято ложное решение о его исправности и ложное решение об отказе исправного датчика.

В случае состояний l = 1 или l = 2 система сохраняет свою работоспособность, при этом принятое решение не снижает ее надежности. Вероятность этого события равна:

В случае состояния l = 3 система также сохраняет свою работоспособность, но в результате принятого ложного решения становится нерезервированной. Вероятность этого события равна:

В случае состояния l = 4 система становится неработоспособной в результате принятия ложного решения об исправности отказавшего датчика. Вероятность этого события равна:

В случае состояния l = 5 система становится неработоспособной в результате принятия ложного решения об исправности отказавшего датчика и ложного решения об отказе исправного датчика. Вероятность такого события равна:

Необходимо разработать алгоритм, максимизирующий вероятность сохранения работоспособного состояния системы P₁ при вероятностях ${{P}_{{Л Р И i}}},{{P}_{{Л Р О i}}}$, $i = \overline {1,2} $, не превышающих допустимые значения. Структура алгоритма может быть синтезирована эвристическим путем на основе анализа проведенных ранее исследований [4–7] и закономерностей изменения выходных сигналов датчиков при наступлении отказа. Параметры $\Pi $ разрабатываемого алгоритма должны принимать значения ${{\Pi }_{{opt}}}$, определяемые как результат решения оптимизационной задачи:

где $\mathbb{R}$ – множество действительных чисел, $P_{{Л Р И }}^{*},Р _{{Л Р О }}^{*}$ – допустимые вероятности ложных решений об исправности и отказе датчика соответственно. Наименование оптимизируемых параметров $\Pi $ и их количество будет представлено в разд. 2.

2. Алгоритм обнаружения отказов. В соответствии с постановкой задачи разрабатываемый универсальный алгоритм обнаружения отказов должен обеспечивать максимум вероятности сохранения работоспособного состояния системы. В [5] был разработан алгоритм обнаружения внезапных отказов типа “обрыв цепи” и “короткое замыкание” в дублированной системе, основанный на обнаружении скачкообразного изменения выходного сигнала в одном из каналов (датчиков). В [4] был предложен двухэтапный алгоритм обнаружения постепенных отказов в дублированной системе, где на первом этапе обнаруживался факт отказа, а на втором этапе осуществлялась локализация отказавшего канала с использованием нечеткой логики. Разработанный в [4] алгоритм позволяет с высокой вероятностью обнаруживать постепенные отказы одного из каналов (датчиков) при условии, что скорость нарастания контролируемого выходного сигнала за счет отказа выше, чем скорость его стабилизации следящей системой. В противном случае обнаружить постепенный отказ, измеряя только выходные сигналы исправного и неисправного каналов (датчиков), невозможно, так как они изменяются в противоположные стороны. Однако в случае, когда в системе в качестве выходного сигнала используют среднеарифметическое значение сигналов от двух датчиков, а система обладает инерционностью, наблюдается следующая закономерность. Среднеарифметическое значение выходных сигналов, просуммированное на нескольких шагах наблюдения при величине каждого шага, меньшем времени отработки возмущающего воздействия следящей системой, изменяется в одну сторону с выходным сигналом отказавшего датчика и в противоположную сторону с выходным сигналом исправного датчика. Для обнаружения внезапного отказа типа “заклинивание” недостаточно контролировать выходные сигналы двух датчиков и их среднеарифметическое значение, необходимо контролировать и входной сигнал системы.

Представим разрабатываемый алгоритм в виде двухэтапной процедуры обнаружения отказов по аналогии с разработанным в [4] алгоритмом. При этом число оцениваемых величин возрастает, так как для обнаружения всех рассматриваемых типов отказов необходимо оценивать: текущие значения выходных сигналов первого и второго датчиков; текущее среднеарифметическое значение выходных сигналов двух датчиков; модуль разности выходных сигналов первого и второго датчиков; запомненные значения выходных сигналов первого и второго датчиков и их среднеарифметического значения до момента обнаружения факта отказа; входной сигнал системы ${{U}_{{в х }}}$.

Кроме того, последовательность обнаружения отказов должна учитывать специфику их воздействия на следящую систему.

Тогда алгоритм обнаружения отказов в следящей системе будет содержать следующие последовательные шаги.

Шаг 1. Обнаружение факта отказа в системе в соответствии с критерием:

где π₁, π₂ – выходные сигналы первого и второго датчиков, $\Delta {{\pi }_{1}}$ – пороговое значение модуля разности выходных сигналов датчиков при обнаружении факта отказа.

Шаг 2. После обнаружения факта отказа (2.1) производится обнаружение внезапных отказов типа “короткое замыкание” и “обрыв цепи”, решение о наличии отказа в первом (втором) датчике принимается при выполнении соответствующих условий:

где ${{\pi }_{1}}(t - \Delta t)$, ${{\pi }_{2}}(t - \Delta t)$ – запомненные значения выходных сигналов датчиков на предыдущем шаге до момента обнаружения факта отказа, $\Delta {{\pi }_{2}}$ – пороговое значение модуля приращения выходного сигнала при обнаружении внезапного отказа.

Шаг 3. В случае если обнаружен факт наступления отказа (2.1) и принято решение об отсутствии внезапных отказов типа “короткое замыкание” и “обрыв цепи”, когда условие (2.2) не выполнено, то обнаруживаются постепенные отказы либо внезапные отказы типа “заклинивание”. Для этого на первом этапе по результатам оценки входного сигнала системы ${{U}_{{{\text{в х }}}}}$ необходимо определить требуемое изменение выходных сигналов датчиков (сигналы не должны изменяться, сигналы должны увеличиваться либо уменьшаться); если сигналы не должны изменяться, то обнаруживается постепенный отказ по результатам сравнения направления изменения контролируемых сигналов в соответствии с критерием, который для первого датчика имеет следующий вид:

где ${{n}_{1}}\Delta t$ – время наблюдения при обнаружении постепенных отказов, ${{n}_{1}}$ – количество шагов наблюдения для обнаружения постепенных отказов, необходимых для обнаружения отказа; r – номер шага; Δπ₃ – пороговое значение выходного сигнала, обусловленное возможным отклонением сигнала от его запомненного значения при воздействии шумов и отсутствии отказов; Δπ₄ – пороговое значение выходного сигнала, обусловленное возможным изменением суммы среднеарифметического сигнала датчиков за время наблюдения в условиях воздействия шумов и отсутствия отказов. Критерий для второго датчика получается путем замены индексов выходных сигналов с единицы на двойку и наоборот.

Шаг 4. В случае если выходные сигналы должны изменяться, то решение о наличии внезапного отказа типа “заклинивание” принимается в соответствии с критерием:

где Δπ₅ – пороговое значение выходного сигнала датчика при обнаружении внезапного отказа типа “заклинивание”, ${{n}_{2}}$ – количество шагов наблюдения для обнаружения отказа типа “заклинивание”.

Шаг 5. В случае если выходные сигналы датчиков должны изменяться, обнаружен факт отказа (2.1) в системе и принято решение об отсутствии внезапных отказов типа “короткое замыкание” и “обрыв цепи”, выражение (2.2), а также не обнаружен отказ типа “заклинивание” (2.4) за требуемое количество шагов наблюдения $f \geqslant {{n}_{2}}$, тогда определяем наиболее опасное отклонение (+ или –) выходного сигнала датчика от его работоспособного состояния (например, при снижении наиболее опасна ошибка, которая приводит к завышению истинной высоты +) и отключаем датчик с минимальным либо максимальным значением выходного сигнала (например, датчик, показывающий максимальную высоту). После того как входной сигнал системы перестает изменяться, подключаем оба датчика, при этом управление системой производим по среднеарифметическому сигналу, а обнаружение отказов – по последовательности, используемой для обнаружения постепенных отказов.

Соответственно для обнаружения рассмотренных выше типов отказов алгоритм должен содержать пять не зависящих от времени параметров: $\Pi = (\Delta {{\pi }_{1}},\;...,\;\Delta {{\pi }_{5}})$, где $\Delta {{\pi }_{1}},\;...,\;\Delta {{\pi }_{5}}$– пороговые значения выходных сигналов датчиков при обнаружении различных типов отказов. Выбор значений параметров для конкретной системы выполняется путем решения задачи оптимизации (1.7). При этом количество шагов наблюдения n₁ и n₂ необходимо определять из условия, что за время наблюдения ${{n}_{1}}\Delta t$, ${{n}_{2}}\Delta t$ воздействие постепенных отказов и отказов типа “заклинивания” не приведет к катастрофическим последствиям.

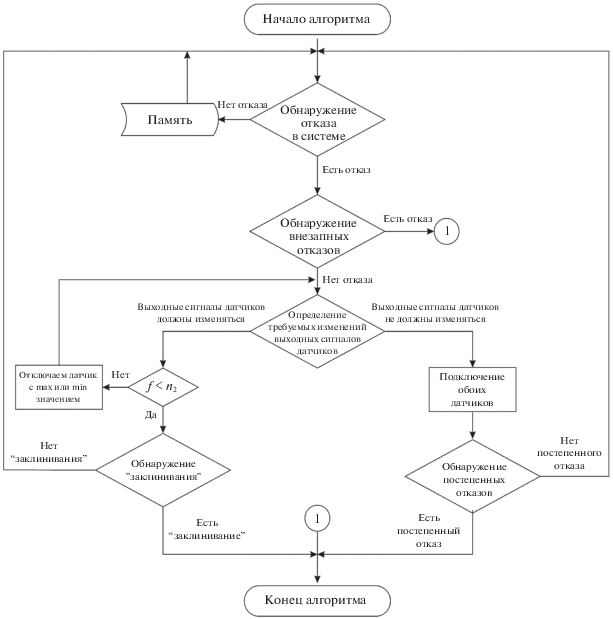
Структурная схема универсального алгоритма обнаружения отказов дублированных датчиков следящей системе представлена на рис. 1.

3. Пример. Проведем сравнительную оценку эффективности обнаружения отказов с использованием разработанного алгоритма и алгоритма обнаружения отказов на основе диагностической модели [6] применительно к контуру стабилизации скорости полета БЛА с дублированием датчиков [7–9].

Принцип обнаружения отказов с использованием диагностической модели применительно к рассматриваемой системе заключается в следующем. На вход диагностической модели контура стабилизации скорости подается ее требуемое значение, при этом на выходе формируется текущее значение скорости ${{V}_{м }}(t)$, которое сравнивается со значениями ${{V}_{1}}(t),{{V}_{2}}(t)$ с выходов датчиков. Решение о наличии отказа в первом (втором) датчике принимается при выполнении соответствующих условий:

где $\Delta {{\pi }_{м }}$ – пороговое значение разности модельного и измеренного датчиком значений скорости.

Будем считать, что параметры модели подобраны идеальным образом, тогда математическая модель типового контура стабилизации скорости без воздействия шумов и отказов полностью соответствует диагностической модели, а порог $\Delta {{\pi }_{м }}$ равен $3{{\sigma }_{в }} + 3{{\sigma }_{д }}$, где ${{\sigma }_{в }}$ – среднеквадратическое отклонение (СКО) скорости, обусловленное турбулентностью атмосферы, ${{\sigma }_{д }}$ – СКО ошибок измерения скорости датчиками. Типовые значения СКО рассматриваемых шумов приведены в [8, 10].

Типовой контур стабилизации скорости БЛА приведен в работе [9]. Путем преобразования структурной схемы контура и с учетом ввода в цепь обратной связи дублированного измерителя скорости получим его представление в виде дифференциального уравнения четвертого порядка, которое в операторной форме имеет вид

где ${{V}_{{и з м }}}(t)$ – значение скорости с выхода дублированного измерителя; ${{W}^{1}}(p) = G_{1}^{1}(p){\text{/}}H_{4}^{1}(p)$ – операторный коэффициент передачи; $p = d{\text{/}}dt$ – оператор дифференцирования; ${{U}^{1}}(t)$ – эквивалентное входное воздействие, представляющее собой сумму требуемого значения скорости ${{V}_{т }}$ с шумовой составляющей скорости, обусловленной атмосферной турбулентностью ${{\xi }_{в }}(t)$ и с приведенными ко входу ошибками измерения скорости каналами дублированного измерителя ${{\xi }_{{и з м 1}}}(t),{\text{ }}{{\xi }_{{и з м 2}}}(t)$, тогда эквивалентное входное воздействие имеет вид:

Полиномы первой $G_{1}^{1}(p)$ и четвертой $H_{4}^{1}(p)$ степени оператора $p$ определяются следующими выражениями:

где ${{g}_{i}},i = \overline {0,1} $, ${{h}_{j}},j = \overline {0,4} $, – коэффициенты, значения которых определяются передаточными числами и постоянными времени динамических звеньев контура стабилизации скорости; при расчетах приняты следующие значения коэффициентов: ${{h}_{0}} = 12.68$, ${{h}_{1}} = 28.1$, ${{h}_{2}} = 14.2$, ${{h}_{3}} = 3.7$, ${{h}_{4}} = 1$, ${{g}_{0}} = 3.6$, ${{g}_{1}} = 0.6$.

Уравнение (3.2) соответствует случаю, когда каналы дублированного измерителя скорости исправны и принято правильное решение об их исправности ($l = 1$ в системе (1.1)). Воспользовавшись методикой, изложенной в [11], преобразуем дифференциальное уравнение четвертого порядка (3.2) в систему четырех дифференциальных уравнений первого порядка вида (1.1) относительно переменных состояния $X = {{\left( {{{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}}} \right)}^{T}}$ со следующими значениями матриц A¹, B:

Выходной величиной контура стабилизации является измеренная дублированными датчиками скорость ${{V}_{{{\text{и з м }}}}}(t)$, которая выражается через переменные состояния соотношением:

В случае, когда состояние системы принимает значения $l = \overline {3,5} $, изменяется вся четвертая строка матрицы A^l, а также изменяется вектор входных воздействий U ^l в зависимости от типа отказа (постепенный или внезапный). Если l = 2, то изменяется только вектор входных воздействий U ^l за счет изменения шумов датчиков.

Проведем математическое моделирование процесса функционирования контура управления скоростью полета БЛА в условиях воздействия на него шумов и отказов. Рассмотрим внезапные отказы, характеризующиеся скачкообразным изменением измеренного значения скорости на выходе отказавшего датчика до максимально возможного в системе значения, равного 100 м/с (“короткое замыкание”), или до минимального, равного 0 м/с значения (“обрыв цепи”). Отказ типа “заклинивание” моделируется как внезапная фиксация измеренного значения скорости на выходе отказавшего датчика. Постепенный отказ моделируется в соответствии с характерным для практики случаем [12], когда приращение $\Delta V(t)$ контролируемого параметра (измеренного значения скорости), обусловленное отказом, изменяется по линейному закону:

где $v$ – детерминированная скорость изменения контролируемого параметра вследствие постепенного отказа; ${{V}_{0}}$ – начальное значение ошибки вследствие постепенного отказа, в рассматриваемом случае ${{V}_{0}} = 0$.

Для каждого типа отказа и фиксированных значений шумов проводилось 10³ экспериментов.

Вероятность сохранения системы в работоспособном состоянии ${{P}_{1}}$ в условиях наступления внезапных отказов типа “обрыв цепи”, “короткое замыкание” и “заклинивание” при обнаружении отказов с использованием как диагностической модели, так и разработанного алгоритма равна 1, а время обнаружения таких отказов при возможностях современных вычислительных систем в обоих случаях сопоставимо.

Диагностическая модель не обнаруживает постепенные отказы, а синтезированный алгоритм позволяет их обнаруживать и обеспечивает вероятность сохранения работоспособного состояния, зависимости которой от параметров шумов ${{\sigma }_{в }}$, ${{\sigma }_{д }}$ и величины ошибки $\Delta V$, обусловленной постепенным отказом, представлены на рис. 2.

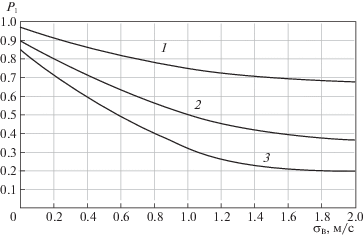
Вероятность сохранения работоспособного состояния системы получена в предположении, что СКО скорости ветра ${{\sigma }_{в }}$ изменяется 0 до 2 м/с, вероятность ложного решения об отказе датчика $Р _{{л р о }}^{*}$ и вероятность ложного решения об исправности датчика $P_{{Л Р И }}^{*}$ фиксированы и равны 0.01, отношение $\Delta V{\text{/}}{{\sigma }_{д }} = 4$ (кривая 1), $\Delta V{\text{/}}{{\sigma }_{д }} = 3$ (кривая 2); $\Delta V{\text{/}}{{\sigma }_{д }} = 2$ (кривая 3); а параметры алгоритма $\Pi = {{\Pi }_{{opt}}}$.

Как видно из приведенных результатов, алгоритм обнаружения отказов в следящих системах с дублированием датчиков позволяет обнаруживать все типы отказов, т.е. является универсальным по отношению к типу отказов.

Заключение. Проведенные исследования позволили разработать универсальный алгоритм обнаружения отказов. Однако на практике для его применения необходимо подстраивать параметры алгоритма $\Pi = (\Delta {{\pi }_{1}},\;...,\;\Delta {{\pi }_{5}})$ в зависимости от возможных внешних шумов и шумов датчиков.

Следует отметить, что способность разработанного алгоритма определять тип отказа облегчает диагностику и ремонт, а также в ряде случаев позволяет избежать аварий. Например, при возникновении постепенного отказа, который ухудшает характеристики датчика, но не приводит к потере аппарата, этот датчик отключается. В дальнейшем при возникновении в оставшемся датчике внезапного отказа датчик с постепенным отказом может быть подключен, что позволит исключить фатальные последствия.