Известия РАН. Теория и системы управления, 2019, № 6, стр. 128-138

АНАЛИТИЧЕСКИЙ АЛГОРИТМ ПОСТРОЕНИЯ ОРБИТАЛЬНОЙ ОРИЕНТАЦИИ КОСМИЧЕСКОГО АППАРАТА ПРИ НЕПОЛНОМ ИЗМЕРЕНИИ КОМПОНЕНТ ВЕКТОРА СОСТОЯНИЯ

Н. Е. Зубов^a, *, А. В. Лапин^a, В. Н. Рябченко^a

^a МГТУ им. Н.Э. Баумана
Москва, Россия

Поступила в редакцию 14.01.2019
После доработки 11.03.2019
Принята к публикации 25.03.2019

DOI: 10.1134/S0002338819040176

Аннотация

Для системы шестого порядка, описывающей вращательное движение космического аппарата, с доступными измерениями пяти компонент вектора состояния аналитически решена задача совместного синтеза модальных регулятора и наблюдателя. Приведены результаты моделирования, описывающего применение синтезированных законов управления и наблюдения к построению орбитальной ориентации космического аппарата.

Введение. Решение практических задач пилотируемой космонавтики в последние годы направлено на реализацию схемы быстрой стыковки [1, 2]. Некоторые препятствия для реализации этой схемы создает значительная длительность построения орбитальной ориентации с использованием информации от инфракрасной вертикали (ИКВ) и датчика угловых скоростей (ДУС). Это видно на циклограмме, представленной в [3]. Работа [3] в какой-то степени решает данную проблему, но она сокращает только начальную часть циклограммы. При этом заключительные ее этапы все еще носят длительный характер. Данная статья, основанная на решении единой задачи наблюдателя состояния и модального управления по оценкам, посвящена сокращению заключительных этапов циклограммы построения орбитальной ориентации.

1. Математическая модель. При построении математической модели углового движения космического аппарата (КА) на орбите используются следующие системы координат (СК) с началом в точке $O$, совпадающей с центром масс (ЦМ) КА:

орбитальная СК (ОСК): $I = O{{x}_{0}}{{y}_{0}}{{z}_{0}}$,

связанная СК (ССК): $E = Oxyz$.

Обозначая нижним индексом с названием СК отображения векторов и матриц на соответствующие базисы, запишем уравнения углового движения КА как абсолютно твердого тела с тензором инерции J на круговой околоземной орбите высотой H (орбитальная угловая скорость ${{\omega }_{0}}$) под действием гравитационного момента ${{{\mathbf{M}}}^{{{\text{грав}}}}}$ от центрального ньютоновского поля тяготения Земли и управляющего момента ${{{\mathbf{M}}}^{{{\text{упр}}}}}$ от реактивных двигателей (РД):

(1.1)

$\left\{ \begin{gathered} {\mathbf{\dot {\theta }}} = {\mathbf{G}}_{E}^{{ - 1}}\left( {{{{\mathbf{w}}}_{E}} - {{{\mathbf{D}}}_{{I \to E}}}{{{\mathbf{\nu }}}_{I}}} \right), \hfill \\ {{{{\mathbf{\dot {w}}}}}_{E}} = {\mathbf{J}}_{E}^{{ - 1}}(({{{\mathbf{J}}}_{E}}{{{\mathbf{w}}}_{E}}) \times {{{\mathbf{w}}}_{E}} + {\mathbf{M}}_{E}^{{{\text{грав}}}} + {\mathbf{M}}_{E}^{{{\text{упр}}}}), \hfill \\ \end{gathered} \right.$

где ${{{\mathbf{w}}}_{E}} = {{\left[ {\begin{array}{*{20}{c}} {{{w}_{x}}}&\vline & {{{w}_{y}}}&\vline & {{{w}_{z}}} \end{array}} \right]}^{{\text{T}}}}$, ${{{\mathbf{\nu }}}_{I}} = {{\left[ {\begin{array}{*{20}{c}} 0&\vline & 0&\vline & { - {{\omega }_{0}}} \end{array}} \right]}^{{\text{T}}}}$, ${\mathbf{M}}_{E}^{{{\text{грав}}}} = 3\omega _{0}^{2}\left( {{{{\mathbf{D}}}_{{I \to E}}}{{{\mathbf{j}}}_{I}}} \right) \times \left( {{{{\mathbf{J}}}_{E}}{{{\mathbf{D}}}_{{I \to E}}}{{{\mathbf{j}}}_{I}}} \right)$, ${{{\mathbf{j}}}_{I}} = {{\left[ {\begin{array}{*{20}{c}} 0&\vline & 1&\vline & 0 \end{array}} \right]}^{{\text{T}}}}$. Здесь ${\mathbf{\theta }} = {{\left[ {\begin{array}{*{20}{c}} \gamma &\vline & \psi &\vline & \vartheta \end{array}} \right]}^{{\text{T}}}}$ – вектор углового положения ССК относительно ОСК, содержащий углы крена $\gamma $, рыскания $\psi $ и тангажа $\vartheta $; ${\mathbf{w}}$ и ${\mathbf{\nu }}$ – векторы абсолютной угловой скорости ССК и ОСК соответственно; G – матрица кинематических уравнений; ${{{\mathbf{D}}}_{{I \to E}}}$ – матрица направляющих косинусов, характеризующая переход $I \to E$; ${\mathbf{j}}$ – орт местной гравитационной вертикали.

Последовательность элементарных поворотов из ОСК в ССК “$\psi \to \vartheta \to \gamma $” соответствует логике работы ИКВ. Матрицы ${{{\mathbf{G}}}_{E}}$ и ${{{\mathbf{D}}}_{{I \to E}}}$ принимают следующий вид:

$\begin{array}{*{20}{c}} {{{{\mathbf{G}}}_{E}} = \left[ {\begin{array}{*{20}{c}} 1&\vline & {\sin \vartheta }&\vline & 0 \\ 0&\vline & {\cos \gamma \cos \vartheta }&\vline & {\sin \gamma } \\ 0&\vline & { - \sin \gamma \cos \vartheta }&\vline & {\cos \gamma } \end{array}} \right],} \\ {{{{\mathbf{D}}}_{{I \to E}}} = \left[ {\begin{array}{*{20}{c}} {\cos \psi \cos \vartheta }&\vline & {\sin \vartheta }&\vline & { - \sin \psi \cos \vartheta } \\ {\sin \gamma \sin \psi - \cos \gamma \cos \psi \sin \vartheta }&\vline & {\cos \gamma \cos \vartheta }&\vline & {\sin \gamma \cos \psi + \cos \gamma \sin \psi \sin \vartheta } \\ {\cos \gamma \sin \psi + \sin \gamma \cos \psi \sin \vartheta }&\vline & { - \sin \gamma \cos \vartheta }&\vline & {\cos \gamma \cos \psi - \sin \gamma \sin \psi \sin \vartheta } \end{array}} \right].} \end{array}$

Требуется для заданного диапазона начальных условий $({{\gamma }_{0}},{\text{ }}{{\psi }_{0}},{\text{ }}{{\vartheta }_{0}},{\text{ }}{{w}_{{x0}}},{\text{ }}{{w}_{{y0}}},{\text{ }}{{w}_{{z0}}})$ по информации с ИКВ и ДУС о векторе наблюдения

${\mathbf{y}} = {{\left[ {\begin{array}{*{20}{c}} \gamma &\vline & \vartheta &\vline & {{{w}_{x}}}&\vline & {{{w}_{y}}}&\vline & {{{w}_{z}}} \end{array}} \right]}^{{\text{T}}}}$

за короткое время (не более 100 c) с помощью управления ${\mathbf{u}} = {\mathbf{M}}_{E}^{{{\text{упр}}}}$ обеспечить трехосную орбитальную стабилизацию КА, т.е. привести вектор состояния

${\mathbf{x}} = {{\left[ {\begin{array}{*{20}{l}} \gamma &\vline & \psi &\vline & \vartheta &\vline & {{{w}_{x}}}&\vline & {{{w}_{y}}}&\vline & {{{w}_{z}}} \end{array}} \right]}^{{\text{T}}}}$

к его программному значению

${{{\mathbf{x}}}_{{{\text{пр}}}}} = {{\left[ {\begin{array}{*{20}{l}} 0&\vline & 0&\vline & 0&\vline & 0&\vline & 0&\vline & { - {{\omega }_{0}}} \end{array}} \right]}^{{\text{T}}}}$

с точностью не хуже 0.3° по углам и 0.1 град/с по компонентам угловой скорости.

Сформулированная задача относится к классу задач поиска управления по неполному вектору состояния динамического объекта [4–8]. Одним из вариантов решения данной задачи методами модального управления является построение для линеаризованной модели регулятора с обратной связью по оценке вектора состояния с одновременным решением задачи оценки.

2. Модальные регулятор и наблюдатель. Пусть линеаризованная модель (1.1) вида

$\left\{ \begin{gathered} {\mathbf{\dot {x}}} = {\mathbf{Ax}} + {\mathbf{Bu}}, \hfill \\ {\mathbf{y}} = {\mathbf{Cx}} \hfill \\ \end{gathered} \right.$

характеризуется вещественными матрицами состояния ${\mathbf{A}} \in {{\mathbb{R}}^{{n \times n}}}$, управления ${\mathbf{B}} \in {{\mathbb{R}}^{{n \times m}}}$ и наблюдения ${\mathbf{C}} \in {{\mathbb{R}}^{{l \times n}}}$ соответствующей размерности. Требуется синтезировать модальный регулятор с матрицей ${\mathbf{K}}$ и наблюдатель с матрицей ${\mathbf{L}}$, обеспечивающие замкнутым системам “объект–регулятор” и “объект–наблюдатель” заданные спектры:

$\begin{array}{*{20}{c}} {\operatorname{eig} \left( {{\mathbf{A}} - {\mathbf{BK}}} \right) = \left\{ {{{\varphi }_{1}},{\text{ }}{{\varphi }_{2}},{\text{ }} \ldots ,{\text{ }}{{\varphi }_{n}}} \right\};} \\ {\operatorname{eig} \left( {{\mathbf{A}} - {\mathbf{LC}}} \right) = \left\{ {{{\psi }_{1}},{\text{ }}{{\psi }_{2}},{\text{ }} \ldots ,{\text{ }}{{\psi }_{n}}} \right\}.} \end{array}$

Модальные регулятор и наблюдатель строятся на основании дуальных свойств управляемости и наблюдаемости, согласно представленному ниже аналитическому алгоритму [9].

1. Для расчетов регулятора и наблюдателя соответственно выполняется декомпозиция пар матриц A, B и A, C следующим образом.

1.1. Задаются нулевые уровни декомпозиции с парами матриц:

(2.1)

$\begin{array}{*{20}{c}} {{{{\mathbf{A}}}_{0}} = {\mathbf{A}},\quad {{{\mathbf{B}}}_{0}} = {\mathbf{B}};} \\ {{{{\mathbf{A}}}_{0}} = {\mathbf{A}},\quad {{{\mathbf{C}}}_{0}} = {\mathbf{C}}} \end{array}$

и определяется количество последующих уровней декомпозиции:

(2.2)

$\begin{array}{*{20}{c}} {{{N}_{m}} = \operatorname{ceil} \left( {{n \mathord{\left/ {\vphantom {n m}} \right. \kern-0em} m}} \right) - 1;} \\ {{{N}_{l}} = \operatorname{ceil} \left( {{n \mathord{\left/ {\vphantom {n l}} \right. \kern-0em} l}} \right) - 1.} \end{array}$

Функция $\operatorname{ceil} $ выдает минимальное целое число, не меньшее ее аргумента.

1.2. Последовательно для каждого из уровней $i = 0,{\text{ }}1,{\text{ }} \ldots ,{\text{ }}{{N}_{m}} - 1$ и $j = 0,{\text{ }}1,{\text{ }} \ldots ,{\text{ }}{{N}_{l}} - 1$ при условиях, что на текущем уровне ранг матрицы управления ${{{\mathbf{B}}}_{i}}$ равен числу ее столбцов, а ранг матрицы наблюдения ${{{\mathbf{C}}}_{j}}$ – числу строк, вводятся переходы на следующие уровни с парами матриц:

(2.3)

$\begin{array}{*{20}{c}} {{{{\mathbf{A}}}_{{i + 1}}} = {\mathbf{B}}_{i}^{{ \bot L}}{{{\mathbf{A}}}_{i}}{\mathbf{B}}_{i}^{{ \bot L + }},\quad {{{\mathbf{B}}}_{{i + 1}}} = {\mathbf{B}}_{i}^{{ \bot L}}{{{\mathbf{A}}}_{i}}{{{\mathbf{B}}}_{i}};} \\ {{{{\mathbf{A}}}_{{j + 1}}} = {\mathbf{C}}_{j}^{{ \bot R + }}{{{\mathbf{A}}}_{j}}{\mathbf{C}}_{j}^{{ \bot R}},\quad {{{\mathbf{C}}}_{{j + 1}}} = {{{\mathbf{C}}}_{j}}{{{\mathbf{A}}}_{j}}{\mathbf{C}}_{j}^{{ \bot R}}.} \end{array}$

Здесь и далее обозначения “$^{{ \bot L}}$” и “$^{{ \bot R}}$” соответствуют левым и правым аннуляторам максимального ранга, а “$^{ + }$” – псевдообратным матрицам [9]. При нарушении указанных условий выполняются скелетные разложения

(2.4)

$\begin{array}{*{20}{c}} {{{{\mathbf{B}}}_{i}} = {{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{B} }}}}_{i}}{{{\mathbf{T}}}_{i}};} \\ {{{{\mathbf{C}}}_{j}} = {{{\mathbf{S}}}_{j}}{{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C} }}}}_{j}}} \end{array}$

и далее используются модификации текущих уровней с парами матриц:

(2.5)

$\begin{array}{*{20}{c}} {{{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} }}}}_{i}} = {{{\mathbf{A}}}_{i}},{\text{ }}{{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{B} }}}}_{i}};} \\ {{{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} }}}}_{j}} = {{{\mathbf{A}}}_{j}},{\text{ }}{{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C} }}}}_{j}}.} \end{array}$

2. Рассчитываются матрицы регуляторов ${{{\mathbf{K}}}_{i}}$ и наблюдателей ${{{\mathbf{L}}}_{j}}$ на всех уровнях декомпозиции пар матриц A, B и A, C в последовательностях $i = N,{\text{ }}N - 1,{\text{ }} \ldots ,{\text{ }}0$ и $j = N,{\text{ }}N - 1,{\text{ }} \ldots ,{\text{ }}0$. Для этого поочередно на каждом из указанных уровней выполняются следующие процедуры.

2.1. Назначаются матрицы ${{{\mathbf{\Phi }}}_{i}}$ и ${{{\mathbf{\Psi }}}_{j}}$ с желаемыми спектрами.

2.2. Рассчитываются матрицы регулятора ${{{\mathbf{K}}}_{i}}$ и наблюдателя ${{{\mathbf{L}}}_{j}}$:

(2.6)

$\begin{gathered} {{{\mathbf{K}}}_{i}} = {\mathbf{B}}_{i}^{ - }{{{\mathbf{A}}}_{i}} - {{{\mathbf{\Phi }}}_{i}}{\mathbf{B}}_{i}^{ - },\quad {\mathbf{B}}_{i}^{ - } = \left\{ \begin{gathered} {\mathbf{B}}_{i}^{{ - 1}},{\text{ }}i = {{N}_{m}}, \hfill \\ {\mathbf{B}}_{i}^{ + } + {{{\mathbf{K}}}_{{i + 1}}}{\mathbf{B}}_{i}^{{ \bot L}},{\text{ }}i < {{N}_{m}}; \hfill \\ \end{gathered} \right. \\ {{{\mathbf{L}}}_{j}} = {{{\mathbf{A}}}_{j}}{\mathbf{C}}_{j}^{ - } - {\mathbf{C}}_{j}^{ - }{{{\mathbf{\Psi }}}_{j}},\quad {\mathbf{C}}_{j}^{ - } = \left\{ \begin{gathered} {\mathbf{C}}_{j}^{{ - 1}},{\text{ }}j = {{N}_{l}}, \hfill \\ {\mathbf{C}}_{j}^{ + } + {\mathbf{C}}_{j}^{{ \bot R}}{{{\mathbf{L}}}_{{j + 1}}},{\text{ }}j < {{N}_{l}}. \hfill \\ \end{gathered} \right. \\ \end{gathered} $

2.3. Если имели место модификации данного уровня (2.5), выполненные с помощью скелетных разложений (2.4), и согласно (2.6) для них определены матрицы регулятора ${{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{K} }}}_{i}}$ и наблюдателя ${{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{L} }}}_{j}}$, то пересчитываются матрицы регулятора ${{{\mathbf{K}}}_{i}}$ и наблюдателя ${{{\mathbf{L}}}_{j}}$ на этом уровне без модификации:

(2.7)

$\begin{array}{*{20}{c}} {{{{\mathbf{K}}}_{i}} = {\mathbf{T}}_{i}^{ + }{{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{K} }}}}_{i}};} \\ {{{{\mathbf{L}}}_{j}} = {{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{L} }}}}_{j}}{\mathbf{S}}_{j}^{ + }.} \end{array}$

2.4. Матрицы регулятора ${\mathbf{K}} = {{{\mathbf{K}}}_{0}}$ и наблюдателя ${\mathbf{L}} = {{{\mathbf{L}}}_{0}}$ являются искомыми.

3. Построение регулятора. Управление, определяемое на борту в дискретные моменты времени с шагом ${{h}_{{\text{б}}}}$ (такт работы бортового вычислителя), удобно синтезировать по непрерывной модели (1.1), в которую оно входит линейно:

(3.1)

$\left\{ \begin{gathered} {\mathbf{\dot {x}}} = {{{\mathbf{f}}}_{{\text{н}}}}({\mathbf{x}}) + {{{\mathbf{B}}}_{{\text{н}}}}{\mathbf{u}}, \hfill \\ {\mathbf{y}} = {{{\mathbf{C}}}_{{\text{н}}}}{\mathbf{x}}. \hfill \\ \end{gathered} \right.$

Для этой модели ${{{\mathbf{f}}}_{{\text{н}}}}({\mathbf{x}})$ – функция состояния, ${{{\mathbf{B}}}_{{\text{н}}}}$ и ${{{\mathbf{C}}}_{{\text{н}}}}$ – соответственно матрицы управления и наблюдения, имеющие вид

${{{\mathbf{f}}}_{{\text{н}}}}({\mathbf{x}}) = \left[ {\begin{array}{*{20}{c}} {{\mathbf{G}}_{E}^{{ - 1}}({\mathbf{\theta }})\left( {{{{\mathbf{w}}}_{E}} - {{{\mathbf{D}}}_{{I \to E}}}({\mathbf{\theta }}){{{\mathbf{\nu }}}_{I}}} \right)} \\ {{\mathbf{J}}_{E}^{{ - 1}}(({{{\mathbf{J}}}_{E}}{{{\mathbf{w}}}_{E}}) \times {{{\mathbf{w}}}_{E}} + {\mathbf{M}}_{E}^{{{\text{грав}}}}({\mathbf{\theta }}))} \end{array}} \right],\quad {{{\mathbf{B}}}_{{\text{н}}}} = \left[ {\begin{array}{*{20}{c}} {{{{\mathbf{0}}}_{{3 \times 3}}}} \\ {{\mathbf{J}}_{E}^{{ - 1}}} \end{array}} \right],\quad {{{\mathbf{C}}}_{{\text{н}}}} = \left[ {\begin{array}{*{20}{c}} 1&\vline & 0&\vline & 0&\vline & 0&\vline & 0&\vline & 0 \\ 0&\vline & 0&\vline & 1&\vline & 0&\vline & 0&\vline & 0 \\ 0&\vline & 0&\vline & 0&\vline & 1&\vline & 0&\vline & 0 \\ 0&\vline & 0&\vline & 0&\vline & 0&\vline & 1&\vline & 0 \\ 0&\vline & 0&\vline & 0&\vline & 0&\vline & 0&\vline & 1 \end{array}} \right].$

Пусть в начале каждого $k{\text{ - го}}$ бортового такта, начиная с некоторого значения $k = {{k}_{{{\text{нач}}}}}$, имеется оценка вектора состояния ${{{\mathbf{\hat {x}}}}_{k}}$ (получение оценки описано в следующем разделе). Линеаризуем модель (3.1) по Тейлору вблизи положения ${{{\mathbf{\hat {x}}}}_{k}}$ в рамках одного вычислительного такта и запишем полученную линеаризованную модель через отклонение ${\mathbf{x}} - {{{\mathbf{x}}}_{{{\text{пр}}}}}$:

(3.2)

$\left\{ \begin{gathered} {\mathbf{\dot {x}}} = {{{\mathbf{\xi }}}_{{\text{н}}}} + {{{\mathbf{A}}}_{{\text{н}}}}({\mathbf{x}} - {{{\mathbf{x}}}_{{{\text{пр}}}}}) + {{{\mathbf{B}}}_{{\text{н}}}}{\mathbf{u}}, \hfill \\ {\mathbf{y}} = {{{\mathbf{C}}}_{{\text{н}}}}{\mathbf{x}}, \hfill \\ \end{gathered} \right.$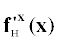

где при расчете ${{{\mathbf{\xi }}}_{{\text{н}}}} = {{{\mathbf{f}}}_{{\text{н}}}}({{{\mathbf{\hat {x}}}}_{k}}) - {\mathbf{f}}_{{\text{н}}}^{{'{\mathbf{x}}}}({{{\mathbf{\hat {x}}}}_{k}})\left( {{{{{\mathbf{\hat {x}}}}}_{k}} - {{{\mathbf{x}}}_{{{\text{пр}}}}}} \right)$ и ${{{\mathbf{A}}}_{{\text{н}}}} = {\mathbf{f}}_{{\text{н}}}^{{'{\mathbf{x}}}}({{{\mathbf{\hat {x}}}}_{k}})$ используется матрица Якоби

, составленная из частных производных функции ${{{\mathbf{f}}}_{{\text{н}}}}({\mathbf{x}})$ по компонентам вектора ${\mathbf{x}}$.

Сформируем закон управления объектом (3.2) по оценке вектора состояния

(3.3)

${{{\mathbf{u}}}_{k}} = {{{\mathbf{u}}}_{0}} - {{{\mathbf{K}}}_{{\text{н}}}}\left( {{{{{\mathbf{\hat {x}}}}}_{k}} - {{{\mathbf{x}}}_{{{\text{пр}}}}}} \right),$

где ${{{\mathbf{u}}}_{0}}$ – добавка от возмущения ${{{\mathbf{\xi }}}_{{\text{н}}}}$, ${{{\mathbf{K}}}_{{\text{н}}}}$ – матрица регулятора по состоянию.

В общем случае возмущение ${{{\mathbf{\xi }}}_{{\text{н}}}} \in {{\mathbb{R}}^{6}}$ из (3.2) изменяется от такта к такту и содержит все шесть ненулевых компонент. Однако при стремлении вектора состояния ${{{\mathbf{x}}}_{k}}$ (и его оценки ${{{\mathbf{\hat {x}}}}_{k}}$) к программному значению ${{{\mathbf{x}}}_{{{\text{пр}}}}}$ возмущение ${{{\mathbf{\xi }}}_{{\text{н}}}}({{{\mathbf{\hat {x}}}}_{k}})$ стремится к величине

${{{\mathbf{\xi }}}_{{\text{н}}}}({{{\mathbf{x}}}_{{{\text{пр}}}}}) = {{\left[ {\begin{array}{*{20}{l}} {{\mathbf{0}}_{3}^{T}}&\vline & {\omega _{0}^{2}\left[ {\begin{array}{*{20}{c}} { - 4{{J}_{{yz}}}}&\vline & {{{J}_{{zx}}}}&\vline & {3{{J}_{{xy}}}} \end{array}} \right]{\mathbf{J}}_{E}^{{ - 1}}} \end{array}} \right]}^{{\text{T}}}},$

поэтому с учетом вида матрицы ${{{\mathbf{B}}}_{{\text{н}}}}$ можно принять добавку ${{{\mathbf{u}}}_{0}}$ равной

(3.4)

${{{\mathbf{u}}}_{0}} = - \omega _{0}^{2}{{\left[ {\begin{array}{*{20}{l}} { - 4{{J}_{{yz}}}}&\vline & {{{J}_{{zx}}}}&\vline & {3{{J}_{{xy}}}} \end{array}} \right]}^{{\text{T}}}}.$

Далее для подстановки в (3.3) описанным выше аналитическим методом синтезируем модальный регулятор с матрицей ${{{\mathbf{K}}}_{{\text{н}}}}$ для пары матриц $({{{\mathbf{A}}}_{{\text{н}}}},{\text{ }}{{{\mathbf{B}}}_{{\text{н}}}})$:

${{{\mathbf{A}}}_{{\text{н}}}} = \left[ {\begin{array}{*{20}{l}} {{{{\mathbf{A}}}_{{{\text{н11}}}}}}&\vline & {{{{\mathbf{A}}}_{{{\text{н12}}}}}} \\ {{{{\mathbf{A}}}_{{{\text{н21}}}}}}&\vline & {{{{\mathbf{A}}}_{{{\text{н22}}}}}} \end{array}} \right],\quad {{{\mathbf{B}}}_{{\text{н}}}} = \left[ {\begin{array}{*{20}{c}} {{{{\mathbf{0}}}_{{3 \times 3}}}} \\ {{\mathbf{J}}_{E}^{{ - 1}}} \end{array}} \right],$

где ${{{\mathbf{A}}}_{{{\text{н11}}}}},{\text{ }}{{{\mathbf{A}}}_{{{\text{н12}}}}},{\text{ }}{{{\mathbf{A}}}_{{{\text{н21}}}}},{\text{ }}{{{\mathbf{A}}}_{{{\text{н22}}}}} \in {{\mathbb{R}}^{{3 \times 3}}}$.

Количество уровней декомпозиции, согласно (2.2), ${{N}_{{\text{н}}}} = 1$.

Зададим спектр замкнутой непрерывной системы “объект–регулятор”:

$\operatorname{eig} \left( {{{{\mathbf{A}}}_{{\text{н}}}} - {{{\mathbf{B}}}_{{\text{н}}}}{{{\mathbf{K}}}_{{\text{н}}}}} \right) = \left\{ {{{\varphi }_{{{\text{н}}1}}},{\text{ }}{{\varphi }_{{{\text{н2}}}}}{\text{, }}{{\varphi }_{{{\text{н3}}}}},{\text{ }}{{\varphi }_{{{\text{н4}}}}}{\text{, }}{{\varphi }_{{{\text{н5}}}}},{\text{ }}{{\varphi }_{{{\text{н6}}}}}} \right\}.$

Нулевой уровень декомпозиции $({{{\mathbf{A}}}_{{\text{н}}}},{\text{ }}{{{\mathbf{B}}}_{{\text{н}}}})$ (2.1)

${{{\mathbf{A}}}_{{{\text{н}}0}}} = {{{\mathbf{A}}}_{{\text{н}}}} \in {{\mathbb{R}}^{{6 \times 6}}},\quad {{{\mathbf{B}}}_{{{\text{н}}0}}} = {{{\mathbf{B}}}_{{\text{н}}}} \in {{\mathbb{R}}^{{6 \times 3}}}.$

Так как $\operatorname{rank} {{{\mathbf{B}}}_{{{\text{н}}0}}} = 3$, перейдем к следующему уровню, вычислив вначале

${\mathbf{B}}_{{{\text{н}}0}}^{{ \bot L}} = \left[ {\begin{array}{*{20}{l}} {{{{\mathbf{I}}}_{3}}}&\vline & {{{{\mathbf{0}}}_{{3 \times 3}}}} \end{array}} \right],\quad {\mathbf{B}}_{{{\text{н}}0}}^{{ \bot L + }} = {\mathbf{B}}_{{{\text{н}}0}}^{{ \bot LT}} = \left[ {\begin{array}{*{20}{c}} {{{{\mathbf{I}}}_{3}}} \\ {{{{\mathbf{0}}}_{{3 \times 3}}}} \end{array}} \right].$

Первый уровень декомпозиции $({{{\mathbf{A}}}_{{\text{н}}}},{\text{ }}{{{\mathbf{B}}}_{{\text{н}}}})$ (2.3)

${{{\mathbf{A}}}_{{{\text{н}}1}}} = {\mathbf{B}}_{{{\text{н}}0}}^{{ \bot L}}{{{\mathbf{A}}}_{{{\text{н}}0}}}{\mathbf{B}}_{{{\text{н}}0}}^{{ \bot L + }} = {{{\mathbf{A}}}_{{{\text{н11}}}}} \in {{\mathbb{R}}^{{3 \times 3}}},\quad {{{\mathbf{B}}}_{{{\text{н}}1}}} = {\mathbf{B}}_{{{\text{н}}0}}^{{ \bot L}}{{{\mathbf{A}}}_{{{\text{н}}0}}}{{{\mathbf{B}}}_{{{\text{н}}0}}} = {{{\mathbf{A}}}_{{{\text{н}}12}}}{\mathbf{J}}_{E}^{{ - 1}} \in {{\mathbb{R}}^{{3 \times 3}}}.$

Предположим, что

(3.5)

$\operatorname{rank} {{{\mathbf{A}}}_{{{\text{н}}12}}} = 3.$

Тогда матрица ${{{\mathbf{B}}}_{{{\text{н}}1}}}$ обратима и можно перейти к расчету регуляторов.

Регулятор на первом уровне декомпозиции $({{{\mathbf{A}}}_{{\text{н}}}},{\text{ }}{{{\mathbf{B}}}_{{\text{н}}}})$. С целью обеспечить единый вид искомой матрицы ${{{\mathbf{K}}}_{{\text{н}}}}$ при диагональном и полном тензорах инерции ${{{\mathbf{J}}}_{E}}$ назначим матрицу с желаемым спектром в параметрической форме [9]

$\begin{array}{*{20}{c}} {{{{{\mathbf{\tilde {\Phi }}}}}_{{{\text{н}}1}}} = {{{\mathbf{B}}}_{{{\text{н}}1}}}{{{\mathbf{\Phi }}}_{{{\text{н}}1}}}{\mathbf{B}}_{{{\text{н}}1}}^{{ - 1}}:}&{\operatorname{eig} {{{{\mathbf{\tilde {\Phi }}}}}_{{{\text{н}}1}}} = \left\{ {{{\varphi }_{{{\text{н4}}}}},{\text{ }}{{\varphi }_{{{\text{н5}}}}},{\text{ }}{{\varphi }_{{{\text{н6}}}}}} \right\}} \end{array}.$

Здесь ${{{\mathbf{\Phi }}}_{{{\text{н}}1}}}$ – матрица с желаемым спектром, присутствующая в классическом выражении для расчета матрицы регулятора (2.6):

${{{\mathbf{K}}}_{{{\text{н}}1}}} = {\mathbf{B}}_{{{\text{н}}1}}^{{ - 1}}{{{\mathbf{A}}}_{{{\text{н}}1}}} - {{{\mathbf{\Phi }}}_{{{\text{н}}1}}}{\mathbf{B}}_{{{\text{н}}1}}^{{ - 1}} = {\mathbf{B}}_{{{\text{н}}1}}^{{ - 1}}({{{\mathbf{A}}}_{{{\text{н}}1}}} - {{{\mathbf{\tilde {\Phi }}}}_{{{\text{н}}1}}}) = {{{\mathbf{J}}}_{E}}{\mathbf{A}}_{{{\text{н}}12}}^{{ - 1}}({{{\mathbf{A}}}_{{{\text{н}}11}}} - {{{\mathbf{\tilde {\Phi }}}}_{{{\text{н}}1}}}).$

Регулятор на нулевом уровне декомпозиции $({{{\mathbf{A}}}_{{\text{н}}}},{\text{ }}{{{\mathbf{B}}}_{{\text{н}}}})$. Рассчитаем псевдообратную и вспомогательную матрицы для (2.6):

$\begin{array}{*{20}{c}} {{\mathbf{B}}_{{{\text{н}}0}}^{ + } = {{{({\mathbf{B}}_{{{\text{н}}0}}^{T}{{{\mathbf{B}}}_{{{\text{н}}0}}})}}^{{ - 1}}}{\mathbf{B}}_{{{\text{н}}0}}^{{\text{T}}} = \left[ {\begin{array}{*{20}{c}} {{{{\mathbf{0}}}_{{3 \times 3}}}}&\vline & {{{{\mathbf{J}}}_{E}}} \end{array}} \right],}&{{\mathbf{B}}_{{{\text{н}}0}}^{ - } = {\mathbf{B}}_{{{\text{н}}0}}^{ + } + {{{\mathbf{K}}}_{{{\text{н}}1}}}{\mathbf{B}}_{{{\text{н}}0}}^{{ \bot L}} = {{{\mathbf{J}}}_{E}}[\begin{array}{*{20}{c}} {{\mathbf{A}}_{{{\text{н}}12}}^{{ - 1}}({{{\mathbf{A}}}_{{{\text{н}}11}}} - {{{{\mathbf{\tilde {\Phi }}}}}_{{{\text{н}}1}}})}&\vline & {{{{\mathbf{I}}}_{3}}} \end{array}].} \end{array}$

По аналогии с первым уровнем декомпозиции назначим матрицу с желаемым спектром в параметрической форме

$\begin{array}{*{20}{c}} {{{{{\mathbf{\tilde {\Phi }}}}}_{{{\text{н0}}}}} = {{{\mathbf{B}}}_{{{\text{н1}}}}}{{{\mathbf{\Phi }}}_{{{\text{н0}}}}}{\mathbf{B}}_{{{\text{н1}}}}^{{ - 1}}:}&{\operatorname{eig} {{{{\mathbf{\tilde {\Phi }}}}}_{{{\text{н0}}}}} = \left\{ {{{\varphi }_{{{\text{н1}}}}},{\text{ }}{{\varphi }_{{{\text{н2}}}}},{\text{ }}{{\varphi }_{{{\text{н3}}}}}} \right\}} \end{array}.$

Здесь ${{{\mathbf{\Phi }}}_{{{\text{н0}}}}}$ – матрица с желаемым спектром, присутствующая в классическом выражении для расчета матрицы регулятора (2.6):

${{{\mathbf{K}}}_{{{\text{н0}}}}} = {\mathbf{B}}_{{{\text{н0}}}}^{ - }{{{\mathbf{A}}}_{{{\text{н0}}}}} - {{{\mathbf{\Phi }}}_{{{\text{н0}}}}}{\mathbf{B}}_{{{\text{н0}}}}^{ - } = {{{\mathbf{J}}}_{E}}[\begin{array}{*{20}{c}} {{{{\mathbf{A}}}_{{{\text{н}}21}}} + {\mathbf{A}}_{{{\text{н}}12}}^{{ - 1}}({{{{\mathbf{\tilde {A}}}}}_{{{\text{н}}11}}}{{{\mathbf{A}}}_{{{\text{н}}11}}} + {{{{\mathbf{\tilde {\Phi }}}}}_{{{\text{н}}0}}}{{{{\mathbf{\tilde {\Phi }}}}}_{{{\text{н}}1}}})}&\vline & {{{{\mathbf{A}}}_{{{\text{н}}22}}} + {\mathbf{A}}_{{{\text{н}}12}}^{{ - 1}}{{{{\mathbf{\tilde {A}}}}}_{{{\text{н}}11}}}{{{\mathbf{A}}}_{{{\text{н}}12}}}} \end{array}],$

где ${{{\mathbf{\tilde {A}}}}_{{{\text{н}}11}}} = {{{\mathbf{A}}}_{{{\text{н}}11}}} - ({{{\mathbf{\tilde {\Phi }}}}_{{{\text{н}}0}}} + {{{\mathbf{\tilde {\Phi }}}}_{{{\text{н}}1}}})$.

Итак, для закона управления (3.3) найдена матрица регулятора ${{{\mathbf{K}}}_{{\text{н}}}} = {{{\mathbf{K}}}_{{{\text{н}}0}}}$:

(3.6)

${{{\mathbf{K}}}_{{\text{н}}}} = {{{\mathbf{J}}}_{E}}[\begin{array}{*{20}{c}} {{{{\mathbf{A}}}_{{{\text{н}}21}}} + {\mathbf{A}}_{{{\text{н}}12}}^{{ - 1}}({{{{\mathbf{\tilde {A}}}}}_{{{\text{н}}11}}}{{{\mathbf{A}}}_{{{\text{н}}11}}} + {{{{\mathbf{\tilde {\Phi }}}}}_{{{\text{н}}0}}}{{{{\mathbf{\tilde {\Phi }}}}}_{{{\text{н}}1}}})}&\vline & {{{{\mathbf{A}}}_{{{\text{н}}22}}} + {\mathbf{A}}_{{{\text{н}}12}}^{{ - 1}}{{{{\mathbf{\tilde {A}}}}}_{{{\text{н}}11}}}{{{\mathbf{A}}}_{{{\text{н}}12}}}} \end{array}].$

Формула (3.6) получена при условии выполнения предположения (3.5) и представляет собой аналитическое решение задачи синтеза регулятора.

Управление (3.3) реализуется на РД, создающих постоянные вращающие моменты $M_{\zeta }^{{{\text{РД}}}}$ вокруг осей ССК $\zeta = x,{\text{ }}y,{\text{ }}z$. Время работы РД, соответствующего знаку управляющего сигнала ${{u}_{{k\zeta }}}$, в рамках $k{\text{ - го}}$ такта предлагается рассчитывать по следующей схеме:

(3.7)

${{\tau }_{{k\zeta }}} = \left\{ \begin{gathered} 0,\quad {{s}_{{k\zeta }}} < {{\tau }_{{\min }}}, \hfill \\ {{s}_{{k\zeta }}},\quad {{\tau }_{{\min }}} \leqslant {{s}_{{k\zeta }}} \leqslant {{h}_{{\text{б}}}} - {{\tau }_{{\min }}}, \hfill \\ {{h}_{{\text{б}}}},\quad {{s}_{{k\zeta }}} > {{h}_{{\text{б}}}} - {{\tau }_{{\min }}}, \hfill \\ \end{gathered} \right.$

где ${{s}_{{k\zeta }}} = {{h}_{{\text{б}}}}{\text{|}}{{{{u}_{{k\zeta }}}} \mathord{\left/ {\vphantom {{{{u}_{{k\zeta }}}} {M_{\zeta }^{{{\text{РД}}}}}}} \right. \kern-0em} {M_{\zeta }^{{{\text{РД}}}}}}{\text{|}}$ – требуемое законом (3.3) время работы РД, ${{\tau }_{{\min }}}$ – минимальное значение импульса и паузы, обусловленное конструкцией РД. Соответствующий управляющий момент от РД будет равен

(3.8)

${{\tilde {u}}_{{k\zeta }}}(t - {{t}_{k}}) = \left\{ \begin{gathered} M_{\zeta }^{{{\text{РД}}}}\operatorname{sign} ({{u}_{{k\zeta }}}),\quad {\text{0}} \leqslant t - {{t}_{k}} < {{\tau }_{{k\zeta }}}, \hfill \\ 0,\quad {{\tau }_{{k\zeta }}} \leqslant t - {{t}_{k}} < {{h}_{{\text{б}}}}. \hfill \\ \end{gathered} \right.$

4. Построение наблюдателя. Для получения оценки ${{{\mathbf{\hat {x}}}}_{k}}$, согласно опыту построения динамических наблюдателей [10], сформируем на основе непрерывной математической модели (3.1) дискретную модель с шагом h₆:

(4.1)

$\left\{ \begin{gathered} {{{\mathbf{x}}}_{{k + 1}}} = {{{\mathbf{f}}}_{{\text{д}}}}({{{\mathbf{x}}}_{k}},{{{{\mathbf{\tilde {u}}}}}_{k}}), \hfill \\ {{{\mathbf{y}}}_{k}} = {{{\mathbf{C}}}_{{\text{д}}}}{{{\mathbf{x}}}_{k}}. \hfill \\ \end{gathered} \right.$

В этой модели ${{{\mathbf{f}}}_{{\text{д}}}}({{{\mathbf{x}}}_{k}},{{{\mathbf{\tilde {u}}}}_{k}})$ – функция состояния, ${{{\mathbf{C}}}_{{\text{д}}}} = {{{\mathbf{C}}}_{{\text{н}}}}$ – матрица наблюдения.

Компоненты (3.8) управляющей функции ${{{\mathbf{\tilde {u}}}}_{k}}$, будучи кусочно-постоянными, внутри каждого такта могут иметь по одному переключению. Моменты времени ${{\tau }_{{kx}}}$, ${{\tau }_{{ky}}}$ и ${{\tau }_{{kz}}}$, в которые на данном такте происходят переключения в каналах x, y и z, в общем случае различны. Поэтому алгоритм расчета функции ${{{\mathbf{f}}}_{{\text{д}}}}({{{\mathbf{x}}}_{k}},{{{\mathbf{\tilde {u}}}}_{k}})$ не ограничивается одной операцией численного интегрирования, а содержит четыре таких операции. Опишем этот алгоритм.

Рассмотрим k-й вычислительный такт. Расположим три числа ${{\tau }_{{kx}}}$, ${{\tau }_{{ky}}}$ и ${{\tau }_{{kz}}}$ в порядке возрастания. Обозначим минимальное число символом через ${{\tau }_{{k1}}}$, соответствующую ему ось (x, y или z) – символом ${{i}_{{k1}}}$, максимальное число – ${{\tau }_{{k3}}}$ (ось ${{i}_{{k3}}}$), а оставшееся число – ${{\tau }_{{k2}}}$ (ось ${{i}_{{k2}}}$). Управляющая функция ${{{\mathbf{\tilde {u}}}}_{k}}(t - {{t}_{k}})$ с компонентами (3.8) на каждом из четырех интервалов изменения ее аргумента $\left[ {0;{\text{ }}{{\tau }_{{k1}}}} \right)$, $\left[ {{{\tau }_{{k1}}};{\text{ }}{{\tau }_{{k2}}}} \right)$, $\left[ {{{\tau }_{{k2}}};{\text{ }}{{\tau }_{{k3}}}} \right)$, $\left[ {{{\tau }_{{k3}}};{\text{ }}{{h}_{{\text{б}}}}} \right)$ принимает строго постоянные значения:

$\begin{array}{*{20}{c}} {{{{{\mathbf{\tilde {u}}}}}_{{k0}}} = {{{\left[ {\begin{array}{*{20}{c}} {{{{\tilde {u}}}_{{k0,x}}}}&\vline & {{{{\tilde {u}}}_{{k0,y}}}}&\vline & {{{{\tilde {u}}}_{{k0,z}}}} \end{array}} \right]}}^{T}}:}&{{{{\tilde {u}}}_{{k0,{{i}_{{k1}}}}}} = {{{\tilde {u}}}_{{k,{{i}_{{k1}}}}}}(0),}&{{{{\tilde {u}}}_{{k0,{{i}_{{k2}}}}}} = {{{\tilde {u}}}_{{k,{{i}_{{k2}}}}}}(0),}&{{{{\tilde {u}}}_{{k0,{{i}_{{k3}}}}}} = {{{\tilde {u}}}_{{k,{{i}_{{k3}}}}}}(0);} \\ {{{{{\mathbf{\tilde {u}}}}}_{{k1}}} = {{{\left[ {\begin{array}{*{20}{c}} {{{{\tilde {u}}}_{{k1,x}}}}&\vline & {{{{\tilde {u}}}_{{k1,y}}}}&\vline & {{{{\tilde {u}}}_{{k1,z}}}} \end{array}} \right]}}^{T}}:}&{{{{\tilde {u}}}_{{k1,{{i}_{{k1}}}}}} = 0,}&{{{{\tilde {u}}}_{{k1,{{i}_{{k2}}}}}} = {{{\tilde {u}}}_{{k,{{i}_{{k2}}}}}}(0),}&{{{{\tilde {u}}}_{{k1,{{i}_{{k3}}}}}} = {{{\tilde {u}}}_{{k,{{i}_{{k3}}}}}}(0);} \\ {{{{{\mathbf{\tilde {u}}}}}_{{k2}}} = {{{\left[ {\begin{array}{*{20}{c}} {{{{\tilde {u}}}_{{k2,x}}}}&\vline & {{{{\tilde {u}}}_{{k2,y}}}}&\vline & {{{{\tilde {u}}}_{{k2,z}}}} \end{array}} \right]}}^{T}}:}&{{{{\tilde {u}}}_{{k2,{{i}_{{k1}}}}}} = 0,}&{{{{\tilde {u}}}_{{k2,{{i}_{{k2}}}}}} = 0,}&{{{{\tilde {u}}}_{{k2,{{i}_{{k3}}}}}} = {{{\tilde {u}}}_{{k,{{i}_{{k3}}}}}}(0);} \\ {{{{{\mathbf{\tilde {u}}}}}_{{k3}}} = {{{\left[ {\begin{array}{*{20}{c}} {{{{\tilde {u}}}_{{k3,x}}}}&\vline & {{{{\tilde {u}}}_{{k3,y}}}}&\vline & {{{{\tilde {u}}}_{{k3,z}}}} \end{array}} \right]}}^{T}}:}&{{{{\tilde {u}}}_{{k3,{{i}_{{k1}}}}}} = 0,}&{{{{\tilde {u}}}_{{k3,{{i}_{{k2}}}}}} = 0,}&{{{{\tilde {u}}}_{{k3,{{i}_{{k3}}}}}} = 0.} \end{array}$

По известному значению вектора состояния ${{{\mathbf{x}}}_{{k0}}} = {{{\mathbf{x}}}_{k}}$ на левом конце k-го такта с помощью четырех последовательных операций численного интегрирования определим значение вектора состояния ${{{\mathbf{x}}}_{{k + 1}}}$ на правом конце k-го такта:

(4.2)

$\begin{gathered} {{{\mathbf{x}}}_{{k1}}} = {{{{\mathbf{\tilde {f}}}}}_{{\text{д}}}}({{{\mathbf{x}}}_{{k0}}},{{{{\mathbf{\tilde {u}}}}}_{{k0}}},{{\tau }_{{k1}}}), \\ {{{\mathbf{x}}}_{{k2}}} = {{{{\mathbf{\tilde {f}}}}}_{{\text{д}}}}({{{\mathbf{x}}}_{{k1}}},{{{{\mathbf{\tilde {u}}}}}_{{k1}}},{{\tau }_{{k2}}} - {{\tau }_{{k1}}}), \\ {{{\mathbf{x}}}_{{k3}}} = {{{{\mathbf{\tilde {f}}}}}_{{\text{д}}}}({{{\mathbf{x}}}_{{k2}}},{{{{\mathbf{\tilde {u}}}}}_{{k2}}},{{\tau }_{{k3}}} - {{\tau }_{{k2}}}), \\ {{{\mathbf{x}}}_{{k + 1}}} = {{{{\mathbf{\tilde {f}}}}}_{{\text{д}}}}({{{\mathbf{x}}}_{{k3}}},{{{{\mathbf{\tilde {u}}}}}_{{k3}}},{{h}_{{\text{б}}}} - {{\tau }_{{k3}}}). \\ \end{gathered} $

Здесь ${{{\mathbf{\tilde {f}}}}_{{\text{д}}}}({{{\mathbf{x}}}_{L}},{{{\mathbf{\tilde {u}}}}_{L}},h)$ – функция, которая по известному значению вектора ${{{\mathbf{x}}}_{L}} = {\mathbf{x}}(t)$ определяет значение вектора ${{{\mathbf{x}}}_{R}} = {\mathbf{x}}(t + h)$ путем численного интегрирования дифференциального уравнения из (3.1) ${\mathbf{\dot {x}}} = {{{\mathbf{f}}}_{{\text{н}}}}({\mathbf{x}}) + {{{\mathbf{B}}}_{{\text{н}}}}{\mathbf{u}}$$({\mathbf{u}}(\tau ) \equiv {{{\mathbf{\tilde {u}}}}_{L}}{\text{ при }}t \leqslant \tau < t + h)$ модифицированным методом Эйлера второго порядка:

(4.3)

${{{\mathbf{\tilde {f}}}}_{{\text{д}}}}({{{\mathbf{x}}}_{L}},{{{\mathbf{\tilde {u}}}}_{L}},h) = {{{\mathbf{x}}}_{L}} + 0.5\left( {{{{{\mathbf{\tilde {\kappa }}}}}_{1}}({{{\mathbf{x}}}_{L}},{{{{\mathbf{\tilde {u}}}}}_{L}},h) + {{{{\mathbf{\tilde {\kappa }}}}}_{2}}({{{\mathbf{x}}}_{L}},{{{{\mathbf{\tilde {u}}}}}_{L}},h)} \right),$

где

$\begin{gathered} {{{{\mathbf{\tilde {\kappa }}}}}_{1}}({{{\mathbf{x}}}_{L}},{{{{\mathbf{\tilde {u}}}}}_{L}},h) = \left( {{{{\mathbf{f}}}_{{\text{н}}}}({{{\mathbf{a}}}_{1}}({{{\mathbf{x}}}_{L}},{{{{\mathbf{\tilde {u}}}}}_{L}})) + {{{\mathbf{B}}}_{{\text{н}}}}{{{{\mathbf{\tilde {u}}}}}_{L}}} \right)h,\quad {{{{\mathbf{\tilde {a}}}}}_{1}}({{{\mathbf{x}}}_{L}},{{{{\mathbf{\tilde {u}}}}}_{L}},h) = {{{\mathbf{x}}}_{L}}, \\ {{{{\mathbf{\tilde {\kappa }}}}}_{2}}({{{\mathbf{x}}}_{L}},{{{{\mathbf{\tilde {u}}}}}_{L}},h) = \left( {{{{\mathbf{f}}}_{{\text{н}}}}({{{\mathbf{a}}}_{2}}({{{\mathbf{x}}}_{L}},{{{{\mathbf{\tilde {u}}}}}_{L}})) + {{{\mathbf{B}}}_{{\text{н}}}}{{{{\mathbf{\tilde {u}}}}}_{L}}} \right)h,\quad {{{{\mathbf{\tilde {a}}}}}_{2}}({{{\mathbf{x}}}_{L}},{{{{\mathbf{\tilde {u}}}}}_{L}},h) = {{{\mathbf{x}}}_{L}} + {{{\mathbf{\kappa }}}_{1}}({{{\mathbf{x}}}_{L}},{{{{\mathbf{\tilde {u}}}}}_{L}},h). \\ \end{gathered} $

Таким образом, функция состояния ${{{\mathbf{f}}}_{{\text{д}}}}({{{\mathbf{x}}}_{k}},{{{\mathbf{\tilde {u}}}}_{k}})$ для дискретной модели (4.1) может быть на основании (4.2) определена как

(4.4)

${{{\mathbf{f}}}_{{\text{д}}}}({{{\mathbf{x}}}_{k}},{{{\mathbf{\tilde {u}}}}_{k}}) = {{{\mathbf{\tilde {f}}}}_{{\text{д}}}}({{{\mathbf{\tilde {f}}}}_{{\text{д}}}}({{{\mathbf{\tilde {f}}}}_{{\text{д}}}}({{{\mathbf{\tilde {f}}}}_{{\text{д}}}}({{{\mathbf{x}}}_{k}},{{{\mathbf{\tilde {u}}}}_{{k0}}},{{\tau }_{{k1}}}),{{{\mathbf{\tilde {u}}}}_{{k1}}},{{\tau }_{{k2}}} - {{\tau }_{{k1}}}),{{{\mathbf{\tilde {u}}}}_{{k2}}},{{\tau }_{{k3}}} - {{\tau }_{{k2}}}),{{{\mathbf{\tilde {u}}}}_{{k3}}},{{h}_{{\text{б}}}} - {{\tau }_{{k3}}}).$

Линеаризуем дискретную модель (4.1) по Тейлору вблизи положения $({{{\mathbf{\hat {x}}}}_{k}},{{{\mathbf{\tilde {u}}}}_{k}})$ в рамках одного шага дискретизации:

(4.5)

$\left\{ \begin{gathered} {{{\mathbf{x}}}_{{k + 1}}} = {{{\mathbf{\xi }}}_{{\text{д}}}} + {{{\mathbf{A}}}_{{\text{д}}}}\left( {{{{\mathbf{x}}}_{k}} - {{{{\mathbf{\hat {x}}}}}_{k}}} \right), \hfill \\ {{{\mathbf{y}}}_{k}} = {{{\mathbf{C}}}_{{\text{д}}}}{{{\mathbf{x}}}_{k}}, \hfill \\ \end{gathered} \right.$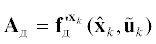

где ${{{\mathbf{\xi }}}_{{\text{д}}}} = {{{\mathbf{f}}}_{{\text{д}}}}({{{\mathbf{\hat {x}}}}_{k}},{{{\mathbf{\tilde {u}}}}_{k}})$,

, а функция

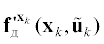представляет собой матрицу Якоби, содержащую частные производные от векторной функции ${{{\mathbf{f}}}_{{\text{д}}}}({{{\mathbf{x}}}_{k}},{{{\mathbf{\tilde {u}}}}_{k}})$ по компонентам вектора ${{{\mathbf{x}}}_{k}}$. Функция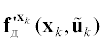

может быть определена как производная от сложной функции (4.4) с учетом (4.2):

(4.6)

${\mathbf{f}}_{{\text{д}}}^{{'{{{\mathbf{x}}}_{L}}}}({{{\mathbf{x}}}_{k}},{{{\mathbf{\tilde {u}}}}_{k}}) = \frac{{\partial {{{\mathbf{x}}}_{{k + 1}}}}}{{\partial {{{\mathbf{x}}}_{{k3}}}}}({{{\mathbf{x}}}_{k}},{{{\mathbf{\tilde {u}}}}_{k}})\frac{{\partial {{{\mathbf{x}}}_{{k3}}}}}{{\partial {{{\mathbf{x}}}_{{k2}}}}}({{{\mathbf{x}}}_{k}},{{{\mathbf{\tilde {u}}}}_{k}})\frac{{\partial {{{\mathbf{x}}}_{{k2}}}}}{{\partial {{{\mathbf{x}}}_{{k1}}}}}({{{\mathbf{x}}}_{k}},{{{\mathbf{\tilde {u}}}}_{k}})\frac{{\partial {{{\mathbf{x}}}_{{k1}}}}}{{\partial {{{\mathbf{x}}}_{k}}}}({{{\mathbf{x}}}_{k}},{{{\mathbf{\tilde {u}}}}_{k}}),$

где

$\begin{gathered} \frac{{\partial {{{\mathbf{x}}}_{{k + 1}}}}}{{\partial {{{\mathbf{x}}}_{{k3}}}}}({{{\mathbf{x}}}_{k}},{{{{\mathbf{\tilde {u}}}}}_{k}}) = {\mathbf{\tilde {f}}}_{{\text{д}}}^{{'{{{\mathbf{x}}}_{L}}}}({{{\mathbf{x}}}_{{k3}}}({{{\mathbf{x}}}_{k}},{{{{\mathbf{\tilde {u}}}}}_{k}}),{{{{\mathbf{\tilde {u}}}}}_{{k3}}},{{h}_{{\text{б}}}} - {{\tau }_{{k3}}}), \\ \frac{{\partial {{{\mathbf{x}}}_{{k3}}}}}{{\partial {{{\mathbf{x}}}_{{k2}}}}}({{{\mathbf{x}}}_{k}},{{{{\mathbf{\tilde {u}}}}}_{k}}) = {\mathbf{\tilde {f}}}_{{\text{д}}}^{{'{{{\mathbf{x}}}_{L}}}}({{{\mathbf{x}}}_{{k2}}}({{{\mathbf{x}}}_{k}},{{{{\mathbf{\tilde {u}}}}}_{k}}),{{{{\mathbf{\tilde {u}}}}}_{{k2}}},{{\tau }_{{k3}}} - {{\tau }_{{k2}}}), \\ \frac{{\partial {{{\mathbf{x}}}_{{k2}}}}}{{\partial {{{\mathbf{x}}}_{{k1}}}}}({{{\mathbf{x}}}_{k}},{{{{\mathbf{\tilde {u}}}}}_{k}}) = {\mathbf{\tilde {f}}}_{{\text{д}}}^{{'{{{\mathbf{x}}}_{L}}}}({{{\mathbf{x}}}_{{k1}}}({{{\mathbf{x}}}_{k}},{{{{\mathbf{\tilde {u}}}}}_{k}}),{{{{\mathbf{\tilde {u}}}}}_{{k1}}},{{\tau }_{{k2}}} - {{\tau }_{{k1}}}), \\ \frac{{\partial {{{\mathbf{x}}}_{{k1}}}}}{{\partial {{{\mathbf{x}}}_{k}}}}({{{\mathbf{x}}}_{k}},{{{{\mathbf{\tilde {u}}}}}_{k}}) = {\mathbf{\tilde {f}}}_{{\text{д}}}^{{'{{{\mathbf{x}}}_{L}}}}({{{\mathbf{x}}}_{k}},{{{{\mathbf{\tilde {u}}}}}_{{k0}}},{{\tau }_{{k1}}}). \\ \end{gathered} $

Здесь ${\mathbf{\tilde {f}}}_{{\text{д}}}^{{'{{{\mathbf{x}}}_{L}}}}({{{\mathbf{x}}}_{L}},{{{\mathbf{\tilde {u}}}}_{L}},h)$ – частная производная от функции (4.3) по аргументу x_L. Она имеет вид

${\mathbf{\tilde {f}}}_{{\text{д}}}^{{'{{{\mathbf{x}}}_{L}}}}({{{\mathbf{x}}}_{L}},{{{\mathbf{\tilde {u}}}}_{L}},h) = {{{\mathbf{I}}}_{6}} + 0.5({\mathbf{\tilde {\kappa }}}_{{\text{1}}}^{{'{{{\mathbf{x}}}_{L}}}}({{{\mathbf{x}}}_{L}},{{{\mathbf{\tilde {u}}}}_{L}},h) + {\mathbf{\tilde {\kappa }}}_{{\text{2}}}^{{'{{{\mathbf{x}}}_{L}}}}({{{\mathbf{x}}}_{L}},{{{\mathbf{\tilde {u}}}}_{L}},h)),$

где

$\begin{gathered} {\mathbf{\tilde {\kappa }}}_{{\text{1}}}^{{'{{{\mathbf{x}}}_{L}}}}({{{\mathbf{x}}}_{L}},{{{{\mathbf{\tilde {u}}}}}_{L}},h) = {\mathbf{f}}_{{\text{н}}}^{'}({{{{\mathbf{\tilde {a}}}}}_{1}}({{{\mathbf{x}}}_{L}},{{{{\mathbf{\tilde {u}}}}}_{L}},h)){\mathbf{\tilde {a}}}_{{\text{1}}}^{{'{{{\mathbf{x}}}_{k}}}}({{{\mathbf{x}}}_{L}},{{{{\mathbf{\tilde {u}}}}}_{L}},h)h,\quad {\mathbf{\tilde {a}}}_{{\text{1}}}^{{'{{{\mathbf{x}}}_{k}}}}({{{\mathbf{x}}}_{L}},{{{{\mathbf{\tilde {u}}}}}_{L}},h) = {{{\mathbf{I}}}_{6}}, \\ {\mathbf{\tilde {\kappa }}}_{{\text{2}}}^{{'{{{\mathbf{x}}}_{L}}}}({{{\mathbf{x}}}_{L}},{{{{\mathbf{\tilde {u}}}}}_{L}},h) = {\mathbf{f}}_{{\text{н}}}^{'}({{{{\mathbf{\tilde {a}}}}}_{2}}({{{\mathbf{x}}}_{L}},{{{{\mathbf{\tilde {u}}}}}_{L}},h)){\mathbf{\tilde {a}}}_{{\text{2}}}^{{'{{{\mathbf{x}}}_{k}}}}({{{\mathbf{x}}}_{L}},{{{{\mathbf{\tilde {u}}}}}_{L}},h)h,\quad {\mathbf{\tilde {a}}}_{{\text{2}}}^{{'{{{\mathbf{x}}}_{k}}}}({{{\mathbf{x}}}_{L}},{{{{\mathbf{\tilde {u}}}}}_{L}},h) = {{{\mathbf{I}}}_{6}} + {\mathbf{\tilde {\kappa }}}_{{\text{1}}}^{{'{{{\mathbf{x}}}_{k}}}}({{{\mathbf{x}}}_{L}},{{{{\mathbf{\tilde {u}}}}}_{L}},h). \\ \end{gathered} $

Таким образом, линеаризованная дискретная модель (4.5) формируется на основе функций (4.4) и (4.6).

Для объекта (4.5), согласно [10], синтезируем наблюдатель полного порядка:

(4.7)

${{{\mathbf{\hat {x}}}}_{{k + 1}}} = {{{\mathbf{\xi }}}_{{\text{д}}}} + {{{\mathbf{L}}}_{{\text{д}}}}\left( {{{{\mathbf{y}}}_{k}} - {{{\mathbf{C}}}_{{\text{д}}}}{{{{\mathbf{\hat {x}}}}}_{k}}} \right).$

Если оценки углов, полученные при расчете, превышают по модулю 180°, то добавляются периоды, кратные 360°, с соответствующим знаком.

Матрица коэффициентов усиления ${{{\mathbf{L}}}_{{\text{д}}}}$ определяется из уравнения ошибки наблюдения ${\mathbf{\varepsilon }} = {\mathbf{x}} - {\mathbf{\hat {x}}}$, сформированного на основании (4.5) и (4.7):

${{{\mathbf{\varepsilon }}}_{{k + 1}}} = \left( {{{{\mathbf{A}}}_{{\text{д}}}} - {{{\mathbf{L}}}_{{\text{д}}}}{{{\mathbf{C}}}_{{\text{д}}}}} \right){{{\mathbf{\varepsilon }}}_{k}}.$

Модальный наблюдатель с матрицей ${{{\mathbf{L}}}_{{\text{д}}}}$ синтезируем описанным выше аналитическим методом для пары матриц $({{{\mathbf{A}}}_{{\text{д}}}},{{{\mathbf{C}}}_{{\text{д}}}})$:

${{{\mathbf{A}}}_{{\text{д}}}} = \left[ {\begin{array}{*{20}{c}} {{{a}_{{11}}}}&\vline & {{{a}_{{12}}}}&\vline & {{{a}_{{13}}}}&\vline & {{{a}_{{14}}}}&\vline & {{{a}_{{15}}}}&\vline & {{{a}_{{16}}}} \\ {{{a}_{{21}}}}&\vline & {{{a}_{{22}}}}&\vline & {{{a}_{{23}}}}&\vline & {{{a}_{{24}}}}&\vline & {{{a}_{{25}}}}&\vline & {{{a}_{{26}}}} \\ {{{a}_{{31}}}}&\vline & {{{a}_{{32}}}}&\vline & {{{a}_{{33}}}}&\vline & {{{a}_{{34}}}}&\vline & {{{a}_{{35}}}}&\vline & {{{a}_{{36}}}} \\ {{{a}_{{41}}}}&\vline & {{{a}_{{42}}}}&\vline & {{{a}_{{43}}}}&\vline & {{{a}_{{44}}}}&\vline & {{{a}_{{45}}}}&\vline & {{{a}_{{46}}}} \\ {{{a}_{{51}}}}&\vline & {{{a}_{{52}}}}&\vline & {{{a}_{{53}}}}&\vline & {{{a}_{{54}}}}&\vline & {{{a}_{{55}}}}&\vline & {{{a}_{{56}}}} \\ {{{a}_{{61}}}}&\vline & {{{a}_{{62}}}}&\vline & {{{a}_{{63}}}}&\vline & {{{a}_{{64}}}}&\vline & {{{a}_{{65}}}}&\vline & {{{a}_{{66}}}} \end{array}} \right],\quad {{{\mathbf{C}}}_{{\text{д}}}} = \left[ {\begin{array}{*{20}{c}} 1&\vline & 0&\vline & 0&\vline & 0&\vline & 0&\vline & 0 \\ 0&\vline & 0&\vline & 1&\vline & 0&\vline & 0&\vline & 0 \\ 0&\vline & 0&\vline & 0&\vline & 1&\vline & 0&\vline & 0 \\ 0&\vline & 0&\vline & 0&\vline & 0&\vline & 1&\vline & 0 \\ 0&\vline & 0&\vline & 0&\vline & 0&\vline & 0&\vline & 1 \end{array}} \right].$

Здесь элементы матрицы ${{{\mathbf{A}}}_{{\text{д}}}}$ рассчитываются с использованием формулы (4.6).

Количество уровней декомпозиции, согласно (2.2), ${{N}_{{\text{д}}}} = 1$. Зададим спектр замкнутой дискретной системы “объект – наблюдатель”:

$\operatorname{eig} \left( {{{{\mathbf{A}}}_{{\text{д}}}} - {{{\mathbf{L}}}_{{\text{д}}}}{{{\mathbf{C}}}_{{\text{д}}}}} \right) = \left\{ {{{\psi }_{{{\text{д}}1}}},{\text{ }}{{\psi }_{{{\text{д2}}}}},{\text{ }}{{\psi }_{{{\text{д3}}}}},{\text{ }}{{\psi }_{{{\text{д4}}}}},{\text{ }}{{\psi }_{{{\text{д5}}}}},{\text{ }}{{\psi }_{{{\text{д6}}}}}} \right\}.$

Нулевой уровень декомпозиции $({{{\mathbf{A}}}_{{\text{д}}}},{\text{ }}{{{\mathbf{C}}}_{{\text{д}}}})$ (2.1):

${{{\mathbf{A}}}_{{{\text{д}}0}}} = {{{\mathbf{A}}}_{{\text{д}}}} \in {{\mathbb{R}}^{{6 \times 6}}},\quad {{{\mathbf{C}}}_{{{\text{д}}0}}} = {{{\mathbf{C}}}_{{\text{д}}}} \in {{\mathbb{R}}^{{5 \times 6}}}.$

Так как $\operatorname{rank} {{{\mathbf{C}}}_{0}} = 5$, перейдем к следующему уровню декомпозиции, вычислив

${\mathbf{C}}_{{{\text{д}}0}}^{{ \bot R}} = {{\left[ {\begin{array}{*{20}{l}} 0&\vline & 1&\vline & 0&\vline & 0&\vline & 0&\vline & 0 \end{array}} \right]}^{{\text{T}}}},\quad {\mathbf{C}}_{{{\text{д}}0}}^{{ \bot R + }} = {\mathbf{C}}_{{{\text{д}}0}}^{{ \bot RT}} = \left[ {\begin{array}{*{20}{l}} 0&\vline & 1&\vline & 0&\vline & 0&\vline & 0&\vline & 0 \end{array}} \right].$

Первый уровень декомпозиции $({{{\mathbf{A}}}_{{\text{д}}}},{\text{ }}{{{\mathbf{C}}}_{{\text{д}}}})$ (2.3):

${{{\mathbf{A}}}_{{{\text{д}}1}}} = {\mathbf{C}}_{{{\text{д}}0}}^{{ \bot R + }}{{{\mathbf{A}}}_{{{\text{д}}0}}}{\mathbf{C}}_{{{\text{д}}0}}^{{ \bot R}} = {{a}_{{22}}} \in {{\mathbb{R}}^{{1 \times 1}}},\quad {{{\mathbf{C}}}_{{{\text{д}}1}}} = {{{\mathbf{C}}}_{{{\text{д}}0}}}{{{\mathbf{A}}}_{{{\text{д}}0}}}{\mathbf{C}}_{{{\text{д}}0}}^{{ \bot R}} = {{\left[ {\begin{array}{*{20}{c}} {{{a}_{{12}}}}&\vline & {{{a}_{{32}}}}&\vline & {{{a}_{{42}}}}&\vline & {{{a}_{{52}}}}&\vline & {{{a}_{{62}}}} \end{array}} \right]}^{{\text{T}}}} \in {{\mathbb{R}}^{{5 \times 1}}}.$

Поскольку $\operatorname{rank} {{{\mathbf{C}}}_{{{\text{д}}1}}} < 5$, выполним скелетное разложение (2.4) ${{{\mathbf{C}}}_{{{\text{д}}1}}} = {{{\mathbf{S}}}_{{{\text{д}}1}}}{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C} }}}_{{{\text{д}}1}}},$ где ${{{\mathbf{S}}}_{{{\text{д}}1}}} = {{{\mathbf{C}}}_{{{\text{д}}1}}}$, ${{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C} }}}_{{{\text{д}}1}}} = 1$, и введем модификацию (2.5) на данном уровне.

Первый модифицированный уровень декомпозиции $({{{\mathbf{A}}}_{{\text{д}}}},{\text{ }}{{{\mathbf{C}}}_{{\text{д}}}})$:

${{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} }}}_{{{\text{д}}1}}} = {{{\mathbf{A}}}_{{{\text{д}}1}}} = {{a}_{{22}}} \in {{\mathbb{R}}^{{1 \times 1}}},\quad {{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C} }}}_{{{\text{д}}1}}} = 1 \in {{\mathbb{R}}^{{1 \times 1}}}.$

Матрица ${{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C} }}}_{{{\text{д}}1}}}$ обратима, поэтому можно перейти к расчету наблюдателей.

Наблюдатель на первом модифицированном уровне декомпозиции $({{{\mathbf{A}}}_{{\text{д}}}},{\text{ }}{{{\mathbf{C}}}_{{\text{д}}}})$. Назначим матрицу с желаемым спектром

${{{\mathbf{\Psi }}}_{{{\text{д}}1}}} = {{\psi }_{{{\text{д}}2}}}.$

Матрица наблюдателя, согласно (2.6), будет иметь вид

${{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{L} }}}_{{{\text{д}}1}}} = {{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} }}}_{{{\text{д}}1}}}{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C} }}_{{{\text{д}}1}}^{{ - 1}} - {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C} }}_{{{\text{д}}1}}^{{ - 1}}{{{\mathbf{\Psi }}}_{{{\text{д}}1}}} = {{\tilde {a}}_{{22}}},$

где ${{\tilde {a}}_{{22}}} = {{a}_{{22}}} - {{\psi }_{{{\text{д}}2}}}$.

Наблюдатель на первом уровне декомпозиции $({{{\mathbf{A}}}_{{\text{д}}}},{\text{ }}{{{\mathbf{C}}}_{{\text{д}}}})$. Псевдообратная матрица перехода

${\mathbf{S}}_{{{\text{д}}1}}^{ + } = {{({\mathbf{S}}_{{{\text{д}}1}}^{T}{{{\mathbf{S}}}_{{{\text{д}}1}}})}^{{ - 1}}}{\mathbf{S}}_{{{\text{д}}1}}^{T} = \frac{{\left[ {\begin{array}{*{20}{c}} {{{a}_{{12}}}}&\vline & {{{a}_{{32}}}}&\vline & {{{a}_{{42}}}}&\vline & {{{a}_{{52}}}}&\vline & {{{a}_{{62}}}} \end{array}} \right]}}{{a_{{12}}^{2} + a_{{32}}^{2} + a_{{42}}^{2} + a_{{52}}^{2} + a_{{62}}^{2}}}.$

Пересчитанная матрица наблюдателя (2.7) равна

${{{\mathbf{L}}}_{{{\text{д}}1}}} = {{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{L} }}}_{{{\text{д}}1}}}{\mathbf{S}}_{{{\text{д}}1}}^{ + } = k\left[ {\begin{array}{*{20}{c}} {{{a}_{{12}}}}&\vline & {{{a}_{{32}}}}&\vline & {{{a}_{{42}}}}&\vline & {{{a}_{{52}}}}&\vline & {{{a}_{{62}}}} \end{array}} \right],$

где $k = {{{{{\tilde {a}}}_{{22}}}} \mathord{\left/ {\vphantom {{{{{\tilde {a}}}_{{22}}}} {(a_{{12}}^{2} + a_{{32}}^{2} + a_{{42}}^{2} + a_{{52}}^{2} + a_{{62}}^{2})}}} \right. \kern-0em} {(a_{{12}}^{2} + a_{{32}}^{2} + a_{{42}}^{2} + a_{{52}}^{2} + a_{{62}}^{2})}}.$

Наблюдатель на нулевом уровне декомпозиции $({{{\mathbf{A}}}_{{\text{д}}}},{\text{ }}{{{\mathbf{C}}}_{{\text{д}}}})$.Рассчитаем псевдообратную и вспомогательную матрицы для (2.6):

${\mathbf{C}}_{{{\text{д}}0}}^{ + } = {\mathbf{C}}_{{{\text{д}}0}}^{T} = \left[ {\begin{array}{*{20}{c}} 1&\vline & 0&\vline & 0&\vline & 0&\vline & 0 \\ 0&\vline & 0&\vline & 0&\vline & 0&\vline & 0 \\ 0&\vline & 1&\vline & 0&\vline & 0&\vline & 0 \\ 0&\vline & 0&\vline & 1&\vline & 0&\vline & 0 \\ 0&\vline & 0&\vline & 0&\vline & 1&\vline & 0 \\ 0&\vline & 0&\vline & 0&\vline & 0&\vline & 1 \end{array}} \right],\quad {\mathbf{C}}_{{{\text{д}}0}}^{ - } = {\mathbf{C}}_{{{\text{д}}0}}^{ + } + {\mathbf{C}}_{{{\text{д}}0}}^{{ \bot R}}{{{\mathbf{L}}}_{{{\text{д}}1}}} = \left[ {\begin{array}{*{20}{c}} 1&\vline & 0&\vline & 0&\vline & 0&\vline & 0 \\ {{{k}_{{12}}}}&\vline & {{{k}_{{32}}}}&\vline & {{{k}_{{42}}}}&\vline & {{{k}_{{52}}}}&\vline & {{{k}_{{62}}}} \\ 0&\vline & 1&\vline & 0&\vline & 0&\vline & 0 \\ 0&\vline & 0&\vline & 1&\vline & 0&\vline & 0 \\ 0&\vline & 0&\vline & 0&\vline & 1&\vline & 0 \\ 0&\vline & 0&\vline & 0&\vline & 0&\vline & 1 \end{array}} \right],$

где введены обозначения: ${{k}_{{12}}} = k{{a}_{{12}}}$, ${{k}_{{32}}} = k{{a}_{{32}}}$, ${{k}_{{42}}} = k{{a}_{{42}}}$, ${{k}_{{52}}} = k{{a}_{{52}}}$ и ${{k}_{{62}}} = k{{a}_{{62}}}$.

Назначим матрицу с желаемым спектром

${{{\mathbf{\Psi }}}_{{{\text{д}}0}}} = \left[ {\begin{array}{*{20}{c}} {{{\psi }_{{{\text{д}}1}}}}&\vline & 0&\vline & 0&\vline & 0&\vline & 0 \\ 0&\vline & {{{\psi }_{{{\text{д}}3}}}}&\vline & 0&\vline & 0&\vline & 0 \\ 0&\vline & 0&\vline & {{{\psi }_{{{\text{д}}4}}}}&\vline & 0&\vline & 0 \\ 0&\vline & 0&\vline & 0&\vline & {{{\psi }_{{{\text{д}}5}}}}&\vline & 0 \\ 0&\vline & 0&\vline & 0&\vline & 0&\vline & {{{\psi }_{{{\text{д}}6}}}} \end{array}} \right].$

Матрица наблюдателя примет вид (2.6)

${{{\mathbf{L}}}_{{{\text{д}}0}}} = {{{\mathbf{A}}}_{{{\text{д}}0}}}{\mathbf{C}}_{{{\text{д}}0}}^{ - } - {\mathbf{C}}_{{{\text{д}}0}}^{ - }{{{\mathbf{\Psi }}}_{{{\text{д}}0}}} = \left[ {\begin{array}{*{20}{c}} {{{{\tilde {a}}}_{{11}}} + {{k}_{{12}}}{{a}_{{12}}}}&\vline & {{{a}_{{13}}} + {{k}_{{32}}}{{a}_{{12}}}}&\vline & {{{a}_{{14}}} + {{k}_{{42}}}{{a}_{{12}}}}&\vline & {{{a}_{{15}}} + {{k}_{{52}}}{{a}_{{12}}}}&\vline & {{{a}_{{16}}} + {{k}_{{62}}}{{a}_{{12}}}} \\ {{{a}_{{21}}} + {{k}_{{12}}}{{a}_{1}}}&\vline & {{{a}_{{23}}} + {{k}_{{32}}}{{a}_{3}}}&\vline & {{{a}_{{24}}} + {{k}_{{42}}}{{a}_{4}}}&\vline & {{{a}_{{25}}} + {{k}_{{52}}}{{a}_{5}}}&\vline & {{{a}_{{26}}} + {{k}_{{62}}}{{a}_{6}}} \\ {{{a}_{{31}}} + {{k}_{{12}}}{{a}_{{32}}}}&\vline & {{{{\tilde {a}}}_{{33}}} + {{k}_{{32}}}{{a}_{{32}}}}&\vline & {{{a}_{{34}}} + {{k}_{{42}}}{{a}_{{32}}}}&\vline & {{{a}_{{35}}} + {{k}_{{52}}}{{a}_{{32}}}}&\vline & {{{a}_{{36}}} + {{k}_{{62}}}{{a}_{{32}}}} \\ {{{a}_{{41}}} + {{k}_{{12}}}{{a}_{{42}}}}&\vline & {{{a}_{{43}}} + {{k}_{{32}}}{{a}_{{42}}}}&\vline & {{{{\tilde {a}}}_{{44}}} + {{k}_{{42}}}{{a}_{{42}}}}&\vline & {{{a}_{{45}}} + {{k}_{{52}}}{{a}_{{42}}}}&\vline & {{{a}_{{46}}} + {{k}_{{62}}}{{a}_{{42}}}} \\ {{{a}_{{51}}} + {{k}_{{12}}}{{a}_{{52}}}}&\vline & {{{a}_{{53}}} + {{k}_{{32}}}{{a}_{{52}}}}&\vline & {{{a}_{{54}}} + {{k}_{{42}}}{{a}_{{52}}}}&\vline & {{{{\tilde {a}}}_{{55}}} + {{k}_{{52}}}{{a}_{{52}}}}&\vline & {{{a}_{{56}}} + {{k}_{{62}}}{{a}_{{52}}}} \\ {{{a}_{{61}}} + {{k}_{{12}}}{{a}_{{62}}}}&\vline & {{{a}_{{63}}} + {{k}_{{32}}}{{a}_{{62}}}}&\vline & {{{a}_{{64}}} + {{k}_{{42}}}{{a}_{{62}}}}&\vline & {{{a}_{{65}}} + {{k}_{{52}}}{{a}_{{62}}}}&\vline & {{{{\tilde {a}}}_{{66}}} + {{k}_{{62}}}{{a}_{{62}}}} \end{array}} \right],$

где ${{\tilde {a}}_{{ii}}} = {{a}_{{ii}}} - {{\psi }_{{{\text{д}}i}}}$, ${{a}_{i}} = {{a}_{{22}}} - {{\psi }_{{{\text{д}}i}}}$, $i = \overline {1, \ldots ,6} $.

Итак, для уравнения наблюдателя (4.7) рассчитана матрица ${{{\mathbf{L}}}_{{\text{д}}}} = {{{\mathbf{L}}}_{{{\text{д}}0}}}$:

(4.8)

${{{\mathbf{L}}}_{{\text{д}}}} = \left[ {\begin{array}{*{20}{c}} {{{{\tilde {a}}}_{{11}}} + {{k}_{{12}}}{{a}_{{12}}}}&\vline & {{{a}_{{13}}} + {{k}_{{32}}}{{a}_{{12}}}}&\vline & {{{a}_{{14}}} + {{k}_{{42}}}{{a}_{{12}}}}&\vline & {{{a}_{{15}}} + {{k}_{{52}}}{{a}_{{12}}}}&\vline & {{{a}_{{16}}} + {{k}_{{62}}}{{a}_{{12}}}} \\ {{{a}_{{21}}} + {{k}_{{12}}}{{a}_{1}}}&\vline & {{{a}_{{23}}} + {{k}_{{32}}}{{a}_{3}}}&\vline & {{{a}_{{24}}} + {{k}_{{42}}}{{a}_{4}}}&\vline & {{{a}_{{25}}} + {{k}_{{52}}}{{a}_{5}}}&\vline & {{{a}_{{26}}} + {{k}_{{62}}}{{a}_{6}}} \\ {{{a}_{{31}}} + {{k}_{{12}}}{{a}_{{32}}}}&\vline & {{{{\tilde {a}}}_{{33}}} + {{k}_{{32}}}{{a}_{{32}}}}&\vline & {{{a}_{{34}}} + {{k}_{{42}}}{{a}_{{32}}}}&\vline & {{{a}_{{35}}} + {{k}_{{52}}}{{a}_{{32}}}}&\vline & {{{a}_{{36}}} + {{k}_{{62}}}{{a}_{{32}}}} \\ {{{a}_{{41}}} + {{k}_{{12}}}{{a}_{{42}}}}&\vline & {{{a}_{{43}}} + {{k}_{{32}}}{{a}_{{42}}}}&\vline & {{{{\tilde {a}}}_{{44}}} + {{k}_{{42}}}{{a}_{{42}}}}&\vline & {{{a}_{{45}}} + {{k}_{{52}}}{{a}_{{42}}}}&\vline & {{{a}_{{46}}} + {{k}_{{62}}}{{a}_{{42}}}} \\ {{{a}_{{51}}} + {{k}_{{12}}}{{a}_{{52}}}}&\vline & {{{a}_{{53}}} + {{k}_{{32}}}{{a}_{{52}}}}&\vline & {{{a}_{{54}}} + {{k}_{{42}}}{{a}_{{52}}}}&\vline & {{{{\tilde {a}}}_{{55}}} + {{k}_{{52}}}{{a}_{{52}}}}&\vline & {{{a}_{{56}}} + {{k}_{{62}}}{{a}_{{52}}}} \\ {{{a}_{{61}}} + {{k}_{{12}}}{{a}_{{62}}}}&\vline & {{{a}_{{63}}} + {{k}_{{32}}}{{a}_{{62}}}}&\vline & {{{a}_{{64}}} + {{k}_{{42}}}{{a}_{{62}}}}&\vline & {{{a}_{{65}}} + {{k}_{{52}}}{{a}_{{62}}}}&\vline & {{{{\tilde {a}}}_{{66}}} + {{k}_{{62}}}{{a}_{{62}}}} \end{array}} \right],$

которая является аналитическим решением задачи синтеза наблюдателя.

5. Числовой пример. В качестве примера рассматривалась ориентация КА типа “Союз” с РД постоянной тяги на круговой околоземной орбите высотой H = 300 км (ω₀ = 0.067 град/с). Уравнения движения (1.1) интегрировались методом Рунге–Кутты IV порядка с шагом модели ${{h}_{{\text{м}}}} = 0.005$ с и бортовым шагом ${{h}_{{\text{б}}}} = 0.2$ с. Время работы РД в рамках каждого бортового шага рассчитывалось по схеме (3.7) , управление от РД – по схеме (3.8) .

Измерения от ИКВ моделировались линейно с насыщением ${{\gamma }_{{\lim }}} = {{\vartheta }_{{\lim }}} = 35^\circ $.

Законы управления синтезировались в соответствии с аналитическими выражениями (3.3), (3.4), (3.6), (4.7), (4.8), полученными для линеаризованных моделей (3.2), (4.1) углового движения КА. Управление начинало рассчитываться с такта ${{k}_{{{\text{нач}}}}} = 6$ (по числу фазовых координат), на котором предполагалось получение адекватной оценки вектора состояния. Начальная оценка угла рысканья равна нулю. Желаемый спектр замкнутой непрерывной системы “объект–регулятор” назначался исходя из возможности реализации быстрого приведения ориентации и поддержания ориентации с заданной точностью на РД постоянной тяги:

$\operatorname{eig} \left( {{{{\mathbf{A}}}_{{\text{н}}}} - {{{\mathbf{B}}}_{{\text{н}}}}{{{\mathbf{K}}}_{{\text{н}}}}} \right) = \left\{ \begin{gathered} \left\{ { - 0.3,{\text{ }} - 0.2,{\text{ }} - 0.2,{\text{ }} - 0.3,{\text{ }} - 0.2,{\text{ }} - 0.2} \right\},{\text{ }}\max (\gamma ,\psi ,\vartheta ) \geqslant 15^\circ ; \hfill \\ \left\{ { - 1.2,{\text{ }} - 0.8,{\text{ }} - 0.8,{\text{ }} - 1.2,{\text{ }} - 0.8,{\text{ }} - 0.8} \right\},{\text{ }}\max (\gamma ,\psi ,\vartheta ) < 15^\circ . \hfill \\ \end{gathered} \right.$

Желаемый спектр замкнутой дискретной системы “объект–наблюдатель” назначался как компромисс между быстродействием наблюдателя и отсутствием колебаний, вызванных периодичностью оценки угла рысканья при его значениях, близких к $ \pm 180^\circ $:

$\operatorname{eig} \left( {{{{\mathbf{A}}}_{{\text{д}}}} - {{{\mathbf{L}}}_{{\text{д}}}}{{{\mathbf{C}}}_{{\text{д}}}}} \right) = \left\{ {0.9,{\text{ }}0.9,{\text{ }}0.9,{\text{ }}0.9,{\text{ }}0.9,{\text{ }}0.9} \right\}.$

Наиболее вероятный диапазон начальных значений вектора состояния рассматривался в виде 6-мерного массива: ${{\gamma }_{0}},{\text{ }}{{\vartheta }_{0}} = - 30^\circ \ldots 30^\circ $, ${{\psi }_{0}} = - 170^\circ \ldots 170^\circ $ с шагом 10°, w_x0, w_y0, ${{w}_{{z0}}} = \pm 0.01$ град/с, т.е. всего было промоделировано $7 \times 7 \times 35 \times 2 \times 2 \times 2 = 13720$ переходных процессов (ПП) с различными начальными условиями (НУ). Во всех случаях требуемая точность 0.3° по углам и 0.1 град/с по компонентам угловой скорости достигается за время ПП не более

${{T}_{{{\text{ПП}}}}} = 60{\text{ с}}$.

В каждом случае подтверждалось нахождение фазовых координат в пределах трубок заданной точности как минимум до момента времени T = 500 c.

Максимальная из 13720 вариантов НУ длительность ПП соответствует варианту № 13 669: ${{\gamma }_{0}} = 30^\circ $, ${{\psi }_{0}} = 170^\circ $, ${{\vartheta }_{0}} = - 30^\circ $, ${{w}_{{x0}}} = 0.01$ град/с, ${{w}_{{y0}}} = {{w}_{{z0}}} = - 0.01$ град/с. Графики ПП для этого варианта представлены на рисунке.

Рисунок.

Переходные процессы при ${{\gamma }_{0}} = 30^\circ $, ${{\psi }_{0}} = 170^\circ $, ${{\vartheta }_{0}} = - 30^\circ $, ${{w}_{{x0}}} = 0.01$ град/с, ${{w}_{{y0}}} = - 0.01$ град/с, ${{w}_{{z0}}} = - 0.01$ град/с; сплошная линия – истинное значение, штриховая линия – значение оценки

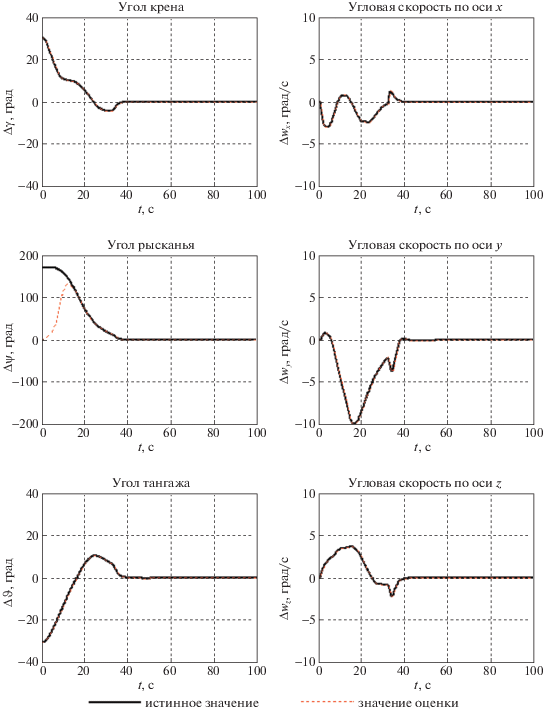
Заключение. В работе с использованием декомпозиционных алгоритмов модального управления и наблюдения осуществлен аналитический синтез регулятора с обратной связью по оценке вектора состояния. Такой подход к решению задачи построения орбитальной ориентации КА позволяет сократить время выполнения режима. Следует заметить, что рассмотренная в статье постановка задачи исследования, вообще говоря, относится к решению проблемы управления при неполной информации. И соответственно данная задача может быть решена в более полном виде с применением подхода, предложенного Фельдбаумом [11 ] , однако получение такого решения в замкнутом виде достаточно проблематично [11 ] .

Кроме того, разработанный авторами декомпозиционный алгоритм модального управления для совместного синтеза регулятора и наблюдателя применяется впервые.

Список литературы

Муртазин Р.Ю. Схемы ускоренного доступа к орбитальной станции для современных космических кораблей // Космич. исслед. 2014. Т. 52. № 2. С. 162–175.
Микрин Е.А., Орловский И.В., Брагазин А.Ф., Усков А.В. Новые возможности автономной системы управления модернизированных кораблей “Союз” и “Прогресс” для реализации быстрой встречи с МКС // Космическая техника и технологии. 2015. № 4. С. 58–67.
Борисенко Н.Ю., Сумароков А.В. Об ускоренном построении орбитальной ориентации грузовых и транспортных кораблей серии “Союз МС” и “Прогресс МС” // Изв. РАН. ТиСУ. 2017. № 5. С. 131–141.
Романенко Л.Г., Романенко А.Г., Самарова Г.Г. Управление продольным движением летательного аппарата при отсутствии в автопилоте сигнала по углу тангажа // Изв. вузов. Авиационная техника. 2014. № 4. С. 25–29.
Зубов Н.Е., Зыбин Е.Ю., Микрин Е.А. и др. Управление по выходу спектром движения космического аппарата // Изв. РАН. ТиСУ. 2014. № 4. С. 111–122.
Зубов Н.Е., Микрин Е.А., Мисриханов М.Ш., Рябченко В.Н. Управление по выходу продольным движением летательного аппарата // Изв. РАН. ТиСУ. 2015. № 5. С. 164–175.
Зубов Н.Е., Микрин Е.А., Мисриханов М.Ш., Рябченко В.Н. Стабилизация взаимосвязанных движений летательного аппарата в каналах тангаж-рысканье при отсутствии информации об угле скольжения // Изв. РАН. ТиСУ. 2015. № 1. С. 95–105.
Зубов Н.Е., Микрин Е.А., Рябченко В.Н., Фомичев А.В. Синтез законов управления боковым движением летательного аппарата при отсутствии информации об угле скольжения. Аналитическое решение // Изв. вузов. Авиационная техника. 2017. № 1. С. 14–20.
Зубов Н.Е., Микрин Е.А., Рябченко В.Н. Матричные методы в теории и практике систем автоматического управления летательных аппаратов. М.: Изд-во МГТУ им. Н.Э. Баумана, 2016. 666 с.
Справочник по теории автоматического управления / Под ред. А.А. Красовского. М.: Наука, 1987. 712 с.
Чаки Ф. Современная теория управления. М.: Мир, 1975. 424 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Теория и системы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал