Известия РАН. Теория и системы управления, 2019, № 6, стр. 163-176

Введение. При движении робота по бездорожью могут возникать разные аварийные ситуации [1]. При отсутствии поломок наиболее катастрофичным представляется случай, когда из-за падения робот оказывается в перевернутой позиции с ногами, ориентированными вверх, и корпусом, лежащим на опорной плоскости. Для многоногого робота с корпусом в виде прямоугольного параллелепипеда [2] обратный переворот корпуса трудновыполним. Возможен спасительный вариант, когда за счет специальной конструкции ног робот может двигаться как в стандартном, так и в перевернутом положении корпуса [3]. Вместе с тем при наличии на борту измерительных устройств, например датчиков, позволяющих осуществлять привязку к местности и к направлению силы тяжести, перевернутое положение корпуса может привести к потере способности робота ориентироваться в пространстве. Чтобы не оказаться беспомощным в аварийной ситуации, робот должен быть снабжен методом, позволяющим вернуть правильную позицию корпуса для возможности его дальнейшего функционирования. Для облегчения задачи переворота корпуса можно воспользоваться резонансными эффектами, которые возникают при определенной форме корпуса за счет специальных движений ног.

Данная статья развивает результаты, представленные в работах [1, 4, 5], в части построения алгоритмов управления поведением робота в экстремальных ситуациях с использованием методов компьютерного экспериментирования. Полная динамическая модель робота формируется автоматически средствами комплекса “Универсальный механизм” [6].

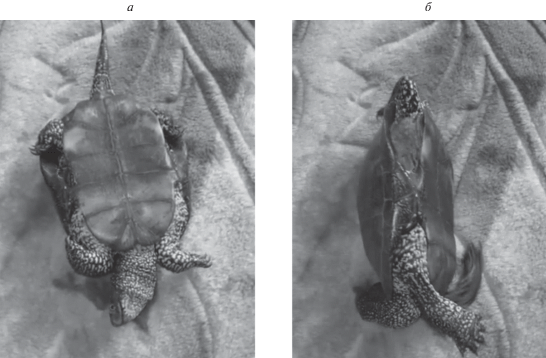
Решаемая задача формулируется следующим образом. В результате непредвиденной случайности шагающий робот оказывается лежащим на спине в положении “вверх ногами”. Он должен без посторонней помощи за счет имеющихся у него ресурсов по управлению перевернуться в исходное рабочее положение, когда ноги находятся в опоре, а корпус – наверху. Подобного рода ситуации нередко встречаются в мире животных и особенно среди насекомых и рептилий, у которых имеется широкий твердый корпус (жуки или черепахи), и все они в процессе эволюции научились преодолевать подобные затруднения. Методы, которые они используют, включают в себя приемы подтягивания и отжимания от опоры [7, 8] (рис. 1, 2).

Ниже предлагается другой метод переворота робота из аварийного в рабочее положение с использованием динамических эффектов, которые возникают, когда робот, будучи в перевернутом положении, начинает без опоры ногами о грунт раскачивать корпус за счет специально сформированного движения ног, обеспечивающего увеличение амплитуды качаний. В результате амплитуда достигает такого значения, что корпус неизбежно переворачивается. Аналогичный прием часто используется любителями качаться на качелях. Очевидно, что в рассматриваемом случае простой периодический закон движения ног не приведет к успеху, так как период качаний корпуса будет зависеть от амплитуды. В статье представлен конструктивно построенный алгоритм решения сформулированной задачи. Этот алгоритм был отработан на программном комплексе “Универсальный механизм” [6] с учетом полной динамики системы в целом, имеющей 24 степени свободы. Представленные результаты компьютерного моделирования свидетельствуют о принципиальной реализуемости предложенного алгоритма управления роботом.

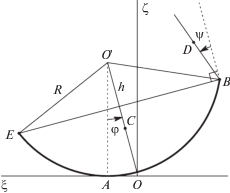
1. Равновесие корпуса в перевернутом положении. Для облегчения процесса переворота корпус шагающего робота в рабочем положении может иметь форму выпуклой вверх части цилиндра, срезанного плоскостью, параллельной оси цилиндра. Рассмотрим следующую модельную задачу. Предположим, что на горизонтальной опорной прямой лежит однородный сегмент круга, имеющий массу M. Сегмент ограничен дугой окружности радиуса $R$ и хордой, отстоящей от центра окружности на расстояние $h$. Дуга окружности сегмента касается опорной прямой в точке A. Сегмент может перекатываться без проскальзывания по опорной прямой, поворачиваясь вокруг центра упомянутой окружности на угол φ, отсчитываемый от вертикального радиуса, направленного в точку $A$ касания сегмента с прямой. Если φ = 0, то сегмент лежит так, что его хорда параллельна опорной прямой (рис. 3).

К правому концу $B$ хорды сегмента плоским шарниром прикреплен стержень (нога) массы m₁, который может вращаться относительно сегмента на угол ψ. Угол $\psi $ отсчитывается от внешнего перпендикуляра к хорде сегмента. Когда $\psi = 0$, стержень направлен перпендикулярно хорде в сторону от опорной прямой. На другом конце хорды в точке E расположена точечная масса m₂, уравновешивающая стержень. Центр масс D стержня расположен на расстоянии $\rho $ от точки B. Центр масс C сегмента расположен на срединном перпендикуляре к хорде на расстоянии r от центра окружности сегмента. Сегмент имеет момент инерции J относительно прямой, проходящей через центр масс сегмента перпендикулярно плоскости сегмента. Момент инерции стержня относительно его центра масс обозначим буквой J_r. Для описания движения воспользуемся системой координат $O\xi \zeta $. Начало O поместим в точку касания сегмента с опорной прямой при φ = 0. Ось $O\xi $ пустим вдоль опорной прямой справа налево. Ось $O\zeta $ направим вертикально вверх. Заметим, что в соответствии с постановкой задачи допустимая величина $\mathop {{\text{tg}}}\nolimits_ \varphi $ ограничена пределами

Для значений $\mathop {{\text{tg}}}\nolimits_ \varphi $, выходящих из диапазона (1.1), следует полагать

Если точка $A$ достигает границы допустимого диапазона, то ее скорость должна стать равной нулю, при этом станет равной нулю скорость точки $E$ либо $B$, и система может испытывать удар. Для простоты исследования, имея в виду изучение вопроса о возможности переворота робота из неудобного положения “вверх ногами”, условие (1.1) принимать во внимание не будем, считая, что вся окружность, частью которой является дуга рассматриваемого сегмента, является твердой, но не имеющей массы.

Найдем координаты указанных характерных точек системы:

где $\alpha = \angle EO{\kern 1pt} 'O$, так что

Центр масс всей механической системы имеет координаты

причем

Пусть декартова система координат $O{\kern 1pt} '\xi {\kern 1pt} '\eta {\kern 1pt} '\zeta {\kern 1pt} '$ жестко связана с сегментом. Ее начало $O{\kern 1pt} '$ совпадает с центром окружности сегмента, ось $O{\kern 1pt} '\xi {\kern 1pt} '$ сонаправлена вектору BE, ось $O{\kern 1pt} '\zeta {\kern 1pt} '$ перпендикулярна оси $O{\kern 1pt} '\xi {\kern 1pt} '$ и ориентирована вверх, ось $O{\kern 1pt} '\eta {\kern 1pt} '$ дополняет систему координат до правоориентированной. Абсолютные координаты центра масс рассматриваемой механической системы можно представить в виде

где суть координаты центра масс механической системы в осях $O{\kern 1pt} '\xi {\kern 1pt} '\eta {\kern 1pt} '\zeta {\kern 1pt} '$.

Рассмотрим сначала равновесие системы в параллельном поле сил тяжести. Согласно формулам (1.4), момент M_a силы тяжести относительно точки A выражается как

Положение равновесия системы достигается там, где ${{M}_{a}} = 0$, т.е. при

Условие (1.7) геометрически соответствует случаю, когда центр масс системы расположен точно над точкой A. Исследуем возможные варианты соотношений параметров системы.

1. Совместно выполнены равенства

Тогда центр масс системы совпадает с центром C опорной окружности. Положение равновесия будет нейтральным и будет иметь место при любом значении угла φ. Как следует из формул (1.5), нейтральное положение равновесия обеспечивается, если

При этом должно быть выполнено условие согласования: ${{\sin }^{2}}\psi + {{\cos }^{2}}\psi = 1$ или

Это условие практически трудновыполнимо. Кроме того, для возможности переворота системы в положении нейтрального равновесия необходимо обеспечить ей некоторый начальный толчок в положительном направлении оси Oξ, что может оказаться невозможным.

2. Выполнены условия

В этом случае центр масс системы расположен справа от линии $O{\kern 1pt} 'C$ (рис. 3) и выше оси $O{\kern 1pt} '\xi {\kern 1pt} '$ или на этой оси. В пределах одного оборота устойчивое положение равновесия будет соответствовать углу $ - \pi < \varphi \leqslant - \pi {\text{/}}2$, а неустойчивое положение равновесия возникает при $0 < \varphi \leqslant \pi {\text{/}}2$. В рассматриваемом случае положение аппарата “вверх ногами” окажется неустойчивым, и под действием силы тяжести он должен перевернуться в устойчивое положение. При этом угол поворота будет отрицательным. В результате поворота точка B окажется ниже точки E, что будет создавать трудности на завершающих этапах маневрирования с целью приведения корпуса в стандартное положение.

3. Выполнены условия

Следовательно, центр масс системы расположен слева от линии $O{\kern 1pt} 'C$ (рис. 3) и выше оси $O{\kern 1pt} '\xi {\kern 1pt} '$ или на этой оси. В пределах одного оборота устойчивое положение равновесия будет соответствовать углу $\pi {\text{/}}2 \leqslant \varphi < \pi $, а неустойчивое положение равновесия возникает при $ - \pi {\text{/}}2 < \varphi \leqslant 0$. Так же, как и в случае 2, аппарат должен перевернуться, но теперь угол поворота окажется положительным, а после переворота точка E окажется ниже точки B. Такой вариант благоприятен для перехода в правильное положение корпуса, так как нога, прикрепленная в точке B, сможет опереться стопой об опорную плоскость. Параметры системы в этом случае должны удовлетворять ограничениям

Эти ограничения можно выполнить при достаточно большой величине ρ и соответствующем угле $\psi $.

2. Раскачивание корпуса робота на спине. Для исследования динамических эффектов при плоскопараллельном движении корпуса и ног, приводящих к увеличению амплитуды колебаний при раскачивании корпуса в аварийной ситуации, предположим, что параметры системы таковы, что перевернутое положение робота оказалось устойчивым при любых значениях угла ψ. Тогда можно попытаться обеспечить переворот робота в нормальное положение посредством циклического изменения угла $\psi $, вызвав тем самым колебания корпуса с увеличивающейся амплитудой. Аналитическое описание процесса раскачивания выполним с помощью теоремы об изменении кинетического момента системы относительно подвижной точки A ([9, с. 409]).

Для того чтобы найти кинетический момент K_A относительно точки A, необходимо знать координаты векторов ${\mathbf{AB}}$, ${\mathbf{AC}}$, ${\mathbf{AD}}$, ${\mathbf{AE}}$:

и координаты абсолютных скоростей точек C, $D$ и $E$:

Обозначим $A{{B}_{r}} = A{{B}_{\xi }}\sin (\varphi + \psi ) + A{{B}_{\zeta }}\cos (\varphi + \psi )$. Тогда кинетический момент K_A имеет вид

где

Следовательно,

где а $\xi _{{cm}}^{'}$, $\zeta _{{cm}}^{'}$ определены формулами (1.5).

Вектор Q количества движения системы имеет координаты

Проекция уравнения изменения кинетического момента относительно подвижной точки A на ось $O\eta $ имеет вид [9]

или, воспользовавшись формулой (2.3), получим

В уравнении (2.6) функцию $\psi (t)$ будем рассматривать как управляющую, изменение которой будет приводить к изменению угла φ, вызывая раскачивание системы в целом. Для простоты исследуем случай кусочно-постоянного управления, мгновенное изменение которого будет происходить в специально подобранные моменты времени с целью достижения переворота корпуса в нормальное положение. Рассмотрим движение при $\ddot {\psi } = \dot {\psi } = 0$. Тогда уравнение (2.6) примет вид

где

В уравнении (2.7) перейдем на участке монотонности функции φ(t) к независимой переменной φ:

Решение уравнения (2.8) имеет вид

Функция $\tau (\varphi )$ имеет вид

В том случае, когда величина ψ постоянна, получим

Отсюда находим уравнение фазовой траектории

Размах колебаний ${{\varphi }_{m}}$ по углу φ соответствует значениям $\dot {\varphi } = 0$. Пусть ${{\dot {\varphi }}_{0}} = 0$. Тогда для определения угла ${{\varphi }_{m}}$ имеем уравнение

или где угол β определен формулами так что угол β отсчитывается от положительного направления оси $O{\kern 1pt} '{\kern 1pt} \zeta {\kern 1pt} '$. В пределах одного оборота уравнение (2.11) имеет два решения. Одно из них, естественно, совпадает с ${{\varphi }_{0}}$, а второе равно

Таким образом, если при движении от значения $\varphi = {{\varphi }_{0}} > 0$ до значения $\varphi = {{\varphi }_{m}}$ принять $\beta = {{\beta }_{1}}$, а при обратном движении от значения $\varphi = {{\varphi }_{m}}$ принять $\beta = {{\beta }_{2}}$, то новое начальное значение угла $\varphi = \varphi _{0}^{{(1)}}$ выразится формулой

и если выбрать ${{\beta }_{1}} - {{\beta }_{2}} > 0$, то окажется $\varphi _{0}^{{(1)}} > {{\varphi }_{0}}$. Указанную процедуру можно повторить n раз. Тогда получим т.е. амплитуда колебаний будет увеличиваться по закону арифметической прогрессии, и со временем неизбежно произойдет переворот системы либо через точку E, либо через точку B.

Представленный выше метод можно назвать “методом амплитудного раскачивания”, так как при его реализации переключение управляющей функции должно происходить в моменты достижения максимального и минимального углов отклонения системы от положения равновесия. Временные интервалы между моментами переключения могут не сохраняться и в большинстве случаев будут расти по мере увеличения амплитуды. Для осуществления этого метода необходимо иметь на борту сенсорную систему, позволяющую с необходимой точностью определять моменты достижения максимального размаха.

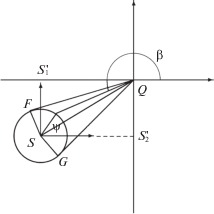
С помощью формул (1.5) и (2.12) найдем зависимость $\beta (\psi )$:

где $S_{1}^{'} = - {{S}_{1}}{\text{/}}({{m}_{1}}\rho )$, $S_{2}^{'} = - {{S}_{2}}{\text{/}}({{m}_{1}}\rho )$. Геометрически формулы (2.15) интерпретируются следующим образом.

Введем вспомогательную координатную плоскость (рис. 4), на которой по оси абсцисс будем откладывать значения $S_{1}^{'}$, а по оси ординат – значения $S_{2}^{'}$. Будем считать, что ${{m}_{1}} \geqslant {{m}_{2}}$. Тогда $S_{1}^{'} < 0$, $S_{2}^{'} \leqslant 0$, что соответствует изображению на рисунке.

В соответствии с формулами (2.15) найдем

где угол γ отсчитывается от положительного направления оси абсцисc и определен формулами

По существу γ есть угол между положительным направлением оси абсцисс и радиус-вектором QS на рис. 4. Из рисунка видно, что в регулярном случае имеем $\gamma \geqslant \pi $. Из формулы (2.16) следует, что когда $\sqrt {{{{(S_{1}^{'})}}^{2}} + {{{(S_{2}^{'})}}^{2}}} > 1$, зависимость $\beta (\psi )$ немонотонна. При $\sqrt {{{{(S_{1}^{'})}}^{2}} + {{{(S_{2}^{'})}}^{2}}} \leqslant 1$ функция $\beta (\psi )$ монотонно возрастает. Исследуем каждый из вариантов.

Вариант 1. Пусть $\sqrt {{{{(S_{1}^{'})}}^{2}} + {{{(S_{2}^{'})}}^{2}}} > 1$. Тогда на рис. 4 круг единичного радиуса с центром в точке S не содержит начало координат Q. Перемена знака производной $d\beta {\text{/}}d\psi $ происходит при значениях угла $\psi $, удовлетворяющих уравнению

Обозначим через

угол между касательной к окружности из точки Q и прямой QS. Подходящие корни уравнения (2.18)соответствуют точкам $G$ и $F$ на рис. 4, принадлежащим касательным к окружности, проведенным из начала координат. Отметим, что в рассматриваемом случае ${{\psi }_{2}} - {{\psi }_{1}} = \pi - 2\chi \geqslant 0$. В диапазоне ${{\psi }_{1}} \leqslant \psi \leqslant {{\psi }_{2}}$ имеем $d\beta {\text{/}}d\psi \leqslant 0$, так что функция $\beta (\psi )$ убывает, а при ${{\psi }_{2}} < \psi < {{\psi }_{1}} + 2\pi $ функция $\beta (\psi )$ возрастает. При этом по конструктивным соображениям должно быть

Рассмотрим практически интересные случаи пересечения рабочей области изменения угла $\psi $ и зон монотонности функции $\beta (\psi )$.

Случай 1: $\pi - \chi \leqslant \gamma \leqslant \pi + \chi $. Тогда $ - \pi {\text{/}}2 \leqslant {{\psi }_{1}} \leqslant 0$ и $0 < {{\psi }_{2}} \leqslant \pi {\text{/}}2$. Следовательно, в диапазоне $ - \pi {\text{/}}2 \leqslant \psi < {{\psi }_{1}}$ функция $\beta (\psi )$ возрастает, далее при ${{\psi }_{1}} \leqslant \psi \leqslant {{\psi }_{2}}$ она убывает, а при ${{\psi }_{2}} < \psi \leqslant \pi {\text{/}}2$ она снова возрастает.

Случай 2: $\pi + \chi \leqslant \gamma \leqslant 3\pi {\text{/}}2 - \chi $. Тогда находим $ - \pi {\text{/}}2 \leqslant {{\psi }_{1}} \leqslant 0$ и ${{\psi }_{2}} \geqslant \pi {\text{/}}2$. Поэтому в диапазоне $ - \pi {\text{/}}2 \leqslant \psi < {{\psi }_{1}}$ функция $\beta (\psi )$ возрастает, а при ${{\psi }_{2}} \leqslant \psi \leqslant \pi {\text{/}}2$ она убывает.

Случай 3: $3\pi {\text{/}}2 - \chi < \gamma \leqslant 3\pi {\text{/}}2 + \chi $. Здесь по-прежнему ${{\psi }_{2}} \geqslant \pi {\text{/}}2$, а $0 \leqslant {{\psi }_{1}} \leqslant \pi {\text{/}}2$. Так же, как и в случае 2, в диапазоне $ - \pi {\text{/}}2 \leqslant \psi < {{\psi }_{1}}$ функция $\beta (\psi )$ возрастает, а при ${{\psi }_{2}} \leqslant \psi \leqslant \pi {\text{/}}2$ она убывает. Но при этом диапазон возрастания этой функции оказывается больше, чем диапазон убывания.

Вариант 2. Пусть $\sqrt {{{{(S_{1}^{'})}}^{2}} + {{{(S_{2}^{'})}}^{2}}} = 1$. Производная $d\beta {\text{/}}d\psi > 0$ для всех значений $\psi \ne \gamma - \pi $ в пределах одного оборота. Для $\psi = \gamma - \pi $ ни производная, ни сама функция $\beta (\psi )$ не определены. Это естественно, так как на рис. 4 при $\psi = \gamma - \pi $ единичная окружность проходит через начало координат Q. В диапазоне $ - \pi {\text{/}}2 \leqslant \psi \leqslant \pi {\text{/}}2$ для раскачивания можно выбирать любые значения ${{\bar {\psi }}_{1}} > {{\bar {\psi }}_{2}}$, кроме $\psi = \gamma - \pi $, и тогда будет выполнено $\beta ({{\bar {\psi }}_{1}}) > \beta ({{\bar {\psi }}_{2}})$.

Вариант 3. Пусть $\sqrt {{{{(S_{1}^{'})}}^{2}} + {{{(S_{2}^{'})}}^{2}}} < 1$. Это значит, что точка Q лежит строго внутри единичного круга на рис. 4. Производная $d\beta {\text{/}}d\psi $ нигде не обращается в нуль и остается положительной. Поэтому функция $\beta (\psi )$ монотонно возрастает и метод раскачивания не имеет никаких особенностей.

Представляется, что в общем случае наиболее употребительным будет вариант 1, случай 2, так как следует ожидать, что масса корпуса с нагрузкой будет превышать суммарную массу ног, а разность ${{m}_{1}} - {{m}_{2}}$ будет невелика. Вместе с тем, возможно, что робот сможет воспользоваться для раскачивания корпуса какими-нибудь местными предметами и тогда полезными могут оказаться и другие рассмотренные варианты.

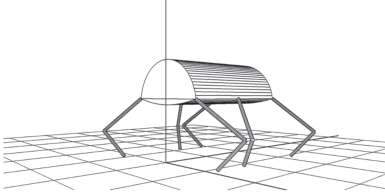
3. Механическая модель робота. Конструкция робота принципиально совпадает с принятой в [1, 10]. Твердый корпус робота имеет форму сложенных по общему прямоугольному плоскому пересечению двух усеченных прямых круговых цилиндров, $a$ – длина плоского пересечения, $b$ – его ширина (рис. 5). Радиус основания цилиндра, соответствующего спине робота, равен $R$, радиус основания цилиндра, соответствующего брюху робота, равен r. Корпус имеет массу m. По бокам плоского пересечения симметрично прикреплены шесть одинаковых двухзвенных ног. Точки прикрепления ног с каждой стороны корпуса расположены на одинаковом расстоянии друг от друга. Отдельная нога состоит из двух твердых звеньев: бедра длины l₁, массы m₁ и голени длины l₂, массы m₂. В отличие от [1, 10] допускается касание поверхности опоры и окружающих предметов любой частью корпуса и стопами ног. Ноги робота не должны иметь взаимных пересечений во все время движения.

Стандартно траектории переносов ног формируются в виде плоских шаговых циклов [1, 2], адаптируемых в зависимости от поверхностей препятствий, скорости движения робота, предписанных следовых точек. Движения ног, соответствующие шаговым циклам, сглаживаются, чтобы сохранить непрерывность как самого движения, так и его скорости [1]. В аварийных ситуациях допускается формирование движений ног непосредственно с помощью их угловых координат.

Предполагается, что роботу известны: собственное положение относительно препятствий и опорной поверхности, несущая способность участков поверхности, выбираемых для опоры, реализовавшиеся шарнирные углы и скорости перемещения как самого робота, так и объектов, выбираемых для опоры. Программные значения шарнирных углов генерируются алгоритмом управления с учетом информации о текущем положении окружающих объектов и о реализовавшейся конфигурации робота при его движении. Реализация программных значений шарнирных углов осуществляется так же, как в [1, 4].

Наличие силового момента в опорных точках не предполагается [2]. Реакции в них должны удовлетворять условию малой деформации опорной поверхности и принадлежать конусам кулоновского трения с заданным коэффициентом [1]. Если требуемая реакция выходит за пределы конуса трения, то возникает проскальзывание. Коэффициент трения предполагается равным единице. Программное движение создается в виде последовательности событий, в начале каждого из которых формируется необходимое движение ног относительно корпуса.

Для первоначальной отработки принципа спасения робота из аварийной ситуации принято, что опорная поверхность представляет собой ровную шероховатую горизонтальную плоскость.

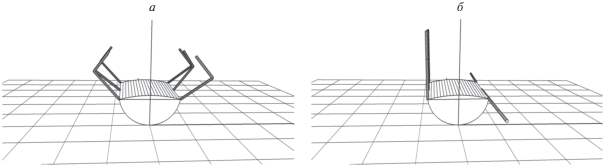
4. Действия робота в аварийной ситуации. Решаемая задача формулируется следующим образом. Пусть в результате несчастного случая робот перевернулся и оказался в позиции, когда он лежит спиной на ровной горизонтальной опорной плоскости ногами вверх (рис. 6, а). Ему необходимо выбрать боковой край корпуса, через который будет выполняться переворот так, чтобы спина оказалась наверху. Спасательные мероприятия происходят в соответствии с перечисленными ниже этапами.

Этап 1. Ноги, точки крепления которых расположены на выбранном для переворота краю, будут пассивны. Их необходимо выпрямить и сложить так, чтобы они, по возможности, не мешали перевороту. Например, переднюю ногу можно направить вперед вдоль корпуса, заднюю – назад вдоль корпуса, а среднюю ногу пустить вперед вдоль корпуса так, чтобы она была прижата к корпусу и примыкала к точке крепления передней ноги (рис. 6, б).

Этап 2. Ноги, которые остались выпрямленными, будут активны. Они начинают раскачивание корпуса путем непосредственного управления их шарнирными углами. При этом все три ноги осуществляют синхронное движение в плоскости, перпендикулярной продольной оси корпуса, при фиксированном угле в колене. Меняются для них только углы ${{\beta }_{i}} \equiv \psi $ между бедром ноги и корпусом. Для более интенсивного раскачивания целесообразно коленный угол всех активных ног максимально развернуть, по возможности приблизив его значение к π. Угол отклонения активных ног от корпуса робота не должен превышать значений π/2. Если это ограничение нарушается, то при больших амплитудах качания корпуса активные ноги, ударяясь об опорную плоскость, могут мешать увеличению амплитуды раскачивания корпуса. Для достижения неограниченного раскачивания корпуса принять периодическую функцию $\psi (t)$ невозможно, так как период колебаний корпуса будет зависеть от амплитуды. Применим метод, изложенный в разд. 3. Обозначим через $\{ t_{j}^{ + },\;j = 1,2,...\} $ последовательность моментов времени, для которых высота точек подвеса пассивных ног над опорной плоскостью минимальна. Пусть также $\{ t_{j}^{ - },\;j = 1,2,...\} $ есть последовательность моментов времени, для которых минимальна высота точек подвеса активных ног при раскачивании. Примем, что индекс j соответствует одному полуциклу колебаний и $t_{j}^{ - } < t_{j}^{ + } < t_{{j + 1}}^{ - }$. Пусть ${{\psi }_{M}}$ – значение угла ψ, при котором активные ноги окажутся наиболее близкими к точкам подвеса пассивных ног, и ${{\psi }_{m}}$ – значение ψ, соответствующее наибольшему допустимому удалению активных ног от точек подвеса пассивных ног при формируемом движении активных ног. Программная зависимость $\psi (t)$ для полного цикла колебаний имеет вид

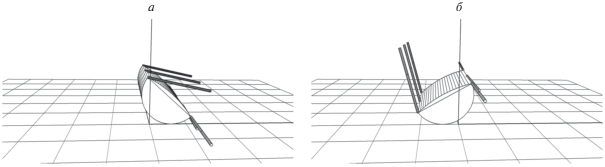
Здесь ${{\psi }_{j}}$ есть то значение угла ψ, которое реализовалось к моменту времени $t_{j}^{ - }$. В частности, если j = 0, то тогда ${{\psi }_{0}}$ равно значению угла ψ, реализовавшемуся к моменту ${{t}_{0}}$ начала раскачивания. Таким образом, раскачивание начинается с перевода активных ног в ближайшее положение к точкам подвеса пассивных ног (рис. 7, а). При этом корпус наклоняется в сторону пассивных ног. Далее угол $\psi $ достигает значения $\psi = {{\psi }_{m}}$, а корпус отклоняется в сторону точек подвеса активных ног (рис. 7, б) (отмашка) и т.д. Величина $\Delta t$ задает интервал времени переходного процесса от одного постоянного значения ψ до другого. Эта величина должна быть меньше времени одного полуцикла. Раскачивание происходит до того момента, когда корпус перевернется вокруг бокового ребра корпуса, соответствующего точкам крепления пассивных ног. Перевернуться вокруг ребра, содержащего точки подвеса активных ног, корпус не может, так как увеличение амплитуды происходит в основном на полуцикле с $\psi = {{\psi }_{M}}$. Заметим, кроме того, что для реализации подобного раскачивания система управления должна иметь возможность достаточно грубо регистрировать моменты достижения амплитудных значений угла поворота корпуса.

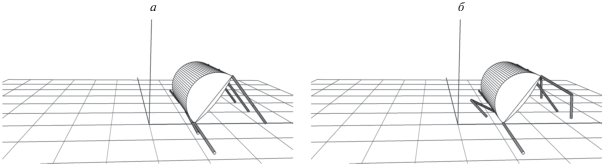
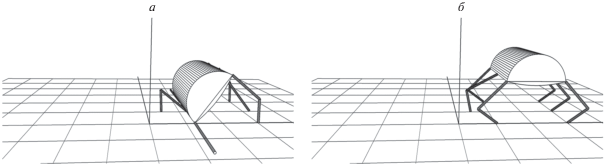
Этап 3. После переворота корпуса робот упрется активными ногами в опорную плоскость (рис. 8, а), и ему необходимо будет встать на ноги. В этой позиции он может переставить тройку ног, в которой передняя и задняя ноги берутся с активной стороны, а средняя нога – с пассивной (рис. 8, б; 9, а). С помощью указанной тройки ног происходит выравнивание корпуса в правильную позицию, и одновременно стопы другой тройки ног переносятся в предписанные точки опоры (рис. 9, б). После этого происходит окончательное выравнивание корпуса и ног в стандартную позицию.

5. Компьютерное моделирование. Компьютерное моделирование осуществлялось аналогично тому, как это было описано в [1, 4]. Управление роботом, закон взаимодействия корпуса и стоп ног с опорой реализованы в виде DLL-библиотеки, подключенной к программному комплексу “Универсальный механизм” [6]. Тем самым создается виртуальная среда обитания робота. Неподвижная опорная поверхность в ней представлена горизонтальной плоскостью. Опорная плоскость, корпус и ноги робота взаимодействуют друг с другом согласно модели трения, основанной на вязкоупругом взаимодействии тел в точках контакта. Управление движением реализуется посредством компьютерного моделирования работы электромеханических приводов шарнирных углов. Выполнение требуемого движения робота осуществляется, как и в реальности, лишь в результате подачи значения управляющего электрического напряжения на модели электромеханических приводов. Соотношение размеров корпуса и звеньев ног имеет вид

Массы корпуса робота и звеньев ног относятся как

Представление о движении корпуса робота и его ног возникает в результате численного интегрирования дифференциальных уравнений полной трехмерной динамики робота. Поскольку в точках контакта объектов предполагается силовое взаимодействие, соответствующая механическая система имеет 24 степени свободы. Уравнения динамики синтезируются автоматически [6]. Результаты компьютерного моделирования отображаются на экране монитора в виде движения геометрических образов исследуемых материальных объектов.

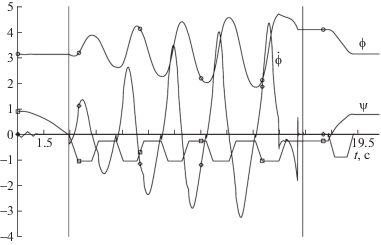
На рис. 10 представлены графики изменения по времени углов $\phi $, $\psi $, а также угловой скорости $\dot {\phi }$. Знаком “$ \circ $” помечена зависимость $\phi (t)$, знаком “$\diamondsuit $” – функция $\dot {\phi }(t)$, а знаком “$\square $” – зависимость $\psi (t)$. Углы даны в радианах. Угол ϕ между строительной вертикалью корпуса и вертикальной осью Oζ в аварийном положении корпуса равен π. Процесс раскачивания происходит в интервале времени, расположенном на рисунке между вертикальными линиями. Видно, что амплитуда колебаний увеличивается монотонно. При этом отклонения угла ϕ несимметричны относительно значения π, поскольку равновесное положение корпуса смещено в сторону пассивных ног. В конце раскачивания происходит переворот корпуса через боковую сторону с точками подвеса пассивных ног. Пассивные ноги, имея конечные размеры, несколько мешают перевороту. Поэтому в конце процесса переворачивания наблюдается нерегулярность. На графике угловой скорости $\dot {\phi }$ видны небольшие скачки, вызванные скачкообразным изменением задаваемой скорости изменения активных ног (см. формулу (4.1)). До начала раскачивания осуществляется подготовка: активные ноги приводятся в выпрямленное вертикальное положение, а пассивные ноги складываются вдоль корпуса. На графике отражены соответствующие кривые и угол $\psi $, отвечающий средней активной ноге. После окончания переворота происходят события этапа 3.

Заключение. Представлено решение новой задачи о спасении автономного инсектоморфного робота, аварийно лежащего на горизонтальной опорной плоскости на спине в положении “вверх ногами”. Для возможности спасения робота предложена специальная форма корпуса в виде сложенных по плоскому сечению двух усеченных прямых круговых цилиндров. Разработан и аналитически обоснован метод амплитудного раскачивания системы в окрестности положения аварийного равновесия, позволяющий использовать кинематические и динамические возможности шагающего робота для самостоятельного спасения. Синтезировано устойчивое резонансное движение системы, обеспечивающее переворот корпуса робота и приведение робота в нормальное рабочее положение.

Предложенные алгоритмы формирования движения робота при спасении из аварийной ситуации были отработаны средствами компьютерного моделирования в программной среде, реализующей расчет взаимодействия трехмерной полной динамической модели механической системы, состоящей из робота, взаимодействующего с горизонтальной опорной плоскостью. В результате аналитического исследования адекватной упрощенной динамической модели системы установлены ограничения на возможность применения разработанного метода, связанные с геометрическими и массовыми характеристиками конструкции робота.

Стабилизация движения робота в окрестности программного движения построена по принципу кусочно-формируемой с дискретностью шага интегрирования обратной связи. Обратная связь рассчитывается по рассогласованиям реальных и программных шарнирных углов с требованием минимальных значений угловых скоростей. Возникающие в шарнирных углах переходные процессы не разрушают требуемое программное движение корпуса робота на всех этапах движения системы.