Известия РАН. Теория и системы управления, 2019, № 6, стр. 103-118

Введение. Эффективным средством дистанционного зондирования являются лазерно-локационные (ЛЛ) системы [1, 2]. Они представляют собой результат естественного слияния технологий радиолокационных и оптико-электронных датчиков и сочетают в себе радиолокационные методы обработки и анализа сигналов с оптическими методами формирования изображений. В зависимости от назначения и конструкции ЛЛ-системы могут обеспечивать при зондировании измерение дальности, скорости, степени деполяризации излучения и т.д. При этом достоверность измерений вероятностным образом связана с отношением сигнал/шум в тракте детектирования отраженного сигнала, которое также может быть измерено известными в радиолокации методами [3].

Особенности формируемой ЛЛ-информации обеспечивают возможность автоматической обработки при решении ряда задач в различных областях применения. С точки зрения систем технического зрения наибольший интерес представляют ЛЛ-датчики, формирующие дальностные 3-D-изображения. В перспективе роботизированные системы на основе информации, формируемой ЛЛ-датчиками, смогут анализировать наблюдаемые сцены, ориентироваться и перемещаться, распознавать образы объектов, принимать решения и т.д. Необходимым этапом обработки изображений для решения задач автоматического распознавания образов и анализа сцен является сегментация [4–9]. Сегментация – это разбиение изображения на непересекающиеся однородные по некоторому признаку области, которые имеют смысловую суть. Как правило, предполагается, что области соответствуют образам объектов или их частям, а границы областей – границам образов объектов. Сегментация изображения является первым шагом на пути автоматического анализа и “понимания” изображения. В частности, если говорить о дальностном ЛЛ-изображении, то сегментация является инструментом построения объемной модели сцены в виде совокупности фрагментов простейших поверхностей (плоскости, цилиндры, сферы, конуса и пр.). Сегментация позволяет перейти от дальностного ЛЛ-изображения (от совокупности не связанных между собой пространственно разнесенных замеров дальности) к геометрической модели сцены в виде совокупности непересекающихся областей с геометрически связанными между собой замерами дальности в пределах каждой области, т.е. к семантическому описанию форм на наблюдаемой сцене.

Семантическая сегментация относится к группе задач обработки изображений прикладного или слабого искусственного интеллекта. При этом в случае сегментации изображений сформированными пассивными датчиками, формализовать критерий качества результатов сегментации, как правило, затруднительно. При сегментации дальностных ЛЛ-изображений критерий качества сегментации формализуем, поскольку появляется возможность математическими методами анализировать форму зондируемой поверхности. Поэтому результативность сегментации ЛЛ-изображений может быть значительно выше, чем сегментации изображений, сформированных пассивными датчиками, которые содержат только косвенные признаки форм объектов (яркость, контраст, текстура и т.п.). Однако в настоящее время методы для сегментации ЛЛ-изображений развиты значительно слабее, чем для телевизионных (ТВ) и тепловизионных (ТП) изображений.

В [10] был предложен, а в [11–13] развит метод выделения плоских поверхностей при сегментации доплеровских и дальностных ЛЛ-изображений. Метод состоит из двух этапов: поиска и последующего наращивания областей, содержащих признаки плоских поверхностей. Поиск плоскостей базируется на аппроксимации фрагмента сцены, попадающего в “скользящее окно”, методом наименьших квадратов исходя из гипотезы, что это фрагмент плоскости, и применении критерия согласия, основанного на распределении χ-квадрат, для принятия решения о верности данной гипотезы. Наращивание областей осуществляется итерационно с помощью критерия максимума апостериорной вероятности и использования марковской модели ЛЛ-изображения. Метод показал высокую эффективность при обработке реальных ЛЛ-изображений.

В настоящее время актуальными являются исследования, направленные на увеличение количества идентифицируемых поверхностей объектов по ЛЛ-изображениям, в частности поверхностей второго порядка (цилиндров, сфер, конусов и т.д.). В данной работе предложен метод и разработаны алгоритмы для выделения на ЛЛ-изображениях фрагментов цилиндрических и сферических поверхностей (труб, градирен, цистерн, нефтехранилищ, водонапорных башен и т.п.) с оценкой их координат и параметров.

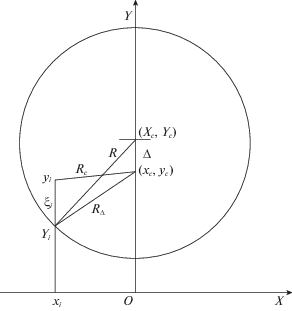
1. Постановка задачи. ЛЛ-система зондирует сцену под настильными углами, формируя растровое дальностное изображение, на которой расположен цилиндрический объект радиуса R с известной ориентацией оси. Центр объекта удален от ЛЛ-системы на расстояние D_c. Будем полагать, что ${{D}_{c}} \gg R$, зондирование производится в малом телесном угле и измерения дальности преобразованы из центральной проекции в Декартову систему координат (СК) OXYZ, начало которой совмещено с ЛЛ-системой, а ось OZ параллельна оси цилиндра (ось OY направлена на объект, ось OX перпендикулярна плоскости OYZ). Без потери общности для краткости будем предполагать, что ось цилиндра вертикальна, а ось OZ направлена вверх. Зондирования производятся только по наблюдаемой части цилиндрического объекта. В соответствии с [3] ошибки измерения дальности ξ имеют нормальное распределение с нулевым математическим ожиданием, а среднее квадратическое отклонение (СКО) оценок времени приема отраженного сигнала τ_с и дальности по i-му измерению определяются выражениями

где τ_с – длительность импульса; С – скорость света; q_i – отношение сигнал/шум. Причем $q_{i}^{2}$ = = S/N. Здесь S – энергия принимаемого сигнала; N – спектральная плотность мощности шума. В силу ${{D}_{c}} \gg R$ будем считать, что направления зондирования коллинеарны оси Y. Рассмотрим случай, когда эффективная ширина диаграммы направленности лазерного луча на местности относительно невелика, что характерно для лазерных локаторов с углом расходимости лазерного излучения менее 1 угл. мин на расстояниях 1–2 км. При этом СКО центра отражения от оси диаграммы направленности составляет единицы сантиметров, что существенно меньше СКО ошибок измерения дальности до отражающей поверхности. Поэтому в дальнейшем будем учитывать только ошибки измерения дальности.

Рассмотрим проекцию цилиндрической поверхности, ее оси, точек зондирования и измерений на горизонтальную плоскость (рис. 1). Примем гипотезу равноточности измерений дальности до всех точек цилиндрической поверхности. Направление зондирования совпадает с осью OY. Очевидно, что координаты точек зондирования X_i,Y_i, i = $\overline {1,n} $, расположены на дуге окружности с центром, имеющим координаты X_с,Y_с в соответствии с выражением:

Измеряются координаты точек зондирования x_i = X_i, y_i = Y_i + ξ_i c СКО σ_ξ. Таким образом, i-м измерением в СК (XOY) является вектор (x_i, y_i), возникающий при координатах точки зондирования X_i, Y_i.

2. Определение радиуса и координат оси цилиндрической поверхности. Рассмотрим результат однократного (i-го) зондирования цилиндрической поверхности как косвенное измерение r_i радиуса R цилиндрической поверхности, имеющей координаты оси X_c, Y_c на горизонтальной плоскости.

Отметим, что решение задачи оценки данных координат при традиционном способе оценки близости измерений к дуге окружности, т.е. путем расчета суммы квадратов отклонений самих косвенных измерений r_i от оценки радиуса, приводит к появлению системы нелинейных уравнений, не имеющей аналитического решения. Поэтому при каждом зондировании будем оценивать косвенные измерения квадрата радиуса $r_{i}^{2}$ вместо r_i. При координатах точки зондирования X_i,Y_i прямое измерение производится с ошибкой ξ_i, т.е. x_i = X_i, y_i = Y_i + ξ_i . Тогда косвенное измерение (r_i)² квадрата радиуса R² имеет вид

Будем рассматривать i-е косвенное измерение (r_i)² квадрата радиуса как реализацию случайной величины r². Учитывая (1.2), легко показать, что математическое ожидание случайной величины r² при известных координатах X_с, Y_с определяется выражением

где D_ξ – дисперсия ошибки ξ.

После очевидных преобразований можно получить выражение для дисперсии косвенного измерения квадрата радиуса в виде

Из (2.3) следует, что даже если принята гипотеза равноточности измерений дальности до всех точек цилиндрической поверхности, косвенные измерения квадрата радиуса не являются равноточными, поскольку зависят от Y_i и неизвестной величины Y_c. Это, вообще говоря, не позволяет для оценки квадрата радиуса использовать среднее арифметическое его измерений в различных точках зондирования. Однако, учитывая простоту вычисления среднего арифметического, целесообразно его использовать для оценки математического ожидания вспомогательной величины $R_{c}^{2}$, с помощью которой можно рассчитать искомую оценку радиуса R на основе процедуры, описанной ниже.

При известных координатах оси цилиндра (т.е. при рассмотрении их в качестве оптимизируемых параметров) выражение для оценки дисперсии случайной величины r² можно использовать в качестве меры близости измерений x_i, y_i, i = $\overline {1,n} $, к дуге окружности:

где

Для оценки координат центра окружности X_c, Y_c определим оптимальные значения параметров x_c, y_c, минимизируя выражение (2.4), т.е. приравняем к нулю частные производные по x_c и y_c:

и решим получившуюся систему уравнений.

После преобразований выражение $\frac{{\partial Q}}{{\partial {{x}_{c}}}}$ примет вид

здесь $\bar {x} = \frac{1}{n}\sum\limits_{i = 1}^n {{{x}_{i}}} $, $\bar {y} = \frac{1}{n}\sum\limits_{i = 1}^n {{{y}_{i}}} $.

Аналогичные преобразования можно провести для $\frac{{\partial Q}}{{\partial {{y}_{c}}}}$. Приравняв к нулю частные производные, можно получить следующую систему линейных уравнений:

где

Решение такой системы позволяет найти аналитические выражения для оценки координат центра дуги окружности в виде

где Δ₁ = b₁a₂₂ – b₂a₁₂, Δ₂ = b₂a₁₁ – b₁a₂₁, Δ = a₁₁a₂₂ – a₂₁a₁₂.

Можно показать, что полученная оценка положения центра окружности является смещенной. Однако величину смещения центра в свою очередь можно оценить. Чтобы получить аналитически оценки смещения центра окружности в условиях наличия ошибок измерения, рассмотрим асимптотический случай, когда количество измерений n → ∞. При этом в соответствии с законом больших чисел оценки математического ожидания и дисперсии оцениваемых величин, полученные по выборке измерений, приближаются по вероятности к соответствующим истинным статистическим характеристикам.

Без потери общности будем считать, что ось OY проходит через центр окружности. В выборке измерений (x₁, …, x_n, …, y₁, … ,y_n, …) при n → ∞ будем рассматривать координату x_i как реализацию случайной величины x, равномерно распределенной в диапазоне [–R, R], где R – радиус окружности (общий случай, когда наблюдается или зондируется лишь часть дуги, будет рассмотрен далее). Величина y_i в соответствии с принятым нормальным законом распределения может быть выражена как y_i = Y_i + ξ_i, где Y_i – координаты точки зондирования, лежащей на окружности при i-м измерении, ξ – нормально распределенная случайная ошибка с характеристиками M(ξ(x)) = 0, $D(\xi (x)) = \sigma _{\xi }^{2}$ для ∀x; Y_i определяется очевидным геометрическим соотношением Y_i = = ${{D}_{c}} - \sqrt {R_{{}}^{2} - x_{i}^{2}} $, где D_c – дальность до центра окружности, отсчитываемая вдоль оси OY.

Допустим, что оценка положения центра окружности сделана с некоторой ошибкой, и предполагаемый центр смещен по оси OY относительно истинного на некоторую величину Δ (рис. 2). В силу симметрии смещение по оси OX стремится к нулю при увеличении количества измерений.

Обозначим через R_c отрезок, связывающий полученное измерение (x_i, y_i) с найденным смещенным центром окружности. Введем отрезок R_Δ, связывающий точку зондирования Y_i, т.е. точку, находящуюся на рассматриваемой окружности с координатами (x_i, Y_i), со смещенным центром (x_c, y_c) с координатами (X_c, Y_c – Δ). Выразим R_c через значение R, измерение (x_i, y_i), величины смещения Δ и ошибки измерения ξ_i. Для i-го измерения имеют место следующие соотношения:

где ${{R}_{\Delta }} = \sqrt {{{{(\sqrt {R_{{}}^{2} - x_{i}^{2}} - \Delta )}}^{2}} + x_{i}^{2}} = \sqrt {R_{{}}^{2} - 2\Delta \sqrt {R_{{}}^{2} - x_{i}^{2}} + {{\Delta }^{2}}} .$

Используя всю выборку измерений, оценим математическое ожидание и дисперсию величины $R_{c}^{2}$ для некоторого значения Δ на основе полученных соотношений и сделанных допущений:

Из того, что случайные величины ξ и x независимы, а M(ξ) = 0, следует

Таким образом,

Далее для случайной величины x, распределенной равномерно в интервале [–R, R], имеем

Величина $M(\sqrt {R_{{}}^{2} - {{x}^{2}}} )$ вычисляется с помощью интегрирования по частям:

Имея в виду, что $M({{\xi }^{2}}) = \sigma _{\xi }^{2},$ $M({{\xi }^{4}}) = 3\sigma _{\xi }^{4},$получаем

Значение Δ, которое доставляет минимум выражению (2.10), соответствует математическому ожиданию $R_{c}^{2}$ для положения центра окружности, найденного с помощью (2.5), (2.6). Чтобы определить значение Δ, доставляющее минимум (2.10), проведем дифференцирование, и полученное выражение приравняем нулю:

Отсюда

Подставив найденное значение смещения центра (2.11) с учетом (2.8) в выражение (2.7), можно получить следующее уравнение относительно радиуса окружности R:

где

В (2.13) вместо величины $M(R_{c}^{2})$ необходимо подставить ее оценку:

Решив бикубическое уравнение (2.12) и взяв положительный корень (моделирование показало, что уравнение имеет только один действительный положительный корень), получаем оценку радиуса окружности $\widehat R$. В свою очередь, подставив оценку радиуса $\widehat R$ в (2.11), определяем смещение центра по оси Y. Увеличив на Δ значение y_c, получаем несмещенную оценку координат центра оси цилиндрической поверхности Y_c = y_c + Δ.

В качестве альтернативы решению (2.12) может быть использована следующая итерационная процедура определения положения центра окружности и ее радиуса.

1. По выборке измерений с помощью решения системы уравнений (2.5) вычисляются начальные координаты положения центра окружности (x_н, y_н).

2. Оценивается величина начального радиуса R₁ (j = 1) с помощью выражения

которое вытекает из (2.2).

3. Используя известное значение σ_ξ и полученное значение радиуса R_j (j = $\overline {1,k} $, где k – количество итераций), по формуле (2.11) вычисляется величина смещения центра по координате, коллинеарной направлению измерений Δ_j.

4. Центр окружности смещается на величину Δ_j в сторону увеличения дальности в точку с координатами (x_ц, y_ц) = (x_н, y_н+ Δ_j).

5. С помощью (2.15) рассчитывается уточненное значение радиуса R_{j + 1} относительно нового положения центра.

Далее процедура повторяется с п. 3. Моделирование показало, что процедура быстро сходится к истинным значениям искомых величин.

Приведенные выше выражения справедливы для случая, когда проекции точек зондирования распределены по всей полуокружности. Аналогичные выражения можно получить для случая, когда проекции точек зондирования находятся только на фрагменте полуокружности. Для построения алгоритма выделения цилиндрических поверхностей на реальных ЛЛ-изображениях целесообразно рассмотреть ситуацию, в которой для выделения цилиндрической поверхности используется лишь часть зондирований, проекции которых соответствуют некоторой дуге окружности, симметрично расположенной относительно оси цилиндра. При этом в представленных выше преобразованиях меняются пределы интегрирования в выражениях (2.8) и (2.9). Введем коэффициент m ∈ (q, 1], где q из практических соображений может быть выбрано как q ≥ 0.1…0.2.

Для случайной величины x, распределенной равномерно в интервале [–mR, mR], имеем

Величина $M(\sqrt {{{R}^{2}} - {{x}^{2}}} )$ аналогично (2.9) вычисляется с помощью интегрирования по частям:

Подставив полученные выражения (2.16), (2.17) в (2.10), проведя дифференцирование и приравняв нулю результат, можно получить величину смещения для рассматриваемого случая наблюдения части дуги окружности:

где

Тогда уравнение (2.12) примет вид

где ${{a}_{1}} = C_{2}^{2};$

Здесь $M(R_{c}^{2})$ оценивается с помощью (2.14).

3. Определение координат центра и радиуса сферической поверхности. Примененный в предыдущем разделе подход может быть обобщен на случай определения координат центра и радиуса сферической поверхности, зондируемой ЛЛ-системой. Последовательность действий полностью аналогична преобразованиям, рассмотренным выше, поэтому изложим результаты вкратце.

В качестве меры близости измерений x_i, y_i ,z_i, i = $\overline {1,n} $, к поверхности сферы аналогично критерию (2.6) будем использовать оценку дисперсии косвенных измерений квадрата радиуса сферы:

где

Для оценки координат центра сферы X_c, Y_c, Z_c определим оптимальные значения параметров x_c, y_c, z_c, минимизируя выражение (3.1), т.е. приравняем к нулю частные производные по x_c, y_c и z_c:

Проведя очевидные преобразования, можно получить следующую систему линейных уравнений:

где

Здесь

Система (3.2) может быть решена по правилу Крамера.

Можно показать, что данная оценка положения центра сферы является смещенной. Чтобы получить оценку смещения центра, проанализируем асимптотический случай, когда количество измерений n → ∞. Без потери общности будем считать, что ось OY проходит через центр сферы. В выборке измерений (x₁, …, x_n, …, y₁, …, y_n, …, z₁, … z_n, …) при n → ∞ будем рассматривать координаты x_i,z_i i-го измерения как реализацию независимых случайных величин x, z, равномерно распределенных на отрезке [–R, R], где R – радиус сферы (предлагаемый подход позволяет получить оценки положения центра сфера и ее радиус и для случая, когда зондируется лишь часть полусферы). Величина y_i может быть выражена как y_i = Y_i + ξ_i, где Y_i – координаты точки зондирования, лежащей на поверхности сферы при i-м измерении, ξ – нормально распределенная случайная ошибка с характеристиками: M(ξ(x)) = 0, $D(\xi (x)) = \sigma _{\xi }^{2}$ для ∀x; Y_i определяется очевидным геометрическим соотношением ${{Y}_{i}} = {{D}_{c}} - \sqrt {R_{{}}^{2} - x_{i}^{2} - z_{i}^{2}} $, где D_c – дальность до центра сферы, отсчитываемая вдоль оси OY. Предположим, что оценка положения центра сделана с некоторой ошибкой и предполагаемый центр смещен по оси OY относительно истинного на некоторую величину Δ. В силу симметрии смещение по осям OX и OZ стремится к нулю при увеличении количества измерений.

Обозначим через R_c отрезок, связывающий полученное измерение (x_i, y_i, z_i) с найденным смещенным центром сферы. Для i-го измерения имеют место следующие соотношения:

Из (3.3) следует

Плотности распределения случайных величин x, z задаются выражениями $p\left( x \right) = p\left( z \right) = 1{\text{/2}}R$. Их совместная плотность распределения с учетом их независимости $p(x,z) = p(x)p(z) = 1{\text{/}}4{{R}^{2}}$. Очевидно, что ${{x}^{2}} + {{z}^{2}} \leqslant {{R}^{2}}$. Вероятность этого события $P({{x}^{2}} + {{z}^{2}} \leqslant {{R}^{2}}) = \pi {{R}^{2}}{\text{/}}4{{R}^{2}} = \pi {\text{/}}4$. Условная плотность вероятности p_c(x, z) распределения координат x,z в круге ${{x}^{2}} + {{z}^{2}} \leqslant {{R}^{2}}$определяется выражением

Тогда

Путем перехода в полярную СК с якобианом преобразования J = ρ можно получить

Тогда

Аналогично

Подставляя найденные выражения для математических ожиданий в (3.5), можно получить

Как и в разд. 2, значение Δ, которое доставляет минимум выражению (3.6), соответствует математическому ожиданию $R_{c}^{2}$ для положения центра окружности, найденного с помощью (3.2). Чтобы определить значение Δ, доставляющее минимум (3.6), проведем дифференцирование и результат приравняем нулю:

Отсюда

Подставив определенное с помощью (3.7) значение смещения центра (3.8) с учетом (3.6) в выражение (3.4), можно получить следующее уравнение относительно радиуса окружности R:

где

Решив бикубическое уравнение с коэффициентами (3.9) и взяв положительный корень, получаем оценку радиуса сферической поверхности $\widehat R$. В свою очередь, подставив оценку радиуса $\widehat R$ в (3.8), определяем смещение центра по оси OY. Увеличив на Δ значение y_c, находим несмещенную оценку координат центра сферической поверхности.

В качестве альтернативы может быть использована итерационная процедура, аналогичная описанной в разд. 2.

Подобные выражения могут быть получены для случая, когда для выделения сферической поверхности используются лишь часть зондирований, которые расположены в некотором круге меньшего радиуса, чем сфера, центр которого расположен на прямой, соединяющей ЛЛ-систему и центр сферы.

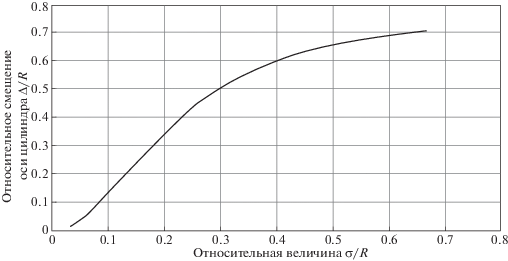
4. Моделирование по синтезированным ЛЛ-изображениям. Для проверки математических положений было проведено моделирование по синтезированным дальностным изображениям. На рис. 3 представлена теоретическая зависимость величины относительного смещения оси цилиндра (Δ_теор/R) от ее истинного положения, от относительной величины СКО измерения дальности (σ_ξ/R). Значение смещения Δ_теор получено с помощью (2.12) для заданного постоянного радиуса R и вариаций значения σ_ξ.

В таблице приведены результаты моделирования для следующих исходных данных: положение оси цилиндра X_c = 0, Y_c = 2000 м, радиус цилиндра R = 3 м, количество измерений в одном эксперименте n = 1000, величина СКО измерения дальности варьировалась от σ_ξ = 0.2 до σ_ξ = 2 м, количество реализаций для каждого значения σ_ξM = 500. В таблице представлены: величины смещения оси цилиндра Δ_теор, рассчитанные с помощью (2.12); усредненные по 500 реализациям координаты оси цилиндра ${{\hat {X}}_{c}}$, ${{\hat {Y}}_{c}}$, полученные при решении системы уравнений (2.7); усредненная оценка радиуса цилиндра $\hat {R}$, найденная с помощью решения уравнения (2.13); усредненная экспериментальная оценка величины смещения Δ_эксп, полученная путем подстановки в (2.12) оценки радиуса цилиндра; скорректированное положение оси цилиндра ${{\bar {Y}}_{c}}$, т.е. ${{\bar {Y}}_{c}} = {{\hat {Y}}_{c}} + {{\Delta }_{{{\text{эксп}}}}}$.

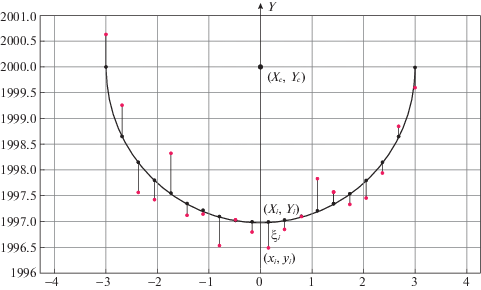
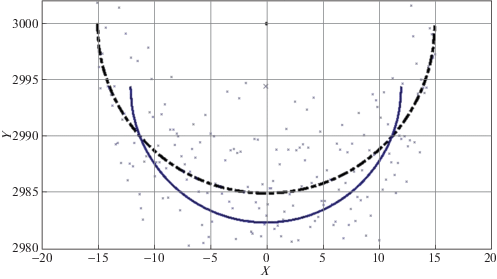
Из таблицы видно, что даже при значительной величине СКО измерения дальности оценка радиуса и положения оси цилиндра производятся с большой точностью, следовательно, полученные выражения корректны. Было проведено моделирование предложенной в разд. 2 итерационной процедуры определения параметров цилиндрической поверхности по выборке измерений. Моделирование подтвердило, что процедура быстро сходится за 2–4 итерации (в зависимости от величины ошибок измерения дальности D_ξ). В качестве примера на рис. 4 представлены результаты моделирования для σ(ξ_D) = 4 м. Штрихпунктирной линией обозначена проекция цилиндрической поверхности с радиусом R = 15 м на горизонтальную плоскость. Точки – проекции измерений на горизонтальную плоскость. Координаты начального положения оси цилиндра (отмечен крестиком) X_н = 0.13 м, Y_н = 1994.63 м. Начальный радиус R_н = 12.21 м. Дуга показана сплошной линией. Начальное смещение положения оси составило Δ = 5.37 м.

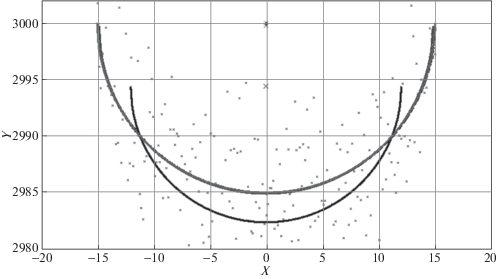
На рис. 5 приведены результаты реализации четырех итераций (наложены друг на друга). Получены следующие значения: оценка радиуса цилиндра R₄ = 15.03 м, ошибка определения положения оси цилиндра по продольной координате ΔY = 0.07 м.

Моделирование определения положения центра и радиуса сферической поверхности также подтвердило корректность выражений (3.2), (3.4), (3.5), (3.8) и (3.9).

5. Алгоритм выделения цилиндрических поверхностей при сегментации реальных ЛЛ-изображений. Полученные выражения для определения координат оси цилиндра и его радиуса были использованы при разработке алгоритма выделения цилиндрических поверхностей при сегментации реальных дальностных ЛЛ-изображений. Алгоритм заключается в следующем. ЛЛ-изображение обрабатывается “скользящим окном” m × n, горизонтальные размеры которого m не превосходят ожидаемую величину диаметра цилиндров (в пикселах), находящихся на сцене. При движении “скользящего окна” существуют положения, когда “окно” расположено на образе цилиндра симметрично относительно его оси. Поэтому для каждого положения “скользящего окна” выполняется проверка нескольких статистических гипотез. Каждая гипотеза заключается в том, что “окно” полностью находится на цилиндрической поверхности так, что ось цилиндра соответствует середине “окна” и горизонтальный размер “окна” составляет некоторую заранее заданную часть диаметра (например, k/10 при k = 1, …, 10). Альтернативой данным гипотезам рассматривается гипотеза, что “окно” расположено на поверхности общего вида или не симметрично относительно оси цилиндра. Для проведения такой проверки гипотез определяются координаты оси цилиндра (x_c, y_c) с помощью выражений (2.5), (2.6). Необходимо отметить, что если анализируемая поверхность не цилиндрическая, а является поверхностью произвольного вида, будут найдены координаты некоторой точки, не имеющей физического смысла. Затем для каждой гипотезы о соотношении горизонтального размера “окна” и диаметра цилиндра рассчитываются радиус R_k и смещение оси Δ_k от ее истинного положения с помощью выражений (2.11)–(2.13) и (2.18), (2.19), после чего координаты оси цилиндра корректируются на величину смещения Δ_k. Если какая-либо гипотеза верна, то положение оси и радиус цилиндра найдены корректно и, следовательно, математические ожидания измерений лежат на поверхности цилиндра, математическое описание которой получено. В соответствии с (1.1) измерения имеют относительно этой поверхности нормальное распределение с нулевым математическим ожиданием. Тогда нормированные ошибки измерений (в результате деления на СКО σ_ξ) являются независимыми случайными величинами с единичной дисперсией и нулевым математическим ожиданием. Поэтому сумма по всем пикселам окна квадратов таких величин, т.е. S_k:

подчинена закону распределения χ-квадрат и доверительная вероятность события ${{S}_{k}} < {{S}_{{{\text{пор}}}}}$ при известном числе измерений дальностей в “окне” n однозначно связана с пороговым значением ${{S}_{{{\text{пор}}}}}$, которое может быть найдено по таблицам для распределения χ-квадрат с n степенями свободы. Если же гипотеза не верна, то величина S_k имеет распределение, отличное от распределения χ-квадрат, причем доверительная вероятность $P({{S}_{k}} < {{S}_{{{\text{пор}}}}})$ будет существенно меньше, чем в случае цилиндрической поверхности. Для принятия или непринятия перечисленных гипотез можно использовать критерий согласия, основанный на использовании табулированных значений распределения χ-квадрат. В отличие от классического применения критериев согласия, например критерия Пирсона, нет необходимости разбивать выборку измерений на интервалы, определять частоты попаданий измерений в эти интервалы и сопоставлять их с теоретическим распределением. Величина S_k по построению имеет распределение χ-квадрат при верности k-й гипотезы и не имеет распределение χ-квадрат в противном случае. Задаваясь желаемой доверительной вероятностью α и сопоставляя величину S_k с пороговым значением ${{S}_{{{\text{пор}}}}}$ (т.е. с рассчитанной “процентной точкой” распределения χ-квадрат), принимается решение о верности одной из гипотез нахождения окна на цилиндрической поверхности с известным радиусом: при ${{S}_{k}} \leqslant \chi _{\alpha }^{2}$ k-я гипотеза принимается, а остальные отклоняются и всем пикселам фрагмента изображения размером 2R_k × n присваивается определенный индекс. Если указанный критерий выполняется для нескольких гипотез, то выбирается гипотеза, для которой S_k минимально. Если не для одной из гипотез не верно условие ${{S}_{k}} \leqslant \chi _{\alpha }^{2}$, то принимается гипотеза нахождения “окна” на поверхности общего вида. Вычисляется новое положение “скользящего окна”, и цикл повторяется. Предложенный подход позволяет провести выделение цилиндрических поверхностей при сегментации ЛЛ-изображений с заранее заданной доверительной вероятностью и определить положение оси и радиус каждого цилиндра. Последующее построение связных образов цилиндров на ЛЛ-изображении может быть произведено на базе эвристических подходов.

Для выделения сферических поверхностей был разработан аналогичный алгоритм.

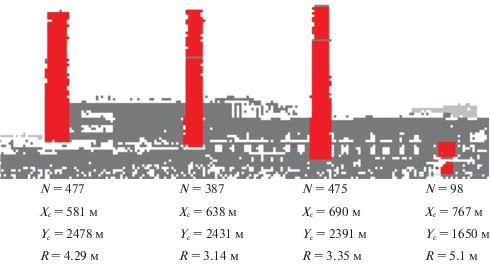
6. Результаты моделирования с использованием реальных ЛЛ-изображений. На рис. 6–8 представлен пример исходного изображения и результаты обработки реального ЛЛ-изображения с применением алгоритма обнаружения фрагментов образов цилиндрических поверхностей на сцене по дальностному ЛЛ-изображению. На рис. 6 приведено изображение промышленно-городской сцены в видимом диапазоне, на рис. 7 – бинарное ЛЛ-изображение той же сцены: белый цвет соответствует принятому отраженному сигналу, черный – отраженный сигнал отсутствует. Изображения, показанные на рис. 6–8, сформированы с помощью активно-пассивного многоспектрального комплекса дистанционного зондирования [14]; на рис. 8 представлены результаты обработки ЛЛ-изображения предложенным алгоритмом.

Под каждой сегментированной областью (более темный тон серого) указано число пикселов N в ней, положение оси X_с, Y_с и радиус цилиндра R. Отметим, что на рис. 8 выделены не только трубы с априори известной формой поверхности, но и цилиндрический бак для хранения горюче-смазочных материалов (в правом нижнем углу обработанного изображения), конфигурация которого не определяется по ТВ-изображению. Цилиндрическая форма данного объекта определена в результате анализа космоснимка. Таким образом, моделирование с использованием реальных ЛЛ-изображений подтвердило работоспособность предложенного алгоритма.

Заключение. Получено аналитическое решение задачи оценки местоположения фрагмента цилиндрической поверхности и его радиуса при обработке дальностного ЛЛ-изображения. Оценки являются оптимальными для случая, когда СКО центра отражения от оси диаграммы направленности существенно меньше СКО ошибок измерения дальности до отражающей поверхности. Предложенные методы и алгоритмы позволяют осуществлять поиск фрагментов таких поверхностей по ЛЛ-изображениям с заданной доверительной вероятностью. Метод обобщен для решения задачи выделения на ЛЛ-изображениях сферических поверхностей.

Предложенный критерий согласия позволяет определять доверительный интервал (для результата обработки измерений в любой области интереса), который соответствует заданной вероятности обнаружения цилиндрических или сферических поверхностей. На основании этого при поиске принимаются решения о сегментировании ЛЛ-изображения, т.е. выделении на нем областей, соответствующих фрагментам цилиндрических или сферических поверхностей.

Работоспособность методов и алгоритмов проверена путем моделирования с использованием реальных ЛЛ-изображений промышленно-городских сцен.