Известия РАН. Теория и системы управления, 2020, № 1, стр. 129-142
РЕАЛИЗАЦИЯ РЕЖИМА ОРБИТАЛЬНОЙ ОРИЕНТАЦИИ ИСКУССТВЕННОГО СПУТНИКА ЗЕМЛИ БЕЗ НАКОПЛЕНИЯ КИНЕТИЧЕСКОГО МОМЕНТА ГИРОСИСТЕМЫ
А. И. Игнатов a, *, В. В. Сазонов b, **
a АО “ГКНПЦ им. М.В. Хруничева”
Москва, Россия
b ИПМ им. М.В. Келдыша РАН
Москва, Россия
* E-mail: general_z@mail.ru
** E-mail: sazonov@keldysh.ru
Поступила в редакцию 17.05.19
После доработки 14.06.19
Принята к публикации 22.07.19
Аннотация
Рассматривается движение искусственного спутника Земли типа “Прогресс”, “Фотон-М” № 4 в различных вариантах режима орбитальной ориентации на низкой околоземной орбите. В качестве исполнительных органов системы управления спутником используется гиросистема (комплекс двигателей-маховиков или гиродинов). Учитывается действие на спутник гравитационного и восстанавливающего аэродинамического моментов. На принципах пропорционально-дифференцирующего регулятора построены законы управления гиростатическим моментом, позволяющие без его накопления поддерживать длительную и достаточно точную ориентацию спутника в окрестности гравитационно устойчивых и неустойчивых положений покоя, существующих в упрощенной задаче (спутник движется по неизменной круговой орбите и испытывает действие только гравитационного момента, гиростатический момент при этом равен нулю).
Введение. Режим орбитальной ориентации искусственного спутника Земли (ИСЗ) применяется для решения ряда задач, в частности, он предпочтителен при проведении космических экспериментов в области микрогравитации [1]. Для поддержания достаточно точной орбитальной ориентации спутника можно использовать различные исполнительные органы системы управления: электроракетные двигатели [2], электромагнитные органы управления [3, 4], а также гиросистему (двигатели-маховики или гиродины) [1, 5]. В данной работе в качестве исполнительного органа системы управления спутника рассматривается гиросистема. При использовании гиросистемы одним из критериев эффективности ее функционирования является скорость накопления гиростатического момента. Эта скорость определяет промежутки времени между разгрузками гиросистемы и должна быть достаточно малой, чтобы обеспечить продолжительные отрезки полета с малым уровнем микроускорений. Ниже рассматриваются законы управления вращательным движением спутника, позволяющие поддерживать его орбитальную ориентацию продолжительное время без насыщения кинетического момента гиросистемы.
1. Уравнения движения спутника. Спутник считаем гиростатом, центр масс которого движется по геоцентрической орбите. Для описания движения спутника будем использовать три правые декартовы системы координат.
Связанная со спутником система координат $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$, образована его главными центральными осями инерции. Начало системы находится в центре масс спутника – точке O. Несколько упрощая модель, полагаем, что оси системы $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ связаны с характерными элементами конструкции спутника. Допустим, что спутник имеет форму прямого кругового цилиндра радиусом ${{R}_{c}}$ и высотой ${{L}_{c}}$ с двумя прикрепленными к нему одинаковыми прямоугольными пластинами – солнечными батареями, суммарной площадью ${{S}_{b}}$. Ось $O{{x}_{1}}$ совпадает с осью цилиндра. Солнечные батареи расположены в плоскости $O{{x}_{1}}{{x}_{3}}$ симметрично относительно оси $O{{x}_{1}}$, стороны батарей параллельны осям $O{{x}_{1}}$ и $O{{x}_{3}}$, ось $O{{x}_{2}}$ перпендикулярна плоскости солнечных батарей. Координаты геометрических центров цилиндра и пластин солнечных батарей обозначим $({{x}_{c}},0,0)$ и $({{x}_{b}},0,0)$ соответственно. Здесь и ниже, если не оговорено особо, компоненты векторов и координаты точек относятся к системе $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$. Базисные орты системы $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ обозначим ${{{\mathbf{e}}}_{1}}$, ${{{\mathbf{e}}}_{2}}$, ${{{\mathbf{e}}}_{3}}$.
В орбитальной системе $O{{X}_{1}}{{X}_{2}}{{X}_{3}}$ оси $O{{X}_{3}}$ и $O{{X}_{2}}$ направлены соответственно вдоль геоцентрического радиус-вектора точки $O$ и вектора кинетического момента орбитального движения спутника. Базисные орты этой системы обозначим ${{{\mathbf{E}}}_{1}}$, ${{{\mathbf{E}}}_{2}}$, ${{{\mathbf{E}}}_{3}}$.
Начало гринвичской системы координат $C{{Y}_{1}}{{Y}_{2}}{{Y}_{3}}$ – точка C, расположенная в центре Земли, плоскость $C{{Y}_{1}}{{Y}_{2}}$ совпадает с плоскостью экватора, ось $C{{Y}_{1}}$ пересекает гринвичский меридиан, ось $C{{Y}_{3}}$ направлена по оси вращения Земли к Северному полюсу. Полагаем, что эта система вращается с постоянной угловой скоростью ${{\omega }_{E}}$ вокруг оси $C{{Y}_{3}}$.
Положение системы $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ относительно систем $O{{X}_{1}}{{X}_{2}}{{X}_{3}}$ и $C{{Y}_{1}}{{Y}_{2}}{{Y}_{3}}$ зададим нормированными кватернионами ${{Q}_{A}}$ и ${{Q}_{B}}$ соответственно. Матрицу перехода от системы $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ к системе $O{{X}_{1}}{{X}_{2}}{{X}_{3}}$ обозначим $A = ({{a}_{{ij}}})_{{i,j = 1}}^{{\,3}}$,${{a}_{{ij}}} = {{{\mathbf{E}}}_{i}}{{{\mathbf{e}}}_{j}}$. Матрицу A параметризируем углами $\gamma $, $\delta $ и $\beta $, которые введем следующим образом [1]. Система $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ может быть получена из системы $O{{X}_{1}}{{X}_{2}}{{X}_{3}}$ тремя последовательными поворотами: 1) на угол $\delta + \pi {\text{/}}2$ вокруг оси $O{{X}_{2}}$, 2) на угол $\beta $ вокруг новой оси $O{{X}_{3}}$, 3) на угол $\gamma $ вокруг оси $O{{X}_{1}}$, полученной после первых двух поворотов и совпадающей с осью $O{{x}_{1}}$. Элементы матрицы A выражаются через углы $\gamma $, $\delta $, $\beta $ по формулам, приведенным в [1], а также через компоненты кватерниона QA по формулам, рассмотренным в [6].
Уравнения движения спутника состоят из двух подсистем. Одна подсистема описывает движение центра масс спутника, другая – движение относительно центра масс (вращательное движение). Первая подсистема записывается в гринвичской системе координат. Ее переменными служат компоненты геоцентрического радиус-вектора ${\mathbf{r}}$ точки O и скорости этой точки ${\mathbf{v}}$ относительно гринвичской системы координат [7]. В ней учитываются нецентральность гравитационного поля Земли и сопротивление атмосферы. Нецентральность поля учитывается с точностью до членов порядка (16,16) включительно в разложении гравитационного потенциала Земли в ряд по шаровым функциям. Атмосфера считается вращающейся вместе с Землей, ее плотность рассчитывается, согласно модели ГОСТ Р 25645.166-2004.
Подсистема уравнений вращательного движения образована уравнениями, выражающими теорему об изменении кинетического момента спутника в его движении относительно центра масс, кинематическими уравнениями для кватерниона QB и уравнениями, описывающими изменение кинетического момента гиросистемы. В уравнениях, выражающих теорему об изменении кинетического момента, учитываются гравитационный и аэродинамический моменты. Гравитационный момент задается аналитическим выражением [8]
Аэродинамический момент вычислен при следующих упрощающих предположениях [8]. Молекулы атмосферы при столкновении со спутником испытывают абсолютно неупругий удар. Взаимное затенение солнечных батарей и корпуса спутника не учитывается. Формула аэродинамического момента имеет вид
Теорема об изменении кинетического момента спутника в его движении относительно центра масс выражается уравнениями
(1.1)
$\frac{{\tilde {d}{\mathbf{K}}}}{{dt}} + \omega \times {\mathbf{K}} = {{{\mathbf{M}}}_{g}} + {{{\mathbf{M}}}_{a}},\quad {\mathbf{K}} = \hat {I}\omega + {\mathbf{H}},$Кинематическое уравнение для кватерниона ${{Q}_{B}}$ имеет вид
(1.2)
$2{{\dot {Q}}_{B}} = {{Q}_{B}} \circ (0,{\mathbf{\omega }}) - (0,{{{\mathbf{\omega }}}_{E}}) \circ {{Q}_{B}},$Чтобы замкнуть подсистему уравнений вращательного движения спутника, надо добавить к (1.1) и (1.2) уравнение, описывающие изменение гиростатического момента спутника H. Это уравнение будет выписано ниже.
Приведем использованные в расчетах числовые значения параметров описанной модели. Параметры спутника: m = 6440 кг, ${{I}_{1}}$ = 2600 кгм2, ${{I}_{2}} = $ 11100 кгм2, ${{I}_{3}}$ = 10900 кгм2, Rc = 1.3 м, Lc= 5.0 м, ${{S}_{b}}$ = 33 м2, ${{x}_{b}}$ = –1 м, ${{x}_{c}} = 0.3$ м. Начальные условия движения центра масс спутника задавались в восходящем узле орбиты в момент 09:10:34 UTC 21.09.2007. Начальные элементы орбиты: высота в апогее 450 км, высота в перигее 400 км, наклонение 63.0°, аргумент широты перигея 53.5°, долгота восходящего узла (отсчитывается от точки среднего весеннего равноденствия эпохи даты). Параметры модели атмосферы: ${{F}_{{10.7}}} = {{F}_{{81}}} = $ 150, ${{A}_{p}}$ = 12.
Начальные условия уравнений (1.1), (1.2) задавались в тот же момент времени, что и начальные условия орбитального движения. Этот момент служил началом отсчета времени – точкой t = 0.
2. Пассивная гравитационная ориентация спутника. Чтобы пояснить этот режим вращательного движения, упростим уравнения (1.1), (1.2), положив H = 0 и отбросив второстепенные факторы. Будем считать, что орбита спутника – круговая радиуса r и неизменна в абсолютном пространстве, ${{{\mathbf{M}}}_{a}} = 0$. В этом случае система (1.1), (1.2) имеет 24 стационарных решения, в которых $\omega = {{\omega }_{0}}{{{\mathbf{E}}}_{2}}$, орты ${{{\mathbf{e}}}_{i}}$ совпадают с ортами $ \pm \,{{{\mathbf{E}}}_{j}},$ $i,j$ = 1, 2, 3, где ${{\omega }_{0}} = \sqrt {{{\mu }_{E}}{\text{/}}{{r}^{3}}} $– среднее движение спутника (орбитальная частота). Эти решения описывают положения равновесия (покой) спутника в орбитальной системе координат [8].
Ограничимся рассмотрением двух стационарных решений системы, задаваемых соотношениями:
(2.1)
${{{\mathbf{e}}}_{1}} = - {{{\mathbf{E}}}_{3}},\quad {{{\mathbf{e}}}_{2}} = {{{\mathbf{E}}}_{2}},\quad {{{\mathbf{e}}}_{3}} = {{{\mathbf{E}}}_{1}},$(2.2)
${{{\mathbf{e}}}_{1}} = {{{\mathbf{E}}}_{1}},\quad {{{\mathbf{e}}}_{2}} = {{{\mathbf{E}}}_{3}},\quad {{{\mathbf{e}}}_{3}} = - {{{\mathbf{E}}}_{2}}.$При выполнении неравенств ${{I}_{1}} < {{I}_{3}} < {{I}_{2}}$ решение (2.1) является устойчивым, а решение (2.2) – неустойчивым [8].
Устойчивое стационарное решение (2.1) можно использовать для реализации режима пассивной трехосной гравитационной ориентации спутника [9].
Исследуя этот режим, положим в (1.1), (1.2) H = 0, остальные параметры оставим без изменений. В этом случае уравнения (1.1), (1.2) уже не имеют решения (2.1), однако они имеют решения, в которых соотношения (2.1) выполнены приближенно. Чтобы ориентированное движение спутника сохранялось более длительное время, такие решения можно выбирать из условия минимума функционала [1]
(2.3)
$\Phi = \int\limits_0^T {{{{\left| {\omega - {{{\tilde {\omega }}}_{0}}{{{\mathbf{E}}}_{2}}} \right|}}^{2}}} dt$.Здесь ${{\tilde {\omega }}_{0}} = c{\text{/}}{{r}^{2}}$, c – модуль орбитального кинетического момента, ${{\tilde {\omega }}_{0}} = {{\tilde {\omega }}_{0}}(t)$ (в случае неизменной круговой орбиты ${{\tilde {\omega }}_{0}} = {{\omega }_{0}}$), значение T приближенно равно нескольким орбитальным периодам $2\pi {\text{/}}{{\tilde {\omega }}_{0}}$. В упрощенной задаче, рассмотренной выше, $Ф = 0$ для положения покоя (2.1) и $Ф > 0$ на решениях, лежащих в окрестности этого положения и не совпадающих с ним. Интеграл в (2.3) можно заменить суммой
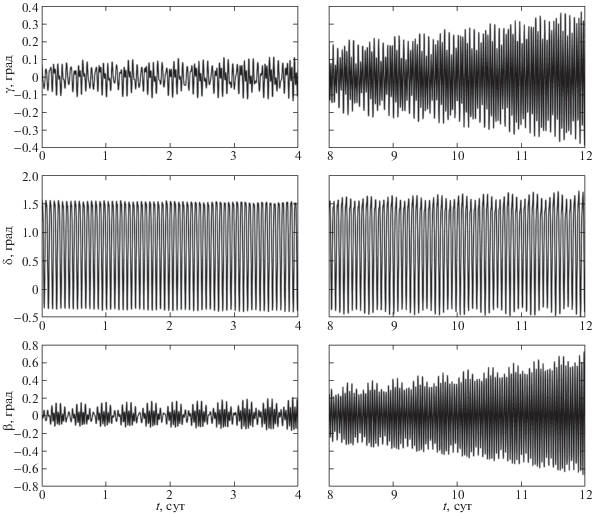
Решения уравнений (1.1), (1.2), доставляющие локальный минимум функционалу $\Phi {\kern 1pt} '$ и близкие положению покоя (2.1), представлены на рис. 1 графиками зависимости от времени углов $\gamma $, $\delta $, $\beta $. Положение спутника в орбитальной системе координат в начальный момент времени задается углами $\gamma (0) = $ 0.06°, $\delta (0) = $ 1.34°, $\beta (0) = $ –0.07°. Начальная угловая скорость спутника:
Решения уравнений найдены на интервале времени 12 сут. Графики в левой части рис. 1 показаны на интервале времени $0 \leqslant t \leqslant 4$ сут, в правой части – на интервале $8 \leqslant t \leqslant 12$ сут. Хорошо видна слабая неустойчивость режима пассивной гравитационной ориентации (см. графики функции $\gamma (t)$ и $\beta (t)$), которая связана с дестабилизирующим действием аэродинамического момента. Колебания спутника вызваны изменением плотности атмосферы и эллиптичностью орбиты. К сожалению, в полной мере использовать возможности режима пассивной гравитационной ориентации не удается из-за неизбежных ошибок в задании начальных условий. Эти ошибки приводят к более быстрому разрушению ориентированного движения, чем показано на рис. 1.
3. Орбитальная ориентация спутника. Орбитальной ориентацией спутника будем называть его движение, близкое заданному положению покоя в орбитальной системе координат. В случае спутника, рассмотренного в разд. 1, технически доступные реализации гиростатического момента ${\mathbf{H}} = {{({{h}_{1}},{{h}_{2}},{{h}_{3}})}^{T}}$ не могут обеспечить существование в течение длительного времени решений уравнений (1.1), (1.2), описывающих точный покой в орбитальной системе, но они могут обеспечить решения, близкие к покою.
Уравнение, описывающее изменение гиростатического момента спутника H, представим как
где Mc – управляющий момент, приложенный к корпусу спутника со стороны гиросистемы. Подстановка (3.1) в уравнение (1.1) приводит его к виду(3.2)
$\hat {I}\frac{{\tilde {d}\omega }}{{dt}} + \omega \times \hat {I}\omega = {{{\mathbf{M}}}_{g}} + {{{\mathbf{M}}}_{а}} + {{{\mathbf{M}}}_{c}}.$Рассмотрим систему уравнений (1.2), (3.2) и выберем момент Mc так, чтобы эта система допускала установившиеся решения, в которых кватернион ${{Q}_{A}}(t)$ был бы близок к заданному постоянному кватерниону Q0, а величина $\left| {\mathbf{H}} \right|$ возрастала бы, по возможности, медленнее. Такой момент будем искать в виде
(3.3)
${{{\mathbf{M}}}_{c}} = - {{\xi }^{2}}\hat {I}\theta - 2\xi \hat {I}(\omega - {{\omega }_{0}}{{{\mathbf{E}}}_{2}}),$Формула (3.3) подразумевает, что на спутнике установлены датчики угловых скоростей и ориентации, по измерениям которых формируется закон управления.
Рассмотрим систему (1.2), (3.2), (3.3). Параметр ξ возьмем настолько большим, чтобы характерное время действия на спутник управляющего момента было существенно меньше аналогичного времени для гравитационного и аэродинамического моментов. Если двумя последними моментами и отличием орбиты от круговой пренебречь, то эту систему, линеаризовав ее по $\theta $, можно привести к виду
Закон управления (3.3) в общем случае обеспечивает поддержание режима ориентации, но не обеспечивает малую скорость возрастания величины $\left| {\mathbf{H}} \right|$. Чтобы уменьшить эту скорость, следует специальным образом выбирать кватернион ориентации Q0. Например, можно взять усредненный кватернион
где ${{Q}_{A}}(t)$ – экстремаль функционала $\Phi {\kern 1pt} '$, $\left\| {\, \cdot \,} \right\|$ – норма кватерниона. Такой выбор можно пояснить следующим образом. Выписанное Q0 доставляет минимум функционалу при ${{Q}_{A}} \approx {{Q}_{0}}$ с использованием вектора бесконечно малого поворота ${\mathbf{\theta }}$ выражение (3.4) можно представить в видеОтсюда следует, что минимизация ${\rm P}$ означает минимизацию возмущенного движения. По смыслу этот функционал близок функционалу (2.3), который приближенно можно записать как
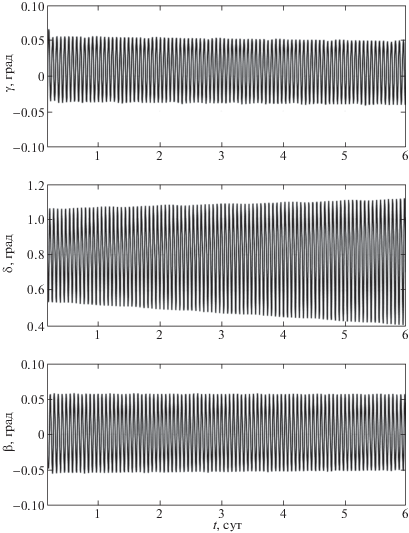
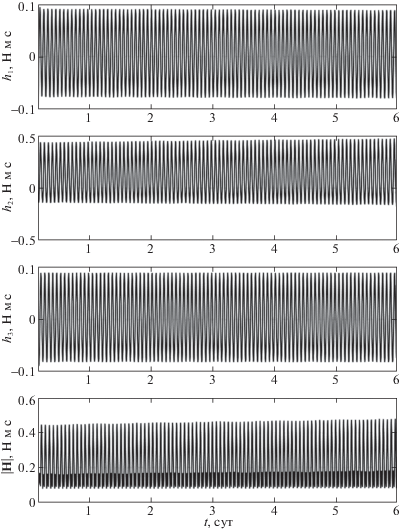
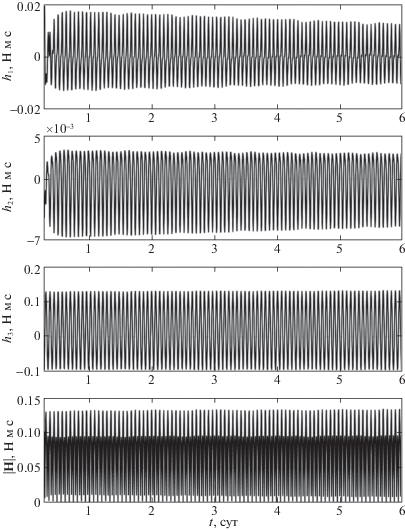
Пример использования закона (3.3) при таком выборе Q0 приведен на рис. 2, 3. Здесь показаны решения системы (1.1), (1.2), (3.1), (3.3) при $\xi = 0.01$ с–1 и кватернионе Q0, полученном усреднением кватерниона ${{Q}_{A}}(t)$ для режима пассивной гравитационной ориентации (см. разд. 2 и рис. 1) в случае T = 2 сут. Усредненные значения углов, соответствующие кватерниону Q0, следующие: $\gamma = - 0.002^\circ $, $\delta = 0.801^\circ $, $\beta = - 0.005^\circ $. Положение спутника в орбитальной системе координат в начальный момент времени задается этими же усредненными значениями углов $\gamma $, $\delta $, $\beta $. Другие начальные условия решения: ${\mathbf{H}}(0) = 0$ и
(3.5)
${{\omega }_{1}}(0) = {{\omega }_{2}}(0) - {{\omega }_{0}} = {{\omega }_{3}}(0) = 0.01\;{\text{град/c}}{\text{.}}$Рис. 2.
Углы ориентации ИСЗ в режиме его орбитальной ориентации (3.1), (3.3) при специальном выборе Q0
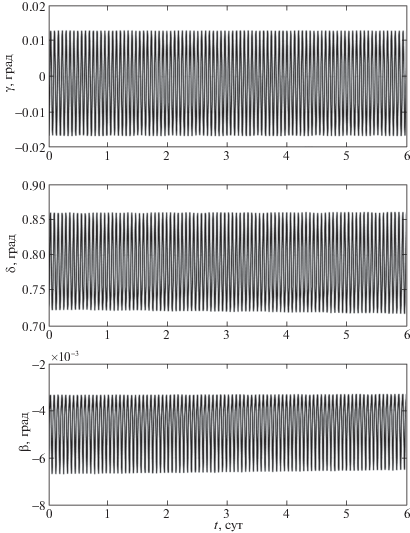
Рис. 3.
Гиростатический момент ИСЗ в режиме его орбитальной ориентации (3.1), (3.3) при специальном выборе Q0
Начальные значения компонент угловой скорости учитывают ошибки в реализации начальных условий вращательного движения спутника. Ошибка в задании угловой скорости наиболее существенна. На рис. 2, 3 на интервалах времени 6 сут изображены графики зависимости от времени углов $\gamma $, $\delta $, $\beta $, компонент ${{h}_{i}}$, i = 1, 2, 3, и модуля гиростатического момента $\left| {\mathbf{H}} \right|$. На графиках не показан начальный участок длительностью 10 мин, иллюстрирующий переходной процесс, обусловленный ошибками в задании начальной угловой скорости (3.5). Колебания спутника в установившемся режиме вызваны изменением плотности атмосферы вдоль орбиты и эллиптичностью последней. Амплитуды установившихся колебаний компонент угловой скорости ограничены значениями:
Следует отметить весьма медленное накопление собственного кинетического момента гиросистемы в построенном решении. Это есть следствие специального выбора кватерниона Q0.
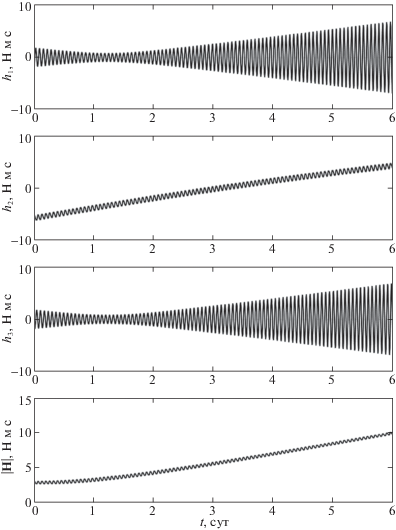
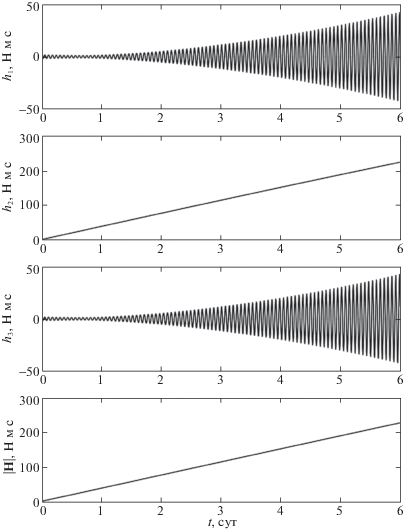
Для сравнения на рис. 4 приведены графики компонент ${{h}_{i}}$, i = 1, 2, 3, и модуля гиростатического момента $\left| {\mathbf{H}} \right|$, полученные в результате интегрирования системы (1.1), (1.2), (3.1), (3.3) с кватернионом ${{Q}_{0}} = (\sqrt 2 {\text{/}}2,0, - \sqrt 2 {\text{/}}2,0)$, соответствующим положению равновесия (2.1). Интегрирование системы уравнений проводилось для начальных условий (3.5) и $\gamma (0) = \delta (0) = \beta (0) = 0$, ${{h}_{1}}(0) = {{h}_{2}}(0) = {{h}_{3}}(0) = 0$ при $\xi $ = 0.01 с–1. Сравнивая полученные результаты, видно, что использование закона управления (3.3) при специальном выборе кватерниона Q0 позволяет уменьшить гиростатический момент спутника, накопленный за 6 сут полета примерно в 22 раза по сравнению с гиростатическим моментом, накопленным за аналогичное время при использовании кватерниона Q0, соответствующего положению равновесия (2.1). В установившемся режиме амплитуды колебаний компонент угловой скорости ${{\omega }_{i}}$, i = 1, 2, 3, полученных с помощью специального выбора кватерниона Q0, практически не изменятся по сравнению с амплитудами, полученными при использовании кватерниона ${{Q}_{0}} = (\sqrt 2 {\text{/}}2,0, - \sqrt 2 {\text{/}}2,0)$.
Рис. 4.
Гиростатический момент ИСЗ в режиме его орбитальной ориентации (3.1), (3.3) при Q0 = $(\sqrt 2 {\text{/}}2,0, - \sqrt 2 {\text{/}}2,0)$
В данном случае применение специального выбора кватерниона Q0 представляет методический интерес для оценок возможностей гиросистемы. Расчет его в реальном времени сложен хотя бы из-за необходимости учета влияния аэродинамического момента на вращательное движение спутника. Однако в использовании специального выбора кватерниона Q0 нет необходимости. Поддержание достаточно точной орбитальной ориентации можно обеспечить без накопления гиростатического момента [12, 13].
4. Орбитальная ориентации спутника в окрестности устойчивого положения равновесия без накопления гиростатического момента. Сначала реализуем такую ориентацию в простейшей ситуации. Орбиту примем круговой и неизменной в абсолютном пространстве, из приложенных к спутнику внешних механических моментов будем учитывать только гравитационный. Теорему об изменении кинетического момента спутника в его движении относительно центра масс запишем в виде
(4.1)
$\frac{{\tilde {d}(\hat {I}\omega + {\mathbf{H}})}}{{dt}} + \omega \times (\hat {I}\omega + {\mathbf{H}}) = 3\omega _{0}^{2}\left( {{{{\mathbf{E}}}_{3}} \times \hat {I}{{{\mathbf{E}}}_{3}}} \right).$Выписанные уравнения дополним уравнениями (1.2), (3.1) и выберем момент Mc таким образом, чтобы полученная система имела стационарные решения, задаваемые формулами (2.1) и H = 0. Примем простой вариант
(4.2)
${{{\mathbf{M}}}_{c}} = {{\hat {K}}_{h}}{\mathbf{H}} - {{\hat {K}}_{\omega }}(\omega - {{\omega }_{0}}{{{\mathbf{e}}}_{2}}),$(4.3)
$\left\{ \begin{gathered} {{I}_{2}}{{{\dot {\omega }}}_{2}} = - {{k}_{{\omega 2}}}({{\omega }_{2}} - {{\omega }_{0}}) + 3\omega _{0}^{2}({{I}_{1}} - {{I}_{3}})\delta + {{k}_{{h2}}}{{h}_{2}}, \hfill \\ \dot {\delta } = {{\omega }_{2}} - {{\omega }_{0}},\quad {{{\dot {h}}}_{2}} = {{k}_{{\omega 2}}}({{\omega }_{2}} - {{\omega }_{0}}) - {{k}_{{h2}}}{{h}_{2}}. \hfill \\ \end{gathered} \right.$(4.4)
$\left\{ \begin{gathered} {{I}_{1}}{{{\dot {\omega }}}_{1}} = - {{k}_{{\omega 1}}}{{\omega }_{1}} + {{\omega }_{0}}({{I}_{2}} - {{I}_{3}}){{\omega }_{3}} + {{k}_{{h1}}}{{h}_{1}}, \hfill \\ {{I}_{3}}{{{\dot {\omega }}}_{3}} = {{\omega }_{0}}({{I}_{1}} - {{I}_{2}}){{\omega }_{1}} - {{k}_{{\omega 3}}}{{\omega }_{3}} + 3\omega _{0}^{2}({{I}_{1}} - {{I}_{2}})\beta + {{k}_{{h3}}}{{h}_{3}}, \hfill \\ \dot {\gamma } = {{\omega }_{1}} - {{\omega }_{0}}\beta ,\quad \dot {\beta } = {{\omega }_{3}} + {{\omega }_{0}}\gamma , \hfill \\ {{{\dot {h}}}_{1}} = {{k}_{{\omega 1}}}{{\omega }_{1}} - {{k}_{{h1}}}{{h}_{1}} - {{\omega }_{0}}{{h}_{3}},\quad {{{\dot {h}}}_{3}} = {{k}_{{\omega 3}}}{{\omega }_{3}} + {{\omega }_{0}}{{h}_{1}} - {{k}_{{h3}}}{{h}_{3}}. \hfill \\ \end{gathered} \right.$Значения коэффициентов ${{k}_{{\omega i}}}$, ${{k}_{{hi}}}$ выберем таким образом, чтобы корни характеристического полинома системы уравнений (4.3), (4.4) лежали в левой полуплоскости комплексного переменного достаточно далеко от мнимой оси. Точнее, критерием качества закона управления (4.2) будем считать степень устойчивости системы уравнений (4.3), (4.4) – взятую с обратным знаком действительную часть самого правого корня ее характеристического полинома. В данном случае этот полином разделяется на полиномы третьего и шестого порядков, являющиеся характеристическими полиномами подсистем (4.3) и (4.4) соответственно.
Полином третьего порядка зависит только от коэффициентов ${{k}_{{h2}}}$ и ${{k}_{{\omega 2}}}$. Выберем их так, чтобы этот полином имел трехкратный действительный корень –α, где $\alpha > 0$ – степень устойчивости. Получаем
Полином шестого порядка содержит только коэффициенты ${{k}_{{h1}}}$, ${{k}_{{h3}}}$, ${{k}_{{\omega {\kern 1pt} 1}}}$ и ${{k}_{{\omega {\kern 1pt} 3}}}$. Примем их значения ${{k}_{{h1}}} = $ 3.00 × 10–4 с–1, ${{k}_{{\omega 1}}} = $ 78.00 Н ⋅ м ⋅ с, ${{k}_{{h3}}} = $ 3.00 × 10–4 с–1, ${{k}_{{\omega 3}}} = $ 26.16 Н ⋅ м ⋅ с. Корни полинома при этом равны
Таким образом, закон управления (4.2) с указанными значениями параметров ${{k}_{{hi}}}$, ${{k}_{{\omega {\kern 1pt} i}}}$ обеспечивает асимптотическую устойчивость стационарного решения (2.3) и H = 0 системы (1.2), (3.2), (4.1), (4.2). Пример использования этого закона в более сложном случае системы (1.1), (1.2), (3.1), (4.2) приведен на рис. 5, 6. Здесь показаны решения системы с начальными условиями (3.5) и $\gamma (0) = \delta (0) = \beta (0) = 0$, ${{h}_{1}}(0) = {{h}_{2}}(0) = {{h}_{3}}(0) = 0$ на интервале времени 6 сут. На рисунках изображены графики зависимости от времени углов $\gamma $, $\delta $, $\beta $, компонент ${{h}_{i}}$, i = 1, 2, 3, и модуля гиростатического момента $\left| {\mathbf{H}} \right|$. На графиках не показан начальный участок длительностью 4 ч, иллюстрирующий переходной процесс, который обусловлен ошибками в задании начальной угловой скорости (3.5). Результаты расчетов показывают, что закон управления (4.2) обеспечивает устойчивую орбитальную ориентацию спутника и гиростатический момент при этом остается ограниченным. В установившемся режиме амплитуды колебаний компонент угловой скорости ограничены следующими значениями:
На рис. 5 видимое увеличение амплитуды колебаний, а также постоянное смещение угла $\delta \approx $0.8° вызваны сопротивлением атмосферы, зависящим от положения Солнца относительно плоскости орбиты спутника. Это положение меняется из-за прецессии плоскости орбиты с угловой скоростью ~5 град/c. За период времени, равный примерно 70 сут, величина постоянного смещения угла δ практически не меняется, амплитуда колебаний меняется в диапазоне от 0.1 до 0.7°, при этом максимальное значение угла $\delta $ не превышает 1.5° [14].
Достоинством закона управления (4.2) (и похожих законов в [1, 15]) является сравнительная простота – для его реализации не нужна информация об ориентации спутника. Недостатки закона (4.2): он поддерживает орбитальную ориентацию только в окрестности устойчивого положения равновесия; характеризующая этот закон степень устойчивости ограничена. Последний недостаток можно устранить, введя в (4.2) слагаемое ${{\hat {K}}_{a}}\theta $ с подходящей матрицей ${{\hat {K}}_{a}} = {\text{diag}}\,{\text{(}}{{k}_{{a1}}}$, ka2, ka3). Способ выбора этой матрицы аналогичен способу, рассмотренному далее в разд. 5.
5. Орбитальная ориентации спутника в окрестности неустойчивого положения равновесия без накопления гиростатического момента. Закон управления гиростатическим моментом возьмем в виде
(5.1)
${{{\mathbf{M}}}_{c}} = {{\hat {K}}_{a}}\theta - {{\hat {K}}_{\omega }}\left( {\omega - {{\omega }_{0}}{{{\mathbf{E}}}_{2}}} \right) + {{\hat {K}}_{h}}{\mathbf{H}},$(5.2)
$\left\{ \begin{gathered} {{I}_{3}}{{{\dot {\omega }}}_{3}} = - {{k}_{{\omega 3}}}({{\omega }_{3}} + {{\omega }_{0}}) + [3\omega _{0}^{2}({{I}_{1}} - {{I}_{2}}) + {{k}_{{a3}}}]\Delta \delta + {{k}_{{h3}}}{{h}_{3}}, \hfill \\ \Delta \dot {\delta } = - ({{\omega }_{3}} + {{\omega }_{0}}),\quad {{{\dot {h}}}_{3}} = {{k}_{{\omega 3}}}({{\omega }_{3}} + {{\omega }_{0}}) - {{k}_{{a3}}}\Delta \delta - {{k}_{{h3}}}{{h}_{3}}; \hfill \\ \end{gathered} \right.$(5.3)
$\left\{ \begin{gathered} {{I}_{1}}{{{\dot {\omega }}}_{1}} = - {{k}_{{\omega 1}}}{{\omega }_{1}} + {{\omega }_{0}}({{I}_{3}} - {{I}_{2}}){{\omega }_{2}} + [3\omega _{0}^{2}\left( {{{I}_{2}} - {{I}_{3}}} \right) + {{k}_{{a1}}}]\Delta \gamma + {{k}_{{\omega 1}}}{{\omega }_{0}}\beta + {{k}_{{h1}}}{{h}_{1}}, \hfill \\ {{I}_{2}}{{{\dot {\omega }}}_{2}} = {{\omega }_{0}}({{I}_{1}} - {{I}_{3}}){{\omega }_{1}} - {{k}_{{\omega 2}}}{{\omega }_{2}} - {{k}_{{\omega 2}}}{{\omega }_{0}}\Delta \gamma + {{k}_{{a2}}}\beta + {{k}_{{h2}}}{{h}_{2}}, \hfill \\ \Delta \dot {\gamma } = {{\omega }_{1}} - {{\omega }_{0}}\beta ,\quad \dot {\beta } = {{\omega }_{2}} + {{\omega }_{0}}\Delta \gamma , \hfill \\ {{{\dot {h}}}_{1}} = {{k}_{{\omega 1}}}{{\omega }_{1}} - {{k}_{{a1}}}\Delta \gamma - {{k}_{{\omega 1}}}{{\omega }_{0}}\beta - {{k}_{{h1}}}{{h}_{1}} - {{\omega }_{0}}{{h}_{2}}, \hfill \\ {{{\dot {h}}}_{2}} = {{k}_{{\omega 2}}}{{\omega }_{2}} + {{k}_{{\omega 2}}}{{\omega }_{0}}\Delta \gamma - {{k}_{{a2}}}\beta + {{\omega }_{0}}{{h}_{1}} - {{k}_{{h2}}}{{h}_{2}}. \hfill \\ \end{gathered} \right.$Значения коэффициентов ${{k}_{{\omega i}}}$, ${{k}_{{ai}}}$, ${{k}_{{hi}}}$ выберем так, чтобы степень устойчивости каждой из них была достаточно большой. Характеристический полином подсистемы (5.2) имеет третий порядок. Потребуем, чтобы он имел действительный корень кратности 3. Отсюда находим коэффициенты ${{k}_{{a3}}}$, ${{k}_{{\omega 3}}}$ и ${{k}_{{h3}}}$:
Подсистема (5.3) имеет порядок 6. Вычисляя характеристические числа ее матрицы, примем следующие значения коэффициентов: ${{k}_{{h1}}}$ = –0.1 с–1, ${{k}_{{\omega 1}}} = $ 300 Н ⋅ м ⋅ с, ${{k}_{{a1}}}$ = –0.11 Н ⋅ м, ${{k}_{{h2}}}$ = = 0.05 с–1, ${{k}_{{\omega 2}}}$ = 300 Н ⋅ м ⋅ с, ${{k}_{{a2}}}$ = –0.1 Н ⋅ м. Характеристические числа при этом равны:
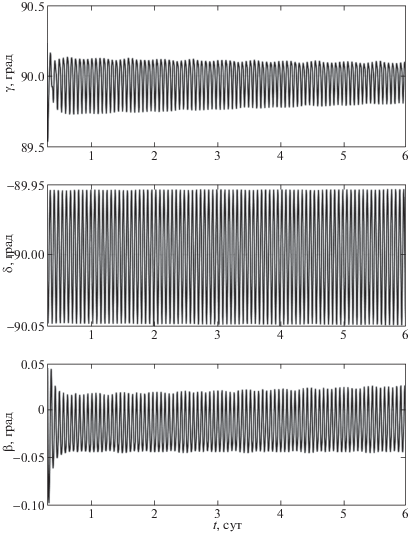
Выбранный закон изменения кинетического момента гиросистемы обеспечивает трехосную орбитальную ориентацию спутника в окрестности положения (2.2). С этой целью вычислим решение системы (1.1), (1.2), (3.1), (5.1). Решения этой системы с начальными условиями γ(0) = = $ - \delta (0) = 90^\circ $, $\beta (0) = 0$, ${{h}_{1}}(0) = {{h}_{2}}(0) = {{h}_{3}}(0) = 0$ и ${{\omega }_{1}}(0) = {{\omega }_{2}}(0) = {{\omega }_{3}}(0) + {{\omega }_{0}} = 0.01$ град/c на интервале времени 6 сут представлены на рис. 7 графиками зависимости от времени углов $\gamma $, $\delta $, $\beta $. На рис. 8 изображены графики зависимости от времени углов компонент ${{h}_{i}}$, i = 1, 2, 3, и модуля гиростатического момента $\left| {\mathbf{H}} \right|$. На графиках не показан начальный участок, длительностью 7 ч, иллюстрирующий переходной процесс, который обусловлен ошибками в задании начальной угловой скорости. Как и в предыдущих примерах, представленные здесь установившиеся колебания вызваны изменением плотности атмосферы и эллиптичностью орбиты. Амплитуды установившихся колебаний компонент угловой скорости ограничены значениями:
Результаты моделирования показали, что закон управления (5.1) обеспечивает достаточно точную стабилизацию спутника в окрестности неустойчивого положения равновесия (2.2), при этом собственный кинетический момент гиросистемы близок к нулю и практически не увеличивается на всем отрезке времени моделирования.
Заключение. В данной работе исследованы простые законы управления гиростатическим моментом, позволяющие без его накопления поддерживать длительную и достаточно точную ориентацию спутника в окрестности гравитационно устойчивых и неустойчивых положений покоя. Для линеаризованной системы уравнений движения спутника получены аналитические зависимости, позволяющие вычислить параметры рассмотренных законов управления. Приведены результаты математического моделирования полной системы уравнений движения спутника, подтверждающие, что предложенные законы управления обеспечивают требуемую ориентацию спутника без накопления гиростатического момента. Полученные результаты могут быть использованы на этапе предварительного проектирования систем управления ориентацией спутника.
Список литературы
Игнатов А.И., Сазонов В.В. Реализация режимов вращательного движения ИСЗ с малым уровнем микроускорений электромеханическими исполнительными органами // Космич. исслед. 2012. Т. 50. № 5. С. 380–393.
Латышев Л.А., Штырлин А.Ф., Непейвода О.М., Сазонов В.В. Использование электроракетных двигателей для реализации режима движения ИСЗ с малым уровнем микроускорений // Препринт ИПМ им. М.В. Келдыша РАН. 2007. № 16.
Абрашкин В.И., Пузин Ю.А., Сазонов В.В. Электромагнитная система управления вращательным движением спутника, обеспечивающая малый уровень микроускорений на его борту // Препринт ИПМ им. М.В. Келдыша РАН. 2010. № 22.
Игнатов А.И., Сазонов В.В. Стабилизация режима гравитационной ориентации искусственного спутника Земли электромагнитной системой управления // Препринт ИПМ им. М.В. Келдыша РАН. 2016. № 28.
Игнатов А.И., Сазонов В.В. Реализация режимов вращательного движения ИСЗ с малым уровнем остаточных микроускорений электромеханическими исполнительными органами // Препринт ИПМ им. М.В. Келдыша РАН. 2008. № 13.
Бранец В.Н., Шмыглевский И.П. Применение кватернионов в задачах ориентации твердого тела. М.: Наука, 1973.
Бажинов И.К., Гаврилов В.П., Ястребов В.Д. и др. Навигационное обеспечение полета орбитального комплекса “Салют-6”–“Союз”–“Прогресс”. М.: Наука, 1985.
Белецкий В.В. Движение искусственного спутника относительно центра масс. М.: Наука, 1965.
Герман А.Д., Гутник С.А., Сарычев В.А. Динамика спутника под действием гравитационного и постоянного моментов // Изв. РАН. ТиСУ. 2017. № 1. С. 128–140.
Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. М.: Мир, 1985.
Малкин И.Г. Теория устойчивости движения. М.: Наука, 1966.
Vadali S.R., Oh H.-S. Space Station Attitude Control and Momentum Management: A Nonlinear Look // Guidance, Control and Dynamics. 1992. V. 15. № 3. P. 577–586.
Зубов Н.Е., Микрин Е.А., Мисриханов М.Ш., Рябченко В.Н. Стабилизация орбитальной ориентации космического аппарата с одновременной разгрузкой кинетического момента инерционных исполнительных органов // Изв. РАН. ТиСУ. 2015. № 4. С. 124–131.
Игнатов А.И., Сазонов В.В. Стабилизация режима орбитальной ориентации искусственного спутника Земли без накопления кинетического момента гиросистемы // Препринт ИПМ им. М.В. Келдыша РАН. 2018. № 2.
Сазонов В.В. Гравитационная ориентация искусственных спутников с гиродинами // Космич. исслед. 1988. Т. 26. № 2. С. 315–317.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления