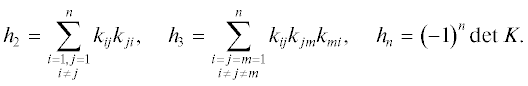Известия РАН. Теория и системы управления, 2020, № 1, стр. 4-10

0. Введение. В теории многосвязных динамических управляемых систем широкое распространение получили два способа описания данного класса систем. Первый из них основан на описании многосвязных систем (МС) через матричные передаточные функции (МПФ) [1, 2], второй – на описании в форме системы дифференциальных уравнений первого порядка в нормальной форме пространства состояний (векторно-матричная форма Коши) [1, 2]. Методы исследования МС, базирующиеся на этих способах описания, реализуются при проектировании в виде комплекса программных средств для электронных вычислительных машин. Такой подход позволяет при заданной начальной информации за короткое время получить конечный результат. При этом, как правило, инженер-проектировщик не в состоянии проследить за физическим процессом формирования конечного результата, например, понять, как влияют изменения параметрических и структурных свойств отдельных подсистем или связей между ними на формирование устойчивости МС в целом. Для этого ему необходимо провести серию целенаправленных численных экспериментов и расчетов.

Другой подход к описанию линейных динамических МС рассмотрен в [3], основанный на структурной декомпозиции МПФ и в выделении характеристик отдельных подсистем и многомерных связей между ними и использовании частотных методов исследования динамических систем. Согласно данному подходу, в [2–7] предложено описание линейных МС через характеристические полиномы M(p) (где p – оператор дифференцирования) физических переменных ${{y}_{i}}(t)$ отдельных подсистем, функционирующих в автономном режиме, и числовые коэффициенты k_ij-связи между ними в полиномиальной векторно-матричной форме:

где ${{M}_{{\text{л}}}} = {\text{diag}}\{ {{M}_{1}}(p),...,{{M}_{n}}(p)\} $, $Y = {{[{{y}_{1}},{{y}_{2}}, \ldots ,{{y}_{n}}]}^{{\text{T}}}}$ – вектор физически реализуемых координат системы, K – матрица числовых коэффициентов связей между подсистемами, в диагонали которой стоят элементы, равные нулю: $B = {\text{diag}}\{ {{b}_{1}},\,{{b}_{2}}....,\,{{b}_{n}}\} $ – матрица коэффициентов входных сигналов; $U = {{[{{u}_{1}},{{u}_{2}}, \ldots ,{{u}_{n}}]}^{{\text{T}}}}$ – вектор входных сигналов.

В данной статье этот подход к описанию МС используется для анализа устойчивости периодических движений в нелинейных МС (НМС) и для оценки значения их параметров.

1. Описание динамической НМС. Рассмотрим управляемую НМС с идентичными (однотипными) нелинейными подсистемами и числовыми коэффициентами ${{k}_{{ij}}}$-связи между ними. Термин “однотипные” применяют не только к системам, состоящим из одинаковых (с технической точки зрения) элементов, но и к МС, сепаратные подсистемы которых имеют одинаковые (однотипные) динамические характеристики. В дальнейшем предполагается использование термина “однотипные” именно в этом смысле. Предполагаем, что каждая нелинейная система и все замкнутые контуры МС, образованные числовыми связями, удовлетворяют условию фильтра, что позволяет нам применять метод гармонической линеаризации [8–10].

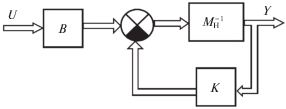
Уравнение гармонически линеаризованной НМС в полиномиальной векторно-матричной форме имеет вид

где a – амплитуда входного гармонического сигнала, ${{M}_{{\text{н}}}} = {\text{diag}}\{ {{M}_{1}}(p{\text{,}}a),...,{{M}_{n}}(p{\text{,}}a)\} $. Отметим, что полиномы ${{M}_{i}}(p,a),\;i = \overline {1,n} $, зависят от $q(a),\;q{\kern 1pt} '(a)$ – коэффициентов гармонической линеаризации. Так как мы рассматриваем МС с однотипными подсистемами, то ${{M}_{i}}(p,a) = M,\;i = \overline {1,n} $.

Структурная схема гармонически линеаризованной НМС представлена на рис. 1.

На основе данного описания требуется решение трех задач:

1) анализа устойчивости состояния равновесия НМС,

2) определения параметров периодических движений (ПД) в НМС, т.е. их амплитуды ${{a}_{{\text{п}}}}$ и частоты ${{\omega }_{{\text{п}}}}$,

3) оценки устойчивости ПД в НМС при вариации ее параметров.

2. Анализ устойчивости состояния равновесия нелинейной многосвязной системы. Для оценки устойчивости динамического и статического состояния равновесия нелинейной МС запишем ее характеристическое уравнение в виде

Раскрыв определитель (2.1), получим относительно характеристического полинома подсистем М алгебраическое уравнение степени, равной порядку матрицы, т.е. количеству физических переменных y_i:

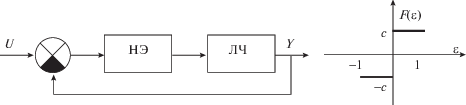
Здесь числовые коэффициенты h_i отражают связи между: h₂ – парами подсистем, h₃ – тройками подсистем, h_n – всеми подсистемами, что соответствует вычислению определителя K. По характеристическому уравнению (2.2) будем изучать статическую устойчивость состояния равновесия нелинейной многосвязной системы (1.1), которое соответствует условию положительности свободного члена характеристического уравнения (2.2) НМС. Полагая, что $M(0,a) = 1$, получим условие статической устойчивости положения равновесия НМС:

Введем понятие критической точки, под которой будем понимать значение корня характеристического уравнения МС, лежащей на ее мнимой оси.

Если в уравнении (2.2) вместо М поставить комплексную переменную z, то получим уравнение критических точек, коэффициенты которых вычисляются по формуле (2.3):

Отметим, что корни z_k уравнения (2.5) лежат на мнимой оси корней характеристического уравнения НМС (2.1), а потому будут служить критическими точками для характеристического уравнения отдельной подсистемы. Тогда для нелинейных систем остается справедливым по содержанию критерий устойчивости положения равновесия линейных МС, предложенный в работе [7].

Критерий устойчивости I. Для устойчивости динамического состояния равновесия однотипной гармонически линеаризованной НМС (1.1) необходимо и достаточно, чтобы при изменении ω от 0 до ±∞ годограф Михайлова М(jω, a) (характеристический полином нелинейной автономной подсистемы) при варьировании амплитуды a в некотором диапазоне охватывал все критические точки уравнения (2.5) (рис. 2).

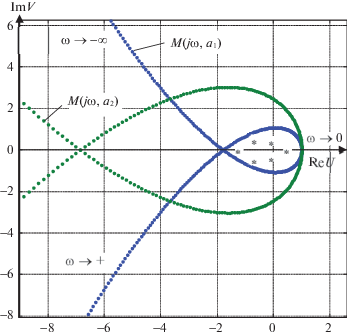
На рис. 2 для устойчивой однотипной шестисвязной нелинейной системы показана деформация кривой Михайлова, соответствующая характеристическому полиному нелинейной подсистемы при вариации амплитуды a входного гармонического сигнала.

3. Оценка значений параметров периодических движений в НМС. Очевидно, что условием наличия ПД в НМС является прохождение кривой Михайлова М(jω, a) через один из множества {z_i} корней уравнения критических точек, т.е. НМС будет находиться на колебательной границе устойчивости.

Пусть в общем случае критической точкой будет корень уравнения (2.5) вида $z_{i}^{*} = {{\alpha }_{i}} + j{{\beta }_{i}}$, через которую проходит кривая Михайлова. Тогда справедливо равенство

Используя частотную форму записи можно уравнение (3.1) представить в виде

Отсюда получим систему из двух уравнений:

Решая систему уравнений (3.3), найдем искомые параметры ПД ${{\omega }_{{\text{п}}}},\;{{a}_{{\text{п}}}}$.

Уравнения (3.1) и (3.2) можно представить и в другой форме:

Из системы уравнений (3.4) также можно получить искомые параметры $({{\omega }_{{\text{п}}}},{{a}_{{\text{п}}}})$ ПД в НМС. При этом искомое значение амплитуды ${{a}_{{\text{п}}}}$ и частоты ${{\omega }_{{\text{п}}}}$ ПД определяются по той кривой Михайлова M(а_п, jω_п), которая пересечет критическую точку $z_{i}^{*}$.

Пример. Требуется исследовать НМС на наличие автоколебаний. НМС состоит из идентичных нелинейных подсистем, связанных друг с другом численными коэффициентами по выходным переменным Y. Нелинейная подсистема представляет собой стандартную структуру, состоящую из нелинейного элемента (НЭ) и линейной части (ЛЧ) (рис. 3).

В качестве НЭ рассматривается реле (рис. 3) с коэффициентами гармонической линеаризации, равным: q(a) = ${{4c} \mathord{\left/ {\vphantom {{4c} {\pi a}}} \right. \kern-0em} {\pi a}}$; c = π; q'(a) = 0.

Пусть передаточная функция ЛЧ равна:

Тогда характеристический полином М гармонически линеаризованного уравнения подсистемы будет равен:

Матрица К коэффициентов связи между подсистемами равна:

Характеристическое уравнение трехсвязной системы имеет вид

При исследовании автономных подсистем параметры автоколебаний ${{\omega }_{{\text{п}}}}$ = 1, ${{a}_{{\text{п}}}}$ = 8. Из (3.6) в соответствии с (2.5) получим уравнение критических точек, заменив М на z:

Коэффициенты h₂ и h₃ характеристического уравнения (3.6) вычислим по формулам (2.3). При заданных числовых значениях коэффициентов связи получим h₂ = 0.8175, h₃ = 1.728, тогда корни уравнения связи (3.7) равны:

Используя частотную форму записи, можно уравнение (3.5) представить в виде (3.1):

Возьмем вещественный корень z₁ = –0.976. Получим систему из двух уравнений (3.3):

Отсюда определим значения параметров ПД:

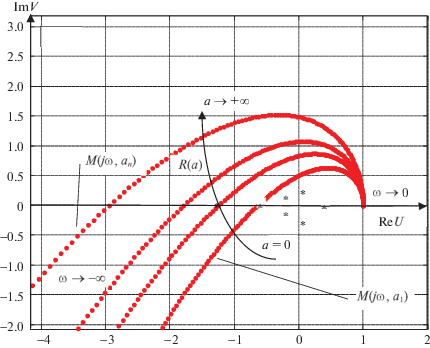
Эту задачу можно решить и графически. Построим годограф функции (3.8) при ω ∈ (0, +∞) и а ∈ (0, +∞). На этой же плоскости расположим собственные значения уравнения критических точек z_i (рис. 4). Из всех корней критическим корнем будет z₁ = –0.976, так как прохождение годографа D(jω, a) через остальные корни соответствует неустойчивой НМС (по вышеприведенному критерию).

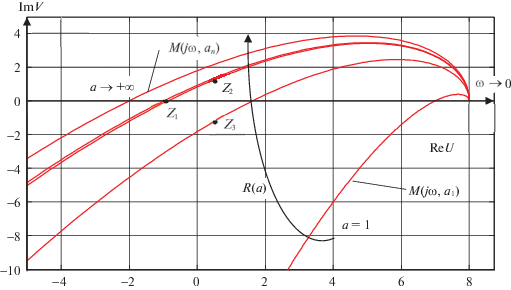
Следовательно, в МС существуют устойчивые ПД с параметрами ${{\omega }_{{\text{п}}}}$ = 1, ${{a}_{{\text{п}}}}$ = 8.976. Отметим, что при числовых связях в МС частота ω подсистем не меняется, а изменяется лишь амплитуда ${{a}_{{\text{п}}}}$ колебаний в МС по сравнению с автономной подсистемой.

4. Анализ устойчивости ПД в НМС. Для анализа устойчивости ПД необходимо определить направление деформации кривой Михайлова M(а, jω) при увеличении амплитуды а. Пусть вектор R(а) и будет определять направление роста амплитуды а.

Далее, пользуясь вышеизложенным критерием устойчивости, проследим, какой станет система (устойчивой или неустойчивой) при движении по вектору R(а) от критической точки.

Если при движении по R(а) в сторону увеличения а кривая Михайлова будет соответствовать устойчивой системе (по критерию I), то амплитуда ПД будут уменьшаться, а если при движении по R(а) в сторону уменьшения амплитуды а кривая Михайлова будет соответствовать неустойчивой системе, то амплитуда ПД будет увеличиваться, т.е. данная критическая точка соответствует устойчивым ПД (рис. 5).

Отсюда можно сформулировать критерии устойчивости ПД в НМС

Критерии устойчивости периодических движений II. При пересечении кривой Михайлова подсистемы с критической точкой уравнения связей, полученные ПД в однотипной НМС будут устойчивыми, если при движении по R(а) в сторону увеличения амплитуды а кривая Михайлова будет соответствовать устойчивой системе. Если же картина будет обратной, то ПД в критической точке будут неустойчивыми.

В примере периодические движения в точке z₁ будут устойчивыми, так как с увеличением амплитуды а кривая Михайлова соответствует устойчивой системе (рис. 4).

Заключение. Предложен критерий устойчивости положения равновесия для однотипной НМС на основе поведения характеристического полинома (кривой Михайлова) нелинейных подсистем относительно критических точек. Описан метод оценки параметров ПД однотипной НМС на основе начальной информации о характеристическом полиноме нелинейной подсистемы (кривой Михайлова) и числовых значениях корней уравнения связи между подсистемами. Рассмотрен критерий устойчивости ПД однотипных НМС на основе деформации кривой Михайлова при вариации амплитуды входного сигнала. Предложенный подход к исследованию НМС развивает дальше подход, известный в классической теории систем автоматического управления.