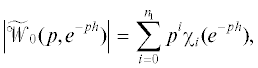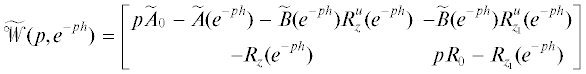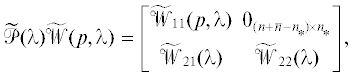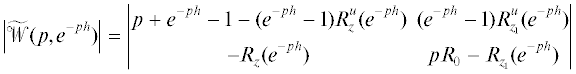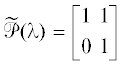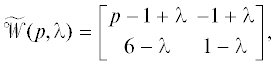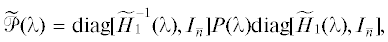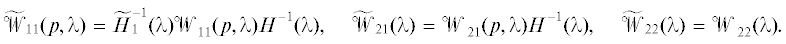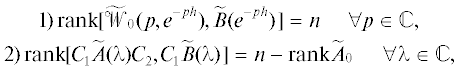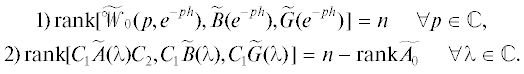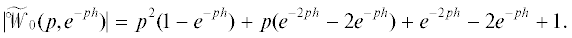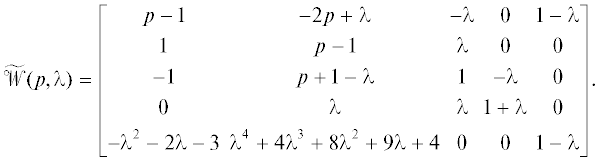Известия РАН. Теория и системы управления, 2020, № 1, стр. 23-43

Введение. Одной из ключевых проблем теории автоматического управления является задача проектирования систем, обладающих заданными свойствами. В связи с этим задачам управления спектром и стабилизации систем с запаздыванием, ставшими на сегодняшний день уже классическими, посвящено достаточно большое количество исследований [1–24] (историю вопроса можно проследить по библиографическим ссылкам в них). Это работы по стабилизации объекта с запаздыванием [1–5], назначению конечного спектра [6–9], спектральной приводимости [10–13] – приведение систем к конечному (но не заданному) спектру, модальной управляемости [14–19].

Известно, что спектр исходной системы с запаздыванием может содержать инвариантные собственные значения, которые возможно исключить из спектра только с помощью интегральных регуляторов [9]. А это значит, что критерии разрешимости задачи модальной управляемости [15, 17, 19] или назначения конечного спектра [7, 8] априори предполагают применение регуляторов интегрального типа. Если исходная система была системой с сосредоточенными запаздываниями, то замкнутая система в случае замыкания ее интегральными регуляторами станет системой с сосредоточенными и распределенными запаздываниями. Интегралы, содержащие распределенное запаздывание, в случае практической реализации заменяются конечными суммами [20], что даже при использовании квадратурных формул высокой точности может привести к нежелательным эффектам [6, 20, 21] (например, к потере устойчивости). В связи с этим представляет интерес возможность управления системой в классе дифференциально-разностных регуляторов, поскольку замкнутая система в этом случае будет содержать только сосредоточенное запаздывание (некоторые уточняющие аспекты приведены в Приложении).

Статья посвящена исследованию задачи управления спектром линейных автономных вполне регулярных дифференциально-алгебраических систем с запаздыванием (иногда говорят [25] о сингулярных или дескрипторных системах). Основной характеристикой таких систем является наличие вырожденной матрицы при производной. Поэтому переменные в таких системах имеют наряду с дифференциальными еще и алгебраические связи. Включение запаздывания в дифференциально-алгебраическую систему позволяет говорить о комбинации двух динамик, соответствующих дифференциальному и разностному уравнениям. Для таких систем представлено два подхода к синтезу дифференциально-разностных регуляторов для управления спектром линейных автономных вполне регулярных дифференциально-алгебраических систем с соизмеримыми запаздываниями в состоянии и управлении. Первый предполагает классическую схему замыкания исходной системы, обеспечивающую характеристическому квазиполиному наперед заданные коэффициенты. Для ее реализации обобщается достаточно часто применяемая в литературе [14, 16, 23, 26] идея, в основе которой лежит выбор столбцов матрицы управляемости (наблюдаемости) специально построенной системы так, чтобы полученная матрица определяла некоторое преобразование подобия, приводящее систему к более простому виду. Чтобы преобразование было обратимым, эта матрица должна быть унимодулярной. Это требование при наличии запаздывания сужает класс управляемых систем. В качестве альтернативы описанной ситуации предложено ограничиться слабой модальной управляемостью [19] – из замкнутой системы выделить подсистему, содержащую исходные переменные разомкнутой системы и независящую от остальных переменных замкнутой системы, характеристический квазиполином которой будет иметь наперед заданный вид (размер замкнутой системы больше размера исходной). Такой подход к построению обратной связи является обобщением использования регуляторов переменной структуры для модальной управляемости [16–18] в случае систем нейтрального типа.

1. Постановка задачи. Пусть задана линейная автономная вполне регулярная дифференциально-алгебраическая система с соизмеримыми запаздываниями в состоянии и управлении:

где $z \in {{\mathbb{R}}^{n}}$ – вектор решения исходной системы, $u \in {{\mathbb{R}}^{r}}$ – вектор кусочно-непрерывного управления; ненулевая матрица ${{\widetilde A}_{0}} \in {{\mathbb{R}}^{{n \times n}}},$ $\widetilde A(\lambda ) \in {{\mathbb{R}}^{{n \times n}}}[\lambda ]$, $\widetilde B(\lambda ) \in {{\mathbb{R}}^{{n \times r}}}[\lambda ]$ (${{\mathbb{R}}^{{i \times j}}}[\lambda ]$ – множество полиномиальных матриц размера i × j); $\lambda $ – оператор сдвига, определяемый для заданного постоянного запаздывания $h = {\text{const}} > 0$ формулой $\lambda f(t) = f(t - h)$ (для произвольной функции $f$). Пусть где ${{\widetilde A}^{{(i)}}} \in {{\mathbb{R}}^{{n \times n}}},$ ${{\widetilde B}^{{(i)}}} \in {{\mathbb{R}}^{{n \times r}}},$ ${{m}_{A}} = \mathop {{\text{deg}}}\nolimits_\lambda A(\lambda )$, ${{m}_{B}} = {\text{de}}{{{\text{g}}}_{\lambda }}B(\lambda )$ (запись $\mathop {{\text{deg}}}\nolimits_\lambda \Upsilon (\lambda )$ обозначает максимальную степень переменной $\lambda $ у элементов полиномиальной матрицы $\Upsilon (\lambda )$ или степень переменной $\lambda $ соответствующего полинома). Тогда выражения $\widetilde A(\lambda )z(t)$ и $\widetilde B(\lambda )u(t)$ в правой части (1.1) имеют вид

Также заметим, что если матрица ${{\tilde {A}}_{0}}$ невырожденная, то $d{\text{/}}dt({{\widetilde A}_{0}}z(t)) = {{\widetilde A}_{0}}\dot {z}(t).$ В случае вырожденной матрицы ${{\tilde {A}}_{0}}$ такое равенство в общем случае не имеет места, поскольку функция $z$ может быть (в отличии от функции ${{\widetilde A}_{0}}z$) не дифференцируемой. Решение системы (1.1) при заданном управлении $u(t),t \in [ - {{m}_{B}}h,0),$ однозначно определяется известными начальными условиями

Напомним, что система (1.1) называется вполне регулярной [19, 27, 28], если степень полинома ${\text{de}}{{{\text{g}}}_{p}}\left| {p{{{\widetilde A}}_{0}} - \widetilde A(0)} \right| = {{n}_{1}}$, где ${{n}_{1}} = {\text{rank}}{{\widetilde A}_{0}}(0 < {{n}_{1}} \leqslant n),$ |⋅| – определитель матрицы. В рамках данной статьи системы (1.1), у которых матрица ${{\tilde {A}}_{0}}$ невырожденная, также будем считать вполне регулярными системам.

Рассмотрим матрицу 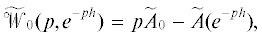которая является характеристической матрицей разомкнутой (u ≡ 0) системы (1.1). Характеристический квазиполином такой системы (1.1) имеет вид

где ${{\chi }_{i}}( \cdot )$, $i = \overline {1,{{n}_{1}}} $ – некоторые полиномы, причем ${{\chi }_{{{{n}_{1}}}}}(0) \ne 0.$

Задача. Пусть задан произвольный квазиполином следующего вида:

где ${{\tilde {d}}_{i}}( \cdot )$ – некоторые полиномы, причем ${{\tilde {d}}_{{{{n}_{0}}}}}(0) \ne 0$, ${{n}_{0}} \geqslant {{n}_{1}}$ – некоторое число, которое будем называть степенью квазиполинома (1.2). Рассмотрим следующее множество значений функции z(t): где $\varrho \in \mathbb{N}$ – любое число (если при некотором t > 0 и $j \in \mathbb{N}$ значение функции $z(t - jh) \in \mathcal{Z}(t)$ неопределенно, то считаем его равным нулю). Требуется замкнуть систему (1.1) обратной связью по состоянию $u(t),$ линейно зависящей от элементов множества $\mathcal{Z}(t)$ при любом фиксированном $\varrho $ и, возможно, от некоторой вспомогательной векторной переменной, удовлетворяющей линейной автономной дифференциально-алгебраической или разностной системе так, чтобы: 1) замкнутая система осталась линейной автономной вполне регулярной дифференциально-алгебраической системой с соизмеримыми запаздываниями; 2) компонента z решения замкнутой системы удовлетворяла линейной автономной вполне регулярной дифференциально-алгебраической системе с соизмеримыми запаздываниями и характеристическим квазиполиномом (1.2).

Для решения задачи будем использовать регулятор

где ${{z}_{1}} \in {{\mathbb{R}}^{{\bar {n}}}}$ – вспомогательная переменная, матрицы $\mathbb{R}_{z}^{u}(\lambda ) \in {{\mathbb{R}}^{{r \times n}}}[\lambda ]$, $\mathbb{R}_{{{{z}_{1}}}}^{u}(\lambda ) \in {{\mathbb{R}}^{{r \times \bar {n}}}}[\lambda ]$, ${{\mathbb{R}}_{0}} \in {{\mathbb{R}}^{{\bar {n} \times \bar {n}}}}$, ${{\mathbb{R}}_{z}}(\lambda ) \in {{\mathbb{R}}^{{\bar {n} \times n}}}[\lambda ]$, ${{\mathbb{R}}_{{{{z}_{1}}}}}(\lambda ) \in {{\mathbb{R}}^{{\bar {n} \times \bar {n}}}}[\lambda ]$ число $\bar {n} \in \{ 0\} \cup \mathbb{N}$ не зависит от n и будет определяться в процессе построения регулятора (1.4) (в случае, когда $\bar {n} = 0,$ дополнительная переменная z₁ и второе уравнение в (1.4) будут отсутствовать). Начальные условия для замкнутой системы (1.1), (1.4) (если они не определяются начальным условием для системы (1.1)) выбираются произвольными непрерывными функциями.

Параметры регулятора (1.4) будем выбирать так, чтобы выполнялось равенство ${\text{de}}{{{\text{g}}}_{p}}\left| {p{{R}_{0}} - {{R}_{{{{z}_{1}}}}}(0)} \right|$ = rankR₀, которое обеспечит требование вполне регулярности замкнутой системы (1.1), (1.4). Обратим внимание, что матрица R₀ может быть нулевой. В этом случае для того, чтобы замкнутая система (1.1), (1.4) была вполне регулярной, будем придерживаться условия $\left| {{{R}_{{{{z}_{1}}}}}(0)} \right| \ne 0$.

Для дальнейшей характеристики системы (1.1), (1.4), с точки зрения разрешимости задачи, введем [19] следующее свойство произвольной матрицы $\Lambda (p,\lambda ) = p{{\Lambda }_{0}} + \widehat \Lambda (\lambda )$, где ${{\Lambda }_{0}} \in {{\mathbb{R}}^{{\phi \times \phi }}}$ – ненулевая матрица, $\widehat \Lambda (\lambda ) \in {{\mathbb{R}}^{{\phi \times \phi }}}[\lambda ]$, $\phi \in \mathbb{N}$. Будем говорить, что матрица $\Lambda (p,\lambda )$ имеет CR-структуру (CR – completely regular), если выполняется условие

Любой матрице, имеющей CR-структуру, можно поставить в соответствие линейную автономную вполне регулярную дифференциально-алгебраическую систему с соизмеримыми запаздываниями. Верно и обратное утверждение. В частности, матрица 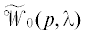имеет CR-структуру.

Пусть

– характеристическая матрица замкнутой системы (1.1), (1.4).

Определение 1. Систему (1.1) назовем модально управляемой [19], если для любого заданного квазиполинома $\widetilde d(p,{{e}^{{ - ph}}})$ вида (1.2) степени ${{n}_{0}} \geqslant {{n}_{1}}$ существует регулятор (1.4), такой, что: 1) матрица 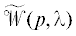имеет CR-структуру; 2) определитель .

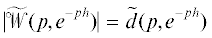Определение 2. Систему (1.1) назовем слабо модально управляемой [19], если для любого заданного квазиполинома $\widetilde d(p,{{e}^{{ - ph}}})$ вида (1.2) степени ${{n}_{0}} \geqslant {{n}_{1}}$ существует регулятор (1.4), такой, что: 1) матрица 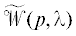имеет CR-структуру; 2) существуют унимодулярная матрица 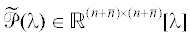(т.е. матрица, для которой 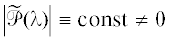) и число ${{n}_{*}} \leqslant \bar {n}$, такие, что выполняется равенство

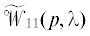где матрица имеет CR-структуру, матрицы 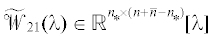, ${{\tilde {\mathcal{W}}}_{{22}}}(\lambda ) \in {{\mathbb{R}}^{{{{n}_{ * }} \times {{n}_{ * }}}}}[\lambda ]$, запись ${{0}_{{{{k}_{1}} \times {{k}_{2}}}}}$ обозначает нулевую матрицу размера ${{k}_{1}} \times {{k}_{2}};$ 3) определитель .

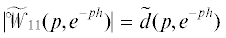Замечание 1. Дадим разъяснение свойства слабой модальной управляемости. Выполнение равенства (1.6) говорит о том, что найдется такой момент времени $\bar {t},\bar {t} > {{m}_{B}},$ что при $t > \bar {t}$ в системе (1.1), замкнутой регулятором (1.4), можно выделить вполне регулярную дифференциально-алгебраическую подсистему с характеристической матрицей 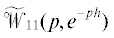и наперед заданным характеристическим квазиполиномом 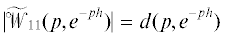, однозначно определяющую величину z. Момент времени $\bar {t} > {{m}_{B}}$ выбирается таким, чтобы при $t > \bar {t}$ было определено решение ${\text{col}}[z(t - {{i}_{1}}h),{{z}_{1}}(t - {{i}_{1}}h)]$ системы, отвечающей характеристической матрице 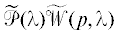, где i₁ = ${\text{de}}{{{\text{g}}}_{\lambda }}\tilde {\mathcal{P}}(\lambda )\tilde {\mathcal{W}}(p,\lambda )$. При этом существование унимодулярной матрицы 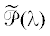позволяет получить указанную подсистему посредством элементарных преобразований уравнений системы (1.1), (1.4), в которые не входит операция дифференцирования. Забегая вперед, отметим, что в компоненты решения подсистемы, отвечающей характеристической матрице 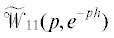, будет входить не только величина z, но и компоненты функции z₁, соответствующие базисным столбцам матрицы R₀ и, возможно, еще некоторые компоненты вектора z₁, а число ${{n}_{*}} \leqslant \bar {n} - {\text{rank}}{{R}_{0}}$. Более детально это будет видно из доказательства необходимости условия теоремы 2 (см. разд. 4). Обратим внимание, что если ${{n}_{ * }} = 0,$ то свойства слабой модальной управляемости и модальной управляемости совпадают ().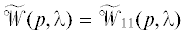

Пример 1. Рассмотрим систему

которая является частным случаем системы (1.1) $({{\widetilde A}_{0}} = 1)$. Эта система не является модально управляемой или стабилизируемой в традиционном смысле [1–9, 14, 15], поскольку в спектр замкнутой системы всегда будет входить число p = 0. Действительно, замыкая систему (1.7) регулятором (1.4), видим, что определитель характеристической матрицы замкнутой системы при p = 0 обращается в ноль.

Покажем, как обратной связью обеспечить устойчивую динамику функции z, определяемую, например, характеристическим полиномом p + 5. Замкнем систему (1.7) регулятором

Тогда управление $u(t) - u(t - h) = z(t - h) - 6z(t)$, $t > \bar {t} = h$. Подставив это выражение в систему (1.7), получим, что функция z при $t > \bar {t}$ удовлетворяет системе $\dot {z}(t) = - 5z(t).$ То же самое: если умножить матрицу

на характеристическую матрицу системы (1.7), (1.8) ($\lambda = {{e}^{{ - ph}}}$) согласно формуле (1.6), получим матрицу, у которой левый верхний блок .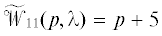

2. Приведение исходной системы к специальному виду. Поскольку характеристическая матрица 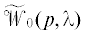($\lambda = {{e}^{{ - ph}}}$) системы (1.1) имеет CR-структуру, то ее можно привести [19, 27] к более простому для исследования виду. Выберем неособые матрицы H и H₁, такие, что ${{H}_{1}}{{\tilde {A}}_{0}}H$ = = ${\text{diag}}\left[ {{{I}_{{{{n}_{1}}}}},{{0}_{{{{n}_{2}} \times {{n}_{2}}}}}} \right]$, где ${{n}_{2}} = n - {{n}_{1}}$. Здесь и ниже для произвольного числа $i \in \mathbb{N}$ $(i > 1)$ единичную матрицу размера i × i будем обозначать ${{I}_{i}}$. Пусть

где ${{A}_{{1j}}}(\lambda ) \in {{\mathbb{R}}^{{{{n}_{1}} \times {{n}_{j}}}}}[\lambda ]$, j = 1, 2, ${{\widehat A}_{{2j}}}(\lambda ) \in {{\mathbb{R}}^{{{{n}_{2}} \times {{n}_{j}}}}}[\lambda ]$, j = 1, 2, ${{B}_{1}}(\lambda ) \in {{\mathbb{R}}^{{{{n}_{1}} \times r}}}[\lambda ]$, ${{\widehat B}_{2}}(\lambda ) \in {{\mathbb{R}}^{{{{n}_{2}} \times r}}}[\lambda ]$. Так как степень ${\text{deg}}\left| {p{{H}_{1}}{{{\widetilde A}}_{0}}H - {{H}_{1}}\widetilde A(0)H} \right| = {{n}_{1}}$, то определитель ${\text{|}}{{\widehat A}_{{22}}}(0){\text{|}} \ne 0$. Положив ${{A}_{{21}}}(\lambda ) = - \widehat A_{{22}}^{{ - 1}}(0){{\widehat A}_{{21}}}(\lambda )$, ${{A}_{{22}}}(\lambda ) = - {{\lambda }^{{ - 1}}}\widehat A_{{22}}^{{ - 1}}(0)({{\widehat A}_{{22}}}(\lambda ) - {{\widehat A}_{{22}}}(0))$, ${{B}_{2}}(\lambda ) = - \widehat A_{{22}}^{{ - 1}}(0){{\widehat B}_{2}}(\lambda )$ и выполнив в системе (1.1) замену переменных $z = H{\text{col}}[x,y]$, $x \in {{\mathbb{R}}^{{{{n}_{1}}}}}$, $y \in {{\mathbb{R}}^{{{{n}_{2}}}}}$, получим новую систему:

Теперь выберем неособые матрицы $\widehat H$ и ${{\widehat H}_{1}}$, такие, что ${{\widehat H}_{1}}{{R}_{0}}\widehat H = {\text{diag}}[{{I}_{{\mathop {\bar {n}}\nolimits_1 }}},{{0}_{{\mathop {\bar {n}}\nolimits_2 \times \mathop {\bar {n}}\nolimits_2 }}}],$ ${{\bar {n}}_{1}} = {\text{rank}}{{R}_{0}}$, ${{\bar {n}}_{2}} = \bar {n} - {{\bar {n}}_{1}}$. Проделав аналогичные преобразования со вторым уравнением в соотношениях (1.4), после соответствующей замены переменных перепишем регулятор (1.4) в виде

где ${{x}_{1}} \in {{\mathbb{R}}^{{\mathop {\bar {n}}\nolimits_1 }}}$, ${{y}_{1}} \in {{\mathbb{R}}^{{\mathop {\bar {n}}\nolimits_2 }}}$ – вспомогательные переменные, величины $X = {\text{col}}[x,{{x}_{1}}]$, $Y = {\text{col}}[y,{{y}_{1}}]$ ${{Q}_{{01}}}(\lambda ) \in {{\mathbb{R}}^{{r \times {{n}_{x}}}}}[\lambda ]$, ${{Q}_{{02}}}(\lambda ) \in {{\mathbb{R}}^{{r \times {{n}_{y}}}}}[\lambda ]$, ${{Q}_{{i1}}}(\lambda ) \in {{\mathbb{R}}^{{\mathop {\bar {n}}\nolimits_i \times {{n}_{x}}}}}[\lambda ]$, ${{Q}_{{i2}}}(\lambda ) \in {{\mathbb{R}}^{{\mathop {\bar {n}}\nolimits_i \times {{n}_{y}}}}}[\lambda ]$, i = 1, 2, ${{n}_{x}} = {{n}_{1}} + {{\bar {n}}_{1}}$, ${{n}_{y}} = {{n}_{2}} + {{\bar {n}}_{2}}$. Поскольку предполагаются известными только элементы множества $\mathcal{Z}(t),$ определяемого формулой (1.3), то приходим к необходимости синтеза регулятора $u(t),$ линейно зависящего от элементов множества: и, возможно, дополнительных переменных ${{x}_{1}}$ и ${{y}_{1}}$.

Замечание 2. Можно выбрать матрицы регулятора (2.2) так, чтобы управление u(t) линейно зависело не только от элементов множества (2.3), но и от $y(t).$ При этом если у полученной замкнутой системы (2.1), (2.2) характеристическая матрица будет иметь CR-структуру, то y(t) линейно выражается через элементы множества ${{\mathcal{Z}}_{1}}(t)$ и вспомогательные переменные.

Свойства модальной управляемости и слабой модальной управляемости для системы (2.1) формулируются аналогично определениям 1 и 2 соответственно.

Дальнейшее исследование свойств модальной управляемости и слабой модальной управляемости будем проводить для системы (2.1). При этом будем осуществлять построение регулятора вида (2.2), а квазиполиному (1.2) поставим в соответствие квазиполином

3. Синтез регуляторов в задаче модальной управляемости. Рассмотрим систему (2.1). Введем матрицу

которая является характеристической матрицей системы (2.1), и матрицу $B(\lambda ) = {\text{col}}[{{B}_{1}}(\lambda ),{{B}_{2}}(\lambda )].$ Замкнем систему (2.1) регулятором (2.2) и через $\mathcal{W}(p,{{e}^{{ - ph}}})$ обозначим характеристическую матрицу замкнутой системы (2.1), (2.2).

Вначале докажем необходимое условие модальной управляемости. Пусть $\mathbb{C}$ – множество комплексных чисел.

Лемма 1. Для того чтобы система (2.1) была модально управляема, необходимо, чтобы одновременно выполнялись два условия:

Доказательство. Доказательство необходимости условия (3.1) принципиальных трудностей не представляет, поэтому останавливаться на этом не будем. Докажем необходимость условия (3.2). Предположим, что регулятор (2.2) обеспечивает замкнутой системе (2.1), (2.2) характеристический квазиполином $d(p,{{e}^{{ - ph}}}) = {{p}^{{{{n}_{0}}}}},$ где ${{n}_{0}} \geqslant {{n}_{1}}$ – некоторое число. Упорядочим переменные замкнутой системы (2.1), (2.2) в виде вектора ${\text{col}}[x,{{x}_{1}},y,{{y}_{1}}]$ и запишем характеристический полином:

где $A_{{ij}}^{{(0)}}(\lambda )$, i = 1, 2, j = 1, 2, – некоторые полиномиальные матрицы подходящих размеров. Пусть определитель ${\text{|}}{{I}_{{{{n}_{y}}}}} - A_{{22}}^{{(0)}}(\lambda ){\text{|}} = {{d}_{0}}(\lambda )$, ${{\Pi }_{0}}(\lambda )$ – матрица, присоединенная к матрице $({{I}_{{{{n}_{y}}}}} - A_{{22}}^{{(0)}}(\lambda ))$, т.е. $({{I}_{{{{n}_{y}}}}} - A_{{22}}^{{(0)}}(\lambda )){{\Pi }_{0}}(\lambda ) = {{d}_{0}}(\lambda ){{I}_{{{{n}_{y}}}}}$. Определим квазиполином

Умножим обе части формулы (3.3) справа на соответствующие части очевидного равенства ${\text{|diag}}[{{I}_{{{{n}_{0}}}}},{{\Pi }_{0}}({{e}^{{ - ph}}})]{\text{|}} = d_{0}^{{{{n}_{y}} - 1}}({{e}^{{ - ph}}})$, в итоге получим квазиполином

С другой стороны, из вида определителя в равенстве (3.4) следует, что квазиполином ${{d}^{*}}(p,{{e}^{{ - ph}}})$ представим в виде

где $\tilde {d}(p,{{e}^{{ - ph}}})$ – некоторый квазиполином, у которого максимальная степень переменной p меньше числа ${{n}_{0}}.$ Сравнивая правые части равенств (3.5) и (3.6), заключаем, что ${{d}_{0}}(\lambda ) \equiv 1$. Записав это тождество в виде где $Q_{{i2}}^{{(1)}}(\lambda )$, $i = 0,2$, – первые ${{n}_{2}}$ столбцов матрицы ${{Q}_{{i2}}}(\lambda )$, а $Q_{{i2}}^{{(2)}}(\lambda )$ – оставшиеся ${{\bar {n}}_{2}}$ столбцов матрицы ${{Q}_{{i2}}}(\lambda )$, видим, что оно не может иметь места, если нарушается условие (3.2). Лемма доказана.

Далее считаем, что условия (3.1) и (3.2) выполнены. В силу условия (3.2) существуют [12] полиномиальные матрицы ${{L}_{{ij}}}(\lambda )$, $i = 1,2$, $j = 1,2$, подходящих размеров, для которых справедливо тождество

где число $r{\text{*}} \in \mathbb{N} \cup \{ 0\} $. Вопрос построения таких матриц обсуждается ниже (см. разд. 5). Систему (2.1) замкнем регулятором: где ${{y}_{1}} \in {{\mathbb{R}}^{{r*}}}$ – вспомогательная переменная, $w = {\text{col}}[{{w}_{1}},{{w}_{2}}]$ – новое управление. Здесь и далее (за исключением случаев, где это может вызвать неоднозначную трактовку) при синтезе регулятора будем предполагать, что переменная t принимает такие значения, при которых решение замкнутой системы определено. Введем матрицы:

Систему (2.1), (3.8) запишем в виде

где величина ${{Y}_{1}} = {\text{col}}[y,{{y}_{1}}].$

Пусть $\Pi (\lambda )$ – матрица, обратная к матрице $({{I}_{{{{n}_{2}} + r{\text{*}}}}} - \lambda {{\overline A }_{{22}}}(\lambda ))$. В силу условия (3.7) матрица $\Pi (\lambda ) \in {{\mathbb{R}}^{{({{n}_{2}} + r{\text{*}}) \times ({{n}_{2}} + r{\text{*}})}}}[\lambda ]$, т.е. является полиномиальной. В системе (3.9) введем новую переменную ${{Y}_{1}} = \Pi (\lambda ){{Y}_{2}},$ в итоге получим систему

где матрица ${{\widetilde A}_{{12}}}(\lambda ) = {{\overline A }_{{12}}}(\lambda )\Pi (\lambda )$. Из вида уравнений системы (3.10) следует, что величина $x$ удовлетворяет системе где $K(\lambda ) = {{A}_{{11}}}(\lambda ) + {{\widetilde A}_{{12}}}(\lambda ){{\overline A }_{{21}}}(\lambda )$, $F(\lambda ) = {{\widetilde A}_{{12}}}(\lambda ){{\overline B }_{2}}(\lambda ) + {{\overline B }_{1}}(\lambda )$.

Перед формулировкой следующего утверждения напомним, что под рангом полиномиальной матрицы понимается наибольший порядок не равного тождественному нулю ее минора.

Лемма 2. Если выполнено условие (3.1), то

Доказательство. Предположим, что условие (3.12) нарушается. Тогда найдется ${{p}_{0}} \in \mathbb{C}$, такое, что выполняется неравенство

Выберем ненулевой вектор $g \in {{\mathbb{R}}^{{{{n}_{1}}}}}$, удовлетворяющий условиям:

Пусть вектор $\bar {g} = [{{g}^{{\text{T}}}},{{g}^{{\text{T}}}}{{\widetilde A}_{{12}}}(\lambda )]$. Можно проверить, что выполняются следующие равенства:

Эти соотношения противоречат условию (3.1). Лемма доказана.

Рассмотрим равенство (3.12). Выберем столбцы ${{f}_{{{{i}_{j}}}}}(\lambda )$, ${{i}_{j}} \in \overline {\{ 1,r + r{\text{*}}\} } $, $j = \overline {1,\alpha } $, матрицы $F(\lambda )$ и числа ${{s}_{j}} \in \mathbb{N}$, $j = \overline {1,\alpha } $, ${{s}_{1}} + ... + {{s}_{\alpha }} = {{n}_{1}}$, так, чтобы каждое число ${{s}_{j}},j = \overline {1,\alpha } ,$ было наибольшим из возможных чисел, при котором система векторных полиномов

линейна независима. Сформулируем достаточное условие модальной управляемости.

Теорема 1. Если матрица

является унимодулярной, то система (2.1) модально управляема.

Доказательство. Пусть задан некоторый квазиполином (2.4) степени ${{n}_{0}} = {{n}_{1}}.$ Вначале рассмотрим случай ${\text{|}}\widehat A_{{22}}^{{ - 1}}(0){\text{|}}\left| {{{H}_{1}}} \right|\left| H \right|{{\widetilde d}_{{{{n}_{0}}}}}(p) \equiv 1$ (см. формулу (1.2)). Поскольку матрица (3.13) является унимодулярной, то система (3.11) обладает свойством модальной управляемости в следующем смысле [14, 16]: существует матрица ${{Q}_{x}}(\lambda ) \in {{\mathbb{R}}^{{(r + r{\text{*}}) \times {{n}_{1}}}}}[\lambda ]$, такая, что

В силу равенства (3.14) определитель

На основании соотношения (3.7) имеем

Умножив обе части формулы (3.15) на соответствующие части последнего тождества, заключаем, что справедливо равенство

Пусть матрица ${{Q}_{x}}(\lambda ) = {\text{col}}[{{Q}_{{01}}}(\lambda ),{{Q}_{{21}}}(\lambda )]$, ${{Q}_{{01}}}(\lambda ) \in {{\mathbb{R}}^{{r \times {{n}_{1}}}}}$, ${{Q}_{{21}}}(\lambda ) \in {{\mathbb{R}}^{{r{\text{*}} \times {{n}_{1}}}}}$. Замкнем систему (2.1) регулятором вида

тогда характеристический квазиполином замкнутой системы (2.1), (3.17) совпадет с квазиполиномом (3.16). При этом регулятор (3.17) есть регулятор (2.2), где ${{Q}_{{02}}}(\lambda ) = [\lambda {{L}_{{11}}}(\lambda ),\lambda {{L}_{{12}}}(\lambda )]$, Q₂₂(λ) = = $[\lambda {{L}_{{21}}}(\lambda ),\lambda {{L}_{{22}}}(\lambda )]$, $x = X$, необходимости в использовании переменной ${{x}_{1}}$ и второго уравнения в соотношениях (2.2) нет.

Теперь остановимся на случае 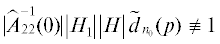. Здесь, в силу определенной схожести с уже рассмотренным случаем, ограничимся только схемой доказательства. Поскольку матрица (3.13) является унимодулярной, то найдутся [14, 16] унимодулярная матрица $\Gamma (\lambda ) \in {{\mathbb{R}}^{{{{n}_{1}} \times {{n}_{1}}}}}[\lambda ],$ определяющая преобразования подобия, и матрица $\widetilde Q(\lambda ) \in {{\mathbb{R}}^{{(r + r{\text{*}}) \times {{n}_{1}}}}}[\lambda ]$, такие, что матрица K⁽¹⁾(λ) = = ${{\Gamma }^{{ - 1}}}(\lambda )(K(\lambda ) + F(\lambda )\widetilde Q(\lambda ))\Gamma (\lambda )$ будет иметь вид

(т.е. от нуля отлична только верхняя наддиагональ матрицы), а столбец $f_{{{{i}_{\alpha }}}}^{{(1)}}(\lambda )$ с номером ${{i}_{\alpha }}$ матрицы ${{\Gamma }^{{ - 1}}}(\lambda )F(\lambda )$ станет $f_{{{{i}_{\alpha }}}}^{{(1)}}(\lambda ) = {\text{col}}[0,0,...,0,1].$ Это позволяет свести исходную задачу к выбору скалярного управления $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{w} $ в виде линейной обратной связи, обеспечивающей системе характеристический квазиполином $d(p,{{e}^{{ - ph}}})$. Несложно проверить, что такой характеристический квазиполином системе (3.18) обеспечит регулятор вида $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{w} (t) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{y} (t)$, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{y} (t)$ = [–d₀(λ), ... ..., $ - {{d}_{{n - 1}}}(\lambda )]\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{x} (t)$ + $(1 - {{d}_{{{{n}_{0}}}}}(\lambda ))\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{y} (t),$ где $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{y} $ – вспомогательная переменная, d_i(p) = ${\text{|}}\hat {A}_{{22}}^{{ - 1}}(0){\text{|}}\left| {{{H}_{1}}} \right|\left| H \right|{{\tilde {d}}_{i}}(p)$, $i = \overline {0,{{n}_{0}}} $. Дальнейшее доказательство незначительно отличается от доказательства уже рассмотренного случая, в силу чего не приводится.

Пусть степень желаемого характеристического квазиполинома ${{n}_{0}} > {{n}_{1}}.$ Тогда систему (3.11) замкнем регулятором

где ${{x}_{1}} \in {{\mathbb{R}}^{{{{n}_{0}} - {{n}_{1}}}}}$ – вспомогательная переменная, $\hat {w} \in {{\mathbb{R}}^{{{{n}_{0}} - {{n}_{1}}}}}$ – новое управление. Можно проверить, что для системы (3.11), (3.19) выполняется условие вида (3.13). Поэтому дальше с ней поступаем так, как это было сделано с системой (3.11). Теорема доказана.

4. Синтез регуляторов в задаче слабой модальной управляемости. Далее понадобятся некоторые вспомогательные сведения и обозначения. Пусть матрица

По аналогии с работами [12, 13, 16–19, 27, 29] определим последовательность векторов ${{q}_{k}}$, $k = m,m + 1, \ldots $, которая является решением разностного уравнения

порождаемого начальным условием ${{q}_{i}} = {{\tilde {q}}_{i}}$, $i = \overline {0,m - 1} $. Последовательность q_k, k = m, $m + 1, \ldots $, определяемая уравнением (4.1), существует в том и только в том случае [29], когда ${{\tilde {q}}_{{m - i}}} = {{T}_{i}}c$, $i = \overline {1,m} $, где ${{T}_{i}} \in {{\mathbb{R}}^{{r \times {{r}_{T}}}}}$ – некоторые матрицы, $c \in {{\mathbb{R}}^{{{{r}_{T}}}}}$ – произвольный постоянный вектор (один и тот же для всех матриц T_i). Процедура построения матриц T_i приведена в работе [29], поэтому здесь не описывается. Отметим, что ее реализация всегда возможна и заключается в решении конечной цепочки однородных алгебраических систем. Обозначим $T = {{T}_{m}}$ и определим матрицу $S \in {{\mathbb{R}}^{{{{r}_{T}} \times {{r}_{T}}}}}$ как решение системы уравнений разрешимость которой следует из определения матриц T_i. Заметим, что будет выполняться равенство

Введем матрицы ${{G}^{{(0)}}} = {{B}^{{(0)}}}T$, ${{G}^{{(i)}}} = {{G}^{{(i - 1)}}}S + {{B}^{{(i)}}}T$, $i = \overline {1,m} $. Обратим внимание, что

Определим матрицу

Для заданной полиномиальной матрицы $B(\lambda )$ матрицу $G(\lambda )$, построенную согласно описанному способу, назовем матрицей дополнительных входов [27] (данный термин оправдывают также доказанные ниже лемма 3 и теорема 2). Представим эту матрицу в виде $G(\lambda ) = {\text{col}}[{{G}_{1}}(\lambda ),{{G}_{2}}(\lambda )],$ где ${{G}_{1}}(\lambda ) \in {{\mathbb{R}}^{{{{n}_{1}} \times {{r}_{T}}}}}[\lambda ],$ ${{G}_{2}}(\lambda ) \in {{\mathbb{R}}^{{{{n}_{2}} \times {{r}_{T}}}}}[\lambda ].$ Системе (4.1) поставим в соответствие систему

где ${{v}^{*}} = {\text{col}}[v_{1}^{*},v_{2}^{*}]$ – новое управление, ${{t}_{0}} > 0$ – некоторый момент времени.

Лемма 3. Пусть для системы (2.1) управление $u(t),\;t > 0$, определяется следующими соотношениями:

где $v_{i}^{*}(t),\;t > 0$, $i = 1,2$, и $\psi (t),\;t \leqslant 0,$ – любые кусочно-непрерывные функции. Тогда при $t > {{t}_{0}}$ = mh система (4.1) будет иметь вид системы (4.2).

Доказательство. Лемма доказывается на основе цепочки равенств [12, 17]:

из которой следует формула

Лемма доказана.

Используя доказательство леммы 2, можно прийти к следующему утверждению.

Следствие 1. Пусть $Q(\lambda ) \in {{\mathbb{R}}^{{{{r}_{T}} \times n}}}[\lambda ]$ – произвольная матрица. Справедлива формула

Установим связь между свойствами модальной управляемостью и слабой модальной управляемостью.

Теорема 2. Для того чтобы система (2.1) была слабо модально управляема, необходимо и достаточно, чтобы система (4.2) была модально управляема.

Доказательство. Необходимость. Пусть система (2.1) слабо модально управляема. Рассмотрим замкнутую систему (2.1), (2.2). Запишем для замкнутой системы (2.1), (2.2) равенство (1.6):

где матрица ${{\mathcal{W}}_{{11}}}(p,\lambda )$ имеет CR-структуру, матрицы ${{\mathcal{W}}_{{21}}}(\lambda ) \in {{\mathbb{R}}^{{{{n}_{ * }} \times (n + \bar {n} - {{n}_{ * }})}}}[\lambda ]$, ${{\mathcal{W}}_{{22}}}(\lambda ) \in {{\mathbb{R}}^{{{{n}_{ * }} \times {{n}_{ * }}}}}[\lambda ]$, унимодулярная матрица $\mathcal{P}(\lambda ) \in {{\mathbb{R}}^{{(n + \bar {n}) \times (n + \bar {n})}}}[\lambda ]$. Выясним, какой переменной будет соответствовать нулевой блок в матрице равенства (4.5). Для этого проведем анализ структуры матрицы $\mathcal{W}(p,\lambda ).$ Будем считать, что характеристической матрице $\mathcal{W}(p,{{e}^{{ - ph}}})$ соответствует вектор решения ${\text{col}}[x,y$, x₁, y₁]. Матрицу $\mathcal{W}(p,\lambda )$ запишем так: где $\lambda = {{e}^{{ - ph}}},$ матрицы $Q_{{ij}}^{{(1)}}(\lambda )$ и $Q_{{ij}}^{{(2)}}(\lambda ),$ $i = \overline {0,2} $, $j = 1,2$, состоят соответственно из первых n_j столбцов матрицы ${{Q}_{{ij}}}(\lambda )$ и оставшихся ${{\bar {n}}_{j}}$ столбцов этой же матрицы ${{Q}_{{ij}}}(\lambda )$, взятых с сохранением порядка их следования. Из структуры матрицы $\mathcal{W}(p,\lambda )$ видно, что если возможно элементарными преобразованиями выделить линейную автономную вполне регулярную подсистему, отвечающую характеристической матрице ${{\mathcal{W}}_{{11}}}(p,\lambda )$ и содержащую в качестве компонент решения переменные x и y, то только за счет домножения определенных строк нижнего правого блока матрицы $\mathcal{W}(p,\lambda )$ и прибавления их к остальным строкам этой матрицы, т.е. ”обнуления элементов”, стоящих в некоторых столбцах правых блоков матрицы ${{\mathcal{W}}_{{11}}}(p,\lambda )$ (второй столбец блоков не учитывается, так как ему соответствует переменная y, которая должна присутствовать в оговоренной выше подсистеме). Действительно, поскольку в третьем столбце блоков матрицы $\mathcal{W}(p,\lambda )$ присутствует переменная p, то применение тех же рассуждений к этому столбцу приводит к необходимости использования операции дифференцирования. На основании проведенного анализа структуры матрицы $\mathcal{W}(p,\lambda )$ заключаем, что нулевому блоку матрицы, стоявшей в равенстве (4.5), соответствуют некоторые компоненты вектора y₁. Очевидно, что такими компонентами можно, не нарушая общности, считать последние ${{n}_{*}}$ компонент вектора y₁. Кроме того, при необходимости можно поменять местами строки матриц, входящих в третье уравнение соотношений (2.2) так, чтобы получить нулевой блок, согласно равенству (4.5).

Приведенный выше анализ позволяет также заключить, что матрица $\mathcal{P}(\lambda )$ с точностью до элементарных преобразований столбцов имеет вид

где матрица ${{\mathcal{P}}_{1}}(\lambda ) \in {{\mathbb{R}}^{{(n + \bar {n} - n{\text{*}}) \times n{\text{*}}}}}[\lambda ]$.

Теперь выясним вид первых $n$ строк матрицы $\mathcal{P}(\lambda )\mathcal{W}(p,\lambda )$, т.е. матрицы ${{\mathcal{W}}_{{11}}}(p,\lambda )$. Матрицы $Q_{{i2}}^{{(2)}}(\lambda )$, $i = 0,2$, представим в виде $Q_{{i2}}^{{(2)}}(\lambda ) = [Q_{{i2}}^{{(21)}}(\lambda ),Q_{{i2}}^{{(22)}}(\lambda )],$ где матрицы $Q_{{i2}}^{{(21)}}(\lambda )$ составлены из первых ${{\bar {n}}_{2}} - {{n}_{ * }}$ столбцов матрицы $Q_{{i2}}^{{(2)}}(\lambda )$ с сохранением порядка их следования, а матрицы $Q_{{i2}}^{{(22)}}(\lambda )$ составлены из оставшихся ${{n}_{ * }}$ столбцов матрицы $Q_{{i2}}^{{(2)}}(\lambda )$ также с сохранением порядка их следования. Проведя рассуждения, аналогичные доказательству необходимости леммы 5 работы [17], можно утверждать: если подсистема, отвечающая характеристической матрице ${{\mathcal{W}}_{{11}}}(p,{{e}^{{ - ph}}})$, не содержит последние ${{n}_{*}}$ компонент вектора ${{y}_{1}},$ то найдется матрица $\widehat Q(\lambda ) \in {{\mathbb{R}}^{{(r + {{r}_{T}}) \times {{n}_{ * }}}}}[\lambda ]$, такая, что

и первые ${{n}_{*}}$ строк матрицы ${{\mathcal{P}}_{1}}$ будут иметь вид (с точностью до элементарных преобразований столбцов) $[B(\lambda ),G(\lambda )]\widehat Q(\lambda ).$ Обозначим

Из структуры матрицы $\mathcal{W}(p,\lambda )$, вида матрицы $\mathcal{P}(\lambda )$ и представления (4.7) следует, что первые $n$ строк матрицы ${{\mathcal{W}}_{{11}}}(p,\lambda )$ будут такими:

Из равенства (4.8) следует, что система (4.2) модально управляема. Необходимость доказана.

Достаточность. Пусть регулятор

обеспечивает системе (4.2), (4.9) характеристический квазиполином $d(p,{{e}^{{ - ph}}}),$ т.е. равенство ${\text{|}}{{\mathcal{W}}^{*}}(p,{{e}^{{ - ph}}}){\text{|}} = d(p,{{e}^{{ - ph}}})$, где ${{\mathcal{W}}^{*}}(p,{{e}^{{ - ph}}})$ – характеристическая матрица системы (4.2), (4.9). Считаем, что матрица ${{\mathcal{W}}^{*}}(p,\lambda )$ имеет CR-структуру. Здесь приняты следующие обозначения: $x_{1}^{*} \in {{\mathbb{R}}^{{\mathop {\bar {n}}\nolimits_1^ * }}}$, $y_{1}^{*} \in {{\mathbb{R}}^{{\mathop {\bar {n}}\nolimits_2^ * }}}$ – вспомогательные переменные, величины ${{X}^{*}} = {\text{col}}[x,x_{1}^{*}]$, ${{Y}^{*}} = {\text{col}}[y,y_{1}^{*}]$, $Q_{{01}}^{*}(\lambda ) \in {{\mathbb{R}}^{{(r + {{r}_{T}}) \times ({{n}_{1}} + \mathop {\bar {n}}\nolimits_1^ * )}}}[\lambda ]$, $Q_{{02}}^{*}(\lambda ) \in {{\mathbb{R}}^{{(r + {{r}_{T}}) \times ({{n}_{2}} + \mathop {\bar {n}}\nolimits_2^ * )}}}[\lambda ]$, $Q_{{11}}^{*}(\lambda ) \in {{\mathbb{R}}^{{\mathop {\bar {n}}\nolimits_1^ * \times ({{n}_{1}} + \mathop {\bar {n}}\nolimits_1^ * )}}}[\lambda ]$, $Q_{{12}}^{*}(\lambda ) \in {{\mathbb{R}}^{{\mathop {\bar {n}}\nolimits_1^ * \times ({{n}_{2}} + \mathop {\bar {n}}\nolimits_2^ * )}}}[\lambda ]$, $Q_{{21}}^{*}(\lambda ) \in {{\mathbb{R}}^{{\mathop {\bar {n}}\nolimits_2^ * \times ({{n}_{2}} + \mathop {\bar {n}}\nolimits_1^ * )}}}[\lambda ]$, $Q_{{22}}^{*}(\lambda ) \in {{\mathbb{R}}^{{\mathop {\bar {n}}\nolimits_2^ * \times ({{n}_{2}} + \mathop {\bar {n}}\nolimits_2^ * )}}}[\lambda ]$. Определим матрицы ${{E}_{1}} = [{{I}_{r}},{{0}_{{r \times {{r}_{T}}}}}]$, ${{E}_{2}} = [{{0}_{{{{r}_{T}} \times r}}},{{I}_{{{{r}_{T}}}}}]$. Используя параметры регулятора (4.9), построим регулятор (2.2), который удобно записать в виде где $X = {\text{col}}[x,{{x}_{1}}] \in {{\mathbb{R}}^{{{{n}_{1}} + \mathop {\bar {n}}\nolimits_1 }}}$, $Y = {\text{col}}[y,{{y}_{{11}}},{{y}_{{12}}}] \in {{\mathbb{R}}^{{{{n}_{2}} + \mathop {\bar {n}}\nolimits_2 + {{r}_{T}}}}}$ (${{y}_{1}} = {\text{col}}[{{y}_{{11}}},{{y}_{{12}}}]$), $\mathop {\bar {n}}\nolimits_1 = \bar {n}_{1}^{*}$, $\mathop {\bar {n}}\nolimits_2 = \bar {n}_{2}^{*} + {{r}_{T}}$. Обоснуем то, что регулятор (4.10) обеспечивает применительно к системе (2.1), (4.10) выполнение трех условий определения 2 при ${{n}_{*}} = {{r}_{T}}$.

Пусть $\mathcal{W}(p,{{e}^{{ - ph}}})$ – характеристическая матрица замкнутой системы (2.1), (4.10). Покажем, что эта матрица имеет CR-структуру, т.е. для этой матрицы $\mathcal{W}(p,{{e}^{{ - ph}}})$ выполняется условие типа (1.5). Рассмотрим формулу (4.6) при ${{n}_{*}} = {{r}_{T}}$. Определим матрицу

В силу следствия выполняется равенство

Заметим, что нижней строке матрицы в правой части равенства (4.12) отвечает последнее равенство в соотношениях (4.10). Пусть $\widetilde \Lambda (p,\lambda ) = \mathcal{P}(\lambda )\mathcal{W}(p,\lambda )$. Поскольку определитель $\left| {P(\lambda )} \right| = 1$, то имеем равенство степеней полиномов ${\text{de}}{{{\text{g}}}_{\lambda }}{\text{|}}\widetilde \Lambda (p,0){\text{|}} = {\text{de}}{{{\text{g}}}_{\lambda }}\left| {\mathcal{W}(p,0)} \right|$. С другой стороны, в силу формулы (4.12), степень этого же полинома ${\text{de}}{{{\text{g}}}_{\lambda }}\left| {\widetilde \Lambda (p,0)} \right| = {\text{de}}{{{\text{g}}}_{\lambda }}{\text{|}}\mathcal{W}{\text{*}}(p,0){\text{|}}$. Значит, справедливо равенство ${\text{de}}{{{\text{g}}}_{\lambda }}\left| {\mathcal{W}(p,0)} \right| = {\text{de}}{{{\text{g}}}_{\lambda }}{\text{|}}\mathcal{W}{\text{*}}(p,0){\text{|}}$. А поскольку в системах (4.2), (4.9) и (2.1), (4.10) дополнительные переменные $x_{1}^{*}$ и ${{x}_{1}}$ определяются одинаковыми уравнениями, то и матрицы при переменной p также являются одинаковыми. Поэтому для матрицы $\mathcal{W}(p,{{e}^{{ - ph}}})$ выполняется равенство типа (1.5), т.е. выполняется первое условие определения 2.

Второе условие определения 2 следует из соотношения (4.12), где следует положить ${{\mathcal{W}}_{{11}}}(p,\lambda ) = \mathcal{W}{\text{*}}(p,\lambda )$, а третье условие определения 3 вытекает из формулы (4.12) и того факта, что матрица $\mathcal{W}{\text{*}}(p,\lambda )$ имеет CR-структуру в силу построения регулятора (4.9). Теорема доказана.

Замечание 3. Получить матрицу ${{\mathcal{W}}_{{11}}}(p,\lambda )$ можно также следующим образом. Перепишем 1-е и 4-е равенства в соотношениях (4.10) в виде

где величины ${{\Omega }_{1}}( \cdot ),\;{{\Omega }_{2}}( \cdot )$ легко усматриваются из (4.10) и не зависят от переменной y₁₂. Замкнув систему (2.1) регулятором (4.13), воспользуемся леммой 3, после чего добавим 2-е и 3-е уравнения из соотношений (4.10). В результате получим систему (4.2), (4.9) c характеристической матрицей ${{\mathcal{W}}_{{11}}}(p,\lambda ) = \mathcal{W}{\text{*}}(p,\lambda )$, при этом переменная y₁₂ будет из этой системы исключена.

Следствие 2. Пусть для системы (4.2) выполняются условия теоремы 1. Тогда система (2.1) слабо модально управляема.

Замечание 4. Пусть регулятор (2.2) и матрица $\mathcal{P}(\lambda )$ построены, согласно доказательству достаточности условий теоремы 2. Если положить

где ${{\widetilde H}_{1}}(\lambda ) = {\text{diag}}[{{I}_{{{{n}_{1}}}}},\widehat A_{{22}}^{{ - 1}}(0)]{{H}_{1}}(\lambda )$, то, переходя в системе (2.1), (2.2) обратно к переменной $z$ и полагая ${{z}_{1}} = {\text{col}}[{{x}_{1}},{{y}_{1}}],$ в определении 2 получим матрицы

5. Некоторые практические аспекты синтеза регуляторов. 5.1. Можно показать [27], что условия (3.1) и (3.2) выполняются в том и только том случае, когда

где ${{C}_{1}},\;{{C}_{2}}$ – фундаментальные матрицы решений линейных алгебраических систем ${{C}_{1}}{{\widetilde A}_{0}} = {{0}_{{{{n}_{2}} \times n}}}$, ${{\widetilde A}_{0}}{{C}_{2}} = {{0}_{{n \times {{n}_{2}}}}}$. Отсюда приходим к следующим утверждениям.

Утверждение 1. Для модальной управляемости системы (1.1) необходимо выполнение условий (5.1).

Пусть матрица $\widetilde G(\lambda )$ является матрицей дополнительных входов для матрицы $\widetilde B(\lambda )$. Тогда найдется матрица H₃, $\left| {{{H}_{3}}} \right| \ne 0$, такая, что $\widetilde G(\lambda ) = {{H}_{3}}G(\lambda )$.

Утверждение 2. Для слабой модальной управляемости системы (1.1) необходимо выполнение следующих условий:

5.2. Условие теоремы 1 формулируется в терминах системы (3.11), которая может определяться неоднозначно. Это связано с неоднозначностью определения матриц ${{L}_{{ij}}}(\lambda )$, $i = 1,2$, $j = 1,2$, удовлетворяющих тождеству (3.7). Рассмотрим два возможных подхода к их построению.

5.2.1. Пусть матрица

Определим матрицы

В силу условия (3.2) справедливо равенство [12]

Поэтому найдется матрица $\widehat L \in {{\mathbb{R}}^{{r \times m(n + r)}}}$, такая, что

Представим матрицу $\hat {L}$ в виде $\widehat L = [{{\widehat L}_{{11}}},...,{{\widehat L}_{{1m}}},{{\widehat L}_{{21}}},...,{{\widehat L}_{{2m}}}],$ где ${{\widehat L}_{{1i}}} \in {{\mathbb{R}}^{{r \times n}}}$, ${{\widehat L}_{{2i}}} \in {{\mathbb{R}}^{{r \times r}}}$, $i = \overline {1,m} $. Положим

Тогда [12] будет выполняться тождество (3.7).

5.2.2. Предположим, что матрицы системы (2.1) имеют вид

Ввиду выполнения условия (1.2) будут иметь место следующие равенства

Условие (5.3) является необходимым [16] для существования $r{\kern 1pt} '\; \times n{\kern 1pt} '\;(r{\kern 1pt} ' = r - r{\kern 1pt} '{\kern 1pt} ')$ матрицы $L(\lambda )$ такой, что выполняется тождество

Достаточные условия существования и способ построения матрицы $L(\lambda ),$ удовлетворяющей (5.5), предложены в статье [16]. Если же матрица $B_{2}^{{(11)}}(\lambda ) = B_{2}^{{(11)}}$, т.е. не зависит от $\lambda $, то условие (5.3) является также [16] и достаточным для существования матрицы $L(\lambda )$. В силу условия (5.4) найдутся полиномиальные матрицы $L_{{ij}}^{'}(\lambda )$, $i = 1,2$, $j = 1,2$, подходящего размера, такие, что

Тогда можно положить (если матрица $L(\lambda )$ существует) ${{L}_{{11}}}(\lambda ) = {\text{diag}}[L(\lambda ),L_{{11}}^{'}(\lambda )]$, L₁₂(λ) = ${\text{col}}[{{0}_{{r{\kern 1pt} ' \times r{\kern 1pt} '{\kern 1pt} '}}},L_{{12}}^{'}(\lambda )]$, ${{L}_{{21}}}(\lambda ) = [{{0}_{{r{\kern 1pt} '{\kern 1pt} ' \times n{\kern 1pt} '}}},L_{{21}}^{'}(\lambda )]$, ${{L}_{{22}}}(\lambda ) = L_{{22}}^{'}(\lambda )$.

Заметим, что все сказанное выше относительно условия (5.3) и следствия из него можно перенести на условие (5.4).

На практике, с целью построения матриц ${{L}_{{ij}}}(\lambda )$, i = 1, 2, j = 1, 2, можно с очевидными изменениями использовать различные комбинации описанных способов, обусловленные конкретным видом пары матриц $\{ {{A}_{{22}}}(\lambda ),{{B}_{2}}(\lambda )\} $.

5.3. Рассмотрим систему (3.11). Наличие запаздывания (особенно в управлении) в большинстве случаев оказывает негативное влияние на существование и синтез регуляторов. В частности, на существование унимодулярной матрицы (3.13). В связи с этим приведем один возможный подход к синтезу регуляторов в случае, когда выбрать унимодулярную матрицу (3.13) невозможно. Если выполнены условия леммы 1, то (см. доказательство леммы 2)

В силу соотношения (5.6) для любого столбца ${{f}_{{{{i}_{0}}}}}(\lambda )$, ${{i}_{0}} \in \{ \overline {1,r + r{\text{*}}} \} $, матрицы $F(\lambda )$ существует (в общем случае не единственная) [7] матрица ${{U}_{{{{i}_{0}}}}}(\lambda ) \in {{\mathbb{R}}^{{(r + r*) \times {{n}_{1}}}}}[\lambda ]$, такая, что

Положив $w(t) = {{U}_{{{{i}_{0}}}}}(\lambda )x(t) + {{e}_{{{{i}_{0}}}}}(\lambda ){{w}_{{{{i}_{0}}}}}(t),$ где ${{e}_{{{{i}_{0}}}}} = {\text{col}}[0,...,0,1,0,...0] \in {{\mathbb{R}}^{{r + r{\text{*}}}}}$ (1 стоит на месте с номером ${{i}_{0}}$), ${{w}_{{{{i}_{0}}}}} \in \mathbb{R}$ – новое управление, приходим к системе

где ${{K}_{{{{i}_{0}}}}}(\lambda ) = K(\lambda ) + F(\lambda )U(\lambda ).$ Матрица (3.13) для этой системы имеет вид

Зачастую, за счет подходящего выбора номера i₀ и матрицы ${{U}_{{{{i}_{0}}}}}(\lambda )$, можно прийти к унимодулярной матрице (5.8).

Пример 2. Пусть матрицы

В данном случае

поэтому получить унимодулярную матрицу (3.13) невозможно. В то же время, выбрав номер i₀ = 2, построим [7] матрицу

Тогда матрица

а матрица (5.8) является унимодулярной.

5.4. Доказательства теорем 1, 2 содержат схемы построения соответствующих регуляторов, которые возможно реализовать в случае любой системы с заданными числовыми параметрами. Проиллюстрируем это примером.

Пример 3. Пусть система (1.1) имеет вид

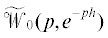Выписав характеристическую матрицу этой системы, видим, что характеристический квазиполином

Рассмотрим вопрос о возможности приведения системы (5.9) к конечному устойчивому спектру.

Проверка условий утверждения 1 показывает, что эта система не является модально управляемой. Вычислив [29] матрицы $T = {\text{col}}[ - 1,1]$, S = 1, $G(\lambda ) = {\text{col}}[ - 1,0,0]$, убеждаемся, что выполнены условия утверждения 2. Проверим достаточные условия слабой модальной управляемости. Для этого воспользуемся теоремой 2. Вначале следует привести исходную систему (5.9) к виду системы (1.1). Выбрав матрицы

выписываем исходную систему в необходимом виде:

Согласно теореме 2, необходимо проверить достаточное условие модальной управляемости (теорема 1) для системы (4.2), т.е. для системы (2.1), у которой вместо матрицы B(λ) взята матрица $[B(\lambda ),G(\lambda )].$ Для этого при построении матриц системы (3.11) матрицу $[B(\lambda ),G(\lambda )]$ будем интерпретировать как матрицу $B(\lambda ),$ а функцию $v{\text{*}}$ – как управление u. Прежде всего построим регулятор (3.8):

Заметим, что если заменить в первом равенстве (5.11) величину ${{y}_{1}},$ согласно второй формуле, то регулятор (5.11) примет вид (3.8). Замкнув регулятором (5.11) систему (5.10), вычисляем матрицы

Условие теоремы 1 выполнено, поскольку матрицу (3.13) можно выбрать так:

Следовательно, исходная система (5.9) слабо модально управляема. Поставим задачу выбора обратной связи так, чтобы у замкнутой системы существовала подсистема с конечным устойчивым спектром, однозначно определяющая функцию z. Поскольку матрицы $K(\lambda )$ и $F(\lambda )$ имеют две строки, то в качестве квазиполинома (1.2) можно взять любой квазиполином не меньше второй степени. Положим, например, $\widetilde d(p) = (p + 1)(p + 2).$ Так как $\left| H \right| = 1$, то полином $d(p) = \widetilde d(p).$

Вернемся к системе (3.11) и доказательству теоремы 1. Вычисляем матрицу

и, применив формулы (3.17), выписываем регулятор (4.9):

Согласно формулам (4.10), имеем регулятор (2.2)

где $X = x$ (переменная ${{x}_{1}}$ не востребована), $Y = {\text{col}}[y,{{y}_{{11}}},{{y}_{{12}}}].$

Переходя к переменным $z$ и ${{z}_{1}},$ окончательно получаем регулятор (1.4):

Заметим, что если положить во втором равенстве регулятора (5.14) $\lambda = 0$, то видно, что величина $z(t)$ входит в управление в виде линейной комбинации $[ - 3, - 1, - 1]{{\widetilde A}_{0}}z(t)$, т.е. требование зависимости регулятора от элементов множества (1.3) выполнено.

Замкнув систему (5.9) регулятором (5.14), приходим к характеристической матрице

Перемножив матрицы (см. формулы (4.6), (4.11)) и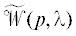 согласно формуле (1.6), получим матрицу, левый верхний блок которой

Непосредственной проверкой убеждаемся, что .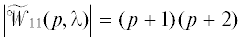

Покажем, как еще можно исключить из замкнутой системы (5.9), (5.14) вторую компоненту вектора ${{z}_{1}}$ и прийти к матрице 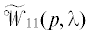. Прежде всего заметим, что в силу второго равенства в соотношениях (5.14)

Подставим в величину $\widetilde B(\lambda )u(t)$ функцию $u,$ определяемую первым равенством в уравнениях (5.14), после этого первые компоненты полученного выражения заменим, согласно формуле (5.15). В итоге видим, что величина

и не зависит от второй компоненты функции ${{z}_{1}}.$ Подставив это выражение в систему (5.9) и дополнив полученные соотношения равенством (которое следует из формул (5.14) и также не зависит от второй компоненты вектора z₁) получим систему (4.2), (4.9) с характеристической матрицей .

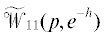Заключение. Предложены необходимые и достаточные условия разрешимости задач модальной управляемости и слабой модальной управляемости линейных автономных вполне регулярных дифференциально-алгебраических систем с соизмеримыми запаздываниями в классе дифференциально-разностных регуляторов. Основные рассуждения статьи носят конструктивный характер, позволяющий в случае заданной системы осуществить синтез соответствующих регуляторов, реализация которого основана на элементарных операциях с полиномиальными матрицами.