Известия РАН. Теория и системы управления, 2020, № 2, стр. 37-63

Введение. Задачи управления детерминированными системами в условиях параметрической неопределенности позволяют учитывать в математической модели неполноту информации о состоянии и параметрах объекта управления, о характере внешних воздействий. Учет в математической модели неопределенных факторов, обусловленный потребностями практики, приводит к необходимости рассматривать движение объекта управления как эволюцию пучка его возможных траекторий. В статье рассматриваются задачи управления пучками траекторий, порожденными только неопределенностью начального состояния, а именно предполагается, что в начальный момент времени состояние системы точно неизвестно, а известно множество ее возможных состояний. К таким пучкам приводятся задачи с параметрической неопределенностью. Качество управления пучком траекторий характеризуется либо средним значением функционала качества управления одной траекторией [1], либо его наибольшим значением [2, 3]. Минимизируя первый функционал, получаем оптимальное в среднем управление пучком. Во втором случае приходим к оптимальному гарантирующему (минимаксному) управлению.

В статье рассматриваются переключаемые системы (ПС), непрерывное движение которых описывается линейными дифференциальными уравнениями, а мгновенные изменения состояния (переключения) – линейными рекуррентными уравнениями. Непрерывное и дискретное движения ПС управляемы. Количество переключений и моменты переключений заранее не заданы. Их выбор также является ресурсом управления, при этом не исключаются процессы с мгновенными многократными переключениями. В постановке задачи используется следующая конструкция показателя качества управления. Задан квадратичный функционал, определяющий качество управления одной траекторией, исходящей из заданного начального состояния. Среднее значение этого функционала (или его максимальное значение) по всем возможным начальным состояниям служит показателем качества управления пучком траекторий в целом. Такая конструкция функционала качества является естественной для практических задач, хотя и не является общей. Например, в задачах управления потоком заряженных частиц [1] используются другие функционалы, учитывающие изменение плотности потока. Таким образом, исследуется линейно-квадратичная (ЛК) задача оптимального в среднем (или оптимального гарантирующего) управления ПС в условиях параметрической неопределенности.

Для ЛК-задач управления непрерывными стохастическими системами доказана теорема разделения [4]: оптимальное в среднем управление стохастической системой совпадает с оптимальным позиционным управлением соответствующей детерминированной системой, в котором используется оптимальная оценка состояния стохастической системы. При таком способе формирования управления задачи оптимального управления и оптимального наблюдения разделены. Их можно решать отдельно. Этот подход получил название принципа разделения. Он широко применяется на практике [5, 6], часто без обоснования, даже для нелинейных систем.

Для ЛК-задачи управления пучками траекторий детерминированных непрерывных систем теорема разделения доказана в [1]: оптимальное в среднем управление линейной системы с квадратичным функционалом качества совпадает с оптимальным управлением одной траекторией этой системы, исходящей из геометрического центра тяжести множества возможных начальных состояний. В этом случае задача наблюдения сводится к нахождению центра тяжести множества возможных состояний. Аналогичный результат справедлив для гарантирующего (минимаксного) управления [7]: оптимальное гарантирующее управление линейной непрерывной системы с квадратичным функционалом качества совпадает с оптимальным управлением одной траекторией этой системы, исходящей из некоторого состояния, принадлежащего выпуклому замыканию множества возможных состояний системы.

Для ЛК-задач управления пучками траекторий непрерывных [1], а также дискретных и непрерывно-дискретных [8] систем выполняется классический принцип (теорема) разделения. Однако для задач управления ПС или системами автоматного типа (САТ), в которых моменты переключения заранее не заданы, а определяются в результате оптимизации, классический принцип разделения не выполняется. Соответствующие контрпримеры ЛК-задач построены в [9, 10]. Причина этого заключается в том, что функция цены (функция Гамильтона–Якоби–Беллмана (ГЯБ)) в ЛК-задаче управления одной траекторией не является квадратичной. Поэтому в системах с переключениями принцип разделения нужно модифицировать. В [9, 10] сформулирован так называемый условный принцип разделения: “оптимальное управление пучком траекторий совпадает с условным оптимальным управлением одной траекторией”, т.е. с управлением, оптимальным при фиксированных моментах переключений. Согласно этому принципу, оптимальная оценка множества возможных состояний находится вместе с моментами переключений в результате конечномерной минимизации функционала качества управления пучком траекторий. Такая процедура оценивания сложнее, чем оценки, применяемые для непрерывных систем, т.е. систем без переключений, либо дискретных или непрерывно-дискретных систем (НДС), в которых моменты переключений заданы.

В статье доказывается теорема разделения для оптимального в среднем и оптимального гарантирующего управлений пучками траекторий детерминированных линейных ПС с квадратичным функционалом качества. Получены уравнения для нахождения оптимальных законов управления. Выделен класс ЛК-задач для систем с “простыми” переключениями, в котором выполняется классический принцип разделения. Рассмотрены академические примеры, демонстрирующие применение условного и классического принципов разделения для ПС. В частности, приведен контрпример ЛК-задачи управления ПС, в котором классический принцип разделения не выполняется, а условный принцип разделения выполняется.

1. Постановки задач. Пусть на заданном промежутке времени $T = [{{t}_{0}},{{t}_{F}}]$ динамическая система совершает N переключений (скачков) в моменты времени t_i, $i = 1,...,N$, образующие неубывающую последовательность $\mathcal{T} = \{ {{t}_{1}},...,{{t}_{N}}\} $:

Между неравными последовательными моментами переключений состояние системы изменяется непрерывно, согласно линейному дифференциальному уравнению:

а в моменты переключений – дискретно в соответствии с линейным рекуррентным уравнением:

В соотношениях (1.2) введены следующие обозначения: $\mathcal{N}\; \triangleq \;\{ i = 0,1,...,N\,{\text{|}}\,{{t}_{i}} < {{t}_{{i + 1}}}\} $ – множество номеров ненулевых (по длине) частичных промежутков ${{T}_{i}}\; \triangleq \;[{{t}_{i}},{{t}_{{i + 1}}})$ непрерывного движения системы; x(t) – состояние системы в момент времени $t \in {{T}_{i}}$, $i \in \mathcal{N}$, $x(t) \in X\; = \;{{\mathbb{R}}^{n}}$; $u(t)$ – управление непрерывным движением системы в момент времени t ∈ T, $u(t) \in U = {{\mathbb{R}}^{p}}$. При ${{t}_{i}} = {{t}_{{i + 1}}}$ дифференциальное уравнение (1.2) опускается ($i \notin \mathcal{N}$), а значение $u({{t}_{i}})$ управления в этой точке t_i несущественно. В уравнении (1.3) ${{x}_{i}}\; \triangleq \;x({{t}_{i}})$ – состояние системы сразу после i-го переключения, ${{x}_{{i - }}}$ – состояние системы непосредственно перед i-м переключением:

${{{v}}_{i}}$ – управление переключением системы в момент ${{t}_{i}} \in \mathcal{T}$, ${{v}_{i}} \in V = {{\mathbb{R}}^{q}}$. Матрицы $A(t)$, $B(t)$ размеров $n \times n$, $n \times p$ ограничены и измеримы на T, матрицы $\hat {A}(t)$, $\hat {B}(t)$ размеров $n \times n$, $n \times q$ ограничены при всех t ∈ T. Предполагаем, что в уравнении (1.3) исключаются так называемые фиктивные переключения, при которых состояние системы не изменяется (${{x}_{i}} = {{x}_{{i - }}}$) и фактического переключения нет. Возможное равенство последовательных моментов в (1.1) означает, что система совершает мгновенные многократные переключения [9, 10].

Множество допустимых программных управлений $\mathcal{W}({{t}_{0}},{{x}_{0}})$ составляют пары $w = (u( \cdot ),v( \cdot ))$, включающие допустимое управление непрерывным движением – ограниченную измеримую на T функцию $u:T \to U$ и управление переключениями:

– последовательность пар $({{t}_{i}},{{v}_{i}})$, $i = 1,...,N$, в которой моменты переключений ${{t}_{i}} \in T$ образуют неубывающую последовательность. Подчеркнем, что количество $N = \left| \mathcal{T} \right|$ переключений и моменты $\mathcal{T} = \{ {{t}_{1}},...,{{t}_{N}}\} $ переключений не фиксированы и у разных допустимых управлений могут не совпадать. При этом не исключается случай отсутствия переключений, когда N = 0 и $v( \cdot ) = \emptyset $ по определению. Допустимое управление $w = (u( \cdot ),v( \cdot ))$ порождает единственную допустимую траекторию $x( \cdot )\; \triangleq \;\{ {{x}_{i}}( \cdot )\} _{{i = 1}}^{N}$, которая на каждом ненулевом (по длине) промежутке T_i, $i \in \mathcal{N}$, представляет собой абсолютно непрерывную функцию $x:{{T}_{i}} \to X$, удовлетворяющую почти всюду T_i дифференциальному уравнению (1.2). В каждый момент переключения ${{t}_{i}} \in \mathcal{T}$ скачки ${{x}_{{i - }}} \to {{x}_{i}}$ = = x(t_i) допустимой траектории удовлетворяют рекуррентному уравнению (1.3), а в начальный момент времени выполняется условие $x({{t}_{0}}) = {{x}_{0}}$.

На множестве $\mathcal{W}({{t}_{0}},{{x}_{0}})$ допустимых управлений задан квадратичный функционал качества

Симметрические матрицы $C(t)$, $\hat {C}(t)$, $F$ порядка n неотрицательно определенные, симметрические матрицы $D(t)$ и $\hat {D}(t)$ размеров $p \times p$ и $q \times q$ положительно определенные, причем матрицы $C(t)$, $D(t)$ ограничены и измеримы, а $\hat {C}(t)$, $\hat {D}(t)$ ограничены на T. Величина $\lambda (t)$ неотрицательная при всех $t \in T$. Слагаемые, зависящие от момента ${{t}_{i}}$, можно рассматривать как затраты (или “штраф”) на переключении ${{x}_{{i - }}} \to {{x}_{i}}$ состояния системы. Отметим, что в функционале (1.4) количество переключений N и моменты переключений ${{t}_{1}}$, …, ${{t}_{N}}$ являются ресурсом управления, так как множество $\mathcal{T} = \{ {{t}_{1}},...,{{t}_{N}}\} $ служит областью определения управления переключениями.

1.1. Задача оптимального управления одной траекторией. Требуется найти минимальное значение функционала (1.4) и оптимальное управление $w^\circ = (u^\circ ( \cdot ),v^\circ ( \cdot )) \in \mathcal{W}({{t}_{0}},{{x}_{0}})$, на котором это значение достигается:

Подчеркнем, что при минимизации (1.5) определяются количество переключений, моменты переключений, управление непрерывным движением системы, а также управление переключениями.

Если наименьшее значение (1.5) не существует, то может быть поставлена задача нахождения минимизирующей последовательности допустимых управлений [11]. Количество переключений у процессов, порождаемых минимизирующей последовательностью управлений, может оставаться конечным или неограниченно возрастать. Бесконечное количество переключений у оптимального процесса становится невозможным, если усилить условие неотрицательности параметра λ(t) в (1.4): $\lambda (t) \geqslant {\text{const}} > 0$. Применение таких “штрафов” в функционале качества исключает последовательности управлений с неограниченным ростом числа переключений как неминимизирующие.

Поставленная задача (1.5) представляет собой так называемую задачу со свободным конечным состоянием и фиксированным временем. В более общей постановке [11] на правый конец траектории могут быть наложены терминальные ограничения.

1.2. Задача оптимального управления с фиксированными моментами переключений. В теории и на практике нередко возникают задачи управления с фиксированными моментами переключений, например, задачи управления дискретными [12, 13] или НДС [14]. Задача минимизации функционала (1.4) на множестве допустимых траекторий с заданными моментами переключений формулируется следующим образом.

Пусть $\mathcal{W}({{t}_{0}},{{x}_{0}}{\kern 1pt} {\text{|}}{\kern 1pt} \mathcal{T})$ – множество допустимых управлений из $\mathcal{W}({{t}_{0}},{{x}_{0}})$, каждое из которых имеет N переключений (1.1), быть может фиктивных, в фиксированные моменты времени $\mathcal{T}$ = {t₁, ..., t_N}. Требуется найти минимальное значение функционала (1.4) на множестве $\mathcal{W}({{t}_{0}},{{x}_{0}}\,{\text{|}}\,\mathcal{T})$ и управление ${{w}_{\mathcal{T}}} \in \mathcal{W}({{t}_{0}},{{x}_{0}}{\kern 1pt} {\text{|}}{\kern 1pt} \mathcal{T})$, на котором это значение достигается:

Такое управление ${{w}_{\mathcal{T}}}$ будем называть условным оптимальным, имея в виду его оптимальность при дополнительном условии – заданных моментах переключений $\mathcal{T} = \{ {{t}_{1}},...,{{t}_{N}}\} $.

Задачи (1.5) и (1.6) связаны. Оптимальное управление $w^\circ \in \mathcal{W}({{t}_{0}},{{x}_{0}})$ получается из условного оптимального управления ${{w}_{\mathcal{T}}} \in \mathcal{W}({{t}_{0}},{{x}_{0}}{\kern 1pt} {\text{|}}{\kern 1pt} \mathcal{T})$ после дополнительной минимизации по моментам переключений $\mathcal{T} = \{ {{t}_{1}},...,{{t}_{N}}\} $:

При оптимизации в (1.7) определяется оптимальный набор переключений $\mathcal{T}^\circ $, соответствующий оптимальному управлению $w^\circ = (u^\circ ( \cdot ),v^\circ ( \cdot ))$. Таким образом, задача (1.5) решается в результате двухэтапной минимизации по моментам переключений (1.7) и условному управлению (1.6). Эта процедура оказывается эффективной для ЛК-задач оптимального управления ПС.

1.3. Задачи оптимального управления пучком траекторий. Пусть в отличие от задачи (1.5) начальное состояние ${{x}_{0}} \in X$ точно неизвестно, а известно множество ${{\sigma }_{0}}$ возможных начальных состояний (${{\sigma }_{0}} \subset X$). Обозначим через $\mathcal{W}({{t}_{0}},{{\sigma }_{0}})$ множество допустимых управлений w = $(u( \cdot ),v( \cdot ))$, каждое из которых порождает допустимую траекторию x(⋅) для любого начального состояния $x({{t}_{0}}) \in {{\sigma }_{0}}$. Объединение этих траекторий образует пучок $t \to \sigma (t)$, исходящий из множества возможных начальных состояний $\sigma ({{t}_{0}}) = {{\sigma }_{0}}$. Предполагается, что в процессе управления никакой дополнительной информации, уточняющей состояние системы, не поступает.

Пусть по-прежнему качество управления одной траекторией характеризуется функционалом (1.4), а качество управления пучком траекторий, исходящих из множества ${{\sigma }_{0}}$, оценивается либо наибольшим (гарантирующим) значением функционала (1.4)

либо его средним значением при этом множество σ₀ считаем либо компактным, либо имеющим положительную меру $\left| {{{\sigma }_{0}}} \right| > 0$ соответственно. В (1.9) измеримую и неотрицательную весовую функцию $\rho :X \to {{\mathbb{R}}_{ + }}$, в частности, можно считать плотностью распределения начального состояния системы, предполагая при этом, что

Требуется найти либо оптимальное гарантирующее (минимаксное) управление ${{w}^{{\text{г}}}}$, либо оптимальное в среднем управление ${{w}^{{\text{с}}}}$, минимизирующие функционалы (1.8), (1.9) соответственно:

Заметим, что множество ${{\sigma }_{0}}$ допустимых состояний можно задавать разными способами. Например, если некоторые координаты вектора состояния в начальный момент времени известны точно, то множество ${{\sigma }_{0}}$ будет отражать неопределенность остальных координат. При этом интегрирование в (1.9) ведется по части координат вектора состояния, а множество ${{\sigma }_{0}}$ должно иметь положительную меру в подпространстве неизмеряемых координат. При моделировании часто ограничиваются конечным числом $M$ траекторий системы. В этом случае множество ${{\sigma }_{0}}$ состоит из M начальных состояний ${{\sigma }_{0}} = \{ x_{0}^{j} \in X{\kern 1pt} {\text{|}}{\kern 1pt} j = 1,...,M\} $. Тогда среднее значение (1.9) заменяется средним арифметическим:

Нередко встречаются задачи, в которых множество возможных состояний принадлежит некоторому многообразию в пространстве состояний $X$, которое задается, например параметрически: ${{\sigma }_{0}} = \{ {{x}_{0}}(s){\kern 1pt} {\text{|}}{\kern 1pt} s \in S\} $, где $s \to {{x}_{0}}(s)$ – заданные на множестве $S$ значения параметров функции. Тогда максимальное (1.8) и среднее (1.9) значения будут определяться на множестве $S$. Возможны и другие способы задания неопределенности. Они, как правило, отражают область приложений исследуемой системы управления.

1.4. Задачи оптимального управления пучком траекторий с фиксированными моментами переключений. Как и в случае управления одной траекторией (см. разд. 1.2), задачи управления пучком траекторий можно рассматривать при дополнительном условии – заданных моментах переключений $\mathcal{T} = \{ {{t}_{1}},...,{{t}_{N}}\} $. Минимизация (1.10) функционалов качества производится на множестве $\mathcal{W}({{t}_{0}},{{x}_{0}}{\kern 1pt} {\text{|}}{\kern 1pt} \mathcal{T})$:

Управление $w_{\mathcal{T}}^{{\text{c}}}$ ($w_{\mathcal{T}}^{{\text{г}}}$) будем называть условным оптимальным в среднем (условным оптимальным гарантирующим), имея в виду его оптимальность при дополнительном условии – заданных моментах переключений $\mathcal{T} = \{ {{t}_{1}},...,{{t}_{N}}\} $. Чтобы из условных управлений $w_{\mathcal{T}}^{{\text{г}}}$ и $w_{\mathcal{T}}^{{\text{c}}}$ получить оптимальные ${{w}^{{\text{г}}}}$ и ${{w}^{{\text{с}}}}$, нужно минимизировать (1.11), (1.12) по моментам переключений $\mathcal{T} = \{ {{t}_{1}},...,{{t}_{N}}\} $:

как это указано в (1.7).

1.5. Задачи управления с “простыми” переключениями. Рассмотрим частный случай ЛК-задачи (1.1)–(1.6), в которой дифференциальное уравнение (1.2) остается прежним, а рекуррентное уравнение (1.4) и функционал качества (1.5) упрощаются:

Действительно, в этой задаче переключения (1.14) особенно простые. Каждая координата вектора состояния получает приращение независимо от других координат. В общем случае (1.3) изменение любой координаты зависит от других координат. Можно сказать, что “простые” переключения не нарушают “ламинарный” характер пучка траекторий. В общем случае переключения придают пучку траекторий некоторую “турбулентность”. Заметим, что скачок ${{x}_{{i - }}} \to {{x}_{i}}$ является параллельным переносом на вектор $\hat {B}({{t}_{i}}){{v}_{i}}$. При нулевом управлении ${{v}_{i}} = 0$ получаем фиктивное переключение (${{x}_{i}} = {{x}_{{i - }}}$), которое исключается. В функционале (1.15) затраты на переключение не зависят от состояния системы. Поэтому при переключении каждая траектория пучка “штрафуется” одинаково. Таким образом, в задачах управления пучками траекторий “простые” переключения меньше других “искажают” динамику непрерывного движения, сохраняя некоторые свойства процессов без переключений. Для системы управления (1.13), (1.14) с функционалом (1.15) ставятся такие же задачи оптимального, оптимального в среднем и оптимального гарантирующего управлений, что и в общем случае (см. разд. 1.1–1.4).

2. Оптимальное управление одной траекторией. Сначала выясним характер зависимости функционала $I({{t}_{0}},{{x}_{0}},w)$ от начального состояния. Пусть $\mathcal{T} = \{ {{t}_{1}},...,{{t}_{N}}\} $ – фиксированное множество моментов переключений. На участках непрерывного изменения состояния системы, например на $[{{t}_{0}},{{t}_{1}}]$, траектория движения системы (1.2) имеет вид

где $\mathcal{C}(t,\tau )$ – матрица Коши, $t \in [{{t}_{0}},{{t}_{1}}]$. Дискретное изменение состояния при переключениях происходит, согласно (1.3), например, если ${{t}_{1}} = {{t}_{0}}$, то ${{x}_{1}} = \hat {A}({{t}_{1}}){{x}_{0}} + \hat {B}({{t}_{1}}){{v}_{1}}$. И в том и другом случае последующее состояние системы аффинно зависит от начального ${{x}_{0}}$. Поэтому текущее состояние $x(t)$, $t \in T$, также является аффинной функцией начального состояния:

Функции k и l зависят от всех моментов переключений ${{t}_{1}},...,{{t}_{i}}$, принадлежащих промежутку $[{{t}_{0}},t]$, причем функция $w \to l(t,w\,{\text{|}}\,{{t}_{1}},...,{{t}_{i}})$ является линейной по управлению $w = (u( \cdot ),v( \cdot ))$, определенному на $[{{t}_{0}},t]$. Подставляя (2.1) в условный функционал качества $I({{t}_{0}},{{x}_{0}},w{\kern 1pt} {\text{|}}{\kern 1pt} \mathcal{T})$, получаем

Здесь $K({{t}_{0}}{\text{|}}{\kern 1pt} \mathcal{T})$ – симметрическая неотрицательно определенная матрица порядка $n$, $L({{t}_{0}},w{\text{|}}{\kern 1pt} \mathcal{T})$ – векторная функция (строка), линейно зависящая от управления $w \in \mathcal{W}({{t}_{0}},{{x}_{0}}{\text{|}}{\kern 1pt} \mathcal{T})$, $M({{t}_{0}},w{\text{|}}{\kern 1pt} \mathcal{T})$ – положительно определенный квадратичный функционал от управления $w \in \mathcal{W}({{t}_{0}},{{x}_{0}}{\text{|}}{\kern 1pt} \mathcal{T})$. Заметим, что при фиксированных моментах переключений $\mathcal{T} = \{ {{t}_{1}},...,{{t}_{N}}\} $ множество допустимых управлений $\mathcal{W}({{t}_{0}},{{x}_{0}}{\text{|}}{\kern 1pt} \mathcal{T})$ можно считать линейным нормированным пространством [15], поскольку его составляют пары $w = (u( \cdot ),v( \cdot ))$ с измеримым ограниченным управлением $u( \cdot ) \in {{L}_{1}}(T,{{\mathbb{R}}^{p}})$ непрерывным движением и конечной последовательностью $v( \cdot ) = \left. {\{ {{v}_{i}}\} } \right|_{{i = 1}}^{N} \in {{\mathbb{R}}^{{qN}}}$ векторов управления переключениями.

На множестве $\mathcal{W}({{t}_{0}},{{x}_{0}}{\text{|}}{\kern 1pt} \mathcal{T})$ функционал (2.2) дифференцируем по управлению, причем производная (Фреше) имеет вид

Обозначение $L{\kern 1pt} '({{t}_{0}}{\text{|}}{\kern 1pt} \mathcal{T}) = L{\kern 1pt} '({{t}_{0}},w{\text{|}}{\kern 1pt} \mathcal{T})$ подчеркивает,  что производная  линейной функции w → → $L({{t}_{0}},w{\text{|}}{\kern 1pt} \mathcal{T})$ не зависит от управления.

Условное оптимальное программное управление ${{w}_{\mathcal{T}}}$ одной траекторией, исходящей из начальной позиции $({{t}_{0}},{{x}_{0}})$, удовлетворяет необходимому условию оптимальности: $I{\kern 1pt} '({{t}_{0}},{{x}_{0}},{{w}_{\mathcal{T}}}) = 0$. Для положительно определенного функционала (2.2) это условие будет также и достаточным. Записывая производную функционала (2.3), вычисленную на условном оптимальном управлении ${{w}_{\mathcal{T}}}$, получаем

Поскольку функционал $w \to M({{t}_{0}},w\,{\text{|}}\,\mathcal{T})$ квадратичный, то уравнение (2.4) представляет собой линейное функциональное уравнение относительно условного оптимального управления ${{w}_{\mathcal{T}}}$.

Заметим, что оптимальное управление $w^\circ = (u^\circ ( \cdot ),v^\circ ( \cdot ))$ также удовлетворяет уравнению (2.4), поскольку оно является условным оптимальным при наилучшем выборе моментов переключений $\mathcal{T}^\circ $, т.е.

3. Оптимальное управление пучком траекторий. Получим теперь условия оптимальности для задач управления пучком траекторий.

3.1. Оптимальное в среднем управление. Запишем выражение для среднего значения функционала (2.2) на множестве ${{\sigma }_{0}}$:

Найдем производную этого функционала по управлению

где $\bar {x} = \bar {x}({{\sigma }_{0}})$ – среднее начальное состояние системы, т.е. центр тяжести множества ${{\sigma }_{0}}$. Приравнивая производную нулевому элементу, получаем необходимое условие оптимальности для управления в среднем:

Сравнивая с (2.4), заключаем, что условное оптимальное в среднем управление $w_{\mathcal{T}}^{{\text{с}}}$ пучком траекторий совпадает с условным оптимальным управлением $\bar {w}_{\mathcal{T}}^{{^{ \circ }}}$ одной траекторией, исходящей из состояния $\bar {x}$. Оптимальное в среднем управление ${{w}^{{\text{с}}}} = ({{u}^{{\text{с}}}}( \cdot ),{{{v}}^{{\text{с}}}}( \cdot ))$ является условным оптимальным управлением с множеством моментов переключений ${{\mathcal{T}}^{{\text{с}}}}$ (это область определения управления ${{v}^{{\text{с}}}}( \cdot )$ переключениями). Поэтому оно также удовлетворяет уравнению (3.1):

Отсюда следует справедливость утверждения.

Теорема разделения для оптимального в среднем управления. Оптимальное в среднем управление пучком траекторий линейных детерминированных ПС с квадратичным функционалом качества совпадает с условным оптимальным управлением одной траекторией, исходящей из центра тяжести множества возможных начальных состояний.

3.2. Оптимальное гарантирующее управление. Функционал (2.2) выпуклый по управлению $w$ при каждом ${{x}_{0}} \in {{\sigma }_{0}}$, а множество ${{\sigma }_{0}}$ компактное. Поэтому функция

является дифференцируемой по направлению и ее субдифференциал имеет вид [16, 17] где $\sigma _{0}^{*} = Arg\mathop {\max }\limits_{x \in {{\sigma }_{0}}} I({{t}_{0}},x,w)$ – множество точек глобального максимума. Это множество худших для  управления  w  возможных  начальных состояний системы. Необходимое условие {0} ∈ ∈  $\partial {{I}^{{\text{г}}}}({{t}_{0}},{{\sigma }_{0}},w_{\mathcal{T}}^{{\text{г}}})$ оптимальности управления $w_{\mathcal{T}}^{{\text{г}}}$ можно записать в виде равенства представляя нулевой элемент субдифференциала выпуклой комбинации производных, вычисленных в точках $x_{i}^{*} \in \sigma _{0}^{*}$, $i = 1,...,m$, глобальных максимумов. Преобразуем эту выпуклую комбинацию, учитывая (2.3): где – некоторая точка выпуклой оболочки множества $\sigma _{0}^{*}$. Необходимое условие оптимальности (3.2) тогда принимает вид

Сравнивая с (2.4) заключаем, что условное оптимальное гарантирующее управление $w_{\mathcal{T}}^{{\text{г}}}$ пучком траекторий совпадает с условным оптимальным управлением $\hat {w}_{\mathcal{T}}^{{^{ \circ }}}$ одной траекторией, исходящей из состояния $\hat {x}$. Оптимальное гарантирующее управление ${{w}^{{\text{г}}}} = ({{u}^{{\text{г}}}}( \cdot ),{{v}^{{\text{г}}}}( \cdot ))$ является условным оптимальным гарантирующим управлением с множеством моментов переключений ${{\mathcal{T}}^{{\text{г}}}}$ (это область определения управления ${{v}^{{\text{г}}}}( \cdot )$ переключениями). Поэтому оно также удовлетворяет уравнению (3.3)

Отсюда следует справедливость утверждения.

Теорема разделения для оптимального гарантирующего управления. Оптимальное гарантирующее управление пучком траекторий линейных детерминированных ПС с квадратичным функционалом качества совпадает с условным оптимальным управлением одной траекторией, исходящей из некоторой точки выпуклого замыкания множества худших для этого управления возможных начальных состояний системы.

Поскольку $\overline {conv} \,\sigma _{0}^{*} \subset \overline {conv} \,{{\sigma }_{0}}$, то можно считать, что точка $\hat {x} = \hat {x}({{\sigma }_{0}}) \in \overline {conv} \,{{\sigma }_{0}}$. Поэтому формулировку теоремы можно упростить, несколько ослабив утверждение.

Следствие. Оптимальное гарантирующее управление пучком траекторий линейных детерминированных ПС с квадратичным функционалом качества совпадает с условным оптимальным управлением одной траекторией, исходящей из некоторой точки выпуклого замыкания множества возможных начальных состояний.

4. Синтез оптимального управления одной траекторией. Для задач (1.5), (1.6) управления одной траекторией в [18] получены достаточные условия оптимальности, в которых функция цены формируется из вспомогательных функций – так называемых моментных функций цены.

Обозначим через $\mathcal{W}(t,x)$ множество допустимых управлений, удовлетворяющих начальному условию $x(t) = x$, каждый из которых имеет конечное число переключений на $[t,{{t}_{F}}]$. Оставшиеся переключения происходят в моменты ${{t}_{1}}$, …, ${{t}_{k}}$, образующие неубывающую последовательность $\mathcal{T} = \{ {{t}_{1}},...,{{t}_{k}}\} $ на промежутке $[t,{{t}_{F}}]$:

Заметим, что количество k оставшихся переключений и сами моменты ${{t}_{1}}$, …, ${{t}_{k}}$ переключений не фиксированы и у разных допустимых управлений могут не совпадать.

На множестве $\mathcal{W}(t,x)$ допустимых управлений определим функционал оставшихся потерь, аналогичный (1.4):

Функция цены $\varphi (t,x)$ по определению равна значению функционала оставшихся потерь (4.2), вычисленному на оптимальном процессе с начальным условием $x(t) = x$. Иначе говоря, функция цены равна минимальному значению функционала оставшихся потерь (4.2) на множестве допустимых управлений $\mathcal{W}(t,x)$:

Если для фиксированной стартовой позиции $(t,x)$ обозначить через w(t, x) = $(u^\circ ( \cdot ),v^\circ ( \cdot )) \in \mathcal{W}(t,x)$ оптимальное программное управление для функционала (4.2), то функции цены будет определяться равенством

Функция $\varphi (t,x{\text{|}}{\kern 1pt} {{t}_{1}},...,{{t}_{k}})$, равная значению функционала оставшихся потерь (4.2), вычисленному на процессе, исходящем из стартовой позиции $(t,x)$, при управлении, которое оптимально среди всех допустимых управлений, имеющих ровно k переключений, быть может фиктивных, которые происходят в моменты времени ${{t}_{1}},...,{{t}_{k}}$, образующие неубывающую последовательность (4.1), называется k-моментной функцией цены [18]. Пусть $\mathcal{W}(t,x{\text{|}}{\kern 1pt} \mathcal{T})$ – множество допустимых управлений из $\mathcal{W}(t,x)$ с k переключениями в моменты $\mathcal{T} = \{ {{t}_{1}},...,{{t}_{k}}\} $. Тогда

Для процессов без переключений, когда $k = 0$ и $\mathcal{T} = \emptyset $, определим 0-моментную функцию цены

где $\mathcal{W}(t,x{\text{|}}{\kern 1pt} \emptyset )$ – множество допустимых управлений без переключений. Если для стартовой позиции $(t,x)$ обозначить через $w(t,x{\text{|}}{\kern 1pt} {{t}_{1}},...,{{t}_{k}}) = ({{u}_{\mathcal{T}}}( \cdot ),{{v}_{\mathcal{T}}}( \cdot )) \in \mathcal{W}(t,x{\text{|}}{\kern 1pt} \mathcal{T})$ условное оптимальное программное управление для функционала (4.2) при заданных моментах переключений $\mathcal{T} = \{ {{t}_{1}}$, ..., t_k}, то моментная функции цены будет определяться равенством

Функцию цены можно выразить через ее моментные функции

Можно сказать, что моментные функции цены представляет собой функцию цены при дополнительных условиях – фиксированных моментах переключений. Функции (4.3), (4.4) аналогичны условным функциям цены, введенным в [19]. Отличие заключается в том, что условные функции цены зависят только от момента первого переключения из k оставшихся, а моментная функция (4.3) зависит от всех моментов переключений (4.1).

4.1. Алгоритм синтеза оптимального позиционного управления. Рекуррентная процедура нахождения моментных функций цены для ПС описана в [18]. Для ЛК-задачи моментные функции цены квадратичные:

где $\Phi $ – симметрическая неотрицательно определенная матрица порядка $n$, непрерывная по совокупности аргументов на области определения ${{t}_{0}} \leqslant t \leqslant {{t}_{1}} \leqslant ... \leqslant {{t}_{k}} \leqslant {{t}_{F}}$. Эти матрицы находятся последовательно, согласно следующему алгоритму.

Шаг 0. Найти матрицу $\Phi (t)$ 0-моментной функции цены $\varphi (t,x\,{\text{|}}\,\emptyset ) = \frac{1}{2}{{x}^{{\text{Т}}}}\Phi (t)x$ (в задаче без переключений), решая дифференциальное уравнение Риккати:

с терминальным условием $\Phi ({{t}_{F}}) = F\,$. Составить матрицу $L(t) = \,{{D}^{{ - 1}}}(t){{B}^{{\text{Т}}}}(t)\,\Phi (t)$ коэффициентов линейного управления: непрерывным движением системы. Положить k = 1 и перейти к шагу 1^k.

Шаг 1^k. Найти матрицу $\Phi ({{t}_{1}}\,{\text{|}}\,{{t}_{1}},...,{{t}_{k}})$ k-моментной функции цены (4.6) в момент $t = {{t}_{1}}$ первого из оставшихся k переключений, решая рекуррентное уравнение:

В правой части уравнения (4.9) $\Phi = \Phi ({{t}_{1}}\,{\text{|}}\,{{t}_{2}},...,{{t}_{k}})$ – матрица ($k - 1$)-моментной функции цены. Составить матрицу

коэффициентов условного оптимального управления переключениями

При k = 1 аргументы ${{t}_{2}},...,{{t}_{k}}$ матриц $\Phi ({{t}_{1}}{\text{|}}{\kern 1pt} {{t}_{2}},...,{{t}_{k}}) = \Phi ({{t}_{1}})$ и $\hat {L}({{t}_{1}}{\text{|}}{\kern 1pt} {{t}_{2}},...,{{t}_{k}}) = \hat {L}({{t}_{1}})$ опускаются.

Шаг 2^k. Найти матрицу $\Phi (t{\text{|}}{\kern 1pt} {{t}_{1}},...,{{t}_{k}})$ k-моментной функции цены (4.6) до первого переключения (при $t < {{t}_{1}}$), решая дифференциальное уравнение Риккати (4.7) с терминальным условием $\Phi ({{t}_{1}}) = \Phi ({{t}_{1}}{\text{|}}{\kern 1pt} {{t}_{1}},...,{{t}_{k}})$. Составить матрицу $L(t{\text{|}}{\kern 1pt} {{t}_{1}},...,{{t}_{k}}) = {{D}^{{ - 1}}}(t){{B}^{{\text{Т}}}}(t)\Phi (t{\text{|}}{\kern 1pt} {{t}_{1}},...,{{t}_{k}})$ коэффициентов линейного управления

непрерывным движением системы до первого переключения.

Проверить условие окончания. Таких условий может быть несколько (см. [18]). Общим условием окончания синтеза служит неравенство

Если (4.12) выполняется для всех позиций $(t,x) \in T \times X$, то оптимальные процессы имеют не более чем k – 1 переключений, и продолжать рекуррентную процедуру синтеза уже не нужно. Это условие очень сложное для проверки. Поэтому при вычислениях, как правило, задают максимальное допустимое количество N переключений. Тогда нужно проверять условие $k > N$. Таким образом, если условие окончания выполняется, то процедура синтеза заканчивается, в противном случае полагаем $k:\, = k + 1$ и переходим к шагу 1^k.

В результате N шагов рекуррентной процедуры находятся матрицы $\Phi (t)$, $\Phi (t{\text{|}}{\kern 1pt} {{t}_{1}})$, …, $\Phi (t{\text{|}}{\kern 1pt} {{t}_{1}},...,{{t}_{N}})$ моментных функции цены (4.6), матрицы $L(t)$, $L(t{\text{|}}{\kern 1pt} {{t}_{1}})$, …, $L(t{\text{|}}{\kern 1pt} {{t}_{1}},...,{{t}_{N}})$ коэффициентов условных оптимальных позиционных управлений (4.8), (4.11) непрерывным движением системы, а также матрицы $\hat {L}(t)$, $\hat {L}(t{\text{|}}{\kern 1pt} {{t}_{1}})$, …, $\hat {L}(t{\text{|}}{\kern 1pt} {{t}_{1}},...,{{t}_{N}})$ коэффициентов условных оптимальных управлений (4.10) переключениями.

4.2. Нахождение условного оптимального процесса управления. С помощью условных оптимальных позиционных управлений (4.8), (4.10), (4.11) можно найти условный оптимальный процесс $(x^\circ ( \cdot ),u^\circ ( \cdot ),v^\circ ( \cdot ))$ с фиксированными моментами $\mathcal{T} = \{ {{t}_{1}},...,{{t}_{N}}\} $ переключений для любого начального состояния ${{x}_{0}} \in X$ системы.

Действительно, пусть система находится в позиции $({{t}_{0}},{{x}_{0}})$, т.е. удовлетворяет начальному условию $x({{t}_{0}}) = {{x}_{0}}$. Если ${{t}_{1}} = {{t}_{0}}$, то первое переключение происходит в начальный момент времени. Система сразу совершает скачок ${{x}_{0}} \to {{x}_{1}}$, согласно уравнению (1.3), под действием управления ${{v}_{1}} = {\mathbf{v}}({{t}_{1}},{{x}_{0}}{\text{|}}{\kern 1pt} {{t}_{2}},...,{{t}_{N}})$. Если ${{t}_{1}} > {{t}_{0}}$, то сначала на промежутке $[{{t}_{0}},{{t}_{1}}]$ происходит непрерывное движение, согласно уравнению (1.2), с программным управлением $u(t) = u(t,x(t){\text{|}}{\kern 1pt} {{t}_{1}},...,{{t}_{N}})$, а в конце этого промежутка из состояния ${{x}_{{1 - }}} = x({{t}_{1}} - 0)$ происходит скачок ${{x}_{{1 - }}} \to {{x}_{1}}$, согласно уравнению (1.3), под действием управления ${{v}_{1}} = {\mathbf{v}}({{t}_{1}},{{x}_{{1 - }}}{\text{|}}{\kern 1pt} {{t}_{2}},...,{{t}_{k}})$. И в том и в другом случае система приходит в позицию $({{t}_{1}},{{x}_{1}})$, в которой выполняются те же действия. Если переключений нет (т.е. $\mathcal{T} = \emptyset $), то непрерывное движение системы совершается, согласно уравнению (1.2), под действием программного управления $u(t) = u(t,x(t))$.

4.3. Вычисление наименьших значений функционала качества. Минимальное значение условного функционала качества при фиксированных переключениях $\mathcal{T} = \{ {{t}_{1}},...,{{t}_{N}}\} $ вычисляется по N-моментной функции цены:

Минимальное значение функционала качества (1.4) с $N$ переключениями находится при оптимизации моментов переключений:

Здесь ${{\mathcal{W}}_{N}}({{t}_{0}},{{x}_{0}})$ – множество допустимых управление из $\mathcal{W}({{t}_{0}},{{x}_{0}})$, имеющих ровно $N$ переключений, быть может фиктивных. Наконец, наименьшее значение функционала качества (1.4) получаем в результате оптимизации количества и моментов переключений:

Найденные при этом число переключений $N^\circ $ и сами моменты переключений ${{\mathcal{T}}^{{^{ \circ }}}} = \{ t_{1}^{{^{ \circ }}},...,t_{{{{N}^{^\circ }}}}^{{^{ \circ }}}\} $ позволяют получить соответствующее оптимальное управление ${{w}^{{^{ \circ }}}} = w({{t}_{0}},{{x}_{0}}{\text{|}}{\kern 1pt} t_{1}^{{^{ \circ }}},...,t_{{{{N}^{^\circ }}}}^{{^{ \circ }}})$.

5. Синтез оптимального управления пучком траекторией. Для решения задач (1.10) управления пучками траекторий используем подход, основанный на доказанном выше принципе разделения: “оптимальное в среднем (или гарантирующее) управление пучком траекторий совпадает с условным оптимальным управлением одной траекторией”, т.е. с управлением, оптимальным при фиксированных моментах переключений. Эта траектория, будем ее называть опорной, может принадлежать пучку или нет. Оптимальное программное управление для опорной траектории можно получить, используя оптимальное позиционное (см. разд. 3, 4). Поэтому остается только выбрать наилучшую опорную траекторию. Для этого достаточно указать ее начальное состояние. Таким образом, если принцип разделения справедлив, то решение задачи оптимального управления пучком можно разделить на два этапа: синтез оптимального позиционного управления одной траекторией и нахождение начального состояния для опорной траектории. На втором этапе фактически строится оценка множества возможных начальных состояний системы, которая затем используется в оптимальном управлении с обратной связью. Как показано выше (см. разд. 2), для ЛК-задачи оптимального в среднем управления пучком лучшей оценкой служит центр тяжести множества возможных начальных состояний. Для оптимального гарантирующего управления лучшую оценку нужно искать в выпуклой оболочке множества начальных состояний.

Синтез оптимальных управлений пучками траекторий можно выполнить при помощи так называемой функции стоимости полуоптимального процесса [10], значение которой $\beta (t,x,\hat {x})$ по определению равно значению функционала оставшихся потерь (4.2):

вычисленному на траектории, исходящей из позиции $(t,x)$, при управлении $\hat {w}$, оптимальном для траектории $\hat {x}( \cdot )$, исходящей из позиции $(t,\hat {x})$. Иначе говоря, функция $\beta (t,x,\hat {x})$ равна значению функционала оставшихся потерь (4.2) на полуоптимальном процессе $(x( \cdot ),\hat {w})$, в котором управление $\hat {w}$ оптимальное (правда, для траектории $\hat {x}( \cdot )$), а траектория x(⋅) неоптимальная, хотя получается при управлении $\hat {w}$. Заметим, что функция цены $\varphi (t,\hat {x})$ показывает стоимость оптимального процесса $(\hat {x}( \cdot ),\hat {w})$, так как по определению $\varphi (t,\hat {x}) = I(t,\hat {x},\hat {w})$. Используя обозначение $w(t,x)$ (см. разд. 4) для оптимального программного управления, определение функции стоимости можно представить в виде

Сравнивая (5.1) с (4.5), заключаем, что при совпадении аргументов $x = \hat {x}$ имеет место равенство

Чтобы получить функцию стоимости $\beta (t,x,\hat {x})$, будем использовать, как и для функции цены, вспомогательные функции – моментные функции стоимости полуоптимального процесса. Значение $\beta (t,x,\hat {x}{\text{|}}{\kern 1pt} {{t}_{1}},...,{{t}_{k}})$ k-моментной функции стоимости равно (по определению) значению функционала оставшихся потерь (4.2), вычисленному на траектории, исходящей из позиции $(t,x)$, при условном оптимальном управлении $\hat {w} = w(t,\hat {x}{\kern 1pt} |{\kern 1pt} {{t}_{1}},...,{{t}_{k}})$ для траектории $\hat {x}( \cdot )$, исходящей из позиции $(t,\hat {x})$:

Иначе говоря, моментная функция равна значению функционала (4.2), вычисленному на полуоптимальном процессе $(x( \cdot ),\hat {w})$, в котором управление $\hat {w}$ является условным оптимальным, а траектория x(⋅) нет. При совпадении состояний $x = \hat {x}$ получаем равенство моментных функций цены и стоимости, аналогичное (5.2):

5.1. Алгоритм построения моментных функций стоимости. Рекуррентная процедура нахождения функции стоимости для ЛК-задачи управления НДС описана в [8]. Для ПС процедура аналогичная. Будем искать моментные функции стоимости квадратичного вида

где $\Phi (t{\text{|}}{\kern 1pt} {{t}_{1}},...,{{t}_{k}}){\kern 1pt} $ – матрица моментной функции цены (4.6), $\Psi (t\,{\text{|}}\,{{t}_{1}},...,{{t}_{k}}){\kern 1pt} $ – симметрическая неотрицательно определенная матрица порядка n, а $\Delta x = x - \hat {x}$ – отклонение состояния $x$ от состояния $\hat {x}$ на опорной траектории. В (5.4) учитывается, что при $\Delta x = 0$ моментные функции стоимости и цены совпадают (5.2). Считаем, что матрицы $\Phi (t{\text{|}}{\kern 1pt} {{t}_{1}},...,{{t}_{k}})$ моментных функций цены найдены, согласно алгоритму разд. 4.1. Поэтому для формирования (5.4) остается получить матрицы $\Psi (t{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{1}},...,{{t}_{k}}){\kern 1pt} $.

Шаг 0. Найти матрицу $\Psi (t)$ 0-моментной функции стоимости

(в задаче без переключений), решая линейное матричное дифференциальное уравнение с нулевым терминальным условием $\Psi ({{t}_{F}}) = 0\,$. Положить k = 1 и перейти к шагу 1^k.

Шаг 1^k. Найти матрицу $\Psi ({{t}_{1}}\,{\text{|}}\,{{t}_{1}},...,{{t}_{k}})$ $k$-моментной функции стоимости (5.4) в момент $t = {{t}_{1}}$ первого из оставшихся k переключений, решая линейное рекуррентное уравнение

В правой части уравнения (5.6): $\Phi = \Phi ({{t}_{1}}{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{2}},...,{{t}_{k}})$, $\Psi = \Psi ({{t}_{1}}{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{2}},...,{{t}_{k}})$ – матрицы ($k - 1$)-моментных функций цены и стоимости соответственно. (При k = 1 аргументы ${{t}_{2}},...,{{t}_{k}}$ матриц $\Phi ({{t}_{1}}{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{2}},...,{{t}_{k}})$ = = Φ(t₁) и $\Psi ({{t}_{1}}{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{2}},...,{{t}_{k}}) = \Psi ({{t}_{1}})$ опускаются.)

Шаг ${{2}^{k}}$. Найти матрицу $\Psi (t{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{1}},...,{{t}_{k}})$ k-моментной функции стоимости (5.4) до первого переключения (при $t < {{t}_{1}}$), решая дифференциальное уравнение (5.5) с терминальным условием $\Psi ({{t}_{1}}) = \Psi ({{t}_{1}}{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{1}},...,{{t}_{k}})$.

Условия окончания рекуррентной процедуры определяются количеством N найденных ранее моментных функций цены (см. разд. 4.1). Если $k < N$, то полагаем $k: = k + 1$ и переходим к шагу 1^k, иначе процесс построения моментных функций стоимости заканчивается.

Сравнивая уравнения (5.5), (5.6) с уравнениями (4.7), (4.9) соответственно, заключаем, что сумма $\Gamma = \Phi + \Psi $ матриц квадратичных форм (5.4) удовлетворяет уравнениям

Точка над Γ в (5.7) обозначает, как обычно, производную по времени t. При k = 0 аргументы ${{t}_{1}},...,{{t}_{k}}$ опускаются: $\Gamma (t{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{1}},...,{{t}_{k}}) = \Gamma (t)$, а терминальное условие (5.8) заменяется на $\Gamma ({{t}_{F}}) = F$. Заметим, что уравнения (5.7), (5.8) линейные, что упрощает их решение. Подставляя $\Psi = \Gamma - \Phi $ в (5.4), приходим к равенству

Преобразуем правую часть (5.9), раскрывая скобки:

Значит, моментную функцию стоимости можно выразить через моментную функцию цены (4.6) следующим образом:

Эта формула фактически является разложением функции стоимости по отклонениям $\Delta x$. При $\Delta x = 0$ приходим к равенству (5.3).

5.2. Синтез оптимального в среднем управления. Согласно теореме разделения (см. разд. 3.1), оптимальное в среднем управление пучком совпадает с условным оптимальным управлением траекторией, исходящей из центра тяжести пучка траекторий. Поэтому сначала находим центр тяжести

множества ${{\sigma }_{0}}$ возможных начальных состояний системы. В частности, если весовая функция постоянная $\rho (x) = 1{\text{/}}mes{{\sigma }_{0}}$, а множество ${{\sigma }_{0}}$ имеет центр симметрии $z({{\sigma }_{0}})$, то центр тяжести совпадает с центром симметрии, т.е. $\bar {x}({{\sigma }_{0}}) = z({{\sigma }_{0}})$. На практике множество возможных состояний часто задается параллелепипедом с длинами ребер $2{{\Delta }_{i}}$, $i = 1,...,n$, или эллипсоидом [20] с симметрической положительно определенной матрицей Q. Центр $z = ({{z}_{1}},...,{{z}_{n}})$ параллелепипеда или эллипсоида является его центром тяжести, т.е. $\bar {x}({{\sigma }_{0}}) = z$. В случае конечного множества ${{\sigma }_{0}} = \{ x_{0}^{1},...,x_{0}^{m}\} $ центр тяжести $\bar {x}({{\sigma }_{0}}) = (x_{0}^{1} + ... + x_{0}^{m}){\text{/}}m$.

После нахождения центра тяжести $\bar {x}$ решаем задачу минимизации:

В результате определяются наименьшее среднее значение $\min {{I}^{{\text{c}}}} = {{I}^{{\text{c}}}}({{t}_{0}},{{\sigma }_{0}},{{w}^{{\text{c}}}})$ функционала (1.9), количество ${{N}^{{\text{c}}}}$ и моменты ${{\mathcal{T}}^{{\text{c}}}} = \{ t_{1}^{{\text{c}}},...,t_{{{{N}^{{\text{c}}}}}}^{{\text{c}}}\} $ переключений наилучшего в среднем условного оптимального управления. После этого находим условное оптимальное программное управление (см. разд. 4.4) для траектории, исходящей из начального состояния $\bar {x}$:

Это управление будет оптимальным в среднем управлением пучком траекторий.

Заметим, что описанная процедура синтеза позволяет получить управление, замкнутое по множеству возможных состояний в виде сложной функции (t₀, σ₀) → $({{t}_{0}},\bar {x}({{\sigma }_{0}}))$ → $w({{t}_{0}},\bar {x}({{\sigma }_{0}}){\kern 1pt} {\text{|}}{\kern 1pt} t_{1}^{{\text{c}}},...,t_{{{{N}^{{\text{c}}}}}}^{{\text{c}}})$. Эту процедуру можно применить для текущей позиции пучка $(t,\sigma )$ с функционалом оставшихся потерь (4.2). Такой подход применяется в задачах с дискретными неточными измерениями [10].

5.3. Синтез оптимального гарантирующего управления. Согласно теореме разделения (см. разд. 3.2), оптимальное гарантирующее управление пучком совпадает с условным оптимальным управлением траекторией, исходящей из некоторой точки выпуклого замыкания множества худших для этого управления возможных начальных состояний системы. Считая фиксированными моменты переключений, рассмотрим функцию

Здесь $\Phi = \Phi ({{t}_{0}}{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{1}},...,{{t}_{N}})$, $\Psi = \Psi ({{t}_{0}}{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{1}},...,{{t}_{N}})$ – симметрические неотрицательно определенные матрицы квадратичной функции (5.4). Найдем точку минимума функции максимума

Напомним, что ${{\sigma }_{0}}$ – компактное множество. Так как функция (5.12) выпуклая по $\hat {x}$ при всех $x \in X$, то функция (5.13) также выпуклая. Ее субдифференциал имеет вид [16, 17]

где $\sigma _{0}^{*}(\hat {x}) = Arg\mathop {\max }\limits_{x \in {{\sigma }_{0}}} \gamma (x,\hat {x})$ – множество точек глобального максимума, а ${{\gamma }_{{\hat {x}}}}(x,\hat {x})$ – производная (градиент) по $\hat {x}$. Если ранг матрицы $\Psi $ равен r, то градиент ${{\gamma }_{{\hat {x}}}}(x,\hat {x}) = {{(\hat {x} - x)}^{{\text{T}}}}\Psi $ является вектором r-мерного подпространства в ${{\mathbb{R}}^{n}}$. Тогда субдифференциал является выпуклым подмножеством r-мерного пространства. Поэтому любой eго элемент, согласно теореме Каратеодори [21], можно представить в виде выпуклой комбинации не более чем (r + 1) точек этого множества. Необходимое (и достаточное) условие экстремума $\{ 0\} \in \partial \,\mathop {\max }\limits_{x \in {{\sigma }_{0}}} \gamma (x,\hat {x})$ при этом можно сформулировать следующим образом: если $\hat {x}$ – точка минимума функции (5.13), то существует $r + 1$ (необязательно различных) градиентов ${{\gamma }_{{\hat {x}}}}(x_{i}^{*},\hat {x})$, $x_{i}^{*} \in \sigma _{0}^{*}$, $i = 0,1,...,r$, выпуклая комбинация которых равна нулевому вектору:

Подставляя производную ${{\gamma }_{{\hat {x}}}}(x,\hat {x}) = {{(\hat {x} - x)}^{{\text{Т}}}}\Psi $ функции (5.12) в (5.14), получаем

В точках $x_{i}^{*}$, $i = 0,1,...,r$, функция (5.12) достигает по $x$ наибольшего значения на множестве ${{\sigma }_{0}}$. Запишем равенство $\gamma (x_{0}^{*},\hat {x}) = \gamma (x_{i}^{*},\hat {x})$ для функции (5.12):

Отсюда получаем

Подставляя (5.15), приходим к равенству

которое выполняется для всех $i = 1,...,r$. Отсюда следует справедливость утверждения.

Лемма. Для того чтобы функция (5.13) достигала своего наименьшего значения в точке $\hat {x}$, необходимо и достаточно, чтобы $\hat {x}$ можно представить в виде выпуклой комбинации

необязательно различных точек $x_{i}^{*} \in \sigma _{0}^{*}$ максимума функции (5.12): с коэффициентами ${{s}_{i}} \geqslant 0$, $i = 0,1,...,r$, ${{s}_{0}} + {{s}_{1}} + ... + {{s}_{r}} = 1$, удовлетворяющими уравнениям (5.16).

Таким образом, точка минимума $\hat {x}$ функции (5.13) принадлежит выпуклой оболочке множества $\sigma _{0}^{*}$ точек глобальных максимумов функции $x \to \gamma (x,\hat {x})$ на множестве ${{\sigma }_{0}}$. Применяя лемму, можно по формуле (5.17) найти точку $\hat {x}$ минимума функции (5.13), а также точку максимума $x_{0}^{*} \in \sigma _{0}^{*}$ функции (5.12). Обе эти точки зависят от моментов переключений ${{t}_{1}},...,{{t}_{N}}$. Поэтому задачу оптимизации переключений можно записать следующим образом:

где $\hat {x} = \hat {x}({{t}_{0}}\,{\text{|}}\,{{t}_{1}},...,{{t}_{N}})$, $x_{0}^{*} = x_{0}^{*}({{t}_{0}}\,{\text{|}}\,{{t}_{1}},...,{{t}_{N}})$ – значения аргументов, при которых функция (5.12) достигает своего минимаксимума:

В результате определяются минимаксное значение $\min {{I}^{{\text{г}}}} = {{I}^{{\text{г}}}}({{t}_{0}},{{\sigma }_{0}},{{w}^{{\text{г}}}})$ функционала (1.8), количество ${{N}^{{\text{г}}}}$ и моменты ${{\mathcal{T}}^{{\text{г}}}} = \{ t_{1}^{{\text{г}}},...,t_{{{{N}^{{\text{г}}}}}}^{{\text{г}}}\} $ переключений наилучшего гарантирующего условного оптимального управления. После этого находим условное оптимальное программное управление (см. разд. 4.4) для траектории, исходящей из начального состояния $\hat {x}$:

Это управление будет оптимальным гарантирующим управлением пучком траекторий.

6. ЛК-задачи управления с “простыми” переключениями. Для ЛК-задачи (1.13)–(1.15) с “простыми” переключениями синтезируем оптимальное в среднем и оптимальное гарантирующее управления. Сначала посмотрим, как упрощаются уравнения для моментных функций цены и стоимости при “простых” переключениях (1.14) вместо переключений (1.3) в общем случае.

6.1. Уравнения для моментных функций цены и стоимости. По сравнению с общей постановкой задачи имеем $\hat {A}(t) = E$ и $\hat {C}(t) = 0$. Так как модель непрерывного движения не меняется, то сохраняются уравнения (4.7), (5.5), (5.7) непрерывного изменения матриц $\Phi $, $\Psi $ и $\Gamma $ моментных функций цены и стоимости. Изменения касаются только модели переключений. Поэтому упрощаются уравнения дискретного изменения моментных функций. Подставляя $\hat {A}(t) = E$ и $\hat {C}(t) = 0$ в уравнение (4.9), получаем

В правой части уравнения (6.1) $\Phi = \Phi ({{t}_{1}}{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{2}},...,{{t}_{k}})$ – матрица ($k - 1$)-моментной функции цены. Как видим, рекуррентное уравнение упрощается незначительно. Оно остается нелинейным матричным уравнением того же вида, что и (4.8). Теперь подставляем матрицы $\hat {A}(t) = E$ и $\hat {C}(t) = 0$ в уравнение (5.8). Получаем

Значит, при переключениях матрица $\Gamma $ не меняется. Следовательно, она не зависит ни от количества переключений, ни самих моментов переключений, а зависит только от текущего времени $\Gamma = \Gamma (t)$. На промежутке времени T матрица $\Gamma $ удовлетворяет уравнению (5.7):

с терминальным условием $\Gamma ({{t}_{F}}) = F$. Поэтому связь (5.10) моментных функций цены и стоимости можно упростить:

Используем это представление для решения задач управления пучками.

6.2. Синтез оптимального в среднем управления. Найдем среднее значение функции (6.2) для оценки $\hat {x}$, совпадающей со средним значением $\bar {x}$. Подставляем $\hat {x} = \bar {x}$ в (6.2) и интегрируем. Учитывая, что среднее значение разности $\Delta x = x - \bar {x}$ нулевое, получаем

Чтобы найти условное оптимальное в среднем управление, нужно минимизировать среднее значение (6.3) количеству $k$ переключений и по моментам переключений ${{t}_{1}},...,{{t}_{k}}$, как это указано (5.11). Очевидно, что этот минимум левой части (6.3) достигается одновременно с минимумом функции $\varphi ({{t}_{0}},\bar {x}{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{1}},...,{{t}_{k}})$ в правой части. Значит, оптимальное в среднем управление пучком траекторий будет совпадать с оптимальным управлением для траектории, исходящей из центра тяжести $\bar {x}$. Таким образом, принцип разделения для задачи оптимального в среднем управления выполняется в этом случае.

Теорема разделения для оптимального в среднем управления с “простыми” переключениями. Для детерминированной ЛК-задачи (1.13)–(1.15) с “простыми” переключениями оптимальное в среднем управление пучком траекторий совпадает с оптимальным управлением одной траекторией, исходящей из центра тяжести множества возможных начальных состояний.

6.3. Синтез оптимального гарантирующего управления. Найдем минимаксное значение функции стоимости (6.2). Пусть максимум достигается в $r + 1$ точках:

т.е. $\sigma _{0}^{*} = \{ x_{0}^{*},x_{1}^{*},...,x_{r}^{*}\} $. Минимум максимума (6.4) по переменной $\hat {x}$ достигается в точке (5.17). Составим выпуклую комбинацию максимальных значений (6.4) с теми же коэффициентами s_i, что и в (5.17). Обозначим $\Delta x_{i}^{*} = x_{i}^{*} - \hat {x}$, $i = 0,1,...,r$. Заметим, что выпуклая комбинация этих векторов равна нулевому вектору: так как ${{s}_{0}} + {{s}_{1}} + ... + {{s}_{r}} = 1$. Поэтому для функции (6.2) получаем

Чтобы найти условное оптимальное гарантирующее управление, нужно минимизировать максимальное значение (6.5) по количеству $k$ переключений и по моментам переключений ${{t}_{1}},...,{{t}_{k}}$, как это указано (5.18). Очевидно, что этот минимум левой части (6.5) достигается одновременно с минимумом функции $\varphi ({{t}_{0}},\hat {x}{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{1}},...,{{t}_{k}})$ в правой части. Значит, оптимальное гарантирующее управление пучком траекторий будет совпадать с оптимальным управлением для траектории, исходящей из точки $\hat {x}$. Таким образом, принцип разделения для задачи оптимального гарантирующего управления выполняется в этом случае.

Теорема разделения для оптимального гарантирующего управления с “простыми” переключениями. Для детерминированной ЛК-задачи (1.13)–(1.15) с “простыми” переключениями оптимальное гарантирующее управление пучком траекторий совпадает с оптимальным управлением одной траекторией, исходящей из некоторой точки выпуклого замыкания множества худших для этого управления возможных начальных состояний системы.

7. Примеры. Рассмотрим примеры применения принципа разделения для синтеза оптимального в среднем и оптимального гарантирующего управлений. В первом примере исследуется система второго порядка со сменой канала управления. Эта ЛК-задача является контрпримером, в котором принцип разделения не выполняется, а условный принцип разделения выполняется. Во втором примере рассматривается ЛК-задача управления с “простыми” переключениями. В этой задаче оптимальные процессы имеют терминальные переключения, т.е. переключения только в начальный и/или конечный моменты времени. Принцип разделения в этом примере выполняется, что и подтверждают расчеты.

Пример 1 (ЛК-задача с переключением канала управления). Пусть на заданном промежутке времени $T = [0,3]$ динамическая система совершает N переключений (скачков) в моменты времени ${{t}_{i}}$, $i = 1,...,N$, которые образуют неубывающую последовательность:

Между неравными последовательными моментами переключений состояние системы изменяется непрерывно, согласно дифференциальным уравнениям:

а в моменты переключений – дискретно в соответствии с рекуррентными уравнениями:

Здесь, как и ранее, $\mathcal{N} = \{ i = 0,1,...,N{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{i}} < {{t}_{{i + 1}}}\} $ – множество номеров ненулевых (по длине) частичных промежутков ${{T}_{i}}\; \triangleq \;[{{t}_{i}},{{t}_{{i + 1}}})$ непрерывного движения системы; x(t) – состояние системы в момент времени $t \in T$, $x = {{({{x}_{1}},{{x}_{2}})}^{{\text{Т}}}} \in {{\mathbb{R}}^{2}}$; u(t) – значение управления непрерывным движением системы в момент времени $t \in T$, $u \in \mathbb{R}$. В уравнении (7.2) ${{x}_{i}}\; \triangleq \;x({{t}_{i}})$ – состояние системы сразу после i-го переключения, ${{x}_{{i - }}}$ – состояние системы непосредственно перед i-м переключением (1.4); ${{v}_{i}}$ – управление переключением системы в момент ${{t}_{i}} \in \mathcal{T}$, $v \in \mathbb{R}$.

Качество процесса управления оценивается квадратичным функционалом

где ${{x}_{0}}$ – начальное состояние системы, $w = (u( \cdot ),v( \cdot ))$ – допустимое управление. Коэффициенты $\lambda = 0.2$ и $\eta = 1000$ определяют затраты на каждое переключение. Количество N и моменты переключений ${{t}_{1}}$, …, ${{t}_{N}}$ заранее не заданы и подлежат оптимизации. Начальное состояние системы точно не известно, а известно множество ${{\sigma }_{0}}$ возможных начальных состояний, представляющее собой параллелограмм с вершинами $(7.5;\,5)$, $(8.5;\,5)$, $(7.5;\,6)$, $(6.5;\,6)$. Требуется найти:

1) оптимальное управление для одной траектории, исходящей из центра ${{\bar {x}}_{0}} = (7.5;\,5.5)$ параллелограмма ABCD;

2) оптимальное в среднем управление ${{w}^{{\text{с}}}}$, минимизирующее среднее значение функционала (7.3):

3) оптимальное гарантирующее (минимаксное) управление ${{w}^{{\text{г}}}}$, минимизирующее максимальное значение функционала (7.3):

В системе (7.1), (7.2) имеется один канал управления: первая координата управляема при непрерывном движении, а вторая – нет (она экспоненциально отклоняется от нуля). В момент переключения фактически происходит взаимная замена координат состояния – неуправляемая координата становится управляемой и наоборот, причем значение первой управляемой координаты корректируется при помощи управления. Таким образом, совершая переключения (т.е. меняя канал управления), можно попеременно управлять координатами системы.

По сравнению с общей постановкой (1.1)–(1.4), (1.8)–(1.10) имеем: ${{t}_{0}} = 0$, ${{t}_{F}} = 3$, $X = {{\mathbb{R}}^{2}}$, U = $\mathbb{R}$, $V = \mathbb{R}$, $D(t) = 1$, $\lambda (t) = \lambda $, $\hat {D} = \eta $,

1. Сначала находим решение ЛК-задачи управления одной траекторией. Моментные функции цены имеют вид (4.6)

где $\Phi (t{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{1}},...,{{t}_{k}}){\kern 1pt} $ – симметрическая неотрицательно определенная матрица второго порядка, а ${{t}_{1}}$, …, ${{t}_{k}}$ – моменты переключений: $0 \leqslant t \leqslant {{t}_{1}} \leqslant ... \leqslant {{t}_{k}} \leqslant 3$. Запишем для элементов матрицы $\Phi $ дифференциальное уравнение Риккати (4.7):

Уравнение для ${{\Phi }_{{21}}}$ опущено, так как ${{\Phi }_{{21}}} = {{\Phi }_{{12}}}$. Согласно алгоритму из разд. 4.1, рекуррентная процедура нахождения моментных функций цены и условного оптимального позиционного управления для рассматриваемой ЛК-задачи следующая.

Шаг 0. Находим элементы матрицы $\Phi (t)$ 0-моментной функции цены $\varphi (t,x{\kern 1pt} {\text{|}}{\kern 1pt} \emptyset ) = \frac{1}{2}{{x}^{{\text{Т}}}}\Phi (t)x$, решая систему дифференциальных уравнений (7.5) с нулевыми терминальными условиями $\Phi (3)$ = 0. Получаем

Составляем матрицу $L(t) = \,({{\Phi }_{{11}}}(t),{{\Phi }_{{12}}}(t))$ коэффициентов оптимального позиционного управления ${\mathbf{u}}(t,x) = - L(t)x$ непрерывным движением без переключений. Полагаем k = 1 и переходим к шагу 1¹.

Шаг 1¹. Находим матрицу $\Phi ({{t}_{1}}\,{\text{|}}\,{{t}_{1}})$ одномоментной функции цены (7.4) в момент $t = {{t}_{1}}$ единственного переключения, решая рекуррентное уравнение (4.9), которое для рассматриваемой ЛК-задачи имеет вид

В правой части уравнения (7.6) стоят элементы матрицы $\Phi ({{t}_{1}})$ 0-моментной функции цены $\varphi (t,x\,{\text{|}}\,\emptyset )$, найденные ранее. Составляем матрицу ${{L}_{{{{t}_{1}}}}} = \,({{\Phi }_{{21}}}({{t}_{1}}),{{\Phi }_{{11}}}({{t}_{1}}))$ коэффициентов оптимального позиционного управления ${\mathbf{v}}({{t}_{1}},x{\kern 1pt} {\text{|}}{\kern 1pt} \emptyset ) = - {{L}_{{{{t}_{1}}}}}x$ единственным переключением системы.

Шаг 2¹. Находим элементы матрицы $\Phi (t\,{\text{|}}\,{{t}_{1}})$ одномоментной функции цены (7.4) до первого переключения (при $t < {{t}_{1}}$), решая систему дифференциальных уравнений (7.5) с терминальным условием (7.6). Получаем

где $\tau = {{t}_{1}} - t$, $\Delta = ch\tau + {{\Phi }_{{11}}}sh\tau $. В правых частях равенств (7.7) стоят элементы матрицы $\Phi ({{t}_{1}}\,{\text{|}}\,{{t}_{1}})$, найденные ранее. Составляем матрицу $L(t{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{1}}) = ({{\Phi }_{{11}}}(t{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{1}}),{{\Phi }_{{12}}}(t{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{1}}))$ коэффициентов оптимального позиционного управления $u(t,x{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{1}}) = - L(t{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{1}})x$ непрерывным движением до переключения. Проверяем условие окончания. Если условие выполняется, то рекуррентная процедура заканчивается, иначе полагаем $k: = k + 1$ и переходим к шагу 1^k. 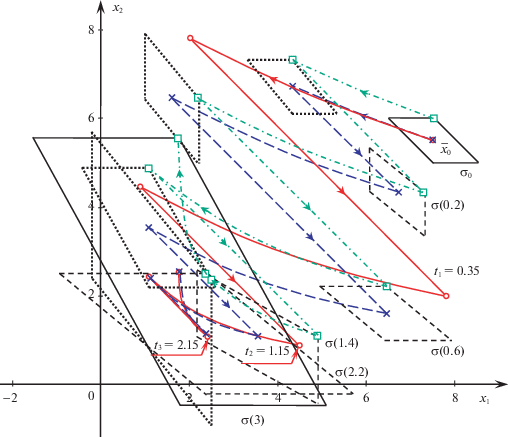При численном решении проверялось условие $\min {{I}_{{k - 1}}} \leqslant \min {{I}_{k}}$, где – минимальное значение функционала (7.3) при фиксированном количестве k переключений. Оптимизация моментов переключений (7.8) выполнялась перебором на сетке с шагом $0.01$ по времени. Для заданного начального состояния были получены следующие значения функционалов:

Так как ${{I}_{3}} < {{I}_{4}}$, то оптимальной оказывается траектория с тремя переключениями в моменты времени: ${{t}_{1}} = 0.35$, ${{t}_{2}} = 1.15$, ${{t}_{3}} = 2.15$. На рис. 1 оптимальная фазовая траектория изображена сплошной линией, начинающейся в точке ${{\bar {x}}_{0}}$, состояния непосредственно до и после переключений отмечены маленькими окружностями, направление движения указано стрелками.

2. Для решения ЛК-задачи управления в условиях неопределенности начального состояния нужно построить функцию стоимости полуоптимального процесса. Моментные функции стоимости имеют вид (5.4)

где $\Phi (t\,{\text{|}}\,{{t}_{1}},...,{{t}_{k}}){\kern 1pt} $ – матрица моментной функции цены (7.4), Ψ(t|t₁, …, t_k) – симметрическая неотрицательно определенная матрица второго порядка, а $\Delta x = x - \hat {x}$ – отклонение состояния $x$ от состояния $\hat {x}$ на опорной траектории. В (7.9) учитывается, что при $\Delta x = 0$ моментные функции стоимости и цены (7.4) совпадают. Матрицы $\Phi (t\,{\text{|}}\,{{t}_{1}},...,{{t}_{k}}){\kern 1pt} $ моментных функций цены найдены в п. 1 решения. Поэтому для формирования (7.9) остается получить матрицы $\Psi (t{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{1}},...,{{t}_{k}}){\kern 1pt} $.

Запишем для элементов матрицы $\Gamma = \Phi + \Psi $ дифференциальное уравнение (5.7):

Уравнение для ${{\Gamma }_{{21}}}$ опущено, так как ${{\Gamma }_{{21}}} = {{\Gamma }_{{12}}}$. Согласно алгоритму (см. разд. 5.1), рекуррентная процедура нахождения моментных функций стоимости для рассматриваемой ЛК-задачи следующая.

Шаг 0. Находим элементы матрицы $\Gamma (t)$, решая систему дифференциальных уравнений (7.10) с нулевыми терминальными условиями $\Gamma (3) = 0$. Получаем

Определяем матрицу $\Psi (t) = \Gamma (t) - \Phi (t)$ 0-моментной функции стоимости

Полагаем k = 1 и переходим к шагу 1¹.

Шаг 1¹. Находим матрицу $\Gamma ({{t}_{1}}{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{1}})$ в момент $t = {{t}_{1}}$ единственного переключения, решая рекуррентное уравнение (5.8), которое для рассматриваемой ЛК-задачи имеет вид

В правой части уравнения (7.11) стоят элементы матрицы $\Gamma ({{t}_{1}})$, найденные ранее.

Шаг 2¹. Находим элементы матрицы $\Gamma (t\,{\text{|}}\,{{t}_{1}})$ одномоментной функции стоимости (5.9) до первого переключения (при $t < {{t}_{1}}$), решая систему дифференциальных уравнений (7.10) с терминальным условием (7.11). Получаем

где $\tau = {{t}_{1}} - t$. В правых частях равенств (7.12) стоят элементы матрицы $\Gamma ({{t}_{1}}{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{1}})$, найденные ранее по формуле (7.11). Определяем матрицу $\Psi (t{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{1}}) = \Gamma (t{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{1}}) - \Phi (t{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{1}})$ одномоментной функции стоимости $\beta (t,x{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{1}})$. Проверяем условие окончания. Если условие выполняется, то рекуррентная процедура заканчивается, иначе полагаем $k: = k + 1$ и переходим к шагу 1^k. При численном решении проверялось условие $\min I_{{k - 1}}^{{\text{c}}} \leqslant \min I_{k}^{{\text{c}}}$, где – минимальное среднее значение функционала (7.3) при фиксированном количестве k переключений. Для заданного множества возможных начальных состояний были получены следующие значения функционалов:

Так как $I_{4}^{{\text{c}}} < I_{5}^{{\text{c}}}$, то оптимальным в среднем оказывается управление с четырьмя переключениями в моменты времени ${{t}_{1}} = 0.2$, ${{t}_{2}} = 0.6$, ${{t}_{3}} = 1.4$, ${{t}_{4}} = 2.2$. Пучок траекторий, соответствующий этому управлению, приведен на рис. 1. Множества возможных состояний, представляющие собой параллелограммы, изображены в начальный и конечный моменты времени сплошными линиями, непосредственно перед переключениями – пунктирными, а после переключения – штриховыми линиями. Траектория, исходящая из центра ${{\bar {x}}_{0}}$ параллелограмма ${{\sigma }_{0}}$, соответствующая оптимальному в среднем управлению, изображена штриховой линией, а характерные состояния – крестиками. Стрелками указано направление движения. Отметим, что эта траектория отличается от оптимальной траектории для того же начального состояния ${{\bar {x}}_{0}}$ (сплошная линия с маленькими окружностями). Значит, принцип разделения не выполняется. Условный принцип разделения выполняется, так как оптимальное в среднем управление является условным оптимальным для траектории, исходящей из центра тяжести.

3. В ЛК-задаче оптимального гарантирующего управления моментные функции стоимости полуоптимального процесса такие же, как в задаче оптимального в среднем управления. Изменяется только условие окончания рекуррентной процедуры. При численном решении проверялось условие $\min I_{{k - 1}}^{{\text{г}}} \leqslant \min I_{k}^{{\text{г}}}$, где

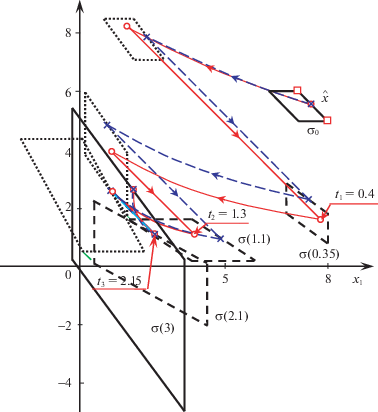
оптимальное гарантирующее (минимаксное) значение функционала (7.3) при фиксированном количестве k переключений. Напомним, что $\sigma _{0}^{*}$ – множество точек глобального максимума функции $x \to \beta (0,x,\hat {x}{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{1}},...,{{t}_{k}})$ на множестве ${{\sigma }_{0}}$. Максимум выпуклой функции на многоугольнике достигается в его вершинах. Практически всегда это одна вершина, поскольку из-за приближенных вычислений получить точное равенство значений функции в двух вершинах невозможно. При этом кажется, что в пучке есть только одна худшая траектория. Однако это впечатление обманчивое. Как правило, худших траекторий в пучке несколько. Для рассматриваемой задачи – две или три. Эти варианты нужно исследовать отдельно, обеспечивая при численном решении равенство значений функционала программно. Для заданного параллелограмма ${{\sigma }_{0}}$ минимум максимального значения (7.13) достигается при k = 3, $\hat {x} = ({\text{7}}{\text{.964;}}\,{\text{5}}{\text{.536}})$. Худшими (по значениям функционала) оказываются две траектории, исходящие из смежных вершин $(8.5;\,5)$, $(7.5;\,6)$ параллелограмма, наиболее удаленных от начала координат. В результате численного решения были получены следующие значения функционалов:

Так как $I_{3}^{{\text{г}}} < I_{4}^{{\text{г}}}$, то оптимальным гарантирующим оказывается управление с тремя переключениями в моменты времени ${{t}_{1}} = {\text{0}}{\text{.35}}$, ${{t}_{2}} = {\text{1}}{\text{.1}}$, ${{t}_{3}} = {\text{2}}.1$. Пучок траекторий, соответствующий этому управлению, представлен на рис. 2. Множества возможных состояний, представляющие собой параллелограммы, изображены в начальный и конечный моменты времени сплошными линиями, непосредственно перед переключениями – пунктирными, а после переключения – штриховыми линиями. Худшие (по значениям функционала) вершины параллелограмма отмечены квадратиками. Между ними находится точка $\hat {x}$ (гарантирующая оценка), отмеченная окружностью и крестиком. Траектория, исходящая из точки $\hat {x}$, соответствующая оптимальному гарантирующему управлению, изображена штриховой линией, а характерные состояния – крестиками. Стрелками указано направление движения. Оптимальная траектория, исходящая из того же начального состояния $\hat {x}$, также имеет три переключения, но в другие моменты времени: ${{t}_{1}} = {\text{0}}{\text{.4}}$, ${{t}_{2}} = {\text{1}}{\text{.3}}$, ${{t}_{3}} = {\text{2}}.15$. Она изображена сплошной линией, а характерные состояния – маленькими окружностями. Отметим, что эти траектории не совпадают. Значит, принцип разделения не выполняется. Условный принцип разделения выполняется, так как оптимальное гарантирующее управление является условным оптимальным для траектории, исходящей из состояния $\hat {x}$.

Пример 2 (ЛК-задача с “простыми” переключениями). Пусть на заданном промежутке времени $T = [0,2]$ динамическая система совершает N переключений (скачков) в моменты времени ${{t}_{i}}$, $i = 1,...,N$, которые образуют неубывающую последовательность $\mathcal{T} = \{ {{t}_{1}},...,{{t}_{N}}\} $:

Между неравными последовательными моментами переключений состояние системы изменяется непрерывно, согласно дифференциальным уравнениям:

а в моменты переключений – дискретно в соответствии с рекуррентными уравнениями:

Здесь, как и ранее, $\mathcal{N} = \{ i = 0,1,...,N{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{i}} < {{t}_{{i + 1}}}\} $ – множество номеров ненулевых (по длине) частичных промежутков ${{T}_{i}} \triangleq [{{t}_{i}},{{t}_{{i + 1}}})$ непрерывного движения системы; $x(t)$ – состояние системы в момент времени $t \in T$, $x = {{({{x}_{1}},{{x}_{2}})}^{{\text{Т}}}} \in {{\mathbb{R}}^{2}}$; $u(t)$ – значение управления непрерывным движением системы в момент времени $t \in T$, $u \in \mathbb{R}$. В уравнении (7.15) ${{x}_{i}} \triangleq x({{t}_{i}})$ – состояние системы сразу после i-го переключения, ${{x}_{{i - }}}$ – состояние системы непосредственно перед i-м переключением (1.4); ${{v}_{i}}$ – управление переключением системы в момент ${{t}_{i}} \in \mathcal{T}$, $v \in \mathbb{R}$.

Качество процесса управления оценивается квадратичным функционалом

где ${{x}_{0}}$ – начальное состояние системы, $w = (u( \cdot ),{v}( \cdot ))$ – программное управление $u( \cdot )$ непрерывным движением и последовательность $v( \cdot ) = \{ {{v}_{i}} = v({{t}_{i}}){\kern 1pt} {\text{|}}{\kern 1pt} {{v}_{i}} \in V,{{t}_{i}} \in \mathcal{T}\} $ дискретных управлений переключениями, $\lambda = 0.1$ – коэффициент, определяющий затраты на переключение. Количество переключений N и моменты переключений ${{t}_{1}}$, …, ${{t}_{N}}$ заранее не заданы и подлежат оптимизации. Начальное состояние системы точно не известно, а известно множество ${{\sigma }_{0}} = [3,\,5] \times [1,\,3]$ возможных начальных состояний, представляющее собой квадрат с центром ${{\bar {x}}_{0}} = (4;\,2)$. Требуется найти:

1) оптимальное управление $\bar {w}$ для одной траектории, исходящей из состояния ${{\bar {x}}_{0}}$;

2) оптимальное в среднем управление ${{w}^{{\text{с}}}}$, минимизирующее среднее значение функционала (7.16):

3) оптимальное гарантирующее (минимаксное) управление ${{w}^{{\text{г}}}}$, минимизирующее максимальное значение функционала (7.16):

ЛК-задача (7.14)–(7.16) является стационарной с “простыми” переключениями, в которой нетерминальные члены функционала зависят только от управления. Нужно минимизировать квадрат отклонения конечного состояния от нулевого при наименьших затратах на управление. Фактически это задача терминального управления с учетом энергетических потерь. По сравнению с общей постановкой (1.1)–(1.4), (1.8)–(1.10) имеем: ${{t}_{0}} = 0$, ${{t}_{F}} = 2$, $X = {{\mathbb{R}}^{2}}$, $U = \mathbb{R}$, $V = \mathbb{R}$, $D = 1$, $\lambda (t) = \lambda $, $\hat {D} = 1$,

А. Сначала докажем, что оптимальные процессы в поставленной задаче имеют переключения только в начальный и/или конечный моменты времени. Действительно, предположим, что оптимальный процесс имеет один момент переключения t₁ внутри промежутка $[0,\,2]$ функционирования системы. Пусть $\delta {{t}_{1}}$ – малая вариация момента переключения. Поскольку на промежутке $({{t}_{1}},2]$ скачков траектории нет, то вариация функционала (7.16) вычисляется обычным образом [22]: $\delta I = \psi ({{t}_{1}})A\hat {B}{{v}_{1}}\delta {{t}_{1}}$, где ${{v}_{1}}$ – управление переключением в момент t₁, а $\psi $ – вектор вспомогательных переменных, удовлетворяющий сопряженной системе: $\dot {\psi }(t) = - \psi (t)A$. Так как момент t₁ оптимальный, а вариация $\delta {{t}_{1}}$ может быть любого знака, заключаем, что $\psi ({{t}_{1}})A\hat {B}{{v}_{1}} = 0$. Оказывается, что в рассматриваемой системе величина $\psi ({{t}_{1}})A\hat {B}{{v}_{1}}$ постоянная. В самом деле, дифференцируя по t₁, получаем $\dot {\psi }({{t}_{1}})A\hat {B}{{v}_{1}} = - \psi ({{t}_{1}}){{A}^{2}}\hat {B}{{v}_{1}} = 0$, так как A² – нулевая матрица. Таким образом, значение функционала не изменится, если оптимальный момент переключения t₁ перенести, например, в конечный момент времени. Аналогичным образом можно перенести все моменты переключений в начало и конец промежутка функционирования. Получим оптимальный процесс с терминальными переключениями.

Б. Выведем уравнения для моментных функций цены в случае терминальных переключений. Предположим, что неубывающая последовательность моментов переключений (1.1) имеет вид

т.е. процесс имеет  j переключений в начальный момент времени t₀ и k переключений в конечный момент ${{t}_{F}}$. Обозначим через ${{\varphi }_{{jk}}}(t,x) = \varphi (t,x{\kern 1pt} {\text{|}}{\kern 1pt} {{t}_{0}},...,{{t}_{0}},{{t}_{F}},...,{{t}_{F}})$ моментную функцию цены, которая, согласно (4.6), квадратичная:

В конечный момент времени ${{t}_{F}}$ матрицы ${{\Phi }_{{0k}}}({{t}_{F}})$, $k = 1,2,...$, квадратичной формы находятся по рекуррентной формуле (4.9):

с начальным условием ${{\Phi }_{{00}}}({{t}_{F}}) = F$. В правой части (7.19) все матрицы вычисляются в момент ${{t}_{F}}$, причем $\Phi = {{\Phi }_{{0\,k - 1}}}({{t}_{F}})$. На промежутке $t \in ({{t}_{0}},{{t}_{F}})$ матрица $\Phi (t) = {{\Phi }_{{0k}}}(t)$ удовлетворяет дифференциальному уравнению Риккати (4.7): с терминальным условием ${{\Phi }_{{0k}}}({{t}_{F}} - 0) = {{\Phi }_{{0k}}}({{t}_{F}})$, $k = 0,1,...$ В начальный момент времени ${{t}_{0}}$ матрица ${{\Phi }_{{jk}}}({{t}_{0}})$, $j = 1,2,...$; $k = 0,1,...$, вычисляется по рекуррентной формуле (4.9): с начальным условием ${{\Phi }_{{0k}}}({{t}_{0}}) = {{\Phi }_{{0k}}}({{t}_{0}} + 0)$. В правой части (7.21) все матрицы имеют аргумент ${{t}_{0}}$ и $\Phi = {{\Phi }_{{j - 1\,\,k}}}({{t}_{0}})$.

Минимальное значение функционала, функцию цены и оптимальное количество терминальных переключений находим, выполняя целочисленную минимизацию функции (7.18):

Как видим, задача с терминальными переключениями решается сравнительно просто.

В. Переходим теперь непосредственно к решению задачи. Запишем уравнения (7.19)–(7.21) для задачи (7.14)–(7.16). Функцию цены (7.18) будем искать в виде

Здесь учтено, что коэффициент $\lambda $ затрат на переключение не зависит от времени. В конечный момент времени $t = 2$ элементы матрицы ${{\Phi }_{{jk}}}$ квадратичной формы (7.23), согласно (7.19), удовлетворяют уравнениям

с начальными условиями ${{\phi }_{{0k}}}(2) = 1$, ${{\psi }_{{0k}}}(2) = 0$, ${{\gamma }_{{0k}}}(2) = 1$. Следовательно,

На промежутке $t \in (0,2)$ элементы матрицы (7.23), согласно (7.20), удовлетворяют системе дифференциальных уравнений:

с терминальными условиями ${{\phi }_{{0k}}}(2 - 0) = 1$, ${{\psi }_{{0k}}}(2 - 0) = 0$, ${{\gamma }_{{0k}}}(2 - 0) = 1{\text{/}}(1 + k)$. Решая (7.24), получаем где $\tau = 2 - t$, $\Delta = [12(1 + k + \tau ) + 4(1 + k){{\tau }^{3}} + {{\tau }^{4}}]{\text{/}}[12(1 + k)]$, $k = 0,1,...$

В начальный момент времени, согласно рекуррентному уравнению (7.21), имеем систему

Начальными условиями для (7.26) служат значения ${{\phi }_{{0k}}}(0)$, ${{\psi }_{{0k}}}(0)$, ${{\gamma }_{{0k}}}(0)$, полученные по формулам (7.25) при $t = 0$. Система (7.26) имеет решение

где ${{\phi }_{{0k}}} = {{\phi }_{{0k}}}(0)$, ${{\psi }_{{0k}}} = {{\psi }_{{0k}}}(0)$, ${{\gamma }_{{0k}}} = {{\gamma }_{{0k}}}(0)$, $j = 0,1,...$; $k = 0,1,...$

1. Найдем оптимальное управление $\bar {w}$ для одной траектории, исходящей из состояния ${{\bar {x}}_{0}}$. Сначала определяем оптимальное количество терминальных переключений, решая задачу целочисленной минимизации (7.22). Минимальное значение функционала $\min I = 2.4194$ получаем при восьми переключениях в начальный момент времени и трех – в конечный, т.е. при j = 8 и k = 3. Оптимальное управление ${{v}_{1}} = ... = {{v}_{8}} = - 0.4525$ переключениями в начальный момент и ${{v}_{9}} = {{v}_{{10}}} = {{v}_{{11}}}$ = 0.4144 – в конечный (вычисления приближенные). Оптимальное программное управление непрерывным движением аффинное: $u(t) = 0.4335\,t - 0.4525$, $0 \leqslant t \leqslant 2$. На рис. 3 оптимальная фазовая траектория представлена сплошной полужирной линией, состояния системы до и после переключения – квадратиками. Стрелками показано направление движения.

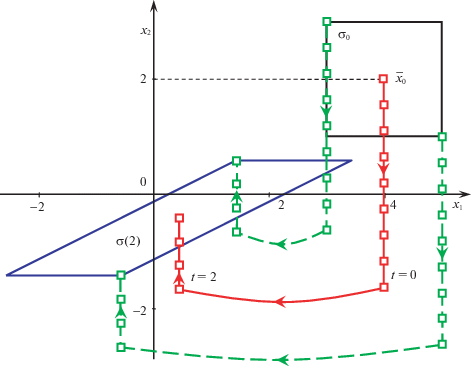
2. Оптимальное в среднем управление ${{w}^{{\text{с}}}}$, минимизирующее среднее значение (7.17) функционала (7.16), совпадает с оптимальным управлением для траектории, исходящей из центра квадрата ${{\sigma }_{0}} = [3,\,5] \times [1,\,3]$, т.е. с управлением $\bar {w}$, найденным в п. 1. Минимальное среднее значение функционала $\min {{I}^{{\text{с}}}} = {\text{3}}{\text{.4194}}$. На рис. 3 представлен оптимальный в среднем пучок траекторий. Множество возможных начальных состояний – квадрат, конечных состояний – параллелограмм. Полужирными линиями изображены траектории, исходящие из центра квадрата и двух его вершин. Стрелками показано направление движения. Так как в этой задаче принцип разделения выполняется, то моментная функция стоимости полуоптимального процесса не нужна для нахождения оптимального в среднем управления.

3. В отличие от задачи управления в среднем для получения минимаксного управления функция стоимости необходима. Она имеет вид (6.2) с функцией цены (7.23) и с матрицей $\Gamma $, которая не зависит от количества переключений:

Выпуклая по $x$ функция (7.27) достигает наибольшего значения в вершинах квадрата ${{\sigma }_{0}}$. Практически всегда это одна вершина, поскольку из-за приближенных вычислений получить точное равенство значений функции в двух вершинах невозможно. При этом кажется, что в пучке есть только одна худшая траектория. Однако это впечатление обманчивое. Как правило, худших траекторий в пучке несколько. Для рассматриваемой задачи – две или три. Эти варианты при численном решении нужно обеспечивать программно. Для заданного квадрата ${{\sigma }_{0}}$ минимум максимального значения

достигается при  j = 8, $k = 3$, $\hat {x} = (4.09;\,2.09)$. Худшими оказывается две траектории, исходящие из противоположных вершин $(3;\,1)$ и $(5;\,3)$. Оптимальное гарантирующее управление пучком совпадает с оптимальным управлением для траектории, исходящей из состояния $\hat {x}$. Она имеет восемь переключений в начальный момент времени и три – в конечный. Минимаксное значение $\min \,\max {{I}^{{\text{г}}}}$ = 7.45987. На рис. 4 представлены начальное и конечное множества возможных состояний (квадрат и параллелограмм соответственно), оптимальная фазовая траектория, исходящая из состояния $\hat {x}$ (сплошная полужирная линия), две худшие траектории пучка (штриховые линии). Состояния непосредственно до и после переключений отмечены маленькими квадратиками, центры квадрата ${{\sigma }_{0}}$ и параллелограмма $\sigma (2)$ – окружностями, а направление движения – стрелками.

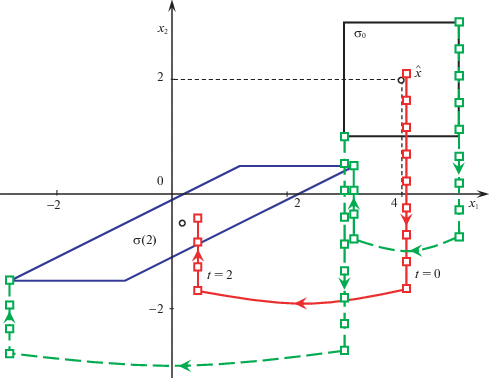
Заключение. Принцип разделения позволяет свести задачу оптимального управления детерминированными системами в условиях параметрической неопределенности к совокупности двух задач – оптимального управления одной траекторией и оптимального наблюдения. Решением задачи наблюдения служит оценка множества возможных состояний, т.е. виртуальное состояние системы, которое при управлении заменяет множество возможных состояний. Эта оценка используется в оптимальном позиционном управлении, полученном при решении задачи управления одной траекторией. Обоснованием такого подхода для ЛК-задач управления пучками траекторий ПС служит доказанный в статье так называемый условный принцип разделения. По сравнению с обычным принципом разделения, справедливым для ЛК-задач управления пучками траекторий непрерывных, дискретных и непрерывно-дискретных систем, условный принцип разделения гораздо сложнее с вычислительной точки зрения. Для его применения нужно вычислить и запомнить моментные функции цены, которые зависят от нарастающего количества моментов переключений. Это существенно повышает требования к вычислительным ресурсам, необходимым для численного решения задачи. Если количество допустимых переключений небольшое из-за технических ограничений, то решение задачи упрощается.

Условный принцип разделения можно применять и для нелинейных ПС. Вычислительные ресурсы при этом также возрастают, так как в отличие от ЛК-задач моментные функции цены уже не будут квадратичными. Их придется задавать приближенно, используя интерполяцию на сетке в пространстве состояний или аппроксимацию. Поскольку принцип разделения для нелинейных систем не выполняется, получаемое управление пучком траекторий не будет оптимальным. Однако на практике это субоптимальное управление часто оказывается вполне приемлемым.