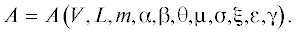Известия РАН. Теория и системы управления, 2020, № 2, стр. 75-82

ОБ ЭНЕРГЕТИЧЕСКИ ЭФФЕКТИВНЫХ РЕЖИМАХ ДВИЖЕНИЯ МОБИЛЬНЫХ РОБОТОВ С ОРТОГОНАЛЬНЫМИ ШАГАЮЩИМИ ДВИЖИТЕЛЯМИ ПРИ ПРЕОДОЛЕНИИ ПРЕПЯТСТВИЙ

Е. С. Брискин^a, b, *, Я. В. Калинин^a, b, М. В. Мирошкина^a

^a Волгоградский государственный технический ун-т
Волгоград, Россия

^b Университет Иннополис
Иннополис, Россия

^* E-mail: dtm@vstu.ru

Поступила в редакцию 20.05.2019
После доработки 07.08.2019
Принята к публикации 30.09.2019

DOI: 10.31857/S0002338820010035

Полный текст (PDF)

Аннотация

Рассматриваются особенности управления движением шагающего робота с ортогональными движителями при преодолении препятствий. Сформулирована задача согласованного управления приводами горизонтального и вертикального перемещения для реализации режима движения, обеспечивающего оптимальность по заданному критерию. Критерием оптимальности выбран минимум тепловых потерь в приводных двигателях. Приводится методика решения поставленной задачи и результаты моделирования.

Введение. Мобильные роботы с шагающими движителями обладают возможностью бесконтактного преодоления препятствий, что является одной из особенностей таких машин [1–4]. В 70–80-е гг. прошлого столетия профессором Н.В. Умновым [1, 5] был предложен вид траектории переноса шагающего движителя (рис. 1). Такой вид предложенной траектории можно объяснить неразвитостью информационно-измерительных систем и необходимостью организовывать взаимодействие стоп движителей с опорной поверхностью без проскальзывания по ней независимо от ее профиля. Но при наличии информации о профиле опорной поверхности и на основе выбираемых показателей качества движения, например, минимума тепловых потерь в приводных двигателях, минимума среднеквадратического ускорения стопы, минимума пройденного пути и др. [6, 7], можно изменять законы движения стопы. По сочетаниям показателей могут быть определены границы парето-оптимальных режимов движения [8] для комплексного показателя качества.

Рис. 1.

Траектория переноса стопы движителя: 1 – абсолютная траектория по Н.В. Умнову; 2 – возможная траектория; 3 – профиль опорной поверхности

Известны методы преодоления запрещенных зон за счет управления походкой [9] для шагающих машин с цикловыми движителями. С точки зрения энергоэффективности, для роботов рассмотрены задачи оптимального управления горизонтальным движением движителей при их переносе из одного положения в другое. Показано, что по критерию минимума тепловых потерь в приводных двигателях выгодно или использовать рекуператоры энергии [10, 11], или отказаться от равномерного движения корпуса робота [12] и применять его в качестве рекуператора. Это подтверждается и исследованиями динамики движения двуногого робота [13].

Для шагающих роботов с ортогональными движителями рассмотрена задача вертикального перемещения стопы движителя и ее переноса в новое положение [14] в соответствии с комплексным критерием качества движения.

Однако задача движения стопы шагающего движителя одновременно в горизонтальном и вертикальном направлениях с точки зрения удовлетворения выбранным показателям качества движения не рассматривалась. Также не рассматривалась задача об определении оптимального по тому или иному критерию движения стопы с ее подъемом и опусканием на опорную поверхность при наличии препятствий.

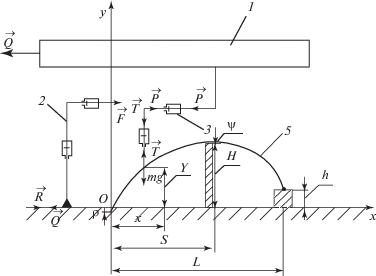
1. Постановка задачи. Рассматривается поступательное с постоянной скоростью корпуса движение робота с ортогональными шагающими движителями, например шагающего робота “Ортоног” [15] (рис. 2). Профиль опорной поверхности, характеризуемый расстоянием S от стопы, вступающей в фазу переноса до препятствия в форме выступа высотой H, расстоянием L до места ее постановки на высоте h от начального уровня (рис. 3), считается известным, например по данным информационно-измерительной системы робота. В каждый момент времени в переносе находится один из движителей массы m.

Рис. 2.

Шагающий робот “Ортоног”

Рис. 3.

Расчетная схема движения робота

Для решения задачи составляются дифференциальные уравнения движения стопы массы m в горизонтальном и вертикальном направлениях и уравнение, описывающее равномерное поступательное движение корпуса робота:

(1.1)

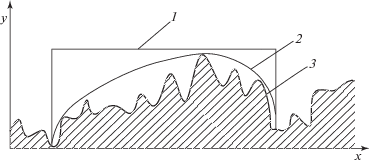
$\left\{ \begin{gathered} m\ddot {x} = P, \hfill \\ m\ddot {y} = T - mg, \hfill \\ 0 = F - Q - P, \hfill \\ \end{gathered} \right.$

где x, y – соответственно горизонтальная и вертикальная координаты стопы движителя в абсолютном движении, g – ускорение свободного падения, Q – сила сопротивления движению робота, обусловленная, например, крюковой нагрузкой и т.п. [16, 17]; F – сила, развиваемая приводом курсового движения, обеспечивающая движение корпуса, P – сила, обеспечивающая горизонтальное перемещение переносимой стопы, T – сила, развиваемая приводом вертикального перемещения стопы.

Формируется показатель качества, характеризующий тепловые потери в приводных двигателях на единицу пути, определяемый выражением

(1.2)

$A = {\alpha }\int\limits_0^{\tau } {({{F}^{2}} + {{P}^{2}}){\text{d}}t + {\beta }\int\limits_0^{\tau } {{{T}^{2}}{\text{d}}t} } ,$

где τ – время переноса стопы; α, β – известные характеристики двигателей горизонтального и вертикального перемещений соответственно.

Ставится задача определения таких законов движения стопы по горизонтали x(t) и вертикали y(t), которые обеспечат как преодоление препятствий и безударное взаимодействие переносимой стопы с опорной поверхностью, так и минимум тепловых потерь А.

2. Метод решения. Метод решения поставленной задачи основан на “разбиении движения” на два этапа с введением управляющих параметров (U – горизонтальная скорость стопы при прохождении над препятствием и τ₁ – время прохождения стопы над препятствием):

первый этап соответствует подъему стопы на участке до препятствия:

(2.1)

$\begin{gathered} 0 < t < {{{\tau }}_{1}},\quad x(0) = 0,\quad \dot {x}(0) = 0,\quad y(0) = 0,\quad \dot {y}(0) = 0, \\ x({{{\tau }}_{1}}) = S,\quad \dot {x}({{{\tau }}_{1}}) = U,\quad y({{{\tau }}_{1}}) = \chi ,\quad \dot {y}({{{\tau }}_{1}}) = \eta , \\ \end{gathered} $

второй этап соответствует опусканию стопы на участке после препятствия:

(2.2)

$\begin{gathered} 0 < t < {\tau } - {{{\tau }}_{1}},\quad x(0) = 0,\quad \dot {x}(0) = U,\quad y(0) = \chi ,\quad \dot {y}(0) = \eta , \\ x({\tau } - {{{\tau }}_{1}}) = L - S,\quad \dot {x}({\tau } - {{{\tau }}_{1}}) = 0,\quad y({\tau } - {{{\tau }}_{1}}) = h,\quad \dot {y}({\tau } - {{{\tau }}_{1}}) = 0, \\ \end{gathered} $

где χ = Н + ρ + ψ – величина подъема стопы, складывающаяся из высоты препятствия Н, величины нормальной деформации грунта ρ и величины гарантированного запаса ψ; η – вертикальная составляющая скорости стопы при прохождении над препятствием. Полное время шага τ в (2.1), (2.2) определяется его длиной L по следовой дорожке и скоростью робота V и для шагающих роботов с движителями на основе сдвоенных механизмов шагания [15]:

(2.3)

${\tau } = \frac{L}{{2V}}.$

На каждом из этапов составляются уравнения Эйлера-Пуассона [18] для двух вариационных задач:

(2.4)

${\delta }{{I}_{1}} = {\delta }\int\limits_0^{\tau } {{{{\Phi }}_{1}}{\text{d}}t} = 0;\quad {\delta }{{I}_{2}} = {\delta }\int\limits_0^{{\tau } - {{{\tau }}_{1}}} {{{{\Phi }}_{2}}{\text{d}}t} = 0,$

где δ – символ изохронной вариации, Ф_j – функция, зависящая от ${{\ddot {x}}_{j}}$ и ${{\ddot {y}}_{j}}$:

(2.5)

${{{\Phi }}_{j}} = {\alpha }[{{(m{{\ddot {x}}_{j}} + Q)}^{2}} + {{(m{{\ddot {x}}_{j}})}^{2}}] + {\beta }{{(m{{\ddot {y}}_{j}} + mg)}^{2}},\quad j = 1,2.$

В общем случае, после решения двух оптимизационных задач (2.4) и вычисления критерия качества по (1.2), его необходимо минимизировать по параметрам τ₁, U, ψ и η. В решаемой задаче ψ и η принимаются равными нулю: ψ = η = 0.

Разбиение изучаемого движения на два этапа и определение оптимального режима на каждом из них не гарантирует оптимальности в целом на двух этапах. Однако выбором управляющих воздействий τ₁ и U этого можно добиться. Действительно, если существует в соответствии с введенным критерием оптимальности режим движения ${{x}_{*}}(t),{{\dot {x}}_{*}}(t)$, который условно представлен в фазовых координатах x, $\dot {x}$ на рис. 4 кривой DB, то, выбрав произвольно управляющие параметры (точку C), можно обеспечить лишь оптимальность на кривых DC и СВ.

Рис. 4.

Разбиение режима движения на два этапа; D, B – начальная и конечная точки фазовых координат; 1 – оптимальный режим на DB; 2, 3 – оптимальные режимы на $D{{C}_{*}}$ и ${{C}_{*}}B$ соответственно

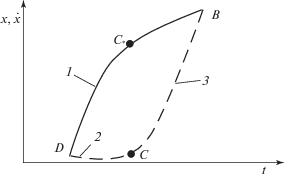
В случае если точку C выбрать на кривой DB (точка ${{C}_{*}}$), то оптимальность режимов $D{{C}_{*}}$ и ${{C}_{*}}B$ приведет к оптимальности (в решаемой задаче – минимуму функционала А) на всем режиме DB. Поэтому после определения оптимальных режимов DC и СВ следует определить такую точку ${{C}_{*}}$ (управляющие параметры τ₁ и U), для которой исследуемый функционал будет минимальным.

Система уравнений Эйлера-Пуассона на каждом из этапов движения имеет форму

(2.6)

$\begin{gathered} \frac{{{{{\text{d}}}^{2}}}}{{{\text{d}}{{t}^{2}}}}\left( {\frac{{\partial {\Phi }}}{{\partial{ \ddot {x}}}}} \right) - \frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{{\partial {\Phi }}}{{\partial{ \dot {x}}}}} \right) + \frac{{\partial {\Phi }}}{{\partial x}} = 0, \\ \frac{{{{{\text{d}}}^{2}}}}{{{\text{d}}{{t}^{2}}}}\left( {\frac{{\partial {\Phi }}}{{\partial{ \ddot {y}}}}} \right) - \frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{{\partial {\Phi }}}{{\partial{ \dot {y}}}}} \right) + \frac{{\partial {\Phi }}}{{\partial y}} = 0 \\ \end{gathered} $

и сводится к виду

(2.7)

$\ddddot x = 0;\quad \ddddot y = 0.$

Решение на каждом из j этапов (j =1, 2) можно представить в виде

(2.8)

$\begin{gathered} {{x}_{j}} = {{x}_{{j0}}} + {{{\dot {x}}}_{{j0}}}t + {{C}_{j}}{{t}^{2}} + {{D}_{j}}{{t}^{3}}, \\ {{y}_{j}} = {{y}_{{j0}}} + {{{\dot {y}}}_{{j0}}}t + {{E}_{j}}{{t}^{2}} + {{G}_{j}}{{t}^{3}}, \\ \end{gathered} $

где постоянные ${{x}_{{j0}}},\;{{\dot {x}}_{{j0}}},$ ${{C}_{j}},\;{{D}_{j}},$ ${{y}_{{j0}}},\;{{\dot {y}}_{{j0}}},$ ${{E}_{j}},\;{{G}_{j}}$ определяются из начальных условий (2.1), (2.2):

(2.9)

$\begin{gathered} {{x}_{{10}}} = 0;\quad {{{\dot {x}}}_{{10}}} = 0;\quad {{C}_{1}} = \frac{{3S}}{{{\tau }_{1}^{2}}} - \frac{U}{{{{{\tau }}_{1}}}};\quad {{D}_{1}} = \frac{U}{{{\tau }_{1}^{2}}} - \frac{{2S}}{{{\tau }_{1}^{3}}}; \\ {{y}_{{10}}} = 0;\quad {{{\dot {y}}}_{{10}}} = 0;\quad {{E}_{1}} = \frac{{3\chi }}{{{\tau }_{1}^{2}}};\quad {{G}_{1}} = - \frac{{2\chi }}{{{\tau }_{1}^{3}}}; \\ {{x}_{{20}}} = 0;\quad {{{\dot {x}}}_{{20}}} = U;\quad {{C}_{2}} = \frac{{3(L - S)}}{{{{{({\tau } - {{{\tau }}_{1}})}}^{2}}}} - \frac{{2U}}{{{\tau } - {{{\tau }}_{1}}}};\quad {{D}_{2}} = \frac{U}{{{{{({\tau } - {{{\tau }}_{1}})}}^{2}}}} - \frac{{2(L - S)}}{{{{{({\tau } - {{{\tau }}_{1}})}}^{3}}}}; \\ {{y}_{{20}}} = H;\quad {{{\dot {y}}}_{{20}}} = 0;\quad {{E}_{2}} = \frac{{3(h - \chi )}}{{{{{({\tau } - {{{\tau }}_{1}})}}^{2}}}};\quad {{G}_{2}} = - \frac{{2(h - \chi )}}{{{{{({\tau } - {{{\tau }}_{1}})}}^{3}}}}. \\ \end{gathered} $

Характерной особенностью полученных уравнений (2.7) и их решений является независимость от массово-геометрических параметров роботов с шагающими движителями, за исключением длины шага L.

При подстановке (2.9) в (2.8) определяется показатель качества (1.2):

(2.10)

$\begin{gathered} A = \int\limits_0^{{{{\tau }}_{1}}} {\{ {\alpha }[{{{\left( {m{{{\ddot {x}}}_{1}} + Q} \right)}}^{2}} + {{{\left( {m{{{\ddot {x}}}_{1}}} \right)}}^{2}}] + {\beta }{{{\left( {m{{{\ddot {y}}}_{1}} + mg} \right)}}^{2}}\} } {\text{d}}t + \\ \, + \int\limits_0^{{\tau } - {{{\tau }}_{1}}} {\{ {\alpha }[{{{\left( {m{{{\ddot {x}}}_{2}} + Q} \right)}}^{2}} + {{{\left( {m{{{\ddot {x}}}_{2}}} \right)}}^{2}}] + {\beta }{{{\left( {m{{{\ddot {y}}}_{2}} + mg} \right)}}^{2}}\} } {\text{d}}t. \\ \end{gathered} $

Предложенный метод и разработанная математическая модель позволяют проводить достаточно большой комплекс исследований, определять влияние внешних геометрических характеристик опорной поверхности и параметров, характеризующих движение робота на выбранный показатель качества – тепловые потери в приводных двигателях на единицу пути. Действительно, задание или определение информационно-измерительной системой величины подъема стопы χ, связанной с высотой преодолеваемого препятствия H, физико-механическими свойствами грунта и величиной гарантированного запаса ψ, положения препятствия относительно первоначального положения стопы S, уровня h опускания переносимой стопы на длине шага L, характеризует профиль опорной поверхности, который оказывает влияние на показатель качества (2.10). Задание этих параметров происходит со стороны информационно-измерительной системы робота в виде

(2.11)

$\chi = \theta L,\quad S = \mu L,\quad h = \sigma L,$

где θ, μ, σ – безразмерные параметры, определяемые на основе данных сканирования местности.

Сила сопротивления движению Q задается из (1.2) также в безразмерном виде с коэффициентом пропорциональности силе тяжести ξ:

(2.12)

$Q = \xi G,$

где G – вес робота.

На показатель качества имеет влияние и характер движения переносимой стопы, что оценивается временем τ₁ и горизонтальной скоростью стопы U в момент ее нахождения над препятствием. Эти параметры являются управляющими воздействиями (2.1), (2.2), которые удобно представлять в безразмерной форме

(2.13)

${{\tau }_{1}} = \varepsilon \tau ,\quad U = \gamma V,$

где ε, γ – безразмерные параметры системы управления робота.

Учитываются и параметры приводных двигателей α, β, влияющие на тепловые потери. Для двигателей постоянного тока с последовательным возбуждением эти параметры пропорциональны активному сопротивлению обмоток [19]. Для других видов двигателей имеют место зависимости, отличные от (2.2) [20].

В совокупности безразмерные параметры совместно с реальными физическими параметрами (скоростью U, длиной шага L и массой движителя m) позволяют на практике определять энергетическую эффективность процесса переноса движителей – тепловые потери в приводных двигателях на единицу пути:

(2.14)

Выявление вида функции (2.14) составляет самостоятельную задачу и имеет важный практический смысл. Определяя эту функцию для конкретного робота, перемещающегося в конкретных эксплуатационных условиях, в результате решения задачи на минимум можно реализовать оптимальный режим движения.

3. Модельная задача энергоэффективного управления роботом “Ортоног”. Рассматривается поступательное перемещение шагающего робота “Ортоног” с прямолинейным движением его центра масс вдоль горизонтальной оси с постоянной скоростью. Длина шага L = 0.91 м, а масса переносимого механизма шагания m = 70 кг. Робот перемещается по горизонтальной деформируемой поверхности (h = 0), характеризуемой безразмерным параметром ξ, который задает различные силы сопротивления. Профиль опорной поверхности (рис. 3) описывается безразмерными параметрами θ = 0.3, μ = 0.2, σ = 0. В реальных условиях это нерегулируемые параметры.

Таким образом, целью решения модельной задачи является апробация метода определения безразмерных параметров управляющих воздействий ε и γ, обеспечивающих оптимальность движения робота по критерию минимума энергозатрат. На графиках (рис. 5–7 ) представлены соответствующие зависимости тепловых потерь на единицу пути А при α = β = 0.0001 (это возможно при использовании одинаковых двигателей в приводах подъема и курсового перемещения, но в итоге если они одинаковые, то эти параметры не влияют на конечный результат) от скорости движения V, силы сопротивления движению ξ, управляющих воздействий ε и γ.

Рис. 5.

Графики зависимости тепловых потерь А на единицу пути от скорости V при различных силах Q: 1 – Q = 500 Н; 2 – Q = ± 1000 Н; 3 – Q = 2000 Н

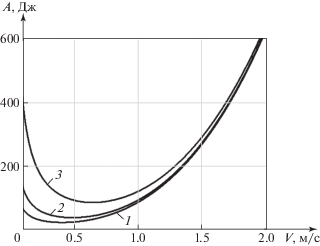
Рис. 6.

График зависимости тепловых потерь А на единицу пути от значения безразмерного параметра ε (τ₁ = = ε · τ) при различных значениях безразмерного параметра γ (U = γ · V): а – V = 0.7 м/с; б – V = 1 м/с; 1 – γ = 2; 2 – γ = 4; 3 – γ = 6

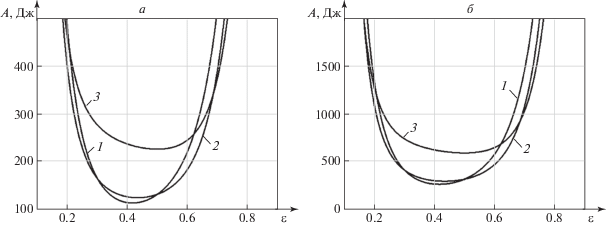
Рис. 7.

График зависимости тепловых потерь А на единицу пути от безразмерного параметра γ (U = γ · V) при различных значениях безразмерного параметра ε (τ₁ = ε · τ): а – V = 0.7 м/с; б – V = 1 м/с; 1 – ε = 0.2; 2 – ε = 0.4; 3 – ε = 0.6

Характерная особенность всех полученных зависимостей состоит в наличии режимов, обеспечивающих минимум тепловых потерь.

Так, на графиках (рис. 5) устанавливается зависимость тепловых потерь на единицу пути А от скорости движения центра масс корпуса робота при ε = 0.3 и γ = 4. Известно, что неуравновешенность шагающего движителя является причиной роста тепловых потерь в двигателях, пропорциональных квадрату скорости [10, 12]. Однако наличие постоянной силы сопротивления вызывает качественное изменение такой закономерности. При малых скоростях тепловые потери на единицу пути имеют тенденцию к снижению и лишь с ростом скорости они возрастают. В связи с этим каждой силе сопротивления соответствует своя оптимальная скорость, причем возрастающая с ростом силы сопротивления. Также интересным фактом является зависимость значений тепловых потерь только от модуля силы сопротивления и независимость от знака этой силы.

На тепловые потери в приводных двигателях на единицу пути влияет также и управление переносом, характеризуемое безразмерными параметрами ε и γ.

Из графиков (рис. 6 и 7 ) следует, что управляющие воздействия влияют на тепловые потери на единицу пути и при их нерациональном выборе последние могут возрастать в несколько раз. Однако их оптимальные значения взаимосвязаны. На графиках (рис. 8) представлены зависимости движения стопы в соответствии с рис. 6, а при оптимальном (ε = 0.4, γ = 2) и неоптимальном (ε = 0.2, γ = 6) управлениях для робота, движущегося со скоростью V = 0.7 м/с, θ = 0.44, μ = 0.2, σ = 0.

Рис. 8.

Графики зависимости перемещения стопы переносимого механизма шагания при различных законах управления и скорости робота V = 0.7 м/с: 1 – координата х при ε = 0.4 и γ = 2 (оптимальный закон движения); 2 – координата у при ε = 0.4 и γ = 2 (оптимальный закон движения); 3 – координата х при ε = 0.2 и γ = 6 (неоптимальный закон движения); 4 – координата у при ε = 0.2 и γ = 6 (неоптимальный закон движения)

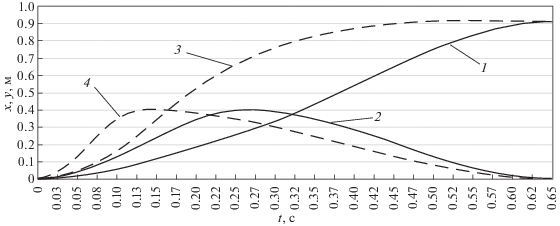
Анализ полученных зависимостей показывает, что отличие в координатах стопы может достигать 50–60%, а потери энергии для оптимального режима составляют 27% от неоптимального режима. Для произвольного режима эти отличия могут быть существенно больше.

Заключение. Сформулирован интегральный показатель, характеризующий качество законов переноса стопы с точки зрения минимума непроизводительных тепловых потерь в приводных двигателях на единицу пути. Введены управляющие воздействия, обеспечивающие реализацию оптимального программного движения переноса движителя. Предложен метод определения закона переноса стопы ортогонального движителя, учитывающий геометрические свойства опорной поверхности и состоящий в разбиении режима движения на этапы с последующим определением управляющих воздействий. Учтены силы сопротивления движению и профиль грунта при формировании оптимального режима переноса движителя.

Установлены закономерности энергоэффективного переноса стопы шагающего движителя в новое положение для шагающего робота, совершающего поступательное движение. Выявлено влияние скорости движения робота на показатель качества, позволяющее для каждой опорной поверхности, характеризуемой ее геометрическими параметрами, и задаваемых сил сопротивления движению определять оптимальную по критерию минимума тепловых потерь в приводных двигателях на единицу пути скорость движения.

Практическая ценность результатов состоит в постановке задачи точного или приближенного определения функции тепловых потерь на единицу пути, что упрощает реализацию оптимального режима движения для конкретного робота в конкретных ситуациях.

Список литературы

Артоболевский И.И., Умнов Н.В. Некоторые проблемы создания шагающих машин // Вестн. АН СССР. 1969 № 2. С. 44.
Охоцимский Д.Е., Голубев Ю.Ф. Механика и управление движением автоматического шагающего аппарата. М.: Наука. Физматлит, 1984. 312 с.
Брискин Е.С., Чернышев В.В., Малолетов А.В. и др. Сравнительный анализ колесных, гусеничных и шагающих машин // Робототехника и техническая кибернетика. 2013. Т. 1. № 1. С. 6–14.
Павловский В.Е. О разработках шагающих машин // Препринт ИПМ им. М.В. Келдыша. 2013. № 101. С. 1–32.
Гончаров С.И., Умнов Н.В. О предельных скоростях движения шагающих машин // Теория механизмов и машин. 1988. № 44. С. 82.
Жога В.В. Система показателей качества шагающих транспортных машин // Справочник. Инженерный журнал с приложением. 1997. № 5. С. 52–54.
Малолетов А.В., Брискин Е.С. Оптимизация структуры, параметров и режимов движения шагающих машин со сдвоенными движителями: монография. Волгоград: ВолгГТУ, 2015. 174 с.
Соболь И.М., Статников Р.Б. Выбор оптимальных параметров в задачах со многими критериями: учеб. пособие для вузов. М.: Дрофа, 2006.
Брискин Е.С. Об управлении походкой шагающей машины “Восьминог” // Мехатроника, автоматизация, управление. 2008. № 5. С. 6–10.
Охоцимский Д.Е., Платонов А.К., Лапшин В.В. Энергетика движения шестиногого шагающего аппарата // Изв. АН СССР. Техн. кибернетика. 1976. № 5. С. 42.
Охоцимский Д.Е., Платонов А.К., Лапшин В.В. Об одном способе рекуперации энергии при движении шагающего аппарата // Изв. АН СССР. МТТ. 1986. № 5. С. 67.
Брискин Е.С., Калинин Я.В. Об энергетически эффективных алгоритмах движения шагающих машин с цикловыми движителями // Изв. РАН. ТиСУ. 2011. № 2. С. 170–176.
Белецкий В.В. Динамика двуногой ходьбы // Изв. АН СССР. МТТ. 1975. № 3. С. 3–13.
Брискин Е.С., Калинин Я.В., Малолетов А.В. и др. Об управлении адаптацией ортогональных шагающих движителей к опорной поверхности // Изв. РАН. ТиСУ. 2017. № 3. С. 184–190.
Брискин Е.С., Вершинина И.П., Малолетов А.В., Шаронов Н.Г. Об управлении движением шагающей машины со сдвоенными ортогонально-поворотными движителями // Изв. РАН. ТиСУ. 2014. № 3. С. 168.
Гуськов В.В. Тракторы. Теория. М.: Машиностроение, 1988. 376 с.
Брискин Е.С., Соболев В.М. Тяговая динамика шагающих машин с ортогональными движениями // Проблемы машиностроения и надежности машин. 1990. № 3. С. 28–34.
Эльсгольц Л.Э. Вариационное исчисление. М.: URSS, 2019. 208 с.
Костенко М.П., Пиотровский Л.М. Электрические машины. В 2-х ч. Ч. 1. Машины постоянного тока. Л.: Энергия, 1972. 543 с.
Брискин Е.С., Калинин Я.В., Малолетов А.В., Чернышев В.В. Об энергетической эффективности цикловых механизмов. Изв. РАН. МТТ. 2014. № 1. С. 18–25.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Теория и системы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал