Известия РАН. Теория и системы управления, 2020, № 2, стр. 27-36

О РОБАСТНОМ КРИТЕРИИ УСТОЙЧИВОСТИ И КОНСТРУИРОВАНИИ ОПТИМАЛЬНЫХ РОБАСТНЫХ СИСТЕМ

М. Г. Зотов^*

МИЭМ НИУ ВШЭ
Москва, Россия

Поступила в редакцию 14.06.2019
После доработки 23.07.2019
Принята к публикации 30.09.2019

DOI: 10.31857/S000233882001014X

Аннотация

На базе критерия Харитонова построен показатель степени робастной устойчивости. Разработаны способы его вычисления. Приведен алгоритм конструирования оптимальной робастной системы управления с заданным значением этого показателя. Эффективность алгоритмов продемонстрирована на числовых примерах.

Введение. При проектировании систем управления требуется, чтобы созданная система функционировала надлежащим образом в широком диапазоне изменений входящих в нее неопределенных параметров. Одним из важнейших свойств, которое система в процессе эксплуатации не должна терять, является устойчивость. При ее потере система становится неработоспособной. В этой связи большое внимание в теории управления уделяется различным критериям робастной устойчивости. В [1] частотный робастный критерий устойчивости строится на базе опорной функции. Согласно теореме, робастная устойчивость полинома при интервальной неопределенности гарантируется, если устойчивы четыре специальных полинома из заданного семейства [2]. Графический критерий Цыпкина–Поляка оперирует уже с одним, а не с четырьмя полиномами и позволяет находить максимальный размах неопределенных параметров [3, 4]. В [5] на основе модифицированных критерия Найквиста и робастного критерия Найквиста [6] предложены другие формы частотных робастных критериев устойчивости. Приведена сравнительная оценка их с критериями из [6]. Важность работ в этом направлении подчеркивается выходом монографии [7].

1. Постановка задачи. Для линейных дифференциальных уравнений с коэффициентами, заданными интервально на базе критерия Харитонова, построить удобные в расчетах оценки величин робастной устойчивости. С использованием полученных оценок разработать алгоритм конструирования оптимальных систем управления с заданной величиной робастной устойчивости.

2. Оценки величины робастной устойчивости. Для того чтобы система с характеристическим интервальным полиномом

(2.1)

$D(s) = {{a}_{0}} + {{a}_{1}}s + ... + {{a}_{{n - 1}}}{{s}^{{n - 1}}} + {{a}_{n}}{{s}^{n}},\quad 0 < {{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} }_{i}} \leqslant {{a}_{i}} \leqslant {{\bar {a}}_{i}},\quad i = \overline {1,n} ,$

была робастно устойчива, необходимо и достаточно, чтобы все полиномы Харитонова

(2.2)

$\begin{gathered} D_{1}^{\chi }(s) = {{{\bar {a}}}_{0}} + {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} }}_{1}}s + {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} }}_{2}}{{s}^{2}} + {{{\bar {a}}}_{3}}{{s}^{3}} + {{{\bar {a}}}_{4}}{{s}^{4}} + {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} }}_{5}}{{s}^{5}} + {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} }}_{6}}{{s}^{6}} + {{{\bar {a}}}_{7}}{{s}^{7}} + ..., \\ D_{2}^{\chi }(s) = {{{\bar {a}}}_{0}} + {{{\bar {a}}}_{1}}s + {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} }}_{2}}{{s}^{2}} + {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} }}_{3}}{{s}^{3}} + {{{\bar {a}}}_{4}}{{s}^{4}} + {{{\bar {a}}}_{5}}{{s}^{5}} + {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} }}_{6}}{{s}^{6}} + {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} }}_{7}}{{s}^{7}} + ..., \\ D_{3}^{\chi }(s) = {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} }}_{0}} + {{{\bar {a}}}_{1}}s + {{{\bar {a}}}_{2}}{{s}^{2}} + {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} }}_{3}}{{s}^{3}} + {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} }}_{4}}{{s}^{4}} + {{{\bar {a}}}_{5}}{{s}^{5}} + {{{\bar {a}}}_{6}}{{s}^{6}} + {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} }}_{7}}{{s}^{7}} + ..., \\ D_{4}^{\chi }(s) = {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} }}_{0}} + {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} }}_{1}}s + {{{\bar {a}}}_{2}}{{s}^{2}} + {{{\bar {a}}}_{3}}{{s}^{3}} + {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} }}_{4}}{{s}^{4}} + {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} }}_{5}}{{s}^{5}} + {{{\bar {a}}}_{6}}{{s}^{6}} + {{{\bar {a}}}_{7}}{{s}^{7}} + ... \\ \end{gathered} $

были устойчивыми [2].

Однако в технических приложениях величина разбросов задается в долях от номинального значения. Исходя из сказанного, полиномы (2.2) запишем в несколько иной форме:

(2.3)

$\begin{gathered} D_{l}^{\chi }(s) = {{D}_{{\text{н}}}}(s) + \delta _{l}^{\chi }(s) = a_{0}^{0}(1 \pm {{\delta }_{0}}) + a_{1}^{0}(1 \pm {{\delta }_{1}})s + ... + a_{{n - 1}}^{0}(1 \pm {{\delta }_{{n - 1}}}){{s}^{{n - 1}}} + a_{n}^{0}(1 \pm {{\delta }_{n}}){{s}^{n}}, \\ l = \overline {1,4} ,\quad {{\delta }_{i}} \geqslant 0,\quad {{D}_{{\text{н}}}}(s) = a_{0}^{0} + a_{1}^{0}s + a_{2}^{0}{{s}^{2}} + \ldots a_{{n - 1}}^{0}{{s}^{{n - 1}}} + a_{n}^{0}{{s}^{n}}, \\ \delta _{l}^{\chi }(s) = \pm a_{0}^{0}{{\delta }_{0}} \pm a_{1}^{0}{{\delta }_{1}}s \pm a_{2}^{0}{{\delta }_{2}}{{s}^{2}} \pm \ldots \pm a_{{n - 1}}^{0}{{\delta }_{{n - 1}}}{{s}^{{n - 1}}} \pm a_{n}^{0}{{\delta }_{n}}{{s}^{n}}, \\ \end{gathered} $

здесь ${{D}_{{\text{н}}}}(s)$ – полином (2.1) при номинальных значениях параметров ${{a}_{i}}$, $a_{i}^{0}$ – номинальное значение параметра ${{a}_{i}}$, $ \pm a_{i}^{0}{{\delta }_{i}}$ – пропорциональная номинальному значению величина отклонения, ${{\underline a }_{i}} = a_{i}^{0}(1 - {{\delta }_{i}})$, ${{\bar {a}}_{i}} = a_{i}^{0}(1 + {{\delta }_{i}})$, $0 \leqslant {{\delta }_{i}} < 1$, δ_i – коэффициент пропорциональности. Полином ${{D}_{{\text{н}}}}(s)$ обладает свойством устойчивости. Модель (2.3) учитывает, что относительно номинального значения $a_{i}^{0}$ разбросы симметричны. Часто величины δ_i совпадают, т.е. ${{\delta }_{i}} = \delta $. Для этого случая соотношение (2.3) будет иметь вид [5]:

(2.4)

$\begin{gathered} D_{l}^{\chi }(s) = {{D}_{{\text{н}}}}(s) + \delta \tilde {D}_{l}^{\chi }(s),\quad l = \overline {1,4} ,\quad \delta > 0, \\ \tilde {D}_{l}^{\chi }(s) = \pm a_{0}^{0} \pm a_{1}^{0}s \pm a_{2}^{0}{{s}^{2}} \pm \ldots \pm a_{{n - 1}}^{0}{{s}^{{n - 1}}} \pm a_{n}^{0}{{s}^{n}}, \\ \end{gathered} $

$\tilde {D}_{l}^{\chi }(s)$ – полиномы отклонения от номинального значения ${{D}_{{\text{н}}}}(s)$.

Необходимо найти такой интервал изменения параметра $\delta $, при котором полиномы $D_{l}^{\chi }(s)$ свойства устойчивости не теряют. Значение одного из концов интервала очевидно: δ = 0. В этом случаe коэффициенты полиномов Харитонова совпадают с номинальным значением ${{D}_{{\text{н}}}}(s)$, а все корни такого полинома лежат в левой полуплоскости. Другой конец интервала $\delta = \delta {\text{*}}$, когда полиномы $D_{l}^{\chi }(s)$ устойчивы, но некоторые из них имеют корни и на мнимой оси. Таким образом, параметр δ должен находиться в интервале $0 \leqslant \delta < \delta {\text{*}}$. Выход из этого интервала приводит к неустойчивости полинома (2.4). Определим значение δ*.

2.1. Решение с использованием критерия Найквиста. Из полиномов $\tilde {D}_{l}^{\chi }(s)$, ${{D}_{{\text{н}}}}(s)$ составим дробно-рациональную функцию

(2.5)

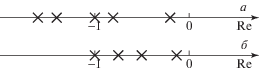
$T_{l}^{\chi }(s) = \frac{{\tilde {D}_{l}^{\chi }(s)}}{{{{D}_{{\text{н}}}}(s)}} = \frac{{ \pm a_{0}^{0} \pm a_{1}^{0}s \pm a_{2}^{0}{{s}^{2}} \pm ... \pm a_{{n - 1}}^{0}{{s}^{{n - 1}}} \pm a_{n}^{0}{{s}^{n}}}}{{a_{0}^{0} + a_{1}^{0}s + a_{2}^{0}{{s}^{2}} + ... + a_{{n - 1}}^{0}{{s}^{{n - 1}}} + a_{n}^{0}{{s}^{n}}}}\quad l = \overline {1,4} ,$

полином $\tilde {D}_{l}^{\chi }(s)$ образуется из полинома ${{D}_{{\text{н}}}}(s)$, в котором знак плюс меняется на знак минус, согласно правилам составления полиномов Харитонова ($ + a_{i}^{0}$, если ${{\bar {a}}_{i}}$, и $ - a_{i}^{0}$, если ${{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} }_{i}}$). Если объекты с передаточными функциями $\delta T_{l}^{\chi }(s)$ охватить отрицательными обратными связями, то в знаменателях передаточных функций, образованных таким образом объектов, будут полиномы Харитонова $D_{l}^{\chi }(s),\;l = \overline {1,4} $, из (2.4). При δ = 1 некоторые коэффициенты $D_{l}^{\chi }(s)$ имеют нулевое значение, и как следствие некоторые из корней $D_{l}^{\chi }(s)$ будут находиться в правой полуплоскости. Для недопустимости этого должно выполняться неравенство $0 \leqslant \delta < 1$.

Годографы $T_{l}^{\chi }(j\omega ),\;l = \overline {1,4} $, при изменении ω от нуля до бесконечности в плоскости комплексного переменного в точках $\omega _{l}^{k},\;k = \overline {1,p} $, пересекают действительную ось Re на интервале $ - \infty ...0$. Возможные точки таких пересечений с действительной осью Re годографов $T_{l}^{\chi }(j\omega ),\;l = \overline {1,4} $, приведены на рис. 1, а. Выделим крайнюю левую точку пересечения. Для нее имеет место соотношение

(2.6)

${{\left. {\mathop {\delta {\text{*}}\min }\limits_{l = \overline {1,4} } \left( {\mathop {\min }\limits_{\omega _{l}^{*}} \operatorname{Re} (T_{l}^{\chi }(j\omega _{l}^{*}))} \right)} \right|}_{{\delta * = 1}}}.$

Рис. 1

Найдем такое значение δ*, чтобы крайняя левая точка пересечения годографами $T_{l}^{\chi }(j\omega )$, $l = \overline {1,4} $, действительной оси, переместилась в точку –1. Такая точка δ* может быть найдена из соотношения

(2.7)

$\mathop {{{\delta }^{*}}\min }\limits_l \left( {\mathop {\min }\limits_{\omega _{l}^{*}} \operatorname{Re} (T_{l}^{\chi }(j\omega _{l}^{*}))} \right) = - 1,\quad l = \overline {1,4} .$

Пересечения годографами $\delta {\text{*}}T_{l}^{\chi }(j\omega ),$ $l = \overline {1,4} $, находятся в точке $( - 1,j0)$ и справа от нее. Никаких пересечений нет на интервале $( - \infty , - 1)$, кроме точки –1, что показано на рис. 1, б. Если для годографов $\delta T_{l}^{\chi }(j\omega ),\;l = \overline {1,4} $ выполняется соотношение $\delta {\text{*}} \geqslant \delta \geqslant 0$, то, согласно критерию Найквиста, этого достаточно, чтобы все четыре полинома Харитонова имели корни только в левой полуплоскости, но при δ = δ* некоторые из корней будут лежать и на мнимой оси. Таким образом, интервал $0 \leqslant \delta < \delta {\text{*}}$ найден. В этом интервале все полиномы Харитонова устойчивы. Величину δ* назовем предельной робастной устойчивостью. Сказанное дополним примером.

Пример 1. Интервальный полином имеет при номинальном значении его параметров вид

${{D}_{{\text{н}}}}(s) = 1 + 6s + 15{{s}^{2}} + 20{{s}^{3}} + 15{{s}^{4}} + 6{{s}^{5}} + {{s}^{6}}$.

Из условия, что отклонение параметров полинома пропорционально их номинальному значению, можно определить величину предельной робастной устойчивости δ*. Для решения поставленной задачи воспользуемся соотношением (2.5), которое запишется в следующем виде:

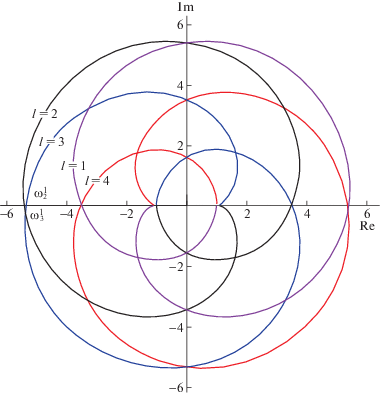
$\begin{gathered} T_{1}^{\chi }(j\omega ) = \frac{{ + 1 - 6(j\omega ) - 15{{{(j\omega )}}^{2}} + {{{20}}^{3}}(j\omega ) + 15{{{(j\omega )}}^{4}} - 6{{{(j\omega )}}^{5}} - {{{(j\omega )}}^{6}}}}{{1 + 6(j\omega ) + 15{{{(j\omega )}}^{2}} + 20{{{(j\omega )}}^{3}} + 15{{{(j\omega )}}^{4}} + 6{{{(j\omega )}}^{5}} + {{{(j\omega )}}^{6}}}}, \\ T_{2}^{\chi }(j\omega ) = \frac{{ + 1 + 6(j\omega ) - 15{{{(j\omega )}}^{2}} - 20{{{(j\omega )}}^{3}} + 15{{{(j\omega )}}^{4}} + 6{{{(j\omega )}}^{5}} - {{{(j\omega )}}^{6}}}}{{1 + 6(j\omega ) + 15{{{(j\omega )}}^{2}} + 20{{{(j\omega )}}^{3}} + 15{{{(j\omega )}}^{4}} + 6{{{(j\omega )}}^{5}} + {{{(j\omega )}}^{6}}}}, \\ T_{3}^{\chi }(j\omega ) = \frac{{ - 1 + 6(j\omega ) + 15{{{(j\omega )}}^{2}} - 20{{{(j\omega )}}^{3}} - 15{{{(j\omega )}}^{4}} + 6{{{(j\omega )}}^{5}} + {{{(j\omega )}}^{6}}}}{{1 + 6(j\omega ) + 15{{{(j\omega )}}^{2}} + 20{{{(j\omega )}}^{3}} + 15{{{(j\omega )}}^{4}} + 6{{{(j\omega )}}^{5}} + {{{(j\omega )}}^{6}}}}, \\ T_{4}^{\chi }(j\omega ) = \frac{{ - 1 - 6(j\omega ) + 15{{{(j\omega )}}^{2}} + 20{{{(j\omega )}}^{3}} - 15{{{(j\omega )}}^{4}} - 6{{{(j\omega )}}^{5}} + {{{(j\omega )}}^{6}}}}{{1 + 6(j\omega ) + 15{{{(j\omega )}}^{2}} + 20{{{(j\omega )}}^{3}} + 15{{{(j\omega )}}^{4}} + 6{{{(j\omega )}}^{5}} + {{{(j\omega )}}^{6}}}}. \\ \end{gathered} $

На рис. 2 приведены годографы соотношений $T_{l}^{\chi }(j\omega ),\;l = \overline {1,4} $. Если в руках исследователя есть изображенные в плоскости комплексного переменного графики функций $T_{l}^{\chi }(j\omega )$, то поиск крайней левой точки пересечения годографами $T_{l}^{\chi }(j\omega )$ действительной оси крайне прост. На рис. 2 эта точка обозначена символом *. В этой точке при $\omega _{2}^{1} = 0.76736$ и $\omega _{3}^{1} = {\text{1}}{\text{.30323}}$ ${\text{Im}}T_{2}^{\chi }(j\omega _{2}^{1})$ = 0 и $\operatorname{Im} T_{3}^{\chi }(j\omega _{3}^{1}) = 0$. Величина предельной робастной устойчивости с учетом рис. 2 определяется соотношением вида (2.7):

${{\delta }^{*}} = {{\left| {\mathop {\min }\limits_{\omega _{2}^{1}} \operatorname{Re} (T_{2}^{\chi }(j\omega _{2}^{1}))} \right|}^{{ - 1}}} = {{\left| {\mathop {\min }\limits_{\omega _{3}^{1}} \operatorname{Re} (T_{3}^{\chi }(j\omega _{3}^{1}))} \right|}^{{ - 1}}} = 0.18613.$

Рис. 2

Результаты проверки полученного решения приведены ниже:

$\begin{gathered} D_{1}^{\chi }(s) = {{D}_{{\text{н}}}}(s) + {{\delta }^{*}}\tilde {D}_{1}^{\chi }(s) = {\text{0}}{\text{.81377}}({{s}^{2}}\;{\text{ + }}\;{\text{4}}{\text{.12702s}}\;{\text{ + }}\;{\text{13}}{\text{.13456)}}({{s}^{2}}\;{\text{ + }}\;{\text{0}}{\text{.14016s}}\;{\text{ + }}\;{\text{0}}{\text{.19821)}} \times \\ \, \times {\text{(s}}\;{\text{ + }}\;{\text{1}}{\text{.30316)(s}}\;{\text{ + }}\;{\text{0}}{\text{.42966),}} \\ D_{2}^{\chi }(s) = {{D}_{{\text{н}}}}(s) + {{\delta }^{*}}\tilde {D}_{2}^{\chi }(s) = {\text{0}}{\text{.81377}}({{s}^{2}}\;{\text{ + }}\;{\text{0}}{\text{.58876)}}({\text{s}}\;{\text{ + }}\;{\text{2}}{\text{.56987)}}({\text{s}}\;{\text{ + }}\;{\text{0}}{\text{.76729)}} \times \\ \, \times ({\text{s}}\;{\text{ + }}\;{\text{5}}{\text{.16623)}}({\text{s}}\;{\text{ + }}\;{\text{0}}{\text{.24304),}} \\ \end{gathered} $

$\begin{gathered} D_{3}^{\chi }(s) = {{D}_{{\text{н}}}}(s) + {{\delta }^{*}}\tilde {D}_{3}^{\chi }(s) = 1.{\text{18623}}({{s}^{2}}\;{\text{ + }}\;{\text{1}}{\text{.69848)}}({\text{s}}\;{\text{ + }}\;{\text{0}}{\text{.38912)}}({\text{s}}\;{\text{ + }}\;{\text{0}}{\text{.19356)}} \times \\ \, \times ({\text{s}}\;{\text{ + }}\;{\text{1}}{\text{.30329)}}({\text{s}}\;{\text{ + }}\;{\text{4}}{\text{.11449),}} \\ D_{4}^{\chi }(s) = {{D}_{{\text{н}}}}(s) + {{\delta }^{*}}\tilde {D}_{4}^{\chi }(s) = 1.{\text{18623}}({{s}^{2}}\;{\text{ + }}\;{\text{0}}{\text{.31421s}}\;{\text{ + }}\;{\text{0}}{\text{.076135)}}({{s}^{2}}\;{\text{ + }}\;{\text{0}}{\text{.70712s}}\;{\text{ + }}\;{\text{5}}{\text{.04517)}} \times \\ \, \times {\text{(s}}\;{\text{ + }}\;{\text{0}}{\text{.76737)(s}}\;{\text{ + }}\;{\text{2}}{\text{.32740)}}{\text{.}} \\ \end{gathered} $

Некоторые корни полиномов $D_{l}^{\chi }(s)$ при $l = 2,\,3$ лежат на мнимой оси, а при $l = 1,\,4$ – только в левой полуплоскости. Полученное решение $\delta {\text{*}} = 0.18613$ постановке задачи удовлетворяет.

2.2. Решение с использованием критерия Гурвица. Рассмотрим соотношения

$\begin{gathered} {{I}_{n}} = \int\limits_0^\infty {k{{{(t)}}^{2}}dt} = \frac{1}{{2\pi j}}\int\limits_{ - j\infty }^{j\infty } {\frac{{B(s)B( - s)}}{{A(s)A( - s)}}} ds = \\ \, = \frac{1}{{2\pi j}}\int\limits_{ - j\infty }^{j\infty } {\frac{{{{c}_{{n - 1}}}{{s}^{{2(n - 1)}}} + {{c}_{{n - 2}}}{{s}^{{2(n - 2)}}} + ... + {{c}_{2}}{{s}^{2}} + {{c}_{0}}}}{{A(s)A( - s)}}} ds = \frac{{{{{( - 1)}}^{{n + 1}}}}}{{2{{a}_{n}}}}\frac{D}{{{{D}^{\gamma }}}}, \\ \int\limits_0^\infty {k(t){{e}^{{ - st}}}dt = {{B(s)} \mathord{\left/ {\vphantom {{B(s)} {A(s)}}} \right. \kern-0em} {A(s)}}} , \\ \end{gathered} $

$A(s) = {{a}_{n}}{{s}^{n}} + {{a}_{{n - 1}}}{{s}^{{n - 1}}} + ... + {{a}_{1}}s + {{a}_{0}},\quad B(s) = {{b}_{{n - 1}}}{{s}^{{n - 1}}} + {{b}_{{n - 2}}}{{s}^{{n - 2}}} + ... + {{b}_{1}}s + {{b}_{0}}.$

Все корни полинома $A(s)$ лежат в левой полуплоскости, $k(t)$ – импульсная переходная функция, ${{D}^{\gamma }}$ – главный определитель Гурвица. Определитель $D$ получается из определителя ${{D}^{\gamma }}$ заменой первого столбца на столбец из коэффициентов ${{c}_{i}},\,\,i = \overline {n - 1,0} $ [8]. Для приведенных выше выражений имеют место предельные соотношения

(2.8)

$\mathop {\lim {{I}_{n}}}\limits_{\operatorname{Re} {{\alpha }_{i}} \to 0} = \infty ,\quad \mathop {\lim {{I}_{n}}}\limits_{{{D}^{\gamma }} \to 0} = \infty ,$

здесь ${{\alpha }_{i}}$ – корни полинома $A(s)$. Из (2.8) следует что, если ${{D}^{\gamma }} = 0$, то какие-то из корней полинома $A(s)$ находятся на мнимой оси. Из сказанного вытекает следующий вывод: если корни $A(s)$ находятся в левой полуплоскости, а коэффициенты $A(s)$ и $B(s)$ в результате поисковых процедур меняются непрерывно, но при этом соблюдается ограничение ${{D}^{\gamma }} > 0$ или ${{I}_{n}} < \infty $, то корни полинома $A(s)$ левую полуплоскость не покидают. Все определители Гурвица для полинома $A(s)$ имеют положительный знак.

Перейдем к алгоритму поиска параметра δ*. Для полиномов Харитонова (2.4) составим главные определители Гурвица. Обозначим их $\Delta _{l}^{\chi }(a_{i}^{0},\,\,\delta ),\,\,l = \overline {1,4} $. Функции $\Delta _{l}^{\chi }(a_{i}^{0},\,\,\delta )$ представляют собой полиномы n-й степени от δ и коэффициентов $a_{i}^{0}$. Построим графики функций $\Delta _{l}^{\chi }(a_{i}^{0},\,\,\delta )$ от переменной δ. Зафиксируем значения δ, при которых $\Delta _{l}^{\chi }(a_{i}^{0},\,\,\delta ) = 0$. Из всех значений δ выберем меньшее. Оно и будет величиной предельной робастной устойчивости:

(2.9)

$\delta {\text{*}} = \mathop {\min }\limits_\delta \Delta _{l}^{\chi }(a_{i}^{0},\delta ),\quad \Delta _{l}^{\chi }(a_{i}^{0},\delta ) = 0.$

Сказанное дополним примером.

Пример 2. Для полинома ${{D}_{{\text{н}}}}(s)$ из примера 1, используя соотношение (2.4), найти величину предельной робастной устойчивости δ*.

Для полиномов Харитонова (2.4) главные определители Гурвица имеют вид

$\begin{gathered} \Delta _{1}^{\chi }(a_{i}^{0},\delta ) = \left[ {\begin{array}{*{20}{c}} {6(1 - \delta )}&{1(1 - \delta )}&0&0&0&0 \\ {20(1 + \delta )}&{15(1 + \delta )}&{6(1 - \delta )}&{1(1 - \delta )}&0&0 \\ {6(1 - \delta )}&{15(1 - \delta )}&{20(1 + \delta )}&{15(1 + \delta )}&{6(1 - \delta )}&{1(1 - \delta )} \\ 0&{1(1 + \delta )}&{6(1 - \delta )}&{15(1 - \delta )}&{20(1 + \delta )}&{15(1 + \delta )} \\ 0&0&0&{1(1 + \delta )}&{6(1 - \delta )}&{15(1 - \delta )} \\ 0&0&0&0&0&{1(1 + \delta )} \end{array}} \right] = \\ \,{\text{ = }} - {\text{32768}}{{\delta }^{6}} - {\text{57344}}{{\delta }^{5}}{\text{ + 660992}}{{\delta }^{4}} - {\text{660992}}{{\delta }^{2}}{\text{ + 57344}}\delta {\text{ + 32768,}} \\ \end{gathered} $

$\begin{gathered} \Delta _{2}^{\chi }(a_{i}^{0},\delta ) = {\text{32768}}{{\delta }^{6}}{\text{ + }}\;{\text{8192}}{{\delta }^{5}} - {\text{710144}}{{\delta }^{4}} - {\text{1371136}}{{\delta }^{3}} - {\text{710144}}{{\delta }^{2}}{\text{ + }}\;{\text{8192}}\delta \;{\text{ + }}\;{\text{32768,}} \\ \Delta _{3}^{\chi }(a_{i}^{0},\delta ) = - {\text{32768}}{{\delta }^{6}}\;{\text{ + }}\;{\text{57344}}{{\delta }^{5}}\;{\text{ + }}\;{\text{660992}}{{\delta }^{4}} - {\text{660992}}{{\delta }^{2}} - {\text{57344}}\delta \;{\text{ + }}\;{\text{32768,}} \\ \Delta _{4}^{\chi }(a_{i}^{0},\delta ) = {\text{32768}}{{\delta }^{6}} - {\text{8192}}{{\delta }^{5}} - {\text{710144}}{{\delta }^{4}}\;{\text{ + }}\;{\text{1371136}}{{\delta }^{3}} - {\text{710144}}{{\delta }^{2}} - {\text{8192}}\delta \;{\text{ + }}\;{\text{32768}}{\text{.}} \\ \end{gathered} $

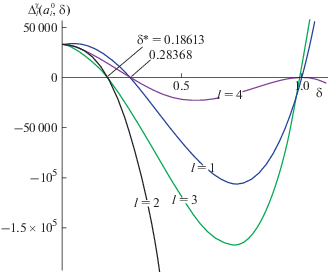
На рис. 3 в зависимости от параметра δ приведены графики функций $\Delta _{l}^{\chi }(a_{i}^{0},\delta ),\;l = \overline {1,4} $. Далее, согласно (2.9), фиксируются значения параметра $\delta $, при которых функция $\Delta _{2}^{\chi }(a_{i}^{0},\delta )$ равна нулю, и из них выбирается минимальное $\delta {\text{*}} = 0.18613$, которое и является показателем предельной робастной устойчивости. Отметим, что при $\delta > \delta {\text{*}}$ функции $\Delta _{l}^{\chi }(a_{i}^{0},\,\,\delta ),\,\,\,l = 2,3$, отрицательные, т.е. полиномы Харитонова $D_{2}^{\chi }(s)$ и $D_{3}^{\chi }(s)$ неустойчивые, а при $\delta < \delta {\text{*}}$ они устойчивы. При $\delta = \delta {\text{*}}$ полиномы $D_{2}^{\chi }(s)$ и $D_{3}^{\chi }(s)$ находятся на грани устойчивости, а $D_{1}^{\chi }(s)$ и $D_{4}^{\chi }(s)$ устойчивы. При δ > $0.28368$ все полиномы неустойчивы.

Рис. 3

2.3. Решение с использованием средств математического программирования. В настоящее время практически все математические пакеты имеют средства, позволяющие решать оптимизационные задачи при ограничениях. Ограничения и сама целевая функция могут носить нелинейный характер. Применительно к рассматриваемой задаче целевая функция может иметь вид $1 - \delta $ и минимизироваться по δ при ограничениях $\delta < 1$, $\Delta _{l}^{\chi }(a_{i}^{0},\delta ) \geqslant 0$. В результате определяется наименьшее значение δ, при котором некоторые ограничения $\Delta _{l}^{\chi }(a_{i}^{0},\delta )$ равны нулю. Иными словами, решается задача поиска минимального значения δ, при котором все четыре полинома Харитонова устойчивы в силу ограничений $\Delta _{l}^{\chi }(a_{i}^{0},\delta ) \geqslant 0$, но у некоторых полиномов корни находятся на мнимой оси. В приложении с использованием программы из пакета Mathcad15 приведено решение задачи для характеристического полинома из примера 1. Полученное решение совпадает с ранее найденным $\delta {\text{*}} = 0.18613$.

3. Алгоритм конструирования оптимальных робастных систем управления. В большинстве практических задач без существенного ухудшения величины основного критерия качества системы возможны значительные отступления от найденных параметров оптимального управляющего устройства. Это характерное свойство оптимальных систем является положительным фактором, так как позволяет в достаточно широких пределах варьировать структуру и параметры управляющего устройства и тем самым удовлетворять многим другим требованиям, предъявляемым к проектируемой системе, в частности, требованиям робастности, сложности и надежности и т.д. [8]. Отметим, что с использованием упомянутого выше положения приведен алгоритм конструирования оптимального управляющего устройства заданной сложности [9].

Перейдем к алгоритму решения задачи. На основе технического задания и опыта конструирования задается структура управляющего устройства и основной критерий качества системы

(3.1)

$I = F\left( {{{W}_{{0{\text{н}}}}}(s),{{W}_{i}}(s)} \right),$

здесь ${{W}_{{{\text{0н}}}}}(s)$ – передаточная функция номинального объекта управления, ${{W}_{i}}(s)$ – передаточные функции звеньев коррекции управляющего устройства, F – функция, отражающая структуру системы.

В результате решения оптимизационной задачи определяются: оптимальное значение критерия качества ${{I}_{{{\text{оп}}}}}$, передаточные функции звеньев коррекции ${{W}_{{i\,{\text{оп}}}}}(s)$ оптимального управляющего устройства, а также характеристический полином спроектированной системы. С использованием одной из методик разд. 2 определяется величина предельной робастной устойчивости $\delta _{{{\text{оп}}}}^{*}$ для спроектированной оптимальной системы. Если степень робастной устойчивости сконструированной системы недостаточна, то передаточные функции звеньев коррекции оптимального регулятора корректируются так, чтобы выполнялось соотношение

(3.2)

${{I}_{{{\text{кор}}}}} \approx {{I}_{{{\text{оп}}}}},\quad \delta _{{{\text{кор}}}}^{*} > \delta _{{{\text{оп}}}}^{*},$

здесь ${{I}_{{{\text{кор}}}}}$ и $\delta _{{{\text{кор}}}}^{*}$ – показатели качества системы и степени ее робастной устойчивости со скорректированным управляющим устройством.

Приведем алгоритм решения этой задачи. Из двух показателей качества системы (3.1) и показателя степени ее робастной устойчивости из разд. 2.3 составим критерий

(3.3)

$I = \mu F\left( {{{W}_{{0{\text{н}}}}}(s),{{W}_{{i\,{\text{оп}}}}}(s)} \right) + (1 - \mu )(1 - \delta ),$

который при различных значениях $\mu $ из интервала $0 - 1$ минимизируется по параметрам передаточных функций управляющего устройства при ограничениях $\Delta _{l}^{\chi }(a_{i}^{0},\,\,\delta ) \geqslant 0$. Начальные значения параметров управляющего устройства совпадают с оптимальными параметрами в ${{W}_{{i\,{\text{оп}}}}}(s)$, найденными ранее. По результатам операции минимизации строятся графики, по которым принимается решение о предпочтительных параметрах передаточных функций управляющего устройства. Алгоритм протестируем примером.

Пример 3. Передаточная функция объекта управления имеет вид

${{W}_{{0{\text{н}}}}}(s) = \frac{{{{Q}_{{0{\text{н}}}}}(s)}}{{{{P}_{{0{\text{н}}}}}(s)}} = \frac{1}{{(s - 0.1)(s + 1)}} = \frac{1}{{{{s}^{2}} + 0.9s - 0.1}}.$

Желаемая передаточная функция системы относительно задающего воздействия равна единице. Необходимо спроектировать управляющее устройство со звеном коррекции в прямой цепи, обеспечивающее близость переходного процесса системы по задающему воздействию к единичному скачку. Передаточная функция относительно этого воздействия имеет вид

$\tilde {H}(s) = \frac{{{{W}_{1}}(s){{W}_{{0{\text{н}}}}}(s)}}{{1 + {{W}_{1}}(s){{W}_{{0{\text{н}}}}}(s)}}.$

Решение задачи проведем с использованием методики из [10].

По постановке задачи запишем функционал, оценивающий качество работы системы:

(3.4)

$\begin{gathered} I\left( {{{W}_{{0{\text{н}}}}}(s),{{W}_{1}}(s)} \right) = \frac{1}{{2\pi j}}\int\limits_{ - j\infty }^{j\infty } {{{{\left| {(1 - \tilde {H}(s))\frac{1}{s}} \right|}}^{2}}ds} + \lambda \frac{1}{{2\pi j}}\int\limits_{ - j\infty }^{j\infty } {{{{\left| {s\tilde {H}(s)} \right|}}^{2}}ds} - \\ \, - {{\rho }_{1}}\left( {\frac{1}{{2\pi j}}\int\limits_{ - j\infty }^{j\infty } {\tilde {H}( - s)\frac{1}{{s + 0.1}}ds + \frac{1}{{2\pi j}}\int\limits_{ - j\infty }^{j\infty } {\tilde {H}(s)\frac{1}{{ - s + 0.1}}ds} } } \right),\quad \tilde {H}(s) = \frac{{{{W}_{{0{\text{н}}}}}(s){{W}_{1}}(s)}}{{1 + {{W}_{{0{\text{н}}}}}(s){{W}_{1}}(s)}}. \\ \end{gathered} $

Первая составляющая обеспечивает близость переходного процесса к единичному скачку, конечность второй составляющей – реализуемость звена коррекции ${{W}_{1}}(s)$, а ее величина оценивает квадратичную интегральную составляющую переходного процесса [11]. Последняя составляющая есть ограничение на компенсацию звеном коррекции ${{W}_{1}}(s)$ правого полюса передаточной функции объекта управления, ${{\rho }_{1}}$ – множитель Лагранжа, $\lambda = 0.01$ – весовой коэффициент, назначаемый исходя из опыта проектирования аналогичных систем. Функционал (3.4) достигает своего минимального значения, если искомая передаточная функция определяется из уравнения Винера–Хопфа вида

$\left( {\lambda (s)( - s) + \frac{1}{{(s)( - s)}}} \right)\tilde {H}(s) - \left( {\frac{1}{{(s)( - s)}} + {{\rho }_{1}}\frac{1}{{s + 0.1}}} \right) = \Gamma (s).$

Здесь $\tilde {H}(s)$ – искомая передаточная функция с полюсами из левой полуплоскости, $\Gamma (s)$ – функция с полюсами из правой полуплоскости. Имея эту информацию о свойствах функций $\tilde {H}(s)$ и $\Gamma (s)$, используя алгоритм решения уравнения Винера–Хопфа [10] при $\lambda = 0.01$, получим

${{\tilde {H}}_{{{\text{оп}}}}}(s) = \frac{{10.914s + 1}}{{{{s}^{3}} + 4.572{{s}^{2}} + 10.447s + 1}}.$

Передаточная функция звена коррекции

${{W}_{{1{\text{оп}}}}}(s) = \frac{{{{V}_{{1{\text{оп}}}}}(s)}}{{{{G}_{{1{\text{оп}}}}}(s)}} = \frac{{{{{\tilde {H}}}_{{{\text{оп}}}}}(s)}}{{{{W}_{{0{\text{н}}}}}(s)(1 - {{{\tilde {H}}}_{{{\text{оп}}}}}(s))}} = \frac{{{{v}_{2}}{{s}^{2}} + {{v}_{1}}s + {{v}_{0}}}}{{{{g}_{2}}{{s}^{2}} + {{g}_{1}}s}} = \frac{{10.914{{s}^{2}} + 11.914s + 1}}{{{{s}^{2}} + 4.672s}}.$

Составляющие функционала (3.4) равны

$\begin{gathered} {{I}_{1}} = \frac{1}{{2\pi j}}\int\limits_{ - j\infty }^{j\infty } {{{{\left| {(1 - \tilde {H}(s))\frac{1}{s}} \right|}}^{2}}ds = 0.356} ,\quad {{I}_{2}} = \frac{1}{{2\pi j}}\int\limits_{ - j\infty }^{j\infty } {{{{\left| {s\tilde {H}(s)} \right|}}^{2}}ds} = 13.316, \\ I = {{\left. {{{I}_{1}} + \lambda {{I}_{2}}} \right|}_{{\lambda = 0.01}}} = 0.489. \\ \end{gathered} $

Для спроектированной оптимальной системы оценим показатель степени робастной устойчивости. С этой целью найдем характеристический полином оптимальной системы:

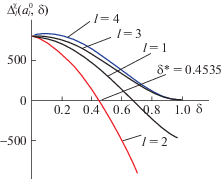
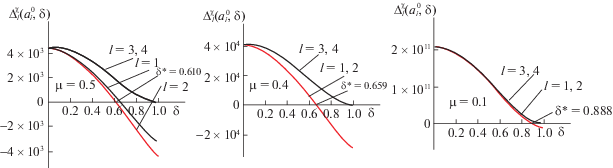
$\begin{gathered} {{D}_{{{\text{оп}}}}}(s) = {{P}_{{0{\text{н}}}}}(s){{G}_{{1{\text{оп}}}}}(s) + {{Q}_{{0{\text{н}}}}}(s){{V}_{{1{\text{оп}}}}}(s) = ({{s}^{2}} + 0.9s - 0.1)({{s}^{2}} + 4.672s) + \\ \, + (10.914{{s}^{2}} + 11.914s + 1) = {{s}^{4}} + 5.572{{s}^{3}} + 15.019{{s}^{2}} + 11.447s + 1. \\ \end{gathered} $

Далее для решения задачи используем алгоритм из разд. 2.2. На основе ${{D}_{{{\text{оп}}}}}(s)$ составим полиномы Харитонова вида (2.4) $D_{l}^{\chi }(s) = {{D}_{{{\text{оп}}}}}(s) + \delta \tilde {D}_{l}^{\chi }(s)$ и по ним – определители, представляющие собой полиномы четвертой степени от параметра δ. На рис. 4 приведены графики зависимости $\Delta _{l}^{\chi }(a_{i}^{0},\delta )$ от δ. Из графиков следует, что у спроектированной оптимальной системы степень робастной устойчивости $\delta _{{{\text{оп}}}}^{*} = 0.4535$. Если она мала, перейдем к процедуре ее увеличения.

Рис. 4

На базе критерия (3.4) из составляющих, оценивающих качество системы, формируется функционал вида (3.3):

(3.5)

$\begin{gathered} I\left( {{{g}_{2}},{{g}_{1}},{{v}_{2}},{{v}_{1}},{{v}_{0}}} \right) = \mu \left( {\frac{1}{{2\pi j}}\int\limits_{ - j\infty }^{j\infty } {{{{\left| {(1 - \tilde {H}(s))\frac{1}{s}} \right|}}^{2}}ds} + \lambda \frac{1}{{2\pi j}}\int\limits_{ - j\infty }^{j\infty } {{{{\left| {s\tilde {H}(s)} \right|}}^{2}}ds} } \right) + (1 - \mu )(1 - \delta ), \\ \tilde {H}(s) = \frac{{{{W}_{{0{\text{н}}}}}(s){{W}_{1}}(s)}}{{1 + {{W}_{{0{\text{н}}}}}(s){{W}_{1}}(s)}} = \frac{{{{Q}_{{0{\text{н}}}}}(s){{V}_{1}}(s)}}{{{{P}_{{0{\text{н}}}}}(s){{G}_{1}}(s) + {{Q}_{{0{\text{н}}}}}(s){{V}_{1}}(s)}} = \\ \, = \frac{{{{v}_{2}}{{s}^{2}} + {{v}_{1}}s + {{v}_{0}}}}{{({{s}^{2}} + 0.9s - 0.1)({{s}^{2}} + {{g}_{1}}s) + ({{v}_{2}}{{s}^{2}} + {{v}_{1}}s + {{v}_{0}})}} = \frac{{{{v}_{2}}{{s}^{2}} + {{v}_{1}}s + {{v}_{0}}}}{{a_{4}^{0}{{s}^{4}} + a_{3}^{0}{{s}^{3}} + a_{2}^{0}{{s}^{2}} + a_{1}^{0}s + a_{0}^{0}}}. \\ \end{gathered} $

Из характеристического полинома системы образуем полиномы Харитонова $D_{l}^{\chi }(s)$, а из них – главные определители Гурвица $\Delta _{l}^{\chi }(a_{i}^{0},\delta )$. Далее при различных значениях $\mu $ из интервала 0–1 решим задачу минимизации функционала (3.5) по параметрам передаточной функции ${{W}_{1}}(s)$ при ограничениях $\Delta _{l}^{\chi }(a_{i}^{0},\delta ) \geqslant 0$. Начальные значения параметров ${{W}_{1}}(s)$ должны совпадать с найденными ранее параметрами ${{W}_{{1{\text{оп}}}}}(s)$. Результаты приведены в таблице. Для их пояснения на рис. 5 при некоторых значениях $\mu $ представлены функции $\Delta _{l}^{\chi }(a_{i}^{0},\delta )$.

Рис. 5

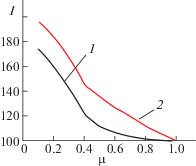
Для упрощения выбора подходящего значения $\mu $ некоторые из параметров качества системы рассмотрены и в графической форме. Так, на рис. 6 приведен график 1, характеризующий процент ухудшения величины основного критерия относительно его оптимального значения ${{I}_{{{\text{оп}}}}}$ = = 0.489, принятого за 100%. График 2 определяет процент увеличения степени робастной устойчивости по отношению к его значению ${{\delta }_{{{\text{оп}}}}} = 0.4535$. Например, при $\mu = 0.5$ критерий качества ухудшается на 11.65%, а робастная устойчивость увеличивается на 34.51%.

Рис. 6

При принятии решения о корректировке оптимальных параметров регулятора необходимо также учитывать тот факт, что параметры характеристического полинома не являются независимыми, а значит, что условия робастной устойчивости являются только достаточными [12].

Таблица 1

μ	${{{v}}_{2}}$	${{{v}}_{1}}$	${{{v}}_{0}}$	g₁	I₁	I₂	I	δ*
0.9	11.555	11.704	1.036	4.980	0.354	13.674	0.491	0.479
0.8	12.377	11.579	1.084	5.391	0.354	14.203	0.496	0.508
0.7	13.474	11.727	1.157	5.992	0.356	14.936	0.506	0.540
0.6	14.925	12.226	1.257	6.828	0.363	15.880	0.522	0.573
0.5	17.395	14.528	1.482	8.732	0.376	17.057	0.546	0.610
0.4	24.029	28.800	2.461	16.413	0.412	17.991	0.592	0.659
0.3	49.719	302.601	7.512	105.651	0.546	14.890	0.695	0.756
0.2	73.523	1778	14.215	458.616	0.650	13.113	0.782	0.838
0.1	88.648	6143	20.263	1334	0.711	13.991	0.851	0.888

Список литературы

Бутковский А.Г. Частотные критерии робастной устойчивости // Изв. РАН. Техн. кибернетика. 1993. № 3. С. 62–82.
Харитонов В.Л. Асимптотическая устойчивость семейства систем линейных дифференциальных уравнений // Диффер. уравнения. 1978. Т. 1. Вып. 11. С. 2086 – 2088.
Поляк Б.Т., Цыпкин Я.З. Частотные критерии робастной устойчивости и апериодичности линейных систем // АиТ. 1990. № 9. С. 45–54.
Поляк Б.Т., Щербаков П.С. Робастная устойчивость и управление. М.: Наука, 2002.
Зотов М.Г. Графическая и алгебраическая формы робастного критерия Харитонова // АиТ. 2015. № 2. С. 61–72.
Поляк Б.Т., Цыпкин Я.З. Робастный критерий Найквиста // АиТ. 1992. № 7. С. 25–31.
Поляк Б.Т., Хлебников М.В., Щербаков П.С. Управление линейными системами при внешних возмущениях: Техника линейных матричных неравенств. М.: ЛЕНАНД/URSS, 2014.
Пугачев В.С., Казаков И.Е., Евланов Л.Г. Основы статистической теории автоматических систем. М.: Машиностроение, 1974.
Зотов М.Г. Алгоритм конструирования оптимальных регуляторов заданной сложности // Изв. РАН ТиСУ. 2017 № 3. С. 3–11.
Зотов М.Г. Многокритериальное конструирование систем автоматического управления. М.: БИНОМ. Лаб. знаний, 2004.
Кухтенко В.И. К расчету корректирующих цепей систем автоматического управления по критерию минимума среднеквадратичной ошибки // АиТ. 1959. № 9. С. 1180–1187.
Ким Д.П. Теория автоматического управления. Т. 1. Линейные системы. М.: Физматлит, 2007.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Теория и системы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал