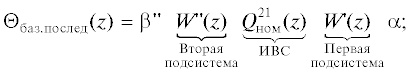Известия РАН. Теория и системы управления, 2020, № 2, стр. 98-110

Введение. Сложность современных и перспективных комплексов оборудования (КО) возрастает из-за неудержимого расширения количества стоящих перед ними задач и ужесточения требований к качеству их решения [1]. По целому ряду преимущественно объективных причин КО формируются путем объединения (интеграции) разрозненных компонентов, предназначенных для выполнения частных функций. При этом разнообразие этих компонентов по предназначению, принципам функционирования, конструктивному исполнению и эффективности предоставляет возможность решать задачи применения комплексов существенно различными способами, достигая разные уровни эксплуатационно-технических показателей [2, 3]. Оперативное, связанное со складывающимися обстоятельствами изменение способа использования КО путем изменения межкомпонентных связей и настроек компонентов называется реконфигурацией [4] или управлением избыточностью [5].

В [5–8] рассматриваются комплексы избыточного оборудования с линейными стационарными моделями, последовательно ставится задача управления избыточностью КО с обеспечением неизменности заданной совокупности передаточных функций, формулируется решение этой задачи с помощью программно-аппаратных средств, названных супервизорами конфигурирования, развивается аналитический подход к формированию множества альтернативных конфигураций избыточных КО, анализируется взаимосвязь аналитических решений с супервизорами конфигурирования КО. Статья [9] содержит условия допустимости выбранной конфигурации неоднородного КО в смысле наличия потенциальной возможности определения такой обработки сигналов в его межкомпонентных связях, при которой система “объект + КО” может выполнять предписанные целевые функции. В [10] приводятся формулы для множеств решений задачи интеграции КО, эквивалентных с позиции целевой функции.

Статья посвящена частному, но весьма важному случаю интеграции КО, когда комплекс конфигурируется таким образом, что возникает последовательность функционально обособленных подсистем. Это характерно, например, для комплексов бортового оборудования подвижных объектов, в частности летательных аппаратов, где выделяются такие традиционные подсистемы, как навигационная и пилотажная системы, а также системы индикации, связи, специального назначения, технического обслуживания и ремонта.

1. Состояние вопроса. В терминах систем с дискретным временем $\tau = 0,1,2,\; \ldots $ поведение динамического объекта и избыточной совокупности динамических компонентов в линейном приближении описывается моделью [8–10]

где ${{y}_{\tau }}$ – метавектор (составной вектор) размерности $m$ выходов всех компонентов на такте $\tau $, ${{x}_{\tau }}$ – метавектор размерности $n$ состояния компонентов и объекта, ${{u}_{\tau }}$ – метавектор размерности $l$ входов компонентов для межкомпонентных связей, ${{{v}}_{\tau }}$ – метавектор размерности $k$ входов компонентов и объекта для внешних воздействий (внешних входов), $D$ – числовая матрица размера $m \times n$ формирования выходов всех компонентов, $A$ – числовая матрица размера $n \times n$ собственной динамики компонентов и объекта, $B$ – числовая матрица размера $n \times l$ эффективности межкомпонентных связей, $G$ – числовая матрица размера $n \times k$ эффективности внешних воздействий.

Объединение компонентов в КО с единой целью функционирования выполняется интегрированной вычислительной средой (ИВС), осуществляющей сбор, обработку и распределение данных между компонентами, используемыми в одной из возможных конфигураций [10]. Функционирование ИВС в линейном приближении описывается моделью

где z – оператор сдвига во времени на один такт вперед [11, 12], $Q(z)$ – дробно-рациональная полиномиальная (по оператору $z$) матрица размера $l \times m$ (передаточная матрица), названная конфигурационной матрицей [7], ${{C}_{{{\text{вх}}}}}$ и ${{C}_{{{\text{вых}}}}}$ – распределительные матрицы размеров $l \times p$ и $q \times m$, т.е. матрицы, содержащие бинарные элементы и не более одного единичного элемента в строке, названные интерфейсными (входной и выходной по отношению к компонентам КО) матрицами [6], E(z) – дробно-рациональная полиномиальная матрица размера $p \times q$, моделирующая обработку вычислительными средствами ИВС всех поступающих данных и названная интеграционной матрицей [6].

Выбор различных пар интерфейсных матриц ${{C}_{{{\text{вх}}}}}$ и ${{C}_{{{\text{вых}}}}}$ связывается преимущественно с конфигурированием КО, а определение значения интеграционной матрицы – с интеграцией КО, хотя такое разделение не является строгим, что иллюстрируется в примере. При этом пара ${{C}_{{{\text{вх}}}}}$ и ${{C}_{{{\text{вых}}}}}$, а также конфигурация в целом считаются допустимыми, если их использование гарантирует потенциальную возможность интеграции комплекса, т.е. существование интеграционной матрицы $E(z)$, при которой выполняется целевая функция.

Целевая функция КО [6] задается формулой

где $\alpha $ и $\beta $ – весовые матрицы размеров $k \times g$ и $f \times m$, $w_{{{{y}_{j}}}}^{{{{{v}}_{i}}}}(z)$ – передаточная функция по внешнему воздействию от i-го входа ${{{v}}_{{i\tau }}}$ к j-му выходу ${{y}_{{j\tau }}}$, $m \times k$ – размер передаточной матрицы: I_n – единичная матрица размера n × n.

Кроме того, вводятся понятия:

а) номинальной конфигурации КО [6], формализуемой номинальными значениями матриц:

при которой целевая функция (1.3) принимает требуемое значение

б) интеграционного базиса [9] (здесь: общий формализм), определяемого формулой

где $W_{{y.{\text{ном}}}}^{{v}}(z)$ и $W_{{y.{\text{ном}}}}^{u}(z)$ – передаточные матрицы системы “объект + КО” по внешнему воздействию ${{{v}}_{\tau }}$ и межкомпонентным связям ${{u}_{\tau }}$ при номинальной конфигурации комплекса, вычисляемые как

Далее использован аппарат канонизации матриц [13, 14]: $\tilde {S}$ – сводный канонизатор произвольной матрицы $S$ ранга r, получаемый из выражения

${{\tilde {S}}^{L}}$ и ${{\tilde {S}}^{R}}$ – левый и правый канонизаторы, удовлетворяющие равенству ${{\bar {S}}^{L}}$ и ${{\bar {S}}^{R}}$– левый и правый делители нуля максимального ранга, удовлетворяющие равенствам

Важным является то, что канонизаторы и делители нуля формируются единой процедурой линейного комбинирования срок и столбцов, предоставляющей благоприятные условия компьютеризации получаемых решений для существенно многомерных моделей технических систем.

В [10] получено, что при выполнении условий допустимости конфигурации с матрицами ${{C}_{{{\text{вх}}}}}$ и ${{C}_{{{\text{вых}}}}}$ [9], заключающихся в проверке равенств

все множество интеграционных матриц $E(z)$, обеспечивающих значение целевой функции (1.5), определяется формулой где $\theta $ и $\vartheta $ – произвольные матрицы подходящих размеров.

Совокупность равенств (1.4)–(1.11) с соответствующими утверждениями будем называть общим формализмом аналитического подхода к управлению избыточностью КО.

2. Методика генерирования альтернативных конфигураций КО. Статьи [9, 10] содержат неявное описание методики генерирования альтернативных конфигураций КО, эквивалентных номинальной по обеспечению значения целевой функции (1.5). Сформулируем здесь эту методику подробно.

Процедура генерирования альтернативных конфигураций упрощенно сводится к выполнению следующих шагов.

Шаг 1. Определение номинальной конфигурации КО (1.4) с использованием доступных конструкторских инструментов (критериев, методов, программ, аналогов, прототипов и пр.), закрепив таким образом номинальные значения интерфейсных $C_{{{\text{вх}}}}^{{{\text{ном}}}}$, $C_{{{\text{вых}}}}^{{{\text{ном}}}}$ и интеграционной ${{E}_{{{\text{ном}}}}}(z)$ матриц.

Шаг 2. Выбор интерфейсных матриц ${{C}_{{{\text{вх}}}}}$ и ${{C}_{{{\text{вых}}}}}$, альтернативных номинальным матрицам $C_{{{\text{вх}}}}^{{{\text{ном}}}}$, $C_{{{\text{вых}}}}^{{{\text{ном}}}}$ и отражающих стремление заказчика и/или разработчика КО к изменению состава применяемых компонентов или перечня их используемых входов и выходов.

Шаг 3. Тестирование новой конфигурации (матриц ${{C}_{{{\text{вх}}}}}$ и ${{C}_{{{\text{вых}}}}}$) на допустимость с применением формул (1.6)–(1.10).

Шаг 4. Отказ от продолжения интеграции КО в конфигурации, выбранной на шаге 2, если конфигурация недопустима (недопустимы матрицы ${{C}_{{{\text{вх}}}}}$ и ${{C}_{{{\text{вых}}}}}$), с переходом к шагу 7.

Шаг 5. Вычисление по формуле (1.11) интеграционных матриц $E(z)$, соответствующих новой конфигурации КО, если конфигурация допустима (допустимы матрицы ${{C}_{{{\text{вх}}}}}$ и ${{C}_{{{\text{вых}}}}}$).

Шаг 6. Целенаправленное изменение интеграционной матрицы $E(z)$ путем варьирования произвольных матричных сомножителей, если таковые присутствуют в общем решении, чтобы удовлетворить различные, в том числе не формализуемые, требования к КО.

Шаг 7. Переход к шагу 2 или окончание процесса генерирования.

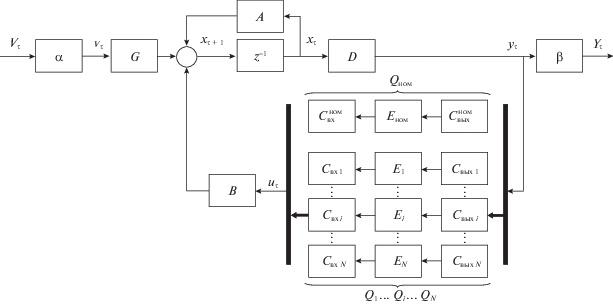
Рисунок 1 иллюстрирует структуру КО с учетом весовых матриц $\alpha $ и $\beta $ на входе и выходе, а также замену номинальной конфигурации КО, формализуемой матрицей ${{Q}_{{{\text{ном}}}}}(z)$, на альтернативные конфигурации, представленные матрицами ${{Q}_{i}}(z)$, $i = \overline {1,N} $. Жирными элементами условно показаны коммутаторы.

Указанные шаги могут быть детализированы и дополнены под влиянием различных обстоятельств и требований прикладного характера.

3. Постановка задачи. Рассмотрим частный случай модели объекта и компонентов (1.1), соответствующий двум функционально обособленным (автономным) подсистемам:

где одним и двумя штрихами отмечены матрицы и части метавекторов (субметавекторы), соответствующие каждой из подсистем в отдельности: $y_{\tau }^{'}$ – размерности $m{\text{'}}$, $y_{\tau }^{{''}}$ – размерности $m{\text{''}}$, при этом $m{\text{'}} + m{\text{''}} = m$, $x_{\tau }^{'}$ – размерности $n{\text{'}}$, $x_{\tau }^{{''}}$ – размерности $n{\text{''}}$, при этом $n{\text{'}} + n{\text{''}} = n$, $u_{\tau }^{'}$ – размерности $l{\text{'}}$, $u_{\tau }^{{''}}$ – размерности $l{\text{''}}$, при этом $l{\text{'}} + l{\text{''}} = l$. Здесь полагается, что множества компонентов различных подсистем функционально не пересекаются. Объект в зависимости от контекста может быть формально отнесен к одной из подсистем.

Пусть помимо общего входа ${{{v}}_{\tau }}$ подсистемы объединяет еще и связь между ними, выраженная блочной структурой конфигурационной матрицы:

где $Q_{{}}^{{21}}(z)$ – блок размера $l{\text{''}} \times m{\text{'}}$, формализующий связь подсистем (а именно первая из них через этот блок воздействует на вторую), $C_{{{\text{вх}}}}^{{''}}$ и $C_{{{\text{вых}}}}^{'}$ – интерфейсные матрицы размеров $l{\text{''}} \times p{\text{''}}$ и $q{\text{'}} \times m{\text{'}}$ на входе второй и на выходе первой подсистем, ${{E}^{{21}}}(z)$ – интеграционная матрица размера $p{\text{''}} \times q{\text{'}}$ блока $Q_{{}}^{{21}}(z)$. Тогда в соответствии с (1.2) общая модель системы “объект + КО” принимает вид

Отсюда передаточная матрица рассматриваемой системы (1.7) выражается формулой

или

Предполагается, что известна по крайней мере одна конфигурация КО, называемая номинальной, при которой конфигурационная матрица (3.1) принимает значение

а при весовых матрицах $\alpha $ и $\beta = \left[ {\begin{array}{*{20}{c}} 0&{\beta {\text{''}}} \end{array}} \right]$ заданное значение целевой функции определяется как заменяющей в данном случае формулу (1.5).

Ставится задача определить условия допустимости конфигурации, задаваемой произвольной парой матриц $C_{{{\text{вх}}}}^{{''}}$ и $C_{{{\text{вых}}}}^{'}$, и в случае удовлетворения этих условий получить формулу для всего множества интеграционных матриц ${{\{ {{E}^{{21}}}(z)\} }_{\kappa }}$, при которых целевая функция (3.3) остается неизменной. Здесь $\kappa $ – собирательное обозначение произвольно варьируемых параметров (матриц), задающих элементы множества.

Результатом решения этой задачи будет частный формализм аналитического подхода к управлению избыточностью в случае последовательного соединения функционально обособленных подсистем КО.

4. Общее решение задачи. Решение поставленной задачи сформулируем в виде теоремы.

Теорема. Конфигурация последовательного соединения двух автономных подсистем КО с передаточными матрицами первой подсистемы

и второй подсистемы где $I{\text{'}}$ и $I{\text{''}}$ – единичные матрицы размером $n{\text{'}} \times n{\text{'}}$ и $n{\text{''}} \times n{\text{''}}$, формализуемая выбором интерфейсных матриц $C_{{{\text{вых}}}}^{'}$ на выходе первой из них и $C_{{{\text{вх}}}}^{{''}}$ на входе второй, является допустимой, если выполняются условия и при этом все множество интеграционных матриц E²¹(z), обеспечивающих неизменность значения целевой функции КО (3.5), выражается формулой где $\Theta _{{{\text{баз}}{\text{.послед}}}}^{{}}(z)$ – интеграционный базис последовательного соединения подсистем (интеграционный базис частного формализма), вычисляемый по формуле $\theta $ и $\vartheta $ – произвольные матрицы подходящих размеров.

Доказательство теоремы приведено в Приложении.

При решении прикладных задач (с последовательным соединением подсистем) методика, изложенная в разд. 2, должна модифицироваться с учетом вновь полученных формул. Подчеркнем, что описанный частный формализм может быть выведен из общего формализма, изложенного в [10].

5. Сравнение общего и частного формализмов. Несомненно, что для последовательности двух подсистем, соединяемых посредством блока Q²¹(z) конфигурационной матрицы (3.4), можно получить решение (4.3)–(4.5) существенно проще, в качестве исходного рассматривая уравнение вида

с соответствующей структурой целевой функции ${{\Phi }_{{{\text{треб}}}}}(z)$. Однако неоспоримую пользу приносит и осуществленный в разд. 2 и 3 “системный” путь получения решения. Он дополнительно, в рамках рассматриваемого частного случая, подтверждает непротиворечивость принятой ранее [10] гипотезы, ставшей основой общего формализма аналитического подхода к управлению избыточностью КО.

Детальное сопоставление общего (1.4)–(1.11) и частного (4.1)–(4.6) формализмов показывает следующее:

при одинаковости структур условий и формул в рассматриваемом частном случае передаточные матрицы (1.7) и (1.8) системы “объект + КО” в целом уступили место передаточным матрицам (4.1) и (4.2), относящимся только к автономным подсистемам;

сказанное выше можно интерпретировать иначе: интеграционный базис общего вида (1.6), фигурирующий в общем формализме и связанный со специально введенной виртуальной системой, названной базисной [10], в рассматриваемом частном случае уступил место передаточной матрице естественной связки последовательных блоков при номинальной конфигурации (4.6):

если передаточные матрицы (1.7) и (1.8) предусматривают соединение компонентов в соответствии с номинальной конфигурацией, то передаточные матрицы (4.1) и (4.2) не зависят от конфигурирования комплекса;

общий формализм (1.4)–(1.11) применим для всевозможных (доступных в рамках используемого математического аппарата) конфигураций, в то время как частный формализм (4.3)–(4.6) может применяться только для интеграции (объединения) подсистем КО, функционирующих исключительно в последовательных связках;

общий формализм (1.4)–(1.11) обладает более широкими возможностями масштабирования, включая как линейное наращивание подсистем “вширь” (каждая подсистема, входящая в КО, может быть представлена последовательностью других подсистем), так и фрактальное усложнение “вглубь” (каждая подсистема, в том числе входящая в последовательную связку, может обладать внутренней структурой со сложными перекрестными связями), в то время как частный формализм допускает только первое из указанных усложнений.

6. Пример. Приведем упрощенную модель навигационной системы (НС), в которой используются измерители линейных перемещений, скоростей и ускорений подвижного объекта (воздушного, наземного, водного).

Движение объекта моделируется перемещением материальной точки. Будем рассматривать модель с дискретным временем $\tau = 0,1,2,\; \ldots $ по одной из линейных координат:

где h – длительность такта, ${{X}_{\tau }}$ – линейная координата, ${{V}_{\tau }}$ – скорость линейного перемещения, ${{a}_{\tau }}$ – ускорение линейного перемещения, ${{{v}}_{\tau }}$ – внешнее управляющее и/или возмущающее воздействие, m – мера инерционности (масса) объекта, $g$ – коэффициент эффективности внешнего воздействия.

При этом компонентами системы являются безынерционные измерители (датчики) положения (ДП) объекта, его скорости (ДС) и ускорения (ДУ) с соответствующими коэффициентами передачи:

входящие в “измерительную” подсистему, а также устройства индикации положения (ИП) и скорости (ИС) объекта, входящие в “индикаторную” подсистему, функционирование которых сводится к задержкам во времени на один такт с соответствующими коэффициентами передачи: где $X_{\tau }^{{{\text{ДП}}}}$, $V_{\tau }^{{{\text{ДС}}}}$ и $a_{\tau }^{{{\text{ДУ}}}}$ – сигналы датчиков, $X_{\tau }^{{{\text{ИП}}}}$ и $V_{\tau }^{{{\text{ИС}}}}$ – сигналы, индицируемые на экранах, табло или стрелочных указателях, $S_{\tau }^{{{\text{ИП}}}}$ и $S_{\tau }^{{{\text{ИС}}}}$ – сигналы на входах индикаторов. Форма и другие характеристики индикации, обусловленные эргономикой и техническими возможностями, выходят за рамки процедуры собственно интеграции НС.

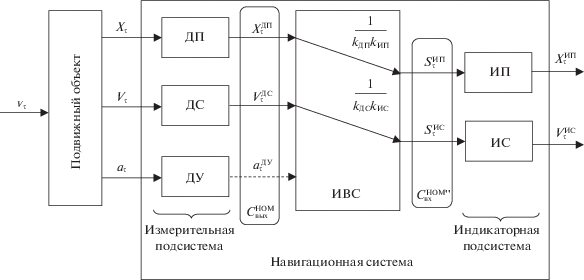
Кроме того, в состав навигационной системы входит ИВС, реализующая различные архитектуры системы. Рисунок 2 иллюстрирует объединенную систему “объект + НС”.

Вводя замены переменных

запишем в матричном виде (3.2) уравнения, описывающие движение объекта и функционирование компонентов НС:

В силу существенной и согласованной разреженности матриц коэффициентов $A$, $B$ и $D$ уравнения (6.1) и (6.2) можно преобразовать к совокупности четырех уравнений:

описывающих раздельно функционирование двух автономных подсистем, которые имеют передаточные матрицы:

В соответствии с рис. 2 последовательное соединение подсистем (6.3) и (6.4) посредством ИВС с передаточной матрицей Q(z) дает объединенную систему “объект + НС” с передаточной матрицей по внешнему воздействию:

Будем полагать, что целевая функция ${{\Phi }_{{{\text{треб}}}}}(z)$ этой системы определяется весовыми матрицами

обуславливающими реакцию индикаторной подсистемы (6.4) в виде показаний ИП $X_{\tau }^{{{\text{ИП}}}} = {{y}_{{4\tau }}}$ и ИС $V_{\tau }^{{{\text{ИС}}}} = {{y}_{{5\tau }}}$ на внешнее воздействие ${{{v}}_{\tau }}$, поступающее на вход объекта в совокупности с измерительной подсистемой (6.3). Конфигурацию простейшей НС формализует статическая (без оператора сдвига во времени z) конфигурационная матрица которой на рис. 2 соответствуют стрелки в пределах ИВС с указанием формул реализуемой обработки данных. Здесь же показаны интерфейсные матрицы $C_{{{\text{вх}}}}^{{{\text{ном''}}}}$ и $C_{{{\text{вых}}}}^{{{\text{ном'}}}}$. Штриховая стрелка – неиспользуемый канал выходного интерфейса.

Целевая функция принимает значение

Такой целевой функции соответствует следующая физическая интерпретация: показания $V_{\tau }^{{{\text{ИС}}}}$ и $X_{\tau }^{{{\text{ИП}}}}$ представляют собой задержанную на один такт z^–1, “проинтегрированную” дважды ${{h}^{2}}{{(z - 1)}^{{ - 2}}}$ и трижды ${{h}^{3}}{{(z - 1)}^{{ - 3}}}$ взвешенную $g{{m}^{{ - 1}}}$ реакцию на входное воздействие ${{{v}}_{\tau }}$.

В таблице представлена совокупность номинальной и других “представительных” конфигураций, выбор которых обусловлен исключительно методическими целями. Здесь же приведены результаты вычислений с использованием частного формализма (4.1)–(4.6).

Результат синтеза включает совокупность базового решения $E_{{{\text{баз}}}}^{{21}}(z)$ и матричного коэффициента ${{\overline {C_{{{\text{вых}}{\kern 1pt} {\text{0}}}}^{'}W{\text{'}}(z)\alpha } }^{L}}$ слагаемого, позволяющего (заданием произвольного сомножителя $\vartheta $) варьировать строки решения без ущерба для целевой функции (6.6). В данном примере для всех допустимых конфигураций (варианты 0–4) матричные коэффициенты варьирования столбцов в формуле (4.5) равны нулю.

Для номинальной конфигурации (вариант 0) базовое решение получилось отличным от значения, фигурирующего в (6.6), что обусловлено выполненной процедурой канонизации матриц (последовательностью преобразований в процессе канонизации). При этом можно убедиться, что полученное множество решений содержит и решение из (6.5), а именно выбор для произвольной матрицы значения

дает исходную интеграционную матрицу:

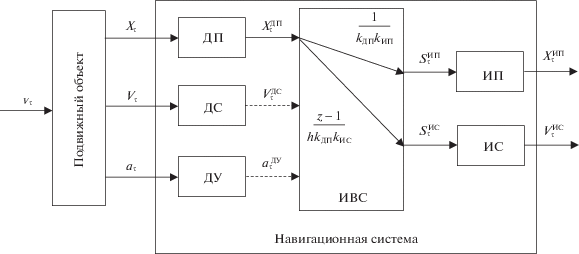
Кроме того, различные значения произвольной матрицы ϑ позволяют получать другие реализации соответствующей конфигурации. Так, при выборе ϑ = 0 ИВС формирует сигналы для индикаторов $S_{\tau }^{{{\text{ИП}}}}$ и $S_{\tau }^{{{\text{ИС}}}}$ только из одного сигнала $X_{\tau }^{{{\text{ДП}}}}$, реализуя разностный аналог дополнительного “дифференцирования” сомножителем ${{(z - 1)} \mathord{\left/ {\vphantom {{(z - 1)} h}} \right. \kern-0em} h}$. При этом конфигурация варианта 0 фактически отождествляется с вариантом 1. Структура системы с указанием формул обработки данных в ИВС показана на рис. 3.

Вариант 1 имеет безальтернативное, т.е. единственное решение, так как оба матричных коэффициента вариаций как столбцов, так и строк равны нулю.

Вариант 2 характеризуется разнообразием возможных вариантов за счет вариаций строк интеграционной матрицы.

Вариант 3 обладает наибольшим разнообразием из приведенных в таблице. Он предусматривает возможность одновременного использования всех трех измерителей с тем или иным комбинированием их сигналов.

Вариант 4 повторяет вариант 1 с дополнительным комбинированием каналов обработки сигнала.

Варианты 5 и 6 относятся к недопустимым конфигурациям, поскольку для них не выполняется одно из условий теоремы. И хотя для варианта, например 5, можно вычислить

их использование для формирования решения дает ошибочный результат в том смысле, что не обеспечивается заданная целевая функция (6.6).

Результаты примера полностью согласуются с элементарными расчетами и физической интерпретацией моделируемого процесса.

Заключение. Для практически важного случая конфигурирования избыточного комплекса оборудования в виде последовательности связанных подсистем в интересах решения задачи его интеграции получен формализм, включающий условия допустимости предварительно выбираемой конфигурации и формулу для всего множества альтернативных связей между компонентами с учетом выполнения заданной целевой функции комплекса.

Область применения полученных результатов не ограничивается только детально рассмотренными в примере комплексами бортового оборудования подвижных объектов и может включать сложные комплексы оборудования, содержащие последовательность взаимовлияющих функционально обособленных подсистем, описываемых линейными стационарными моделями.