Известия РАН. Теория и системы управления, 2020, № 2, стр. 5-16
МЕТОД ПОСТРОЕНИЯ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ В УПРАВЛЯЕМОЙ ДИНАМИЧЕСКОЙ СИСТЕМЕ С ЦИЛИНДРИЧЕСКИМ ФАЗОВЫМ ПРОСТРАНСТВОМ
Л. А. Климина *
НИИ механики МГУ
Москва, Россия
* E-mail: klimina@imec.msu.ru
Поступила в редакцию 12.08.2019
После доработки 02.10.2019
Принята к публикации 25.11.2019
Аннотация
Рассматривается управляемая механическая система с одной степенью свободы, описываемой угловой координатой. Система находится под действием консервативных и неконсервативных сил. Предполагается, что соответствующая динамическая система содержит варьируемый параметр, описывающий коэффициент усиления управляющего воздействия. Предложен итерационный численно-аналитический метод, предназначенный для формирования авторотационных режимов с заданными свойствами. Сформулированы условия орбитальной устойчивости таких режимов. Предложенный подход представляет собой модификацию метода Андронова–Понтрягина, и, в отличие от последнего, может быть применен не только к системам, близким к гамильтоновым, но и к некоторому классу систем, не содержащих малого параметра. Приведен пример применения метода к модели аэродинамического маятника. Показана возможность расширить область сходимости метода путем использования процедуры продолжения по параметру.
Введение. Автоколебания/авторотации представляют собой базовые программные режимы для широкого спектра систем (например, для технических устройств, биомеханических объектов, нейронных сетей) и активно изучаются в литературе. Зачастую соответствующие математические модели представлены динамическими системами второго порядка: модели маятников, часов, лазеров [1–5], аэрогидродинамических и аэроупругих систем [6–9], электромеханических систем [10–13], деформируемых твердых тел [14], моделирование процесса ходьбы [15, 16], модель ФитцХью–Нагумо для нейрона [17]. В большинстве перечисленных работ рассматриваются автономные динамические системы. Для последних изучаются, в том числе, вопросы формирования автоколебательных/авторотационных режимов.
Отметим, что в настоящей работе мы используем термин автоколебания/авторотации, введенный в [18]. В то же время известны альтернативные, несколько отличающиеся определения авторотации, например [19]. В работе [2] подробно обсуждается взаимосвязь эффекта авторотации с различными физическими принципами, приводятся примеры соответствующих динамических моделей.
Среди последних работ, систематизирующих методы поиска периодических решений динамических систем, можно отметить статьи [20, 21]. Выделяется несколько базовых направлений, по которым развиваются методы поиска периодических решений, непосредственно коррелированные с методами формирования заданных периодических движений управляемых систем. Во-первых, это методы, основанные на прямом численном интегрировании системы. Они подразумевают процесс “пристрелки”, зачастую используют процедуру продолжения по параметру, искусственную параметризацию и другие оригинальные подходы [22, 23]. Для таких методов практически отсутствует ограничение на порядок системы. Однако сходимость может существенно замедляться, когда параметры близки значениям, при которых происходит вырождение: например, возникновение кратных или неизолированных периодических решений.
Помимо этого широко востребованы проекционные методы, в рамках которых периодическое решение раскладывается по некоторому базису (часто используют гармонические функции), например [24–30]. В последнее время в этой области появляются работы с выраженным акцентом на итерационный процесс [5, 7, 20, 31, 32], в том числе не подразумевающие наличия малого параметра [33]. К достоинствам проекционных методов относятся универсальность, возможность применения для систем высокого порядка. Недостатки: скорость сходимости естественным образом снижается при наличии высоких гармоник в искомом решении. Кроме того, если рассмотреть первые гармоники как решение определенной порождающей системы, то такая “порождающая система нулевого приближения” линейна.
Третий класс подходов – методы, использующие порождающие системы. В последние годы методы, близкие к подходу [34–36], развиваются и применяются, например, в [37, 38]. Для таких подходов отсутствует ограничение на размерность системы. Однако порождающая система нулевого приближения линейна и, кроме того, в случае автономной системы требуется вспомогательная замена переменных.
Методы порождающих систем, основанные на модификации метода Андронова–Понтрягина [18, 39], применимы к автономным системам без дополнительных замен, используют сколь угодно нелинейную систему нулевого приближения. Такие подходы предложены и апробированы для описания автоколебаний систем второго порядка, в том числе управляемых [40, 41]. Однако распространение на системы более высокого порядка на данный момент отсутствует.
В настоящей работе, в отличие от статей [40, 41], дополнительно предполагается, что правая часть динамической системы является $2\pi $-периодической по фазовой координате. Таким образом, фазовое пространство системы может быть представлено в виде цилиндра. Автоколебаниям системы соответствуют циклы, охватывающие одну или несколько неподвижных точек, а авторотациям – замкнутые траектории, охватывающие фазовый цилиндр. Для формирования автоколебаний такой системы, обладающих заданными свойствами, можно применить методы [40, 41]. Для формирования авторотаций можно воспользоваться модификацией этих методов, которая предлагается в настоящей работе. Метод может быть применен не только для построения управления, но и для поиска периодических решений автономной динамической системы с цилиндрической фазовой поверхностью. Рассматривается пример применения метода к задаче об авторотациях аэродинамического маятника, управляющее воздействие на который представлено моментом в шарнире маятника, пропорциональным угловой скорости маятника.
Метод, предложенный в данной статье, совместно с подходом [41] образуют единый алгоритм, позволяющий осуществлять формирование периодических колебательных/ротационных движений управляемой механической системы с одной степенью свободы, обладающих заданными свойствами.
1. Постановка задачи. Рассмотрим механическую систему с одной угловой координатой $\varphi $. Пусть движение системы описывается безразмерными уравнениями следующего вида:
(1.1)
$\begin{gathered} \dot {\varphi } = \frac{{\partial H(\varphi ,\omega )}}{{\partial \omega }}, \\ \dot {\omega } = - \frac{{\partial H(\varphi ,\omega )}}{{\partial \varphi }} + a\left( {Q(\varphi ,\omega ) - u(\varphi ,\omega )} \right), \\ u(\varphi ,\omega ) = bf(\varphi ,\omega ). \\ \end{gathered} $Здесь точкой обозначена производная по безразмерному времени $\tau $; $\omega $ – безразмерный импульс; $H(\varphi ,\omega ) = 0.5{{k}^{{ - 1}}}(\varphi ){{\omega }^{2}} + P(\varphi )$ – функция Гамильтона, описывающая полную механическую энергию системы; $k(\varphi ) > 0$ – аналитическая функция, определяемая структурой кинетической энергии системы; $P(\varphi ) \geqslant 0$ – аналитическая функция, описывающая потенциальную энергию системы; a > 0 – безразмерный коэффициент; $Q(\varphi ,\omega )$ – безразмерная обобщенная сила, соответствующая внешним неконсервативным силам (аналитическая функция); $u(\varphi ,\omega )$ – управление. Предполагается, что управление есть произведение коэффициента b, который подлежит выбору, и некоторой заданной функции $f(\varphi ,\omega )$, характеризующей структуру обратной связи и обладающей следующим свойством: $\omega f(\varphi ,\omega ) > 0$ при $\omega \ne 0$. Таким образом, параметр b отвечает повороту векторного поля системы (1.1) [18]. Предполагается, что правая часть системы (1.1) является $2\pi $-периодической по угловой координате $\varphi $ функцией. Таким образом, фазовое пространство $(\varphi ,\omega )$ системы (1.1) может быть представлено как фазовый цилиндр $(\varphi \bmod 2\pi ,\omega )$.
Задача данной работы состоит в том, чтобы для заданного $h$ установить достаточные условия существования значения $b = \tilde {b}(h)$, такого, что система (1.1) при $b = \tilde {b}(h)$ обладает 2π-периодической по $\varphi $ фазовой траекторией, на которой среднее по времени значение функции $H(\varphi ,\omega )$ равно h. Если такое значение $b = \tilde {b}(h)$ существует, то найти его и соответствующую периодическую траекторию $\omega = \tilde {\omega }(\varphi ,h)$, определить, является ли эта траектория притягивающей, и если является, то указать область притяжения. Помимо этого, требуется указать диапазон значений h, которые возможно реализовать при управлении выбранной структуры.
Ограничимся положительными значениями $\omega $, поскольку отрицательные можно рассмотреть полностью аналогично. Отметим, что предложенный далее подход легко обобщить на случай, когда требуется обеспечить определенное среднее значение угловой скорости авторотации, и на другие подобные задачи формирования авторотационных режимов с заданными свойствами.
2. Достаточные условия существование периодической траектории. Пусть максимальное значение ${{P}_{0}}$ функции $P(\varphi )$ достигается при некотором $\varphi = {{\varphi }_{0}}$. Будем рассматривать значения $h > {{P}_{0}}$. Будем характеризовать $2\pi $-периодическую траекторию значением ${{\omega }_{0}} = {{\left. \omega \right|}_{{\varphi = {{\varphi }_{0}}}}}$ на этой траектории. Рассмотрим интервал ${{\omega }_{0}} \in (0,\Omega )$, где $\Omega $ – некоторая положительная константа, выбранная так, что если $2\pi $-периодическая траектория с заданным средним значением h функции $H(\varphi ,\omega )$ существует, то она заведомо расположена внутри полосы ${{\omega }_{0}} \in (0,\Omega )$ фазового цилиндра.
Решим вспомогательную задачу. Пусть задано некоторое значение ${{\omega }_{0}} \in (0,\Omega )$. Фазовой точке $({{\varphi }_{0}},{{\omega }_{0}})$ отвечает некоторая величина ${{h}_{0}} = H({{\varphi }_{0}},{{\omega }_{0}})$. Сформулируем достаточные условия, при которых существует значение $\hat {b}({{\omega }_{0}})$ параметра b, обеспечивающее в системе (1.1) наличие $2\pi $-периодической траектории, проходящей через фазовую точку $({{\varphi }_{0}},{{\omega }_{0}})$. Отметим, что в силу свойств поворота векторного поля [18], если такое значение $\hat {b}({{\omega }_{0}})$ существует, оно единственно.
Отметим, что функция $\hat {b}({{\omega }_{0}})$ удовлетворяет определению функции предельных циклов, введенному в [42], а предложенный далее метод вычисления этой функции альтернативен подходам [42, 43].
Определим последовательные приближения следующего вида:
(2.1)
$\begin{gathered} {{y}_{0}}(\varphi ,{{\omega }_{0}}) = \sqrt {2k(\varphi )({{h}_{0}} - P(\varphi ))} , \\ {{b}_{0}}({{\omega }_{0}}) = {{\left( {\int\limits_0^{2\pi } {f\left( {\varphi ,{{y}_{0}}(\varphi ,{{\omega }_{0}})} \right)} d\varphi } \right)}^{{ - 1}}}\int\limits_0^{2\pi } {Q\left( {\varphi ,{{y}_{0}}(\varphi ,{{\omega }_{0}})} \right)} d\varphi ; \\ \end{gathered} $(2.2)
$\begin{gathered} {{y}_{n}}(\varphi ,{{\omega }_{0}}) = \operatorname{Re} \sqrt {2k(\varphi )\left( {{{h}_{0}} - P(\varphi ) + a\int\limits_{{{\varphi }_{0}}}^\varphi {\left( {Q\left( {\vartheta ,{{y}_{{n - 1}}}(\vartheta ,{{\omega }_{0}})} \right) - {{b}_{{n - 1}}}f\left( {\vartheta ,{{y}_{{n - 1}}}(\vartheta ,{{\omega }_{0}})} \right)} \right)} d\vartheta } \right)} {\kern 1pt} {\kern 1pt} , \\ {{b}_{n}}({{\omega }_{0}}) = {{\left( {\int\limits_0^{2\pi } {f\left( {\varphi ,{{y}_{n}}(\varphi ,{{\omega }_{0}})} \right)} d\varphi } \right)}^{{ - 1}}}\int\limits_0^{2\pi } {Q\left( {\varphi ,{{y}_{n}}(\varphi ,{{\omega }_{0}})} \right)} d\varphi ,\quad n \geqslant 1. \\ \end{gathered} $Здесь ${{y}_{n}}(\varphi ,{{\omega }_{0}})$ – построенная на n-м шаге аппроксимация 2π-периодической фазовой траектории; ${{b}_{n}}({{\omega }_{0}})$ – полученная на n-м шаге аппроксимация искомого значения коэффициента усиления управляющего воздействия.
Утверждение 1. Если последовательность ${{y}_{n}}(\varphi ,{{\omega }_{0}})$ сходится к некоторому пределу $\hat {y}(\varphi ,{{\omega }_{0}})$ > 0 при всех φ, то и последовательность ${{b}_{n}}({{\omega }_{0}})$ сходится к некоторому пределу $\hat {b}({{\omega }_{0}})$, при этом функция $\hat {y}(\varphi ,{{\omega }_{0}})$ представляет собой 2π-периодическую траекторию, существующую в системе (1.1) при $b = \hat {b}({{\omega }_{0}})$ и проходящую через точку $({{\varphi }_{0}},{{\omega }_{0}})$.
Утверждение 1 описывает достаточные условия существования периодической траектории системы (1.1), проходящей через точку $({{\varphi }_{0}},{{\omega }_{0}})$, и соответствующего значения параметра $\hat {b}({{\omega }_{0}})$. Аналоги утверждения 1 для системы второго порядка на плоскости предложены в работах [40] (случай системы с центральной симметрией) и [41] (общий случай). Доказательство утверждения 1 аналогично доказательству подобного утверждения, приведенного в [40]. Значение параметра a влияет на скорость сходимости итераций (2.2) и на сам факт сходимости.
Нулевое приближение (2.1) совпадает с результатом применения метода Андронова–Понтрягина, предложенного в [18, 39]. Порождающая система нулевого приближения – гамильтонова система с функцией Гамильтона $H(\varphi ,\omega )$ может быть сколь угодно нелинейна.
Если итерации (2.2) не сходятся, это, вообще говоря, не означает отсутствия искомого значения параметра $b = \hat {b}({{\omega }_{0}})$. Иными словами, условия утверждения 1 являются достаточными, но не являются необходимыми для существования периодической траектории. Можно привести соответствующие примеры. В частности, далее рассмотрим пример, когда при помощи продолжения по параметру можно модифицировать предложенный метод и расширить область сходимости итераций (2.2).
Итак, предположим, что для заданного ${{\omega }_{0}} \in (0,\Omega )$ итерации (2.2) сходятся. Для решения основной задачи вычислим среднее значение $\tilde {h}({{\omega }_{0}})$ функции $H(\varphi ,\omega )$ вдоль найденной периодической траектории $\hat {y}(\varphi ,{{\omega }_{0}}) = \left( {\hat {\varphi }(\tau ,{{\omega }_{0}}),\hat {\omega }(\tau ,{{\omega }_{0}})} \right)$, существующей в системе (1.1) при $b = \hat {b}({{\omega }_{0}})$:
(2.3)
$\tilde {h}({{\omega }_{0}}) = \frac{1}{T}\int\limits_0^T {H\left( {\hat {\varphi }(\tau ,{{\omega }_{0}}),\hat {\omega }(\tau ,{{\omega }_{0}})} \right)} d\tau = {{\left( {\int\limits_0^{2\pi } {\frac{1}{{\hat {y}(\varphi ,{{\omega }_{0}})}}} d\varphi } \right)}^{{ - 1}}}\int\limits_0^{2\pi } {\frac{{H(\varphi ,\hat {y}(\varphi ,{{\omega }_{0}}))}}{{\hat {y}(\varphi ,{{\omega }_{0}})}}} d\varphi .$Отметим, что значение $\tilde {h}({{\omega }_{0}})$ вычисляется с использованием найденной ранее траектории $\hat {y}(\varphi ,{{\omega }_{0}})$ и значения $b = \hat {b}({{\omega }_{0}})$.
Применим алгоритм (2.1)–(2.3) для “всех” значений ${{\omega }_{0}} \in (0,\Omega )$: при численной реализации зададим некоторый шаг по ω0. Предположим, что для всех таких ω0 итерации (2.2) сходятся. Тогда мы получим зависимость между средним уровнем h функции $H(\varphi ,\omega )$ (механической энергии) на 2π-периодических траекториях (авторотациях) и величиной коэффициента b усиления управляющего воздействия. Эта зависимость параметризована величиной ω0. Другими словами, $\tilde {b}\left( h \right) = \left\{ {\left. {\hat {b}\left( {{{\omega }_{0}}} \right)} \right|\tilde {h}({{\omega }_{0}}) = h} \right\}$.
Зависимость $\tilde {h}({{\omega }_{0}})$, вообще говоря, может оказаться немонотонной, и тогда зависимость $\tilde {b}\left( h \right)$ будет неоднозначной. В последнем случае можно выбрать любое из значений $\tilde {b}\left( h \right)$ в качестве искомого коэффициента усиления управляющего сигнала, в частности, то значение, при котором шире область притяжения соответствующего установившегося режима.
3. Устойчивость и области притяжения. Имеет место следующее утверждение, позволяющее установить свойство притяжения цикла.
Утверждение 2. Если при некотором значении ${{\omega }_{0}} = {{\omega }_{{01}}}$ производная функции $\hat {b}({{\omega }_{0}})$ отрицательна, то при $b = \hat {b}({{\omega }_{{01}}})$ 2π-периодическая траектория системы (1.1), проходящая через точку $({{\varphi }_{0}},{{\omega }_{{01}}})$, является орбитально устойчивой; если же производная функции $\hat {b}({{\omega }_{0}})$ при ${{\omega }_{0}} = {{\omega }_{{01}}}$ положительна, то при $b = \hat {b}({{\omega }_{{01}}})$ 2π-периодическая траектория системы (1.1), проходящая через точку $({{\varphi }_{0}},{{\omega }_{{01}}})$, является неустойчивой.
Это утверждение вытекает из свойств поворота векторного поля.
Опишем области притяжения 2π-периодических траекторий, существующих при различных значениях параметра b в полосе ${{\omega }_{0}} \in (0,\Omega )$ фазового цилиндра. Предположим, что получена (как описано выше) зависимость $b = \hat {b}({{\omega }_{0}})$ для ${{\omega }_{0}} \in (0,\Omega )$. Если для двух или более значений ω0 соответствующие значения $\hat {b}({{\omega }_{0}})$ одинаковы, то при таком значении $b = \hat {b}({{\omega }_{0}})$ существует несколько 2π-периодических траекторий и неустойчивые периодические траектории ограничивают области притяжения орбитально устойчивых. Если 2π-периодическая траектория с наименьшим значением ω0 притягивающая, то ее область притяжения может быть ограничена снизу либо неустойчивым циклом, который можно искать, например, методом [41], либо сепаратрисами седловых точек, которые требуется исследовать отдельно, например, путем прямого численного интегрирования системы.
4. Продолжение по параметру a. Для того чтобы расширить область сходимости итераций (2.2), предложим процедуру, подобную методу продолжения по параметру применительно к параметру a. Предположим, что для некоторого заданного $a = {{a}_{1}}$ найдено (путем применения итераций (2.2)) значение $\hat {b}({{\omega }_{0}})$ и построена функция $\hat {y}(\varphi ,{{\omega }_{0}})$. Тогда для значения $a = {{a}_{2}} > {{a}_{1}}$ используем пару $\hat {b}({{\omega }_{0}})$ и $\hat {y}(\varphi ,{{\omega }_{0}})$ в качестве нулевого приближения итераций (2.2) вместо пары (2.1).
Эта модификация позволяет расширить область сходимости итераций (2.2). Подобная процедура продолжения по параметру a может быть применена и для расширения области сходимости методов [40, 41], предназначенных для поиска циклов систем на плоскости.
Рассмотрим пример применения метода (2.1)–(2.3), включающий анализ областей притяжения построенных периодических решений. На этом примере проиллюстрируем скорость сходимости метода, а также расширение области сходимости за счет продолжения по параметру a.
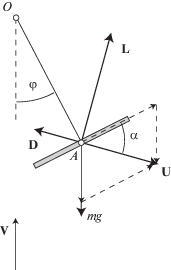
5. Пример применения метода: авторотация маятника в потоке. Применим утверждения 1 и 2 для описания авторотаций тяжелого аэродинамического маятника в вертикальном потоке воздуха (рис. 1). Такой маятник может выступать в качестве модели малой ветроэнергетической установки, предназначенной для работы в восходящем потоке (например, около высотного знания). В этом случае на оси маятника устанавливается ротор электрогенератора установки, а в качестве управляющего воздействия выступает регулирование внешнего сопротивления в локальной цепи электрогенератора. Подобные модели ветроустановок (в горизонтальном потоке) и стратегии управления внешним сопротивлением обсуждаются в работах [44–49].
Аэродинамический маятник представляет собой твердое тело в потоке воздуха. Маятник может вращаться вокруг неподвижной горизонтальной оси $O$. Он состоит из державки OA длины r и жестко прикрепленной к ней лопасти–пластины. Пластина перпендикулярна державке. Центр масс маятника совпадает с точкой A. Маятник расположен в поле силы тяжести. Вектор ${\mathbf{V}}$ скорости потока направлен вертикально вверх. Плотность потока обозначим $\rho $.
Далее используются следующие обозначения: $\varphi $ – угол поворота державки OA, отсчитывается от вертикали; $\omega = r{{V}^{{ - 1}}}d\varphi {\text{/}}dt$ – безразмерная угловая скорость маятника; $m$ – масса маятника; J – момент инерции маятника относительно оси вращения O; $S$ – характерная площадь пластины; $U$ – воздушная скорость точки A; $\alpha = {\text{arctg}}(\cos \varphi {\text{/}}(\omega - \sin \varphi ))$ – мгновенный угол атаки (угол между вектором U и пластиной); D – сила сопротивления; L – подъемная сила; ${{C}_{D}}(\alpha )$, ${{C}_{L}}(\alpha )$ – безразмерные коэффициенты силы сопротивления и подъемной силы.
Аэродинамическое воздействие на маятник описывается на основе квазистационарного подхода [44, 50]:
Аэродинамические коэффициенты аппроксимируются следующими функциями, отражающими их характерные свойства:
Предполагается, что вал маятника соединен с ротором электрогенератора, подключенного к локальной внешней цепи. Электромеханический момент, действующий на ротор электрогенератора, описывается функцией ${{B}_{R}} = - B\omega $, $B > 0$ (аналогично [44]). Коэффициент $B$ характеризует нагрузку со стороны потребителей энергии в цепи генератора. Значение этого коэффициента может регулироваться путем подключения/отключения потребителей и может выступать в качестве управления, как, например, в работе [48].
Представим уравнения движения системы в форме системы вида (1.1) (точкой обозначена производная по безразмерному времени $\tau = Vt{\text{/}}r$):
(5.1)
$\begin{gathered} \dot {\varphi } = \omega , \\ \dot {\omega } = - p\sin \varphi + a\left( {Q(\varphi ,\omega ) - b\omega } \right), \\ Q(\varphi ,\omega ) = - \sqrt {{{{(\omega - \sin \varphi )}}^{2}} + {{{\cos }}^{2}}\varphi } \left( {{{C}_{L}}(\alpha )\cos \varphi + {{C}_{D}}(\alpha )(\omega - \sin \varphi )} \right), \\ f(\varphi ,\omega ) = \omega , \\ a = \frac{{\rho S{{r}^{3}}}}{{2J}},\quad b = \frac{{2B}}{{\rho Sr{{V}^{2}}}},\quad p = \frac{{mg{{r}^{3}}}}{{J{{V}^{2}}}}. \\ \end{gathered} $В данном примере $k(\varphi ) \equiv 1$, $P(\varphi ) = - p\cos \varphi $, максимальное значение потенциальной энергии достигается при угле ${{\varphi }_{0}} = \pi $.
Далее рассмотрим задачу построения зависимости $b = \hat {b}({{\omega }_{0}})$. Последующий переход к зависимости $\tilde {b}\left( h \right)$ может быть выполнен очевидным образом по формуле (2.3).
Ограничимся случаем p = 1. Будем рассматривать область $\omega > 0$ (при численном счете: $\omega > 0.01$). Область $\omega < 0$ может быть рассмотрена аналогично.
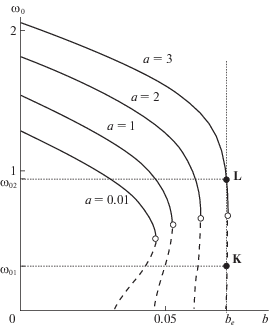
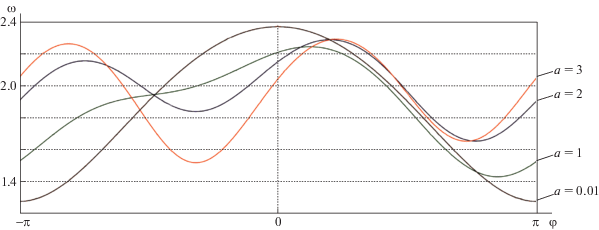
Применим утверждение 1 для описания зависимости авторотационных режимов маятника от параметра b. На рис. 2 представлена эволюция соответствующих бифуркационных диаграмм при нескольких значениях ai параметра a. Для каждого значения a = ai итерационный процесс (2.2) реализовывался численно, пока номер n не достигал такого значения $n = {{n}_{i}}({{a}_{i}})$, при котором невязка
На рис. 2 сплошные линии отвечают орбитально устойчивым 2π-периодическим траекториям, пунктирные линии – неустойчивым. Белая (выколотая) точка на каждой кривой соответствует слиянию притягивающей и отталкивающей траекторий.
Например, при $a = 3$, $b = {{b}_{e}} = 0.071$ существует две $2\pi $-периодические траектории: отталкивающая траектория, на которой $\tilde {y}(\pi ) = {{\omega }_{{01}}} \approx 0.33$, и притягивающая траектория, на которой $\tilde {y}(\pi )$ = = ${{\omega }_{{02}}} \approx 0.94$. Соответствующие точки бифуркационной диаграммы обозначены на рис. 2 буквами “K” и “L”.
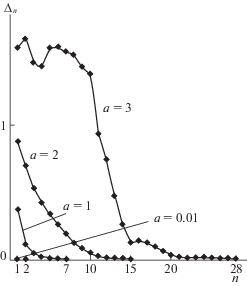
Из рис. 3 видно, что при a = 0.01 уже нулевое приближение (2.1) для периодической траектории, определяемое методом Андронова–Понтрягина [18, 39], является весьма точным. При таком “малом” значении параметра a начальное приближение лишь “незначительно” улучшается последующими итерациями (2.2). В то же время при значениях a порядка единицы итерации (2.2) существенно уменьшают значение невязки с ростом n. Чем больше a, тем больше начальная невязка и тем медленнее она уменьшается.
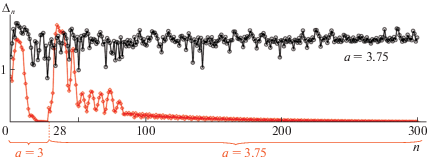
Рисунок 4 иллюстрирует, что при $a \approx 3.7$ сходимость (2.1)–(2.2) теряется (график с точками), но может быть восстановлена путем замены нулевого приближения (2.1) на приближение, полученное по итогам выполнения итераций (2.2) для значения $a = 3$ (график с ромбиками).
6. Примеры фазовых траекторий. Каждая точка построенных диаграмм (рис. 2) отвечает функции ${{y}_{{{{n}_{i}}}}}(\varphi ,{{\omega }_{0}})$, построенной в ходе реализации итераций (2.2). Эта функция аппроксимирует периодическую траекторию системы (5.1), существующую при $a = {{a}_{i}}$, $b = {{b}_{{{{n}_{i}}}}}({{\omega }_{0}})$. На основе полученной информации об этих функциях можно проиллюстрировать эволюцию периодической траектории при изменении параметра a при фиксированном значении b. Пример приведен на рис. 5. Представлен случай b = 0 (свободная авторотация маятника в потоке).
C другой стороны, при фиксированном a соответствующая бифуркационная кривая (рис. 2) описывает эволюцию периодических траекторий при изменении параметра b.
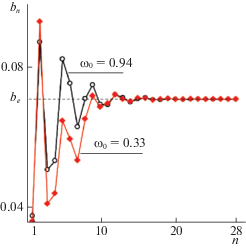
Проиллюстрируем более детально случай, когда в системе (5.1) существуют одновременно две периодические траектории. На рис. 6 представлены аппроксимации ${{y}_{n}}(\varphi ,{{\omega }_{0}})$ периодических траекторий, полученные для a = 3, $b = 0.071$. Приведено несколько итераций, включая нулевую, которая полностью совпадает с одной из траекторий математического маятника, проходящей через фазовую точку $(\pi ,{{\omega }_{0}})$. Для притягивающей траектории ${{\omega }_{0}} = 0.94$, для отталкивающей ${{\omega }_{0}} = 0.33$. Соответствующие этим итерациям приближения ${{b}_{n}}({{\omega }_{0}})$ показаны на рис. 7.
Рис. 6.
Итерационные приближения для притягивающей (“L”) и отталкивающей (“K”) $2\pi $-периодических траекторий, существующих в системе (5.1) при a = 3, $b = 0.071$
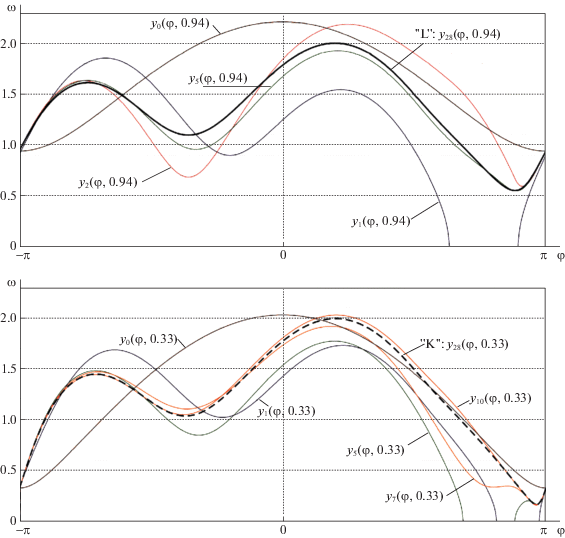
Рис. 7.
Итерационные приближения ${{b}_{n}}({{\omega }_{0}})$ при a = 3: случаи ${{\omega }_{0}} = 0.33$ и ${{\omega }_{0}} = 0.94$
На рис. 8 представлены элементы фазового портрета системы (5.1) при a = 3, $b = 0.071$. Показаны приближения периодических траекторий “K” и “L”, построенные предложенным итерационным методом, а также траектории, полученные путем прямого численного интегрирования системы при различных начальных условиях (метод Рунге–Кутты). Начальное значение угла на всех траекториях $\varphi (0) = - \pi $.
Рис. 8.
Элементы фазового портрета системы при a = 3, $b = 0.071$ (сравнение предложенного метода с методом Рунге–Кутты)
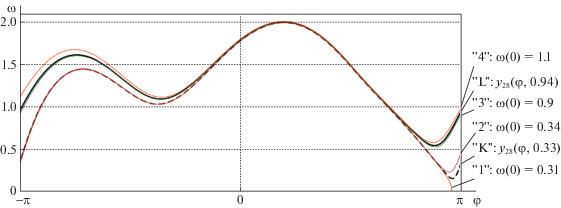
Из рис. 8 видно, что найденные приближения для периодических траекторий полностью согласуются с элементами фазового портрета, полученными путем прямого численного интегрирования.
Чем меньше значение a, тем слабее влияние аэродинамических сил по сравнению с гравитацией. Это обстоятельство заметно сказывается на авторотациях маятника. Для небольших a периодические фазовые траектории близки к траекториям математического маятника. В этом случае они могут быть с высокой точностью описаны методом Андронова–Понтрягина [18, 39]. C увеличением параметра a отличие периодических траекторий от траекторий математического маятника усиливается (рис. 5); бифуркационная кривая авторотационных режимов все более отличается от случая $a \ll 1$, описанного методом Андронова–Понтрягина (рис. 2). Эволюция периодических траекторий системы (5.1) при увеличении параметра a является яркой иллюстрацией того, как усиление неконсервативных воздействий влияет на характер авторотаций.
Для рассмотренного примера можно отметить следующие закономерности: притягивающие авторотационные режимы существуют в широком диапазоне значений параметра b. Этот диапазон расширяется при увеличении параметра a. В то время как интервал значений b, при которых существует отталкивающий авторотационный режим, сужается при увеличении параметра a.
7. Сравнение метода с другими подходами. Для решения рассмотренной задачи можно было использовать и другие методы, при этом возникли бы другие преимущества и недостатки. Например, использование метода прямого численного интегрирования в сочетании с методом стрельбы позволило бы расширить исследуемый диапазон по параметру a (снять проблему замедления сходимости при увеличении a). Однако при относительно небольших a, а также в окрестности слияния притягивающего и отталкивающего режимов, напротив, метод стрельбы медленно сходится, а предложенный метод работает эффективно (рис. 3).
Преимуществами предложенного метода по сравнению с другими численно-аналитическими подходами являются, в частности, существенная нелинейность порождающей системы нулевого приближения, а также возможность ускорения сходимости путем использования процедуры продолжения по параметру a.
8. Связь построенных периодических траекторий с интегрируемой системой. Из Утверждения 1 и альтернативного ему утверждения для систем с плоским фазовым пространством, полученного в [41], получаем красивое свойство периодических решений автономной системы второго порядка:
Утверждение 3. Рассмотрим семейство систем второго порядка вида (1.1), параметризованное параметром b (при этом $a = {{a}_{0}} = {\text{const}}$). Пусть на некоторой области $\Omega $ фазового цилиндра определена функция $b = \beta (\varphi ,\omega ) = {{\left. {\hat {b}(\omega )} \right|}_{{\varphi = {{\varphi }_{0}}}}}$, обеспечивающая в системе наличие периодической траектории, проходящей через точку $({{\varphi }_{0}},\omega )$ и постоянная вдоль каждой такой траектории (в частности, такая функция определена пределом последовательностей (2.2), если итерации сходятся). Тогда существует интегрируемая система второго порядка, такая, что каждая ее фазовая траектория, расположенная в области $\Omega $, представляет собой периодическое решение системы вида (1.1), существующее при некотором значении параметра b. Функция $\beta (\varphi ,\omega )$ представляет собой первый интеграл этой системы. И тогда все периодические траектории всех систем семейства (1.1), расположенные в области Ω, являются траекториями одной и той же интегрируемой системы с первым интегралом $\beta (\varphi ,\omega )$.
Заключение. Предложенный итерационный метод позволяет описывать 2π-периодические траектории автономной динамической системы с цилиндрической фазовой поверхностью, а также формировать периодические траектории с заданными свойствами путем выбора значения коэффициента усиления управляющего воздействия. Метод основан на идеях подхода Андронова–Понтрягина [18, 39] и расширяет область применения этих идей на класс систем, не содержащих малого параметра.
Помимо этого предложена процедура продолжения по параметру, позволяющая расширить область сходимости метода.
Эффективность метода и скорость сходимости проиллюстрированы на примере задачи формирования авторотационных режимов движения аэродинамического маятника, представляющего собой рабочий элемент ветроэнергетической системы. Описана эволюция режимов авторотации при изменении параметров модели.
Описаны преимущества метода по сравнению с другими известными подходами. Основные преимущества достигаются, когда значения параметров модели относительно близки к случаю гамильтоновой системы, а также к случаю бифуркации слияния периодических решений.
Список литературы
Решмин C.А., Черноусько Ф.Л. Оптимальное по быстродействию управление перевернутым маятником в форме синтеза // Изв. РАН. ТиСУ. 2006. № 3. С. 51–62.
Jenkins A. Self-Oscillation // Physics Reports. 2013. V. 525. № 2. P. 167–222.
Morozov A.D., Kostromina O.S. On Periodic Perturbations of Asymmetric Duffing–Van-der-Pol Equation // Intern. J. Bifurc. Chaos. 2014. V. 24. № 5. P. 1450061.
Formalskii A.M. Stabilization and Motion Control of Unstable Objects. Berlin/Boston: Walter de Gruyter, 2015.
Gasull A., Geyer A., Mañosas F. On the Number of Limit Cycles for Perturbed Pendulum Equations // J. Differential Equations. 2016. V. 261. № 3. P. 2141–2167.
Klimina L., Dosaev M., Selyutskiy Yu. Asymptotic Analysis of the Mathematical Model of a Wind-powered Vehicle // Applied Mathematical Modelling. 2017. V. 46. P. 691–697.
Berci M., Dimitriadis G. A Combined Multiple Time Scales and Harmonic Balance Approach for the Transient and Steady-State Response of Nonlinear Aeroelastic Systems // J. Fluids and Structures. 2018. V. 80. P. 132–144.
Rostami A.B., Fernandes A.C. Mathematical Model and Stability Analysis of Fluttering and Autorotation of an Articulated Plate into a Flow // Communications in Nonlinear Science and Numerical Simulation. 2018. V. 56. P. 544–560.
Selyutskiy Y.D. On Dynamics of an Aeroelastic System with Two Degrees of Freedom // Applied Mathematical Modelling. 2019. V. 67. P. 449–455.
Fernandes A.C., Rostami A.B. Hydrokinetic Energy Harvesting by an Innovative Vertical Axis Current Turbine // Renewable Energy. 2015. V. 81. P. 694–706.
Chen C., Zanette D.H., Guest J.R., Czaplewski D.A., López D. Self-Sustained Micromechanical Oscillator with Linear Feedback // Physical Review Letters. 2016. V. 117. № 1. 017203.
Jia B., Smallbone A., Feng H., Tian G., Zuo Z., Roskilly A.P. A Fast Response Free-Piston Engine Generator Numerical Model for Control Applications // Applied Energy. 2016. V. 162. P. 321–329.
Dosaev M., Klimina L., Selyutskiy Y. Wind Turbine Based on Antiparallel Link Mechanism // New Trends in Mechanism and Machine Science. 2017. V.43. P. 543–550.
Amabili M. Nonlinear Damping in Large-Amplitude Vibrations: Modelling and Experiments // Nonlinear Dyn. 2018. V. 93. P. 1–14.
Erlicher S., Trovato A., Argoul P. Modeling the Lateral Pedestrian Force on a Rigid Floor by a Self-sustained Oscillator // Mechanical Systems and Signal Processing. 2010. V. 24. № 5. P. 1579–1604.
Aoustin Y., Formal’sky A.M. Control Design for a Biped: Reference Trajectory Based on Driven Angles as Functions of the Undriven Angle // J. Computer and Systems Sciences International. 2003. V. 42. № 4. P. 645–662.
Rocsoreanu C., Georgescu A., Giurgiteanu N. The FitzHugh-Nagumo Model: Bifurcation and Dynamics. Springer Science & Business Media, 2012.
Андронов А.А., Леонтович Е.А., Гордон И.И., Майер А.Г. Теория бифуркаций динамических систем на плоскости. М.: Наука, 1967.
Lugt H.J. Autorotation // Ann. Rev. Fluid Mech. 1983. V. 15. № 1. P. 123–147.
Dudkowski D., Jafari S., Kapitaniak T., Kuznetsov N.V., Leonov G.A., Prasad A. Hidden Attractors in Dynamical Systems // Physics Reports. 2016. V. 637. P. 1–50.
Renson L., Kerschen G., Cochelin B. Numerical Computation of Nonlinear Normal Modes in Mechanical Engineering // J. Sound and Vibration. 2016. V. 364. P. 177–206.
Bindel D., Friedman M., Govaerts W., Hughes J., Kuznetsov Y.A. Numerical Computation of Bifurcations in Large Equilibrium Systems in Matlab // J. Computational and Applied Mathematics. 2014. V. 261(0). P. 232–248.
Monovasilis T., Kalogiratou Z., Ramos H., Simos T.E. Modified Two-Step Hybrid Methods for the Numerical Integration of Oscillatory Problems // Mathematical Methods in the Applied Sciences. 2017. V. 40. № 14. P. 5286–5294.
Delamotte B. Nonperturbative (but Approximate) Method for Solving Differential Equations and Finding Limit Cycles // Physical Review Letters. 1993. V. 70. № 22. P. 3361.
He J.H. Determination of Limit Cycles for Strongly Nonlinear Oscillators // Physical Review Letters. 2003. V. 90. № 17. P. 174301.
He J.H. Limit Cycle and Bifurcation of Nonlinear Problems // Chaos, Solitons & Fractals. 2005. V. 26. № 3. P. 827–833.
Leonov G.A. Efficient Methods in the Search for Periodic Oscillations in Dynamical Systems // J. Applied Mathematics and Mechanics. 2010. V. 74. № 1. P. 24–50.
Momeni M., Jamshidi N., Barari A., Ganji D.D. Application of He’s Energy Balance Method to Duffing-Harmonic Oscillators // Intern. J. Computer Mathematics. 2011. V. 88. № 1. P. 135–144.
Брагин В.О., Вагайцев В.И., Кузнецов Н.В., Леонов Г.А. Алгоритмы поиска скрытых колебаний в нелинейных системах. Проблемы Айзермана, Калмана и цепи Чуа // Изв. РАН. ТиСУ. 2011. № 4. С. 3–36.
Klimenko A.A., Mikhlin Y.V., Awrejcewicz J. Nonlinear Normal Modes in Pendulum Systems // Nonlinear Dynamics. 2012. V. 70. № 1. P. 797–813.
Leonov G.A., Kuznetsov N.V. Hidden Oscillations in Dynamical Systems. 16 Hilbert’s Problem, Aizerman’s and Kalman’s Conjectures, Hidden Attractors in Chua’s Circuits // J. Mathematical Sciences. 2014. V. 201. № 5. P. 645–662.
Lewis A.P. Refined Analytical Approximations to Limit Cycles for Non-Linear Multi-Degree-of-Freedom Systems // Intern. J. Non-Linear Mechanics. 2019. V. 110. P. 58–68.
Buonomo A., Schiavo A.L. A Constructive Method for Finding the Periodic Response of Nonlinear Circuits // IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications. 2003. V. 50. № 7. P. 885–893.
Cesari L., Hale J.K. A New Sufficient Condition for Periodic Solutions of Weakly Nonlinear Differential Systems // Proc. American Mathematical Society. 1957. V. 8. № 4. P. 757–764.
Samoilenko A.M. Numerical Analytical Method of Investigating Periodic Systems of Ordinary Differential Equations. I // Ukrainskij Matematicheskij Zhurnal. 1965. V. 17. № 04. P. 82–93.
Rontó M.I., Samoilenko A.M., Trofimchuk S.I. The Theory of the Numerical-Analytic Method: Achievements and New Trends of Development. IV // Ukrainian Mathematical J. 1998. V. 50. № 12. P. 1888–1907.
Rontó A., Rontó M., Shchobak N. Constructive Analysis of Periodic Solutions with Interval Halving // Boundary Value Problems. 2013. V. 2013. № 1. P. 57.
Буданов В.М. Метод неопределенных частот // Фундамент. и прикл. матем. 2018. V. 22. № 2. P. 59–71.
Понтрягин Л.С. О динамических системах, близких к гамильтоновым // ЖЭТФ. 1934. Т. 4. № 9. С. 234–238.
Климина Л.А. Метод поиска периодических траекторий центрально-симметричных динамических систем на плоскости // Дифференц. уравнения. 2019. Т. 55. № 2. С. 159–168.
Климина Л.А., Селюцкий Ю.Д. Метод построения периодических решений в управляемой динамической системе второго порядка // Изв. РАН. ТиСУ. 2019. № 4. С. 3–15.
Cherkas L.A., Grin’ A.A. Limit Cycle Function of the Second Kind for Autonomous Systems on the Cylinder // Differential Equations. 2011. V. 47. № 4. P. 462–470.
Cherkas L., Grin A., Schneider K.R. On the Approximation of the Limit Cycles Function // Electronic J. Qualitative Theory of Differential Equations. 2007. V. 2007. № 28. P. 1–11.
Досаев М.З., Самсонов В.А., Селюцкий Ю.Д. О динамике малой ветроэлектростанции // ДАН. 2007. Т. 416. № 1. С. 50–53.
Досаев М.З., Самсонов В.А., Селюцкий Ю.Д., Вен-Лон Лю, Чин-Хуэй Линь. Бифуркации режимов функционирования малых ветроэлектростанций и оптимизация их характеристик // Изв. РАН. МТТ. 2009. № 2. С. 59–66.
Andronov P.R., Dosaev M.Z., Dynnikova G.Y., Selyutskii Y.D., Strekalov S.D. Modeling of Oscillating Wind Turbine // J. Machinery Manufacture and Reliability. 2009. V. 38. № 4. P. 383–387.
Dosaev M., Holub A., Klimina L. Preferable Operation Modes of a Wind Turbine with a Differential Planetary Gearbox // New Trends in Mechanism and Machine Science. 2015. V. 24. P. 545–552.
Shalimova E., Klimina L., Lin K.H. On Behavior of a Double Rotor HAWT with a Differential Planet Gear // Technische Mechanik. 2017. V. 37. № 2–5. P. 394–399.
Selyutskiy Y.D. On the Dynamics of Small Wind Power Generators // Mathematical Models and Computer Simulations. 2018. V. 10. № 4. P. 494–500.
Самсонов В.А., Селюцкий Ю.Д. Сопоставление различных форм записи уравнений движения тела в потоке среды // Изв. РАН. МТТ. 2008. № 1. С. 171–178.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления