Известия РАН. Теория и системы управления, 2020, № 2, стр. 156-167

Введение. В настоящее время в Российской Федерации прослеживается тенденция к значительному увеличению группировки космических аппаратов (КА) дистанционного зондирования Земли (ДЗЗ). Это приводит к тому, что в данный момент проводятся значительные исследования в области создания современных автоматических систем, предназначенных для съемок поверхности Земли из космоса. Результатом этих исследований становится разработка новых технологических платформ спутников [1], а также использование уже имеющихся возможностей для отработки новых технологий ДЗЗ [2, 3]. В данной статье рассматривается управление ориентацией перспективного КА. Аппарат предназначен для съемки заданных районов земной поверхности с высоким пространственным разрешением. Ввиду требований к все более увеличивающейся производительности КА, а также необходимости реализации им площадных съемок и коридорных съемок предполагается, что основными исполнительными органами для управления угловым движением являются двухстепенные силовые гироскопы. За счет того, что управляющий момент, действующий на КА, создается в основном путем поворота вокруг оси подвеса ротора гироскопа, имеющего постоянную скорость вращения, управляющий момент системы гиродинов на порядки превосходит управляющий момент маховиков. В этом случае набор и гашение угловой скорости во время проведения разворотов КА происходят на порядок быстрее. В результате продолжительность программных разворотов значительно сокращается. Таким образом, использование двухстепенных силовых гироскопов позволяет резко увеличить количество съемок в сеансах наблюдений, по сравнению с системой управления движением, использующей маховики [1], а также обеспечить реализацию требуемых видов съемок.

1. Постановка задачи. При использовании двухстепенных силовых гироскопов следует рассматривать несколько различных режимов управления КА. В случае, когда гиродины на начальном участке полета еще не введены в эксплуатацию или находятся в режиме набора требуемого кинетического момента (раскрутки), управление угловым движением КА ведется с помощью двигателей ориентации. При достижении требуемого кинетического момента всех используемых для управления гиродинов контур управления ориентацией начинает применять их в качестве исполнительных органов, при этом двигатели ориентации отключаются. Также возможно появление различных нештатных ситуаций, таких, как, например, рестарт бортовой цифровой вычислительной машины или нехватка электропитания. При таких ситуациях возможны отключения электропитания приводов главной оси гиродинов, в результате система двухстепенных силовых гироскопов переходит в режим плавного торможения (выбега) и для управления угловым движением также могут быть задействованы двигатели ориентации.

Ввиду особенностей изготовления гиродинов невозможно достичь их идентичных технических характеристик. В связи с этим в процессе набора кинетического момента или в процессе торможения нарастание или уменьшение кинетического момента различных силовых гироскопов происходит неодинаково. Эта неодинаковость ведет к тому, что в режимах их раскрутки и торможения на КА может постоянно действовать возмущающий момент, вызванный неравномерностью изменения кинетического момента различных гиродинов, который необходимо парировать двигателями ориентации. Действие возмущающего момента приводит к значительным расходам топлива двигателями ориентации для стабилизации КА.

Для сокращения расхода топлива предлагается рассмотреть возможность управления угловым движением КА с использованием гиродинов с неполным кинетическим моментом с учетом того, что кинетический момент разных гиродинов может отличаться. Требуется построить законы управления скоростью прецессии гиродинов такой системы, а также показать принципиальную реализуемость такого режима управления.

Предполагается, что, как и в [4], моменты инерции КА вокруг осей x, y, z равны соответственно: 800; 500 и 800 кгм², а для управления угловым движением используются имеющиеся в настоящее время в Российской Федерации двухстепенные силовые гироскопы производства “Научно-исследовательского института командных приборов” с кинетическим моментом 60 Нмс [5]. Максимальная и минимальная угловые скорости прецессии гиродина составляют соответственно 57.3 и 0.0069 град/с. Угол поворота подвеса неограничен и измеряется в диапазоне [0, 2π] . Погрешность выдачи информации об угловом положение подвеса составляет 3′, дискретность измерения кинетического момента – 0.0032 Нмс, диапазон измерений от 0 до 105 Нмс. Информация об угле поворота подвеса гиродина и величине его кинетического момента измеряется контроллером гиродина и отправляется в бортовой компьютер на каждом такте управления. Дополнительно следует отметить, что в режиме набора кинетического момента, для недопущения излишнего энергопотребления системы гиродинов, допускается вращение привода прецессии со скоростью не более 2 град/с, в то время как максимальная скорость вращения привода прецессии составляет 57.3 град/с.

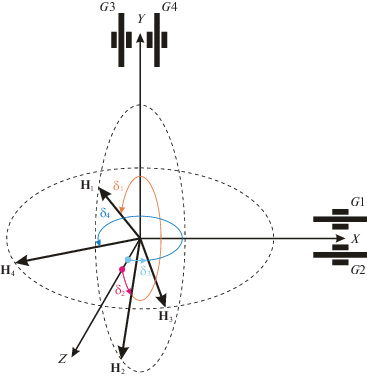
2. Кинематическая схема установки силовых гироскопов. Введем связанную с КА систему координат Oxyz. Считаем, что КА – осесимметричное тело с продольной осью y. Как и в [4], будем считать, что силовые гироскопы расположены попарно параллельно (рис. 1): оси прецессии двух из них (G1 и G2 на рис. 1) параллельны оси Ox КА, а двух других (G3 и G4 на рис. 1) параллельны оси Oy КА. Отсчет углов в векторе прецессии ${\mathbf{\delta }} = {{\left( {{{\delta }_{1}},{{\delta }_{2}},{{\delta }_{3}},{{\delta }_{4}}} \right)}^{{\text{T}}}}$ будем вести от оси Oz. В результате величина кинетического момента такой системы двухстепенных силовых гироскопов будет определяться по формуле

где ${\mathbf{h}} = {{\left( {\begin{array}{*{20}{c}} {{{h}_{1}},}&{{{h}_{2}},}&{{{h}_{3}},}&{{{h}_{4}}} \end{array}} \right)}^{{\text{T}}}}$ – вектор величин кинетического момента силовых гироскопов, по сути, модули векторов кинетических моментов отдельных гиродинов которые будем считать различными. Как видно из (2.1), область вариации кинетического момента $S$ такой системы силовых гироскопов, несмотря на принятые различия кинетических моментов отдельных гиродинов, так же, как и в случае их одинаковости, имеет отчетливо выраженную вытянутую форму вдоль оси z. Размеры $S$ по осям связанной системы координат Ox, Oy, Oz составляют ±$\left( {{{h}_{3}} + {{h}_{4}}} \right)$; ±$\left( {{{h}_{1}} + {{h}_{2}}} \right)$; ±$\left( {{{h}_{1}} + {{h}_{2}} + {{h}_{3}} + {{h}_{4}}} \right)$ соответственно. На рис. 2 изображены проекции $S$ на плоскости Oxy, Oxz и Oyz. Область вариации кинетического момента такой гиросистемы ограничена поверхностью $S{\text{*}}$, на рис. 3 изображена данная поверхность в трехмерном виде.

Как и в [6], будем считать, что контур управления ориентацией КА с гиродинами в качестве основных исполнительных органов состоит из ряда последовательных блоков. Вначале решается задача выделения из измерений угловой скорости, искаженных упругими колебаниями конструкции и шумами измерителей, оценок скорости твердого тела и кинематических параметров управления. Для решения этой задачи служит фильтр упругих колебаний на основе оптимального линейного фильтра Калмана, описанного, например, в [7–9]. На основе этих кинематических параметров проводится расчет требуемого управляющего момента, создаваемого силовыми гироскопами по алгоритмам, рассмотренным в [4, 6]. Далее, для стабилизации упругих колебаний солнечных батарей и корпуса КА требуемый управляющий момент пропускается через фильтр высоких частот. В конечном итоге рассчитанный требуемый управляющий момент распределяется на систему гиродинов.

3. Формирование скоростей прецессии гиродинов. Алгоритмы управления системой, включающей четыре гиродина с попарно параллельными осями прецессии, с одинаковой величиной кинетического момента отдельных гироскопов, приведены в работах [4, 10–12].

Как и в [4, 10, 11], для формирования закона управления рассматривается задача нахождения скоростей прецессии ${{\dot {\delta }}_{i}}$, $i = \overline {1,4} $, при которых система силовых гироскопов реализует требуемый для системы управления движением КА управляющий момент ${{{\mathbf{M}}}_{{req}}}$:

где управляющий момент ${{{\mathbf{M}}}_{{cont}}}$ для системы гироскопов с различной величиной кинетического момента определяется изменением углов прецессии ${{{\mathbf{M}}}_{{cont}}} = - {\mathbf{DG}}\dot {\delta }$, здесь ${\mathbf{D}} = \left( {\begin{array}{*{20}{c}} {{{m}_{1}},}&{{{m}_{2}},}&{...,}&{{{m}_{4}}} \end{array}} \right)$ – матрица Якоби размером 3 × 4, столбцы которой – векторы управляющих моментов m_i = = $(\partial {{{\mathbf{H}}}_{i}}{\text{/}}\partial {{\delta }_{i}}){\text{/}}{{h}_{i}}$, i = $\overline {1{\text{,}}4} $; $\dot {\delta } = {{\left( {{{{\dot {\delta }}}_{1}},{{{\dot {\delta }}}_{2}},...,{{{\dot {\delta }}}_{4}}} \right)}^{{\text{T}}}}$ – вектор скоростей прецессии гиродинов. Для рассматриваемой системы четырех гиродинов с попарно параллельными осями матрица D может быть рассчитана с использованием (2.1) и имеет вид

Матрица G, зависящая от кинетических моментов роторов отдельных гиродинов, может быть представлена следующим образом:

Обозначим через

а также, введя обозначение ${\mathbf{M}}_{{req}}^{*} = {{{\mathbf{M}}}_{{req}}} + \omega \times {\mathbf{H}}$ и учитывая (3.1), получим

Для определения скоростей прецессии, как и в [7, 13], будем минимизировать функцию вида

при условии (3.4). Здесь $\rho \left( {\delta {\text{*}}} \right) \geqslant 0$ – весовая функция, имеющая размерность угловой скорости, суть которой описана в [4] а компоненты 4-мерного вектора f равны где $\Phi $ – функция от углов прецессии гиродинов. Целью выбора критерия (3.5) является, наряду с минимизацией энергопотребления приводов прецессии гиродинов (квадратичный член в (3.5)), также и минимизация функции взаимного расположения векторов кинетических моментов гиродинов (линейный член в (3.5)) с целью избегания попадания в особые ситуации.

Задача минимизации функции (3.5) при условии (3.4) решается методом множителей Лагранжа. Для этого запишем функцию Лагранжа F в виде

где ${\mathbf{\lambda }} = {{\left( {\begin{array}{*{20}{c}} {{{\lambda }_{1}}}&{{{\lambda }_{2}}}&{{{\lambda }_{3}}} \end{array}} \right)}^{{\text{T}}}}$ – вектор множителей Лагранжа. Проведя дифференцирование функции F в (3.7) по $\dot {\delta }$ и $\lambda $, получим следующую систему из семи уравнений с семью неизвестными:

Выразив из (3.8) $\dot {\delta }{\text{*}}$ через ${\mathbf{\lambda }}$ и подставив в (3.9), найдем выражения для коэффициентов Лагранжа:

Подставив получившиеся коэффициенты Лагранжа в (3.8), найдем закон управления скоростями прецессии системы:

где E – единичная матрица.

В результате, с учетом (3.3) закон управления скоростями прецессии может быть определен из (3.11):

Обозначим вторую составляющую вектора скорости прецессии в (3.12) через

Как и в [4], ${{\dot {\delta }}_{P}}$ не создает управляющий момент, а перераспределяет векторы кинетических моментов отдельных гиродинов относительно неизменного суммарного вектора, чтобы избежать попадания гиросистемы в особые точки [14].

В качестве $\Phi $ будем использовать следующую функцию:

где квадрат вектора понимается как скалярный, т.е. ${{{\mathbf{a}}}^{2}} = {{\left| {\mathbf{a}} \right|}^{2}}$.

Закон управления скоростями прецессии дополняется алгоритмами, исключающими вырождение при расчете в (3.12) и (3.13) обратной матрицы ${{({\mathbf{D}}{{{\mathbf{D}}}^{{\text{T}}}})}^{{ - 1}}}$ и ограничивающими скорости прецессии $\dot {\delta }$, приведенными в [4, 11].

В процессе управления осуществляется максимизация управляющего момента, развиваемого системой гиродинов.

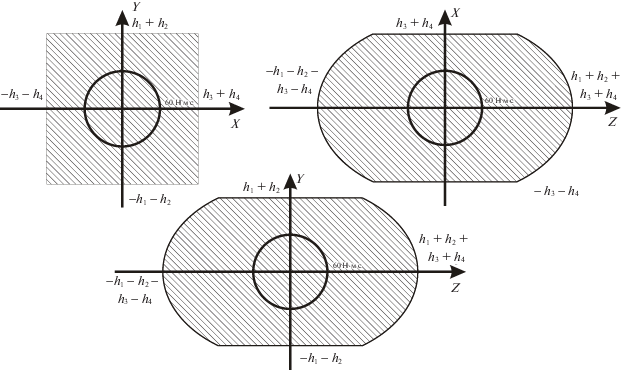
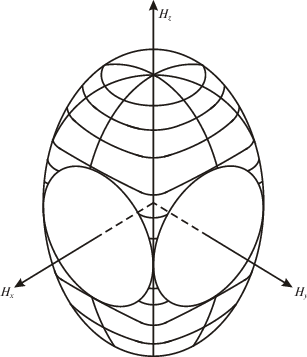
4. Исследование влияния разницы величин кинетического момента отдельных гиродинов на положение особых точек системы. В пространстве вектора H существуют состояния, где ранг матрицы Грама ${\mathbf{D}}{{{\mathbf{D}}}^{{\text{T}}}}$ меньше трех. Такие положения вектора H, в которых происходит частичная потеря управляемости, называются особыми точками. Данные точки могут образовывать целые поверхности внутри области $S$, такие поверхности будем далее называть особыми. Следует отметить, что граница области $S$ также является особой поверхностью. Различают особые точки двух типов – проходимые и непроходимые [14]. Пусть в особой точке гиродины расположены так, что нельзя выдать управляющий момент по нормали к особой поверхности в этой точке n*, тогда возможен случай, когда, перераспределяя векторы кинетических моментов отдельных гиродинов относительно неизменного суммарного вектора H, можно добиться создания управляющего момента по направлению n*. Такая особая точка называется проходимой. В случае если никаким перераспределением векторов кинетических моментов отдельных гиродинов относительно неизменного суммарного вектора H нельзя обеспечить выдачу управляющего момента по одному из двух направлений нормали к поверхности n*, то особая точка называется непроходимой. Очевидно, что $S{\text{*}}$ – непроходимая особая поверхность. Таким образом, для любой гиросистемы всегда существует хотя бы одна непроходимая особая поверхность, являющаяся границей области $S$.

Гиросистемы, включающие попарно параллельные группы гиродинов с равными по величине кинетическими моментами, не содержат непроходимых особых поверхностей [14] внутри области вариации кинетического момента $S$. Напротив, неравенство модулей векторов кинетических моментов отдельных гиродинов приводит к их появлению.

Пусть модули векторов внутри каждой из пар гироскопов G1, G2 и G3, G4 не равны между собой. Положим модули векторов ${{{\mathbf{H}}}_{1}}$–${{{\mathbf{H}}}_{4}}$ равными следующим значениям:

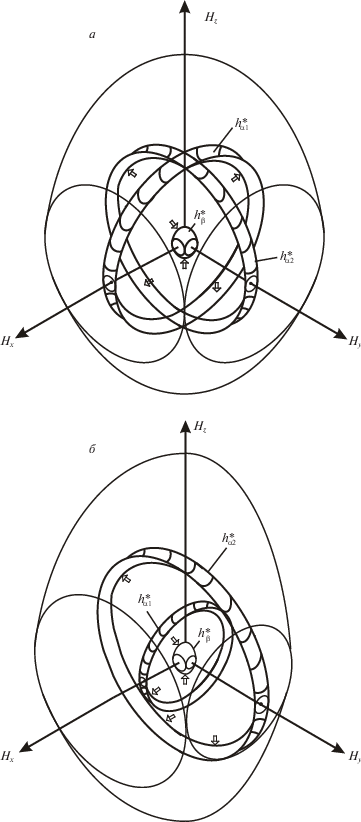
где $\Delta h$ – разница модулей векторов кинетических моментов внутри пар 1, 2 и 3, 4.

В этом случае гиросистема имеет непроходимые особые поверхности внутри области вариации кинетического момента $S$. На рис. 4, а, эти поверхности обозначены через $h_{{\alpha 1}}^{*}$, $h_{{\alpha 2}}^{*}$ и $h_{\beta }^{*}$. На координатных осях отложены безразмерные величины ${{H}_{x}}$, ${{H}_{y}}$, ${{H}_{z}}$.

При этом поверхность $h_{{\alpha 1}}^{*}$ возникает вследствие неравенства модулей векторов кинетических моментов в паре G1, G2, а поверхность $h_{{\alpha 2}}^{*}$ – вследствие неравенства модулей в паре G3, G4. Поверхность $h_{\beta }^{*}$ возникает только в случае неравенства модулей векторов кинетических моментов внутри обеих пар.

В случае если величины кинетических моментов всех гиродинов не равны между собой, то внешний вид области вариации кинетического момента и непроходимых поверхностей $h_{{\alpha 1}}^{*}$, $h_{{\alpha 2}}^{*}$ и $h_{\beta }^{*}$ внутри этой области имеет вид, изображенный на рис. 4, б. Как видно из данного рисунка, область вариации и непроходимая поверхность $h_{\beta }^{*}$ искажаются в соответствии с величинами максимального кинетического момента, который может создать каждая пара. С другой стороны, размеры поверхностей $h_{{\alpha 1}}^{*}$ и $h_{{\alpha 2}}^{*}$ также изменяются в соответствии с величинами кинетических моментов гиродинов.

Значения вектора H, соответствующие непроходимой поверхности $h_{{\alpha 1}}^{*}$, реализуется в пространстве вектора ${\mathbf{\delta }}$ при

Для поверхности $h_{{\alpha 2}}^{*}$ имеем следующие соотношения:

Примером, иллюстрирующим реализацию значений вектора H, соответствующих точкам поверхности $h_{\beta }^{*}$, могут служить, в частности, следующие соотношения:

Поверхности $h_{{\alpha 1}}^{*}$, $h_{{\alpha 2}}^{*}$ и $h_{\beta }^{*}$ непроходимы в направлениях, указанных на рис. 4 стрелками.

Рассмотрим подробно поверхности $h_{{\alpha 1}}^{*}$ и $h_{{\alpha 2}}^{*}$. Каждая из этих поверхностей состоит из двух лепестков, которые можно условно обозначить $h_{{\alpha 1}}^{*}\left( { + z} \right)$ и $h_{{\alpha 1}}^{*}\left( { - z} \right)$ и соответственно $h_{{\alpha 2}}^{*}\left( { + z} \right)$ и $h_{{\alpha 2}}^{*}\left( { - z} \right)$. Данные поверхности являются гладкими продолжениями границы области $S$, ограничивающей ее внутрь. Поверхность $h_{\beta }^{*}$ находится в центре области $S$ и состоит из двух частей, которые обозначим $h_{\beta }^{*}\left( { + z} \right)$ и $h_{\beta }^{*}\left( { - z} \right)$.

Наличие непроходимых особых поверхностей внутри $S$ связано с разбиением множества G реализаций вектора H в пространстве вектора $\delta = {{\left( {{{\delta }_{1}},{{\delta }_{2}},{{\delta }_{2}},{{\delta }_{4}}} \right)}^{{\text{T}}}}$ на изолированные подмножества [15]. Для данной схемы расположения гиродинов при неравенстве модулей их кинетических моментов между собой в определенных частях области $S$ количество изолированных подмножеств равно двум или трем. Соответственно при приближении траектории H(t) в области S к непроходимой поверхности одно из изолированных подмножеств сужается и в момент достижения H(t) этой поверхности вырождается, обращаясь в точку.

Следует заметить, что и после окончания процесса раскрутки гиродинов внутри области S из-за неравенства модулей векторов кинетических моментов гиродинов между собой (в пределах ±0.8% от номинальной величины 60 Нмс) непроходимые особые поверхности будут присутствовать.

5. Алгоритмы обхода непроходимых особых поверхностей. Наличие непроходимых особых поверхностей внутри области $S$ вызывает значительные трудности при управлении данной гиросистемой. Например, при изменении траектории H(t) по оси Oz от начала координат к границам области $S$ нельзя избежать попадания гиросистемы в позиции, соответствующие одной из двух особых поверхностей $h_{{\alpha 1}}^{*}$ или $h_{{\alpha 2}}^{*}$ (какой именно – зависит от начальных положений ${{\delta }_{i}}$, $i = \overline {1,4} $). В случае изменения траектории H(t) по оси Oz в направлении от границ области $S$ к началу координат О гиросистема попадает в положения, соответствующие непроходимой поверхности $h_{\beta }^{*}$. Для преодоления данных поверхностей необходимо совершить в трехмерном пространстве вектора H “обходной маневр”. Так, для преодоления поверхности $h_{{\alpha 1}}^{*}$ следует вывести траекторию H(t) за пределы области ${{Q}_{\alpha }}$, ограниченной поверхностью $h_{{\alpha 1}}^{*}$ и двумя плоскостями, каждая из которых параллельна плоскости Oxz и проходит через точки ${{H}_{y}} = \Delta h$ и ${{H}_{y}} = - \Delta h$ соответственно.

Такой маневр предусматривает обязательную перестройку гироскопической системы, неизбежно приводящую к нарушению равенства ${\mathbf{H}} = {\mathbf{H}}{\text{*}}$, где ${\mathbf{H}}{\text{*}} \in h_{{\alpha 1}}^{*}$. В режиме поддержания ориентации такое вынужденное изменение траектории H(t) приводит к ошибкам ориентации КА при любом законе управления скоростями прецессии.

Обозначим через n нормаль к особой поверхности в точке попадания траектории конца вектора H на данную поверхность. Пусть особая поверхность непроходима в направлении ${\mathbf{n}}$. Если векторы кинетических моментов всех гиродинов имеют положительную проекцию на нормаль, то данная особая поверхность является частью поверхности $S{\text{*}}$, ограничивающей область вариации кинетического момента гиросистемы. Все другие особые поверхности можно получить из данной, изменяя угол прецессии у одного или нескольких гиродинов на π. Поверхности $h_{{\alpha 1}}^{*}$ и $h_{{\alpha 2}}^{*}$ являются гладкими продолжениями поверхности, ограничивающей область вариации внутрь данной области и для них существует один гиродин, вектор кинетического момента которого имеет отрицательную проекцию на нормаль ${\mathbf{n}}$. У трех остальных гиродинов векторы кинетического момента имеют положительные проекции на ${\mathbf{n}}$ (см. (4.1) и (4.2)).

Алгоритм обхода непроходимых особых поверхностей $h_{{\alpha 1}}^{*}$ и $h_{{\alpha 2}}^{*}$ реализуется по следующей логике. О достижении границы непроходимой поверхности можно судить по нахождению конца вектора H в части области $S$, содержащей какой-либо лепесток поверхности $h_{{\alpha i}}^{*}$, $i = 1,2$ (например, для поверхности $h_{{\alpha 1}}^{*}$ часть области, содержащая данную поверхность, определяется по следующим условиям: часть области расположена вне цилиндра с высотой параллельной оси x радиусом $0.85\left( {{{h}_{3}} + {{h}_{4}}} \right)$ и внутри области, ограниченной плоскостями ${{H}_{y}} = 1.2 \cdot \Delta h$ и ${{H}_{y}} = - 1.2 \cdot \Delta h$), и уменьшению детерминанта матрицы Грама $d = {\text{|}}{\mathbf{D}}{{{\mathbf{D}}}^{{\text{T}}}}{\text{|}}$ меньше некоторой малой величины ${{\varepsilon }_{0}}$. После чего определяется гиродин, вектор кинетического момента которого имеет отрицательную проекцию на n. Далее происходит поворот вектора кинетического момента данного гиродина с максимальной угловой скоростью вокруг оси прецессии, чтобы проекция вектора кинетического момента на ${\mathbf{n}}$ стала положительной. Поворот производится в кратчайшем направлении. Поворот заканчивается, когда угол между вектором кинетического момента и нормалью становится менее 45°. При проведении такого маневра данный гиродин исключается из контура управления на время его поворота (для этого достаточно обнулить столбец в матрице D из (3.2), соответствующий данному гиродину). Остальные гиродины, по возможности, компенсируют момент, создаваемый поворачиваемым гиродином.

Для $h_{\beta }^{*}$, согласно (4.3), существуют два гиродина, векторы кинетических моментов которых имеют отрицательные проекции на нормаль ${\mathbf{n}}$ к этой поверхности. Алгоритм обхода непроходимых поверхностей $h_{\beta }^{*}$ строится по такой же логике, как и обход поверхностей $h_{{\alpha i}}^{*}$, $i = 1,2$. При этом поворачивается один из двух гиродинов, векторы кинетических моментов которых имеют отрицательную проекцию на нормаль.

Подобные алгоритмы обхода непроходимых особых поверхностей использовались при управлении ориентацией станции “Мир” в случаях отказов отдельных гиродинов [15].

6. Результаты математического моделирования. Для оценки возможности стабилизации КА при осуществлении раскрутки силовых гироскопов было проведено математическое моделирование. При моделировании использовались штатные бортовые программы контура управления ориентацией. Величина такта управления предполагалась равной 0.2 с. Применялись циклограммы обмена бортового компьютера с моделью датчика угловой скорости и моделью гиродинов, соответствующие протоколам обмена между реальной аппаратурой.

При проведении моделирования в динамической модели КА учитывались упругие тоны колебаний конструкции КА до 10 Гц с максимальными разбросами динамических параметров.

Параметры управления и массово-инерционные характеристики аппарата использовались такие же, как и в [4]. Передаточная функция привода прецессии гиродина, так же как в работе [16], представлялась в виде колебательного звена:

где ${{\omega }_{C}}$ – задаваемая угловая скорость прецессии, $\omega $ – реальная скорость прецессии.

Максимальная допустимая угловая скорость прецессии гиродина в режиме раскрутки составляет 2 град/с, минимальная – 0.0069 град /с. При моделировании считалось, что возможно задание любой скорости в диапазоне от минимальной до максимальной с шагом, равным минимальной скорости. К динамике привода прецессии (6.1) прибавлялась дополнительная ошибка отработки, которая предполагалась равной ±(1%+0.0069 град/с) от заданной скорости. Следует также отметить, что при математическом моделировании учитывались возмущающие моменты, создаваемые приводами главной оси гиродинов в процессе раскрутки и поддержания скоростей вращения роторов.

Одной из основных целей моделирования являлось доказательство возможности стаблилизации КА с использованием рассмотренной системы двухстепенных силовых гироскопов с различной величиной кинетического момента отдельных гиродинов и ограниченными возможностями управления. Моделировался режим стабилизации КА в режиме раскрутки привода главной оси силовых гироскопов, управление угловым движением осуществлялось с помощью этих же гироскопов. Следует отметить, что наибольший интерес при проведении моделирования режимов ориентации КА при неравных кинетических моментах представляют вопросы преодоления непроходимых особых поверхностей. С этой целью в процессе моделирования была выбрана траектория изменения вектора H(t), проходящая через поверхности $h_{\alpha }^{*}$ и $h_{\beta }^{*}$.

Моделирование строилось по следующей схеме: в начальный момент времени ($t = - 100$ с) вектор кинетических моментов ${\mathbf{h}} = {{\left( {\begin{array}{*{20}{c}} {{{h}_{1}},}&{{{h}_{2}},}&{{{h}_{3}},}&{{{h}_{4}}} \end{array}} \right)}^{{\text{T}}}}$ отдельных силовых гироскопов принимает значение: (20, 25, 20, 25) Нмс и его компоненты равномерно увеличиваются со скоростью раскрутки 0.0125 Нм до конечной величины 60 Нмс. Суммарный кинетический момент равен нулю. КА ориентируется в инерциальной – солнечной ориентации [17] с осью $ + y$ на Солнце.

Для того чтобы траектория H(t) гарантированно прошла через поверхности $h_{\alpha }^{*}$ и $h_{\beta }^{*}$, сначала, в момент времени t = 0 с, задается момент возмущающих сил в инерциальной системе координат по оси z, равный ${{M}_{{dist}}} = - 0.1$ Нмс, который действует в течение 1000 с. При действии такого момента суммарный кинетический момент гиросистемы будет изменяться в направлении $ - z$. Траектория H(t) непременно упрется в поверхность $h_{\alpha }^{*}$, после чего гиросистема совершит обходной маневр для ее преодоления. Затем возмущающий момент меняет знак на противоположный (величина момента при этом сохраняется). Действие положительного момента продолжается 1500 с. В этом случае суммарный кинетический момент гиросистемы будет изменяться в направлении +z и траектория H(t) рано или поздно упрется в поверхность $h_{\beta }^{*}$, что потребует реализации обходного маневра для ее преодоления. При моделировании задавалась следующая величина границы детерминанта матрицы Грама, при достижении которой начинается маневр обхода особой поверхности ${{\varepsilon }_{0}} = 0.02$.

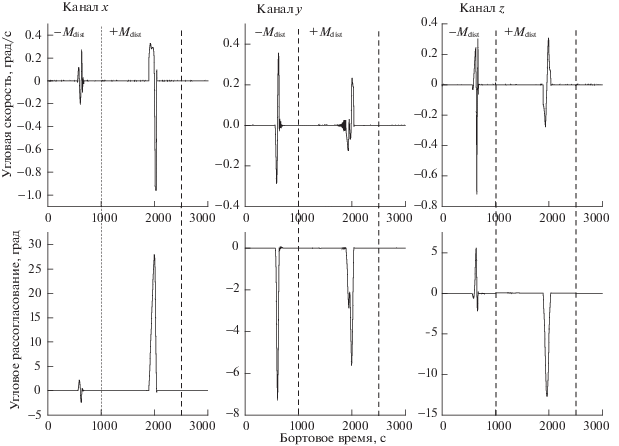
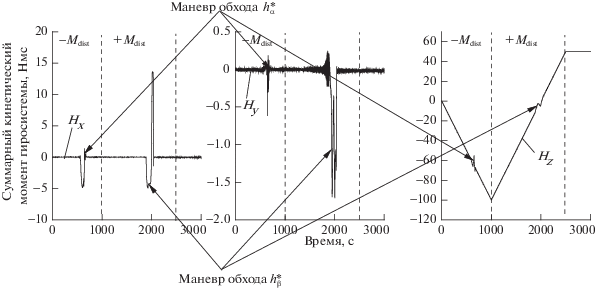
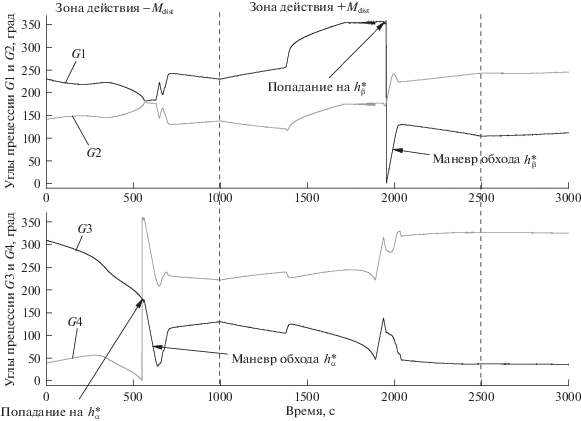
На рис. 5 представлены графики изменений компонент угловой скорости КА относительно требуемой угловой скорости и углов Крылова рассогласования от заданной ориентации при проведении математического моделирования. На рис. 6 рассмотрены графики изменений компонент суммарного кинетического момента гиросистемы, а на рис. 7 – поведение углов прецессии отдельных гиродинов.

На рис. 5–7 видно, что при движении H(t) в направлении $ - z$ на 562 с траектория H(t) натыкается на непроходимую особую поверхность $h_{{\alpha 2}}^{*}\left( { - z} \right)$ и начинается ее обход. При движении H(t) в направлении $ + z$ на 1889 с траектория H(t) соприкасается с непроходимой особой поверхностью $h_{\beta }^{*}\left( { - z} \right)$ и совершается обход этой поверхности. Обход начинается при выполнении условия $d = \left| {{\mathbf{D}}{{{\mathbf{D}}}^{{\text{T}}}}} \right| < {{\varepsilon }_{0}}$. Следует отметить, что максимальная допустимая угловая скорость прецессии гиродинов при нераскрученных роторах составляет 2 град/с, это обстоятельство значительно удлиняет продолжительность поворотов гиродинов. Из графиков на рис. 5 видно, что маневр обхода особых непроходимых поверхностей $h_{{\alpha 1}}^{*}$, $h_{{\alpha 2}}^{*}$ и $h_{\beta }^{*}$ приводит к кратковременному ухудшению ориентации КА, на время не более 120–150 с, что в целом допускается в таком режиме полета. Отклонение оси $ + y$ от направления на Солнце при обходе поверхности $h_{{\alpha 2}}^{*}$ составляет не более 10°, а при обходе поверхности $h_{\beta }^{*}$ – не более 30°.

Примерно к 3300-й с раскрутка всех гиродинов закачивается.

Заключение. Рассмотрен режим управления угловым движением КА с гиродинами в качестве исполнительных органов, которые имеют неполный уровень кинетического момента. Показывается, что при различном уровне кинетического момента отдельных гиродинов внутри области вариации кинетического момента такой гиросистемы возникает ряд непроходимых особых поверхностей. Приводятся алгоритмы обхода этих поверхностей и показывается принципиальная возможность обеспечения стабилизации КА. С помощью результатов математического моделирования демонстрируется способность реализации данным спутником задачи управления угловым движением с использованием гиродинов с различной величиной кинетического момента и иллюстрируется эффективность предложенных алгоритмов.