1. На главную
  2. Электронные версии
  3. Известия РАН. Теория и системы управления
  4. № 2, 2020

Известия РАН. Теория и системы управления, 2020, № 2, стр. 17-26

Управление линейной mimo-системой по вектору измерения с использованием многоуровневой декомпозиции

Н. Е. Зубов a, *, Е. А. Микрин b, В. Н. Рябченко a

a МГТУ им. Н.Э. Баумана
Москва, Россия

b ПАО “РКК “Энергия”
Москва, Россия

* E-mail: nik.zubov@gmail.com

Поступила в редакцию 28.04.2019
После доработки 08.11.2019
Принята к публикации 25.11.2019

Полный текст (PDF)

Аннотация

Разработан вариант метода синтеза управления линейной MIMO-системой по вектору выхода, обеспечивающий заданный спектр многомерной динамической системы в пространстве состояний. В основе лежит принцип дуальности задачи управления MIMO-системой по вектору состояния и задачи построения наблюдателя состояния. Алгоритм без каких-либо изменений применим как для непрерывного, так и для дискретного случаев описания математической модели MIMO-системы, не имеет ограничений по заданию элементов спектра замкнутой MIMO-системы, позволяет получать решения задач синтеза в аналитическом виде и осуществлять параметризацию множества эквивалентных законов управления с обратной связью. Приведен пример аналитического синтеза закона управления гипотетическим летательным аппаратом.

Введение. Задача управления спектром движения (полюсами, собственными значениями) линейной динамической MIMO-системой (multi input multi output) по вектору выхода системы относится в теории систем к разряду классических [1–11], однако до сих пор не имеет исчерпывающего решения и относится к задаче высокого уровня сложности [9]. В данной статье рассматривается метод синтеза закона управления с использованием принципа дуальности задачи управления по вектору состояния и задачи построения наблюдателя состояния по вектору измерения.

1. Декомпозиция динамической системы и подход к синтезу закона управления. Будем рассматривать MIMO-систему следующего вида:

(1.1)
$\sigma x(t) = Ax(t) + Bu(t){\text{,}}\quad y(t) = Cx(t),$
где t – непрерывное $t \in {{\mathbb{R}}_{ + }} = [0, + \infty )$ или дискретное $t \in {{\mathbb{N}}_{0}} = \{ 0,1,2, \ldots \} $ время; $x \in {{\mathbb{R}}^{n}}$ – вектор состояния; $u \in {{\mathbb{R}}^{r}}$ – вектор входа; $y \in {{\mathbb{R}}^{m}}$ – вектор выхода; $\mathbb{R}$ – множество действительных чисел; $m + r > n$; σ – символ оператора дифференцирования $\sigma x(t)\mathop \doteq \limits^. \dot {x}(t)$ или оператора сдвига $\sigma x(t) \doteq x(t + 1)$.

Предполагается, что спектр MIMO-системы (1.1) совпадает с множеством собственных значений матрицы A и равен

${\text{eig}}\left( A \right) = \{ {{\lambda }_{i}} \in \mathbb{C}:\;\det \left( {{{\lambda }_{i}}{{I}_{n}} - A} \right) = 0,\;i = \overline {1,n} \} $,
где In – единичная матрица размера $n \times n$, $\mathbb{C}$ – множество комплексных чисел (комплексная плоскость).

Рассматриваемый здесь метод предполагает выполнение алгоритма, содержащего два шага:

1) многоуровневая декомпозиция динамической системы с помощью техники ортогональных делителей нуля и псевдообратных матриц, т.е. декомпозиции матриц A, B и C (процесс “сверху–вниз”);

2) собственно синтез закона управления с использованием декомпозированных на соответствующих уровнях MIMO-систем, т.е. формировании (“сборки”) матрицы регулятора в законе управления u(t) = –Fy(t) (процесс “снизу–вверх”).

Указанное ранее применение принципа дуальности понимается в том смысле, что синтез закона управления по вектору выхода MIMO-системы (регулятора по выходу) равносилен синтезу наблюдателя Люэнбергера (наблюдателя состояния).

Введем в рассмотрение многоуровневую декомпозицию MIMO-системы (1.1) следующего вида:

нулевой уровень декомпозиции

(1.2)
${{A}_{0}} = A,\quad {{B}_{0}} = B,\quad {{C}_{0}} = C{\text{,}}$

первый уровень декомпозиции

(1.3)
${{A}_{1}} = {{(С_{0}^{{R \bot }})}^{ + }}{{A}_{0}}С_{0}^{{R \bot }},\quad {{B}_{1}} = {{(С_{0}^{{R \bot }})}^{ + }}{{A}_{0}}{{B}_{0}},\quad {{C}_{1}} = {{C}_{0}}{{A}_{0}}С_{0}^{{R \bot }},$

k-й уровень декомпозиции ($1 < k < M$)

(1.4)
${{A}_{k}} = {{(С_{{k - 1}}^{{R \bot }})}^{ + }}{{A}_{{k - 1}}}С_{{k - 1}}^{{R \bot }},\quad {{B}_{k}} = {{(С_{{k - 1}}^{{R \bot }})}^{ + }}{{A}_{{k - 1}}}{{B}_{{k - 1}}},\quad {{C}_{k}} = {{C}_{{k - 1}}}{{A}_{{k - 1}}}С_{{k - 1}}^{{R \bot }},$

M-й уровень декомпозиции

(1.5)
${{A}_{M}} = {{(С_{{M - 1}}^{{R \bot }})}^{ + }}{{A}_{{M - 1}}}С_{{M - 1}}^{{R \bot }},\quad {{B}_{M}} = {{(С_{{M - 1}}^{{R \bot }})}^{ + }}{{A}_{{M - 1}}}{{B}_{{M - 1}}},\quad {{C}_{M}} = {{C}_{{M - 1}}}{{A}_{{M - 1}}}С_{{M - 1}}^{{R \bot }}.$

Здесь $M = {\text{ceil}}(n{\text{/}}m) - 1$, где ${\text{ceil}}\,( * )$ – операция округления числа “$ * $” в сторону большего значения,  т.е. ceil(1.2) = 2, ceil(2.5) = 3 и т.д.; индексом “$R \bot $” обозначен правый делитель нуля [11–17], а индексом “$ + $” – псевдообратные матрицы Мура–Пенроуза [11–17].

Рассмотрим далее собственно синтез закона управления по вектору выхода на основе управления спектром декомпозированных MIMO-систем на соответствующих уровнях (в обратном порядке):

M-й уровень декомпозиции

(1.6)
${{F}_{M}} = B_{M}^{ + }(C_{M}^{ + }{{\Phi }_{M}} - {{A}_{M}}C_{M}^{ + }),$

k-й уровень декомпозиции ($k = \overline {0,М - 1} $)

(1.7)
${{F}_{k}} = B_{k}^{ + }(C_{k}^{ - }{{\Phi }_{k}} - {{A}_{k}}C_{k}^{ - }),\quad C_{k}^{ - } = C_{k}^{ + } - C_{k}^{{R \bot }}B_{k}^{{}}{{F}_{{k + 1}}}.$

Следовательно, первая формула выражения (1.7) при k = 0 представляет собой матрицу коэффициентов обратной связи регулятора по выходу и собственно решение задачи синтеза управления по выходу.

2. Основной теоретический результат. Справедливо утверждение.

Теорема. Пусть следующие матрицы существуют и попарно полностью управляемые:

(2.1)
$G_{M}^{{}} = {{(B_{M}^{ \bot }C_{M}^{ + })}^{ + }}B_{M}^{ \bot }{{A}_{M}}C_{M}^{ + },\quad H_{M}^{{}} = {{(B_{M}^{ \bot }C_{M}^{ + })}^{{R \bot }}},$
(2.2)
$G_{k}^{{}} = {{(B_{k}^{ \bot }C_{k}^{ - })}^{ + }}B_{k}^{ \bot }{{A}_{k}}C_{k}^{ - },\quad H_{k}^{{}} = {{(B_{k}^{ \bot }C_{k}^{ - })}^{{R \bot }}},$
где $\,k = \overline {0,М - 1} $, тогда существует непустое множество матриц Ki, $i = \overline {0,M} $, таких, что
(2.3)
${{\Phi }_{i}} = {{G}_{i}} + {{H}_{i}}K_{i}^{{}} = {{(B_{i}^{ \bot }C_{i}^{ - })}^{ + }}B_{i}^{ \bot }{{A}_{i}}C_{i}^{ - } + {{(B_{i}^{ \bot }C_{i}^{ - })}^{{R \bot }}}K_{i}^{{}},$
и для (1.6), (1.7) соответственно выполняются равенства

(2.4)
${\text{eig}}\left( {{{A}_{M}} + {{B}_{M}}{{F}_{M}}{{C}_{M}}} \right) = {\text{eig(}}{{\Phi }_{M}}{\text{),}}$
(2.5)
${\text{eig}}\left( {{{A}_{k}} + {{B}_{k}}{{F}_{k}}{{C}_{k}}} \right) = \bigcup\limits_{i = k}^M {{\text{eig(}}{{\Phi }_{i}}{\text{)}}} ,\quad (k = \overline {0,М - 1} ),$
(2.6)
${\text{eig}}\left( {{{A}_{0}} + {{B}_{0}}{{F}_{0}}{{C}_{0}}} \right) = {\text{eig}}\left( {A + BFC} \right) = \bigcup\limits_{i = 0}^M {{\text{eig(}}{{\Phi }_{i}}{\text{)}}} \doteq \Lambda .$

Здесь индексом “$\, \bot $” обозначена ортогональная матрица левого делителя нуля [11], а при i = M имеет место равенство $C_{M}^{ - } = C_{M}^{ + }$.

Доказательство теоремы приведено в Приложении.

Как и в материалах, представленных в [12–17], в теореме при преобразованиях используются только ортогональные и псевдообратные матрицы, что позволяет, по крайней мере, не ухудшать обусловленность получаемых уравнений. Приведенный теоретический результат применим как для непрерывного, так и для дискретного случаев описания MIMO-системы (1.1), не имеет ограничений по заданию элементов спектра замкнутой MIMO-системы, позволяет получать решения задачи синтеза в аналитическом виде и осуществлять параметризацию множества эквивалентных законов управления с обратной связью. Это подтверждается, в том числе, математическим моделированием, результаты которого демонстрируют высокую точность управления спектром и практическое отсутствие ограничений на размерность MIMO-системы (1.1).

3. Аналитический синтез управления стабилизацией бокового движения маневренного летательного аппарата. Рассмотрим задачу управления движением маневренного летательного аппарата (ЛА) в горизонтальной плоскости (боковой канал движения и управления). В качестве органов управления будем использовать элероны, руль направления, переднее вертикальное оперение и отклоняемый вектор тяги двигателя. В этом случае линеаризованные уравнения бокового канала в отклонениях в соответствии с [18, 19] будут иметь вид

(3.1)
$\left[ {\begin{array}{*{20}{c}} {\dot {\beta }} \\ {{{{\dot {\omega }}}_{x}}} \\ {{{{\dot {\omega }}}_{y}}} \\ {\dot {\gamma }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{a}_{{11}}}}&{{{a}_{{12}}}}&{{{a}_{{13}}}}&{{{a}_{{14}}}} \\ {{{a}_{{21}}}}&{{{a}_{{22}}}}&{{{a}_{{23}}}}&0 \\ {{{a}_{{31}}}}&{{{a}_{{32}}}}&{{{a}_{{33}}}}&0 \\ 0&1&{{{a}_{{43}}}}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \beta \\ {{{\omega }_{x}}} \\ {{{\omega }_{y}}} \\ \gamma \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{{b}_{{11}}}}&0&{{{b}_{{13}}}}&0 \\ {{{b}_{{21}}}}&{{{b}_{{22}}}}&{{{b}_{{23}}}}&{{{b}_{{24}}}} \\ {{{b}_{{31}}}}&{{{b}_{{32}}}}&{{{b}_{{33}}}}&{{{b}_{{34}}}} \\ 0&0&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\delta }_{э}}} \\ {{{\delta }_{{\text{н}}}}} \\ {{{\delta }_{{{\text{ОВТ}}}}}} \\ {{{\delta }_{{{\text{п}}{\text{.о}}}}}} \end{array}} \right]$.

Здесь $\beta $ – угол скольжения; ${{\omega }_{x}}$ – угловая скорость крена; ${{\omega }_{y}}$ – угловая скорость рыскания; $\gamma $ – угол крена; ${{\alpha }_{0}}$ – угол атаки; ${{\vartheta }_{0}}$ – угол тангажа; ${{\delta }_{{\text{н}}}}$ – угол отклонения рулей направления; ${{\delta }_{э}}$ – угол отклонения элеронов; ${{\delta }_{{{\text{ОВТ}}}}}$ – угол отклонения вектора тяги; ${{\delta }_{{{\text{п}}{\text{.о}}}}}$ – угол отклонения переднего вертикального оперения; ${{a}_{{ij}}}$, ${{b}_{{ij}}}$ – коэффициенты линеаризации [19, 20].

Как видно, особенностью модели (3.1) является неполнота ранга матрицы управления, обусловленное “избыточностью” органов управления в боковой плоскости

В обозначениях (1.1) матрицы А и В с учетом (3.1) запишутся так:

(3.2)
$A = \left[ {\begin{array}{*{20}{c}} {{{a}_{{11}}}}&{{{a}_{{12}}}}&{{{a}_{{13}}}}&{{{a}_{{14}}}} \\ {{{a}_{{21}}}}&{{{a}_{{22}}}}&{{{a}_{{23}}}}&0 \\ {{{a}_{{31}}}}&{{{a}_{{32}}}}&{{{a}_{{33}}}}&0 \\ 0&1&{{{a}_{{43}}}}&0 \end{array}} \right],\quad B = \left[ {\begin{array}{*{20}{c}} {{{b}_{{11}}}}&0&{{{b}_{{13}}}}&0 \\ {{{b}_{{21}}}}&{{{b}_{{22}}}}&{{{b}_{{23}}}}&{{{b}_{{24}}}} \\ {{{b}_{{31}}}}&{{{b}_{{32}}}}&{{{b}_{{33}}}}&{{{b}_{{34}}}} \\ 0&0&0&0 \end{array}} \right].$

Зададим матрицу выхода следующим образом:

(3.3)
$C = \left[ {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&0&0&1 \end{array}} \right],$
что соответствует отсутствию информации об угловых скоростях движения ЛА.

Пусть требуется найти в явном виде формулу закона управления (регулятора), обеспечивающего замкнутой системе “ЛА + система управления” следующий (вообще говоря, произвольный) спектр:

(3.4)
$\Lambda = \{ {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }_{1}},{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }_{2}},{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }_{3}},{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }_{4}}\} \subset \mathbb{C}.$

Следует заметить, что аналитическое решение указанной задачи синтеза нельзя получить ранее опубликованными авторами методами в силу неполноты ранга матрицы $B$ (3.2).

Для системы (1.1) с матрицами (3.2), (3.3) рассмотрим многоуровневую декомпозицию, определенную в разд. 1, имеющую в данном случае два уровня декомпозиции: нулевой (1.2) и первый (1.3), для которых

(3.5)
$B_{0}^{ \bot } = \left[ {\begin{array}{*{20}{c}} 0&0&0&1 \end{array}} \right],\quad {{C}^{{R \bot }}} = \left[ {\begin{array}{*{20}{c}} 0&0 \\ 0&{ - 1} \\ 1&0 \\ 0&0 \end{array}} \right],\quad B_{0}^{ + } = \left[ {\begin{array}{*{20}{c}} {b_{{11}}^{ + }}&{b_{{12}}^{ + }}&{b_{{13}}^{ + }}&{b_{{14}}^{ + }} \\ {b_{{21}}^{ + }}&{b_{{22}}^{ + }}&{b_{{23}}^{ + }}&{b_{{24}}^{ + }} \\ {b_{{31}}^{ + }}&{b_{{32}}^{ + }}&{b_{{33}}^{ + }}&{b_{{34}}^{ + }} \\ {b_{{41}}^{ + }}&{b_{{42}}^{ + }}&{b_{{43}}^{ + }}&{b_{{44}}^{ + }} \end{array}} \right],\quad {{C}_{p}} = \left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&0 \\ 0&0 \\ 0&1 \end{array}} \right],$
${{({{C}^{{R \bot }}})}^{ + }} = \left[ {\begin{array}{*{20}{c}} 0&0&1&0 \\ 0&{ - 1}&0&0 \end{array}} \right]{\text{,}}\quad {{A}_{1}} = \left[ {\begin{array}{*{20}{c}} {{{a}_{{33}}}}&{ - {{a}_{{32}}}} \\ { - {{a}_{{23}}}}&{{{a}_{{22}}}} \end{array}} \right],\quad {{B}_{1}} = \left[ {\begin{array}{*{20}{c}} {b_{{11}}^{1}}&{b_{{12}}^{1}}&{b_{{13}}^{1}}&{b_{{14}}^{1}} \\ {b_{{21}}^{1}}&{b_{{22}}^{1}}&{b_{{23}}^{1}}&{b_{{24}}^{1}} \end{array}} \right],$
${{C}_{1}} = \left[ {\begin{array}{*{20}{c}} {{{a}_{{13}}}}&{ - {{a}_{{12}}}} \\ {{{a}_{{43}}}}&{ - 1} \end{array}} \right].$

Здесь элементы матрицы $B_{0}^{ + }$ из (3.5) в силу неполноты ее ранга вычислены в соответствии с [1] на основании следующей оригинальной формулы псевдообратной матрицы [21]:

$B_{0}^{ + } = {{[B_{0}^{{}} + {{(B_{0}^{{R \bot }}B_{0}^{ \bot })}^{{\text{т}}}}]}^{{ - 1}}} - B_{0}^{{R \bot }}B_{0}^{ \bot }$
и в силу их громоздкости здесь не приводятся. При этом компоненты матрицы ${{B}_{1}}$ равны:

$\begin{gathered} b_{{11}}^{1} = {{a}_{{31}}}{{b}_{{11}}} + {{a}_{{32}}}{{b}_{{21}}} + {{a}_{{33}}}{{b}_{{31}}},\quad b_{{12}}^{1} = {{a}_{{32}}}{{b}_{{22}}} + {{a}_{{33}}}{{b}_{{32}}},\quad b_{{13}}^{1} = {{a}_{{31}}}{{b}_{{13}}} + {{a}_{{32}}}{{b}_{{23}}} + {{a}_{{33}}}{{b}_{{33}}},\, \\ b_{{14}}^{1} = {{a}_{{32}}}{{b}_{{24}}} + {{a}_{{33}}}{{b}_{{34}}},\quad b_{{21}}^{1} = - {{a}_{{21}}}{{b}_{{11}}} - {{a}_{{22}}}{{b}_{{21}}} - {{a}_{{23}}}{{b}_{{31}}},\quad b_{{22}}^{1} = - {{a}_{{22}}}{{b}_{{22}}} - {{a}_{{23}}}{{b}_{{32}}}, \\ b_{{23}}^{1} = - {{a}_{{21}}}{{b}_{{13}}} - {{a}_{{22}}}{{b}_{{23}}} - {{a}_{{23}}}{{b}_{{33}}},\quad b_{{24}}^{1} = - {{a}_{{22}}}{{b}_{{24}}} - {{a}_{{23}}}{{b}_{{34}}}. \\ \end{gathered} $

Для проверки условий управляемости на первом уровне декомпозиции, определенных в теореме, вычислим следующие матрицы:

$C_{1}^{ + } = \frac{1}{{{{a}_{{13}}} - {{a}_{{12}}}{{a}_{{43}}}}}\left[ {\begin{array}{*{20}{c}} 1&{ - {{a}_{{12}}}} \\ {{{a}_{{43}}}}&{ - {{a}_{{13}}}} \end{array}} \right],\quad B_{1}^{ \bot } = \left[ {\begin{array}{*{20}{c}} 0&0 \end{array}} \right],$
(3.6)
$H_{1}^{{}} = {{(B_{1}^{ \bot }C_{1}^{ + })}^{{R \bot }}} = I_{2}^{{}},\quad H_{1}^{ + } = I_{2}^{{}},$
${{G}_{1}} = {{(B_{1}^{ \bot }C_{1}^{ + })}^{ + }}B_{1}^{ \bot }{{A}_{1}}C_{1}^{ - } = \left[ {\begin{array}{*{20}{c}} 0&0 \\ 0&0 \end{array}} \right].$

Вычислим для первого уровня декомпозиции ранг следующей блочной матрицы:

${\text{rank}}[\begin{array}{*{20}{c}} {H_{1}^{{}}}&{{{G}_{1}}H_{1}^{{}}} \end{array}] = 2,$
что совпадает с числом измеряемых компонент вектора состояния m = 2. Следовательно, первый уровень удовлетворяет критерию управляемости, определенному в теореме.

Далее в соответствии с введенной формой регулятора (1.6), (1.7) зададим матрицу, собственные значения которой будут “приписаны” MIMO-системе на первом уровне декомпозиции. В силу очевидной обратимости матриц (3.6) для первого уровня декомпозиции мы вправе выбрать любую матрицу ${{{\text{Ф}}}_{1}}$, обладающую заданным спектром. Для простоты положим

${{{\text{Ф}}}_{1}} = \left[ {\begin{array}{*{20}{c}} {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{1}}}&0 \\ 0&{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{2}}} \end{array}} \right]$
и вычислим псевдообратную матрицу
$B_{1}^{ + } = \left[ {\begin{array}{*{20}{c}} {b_{{11}}^{{1 + }}}&{b_{{12}}^{{1 + }}} \\ {b_{{21}}^{{1 + }}}&{b_{{22}}^{{1 + }}} \\ {b_{{31}}^{{1 + }}}&{b_{{32}}^{{1 + }}} \\ {b_{{41}}^{{1 + }}}&{b_{{42}}^{{1 + }}} \end{array}} \right],$
где при условии, что
$\begin{gathered} \Delta = {{(b_{{11}}^{1})}^{2}}{{(b_{{22}}^{1})}^{2}} + {{(b_{{11}}^{1})}^{2}}{{(b_{{23}}^{1})}^{2}} + {{(b_{{11}}^{1})}^{2}}{{(b_{{24}}^{1})}^{2}} - 2b_{{11}}^{1}b_{{12}}^{1}b_{{21}}^{1}b_{{22}}^{1} - 2b_{{11}}^{1}b_{{13}}^{1}b_{{21}}^{1}b_{{23}}^{1} - 2b_{{11}}^{1}b_{{14}}^{1}b_{{21}}^{1}b_{{24}}^{1} + \\ + \;{{(b_{{12}}^{1})}^{2}}{{(b_{{21}}^{1})}^{2}} + {{(b_{{12}}^{1})}^{2}}{{(b_{{23}}^{1})}^{2}} + {{(b_{{12}}^{1})}^{2}}{{(b_{{24}}^{1})}^{2}} - 2b_{{12}}^{1}b_{{13}}^{1}b_{{22}}^{1}b_{{23}}^{1} - 2b_{{12}}^{1}b_{{14}}^{1}b_{{22}}^{1}b_{{24}}^{1} + {{(b_{{13}}^{1})}^{2}}{{(b_{{21}}^{1})}^{2}} + \\ + \;{{(b_{{13}}^{1})}^{2}}{{(b_{{22}}^{1})}^{2}} + {{(b_{{13}}^{1})}^{2}}{{(b_{{24}}^{1})}^{2}} - 2b_{{13}}^{1}b_{{14}}^{1}b_{{23}}^{1}b_{{24}}^{1} + {{(b_{{14}}^{1})}^{2}}{{(b_{{21}}^{1})}^{2}} + {{(b_{{14}}^{1})}^{2}}{{(b_{{22}}^{1})}^{2}} + {{(b_{{14}}^{1})}^{2}}{{(b_{{23}}^{1})}^{2}} \ne 0, \\ \end{gathered} $
обозначены

$\begin{gathered} b_{{11}}^{{1 + }} = {{[b_{{11}}^{1}{{{(b_{{22}}^{1})}}^{2}} - b_{{12}}^{1}b_{{21}}^{1}b_{{22}}^{1} + b_{{11}}^{1}{{{(b_{{23}}^{1})}}^{2}} - b_{{13}}^{1}b_{{21}}^{1}b_{{23}}^{1} + b_{{11}}^{1}{{{(b_{{24}}^{1})}}^{2}} - b_{{14}}^{1}b_{{21}}^{1}b_{{24}}^{1}]} \mathord{\left/ {\vphantom {{[b_{{11}}^{1}{{{(b_{{22}}^{1})}}^{2}} - b_{{12}}^{1}b_{{21}}^{1}b_{{22}}^{1} + b_{{11}}^{1}{{{(b_{{23}}^{1})}}^{2}} - b_{{13}}^{1}b_{{21}}^{1}b_{{23}}^{1} + b_{{11}}^{1}{{{(b_{{24}}^{1})}}^{2}} - b_{{14}}^{1}b_{{21}}^{1}b_{{24}}^{1}]} \Delta }} \right. \kern-0em} \Delta }, \\ b_{{12}}^{{1 + }} = {{[b_{{21}}^{1}{{{(b_{{12}}^{1})}}^{2}} - b_{{11}}^{1}b_{{22}}^{1}b_{{12}}^{1} + b_{{21}}^{1}{{{(b_{{13}}^{1})}}^{2}} - b_{{11}}^{1}b_{{23}}^{1}b_{{13}}^{1} + b_{{21}}^{1}{{{(b_{{14}}^{1})}}^{2}} - b_{{11}}^{1}b_{{24}}^{1}b_{{14}}^{1}]} \mathord{\left/ {\vphantom {{[b_{{21}}^{1}{{{(b_{{12}}^{1})}}^{2}} - b_{{11}}^{1}b_{{22}}^{1}b_{{12}}^{1} + b_{{21}}^{1}{{{(b_{{13}}^{1})}}^{2}} - b_{{11}}^{1}b_{{23}}^{1}b_{{13}}^{1} + b_{{21}}^{1}{{{(b_{{14}}^{1})}}^{2}} - b_{{11}}^{1}b_{{24}}^{1}b_{{14}}^{1}]} \Delta }} \right. \kern-0em} \Delta }, \\ b_{{21}}^{{1 + }} = {{[b_{{12}}^{1}{{{(b_{{21}}^{1})}}^{2}} - b_{{11}}^{1}b_{{22}}^{1}b_{{21}}^{1} + b_{{12}}^{1}{{{(b_{{23}}^{1})}}^{2}} - b_{{13}}^{1}b_{{22}}^{1}b_{{23}}^{1} + b_{{12}}^{1}{{{(b_{{24}}^{1})}}^{2}} - b_{{14}}^{1}b_{{22}}^{1}b_{{24}}^{1}]} \mathord{\left/ {\vphantom {{[b_{{12}}^{1}{{{(b_{{21}}^{1})}}^{2}} - b_{{11}}^{1}b_{{22}}^{1}b_{{21}}^{1} + b_{{12}}^{1}{{{(b_{{23}}^{1})}}^{2}} - b_{{13}}^{1}b_{{22}}^{1}b_{{23}}^{1} + b_{{12}}^{1}{{{(b_{{24}}^{1})}}^{2}} - b_{{14}}^{1}b_{{22}}^{1}b_{{24}}^{1}]} \Delta }} \right. \kern-0em} \Delta }, \\ b_{{22}}^{{1 + }} = {{[b_{{22}}^{1}{{{(b_{{11}}^{1})}}^{2}} - b_{{12}}^{1}b_{{21}}^{1}b_{{11}}^{1} + b_{{22}}^{1}{{{(b_{{13}}^{1})}}^{2}} - b_{{12}}^{1}b_{{21}}^{1}b_{{23}}^{1} + b_{{22}}^{1}{{{(b_{{14}}^{1})}}^{2}} - b_{{12}}^{1}b_{{24}}^{1}b_{{14}}^{1}]} \mathord{\left/ {\vphantom {{[b_{{22}}^{1}{{{(b_{{11}}^{1})}}^{2}} - b_{{12}}^{1}b_{{21}}^{1}b_{{11}}^{1} + b_{{22}}^{1}{{{(b_{{13}}^{1})}}^{2}} - b_{{12}}^{1}b_{{21}}^{1}b_{{23}}^{1} + b_{{22}}^{1}{{{(b_{{14}}^{1})}}^{2}} - b_{{12}}^{1}b_{{24}}^{1}b_{{14}}^{1}]} \Delta }} \right. \kern-0em} \Delta }, \\ \end{gathered} $
$\begin{gathered} b_{{31}}^{{1 + }} = {{[b_{{13}}^{1}{{{(b_{{21}}^{1})}}^{2}} - b_{{11}}^{1}b_{{23}}^{1}b_{{21}}^{1} + b_{{13}}^{1}{{{(b_{{22}}^{1})}}^{2}} - b_{{12}}^{1}b_{{23}}^{1}b_{{22}}^{1} + b_{{13}}^{1}{{{(b_{{24}}^{1})}}^{2}} - b_{{14}}^{1}b_{{23}}^{1}b_{{24}}^{1}]} \mathord{\left/ {\vphantom {{[b_{{13}}^{1}{{{(b_{{21}}^{1})}}^{2}} - b_{{11}}^{1}b_{{23}}^{1}b_{{21}}^{1} + b_{{13}}^{1}{{{(b_{{22}}^{1})}}^{2}} - b_{{12}}^{1}b_{{23}}^{1}b_{{22}}^{1} + b_{{13}}^{1}{{{(b_{{24}}^{1})}}^{2}} - b_{{14}}^{1}b_{{23}}^{1}b_{{24}}^{1}]} \Delta }} \right. \kern-0em} \Delta }, \\ b_{{32}}^{{1 + }} = {{[b_{{23}}^{1}{{{(b_{{11}}^{1})}}^{2}} - b_{{13}}^{1}b_{{21}}^{1}b_{{11}}^{1} + b_{{23}}^{1}{{{(b_{{12}}^{1})}}^{2}} - b_{{13}}^{1}b_{{22}}^{1}b_{{12}}^{1} + b_{{23}}^{1}{{{(b_{{14}}^{1})}}^{2}} - b_{{13}}^{1}b_{{24}}^{1}b_{{14}}^{1}]} \mathord{\left/ {\vphantom {{[b_{{23}}^{1}{{{(b_{{11}}^{1})}}^{2}} - b_{{13}}^{1}b_{{21}}^{1}b_{{11}}^{1} + b_{{23}}^{1}{{{(b_{{12}}^{1})}}^{2}} - b_{{13}}^{1}b_{{22}}^{1}b_{{12}}^{1} + b_{{23}}^{1}{{{(b_{{14}}^{1})}}^{2}} - b_{{13}}^{1}b_{{24}}^{1}b_{{14}}^{1}]} \Delta }} \right. \kern-0em} \Delta }, \\ b_{{41}}^{{1 + }} = {{[b_{{14}}^{1}{{{(b_{{21}}^{1})}}^{2}} - b_{{11}}^{1}b_{{24}}^{1}b_{{21}}^{1} + b_{{14}}^{1}{{{(b_{{22}}^{1})}}^{2}} - b_{{12}}^{1}b_{{24}}^{1}b_{{22}}^{1} + b_{{14}}^{1}{{{(b_{{23}}^{1})}}^{2}} - b_{{13}}^{1}b_{{24}}^{1}b_{{23}}^{1}]} \mathord{\left/ {\vphantom {{[b_{{14}}^{1}{{{(b_{{21}}^{1})}}^{2}} - b_{{11}}^{1}b_{{24}}^{1}b_{{21}}^{1} + b_{{14}}^{1}{{{(b_{{22}}^{1})}}^{2}} - b_{{12}}^{1}b_{{24}}^{1}b_{{22}}^{1} + b_{{14}}^{1}{{{(b_{{23}}^{1})}}^{2}} - b_{{13}}^{1}b_{{24}}^{1}b_{{23}}^{1}]} \Delta }} \right. \kern-0em} \Delta }, \\ b_{{42}}^{{1 + }} = {{[b_{{24}}^{1}{{{(b_{{11}}^{1})}}^{2}} - b_{{14}}^{1}b_{{21}}^{1}b_{{11}}^{1} + b_{{24}}^{1}{{{(b_{{12}}^{1})}}^{2}} - b_{{14}}^{1}b_{{22}}^{1}b_{{12}}^{1} + b_{{24}}^{1}{{{(b_{{13}}^{1})}}^{2}} - b_{{14}}^{1}b_{{23}}^{1}b_{{13}}^{1}]} \mathord{\left/ {\vphantom {{[b_{{24}}^{1}{{{(b_{{11}}^{1})}}^{2}} - b_{{14}}^{1}b_{{21}}^{1}b_{{11}}^{1} + b_{{24}}^{1}{{{(b_{{12}}^{1})}}^{2}} - b_{{14}}^{1}b_{{22}}^{1}b_{{12}}^{1} + b_{{24}}^{1}{{{(b_{{13}}^{1})}}^{2}} - b_{{14}}^{1}b_{{23}}^{1}b_{{13}}^{1}]} \Delta }} \right. \kern-0em} \Delta }. \\ \end{gathered} $

На основании формулы (1.7) при k = 1 для первого уровня будем иметь

${{F}_{1}} = B_{1}^{ + }(C_{1}^{ - }{{\Phi }_{1}} - {{A}_{1}}C_{1}^{ + }) = \left[ {\begin{array}{*{20}{c}} {f_{{11}}^{1}}&{f_{{12}}^{1}} \\ {f_{{21}}^{1}}&{f_{{22}}^{1}} \\ {f_{{31}}^{1}}&{f_{{32}}^{1}} \\ {f_{{41}}^{1}}&{f_{{42}}^{1}} \end{array}} \right],$
где

$\begin{gathered} f_{{11}}^{1} = {{(a_{{23}}^{{}}b_{{12}}^{{1 + }} - {{a}_{{33}}}b_{{11}}^{{1 + }} + b_{{11}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{1}} - {{a}_{{22}}}{{a}_{{43}}}b_{{12}}^{{1 + }} + {{a}_{{32}}}{{a}_{{43}}}b_{{11}}^{{1 + }} + {{a}_{{43}}}b_{{12}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{1}})} \mathord{\left/ {\vphantom {{(a_{{23}}^{{}}b_{{12}}^{{1 + }} - {{a}_{{33}}}b_{{11}}^{{1 + }} + b_{{11}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{1}} - {{a}_{{22}}}{{a}_{{43}}}b_{{12}}^{{1 + }} + {{a}_{{32}}}{{a}_{{43}}}b_{{11}}^{{1 + }} + {{a}_{{43}}}b_{{12}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{1}})} {\left( {{{a}_{{13}}} - {{a}_{{12}}}{{a}_{{43}}}} \right)}}} \right. \kern-0em} {\left( {{{a}_{{13}}} - {{a}_{{12}}}{{a}_{{43}}}} \right)}}, \\ f_{{12}}^{1} = - {{(a_{{12}}^{{}}{{a}_{{23}}}b_{{12}}^{{1 + }} - {{a}_{{13}}}{{a}_{{22}}}b_{{12}}^{{1 + }} - {{a}_{{12}}}{{a}_{{33}}}b_{{11}}^{{1 + }} + {{a}_{{13}}}{{a}_{{32}}}b_{{11}}^{{1 + }} + {{a}_{{12}}}b_{{11}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{2}} + {{a}_{{13}}}b_{{12}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{2}})} \mathord{\left/ {\vphantom {{(a_{{12}}^{{}}{{a}_{{23}}}b_{{12}}^{{1 + }} - {{a}_{{13}}}{{a}_{{22}}}b_{{12}}^{{1 + }} - {{a}_{{12}}}{{a}_{{33}}}b_{{11}}^{{1 + }} + {{a}_{{13}}}{{a}_{{32}}}b_{{11}}^{{1 + }} + {{a}_{{12}}}b_{{11}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{2}} + {{a}_{{13}}}b_{{12}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{2}})} {\left( {{{a}_{{13}}} - {{a}_{{12}}}{{a}_{{43}}}} \right)}}} \right. \kern-0em} {\left( {{{a}_{{13}}} - {{a}_{{12}}}{{a}_{{43}}}} \right)}}, \\ \end{gathered} $
$\begin{gathered} f_{{21}}^{1} = {{(a_{{23}}^{{}}b_{{22}}^{{1 + }} - {{a}_{{33}}}b_{{21}}^{{1 + }} + b_{{21}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{1}} - {{a}_{{22}}}{{a}_{{43}}}b_{{22}}^{{1 + }} + {{a}_{{32}}}{{a}_{{43}}}b_{{21}}^{{1 + }} + {{a}_{{43}}}b_{{22}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{1}})} \mathord{\left/ {\vphantom {{(a_{{23}}^{{}}b_{{22}}^{{1 + }} - {{a}_{{33}}}b_{{21}}^{{1 + }} + b_{{21}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{1}} - {{a}_{{22}}}{{a}_{{43}}}b_{{22}}^{{1 + }} + {{a}_{{32}}}{{a}_{{43}}}b_{{21}}^{{1 + }} + {{a}_{{43}}}b_{{22}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{1}})} {\left( {{{a}_{{13}}} - {{a}_{{12}}}{{a}_{{43}}}} \right)}}} \right. \kern-0em} {\left( {{{a}_{{13}}} - {{a}_{{12}}}{{a}_{{43}}}} \right)}}, \\ f_{{22}}^{1} = - {{(a_{{12}}^{{}}{{a}_{{23}}}b_{{22}}^{{1 + }} - {{a}_{{13}}}{{a}_{{22}}}b_{{22}}^{{1 + }} - {{a}_{{12}}}{{a}_{{33}}}b_{{21}}^{{1 + }} + {{a}_{{13}}}{{a}_{{32}}}b_{{21}}^{{1 + }} + {{a}_{{12}}}b_{{21}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{2}} + {{a}_{{13}}}b_{{22}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{2}})} \mathord{\left/ {\vphantom {{(a_{{12}}^{{}}{{a}_{{23}}}b_{{22}}^{{1 + }} - {{a}_{{13}}}{{a}_{{22}}}b_{{22}}^{{1 + }} - {{a}_{{12}}}{{a}_{{33}}}b_{{21}}^{{1 + }} + {{a}_{{13}}}{{a}_{{32}}}b_{{21}}^{{1 + }} + {{a}_{{12}}}b_{{21}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{2}} + {{a}_{{13}}}b_{{22}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{2}})} {{{a}_{{13}}} - {{a}_{{12}}}{{a}_{{43}}}}}} \right. \kern-0em} {{{a}_{{13}}} - {{a}_{{12}}}{{a}_{{43}}}}}, \\ \end{gathered} $
$\begin{gathered} f_{{31}}^{1} = {{(a_{{23}}^{{}}b_{{32}}^{{1 + }} - {{a}_{{33}}}b_{{31}}^{{1 + }} + b_{{31}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{1}} - {{a}_{{22}}}{{a}_{{43}}}b_{{32}}^{{1 + }} + {{a}_{{32}}}{{a}_{{43}}}b_{{31}}^{{1 + }} + {{a}_{{43}}}b_{{32}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{1}})} \mathord{\left/ {\vphantom {{(a_{{23}}^{{}}b_{{32}}^{{1 + }} - {{a}_{{33}}}b_{{31}}^{{1 + }} + b_{{31}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{1}} - {{a}_{{22}}}{{a}_{{43}}}b_{{32}}^{{1 + }} + {{a}_{{32}}}{{a}_{{43}}}b_{{31}}^{{1 + }} + {{a}_{{43}}}b_{{32}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{1}})} {\left( {{{a}_{{13}}} - {{a}_{{12}}}{{a}_{{43}}}} \right)}}} \right. \kern-0em} {\left( {{{a}_{{13}}} - {{a}_{{12}}}{{a}_{{43}}}} \right)}}, \\ f_{{32}}^{1} = - {{(a_{{12}}^{{}}{{a}_{{23}}}b_{{32}}^{{1 + }} - {{a}_{{13}}}{{a}_{{22}}}b_{{32}}^{{1 + }} - {{a}_{{12}}}{{a}_{{33}}}b_{{31}}^{{1 + }} + {{a}_{{13}}}{{a}_{{32}}}b_{{31}}^{{1 + }} + {{a}_{{12}}}b_{{31}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{2}} + {{a}_{{13}}}b_{{32}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{2}})} \mathord{\left/ {\vphantom {{(a_{{12}}^{{}}{{a}_{{23}}}b_{{32}}^{{1 + }} - {{a}_{{13}}}{{a}_{{22}}}b_{{32}}^{{1 + }} - {{a}_{{12}}}{{a}_{{33}}}b_{{31}}^{{1 + }} + {{a}_{{13}}}{{a}_{{32}}}b_{{31}}^{{1 + }} + {{a}_{{12}}}b_{{31}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{2}} + {{a}_{{13}}}b_{{32}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{2}})} {\left( {{{a}_{{13}}} - {{a}_{{12}}}{{a}_{{43}}}} \right)}}} \right. \kern-0em} {\left( {{{a}_{{13}}} - {{a}_{{12}}}{{a}_{{43}}}} \right)}}, \\ \end{gathered} $
$\begin{gathered} f_{{41}}^{1} = {{(a_{{23}}^{{}}b_{{42}}^{{1 + }} - {{a}_{{33}}}b_{{41}}^{{1 + }} + b_{{21}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{1}} - {{a}_{{22}}}{{a}_{{43}}}b_{{42}}^{{1 + }} + {{a}_{{32}}}{{a}_{{43}}}b_{{41}}^{{1 + }} + {{a}_{{43}}}b_{{42}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{1}})} \mathord{\left/ {\vphantom {{(a_{{23}}^{{}}b_{{42}}^{{1 + }} - {{a}_{{33}}}b_{{41}}^{{1 + }} + b_{{21}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{1}} - {{a}_{{22}}}{{a}_{{43}}}b_{{42}}^{{1 + }} + {{a}_{{32}}}{{a}_{{43}}}b_{{41}}^{{1 + }} + {{a}_{{43}}}b_{{42}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{1}})} {\left( {{{a}_{{13}}} - {{a}_{{12}}}{{a}_{{43}}}} \right)}}} \right. \kern-0em} {\left( {{{a}_{{13}}} - {{a}_{{12}}}{{a}_{{43}}}} \right)}}, \\ f_{{42}}^{1} = - {{(a_{{12}}^{{}}{{a}_{{23}}}b_{{42}}^{{1 + }} - {{a}_{{13}}}{{a}_{{22}}}b_{{42}}^{{1 + }} - {{a}_{{12}}}{{a}_{{33}}}b_{{41}}^{{1 + }} + {{a}_{{13}}}{{a}_{{32}}}b_{{41}}^{{1 + }} + {{a}_{{12}}}b_{{41}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{2}} + {{a}_{{13}}}b_{{42}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{2}})} \mathord{\left/ {\vphantom {{(a_{{12}}^{{}}{{a}_{{23}}}b_{{42}}^{{1 + }} - {{a}_{{13}}}{{a}_{{22}}}b_{{42}}^{{1 + }} - {{a}_{{12}}}{{a}_{{33}}}b_{{41}}^{{1 + }} + {{a}_{{13}}}{{a}_{{32}}}b_{{41}}^{{1 + }} + {{a}_{{12}}}b_{{41}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{2}} + {{a}_{{13}}}b_{{42}}^{{1 + }}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{2}})} {\left( {{{a}_{{13}}} - {{a}_{{12}}}{{a}_{{43}}}} \right)}}} \right. \kern-0em} {\left( {{{a}_{{13}}} - {{a}_{{12}}}{{a}_{{43}}}} \right)}}. \\ \end{gathered} $

Для вычисления матрицы $C_{0}^{ - }$, необходимой для определения регулятора нулевого уровня, воспользуемся второй формулой в (1.7). В результате получим

$C_{0}^{ - } = C_{0}^{ + } - C_{0}^{{R \bot }}B_{0}^{{}}{{F}_{1}} = \left[ {\begin{array}{*{20}{c}} 1&0 \\ {c_{{21}}^{m}}&{c_{{22}}^{m}} \\ {c_{{32}}^{m}}&{c_{{33}}^{m}} \\ 0&1 \end{array}} \right].$
Здесь

$c_{{21}}^{m} = b_{{21}}^{1}f_{{11}}^{1} + b_{{22}}^{1}f_{{21}}^{1} + b_{{23}}^{1}f_{{31}}^{1} + b_{{24}}^{1}f_{{41}}^{1},\quad c_{{22}}^{m} = b_{{21}}^{1}f_{{12}}^{1} + b_{{22}}^{1}f_{{22}}^{1} + b_{{23}}^{1}f_{{32}}^{1} + b_{{24}}^{1}f_{{42}}^{1},$
$c_{{32}}^{m} = - b_{{11}}^{1}f_{{11}}^{1} - b_{{12}}^{1}f_{{21}}^{1} - b_{{13}}^{1}f_{{31}}^{1} - b_{{14}}^{1}f_{{41}}^{1},\quad c_{{33}}^{m} = - b_{{11}}^{1}f_{{12}}^{1} - b_{{12}}^{1}f_{{22}}^{1} - b_{{13}}^{1}f_{{32}}^{1} - b_{{14}}^{1}f_{{42}}^{1}.$

В соответствии с теоремой проанализируем соблюдение условия управляемости MIMO-системы на нулевом уровне декомпозиции, для чего определим матрицы

$G_{0}^{{}} = {{(B_{0}^{ \bot }C_{0}^{ - })}^{ + }}B_{0}^{ \bot }{{A}_{0}}C_{0}^{ - } = \left[ {\begin{array}{*{20}{c}} 0&0 \\ {a_{{21}}^{a}}&{a_{{22}}^{a}} \end{array}} \right],\quad H_{0}^{{}} = {{(B_{0}^{ \bot }C_{0}^{ - })}^{{R \bot }}} = \left[ {\begin{array}{*{20}{c}} 1 \\ 0 \end{array}} \right],$
где

$a_{{21}}^{a} = с_{{21}}^{m} + {{a}_{{43}}}с_{{32}}^{m},\quad a_{{22}}^{a} = с_{{22}}^{m} + {{a}_{{43}}}с_{{33}}^{m}\,.$

Вычислим для нулевого уровня декомпозиции ранг следующей блочной матрицы:

${\text{rank}}[\begin{array}{*{20}{c}} {H_{0}^{{}}}&{{{G}_{0}}H_{0}^{{}}} \end{array}] = 2,$
что совпадает с числом измеряемых компонент вектора состояния, т.е. m = 2. Следовательно, нулевой уровень также удовлетворяет критерию управляемости, определенному в теореме.

Теперь следует найти Φ0 для нулевого уровня декомпозиции. Для этого осуществим декомпозицию матриц $H_{0}^{{}}$, ${{G}_{0}}$ нулевого уровня на два подуровня и вычислим соответствующие матрицы. В результате получим

${{\left( {{{H}_{0}}} \right)}_{0}} = {{H}_{0}},\quad \left( {{{H}_{0}}} \right)_{0}^{ \bot } = \left[ {\begin{array}{*{20}{c}} 0&1 \end{array}} \right],$
$\left( {{{H}_{0}}} \right)_{0}^{ + } = \left[ {\begin{array}{*{20}{c}} 1&0 \end{array}} \right],\quad {{\left( {{{G}_{0}}} \right)}_{1}} = \left( {{{H}_{0}}} \right)_{0}^{ \bot }{{G}_{0}}\left( {{{H}_{0}}} \right)_{0}^{{ \bot T}} = a_{{22}}^{a},$
${{\left( {{{H}_{0}}} \right)}_{1}} = \left( {{{H}_{0}}} \right)_{0}^{{}}{{G}_{0}}{{H}_{0}} = a_{{21}}^{a},$
$\left( {{{H}_{0}}} \right)_{1}^{ + } = {{(a_{{21}}^{a})}^{{ - 1}}}.$

Назначим собственное значение ${{\left( {{{{\text{Ф}}}_{0}}} \right)}_{1}} = {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }_{3}}$ и вычислим матрицу коэффициентов обратной связи первого подуровня нулевого уровня декомпозиции. Следовательно, имеем

${{k}_{1}} = - (a_{{22}}^{a} - {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }_{3}}){\text{/}}a_{{21}}^{a}.$

Вычислим матрицу

$\left( {{{H}_{0}}} \right)_{0}^{ - } = \left( {{{H}_{0}}} \right)_{0}^{ + } - {{k}_{1}}\left( {{{H}_{0}}} \right)_{0}^{ \bot } = [\begin{array}{*{20}{c}} 1&{(a_{{22}}^{a}} \end{array} - {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }_{3}}){\text{/}}a_{{21}}^{a}].$

Далее назначим собственное значение ${{\left( {{{{\text{Ф}}}_{0}}} \right)}_{0}} = {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }_{4}}$ и найдем матрицу K0 по формуле

${{K}_{0}} = {{\left( {{{{\text{Ф}}}_{0}}} \right)}_{0}}\left( {{{H}_{0}}} \right)_{0}^{ - } - \left( {{{H}_{0}}} \right)_{0}^{ - }{{G}_{0}} = [\begin{array}{*{20}{c}} {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{3}} - a_{{22}}^{a} + {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{4}}}&{ - (a_{{22}}^{a} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{3}})(a_{{22}}^{a} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{4}}){\text{/}}a_{{21}}^{a}} \end{array}].$

В результате с использованием выражения (2.3) получим искомую матрицу ${{{\text{Ф}}}_{0}}$ с собственными значениями ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }_{3}}$, ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }_{4}}$, а именно

${{{\text{Ф}}}_{0}} = \left[ {\begin{array}{*{20}{c}} {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{3}} - a_{{22}}^{a} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }&{ - (a_{{22}}^{a} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{3}})(a_{{22}}^{a} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{4}}){\text{/}}a_{{21}}^{a}} \\ {a_{{21}}^{a}}&{a_{{22}}^{a}} \end{array}} \right].$

Используя полученные выше выражения для $C_{0}^{ + }$, $C_{0}^{{R \bot }}$, ${{F}_{1}}$ вычисляем

$C_{0}^{ - } = C_{0}^{ + } - C_{0}^{{R \bot }}B_{0}^{{}}{{F}_{1}}$
и, применяя первую формулу из (1.7), в конечном итоге будем иметь следующую формулу регулятора в законе управления по вектору выхода:
(3.7)
$F = {{F}_{0}} = B_{0}^{ + }(C_{0}^{ - }{{\Phi }_{0}} - {{A}_{0}}C_{0}^{ - }) = \left[ {\begin{array}{*{20}{c}} {{{F}_{{11}}}}&{{{F}_{{12}}}} \\ {{{F}_{{21}}}}&{{{F}_{{22}}}} \\ {{{F}_{{31}}}}&{{{F}_{{32}}}} \\ {{{F}_{{41}}}}&{{{F}_{{42}}}} \end{array}} \right],$
где для компактности записи введены обозначения:

$\begin{gathered} {{F}_{{11}}} = - b_{{14}}^{ + }(c_{{21}}^{m} - a_{{21}}^{a} + {{a}_{{43}}}c_{{32}}^{m}) - b_{{12}}^{ + }[{{a}_{{21}}} + {{a}_{{22}}}c_{{21}}^{m} + {{a}_{{23}}}c_{{32}}^{m} - a_{{21}}^{a}c_{{22}}^{m} - c_{{21}}^{m}({{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{3}} - a_{{22}}^{a} + {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{4}})] - \\ - \;b_{{13}}^{ + }[{{a}_{{31}}} + {{a}_{{32}}}c_{{21}}^{m} + {{a}_{{33}}}c_{{32}}^{m} - a_{{21}}^{a}c_{{33}}^{m} - c_{{32}}^{m}({{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{3}} - a_{{22}}^{a} + {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{4}})] - b_{{11}}^{ + }({{a}_{{11}}} + a_{{22}}^{a} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{3}} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{4}} + \\ + \;{{a}_{{12}}}c_{{21}}^{m} + {{a}_{{13}}}c_{{32}}^{m}), \\ {{F}_{{12}}} = - b_{{12}}^{ + }[{{a}_{{22}}}c_{{22}}^{m} + a_{{23}}^{{}}c_{{33}}^{m} - a_{{22}}^{a}c_{{22}}^{m} + c_{{21}}^{m}(a_{{22}}^{a} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{3}})(a_{{22}}^{a} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{4}}){\text{/}}a_{{21}}^{a}] - b_{{13}}^{ + }[{{a}_{{32}}}c_{{22}}^{m} + a_{{33}}^{{}}c_{{33}}^{m} - \\ - \;a_{{22}}^{a}c_{{33}}^{m} + c_{{32}}^{m}(a_{{22}}^{a} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{3}})(a_{{22}}^{a} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{4}}){\text{/}}a_{{21}}^{a}] - b_{{14}}^{ + }(c_{{22}}^{m} - a_{{22}}^{a} + {{a}_{{43}}}c_{{33}}^{m}) - b_{{11}}^{ + }[{{a}_{{14}}} + {{a}_{{12}}}c_{{22}}^{m} + {{a}_{{13}}}c_{{33}}^{m} + \\ + \;(a_{{22}}^{a} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{3}})(a_{{22}}^{a} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{4}}){\text{/}}a_{{21}}^{a}], \\ \end{gathered} $
$\begin{gathered} {{F}_{{31}}} = - b_{{34}}^{ + }(c_{{21}}^{m} - a_{{21}}^{a} + {{a}_{{43}}}c_{{32}}^{m}) - b_{{32}}^{ + }[{{a}_{{21}}} + {{a}_{{22}}}c_{{21}}^{m} + {{a}_{{23}}}c_{{32}}^{m} - a_{{21}}^{a}c_{{22}}^{m} - c_{{21}}^{m}({{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{3}} - a_{{22}}^{a} + {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{4}})] - \\ - \;b_{{33}}^{ + }[{{a}_{{31}}} + {{a}_{{32}}}c_{{21}}^{m} + {{a}_{{33}}}c_{{32}}^{m} - a_{{21}}^{a}c_{{33}}^{m} - c_{{32}}^{m}({{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{3}} - a_{{22}}^{a} + {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{4}})] - b_{{31}}^{ + }({{a}_{{11}}} + a_{{22}}^{a} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{3}} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{4}} + {{a}_{{12}}}c_{{21}}^{m} + {{a}_{{13}}}c_{{32}}^{m}), \\ {{F}_{{32}}} = - b_{{32}}^{ + }[{{a}_{{22}}}c_{{22}}^{m} + a_{{23}}^{{}}c_{{33}}^{m} - a_{{22}}^{a}c_{{22}}^{m} + c_{{21}}^{m}(a_{{22}}^{a} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{3}})(a_{{22}}^{a} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{4}}){\text{/}}a_{{21}}^{a}] - b_{{33}}^{ + }[{{a}_{{32}}}c_{{22}}^{m} + a_{{33}}^{{}}c_{{33}}^{m} - a_{{22}}^{a}c_{{33}}^{m} + \\ + \;c_{{32}}^{m}(a_{{22}}^{a} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{3}})(a_{{22}}^{a} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{4}}){\text{/}}a_{{21}}^{a}] - b_{{34}}^{ + }(c_{{22}}^{m} - a_{{22}}^{a} + {{a}_{{43}}}c_{{33}}^{m}) - b_{{31}}^{ + }[{{a}_{{14}}} + {{a}_{{12}}}c_{{22}}^{m} + {{a}_{{13}}}c_{{33}}^{m} + \\ + \;(a_{{22}}^{a} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{3}})(a_{{22}}^{a} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{4}}){\text{/}}a_{{21}}^{a}], \\ \end{gathered} $
$\begin{gathered} {{F}_{{41}}} = - b_{{44}}^{ + }(c_{{21}}^{m} - a_{{21}}^{a} + {{a}_{{43}}}c_{{32}}^{m}) - b_{{42}}^{ + }[{{a}_{{21}}} + {{a}_{{22}}}c_{{21}}^{m} + {{a}_{{23}}}c_{{32}}^{m} - a_{{21}}^{a}c_{{22}}^{m} - c_{{21}}^{m}({{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{3}} - a_{{22}}^{a} + {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{4}})] - \\ - \;b_{{43}}^{ + }[{{a}_{{31}}} + {{a}_{{32}}}c_{{21}}^{m} + {{a}_{{33}}}c_{{32}}^{m} - a_{{21}}^{a}c_{{33}}^{m} - c_{{32}}^{m}({{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{3}} - a_{{22}}^{a} + {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{4}})] - b_{{41}}^{ + }({{a}_{{11}}} + a_{{22}}^{a} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{3}} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{4}} + {{a}_{{12}}}c_{{21}}^{m} + {{a}_{{13}}}c_{{32}}^{m}), \\ {{F}_{{42}}} = - b_{{42}}^{ + }[{{a}_{{22}}}c_{{22}}^{m} + a_{{23}}^{{}}c_{{33}}^{m} - a_{{22}}^{a}c_{{22}}^{m} + c_{{21}}^{m}(a_{{22}}^{a} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{3}})(a_{{22}}^{a} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{4}}){\text{/}}a_{{21}}^{a}] - b_{{43}}^{ + }[{{a}_{{32}}}c_{{22}}^{m} + a_{{33}}^{{}}c_{{33}}^{m} - a_{{22}}^{a}c_{{33}}^{m} + \\ + \;c_{{32}}^{m}(a_{{22}}^{a} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{3}})(a_{{22}}^{a} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{4}}){\text{/}}a_{{21}}^{a}] - b_{{44}}^{ + }(c_{{22}}^{m} - a_{{22}}^{a} + {{a}_{{43}}}c_{{33}}^{m}) - b_{{41}}^{ + }[{{a}_{{14}}} + {{a}_{{12}}}c_{{22}}^{m} + {{a}_{{13}}}c_{{33}}^{m} + \\ + \;(a_{{22}}^{a} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{3}})(a_{{22}}^{a} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } }}_{4}}){\text{/}}a_{{21}}^{a}]. \\ \end{gathered} $

Регулятор (3.7) представляет собой аналитическое решение рассматриваемой задачи синтеза и обеспечивает боковому управляемому движению гипотетического ЛА спектр (3.4).

Аналогичным образом можно получить решение в численном виде. Допустим, требуется обеспечить замкнутой системе “ЛА + система управления” следующий спектр:

(3.8)
$\Lambda = \left\{ { - 0.24 \pm 0.12i,\; - 2.2,\; - 0.28} \right\},$
когда матрицы A и B имеют вид

(3.9)
$A = \left[ {\begin{array}{*{20}{c}} { - 0.1720}&{0.0631}&{0.9980}&{0.0510} \\ { - 26.0500}&{ - 2.7490}&{ - 0.5330}&0 \\ { - 4.3370}&{ - 0.0060}&{ - 0.3010}&0 \\ 0&1&{ - 0.0632{\text{ }}}&0 \end{array}} \right],$
(3.10)
$B = \left[ {\begin{array}{*{20}{c}} { - 0.0340}&0&{ - 0.0100}&0 \\ { - 4.7570}&{ - 18.6640}&{ - 1.5000}&{ - 20.0000} \\ { - 3.0700}&{0.6660}&{ - 1.0000}&{ - 1.0000} \\ 0&0&0&0 \end{array}} \right].$

Пусть начальное значение вектора состояния в системе единиц СИ равно:

(3.11)
$\left[ {\begin{array}{*{20}{c}} {{{\beta }_{0}}} \\ {{{\omega }_{{x0}}}} \\ {{{\omega }_{{y0}}}} \\ {{{\gamma }_{0}}} \end{array}} \right]{\text{ = }}\left[ {\begin{array}{*{20}{c}} { - 0.0938} \\ { - 0.0243} \\ { - 0.0220} \\ {0.0209} \end{array}} \right].$

Числовое значение матрицы F в соответствии с (3.7) будет следующим:

(3.12)
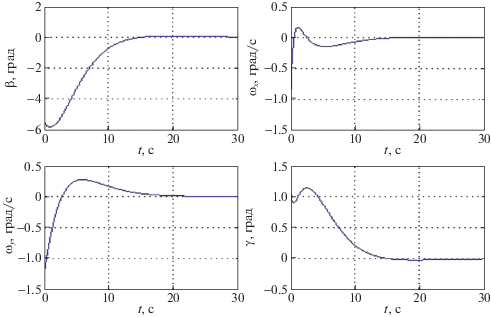
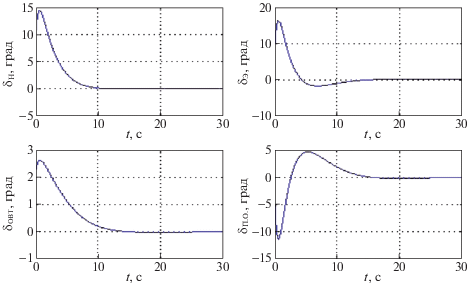
$F = \left[ {\begin{array}{*{20}{c}} { - {\text{5}}{\text{.1600}}}&{ - {\text{16}}{\text{.8687}}} \\ { - {\text{7}}{\text{.6761}}}&{ - {\text{30}}{\text{.7344}}} \\ { - {\text{0}}{\text{.6561}}}&{ - {\text{1}}{\text{.2635}}} \\ {{\text{7}}{\text{.1490}}}&{{\text{32}}{\text{.8486}}} \end{array}} \right].$

Графики переходных процессов и величин управляющих воздействий для заданного спектра (3.8), модели ЛА (3.9)–(3.11) и матрицы регулятора (3.12) приведены соответственно на рис. 1 и 2. При этом вычисление спектра матрицы A + BFС дает

${\text{eig}}\left( {A + BFC} \right) = \left\{ { - 0.24 \pm 0.12i,\; - 2.2,\; - 0.28} \right\},$
Рис. 1
Рис. 2

что, согласно (3.8), и требовалось получить.

Заключение. Представлен алгоритм синтеза закона управления линейной MIMO-системой с обратной связью по вектору выхода, обеспечивающий заданный спектр многомерной динамической системы в пространстве состояний. Сформулирована и доказана соответствующая теорема.

В основе предлагаемого подхода лежит принцип дуальности задачи управления MIMO-системой по вектору состояния и задачи построения наблюдателя состояния. Алгоритм без каких-либо изменений применим как для непрерывного, так и для дискретного случаев описания математической модели MIMO-системы, не имеет никаких ограничений по заданию элементов спектра замкнутой MIMO-системы, позволяет получать аналитические решения задачи синтеза и осуществлять параметризацию множества эквивалентных законов управления с обратной связью.

Возможности метода продемонстрированы на решении задачи управления боковым движением моделью гипотетического ЛА. Особенностью данной модели является неполнота ранга матрицы управления, обусловленная “избыточностью” органов управления в боковой плоскости.

Список литературы

  1. Bhattachrya S. Sparsity Based Ceedback Design: A new Paradigm in Opportunistic Sensing // Proc. American Control Conf. St. Louis, 2011. P. 3704–3709.

  2. Blumthaler I., Oberst U. Design, Parameterization, and Pole Placement of Stabilizing Output Feedback Compensators Via Injective Cogenerator Quotient Signal Modules // Linear Algebra Appl. 2012. V. 436 (5-2). P. 963–1000.

  3. Eremenko A., Gabrielov A. Pole Placement by Static Output Feedback for Generic Linear Systems // SIAM J. Contr. Opt. 2002. V. 41 (1). P. 303–312.

  4. Franke M. Eigenvalue Assignment by Static Output Feedback – on a new Solvability Condition and the Computation of Low Gain Feedback Matrices // Intern. J. Contr. 2014. V. 87 (1). P. 64–75.

  5. Kaiyang Yanga, Orsi R. Generalized Pole Placement Via Static Output Feedback: A Methodology Based on Projections // Automatica. 2006. V. 42. P. 2143–2150.

  6. Peretz Y. A Randomized Approximation Algorithm for the Minimal-Norm Static-Output-Feedback Problem // Automatica. 2016. V. 63. P. 221–234.

  7. Shimjith S.R., Tiwari A.P., Bandyopadhyay B. Modeling and Control of a Large Nuclear Reactor. Berlin, Heidelberg: Springer-Verlag, 2013.

  8. Wang X.A. On Linear Solutions of the Output Feedback Pole Assignment Problem // IEEE Trans. Autom. Contr. 2013. V. 58(9). P. 2354–2359.

  9. Fu M. Pole Placement Via Static Output Feedback is NP-hard // IEEE Trans. Autom. Contr. 2004. V. 49 (5). P. 855–857.

  10. Van der Woude J.W. A Note on Pole Placement by Static Output Feedback for Single. Input Systems // Systems & Control Letters. 1988. V. 11. P. 285–287.

  11. Зубов Н.Е., Микрин Е.А., Мисриханов М.Ш., Рябченко В.Н. Управление по выходу спектром дескрипторной динамической системы // ДАН. 2016. Т. 468. № 2. С. 134–136.

  12. Зубов Н.Е., Лапин А.В., Микрин Е.А., Рябченко В.Н. Управление по выходу спектром линейной динамической системы на основе подхода Ван-дер-Воуда // ДАН. 2017. Т. 476. № 3. С. 260–263.

  13. Зубов Н.Е., Микрин Е.А., Олейник А.С. и др. Оценка угловой скорости космического аппарата в режиме орбитальной стабилизации по результатам измерений датчика местной вертикали // Вестн. МГТУ. Приборостроение. 2014. № 5. С. 3–15.

  14. Зубов Н.Е., Микрин Е.А., Мисриханов М.Ш., Рябченко В.Н. Стабилизация взаимосвязанных движений летательного аппарата в каналах тангаж-рысканье при отсутствии информации об угле скольжения // Изв. РАН. ТиСУ. 2015. № 1. С. 95–105.

  15. Зубов Н.Е., Микрин Е.А., Мисриханов М.Ш., Рябченко В.Н. Управление по выходу продольным движением летательного аппарата // Изв. РАН. ТиСУ. 2015. № 5. С. 164–175.

  16. Зубов Н.Е., Микрин Е.А., Рябченко В.Н. и др. Синтез законов управления боковым движением летательного аппарата при отсутствии информации об угле скольжения. Аналитическое решение // Изв. вузов. Авиационная техника. 2017. № 1. С. 14–20.

  17. Зубов Н.Е., Микрин Е.А., Рябченко В.Н. Матричные методы в теории и практике систем автоматического управления летательными аппаратами. М.: Изд-во МГТУ им. Н.Э. Баумана, 2016. 666 с.

  18. Рябченко В.Н. Вложение систем. Нерегулярные законы управления // АиТ. 2001. № 7. С. 198–210.

  19. Боднер В.А. Системы управления летательными аппаратами. М.: Машиностроение, 1973. 504 с.

  20. Буков В.Н. Адаптивные прогнозирующие системы управления полетом. М.: Наука, 1987. 230 с.

  21. Зубов Н.Е., Рябченко В.Н. О вычислении псевдообратной матрицы. Общий случай // Вестн. МГТУ. Естественные науки. 2018. № 1 (76). С. 16–25.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Теория и системы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал