Известия РАН. Теория и системы управления, 2020, № 3, стр. 148-163
ПРИМЕНЕНИЕ ОБОБЩЕННЫХ ПОЛИНОМОВ БАТТЕРВОРТА ДЛЯ СТАБИЛИЗАЦИИ ПОЛОЖЕНИЯ РАВНОВЕСИЯ КОСМИЧЕСКОЙ СТАНЦИИ
К. А. Богданов a, А. В. Зыков a, А. В. Субботин a, А. В. Сумароков a, *, С. Н. Тимаков a
a ПАО “Ракетно-космическая корпорация “Энергия” им. С.П. Королёва”
МО, Королёв, Россия
* E-mail: anton.sumarokov@rsce.ru
Поступила в редакцию 24.04.2019
После доработки 06.11.2019
Принята к публикации 27.01.2020
Аннотация
Рассматривается задача поиска и удержания в положении динамического равновесия Международной космической станции. Равновесная ориентация Международной космической станции определяется действующей на нее суперпозицией гравитационного, гироскопического и аэродинамического моментов. В роли исполнительных органов в данной задаче выступает система силовых гироскопов, установленных на космической станции. На примере данной задачи рассматривается возможность применения метода последовательного замыкания мод движения для синтеза закона управления multi input multi output (MIMO) – многомерной многосвязной динамической системой. В качестве эталонного полинома, определяющего размещение полюсов замкнутой системы, предлагается использовать обобщенный полином Баттерворта. С помощью математического моделирования работы системы управления в режиме поиска и поддержания динамического равновесия демонстрируется преимущество применения обобщенных полиномов Баттерворта по сравнению с классическими полиномами Баттерворта.
Введение. Международная космическая станция (МКС) является уникальной космической лабораторией, на базе которой проводятся различные космические эксперименты [1, 2], наблюдения за поверхностью Земли [3], отрабатываются различные новые технологии и новое оборудование, позволяющие обеспечить продолжительное пребывание человека в космосе, а также постоянное присутствие человека на низкой околоземной орбите. При управлении угловым движением таких крупногабаритных космических конструкций, какой является МКС, неизбежно возникает ряд ограничений. Одно из этих ограничений – малая величина управляющего момента исполнительных органов по сравнению с размерами конструкции. В результате, поддержание любой произвольной ориентации такой конструкции может повлечь воздействие на нее значительного гравитационного момента, борьба с которым при помощи двигателей ориентации может привести к большому расходу топлива. При использовании инерционных исполнительных органов значительные величины возмущающих моментов могут привести к их насыщению и потребовать разгрузки накопленного кинетического момента. Наиболее эффективным является подержание ориентации такой конструкции вблизи положения гравитационного равновесия [4]. Однако определение такого положения затруднено воздействием изначально неопределенного аэродинамического момента. В результате равновесная ориентация МКС определяется действующей на нее суперпозицией гравитационного, гироскопического и аэродинамического моментов. В роли исполнительных органов в данной задаче будем использовать систему силовых гироскопов. Управление угловым положением станции происходит за счет управляющего момента, создаваемого силовыми гироскопами [5]. Рассматривается угловое положение МКС по всем трем каналам – крена, рысканья и тангажа. В силу автономности канала тангажа (каналы крена и рысканья гироскопически связаны), синтез закона управления проводится отдельно для канала тангажа и для каналов крен-рысканье. Для учета изначально неопределенного аэродинамического момента вектор состояния, описывающий исследуемый объект управления, должен содержать несколько компонент, характеризующих его влияние на ориентацию КА. Этот момент идентифицируется в алгоритме управления МКС.
Гироскопическая связь каналов крена и рысканья делает невозможным построение отдельного закона управления для каждого из каналов управления, что приводит к проблеме синтеза системы управления с более чем одним входным сигналом. Более того, “расширение” вектора состояния с целью учета переменных, отвечающих за аэродинамику, значительно увеличивает размерность объекта управления и как следствие увеличивает сложность синтеза закона управления данной системой. Подобная задача решалась авторами в [6], однако там при синтезе закона управления данной системой в качестве эталонного полинома, определяющего размещение полюсов замкнутой системы, применялся классический полином Баттерворта. В данной работе вводится понятие обобщенных полиномов Баттерворта и показывается преимущество их использования при решении поставленной задачи по сравнению с классическими. Кроме того, введение обобщенного полинома Баттерворта позволяет достаточно просто и наглядно распространить на динамические системы MIMO понятия запаса устойчивости, степени колебательности и быстродействия.
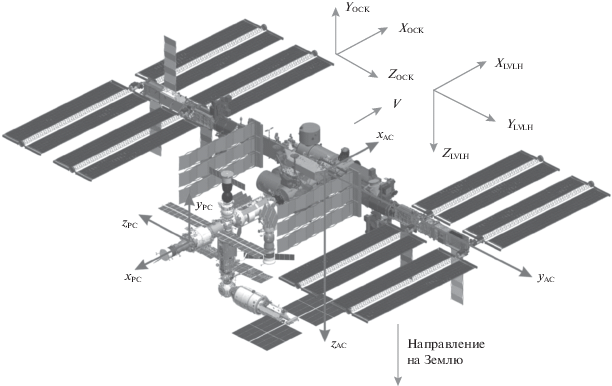
1. Постановка задачи. В качестве орбитальной системы координат [7, 8] будем использовать систему LVLH (Local Vertical – Local Horizontal). В данной системе началом координат является центр масс МКС, ось OX направлена вдоль вектора орбитальной скорости, ось OZ – из центра масс объекта управления в центр земли, ось OY дополняет систему координат до правой тройки. В качестве связанной системы координат будем использовать систему американского сегмента (АС), оси которой совпадают с осями координат системы LVLH в режиме орбитальной ориентации (рис. 1).
Будем считать, что в качестве исполнительных органов используется система из четырех трехстепенных силовых гироскопов АС. Кинетический момент каждого гироскопа составляет 4750 Нмс, а область вариации кинетического момента такой системы представляет сферу радиусом 19 000 Нмс.
Динамика объекта управления, в данном случае МКС, описывается динамическими уравнениями Эйлера при воздействии гравитационного и аэродинамического моментов (1.1) и кинематическими уравнениями в кватернионной форме (1.2):
(1.1)
$J{{\dot {\omega }}_{{abs}}} + {{\omega }_{{abs}}} \times J{{\omega }_{{abs}}} + \dot {h} + {{\omega }_{{abs}}} \times h = 3\frac{\mu }{{{{r}^{3}}}}\frac{r}{r} \times J\frac{r}{r} + {{М}^{{aero}}},$(1.2)
$2{\mathbf{\dot {N}}}_{{\mathbf{i}}}^{{\mathbf{e}}} = {\mathbf{N}}_{{\mathbf{i}}}^{{\mathbf{e}}} \circ {{({{{\mathbf{\omega }}}_{{{\mathbf{abs}}}}})}_{{\mathbf{e}}}} - {{({{{\mathbf{\omega }}}_{0}})}_{{\mathbf{i}}}} \circ {\mathbf{N}}_{{\mathbf{i}}}^{{\mathbf{e}}}{\text{ ,}}$В [6–10] показано, что при малости углов отклонения связанного базиса от положения гравитационного равновесия по каналам крена рыскания и тангажа, а также их производных уравнения (1.1) и (1.2) можно линеаризовать вблизи положения гравитационного равновесия. В результате, применяя теорему об изменении кинетического момента отдельно к корпусу МКС и отдельно к силовым гироскопам, можно записать линеаризованную систему уравнений:
(1.3)
$\begin{gathered} {{J}_{x}}\ddot {\gamma } = 4\omega _{0}^{2}({{J}_{z}} - {{J}_{y}})\gamma - {{\omega }_{0}}({{J}_{x}} - {{J}_{y}} + {{J}_{z}})\dot {\psi } - {{u}_{x}} + M_{x}^{{aero}}, \\ {{J}_{y}}\ddot {\theta } = 3\omega _{0}^{2}({{J}_{z}} - {{J}_{x}})\theta - {{u}_{y}} + M_{y}^{{aero}}, \\ {{J}_{z}}\ddot {\psi } = \omega _{0}^{2}({{J}_{x}} - {{J}_{y}})\psi + {{\omega }_{0}}({{J}_{x}} - {{J}_{y}} + {{J}_{z}})\dot {\gamma } - {{u}_{z}} + M_{z}^{{aero}}, \\ {{{\dot {h}}}_{x}} = {{h}_{z}}{{\omega }_{0}} + {{u}_{x}}, \\ {{{\dot {h}}}_{y}} = {{u}_{y}}, \\ {{{\dot {h}}}_{z}} = - {{h}_{x}}{{\omega }_{0}} + {{u}_{z}}, \\ \end{gathered} $При несущественном ущемлении общности окончательных результатов будем полагать, что реальное положение равновесия космической станции находится вблизи ее гравитационного положения (в пределах нескольких градусов), в силу этого линеаризация в форме (1.3) остается уместной.
Для расчета аэродинамического момента, действующего на станцию, будем использовать зеркально-диффузионную аэродинамическую модель обтекания свободно молекулярным потоком набегающих частиц. Суть этой модели заключается в том, что часть молекул набегающего потока претерпевает абсолютно упругое соударение, а остальная часть молекул в набегающем потоке претерпевает абсолютно неупругое соударение с корпусом объекта управления. Если аппроксимировать всю поверхность МКС набором Npl плоских поверхностей, представляющих собой поперечные сечения модулей и вращающиеся панели солнечных батарей, то, согласно этой модели, аэродинамический момент определяется следующим выражением:
(1.4)
${\mathbf{M}}_{{}}^{{aero}} = \frac{{\rho V_{0}^{2}}}{2}\left[ {2c\sum\limits_{i = 1}^{{{N}_{{pl}}}} {{{A}_{i}}\left| {\left( {{{{\mathbf{n}}}_{i}} \times {\mathbf{I}}} \right)} \right|\left[ {{\mathbf{I}} \times {{{\mathbf{r}}}_{i}}} \right]} + 4\left( {1 - c} \right)\sum\limits_{i = 1}^{{{N}_{{pl}}}} {{{A}_{i}}\left| {\left( {{{{\mathbf{n}}}_{i}} \times {\mathbf{I}}} \right)} \right|\left( {{{{\mathbf{n}}}_{i}} \times {\mathbf{I}}} \right)\left[ {{{{\mathbf{n}}}_{i}} \times {{{\mathbf{r}}}_{i}}} \right]} } \right].$Здесь $\rho $ – плотность атмосферы; V0 – скорость набегающего потока; $c$ – коэффициент диффузии; ${{{\mathbf{n}}}_{i}}$ – единичный вектор нормали к i-й аппроксимирующей плоскости; I – единичный вектор в направлении против набегающего потока; ${{{\mathbf{r}}}_{i}}$ – эффективный радиус-вектор из центра масс станции к центру давления i-й аппроксимирующей плоскости; Ai – площадь i-й аппроксимирующей плоскости.
При вычислении аэродинамических моментов, согласно (1.4), использовалась упрощенная модель плотности атмосферы, учитывающая лишь суточные колебания атмосферы. Зависимость плотности атмосферы от времени определяется следующим выражением:
(1.5)
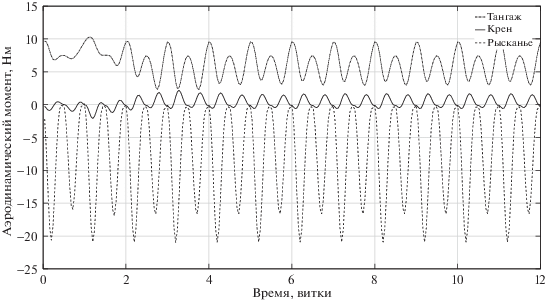
$\rho = ({{\rho }^{{{\text{max}}}}} - {{\rho }^{{{\text{min}}}}}){{\left| {\cos \left( {\frac{{{{\omega }_{0}}t - {{\phi }_{0}}}}{2}} \right)} \right|}^{\alpha }} + {{\rho }^{{{\text{min}}}}},$Для более точного определения равновесной ориентации космической станции в контур управления была введена бортовая модель, содержащая упрощенный вариант выражения для аэродинамического момента [11–13]. Эта модель представляет собой три первые гармоники ${{\omega }_{0}}$, $2{{\omega }_{0}}$, $3{{\omega }_{0}}$ разложения выражения для аэродинамического момента по витку:
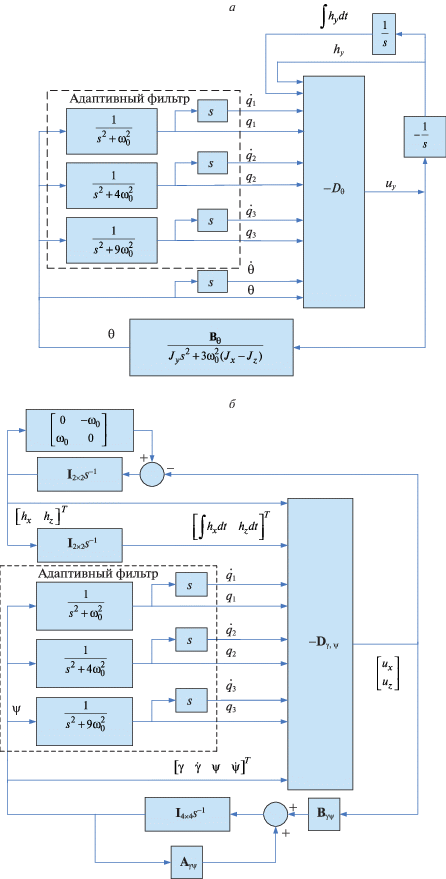
Фактические значения амплитуд Aij (где i = 0, 1, 2, 3; j = $\gamma $, $\psi $, $\theta $) и фаз ${{\phi }_{1}}$, ${{\phi }_{2}}$, ${{\phi }_{3}}$ коэффициентов в разложении аэродинамического момента в ряд по доминирующим частотам ${{\omega }_{0}}$, $2{{\omega }_{0}}$, $3{{\omega }_{0}}$ неизвестны и идентифицируются адаптивным наблюдателем в процессе выведения станции в положение равновесия. В силу вышеупомянутого факта, для учета воздействия аэродинамического момента на МКС к системе (1.3) необходимо добавить еще несколько уравнений [11–13], представляющих собой осцилляторы с орбитальной, двух- и трехорбитальной частотами:
(1.6)
$\begin{gathered} {{{\ddot {q}}}_{{1\psi }}} = \psi - \omega _{0}^{2}{{q}_{{1\psi }}} \hfill \\ {{{\ddot {q}}}_{{2\psi }}} = \psi - 4\omega _{0}^{2}{{q}_{{2\psi }}} \hfill \\ {{{\ddot {q}}}_{{3\psi }}} = \psi - 9\omega _{0}^{2}{{q}_{{3\psi }}},\quad \hfill \\ \end{gathered} $ $\begin{gathered} {{{\ddot {q}}}_{{1\theta }}} = \theta - \omega _{0}^{2}{{q}_{{1\theta }}}, \hfill \\ {{{\ddot {q}}}_{{2\theta }}} = \theta - 4\omega _{0}^{2}{{q}_{{2\theta }}}, \hfill \\ {{{\ddot {q}}}_{{3\theta }}} = \theta - 9\omega _{0}^{2}{{q}_{{3\theta }}}, \hfill \\ \end{gathered} $Дополнительно следует отметить, что доминирующие частоты в выражении, определяющем аэродинамический момент, соответствуют орбитальной угловой скорости МКС, удвоенной и утроенной орбитальной угловой скорости, что на порядок меньше частот упругих колебаний корпуса станции. Это обстоятельство исключает их взаимную корреляцию, которая могла бы вызвать неустойчивость контура управления.
2. Описание объекта управления в пространстве состояний. Для построения регулятора необходимо описать динамику объекта управления в пространстве состояний. Уравнение (1.3) демонстрирует, что каналы крена и рысканья гироскопически связаны между собой, а канал тангажа является автономным. Поэтому при рассмотрении МКС как объекта управления целесообразно отдельно описывать связанные каналы крена и рысканья и отдельно – канал тангажа.
Расширенный вектор состояния ${\mathbf{x}}$ и вектор управления ${\mathbf{u}}$ для системы каналов крена и рысканья и для системы канала тангажа соответственно будут иметь следующий вид:
(2.1)
${{{\mathbf{x}}}_{{{\mathbf{\gamma \psi }}}}} = {{\left[ {\begin{array}{*{20}{c}} \gamma &{\dot {\gamma }}&{{{h}_{x}}}&{\int {{{h}_{x}}} dt}&\psi &{\dot {\psi }}&{{{h}_{z}}}&{\int {{{h}_{z}}} dt}&{{{q}_{{1\psi }}}}&{{{{\dot {q}}}_{{1\psi }}}}&{{{q}_{{2\psi }}}}&{{{{\dot {q}}}_{{2\psi }}}}&{{{q}_{{3\psi }}}}&{{{{\dot {q}}}_{{3\psi }}}} \end{array}} \right]}^{{\text{т}}}},$(2.2)
${{{\mathbf{u}}}_{{{\mathbf{\gamma \psi }}}}} = {{\left[ {\begin{array}{*{20}{c}} {{{u}_{x}}}&{{{u}_{z}}} \end{array}} \right]}^{{\text{т}}}},$(2.3)
${{{\mathbf{x}}}_{{\mathbf{\theta }}}} = {{\left[ {\begin{array}{*{20}{c}} \theta &{\dot {\theta }}&{{{h}_{y}}}&{\int {{{h}_{y}}} dt}&{{{q}_{{1\theta }}}}&{{{{\dot {q}}}_{{1\theta }}}}&{{{q}_{{2\theta }}}}&{{{{\dot {q}}}_{{2\theta }}}}&{{{q}_{{3\theta }}}}&{{{{\dot {q}}}_{{3\theta }}}} \end{array}} \right]}^{{\text{т}}}},$(2.4)
${{{\mathbf{u}}}_{{\mathbf{\theta }}}} = \left[ {\begin{array}{*{20}{c}} {{{u}_{y}}} \end{array}} \right].$В пространстве состояний объект управления, который представляет собой MIMO динамическую систему, описывается следующими уравнениями:
(2.5)
${{{\mathbf{\dot {x}}}}_{{{\mathbf{\gamma \psi }}}}} = {{{\mathbf{A}}}_{{{\mathbf{\gamma \psi }}}}}{{{\mathbf{x}}}_{{{\mathbf{\gamma \psi }}}}} + {{{\mathbf{B}}}_{{{\mathbf{\gamma \psi }}}}}{{{\mathbf{u}}}_{{{\mathbf{\gamma \psi }}}}},$(2.6)
${{{\mathbf{\dot {x}}}}_{{\mathbf{\theta }}}} = {{{\mathbf{A}}}_{{\mathbf{\theta }}}}{{{\mathbf{x}}}_{{\mathbf{\theta }}}} + {{{\mathbf{B}}}_{{\mathbf{\theta }}}}{{{\mathbf{u}}}_{{\mathbf{\theta }}}},$ ${{{\mathbf{A}}}_{{\mathbf{\theta }}}} = \left[ {\begin{array}{*{20}{c}} 0&1&0&0&0&0&0&0&0&0 \\ {{{M}_{y}}}&0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0&0 \\ 0&0&1&0&0&0&0&0&0&0 \\ 0&0&0&0&0&1&0&0&0&0 \\ 1&0&0&0&{ - \omega _{0}^{2}}&0&0&0&0&0 \\ 0&0&0&0&0&0&0&1&0&0 \\ 1&0&0&0&0&0&{ - 4\omega _{0}^{2}}&0&0&0 \\ 0&0&0&0&0&0&0&0&0&1 \\ 1&0&0&0&0&0&0&0&{ - 9\omega _{0}^{2}}&0 \end{array}} \right];\quad {{{\mathbf{B}}}_{{\mathbf{\theta }}}} = \left[ {\begin{array}{*{20}{c}} 0 \\ { - 1{\text{/}}{{J}_{y}}} \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{array}} \right],$
${{{\mathbf{A}}}_{{\mathbf{\theta }}}} = \left[ {\begin{array}{*{20}{c}} 0&1&0&0&0&0&0&0&0&0 \\ {{{M}_{y}}}&0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0&0 \\ 0&0&1&0&0&0&0&0&0&0 \\ 0&0&0&0&0&1&0&0&0&0 \\ 1&0&0&0&{ - \omega _{0}^{2}}&0&0&0&0&0 \\ 0&0&0&0&0&0&0&1&0&0 \\ 1&0&0&0&0&0&{ - 4\omega _{0}^{2}}&0&0&0 \\ 0&0&0&0&0&0&0&0&0&1 \\ 1&0&0&0&0&0&0&0&{ - 9\omega _{0}^{2}}&0 \end{array}} \right];\quad {{{\mathbf{B}}}_{{\mathbf{\theta }}}} = \left[ {\begin{array}{*{20}{c}} 0 \\ { - 1{\text{/}}{{J}_{y}}} \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{array}} \right],$3. Обобщенные полиномы Баттерворта. В [6] при синтезе закона управления системой в качестве эталонного полинома, определяющего размещение полюсов замкнутой системы, применялся классический полином Баттерворта. Основным достоинством полинома Баттерворта является тот факт, что он обладает максимально гладкой амплитудно-частотной характеристикой (АЧХ) на частотах пропускания, что делает данный тип полиномов хорошим вариантом для построения фильтров.
Классический полином Баттерворта определяется следующим образом:
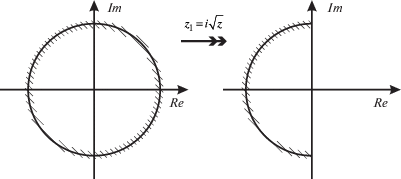
На комплексной плоскости корни полиномов Баттерворта равномерно расположены в левой полуплоскости на окружности радиусом ${{\omega }_{c}}$ и центром в начале координат. Корни классического полинома Баттерворта можно получить путем конформного преобразования точек, равномерно распределенных по окружности симметрично относительно точки –π (рис. 4):
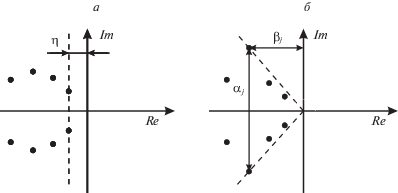
Следует отметить, что эталонный полином определяет расположение корней замкнутой системы и, как следствие, характер переходного процесса. Для оценки качества переходного процесса используют такие критерии, как степень устойчивости и степень колебательности [14, 15]. Степень устойчивости численно равна абсолютному значению действительной части ближайшего к мнимой оси корня $\eta $ (рис. 5, а). Чем больше степень устойчивости, тем быстрее затухает переходный процесс. Также можно отметить, что достаточно большой коэффициент устойчивости динамической системы делает систему управления более робастной, т.е. не теряющей устойчивость при некоторых изменениях в значениях параметров системы.
Еще одним критерием качества динамической системы является степень колебательности (рис. 5, б). Если из начала координат провести лучи через два комплексно-сопряженных корня так, чтобы все остальные корни оказались между этими лучами, то степенью колебательности называется отношение
Чем меньше значение m, тем быстрее затухает колебательный процесс. Идеальным вариантом эталонного полинома, обладающего низкой степенью колебательности, является бином Ньютона. Степень колебательности динамической системы, корни которой лежат согласно биному Ньютона, равна нулю, а степень устойчивости такой системы будет равна параметру ω0. Существенным же недостатком использования данного типа полиномов для построения систем управления является высокая чувствительность расположения корней к изменениям параметров системы (низкая робастность системы) [16], так как при кратных корнях нарушается гладкость зависимости расположения корней характеристического уравнения от коэффициентов (дискриминант характеристического полинома обращается в нуль). Существует ненулевая вероятность, что при малейшем возмущении одного из параметров системы управления корни полинома данного типа могут “уползти” в правую полуплоскость комплексной плоскости, т.е. сделать систему управления неустойчивой.
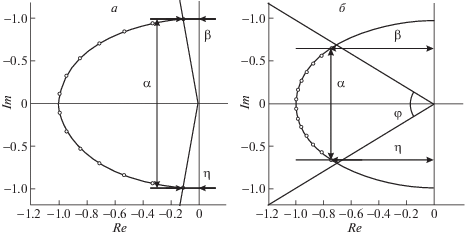
Если рассчитать степень устойчивости и степень колебательности для корней классических полиномов Баттерворта, то можно видеть, что построенная система управления будет обладать высокой степенью колебательности и низкой степенью устойчивости. Действительно, самая правая пара комплексно-сопряженных корней расположена слишком близко к мнимой оси, и при росте размерности динамической системы управления степень устойчивости будет стремиться к нулю, а степень колебательности – к бесконечности (рис. 6, а).
Одним из решений данной проблемы может стать введение нового параметра, отвечающего за удаленность самой правой пары корней данного семейства полиномов от комплексной оси. Если равномерно расположить все корни на окружности в левой полуплоскости так, чтобы они лежали между двумя симметричными лучами, проведенными из начала координат, то степень колебательности такого полинома значительно уменьшится, а степень устойчивости наоборот возрастет (рис. 6, б). В дальнейшем подобный тип полиномов будем называть обобщенными полиномами Баттерворта. Обобщенные полиномы Баттерворта получаются из классических полиномов Баттерворта введением варьируемого параметра $\varphi $, определяющего величину дуги, на которой располагаются корни. Аналитическая запись данного полинома выглядит следующим образом:
(3.2)
$\mathop \prod \limits_{k = 1}^n \left( {s - {{\omega }_{c}}\exp \left( {i\left( {\frac{{\varphi \left( {2k - 1} \right)}}{{2n}} + \pi - \frac{\varphi }{2}} \right)} \right)} \right),$При уменьшении параметра $\varphi $ степень устойчивости замкнутой системы, построенной, согласно эталонному полиному данного типа, будет возрастать, а степень колебательности – наоборот уменьшаться. При φ = 0 корни полинома будут лежать в одной точке на действительной оси, что говорит о том, что бином Ньютона можно считать предельным случаем обобщенного полинома Баттерворта при φ → 0.
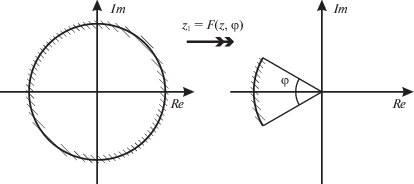
Аналогично (3.1) можно найти конформное преобразование точек, равномерно распределенных по окружности симметрично относительно точки –π к корням обобщенного полинома Баттерворта (рис. 7). Для этого представим начальное распределение точек в виде
(3.3)
${{z}^{k}} = {{\omega }_{c}}\left[ {\cos \left( {\frac{{(2k - 1)2\pi }}{n}} \right) + i\sin \left( {\frac{{(2k - 1)2\pi }}{n}} \right)} \right] = {{\omega }_{c}}{{e}^{{i\left( {\frac{{(2k - 1)2\pi }}{n}} \right)}}},\quad k \leqslant n.$После конформного преобразования требуется получить следующее распределение:
(3.4)
$z_{1}^{k} = {{\omega }_{c}}\left[ {\cos \left( {\frac{{\varphi \left( {2k - 1} \right)}}{{2n}} + \pi - \frac{\varphi }{2}} \right) + i\sin \left( {\frac{{\varphi \left( {2k - 1} \right)}}{{2n}} + \pi - \frac{\varphi }{2}} \right)} \right] = {{\omega }_{c}}{{e}^{{i\left( {\frac{{\varphi \left( {2k - 1} \right)}}{{2n}} + \pi - \frac{\varphi }{2}} \right)}}}.$Очевидно, что с учетом того, что
В результате искомое конформное преобразование имеет вид
(3.5)
${{z}_{1}} = F\left( {z,\varphi } \right) = \omega _{c}^{{1 - \frac{\varphi }{{2\pi }}}}{{e}^{{i\left( {\pi - \frac{\varphi }{2}} \right)}}}{{z}^{{\frac{\varphi }{{2\pi }}}}}.$Нетрудно проверить, что при φ = π (3.5) переходит в (3.1), а при $\varphi \to 0$ – в корни бинома Ньютона ${{z}_{1}} = - \omega _{c}^{{}}$.
В результате можно сделать вывод, что обобщенные полиномы Баттерворта являются довольно удобным вариантом для использования в качестве эталонных при модальном синтезе систем управления, так как выбором параметра $\varphi $ можно добиться необходимой степени устойчивости и степени колебательности. При этом такие полиномы не имеют кратных корней, что дает возможность обеспечить робастность системе управления.
4. Синтез закона управления. Результаты математического моделирования. Для синтеза регулятора используем в качестве эталонного полинома обобщенный полином Баттерворта (3.2). Порядок полинома системы в каналах крена и рысканья (2.5) n = 14, а для системы в канале тангажа (2.6) n = 10. Были выбраны следующие параметры размещения корней замкнутой системы: ${{\omega }_{c}}$ = ω0, где ${{\omega }_{0}}$ – абсолютная угловая скорость движения приборного базиса МКС (угловая скорость орбитального движения), $\varphi = \pi {\text{/}}6$.
Для построения регулятора требуется найти такие законы управления [15]
(4.1)
${{{\mathbf{\dot {x}}}}_{{{\mathbf{\gamma \psi }}}}} = ({{{\mathbf{A}}}_{{{\mathbf{\gamma \psi }}}}} - {{{\mathbf{B}}}_{{{\mathbf{\gamma \psi }}}}}{{{\mathbf{D}}}_{{{\mathbf{\gamma \psi }}}}}){{{\mathbf{x}}}_{{{\mathbf{\gamma \psi }}}}},$(4.2)
${{{\mathbf{\dot {x}}}}_{{\mathbf{\theta }}}} = {\mathbf{(}}{{{\mathbf{A}}}_{{\mathbf{\theta }}}} - {{{\mathbf{B}}}_{{\mathbf{\theta }}}}{{{\mathbf{D}}}_{{\mathbf{\theta }}}}{\mathbf{)}}{{{\mathbf{x}}}_{{\mathbf{\theta }}}}$Следует дополнительно отметить, что путем задания параметра ${{\omega }_{c}}$ в (3.3) расположение корней эталонного полинома для дальнейшего расчета коэффициентов обратной связи подбиралось таким образом, чтобы максимальная величина кинетического момента силовых гироскопов была значительно ниже предельного значения выбранной системы исполнительных органов.
Для поиска числовых значений коэффициентов матриц обратной связи ${{{\mathbf{D}}}_{{{\mathbf{\gamma \psi }}}}}$ и ${{{\mathbf{D}}}_{{\mathbf{\theta }}}}$ используем метод последовательного замыкания мод движения [6]. В результате получаем следующие значения матриц коэффициентов обратной связи:
Следует заметить, что похожие задачи решались ранее, например в [18–22], однако в данных работах используется аналитический алгоритм модального синтеза, позволяющий получать аналитические выражения для коэффициентов обратной связи. В силу высокой размерности вектора состояния (в частности, из-за учета аэродинамических возмущений, в отличие от похожей задачи, рассмотренной в [18], размерность вектора состояния значительно возрастает) применение аналитических алгоритмов модального синтеза будет затруднено, поскольку выражения для коэффициентов обратной связи могут быть очень громоздкими и неудобными для использования. В данной статье, в отличие от [18–20], для расчета матрицы коэффициентов обратной связи применяется численный алгоритм, позволяющий за несколько итераций получить непосредственно значения указанных коэффициентов.
Для подтверждения правильности выбранной концепции управления было проведено математическое моделирование углового движения МКС (далее по тексту – закон управления 1). Дополнительно сравнивались результаты полученного моделирования с результатами из [6] для системы управления, которая была построена методом модального управления по классическому полиному Баттерворта (далее по тексту – закон управления 2).
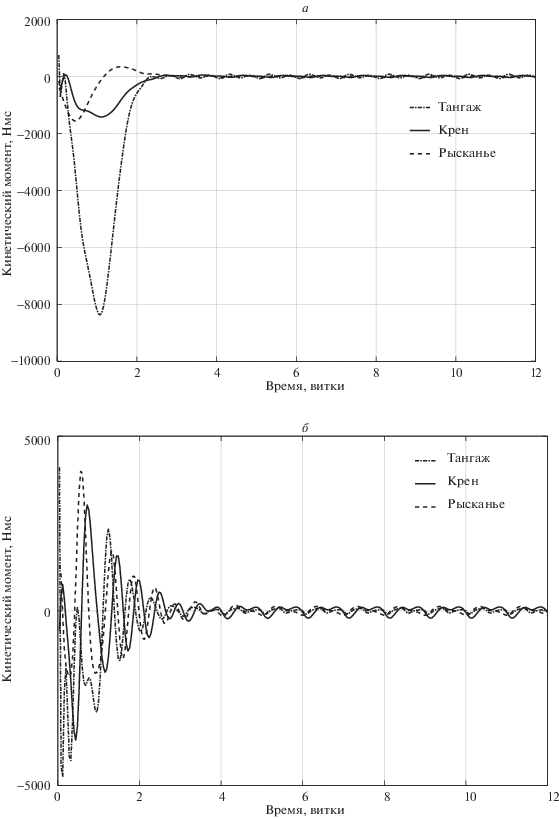
Математическое моделирование проводилось в среде MATLAB. При этом в бортовом регуляторе использовались линеаризованные уравнения движения (1.3), а поведение системы анализировалось по исходной нелинейной системе (1.1)–(1.2), (1.4)–(1.5). Результаты математического моделирования представлены на рис. 8–10. На рис. 8, а рассмотрено поведение углов рассогласования по каналам крена, рысканья и тангажа относительно заданной ориентации при использовании закона управления 1, на рис. 8, б – поведение углов рассогласования по каналам крена, рысканья и тангажа относительно заданной ориентации с помощью закона управления 2. На рис. 9, а продемонстрировано поведение компонент угловой скорости по каналам крена, рысканья и тангажа при использовании закона управления 1, на рис. 9, б – поведение компонент угловой скорости по каналам крена, рысканья и тангажа с помощью закона управления 2. На рис. 10, а приведено поведение компонент кинетического момента по каналам крена, рысканья и тангажа при использовании закона управления 1, на рис. 10, б – поведение компонент кинетического момента по каналам крена, рысканья и тангажа с помощью закона управления 2.
Рис. 8.
Поведение углов рассогласования орбитального базиса при поиске и поддержании равновесной ориентации, а – закон управления 1, б – закон управления 2
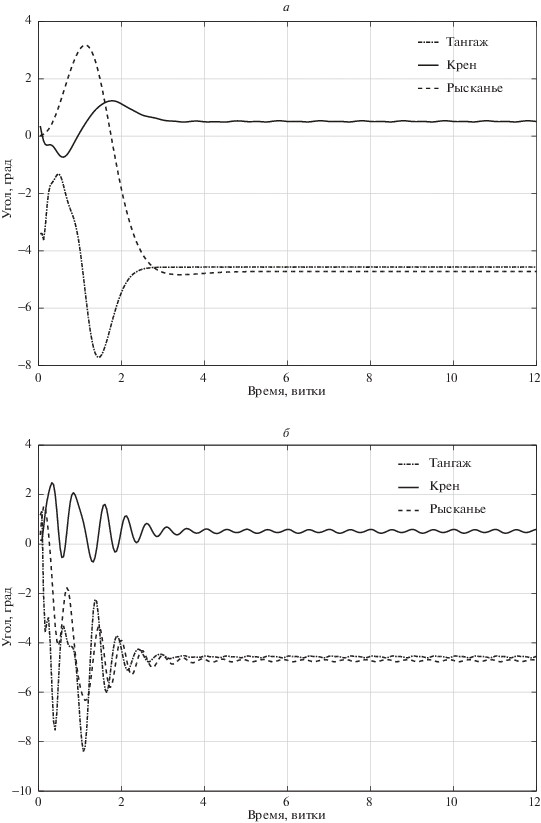
Рис. 9.
Поведение угловых скоростей при поиске и поддержании равновесной ориентации, а – закон управления 1, б – закон управления 2
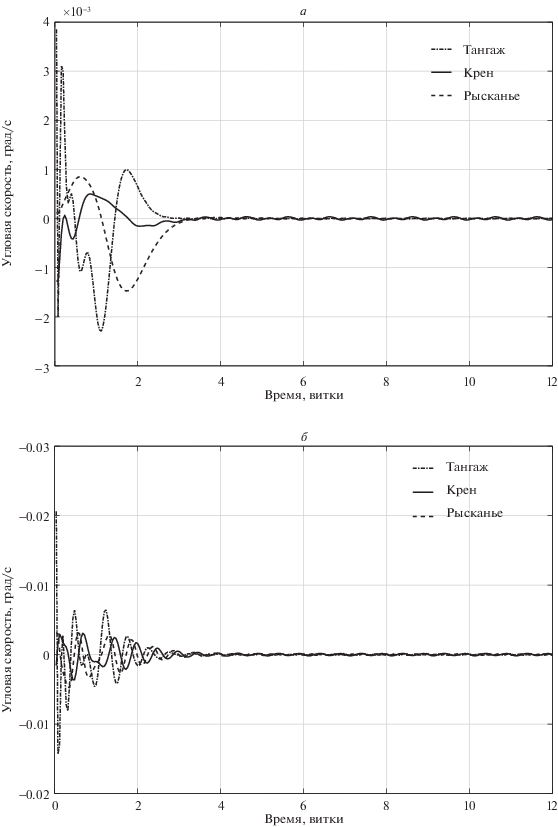
Рис. 10.
Поведение кинетического момента силовых гироскопов при поиске и поддержании равновесной ориентации, а – закон управления 1, б – закон управления 2
Результаты математического моделирования углового движения МКС показывают, что переходный процесс, динамику которого определяют корни обобщенного полинома Баттерворта (закон управления 1), имеет менее выраженную осцилляционную составляющую и проходит более “плавно”. Переходный процесс, определяющийся корнями классического полинома Баттерворта (закон управления 2), напротив, демонстрирует высокую колебательность. Более того, начальная амплитуда компонент вектора состояния ниже в переходном процессе, который задается корнями обобщенного полинома Баттерворта. Таким образом, на основании полученных результатов можно сделать вывод, что обобщенный полином Баттерворта является более подходящим эталонным полиномом для модального синтеза многомерных многосвязных динамических систем.
Заключение. В работе решена задача построения закона управления ориентацией МКС. За основу математической модели динамики МКС были взяты линеаризованные уравнения углового движения космического аппарата, несущего вращающиеся массы с учетом воздействия гравитационного и аэродинамического моментов. Для решения задачи модального синтеза систем управления многомерных многосвязных систем были выбраны обобщенные полиномы Баттерворта. С использованием алгоритма последовательного замыкания методом модального синтеза был получен регулятор, соответствующий обобщенному полиному Баттерворта. Результаты математического моделирования продемонстрировали как работоспособность алгоритма последовательного замыкания в задачах синтеза регуляторов большой размерности, так и правильность выбора обобщенного полинома Баттерворта как эталонного. Сравнение переходного процесса, определяемого корнями обобщенного полинома Баттерворта, показывает меньшую колебательность, а также меньшую начальную амплитуду компонент углов и угловых скоростей МКС, чем переходный процесс, определяемый корнями классического полинома Баттерворта.
Список литературы
Сумароков А.В. О бортовом алгоритме усреднения параметров орбитального движения Международной космической станции в эксперименте ICARUS // Изв. РАН. ТиСУ. 2018. № 2. С. 102–111.
Воронин Ф.А., Назаров Д.С., Пахмутов П.А. и др. О принципах разработки программного обеспечения информационно-управляющей системы российского сегмента Международной космической станции // Вестн. МГТУ им. Н.Э. Баумана. Сер. Приборостроение. 2018. № 2. С. 69–86.
Беляев М.Ю., Десинов Л.В., Караваев Д.Ю. и др. Особенности проведения и использования результатов съемок земной поверхности, выполняемой экипажами Российского сегмента МКС // Космическая техника и технологии. 2015. № 1. С. 17–30.
Зубов Н.Е., Микрин Е.А., Мисриханов М.Ш., Рябченко В.Н., Тимаков С.Н., Черемных Е.А. Идентификация положения равновесной ориентации Международной космической станции как задача матричного пополнения с устойчивостью // Изв. РАН. ТиСУ. 2012. № 2. С. 130–144.
Платонов В.Н., Сумароков А.В. Исследование возможности обеспечения точностных характеристик стабилизации перспективного космического аппарата дистанционного зондирования Земли // Изв. РАН. ТиСУ. 2018. № 4.
Тимаков С.Н., Богданов К.А., Нефедов С.Е. Метод последовательного замыкания мод движения для многомерных, многосвязных динамических систем // Вестн. МГТУ им. Н.Э. Баумана. Сер. Приборостроение. 2014. № 5. С. 40–59.
Борисенко Н.Ю., Сумароков А.В. Об ускоренном построении орбитальной ориентации грузовых и транспортных кораблей серий “Союз МС” и “Прогресс МС” // Изв. РАН. ТиСУ. 2017. № 5. С. 131–141.
Сумароков А.В., Тимаков С.Н. Об одной адаптивной системе управления угловым движением спутника связи // Изв. РАН. ТиСУ. 2008. № 5. С. 131–141.
Бранец В.Н., Платонов В.Н., Сумароков А.В., Тимаков С.Н. О стабилизации спутника связи, несущего маховики, без использования датчиков углов и угловых скоростей // Изв. РАН. ТиСУ. 2008. № 1. С. 106–116.
Ефимов Д.А., Сумароков А.В., Тимаков С.Н. О гиростабилизации спутника связи в отсутствии измерений угловой скорости // Изв. РАН. ТиСУ. 2012. № 5. С. 119–128.
Harduvel J.T. Continuous Momentum Management of Earth-Oriented Spacecraft // J. Guidance, Control and Dynamics. 1992. V. 15. № 6. P. 1417–1426.
Wie B. et al. A New Momentum Management Controller for the Space Station // J. Guidance, Control and Dynamics. 1989. V. 12. № 5. P. 714–722.
Warren W., Wie B., Geller D. Periodic-Disturbance Accommodating Control of the Space Station for Asymptotic Momentum Management // J. Guidance, Control and Dynamics. 1990. V. 13. № 6. P. 984–992.
Воронов А.А. Теория автоматического управления. Ч. 1. М.: Высш. шк., 1986. 367 с.
Квакернаак Х., Сиван Р. Линейные оптимальные системы управления. М.: Мир, 1977. 650 с.
Филимонов А.Б., Филимонов Н.Б. О пpоблеме неpобастности спектpа в задачах модального управления // Мехатроника, автоматизация и управление. 2011. № 10. С. 8–13.
Демидович Б.П. Лекции по математической теории устойчивости. М.: Наука, Физматлит, 1967. 472 с.
Зубов Н.Е., Микрин Е.А., Мисриханов М.Ш., Рябченко В.Н. Синтез развязывающих законов стабилизации орбитальной ориентации космического аппарата // Изв. РАН. ТиСУ. 2012. № 1. С. 92–108.
Зубов Н.Е., Микрин Е.А., Мисриханов М.Ш., Рябченко В.Н. Модификация метода точного размещения полюсов и его применение в задачах управления движением космического аппарата // Изв. РАН. ТиСУ. 2013. № 2. С. 118–132.
Зубов Н.Е., Микрин Е.А., Мисриханов М.Ш., Рябченко В.Н. Стабилизация взаимосвязанных движений летательного аппарата в каналах тангаж-рыскание при отсутствии информации об угле скольжения. Аналитический синтез // Изв. РАН. ТиСУ. 2015. № 1. С. 95–105.
Мисриханов М.Ш., Рябченко В.Н. Размещение полюсов в больших динамических системах с многими входами и выходами // ДАН. 2011. Т. 439. № 4. С. 464–466.
Зубов Н.Е., Зыбин Е.Ю., Микрин Е.А., Мисриханов М.Ш., Пролетарский А.В., Рябченко В.Н. Управление по выходу спектром движения космического аппарата // Изв. РАН. ТиСУ. 2014. № 4. С. 111–122.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления