Известия РАН. Теория и системы управления, 2020, № 3, стр. 75-80

Введение. Минимакс при транспортных ограничениях [1] имеет ряд обобщений [2, 3]. Еще одним таким обобщением является развитие, связанное с гиперграфами. Известно, что гиперграф [4] – это множество гиперребер на заданном множестве вершин [5]. Тогда k-однородным гиперграфом (k – 1-комплексом [6]) называют гиперграф, у которого каждое гиперребро инцидентно ровно k вершинам [7]. Соответственно над k-однородными гиперграфами, определенными над одним и тем же множеством вершин, действуют все классические для графов операции: пересечение, объединение, вычитание, дополнение. Кроме того, добавим операции “симметрическая разность”, “эквивалентность”, а также дополнения к объединению и пересечению. В [8] показано, что множество k-однородных гиперграфов с операциями пересечения и объединения является алгеброй. При этом для каждого гиперграфа существует вектор его степеней вершин [9]. Однако задача нахождения вектора степеней вершин от гиперграфа – результата операции над однородными гиперграфами связана либо с построением соответствующего гиперграфа, либо c выполнением алгоритма над матрицами смежности. Но следует учитывать, что нахождения вектора степеней вершин по матрице смежности имеет сложность $O({{n}^{k}})$. В работе рассматриваем способ нахождения векторов степеней вершин от ряда операций над однородными гиперграфами через вектор степени вершин от пересечения гиперграфов. Данный способ позволяет сократить объем вычислений и ускорить нахождение векторов от результатов операций над однородными гиперграфами.

1. Операции над k-однородными гиперграфами. Для начала следует отметить, что все k-однородные гиперграфы, которые здесь будут рассматриваться, относятся к одному и тому же классу – ненаправленные, без петель, с весами гиперребер, равными 1. Соответственно в дальнейшем это будет подразумеваться.

Теперь определим операции над однородными гиперграфами, которые нам потребуются в дальнейшем. Пусть даны два таких гиперграфа G₁ и G₂ с одинаковым множеством вершин, тогда обозначим операции над ними следующим образом:

${{G}_{1}} \cup {{G}_{2}}$ – объединение гиперребер G₁ и G₂ (OR);

${{G}_{1}} \cap {{G}_{2}}$ – пересечение гиперребер G₁ и G₂ (AND);

${{G}_{1}}{\text{/}}{{G}_{2}}$ – вычитание гиперребер G₂ из G₁;

${{\bar {G}}_{1}}$ и ${{\bar {G}}_{2}}$ – дополнения гиперграфов G₁ и G₂ соответственно (NOT);

${{G}_{1}} \oplus {{G}_{2}}$ – “симметричная разность” гиперребер G₁ и G₂ (XOR);

${{G}_{1}} \equiv {{G}_{2}}$ – “эквивалентность” наличия гиперребер или их отсутствия в G₁ и G₂ (EQV);

${{G}_{1}}\bar { \cup }{{G}_{2}}$ – дополнение к объединению гиперграфов (NOR);

${{G}_{1}}\bar { \cap }{{G}_{2}}$ – дополнение к пересечению гиперграфов (NAND).

Рассмотрим пример, иллюстрирующий действие представленных операций.

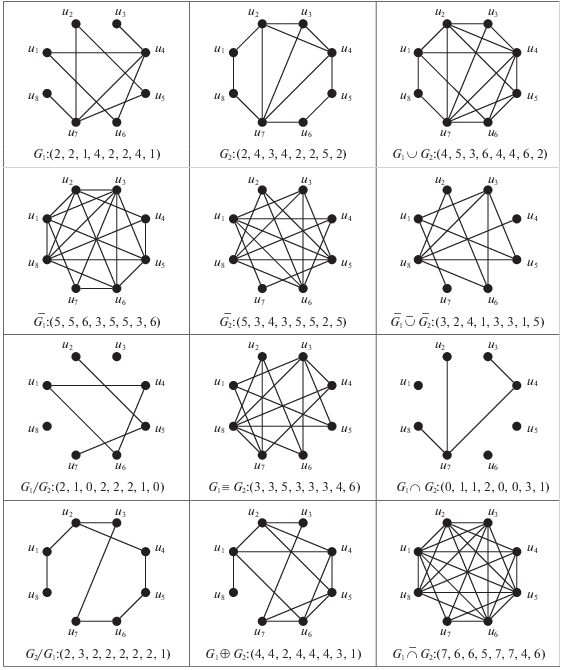
Пример 1. Пусть заданы 2-однородные гиперграфы (графы) ${{G}_{1}}$ и G₂ на восьми вершинах. Графы ${{G}_{1}}$ и G₂, а также полученные в результате выполнения операций над ними представлены на рисунке. Там же приведены векторы степеней вершин соответствующих графов.

Вспомним известные свойства вектора степеней вершин однородного гиперграфа. Пусть $G$ – k-однородный гиперграф на n вершинах и $A(G) = ({{a}_{1}}, \ldots ,{{a}_{n}})$ – вектор степеней его вершин. Тогда справедливо следующее неравенство:

где ${{u}_{i}}$ – вершина гиперграфа $G$, $C_{n}^{k}$ – число сочетаний из n по k элементов, а $i = \overline {1,n} $.

Зададим ${{G}_{F}}$ как полный k-однородный гиперграф на n вершинах, тогда $A({{G}_{F}}) = (C_{{n - 1}}^{{k - 1}}, \ldots ,C_{{n - 1}}^{{k - 1}})$. Если ${{G}_{0}}$ – вполне несвязанный гиперграф на n вершинах, то $A({{G}_{0}}) = (0, \ldots ,0)$.

2. Векторы степеней вершин от результатов операций над однородными гиперграфами. Теперь рассмотрим связь между вектором степеней вершин от операции дополнения для k-однородных гиперграфов и вектором самого гиперграфа.

Теорема 1. Пусть дан k-однородный гиперграф $G$ и его вектор степеней вершин $A(G)$, тогда вектор степеней вершин $\overline G $ равен

Доказательство теоремы вытекает из определения дополнения однородного гиперграфа G: так как в дополнении присутствуют все гиперребра, отсутствующие в $G$, но присутствующие в полном k-однородном гиперграфе на тех же вершинах, что и $G$.

Замечание 1. Пусть дан k-однородный гиперграф $G$ и его вектор степеней вершин $A(G)$, тогда сумма векторов $A(G)$ и $A(\overline G )$ равна вектору k-полного однородного гиперграфа, построенного на тех же вершинах, что и $G$.

Покажем связь между векторами от объединения и пересечения однородных гиперграфов.

Теорема 2. Пусть даны $k$-однородные гиперграфы ${{G}_{1}}$ и ${{G}_{2}}$, а также их векторы ${{A}_{1}} = A({{G}_{1}})$ и ${{A}_{2}} = A({{G}_{2}})$, тогда

Доказательство. При объединении однородных гиперграфов объединяются множества ребер. Таким образом, при наличии гиперребра в любом из гиперграфов в результирующем гиперграфе оно тоже будет присутствовать. Однако при сложении координат вектора в случае, если гиперребро принадлежит обоим гиперграфам, мы посчитаем его дважды. Другими словами, разница между ${{A}_{3}}$ и суммой векторов гиперграфов ${{G}_{1}}$ и ${{G}_{2}}$ равна вектору, который построен из гиперграфа, имеющего только те ребра, что есть у обоих гиперграфов. Но вектор, у которого учтены только ребра, принадлежащие обоим гиперграфам, это вектор $A({{G}_{1}} \cap {{G}_{2}})$. Таким образом ${{A}_{1}} + {{A}_{2}} - {{A}_{3}} = A({{G}_{1}} \cap {{G}_{2}})$. Что и требовалось доказать.

Следующая теорема может быть сформулирована независимо от предыдущей, но может быть и ее следствием.

Теорема 3. Пусть даны k-однородные гиперграфы ${{G}_{1}}$ и ${{G}_{2}}$, а также их векторы ${{A}_{1}} = A({{G}_{1}})$ и ${{A}_{2}} = A({{G}_{2}})$, тогда

Доказательство аналогично предыдущей теореме.

Теперь покажем, что можно выразить все операции через одну из уже определенных нами операций. Для демонстрации возьмем пересечение как базисную операцию над векторами.

Перейдем к вектору от операции разности однородных гиперграфов.

Теорема 4. Пусть даны k-однородные гиперграфы ${{G}_{1}}$ и ${{G}_{2}}$, а также их векторы ${{A}_{1}} = A({{G}_{1}})$ и ${{A}_{2}} = A({{G}_{2}})$, тогда

Доказательство аналогично теореме 2.

Теперь рассмотрим связь векторов и операции эквивалентности.

Теорема 5. Пусть даны k-однородные гиперграфы ${{G}_{1}}$ и ${{G}_{2}}$, а также их векторы ${{A}_{1}} = A({{G}_{1}})$ и ${{A}_{2}} = A({{G}_{2}})$, тогда

Доказательство. Операцию эквивалентности можно представить как

Теперь возьмем вектор от полученного гиперграфа:

При этом $A(({{G}_{1}} \cap {{G}_{2}}) \cap ({{G}_{1}}\overline \cup {{G}_{2}})) = A({{G}_{0}})$, так как $({{G}_{1}} \cap {{G}_{2}}) \cap ({{G}_{1}}\overline \cup {{G}_{2}}) = \emptyset $. Следовательно,

Отсюда легко получить следующую теорему.

Теорема 6. Пусть даны k-однородные гиперграфы ${{G}_{1}}$ и ${{G}_{2}}$, а также их векторы ${{A}_{1}} = A({{G}_{1}})$ и ${{A}_{2}} = A({{G}_{2}})$, тогда

Доказательство. Данное утверждение легко доказывается, если вспомнить, что гиперграф ${{G}_{1}} \oplus {{G}_{2}} = \overline {{{G}_{1}} \equiv {{G}_{2}}} $.

Единственное препятствие для простого расчета вектора от результата любой из предложенных операций состоит в том, что нужно находить вектор от пересечения k-однородных гиперграфов. Для данной проблемы можно предложить следующее решение.

Замечание 2. Пусть даны k-однородные гиперграфы ${{G}_{1}}$ и ${{G}_{2}}$ и их матрицы смежности X₁ и X₂ соответственно. Тогда для вектора $A({{G}_{1}} \cap {{G}_{2}}) = ({{a}_{1}}, \ldots ,{{a}_{n}})$ его координаты можно найти следующим образом:

Проиллюстрируем полученные результаты на примере.

Пример 2. Рассмотрим векторы, представленные в примере 1: ${{A}_{1}} = A({{G}_{1}}) = (2,2,1,4,2,2,4,1)$ и ${{A}_{2}} = A({{G}_{2}}) = (2,4,3,4,2,2,5,2)$. Также возьмем вектор ${{A}_{3}} = A({{G}_{1}} \cap {{G}_{2}}) = (0,1,1,2,0,0,3,1)$.

Так как ${{G}_{1}}$ и ${{G}_{2}}$ – это графы (2-однородные гиперграфы), то вектор полного графа на восьми вершинах будет равен ${{A}_{F}} = A({{G}_{F}}) = (7,7,7,7,7,7,7,7)$.

Теперь мы можем найти векторы для других операций:

При сравнении с примером 1 видим, что все векторы найдены верно.

В заключение рассмотрим пример с 5-однородными гиперграфами.

Пример 3. Пусть заданы два 5-однородных гиперграфа ${{G}_{1}} = {{G}_{1}}({{S}_{1}},V)$ и ${{G}_{2}} = {{G}_{2}}({{S}_{2}},V)$, где $V = {{u}_{1}}, \ldots ,{{u}_{7}}$ – множество вершин, ${{S}_{1}}$ и ${{S}_{2}}$ – множества гиперребер. Зададим гиперребра из множества $S$ в упрощенном виде как наборы по 5 чисел-индексов вершин:

Легко находим векторы степеней вершин ${{A}_{1}} = A({{G}_{1}}) = (5,5,6,5,5,7,7)$ и A₂ = A(G₂) = (10, 11, 11, $12,10,10,11)$. Также легко определить вектор полного 5-однородного гиперграфа на семи вершинах: ${{A}_{F}} = (15,15,15,15,15,15,15)$.

Далее построим гиперграф-пересечение ${{G}_{3}} = {{G}_{3}}({{S}_{3}},V) = {{G}_{1}} \cap {{G}_{2}}$, где ${{S}_{3}} = {{S}_{1}} \cap {{S}_{2}}$:

Соответственно вектор ${{A}_{3}} = A({{G}_{1}} \cap {{G}_{2}}) = (3,3,4,3,3,4,5)$. Следовательно, векторы остальных гиперграфов-результатов операций равны:

В завершение примера построим множества гиперребер для гиперграфов-результатов рассматриваемых операций. Убедиться в соответствии найденных векторов построенным гиперграфам несложно:

Заключение. Таким образом мы получили способ нахождения вектора от результата любой из рассматриваемых операций через вектор от пересечения k-однородных гиперграфов, который также можно легко определить через матрицу смежности. В частном случае, алгоритм для вычисления вектора от пересечения графов имеет сложность O(n^k), но, вычислив один раз вектор пересечения, можно рассчитать остальные операции со сложностью O(n).