Известия РАН. Теория и системы управления, 2020, № 3, стр. 164-176
СТАБИЛИЗАЦИЯ РЕЖИМА СОЛНЕЧНОЙ ОРИЕНТАЦИИ ИСКУССТВЕННОГО СПУТНИКА ЗЕМЛИ БЕЗ НАКОПЛЕНИЯ КИНЕТИЧЕСКОГО МОМЕНТА ГИРОСИСТЕМЫ
А. И. Игнатов *
АО “ГКНПЦ им. М.В. Хруничева”
Москва, Россия
* E-mail: general_z@mail.ru
Поступила в редакцию 14.11.2019
После доработки 26.11.2019
Принята к публикации 27.01.2020
Аннотация
Исследуется движение искусственного спутника Земли в различных вариантах режима солнечной ориентации на низкой околоземной орбите. Спутник по форме близок к цилиндру с двумя панелями солнечных батарей. Не поворачивающиеся панели батарей расположены вдоль продольной оси спутника симметрично относительно нее. В режиме солнечной ориентации нормаль к плоскости солнечных батарей спутника неизменно направлена на Солнце, продольная ось лежит вблизи плоскости орбиты, абсолютная угловая скорость спутника весьма мала. В качестве исполнительных органов системы управления спутником используется гиросистема (комплекс двигателей-маховиков или гиродинов). Рассматривается два варианта закона управления собственным кинетическим моментом гиросистемы. Первый вариант обеспечивает только затухание возмущенного движения спутника в окрестности положения покоя с требуемой скоростью. Второй вариант дополнительно ограничивает рост накапливаемого кинетического момента гиросистемы за счет управления углом поворота спутника вокруг нормали к плоскости солнечных батарей.
Введение. Режим солнечной ориентации часто используется в процессе эксплуатации искусственных спутников Земли, поскольку обеспечивает максимальный приток электроэнергии на борт. В данной работе исследуется поддержание режима солнечной ориентации спутника на низкой околоземной орбите с помощью гиросистемы в течение длительного времени. Гиросистема может состоять из комплекса управляющих двигателей-маховиков или гиродинов. При использовании гиросистемы одним из основных требований к режиму ориентации спутника является малая скорость накопления собственного кинетического момента гиросистемы (гиростатического момента) для увеличения интервалов времени между проведением разгрузок. Накопление гиростатического момента происходит за счет воздействия на спутник гравитационного и аэродинамического моментов. Рассматривается два варианта закона управления гиростатическим моментом спутника. Первый вариант обеспечивает затухание возмущенного движения спутника в окрестности положения его солнечной ориентации, второй вариант дополнительно ограничивает накопление гиростатического момента за счет управления углом поворота спутника вокруг нормали к плоскости солнечных батарей.
1. Уравнения движения спутника. Спутник считаем гиростатом, центр масс которого движется по геоцентрической орбите. Для описания движения спутника будем использовать три правые декартовы системы координат.
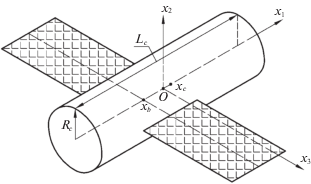
1. Связанная система координат – $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$, образованная главными центральными осями инерции спутника. Начало системы находится в центре масс спутника – точке O. Полагаем, что спутник имеет форму прямого кругового цилиндра (рис. 1) радиуса ${{R}_{c}}$ и высоты ${{L}_{c}}$, с двумя прикрепленными к нему одинаковыми прямоугольными пластинами – солнечными батареями суммарной площади ${{S}_{b}}$. Ось цилиндра совпадает с осью $O{{x}_{1}}$. Солнечные батареи расположены в плоскости $O{{x}_{1}}{{x}_{3}}$ симметрично относительно оси $O{{x}_{1}}$, стороны батарей параллельны осям $O{{x}_{1}}$ и $O{{x}_{3}}$, ось $O{{x}_{2}}$ перпендикулярна плоскости солнечных батарей. Светочувствительная сторона солнечных батарей обращена к полупространству x2 > 0. Координаты геометрических центров цилиндра и пластин солнечных батарей обозначим $({{x}_{c}},0,0)$ и $({{x}_{b}},0,0)$ соответственно, базисные орты этой системы – ${{{\mathbf{e}}}_{1}},\;{{{\mathbf{e}}}_{2}},\;{{{\mathbf{e}}}_{3}}.$ Ниже, если не оговорено особо, компоненты векторов и координаты точек относятся к системе $O{{x}_{1}}{{x}_{2}}{{x}_{3}}.$
2. Гринвичская система координат – ${{O}_{E}}{{y}_{1}}{{y}_{2}}{{y}_{3}}$. Точка OE – центр Земли, плоскость ${{O}_{E}}{{y}_{1}}{{y}_{2}}$ совпадает с плоскостью экватора, ось ${{O}_{E}}{{y}_{1}}$ пересекает гринвичский меридиан, ось ${{O}_{E}}{{y}_{3}}$ направлена к Северному полюсу.
3. Квазиинерциальная система координат – ${{O}_{E}}{{Z}_{1}}{{Z}_{2}}{{Z}_{3}}$. Ось ${{O}_{E}}{{Z}_{2}}$ параллельна вектору кинетического момента орбитального движения спутника, ось ${{O}_{E}}{{Z}_{3}}$ лежит в плоскости экватора и направлена в восходящий узел оскулирующей орбиты спутника. Базис этой системы образован ортами ${{{\mathbf{E}}}_{1}},\;{{{\mathbf{E}}}_{2}},\;{{{\mathbf{E}}}_{3}}$.
Матрицу перехода от системы ${{O}_{E}}{{Z}_{1}}{{Z}_{2}}{{Z}_{3}}$ к системе ${{O}_{E}}{{y}_{1}}{{y}_{2}}{{y}_{3}}$ обозначим $C = \left\| {{{c}_{{ij}}}} \right\|_{{i,j = 1}}^{3}$, где cij – косинус угла между осями ${{O}_{E}}{{y}_{i}}$ и ${{O}_{E}}{{Z}_{j}}$. Элементы этой матрицы выражаются через координаты и компоненты скорости центра масс спутника в гринвичской системе координат. Матрица $A = \left\| {{{a}_{{ij}}}} \right\|_{{i,j = 1}}^{3}$ – матрица перехода от системы $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ к системе ${{O}_{E}}{{Z}_{1}}{{Z}_{2}}{{Z}_{3}}$; ${{a}_{{ij}}} = {{{\mathbf{E}}}_{i}} \cdot {{{\mathbf{e}}}_{j}}$ – косинус угла между осями ${{O}_{E}}{{Z}_{i}}$ и $O{{x}_{j}}$; $B = \left\| {{{b}_{{ij}}}} \right\|_{{i,j = 1}}^{3}$ – матрица перехода от системы $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ к системе ${{O}_{E}}{{y}_{1}}{{y}_{2}}{{y}_{3}}$; bij – косинус угла между осями ${{O}_{E}}{{y}_{i}}$ и $O{{x}_{j}}$. Тогда справедливо соотношение $B = CA$.
Положение системы $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$, относительно системы ${{O}_{E}}{{Z}_{1}}{{Z}_{2}}{{Z}_{3}}$, будем также задавать углами $\psi $, $\theta $ и $\varphi $, которые введем следующим образом. Если точку ${{O}_{E}}$ перенести в точку O, то систему ${{O}_{E}}{{Z}_{1}}{{Z}_{2}}{{Z}_{3}}$ можно перевести в систему $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ тремя последовательными поворотами: 1) на угол $\psi $ вокруг оси ${{O}_{E}}{{Z}_{2}}$, 2) на угол ${\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2} - \theta $ вокруг новой оси ${{O}_{E}}{{Z}_{1}}$, 3) на угол $\varphi + \pi $ вокруг новой оси ${{O}_{E}}{{Z}_{2}}$, совпадающей с осью $O{{x}_{2}}$. Элементы матрицы A выражаются через эти углы с помощью следующих формул:
(1.1)
$\begin{gathered} {{a}_{{11}}} = - \cos \varphi \cos \psi + \sin \varphi \sin \psi \sin \theta ,\quad {{a}_{{12}}} = \sin \psi \cos \theta , \\ {{a}_{{13}}} = - \sin \varphi \cos \psi - \cos \varphi \sin \psi \sin \theta , \\ {{a}_{{21}}} = - \sin \varphi \cos \theta ,\quad {{a}_{{22}}} = \sin \theta ,\quad {{a}_{{23}}} = \cos \varphi \cos \theta , \\ {{a}_{{31}}} = \cos \varphi \sin \psi + \sin \varphi \cos \psi \sin \theta , \\ {{a}_{{32}}} = \cos \psi \cos \theta ,\quad {{a}_{{33}}} = \sin \varphi \sin \psi - \cos \varphi \cos \psi \sin \theta . \\ \end{gathered} $Уравнения движения спутника состоят из двух подсистем. Одна подсистема описывает движение центра масс спутника в гринвичской системе координат. Она образована уравнениями для компонент радиуса-вектора ${\mathbf{r}}$ этого центра масс и компонент вектора ${\mathbf{v}}$ его относительной скорости [1] . В уравнениях учитываются нецентральность гравитационного поля Земли и сопротивление атмосферы. Нецентральность поля учитывается с точностью до членов порядка (16, 16) включительно в разложении гравитационного потенциала Земли в ряд по шаровым функциям. Атмосфера считается вращающейся вместе с Землей, ее плотность рассчитывается согласно модели ГОСТ Р 25645.166-2004. Параметры атмосферы и баллистический коэффициент спутника считаются неизменными, это упрощение не влияет на точность описания его вращательного движения.
Другая подсистема описывает движение спутника относительно центра масс (вращательное движение). Она образована уравнениями, выражающими теорему об изменении кинетического момента спутника в его движении относительно центра масс, кинематическими уравнениями Пуассона для элементов первых двух строк матрицы $B$ и уравнениями, описывающими изменение кинетического момента гиросистемы. В уравнениях, выражающих теорему об изменении кинетического момента спутника, учитываются гравитационный и аэродинамический моменты. Гравитационный момент задается формулой [2]
(1.2)
${{{\mathbf{M}}}_{g}} = 3\frac{{{{\mu }_{E}}}}{{{{r}^{5}}}}({\mathbf{r}} \times \hat {I}{\mathbf{r}}),\quad r = {\text{|}}{\mathbf{r}}{\text{|}},\quad \hat {I} = {\text{diag}}({{I}_{1}},{{I}_{2}},{{I}_{3}}),$Формула аэродинамического момента имеет вид
Подсистема уравнений вращательного движения спутника имеет вид
(1.3)
$\begin{gathered} \hat {I}\frac{{\tilde {d}{\mathbf{\omega }}}}{{dt}} + {\mathbf{\omega }} \times \hat {I}{\mathbf{\omega }} = 3\frac{{{{\mu }_{E}}}}{{{{r}^{5}}}}({\mathbf{r}} \times \hat {I}{\mathbf{r}}) + p({\mathbf{v}} \times {{{\mathbf{e}}}_{1}}) + {{{\mathbf{M}}}_{c}}, \\ \frac{{\tilde {d}{{{\mathbf{b}}}_{1}}}}{{dt}} + {\mathbf{\omega }} \times {{{\mathbf{b}}}_{1}} = {{\omega }_{E}}{{{\mathbf{b}}}_{2}},\quad \frac{{\tilde {d}{{{\mathbf{b}}}_{2}}}}{{dt}} + {\mathbf{\omega }} \times {{{\mathbf{b}}}_{2}} = - {{\omega }_{E}}{{{\mathbf{b}}}_{1}}, \\ \end{gathered} $Чтобы замкнуть подсистему уравнений вращательного движения (1.3), надо добавить к ней уравнение, описывающее изменение гиростатического момента спутника. Это уравнение запишем в виде
(1.4)
$\frac{{\tilde {d}{\mathbf{H}}}}{{dt}} + {\mathbf{\omega }} \times {\mathbf{H}} = - {{{\mathbf{M}}}_{c}},$В расчетах использовались следующие параметры описанной модели. Параметры спутника: $m = $ 6440 кг, ${{I}_{1}} = $ 2600 кг ∙ м2, ${{I}_{2}} = $ 11 100 кг ∙ м2, ${{I}_{3}} = $ 10 900 кг ∙ м2, Rc = 1.3 м, ${{L}_{c}}$ = 5.0 м, ${{S}_{b}}$ = 33 м2, xb = –1 м, xc = 0.3 м. Параметры модели атмосферы: ${{F}_{{10.7}}} = $ ${{F}_{{81}}} = $ 150, ${{A}_{p}}$ = 12.
Рассматриваются два варианта начальных условий движения центра масс спутника. Соответствующие им решения уравнений орбитального движения назовем орбитами I и II. Начальные условия орбиты I задавались в момент 07:13:07 UTC 05.05.2013. На этот момент времени элементы орбиты составляли: высота в апогее 575.2 км, высота в перигее 546.8 км, наклонение 64.87°, аргумент широты перигея –124.65°, долгота восходящего узла (отсчитывается от точки весеннего равноденствия эпохи даты) –16.73°. В этом случае максимальное значение угла $\vartheta $ между ортом направления “Земля–Солнце” и плоскостью орбиты спутника составляет ~47°. Начальные условия орбиты II задавались аналогичным образом в момент 07:13:07 UTC 21.12.2013. На этот момент времени численные значения параметров орбиты II принимались такими же, как и для орбиты I, за исключением значения долготы восходящего узла, равного –150.03°. В случае орбиты II максимальное значение угла $\vartheta $ составляет ~88°. Таким образом орбиты I и II существенно по-разному расположены относительно Солнца.
Начальные условия уравнений (1.3), (1.4) задавались в тот же момент времени, что и начальные условия орбитального движения. Этот момент служил началом отсчета времени – точкой $t$ = 0.
2. Трехосная солнечная ориентация спутника. Сперва рассмотрим режим трехосной солнечной ориентации спутника, в котором нормаль к плоскости солнечных батарей (ось Ox2) неизменно направлена на Солнце, продольная ось Ox1 лежит в плоскости орбиты, абсолютная угловая скорость спутника мала.
Реализуем построение закона управления гиросистемой в упрощенной ситуации, когда внешние моменты на спутник не действуют, орбита спутника и направление на Солнце неизменны в абсолютном пространстве. Тогда первое уравнение системы (1.3) принимает вид
(2.1)
$\hat {I}\frac{{\tilde {d}{\mathbf{\omega }}}}{{dt}} + {\mathbf{\omega }} \times \hat {I}{\mathbf{\omega }} = {{{\mathbf{M}}}_{c}}.$Пусть s – орт направления “Земля–Солнце”. В этом случае орт ${\mathbf{n}} = ({\mathbf{s}} \times {{{\mathbf{E}}}_{2}}){\text{/|}}{\mathbf{s}} \times {{{\mathbf{E}}}_{2}}{\text{|}}$ лежит в плоскости орбиты спутника и ортогонален орту s. Изменение ортов s и n в системе $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ описывается уравнениями
(2.2)
$\frac{{\tilde {d}{\mathbf{s}}}}{{dt}} + {\mathbf{\omega }} \times {\mathbf{s}} = 0,\quad \frac{{\tilde {d}{\mathbf{n}}}}{{dt}} + {\mathbf{\omega }} \times {\mathbf{n}} = 0.$Зададим функцию ${{{\mathbf{M}}}_{c}} = {{{\mathbf{M}}}_{c}}({\mathbf{\omega }},{\mathbf{s}},{\mathbf{n}})$ так, чтобы система (2.1), (2.2) имела асимптотически устойчивое стационарное решение
(2.3)
${\mathbf{\omega }} = 0,\quad {{{\mathbf{e}}}_{1}} = {\mathbf{n}},\quad {{{\mathbf{e}}}_{2}} = {\mathbf{s}}.$Возьмем
(2.4)
${{{\mathbf{M}}}_{c}} = l({{{\mathbf{e}}}_{2}} \times {\mathbf{s}} + {{{\mathbf{e}}}_{1}} \times {\mathbf{n}}) - \hat {W}{\mathbf{\omega }},$Система (2.1), (2.2), (2.4) допускает стационарное решение (2.3). Вдоль произвольного решения этой системы
Здесь E – полная энергия системы, точка над буквой означает дифференцирование по времени $t$. Взяв E в качестве функции Ляпунова, можно с помощью теоремы Барбашина–Красовского [4] установить асимптотическую устойчивость решения (2.3).
Для упрощения выбора параметров управления (2.4) запишем
(2.5)
${{{\mathbf{M}}}_{c}} = {{\xi }^{2}}\hat {I}({{{\mathbf{e}}}_{2}} \times {\mathbf{s}} + {{{\mathbf{e}}}_{1}} \times {\mathbf{n}}) - 2\xi \hat {I}\hat {D}{\mathbf{\omega }},$Линеаризуем систему (2.1), (2.2), (2.5) в окрестности стационарного решения (2.3). Пусть δ = ${{({{\delta }_{1}},{{\delta }_{2}},{{\delta }_{3}})}^{T}}$ – вектор бесконечно малого поворота из положения ${{{\mathbf{e}}}_{1}} = {\mathbf{n}}$, ${{{\mathbf{e}}}_{2}} = {\mathbf{s}}$. В окрестности решения (2.3) выполнены соотношения ${\mathbf{\omega }} \approx {\mathbf{\dot {\delta }}}$, ${\mathbf{s}} \approx {{{\mathbf{e}}}_{2}} - {\mathbf{\delta }} \times {{{\mathbf{e}}}_{2}},$ ${\mathbf{n}} \approx {{{\mathbf{e}}}_{1}} - {\mathbf{\delta }} \times {{{\mathbf{e}}}_{1}}$, и систему (2.1), (2.5) можно привести к виду
Выписанная система асимптотически устойчива, ее произвольное решение допускает оценку $\left\| {{\mathbf{\delta }}(t)} \right\| \leqslant \kappa \left\| {{\mathbf{\delta }}(0)} \right\|\exp ( - \xi t)$, где $\kappa $ – положительная постоянная, не зависящая от ${\mathbf{\delta }}\,(0)$. Согласно теореме Малкина об устойчивости при постоянно действующих возмущениях [5] , можно ожидать, что режим солнечной ориентации при достаточно большом значении $\xi $ будет устойчив и с учетом действия на спутник внешних возмущающих моментов. Параметр ξ возьмем настолько большим, чтобы характерное время действия на спутник управляющего момента, равное $1{\text{/}}\xi $, было существенно меньше аналогичного времени для гравитационного и аэродинамического моментов, которыми пренебрегаем. При подходящем выборе параметра ξ и реальной орбите возмущенное движение спутника в окрестности положения покоя (2.3) будет затухать с требуемой скоростью. Ниже принято, что ξ = 0.01 с–1. Полагаем, что закон управления (2.5) формируется в соответствии с показаниями установленных на спутнике датчиков ориентации и угловой скорости.
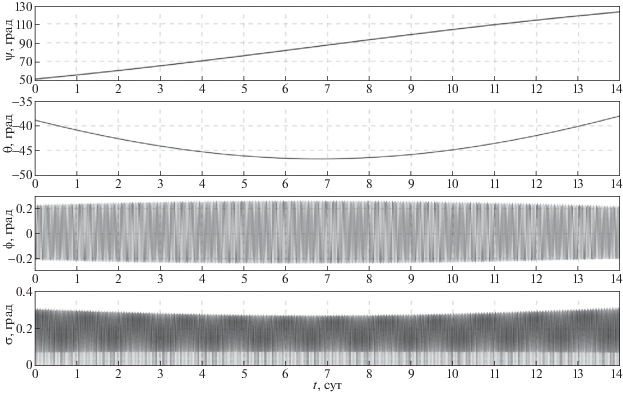
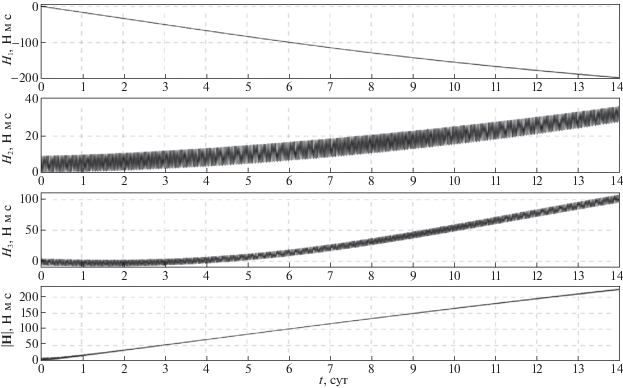
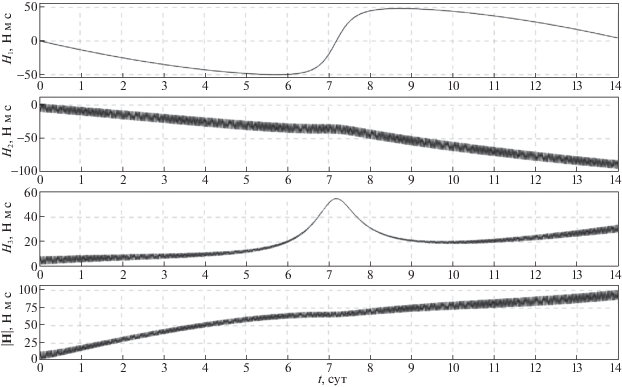
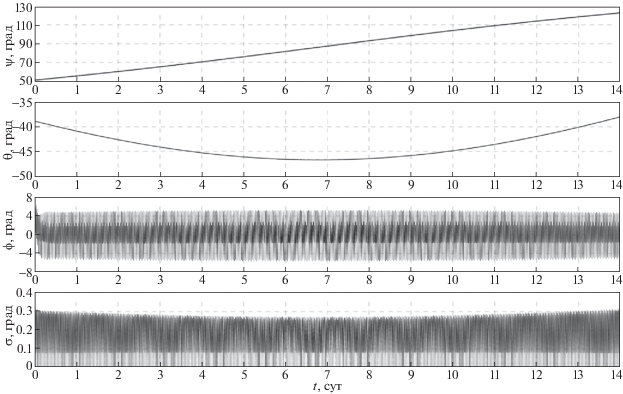
3. Моделирование режима трехосной солнечной ориентации спутника. Покажем возможности гиросистемы спутника при реализации выбранного закона изменения управляющего момента (2.5). С этой целью вычислим решение системы (1.3), (1.4), (2.5). Компоненты орта s в гринвичской системе координат рассчитывались по приближенным формулам [6] . Начальные условия системы (1.3), (1.4), (2.5) в момент времени t = 0 задавались следующим образом. Спутник в гринвичской системе координат занимает положение (2.3), т.е. ${{{\mathbf{e}}}_{1}} = {\mathbf{n}}$, ${{{\mathbf{e}}}_{2}} = {\mathbf{s}}$. Гиростатический момент спутника H(0) = 0. Начальные значения компонент угловой скорости ${{\omega }_{i}}$ задавались с учетом ошибок в их реализации: ${{\omega }_{1}}(0) = {{\omega }_{2}}(0) = {{\omega }_{3}}(0)$ = 0.01 град/с. Результаты расчетов движения спутника, полученные в рамках принятой модели для орбиты I, приведены на рис. 2, 3, для орбиты II – на рис. 4, 5. Эти результаты представлены графиками зависимости от времени углов $\psi $, $\theta $, $\varphi $ и угла $\sigma = \arccos \left( {{\mathbf{s}} \cdot {{{\mathbf{e}}}_{2}}} \right)$. На рисунках также представлены графики компонент гиростатического момента ${{H}_{i}}$, $i = $ 1, 2, 3, и модуля вектора гиростатического момента |H|. Все графики на рис. 2–5 построены на интервалах времени 14 сут. Переходный процесс (процесс гашения возмущенного движения), обусловленный ошибками в задании начальной угловой скорости, длится менее 10 мин и из-за масштаба на рисунках не виден. Результаты моделирования показывают, что для обоих рассматриваемых вариантов орбит использование закона управления (2.5) обеспечивает трехосную солнечную ориентацию спутника и затухание его возмущенного движения в окрестности положения покоя (2.3). Экстремумы на графиках углов и компонент вектора H, представленных на рис. 4, 5, соответствуют максимальному значению угла между плоскостью орбиты спутника и ортом направления “Земля–Солнце”. Амплитуды установившихся колебаний компонент абсолютной угловой скорости спутника ограничены следующими значениями, град/c: ${\text{|}}{{\omega }_{1}}{\text{|}} < $ 1 × 10–4, ${\text{|}}{{\omega }_{2}}{\text{|}} < $ 2 × 10–3, ${\text{|}}{{\omega }_{3}}{\text{|}} < $ 7 × 10–4.
При этом величина модуля вектора гиростатического момента |H| неограниченно возрастает на всем интервале времени. Чтобы ограничить рост гиростатического момента спутника, не нарушая режим его солнечной ориентации, ниже предложен соответствующий закон управления.
4. Реализация режима солнечной ориентации спутника без накопления кинетического момента гиросистемы. Рассмотрим возможность использования закона управления, позволяющего не только обеспечить затухание возмущенного движения спутника в окрестности положения покоя с требуемой скоростью, но и дополнительно ограничить рост накапливаемого гиростатического момента спутника. Чтобы не нарушать режим солнечной ориентации спутника, накопление гиростатического момента будем контролировать только за счет управления углом поворота спутника вокруг орта ${{{\mathbf{e}}}_{2}} = {\mathbf{s}}$.
Рассмотрим функцию $F = ({\mathbf{K}}\hat {W}{\mathbf{K}}){\text{/}}2$, где ${\mathbf{K}} = {{({{K}_{1}},{{K}_{2}},{{K}_{3}})}^{T}}$ – кинетический момент спутника в его движении относительно центра масс. Примем, что из всех внешних моментов на спутник действует только гравитационный, т.е. ${\mathbf{\dot {K}}} = {{{\mathbf{M}}}_{g}}$. Тогда
(4.1)
${{\ddot {\varphi }}_{c}} + \chi {{\dot {\varphi }}_{c}} + \frac{{df}}{{d{{\varphi }_{c}}}} = 0,\quad \chi = {\text{const}} > 0.$Изменение угла ${{\varphi }_{c}}$ будем считать быстрым – с характерным временем намного меньше орбитального периода. В этом движении можно приближенно принять ${\mathbf{\omega }} = {{\dot {\varphi }}_{c}}\,{{{\mathbf{e}}}_{2}}$ и орт ${\mathbf{\gamma }}$ считать неизменным в абсолютном пространстве. Тогда изменение вектора K и орта ${\mathbf{\gamma }}$ относительно системы $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ будет описываться уравнениями
Найдем $df{\text{/}}d{{\varphi }_{c}}$. Заметим, что $\dot {f} = {{\dot {\varphi }}_{c}}(df{\text{/}}d{{\varphi }_{c}})$. С другой стороны, $\dot {f}$ можно представить в виде
При рассматриваемых допущениях имеем
Здесь
Положим, что $\hat {W} = {\text{diag}}({{W}_{1}},{{W}_{2}},{{W}_{3}})$, тогда, преобразовав слагаемые, стоящие в фигурных скобках, получим
(4.2)
$\begin{gathered} \frac{{df}}{{d{{\varphi }_{c}}}} = \frac{{\dot {f}}}{{{{{\dot {\varphi }}}_{c}}}} = \tilde {f} = - \frac{{3{{\mu }_{E}}}}{{{{r}^{3}}}}\left\{ { - \left[ {{{W}_{3}}\left( {{{I}_{2}} - {{I}_{1}}} \right) - {{W}_{1}}\left( {{{I}_{2}} - {{I}_{3}}} \right)} \right]{{\gamma }_{1}}{{\gamma }_{2}}{{K}_{1}} + } \right. \\ \, + \left. {{{W}_{2}}\left( {{{I}_{3}} - {{I}_{1}}} \right)(\gamma _{1}^{2} - \gamma _{3}^{2}){{K}_{2}} + \left[ {{{W}_{3}}\left( {{{I}_{2}} - {{I}_{1}}} \right) - {{W}_{1}}\left( {{{I}_{2}} - {{I}_{3}}} \right)} \right]{{\gamma }_{2}}{{\gamma }_{3}}{{K}_{3}}} \right\}. \\ \end{gathered} $При $\hat {W} = \kappa \,diag(1,1,1)$, где $\kappa = {\text{const}}$ > 0, выражение (4.2) представляет собой закон управления, описанный в [7] . Рассмотрим случай, когда
Выражение (4.2) теперь примет вид
(4.3)
$.\tilde {f} = - \frac{{3{{\mu }_{E}}}}{{{{r}^{3}}}}[ - ({{\kappa }_{3}} - {{\kappa }_{1}}){{\gamma }_{1}}{{\gamma }_{2}}{{K}_{1}} + {{\kappa }_{2}}(\gamma _{1}^{2} - \gamma _{3}^{2}){{K}_{2}} + ({{\kappa }_{3}} - {{\kappa }_{1}}){{\gamma }_{2}}{{\gamma }_{3}}{{K}_{3}}].$Такой закон в общем случае оказался более эффективным.
Если орбита спутника близка к круговой, то (4.3) можно заменить выражением
(4.4)
$\tilde {f} = - 3\omega _{0}^{2}[ - \left( {{{\kappa }_{3}} - {{\kappa }_{1}}} \right){{\gamma }_{1}}{{\gamma }_{2}}{{K}_{1}} + {{\kappa }_{2}}(\gamma _{1}^{2} - \gamma _{3}^{2}){{K}_{2}} + \left( {{{\kappa }_{3}} - {{\kappa }_{1}}} \right){{\gamma }_{2}}{{\gamma }_{3}}{{K}_{3}}],$Движение спутника, близкое движению вокруг орта ${{{\mathbf{e}}}_{2}}$, согласно уравнению (4.1), может быть реализовано, если управляющий момент (2.5) дополнить слагаемым
В этом случае векторное уравнение, описывающее изменение гиростатического момента ${\mathbf{H}}$, принимает вид
(4.6)
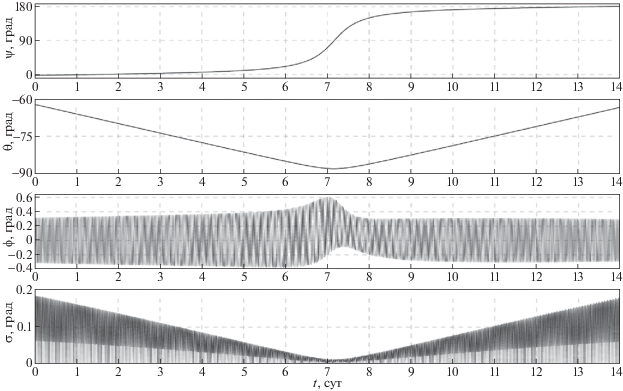
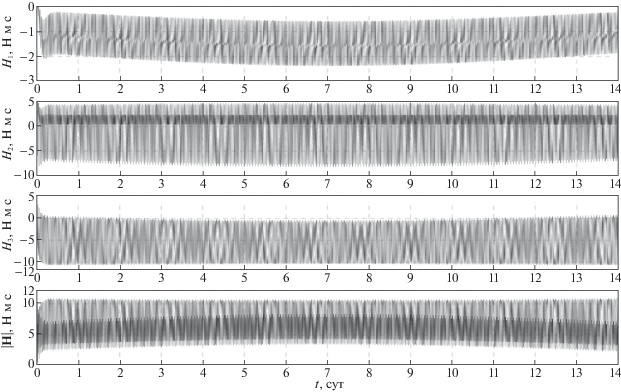
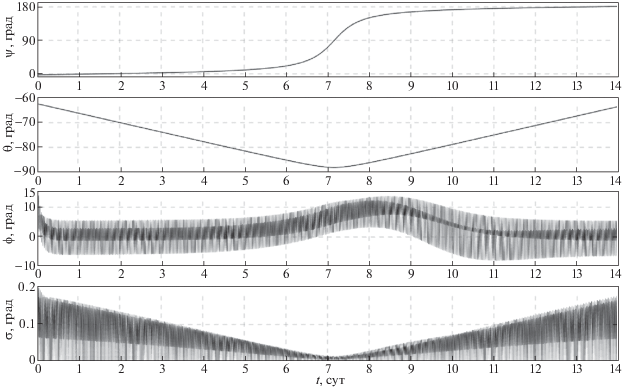
$\frac{{\tilde {d}{\mathbf{H}}}}{{dt}} + {\mathbf{\omega }} \times {\mathbf{H}} = - ({{{\mathbf{M}}}_{c}} + {\mathbf{M}}_{c}^{'}).$5. Реализация режима солнечной ориентации спутника без накопления кинетического момента гиросистемы. Покажем, что выбранный закон изменения управляющего момента (2.5), (4.5) действительно обеспечивает солнечную ориентацию спутника и при этом ограничивает накопление гиростатического момента. С этой целью вычислим решение системы (1.3), (2.5), (4.5), (4.6) при $\chi = 2\xi $, $\xi $ = 0.01 с–1, ${{\kappa }_{1}} = $${{\kappa }_{2}} = $ 1 (Н ∙ м ∙ с)–1, ${{\kappa }_{3}} = $ 3 (Н ∙ м ∙ с)–1 с начальными условиями в момент времени t = 0, заданными как в разд. 3. Результаты расчетов движения спутника, полученные в рамках принятой модели для орбиты I, приведены на рис. 6, 7, для орбиты II – на рис. 8, 9. Результаты моделирования представлены графиками зависимости от времени углов $\psi $, $\theta $, $\varphi $ и угла $\sigma $. На рисунках также показаны графики компонент гиростатического момента ${{H}_{i}}$, $i$ = 1, 2, 3, и модуля вектора гиростатического момента ${\text{|}}{\mathbf{H}}{\text{|}}$. Все графики на рис. 6–9 построены на интервалах времени 14 сут. На этих рисунках переходный процесс, обусловленный ошибками в задании начальной угловой скорости, длится менее 10 мин и из-за масштаба не виден. Результаты моделирования показывают, что использование закона управления (2.5), (4.5) обеспечивает солнечную ориентацию спутника и затухание возмущенного движения спутника в окрестности положения покоя для обеих рассматриваемых орбит.
Амплитуды установившихся колебаний компонент абсолютной угловой скорости спутника ограничены следующими значениями, град/c: ${\text{|}}{{\omega }_{1}}{\text{|}} < $ 1.5 × 10–4, ${\text{|}}{{\omega }_{2}}{\text{|}} < $ 0.03, ${\text{|}}{{\omega }_{3}}{\text{|}} < $ 8 × 10–4. При численном моделировании системы (1.3), (2.5), (4.5), (4.6) использование выражения (4.3) или (4.4) в законе управления (4.5) не дает видимой разницы в полученных решениях, что обусловлено формой орбиты спутника, близкой к круговой. Величина накапливаемого гиростатического момента спутника для орбиты I остается ограниченной значением ${\text{|}}{\mathbf{H}}{\text{|}}$ < 12 Н ∙ м ∙ с (см. рис. 7). В случае движения спутника по орбите II, когда Солнце относительно плоскости орбиты поднимается достаточно высоко $(\vartheta $ > 75°), значение ${\text{|}}{\mathbf{H}}{\text{|}}$ начинает возрастать (см. рис. 9), достигая своего максимума ${\text{|}}{\mathbf{H}}{\text{|}} = $ 31 Н ∙ м ∙ с при $\vartheta \approx $ 88°. В дальнейшем, по мере уменьшения $\vartheta $, происходит разгрузка гиросистемы до значения ${\text{|}}{\mathbf{H}}{\text{|}}$ < 12 Н ∙ м ∙ с. Чтобы избежать нежелательного роста кинетического момента гиросистемы при значении $\vartheta ,$ близком к максимальному в случае орбиты II (см. рис. 9), можно при достижении некоторого заранее выбранного порогового значения $\vartheta $ переориентировать спутник в режим орбитальной ориентации без накопления собственного кинетического момента гиросистемы [8–10] .
6. Использование режима орбитальной ориентации спутника. В случае, когда положение Солнца относительно плоскости орбиты характеризуется соотношением $\vartheta $ > 75°, в качестве режима вращательного движения спутника можно использовать орбитальную ориентацию. Этот режим можно реализовать без накопления собственного кинетического момента гиросистемы [8–10] . В данном случае орбитальной ориентацией спутника будем называть его движение, при котором ${{{\mathbf{e}}}_{2}} = \pm {{{\mathbf{E}}}_{2}}$ и ${{{\mathbf{e}}}_{1}} = \pm {\mathbf{r}}$. При указанном положении Солнца режим орбитальной ориентации обеспечивает приемлемый энергосъем с солнечных батарей. Для рассматриваемой орбиты II требуемая орбитальная ориентация спутника задается соотношениями ${{{\mathbf{e}}}_{2}} = - {{{\mathbf{E}}}_{2}}$, поскольку в системе координат ${{O}_{E}}{{Z}_{1}}{{Z}_{2}}{{Z}_{3}}$ Солнце расположено в полупространстве ${{Z}_{2}}$ < 0. Для определенности зададим положение спутника соотношениями ${{{\mathbf{e}}}_{1}} = - {\mathbf{r}}$ и ${\mathbf{\omega }} = - {{\omega }_{0}}{{{\mathbf{e}}}_{2}}.$
Для реализации режима орбитальной ориентации спутника закон управления его гиростатическим моментом примем в виде
(6.1)
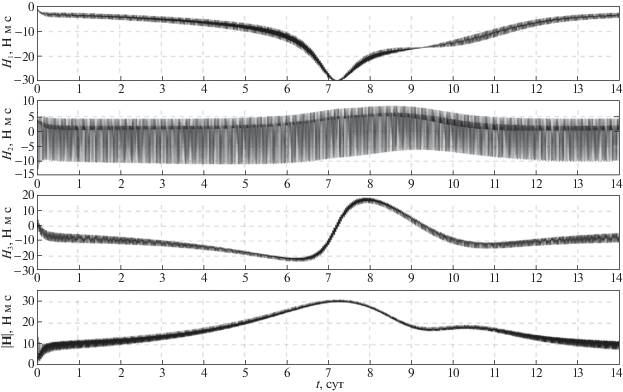
${{{\mathbf{M}}}_{c}} = {{\xi }^{2}}\hat {I}\left( {{\mathbf{\gamma }} \times {{{\mathbf{e}}}_{1}} + {{{\mathbf{e}}}_{2}} \times {{{\mathbf{E}}}_{2}}} \right) - 2\xi \hat {I}\left( {{\mathbf{\omega }} - {{\omega }_{0}}{{{\mathbf{e}}}_{2}}} \right) + 4\xi {\mathbf{H}},$Результаты расчетов движения спутника для орбиты II при последовательном использовании законов управления (2.5), (4.5) и (6.1) представлены на рис. 10, 11. Моделирование движения спутника проводилось по следующему сценарию. С момента времени t = 0 до наступления момента времени выполнения условия $\vartheta $ > 75° и с наступления момента времени выполнения условия $\vartheta $ < 75° до окончания моделирования для управления спутником использовался закон управления (2.5), (4.5). На интервале времени моделирования движения спутника, на котором выполнялось условие $\vartheta \; \geqslant $ 75°, для управления использовался закон (6.1). Переходные процессы, возникающие при последовательной смене законов управления, показаны на рис. 10. Значения начальных условий системы в момент времени t = 0 и значения параметров закона управления (2.5), (4.5) задавались, как в разд. 3 и 5. Параметры закона управления (6.1): ${{\omega }_{0}} = 1.09 \times {{10}^{{ - 3}}}$ с–1, $\xi $ = 0.01 с–1. На рис. 10 приведены графики компонент гиростатического момента ${{H}_{i}}$, i = 1, 2, 3, и модуля вектора гиростатического момента ${\text{|}}{\mathbf{H}}{\text{|}}$. Графики в левой части рисунка показаны на интервале времени $0 \leqslant t \leqslant 4$ сут, в правой части – на интервале $10 \leqslant t \leqslant 14$ сут. На рис. 10 видно, что гиростатический момент, накапливаемый в процессе переориентации спутника из режима солнечной ориентации в орбитальную и обратно, разгружается за относительно короткий интервал времени. Это обусловлено выбором коэффициентов соответствующих законов управления (4.5) и (6.1). На рис. 11 на интервале времени 14 сут показан график освещенности панелей солнечных батарей спутника. Освещенность выражена в процентах, 100% достигаются в положении, в котором орты ${{{\mathbf{e}}}_{2}}$ и ${\mathbf{s}}$ коллинеарны. График построен с учетом прохождения спутника через тень Земли. Функция, характеризующая тень Земли, использовалась в виде
где ${{R}_{E}}$ = 6378 км – радиус Земли, принятой шаром. В тени Земли ($\varsigma \leqslant 0$) освещенность панелей солнечных батарей спутника принималась равной 0%.Рис. 10.
Гиростатический момент спутника при последовательном использовании двух законов управления (орбита II)
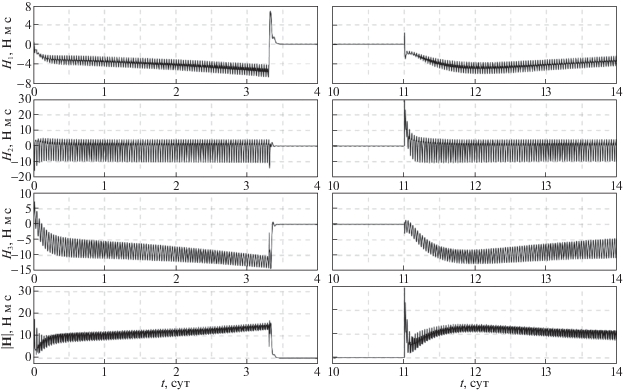
Рис. 11.
Освещенность панелей солнечных батарей спутника при последовательном использовании двух законов управления (орбита II)
Рассмотренный в данной работе дополнительный управляющий момент (4.5) можно использовать не постоянно. К примеру, можно поддерживать солнечную ориентацию спутника с помощью закона (2.5), а дополнительный управляющий момент (4.5) применять время от времени для разгрузки накопленного гиростатического момента спутника [7] . Альтернативный способ реализации солнечной ориентации спутника с одновременной разгрузкой кинетического момента гиросистемы при помощи гравитационного момента предложен в [11] .
Заключение. Построены и исследованы два варианта закона управления гиростатическим моментом, позволяющего поддерживать длительную и достаточно точную солнечную ориентацию искусственного спутника Земли. Первый вариант представляет собой пропорционально-дифференцирующий регулятор традиционной структуры, который обеспечивает затухание возмущенного движения спутника в окрестности положения покоя с требуемой скоростью. При этом происходит постоянный рост гиростатического момента, вызванный действием на спутник гравитационного и аэродинамического моментов. В работе предложен второй вариант закона управления гиростатическим моментом спутника, дополняющий первый. Преимущество его использования состоит в том, что он позволяет ограничить рост гиростатического момента при поддержании достаточно точной солнечной ориентации спутника в течении длительного времени. Приведены результаты математического моделирования системы уравнений движения спутника, подтверждающие работоспособность рассмотренных вариантов закона управления при различных вариантах положения Солнца относительно плоскости орбиты. Полученные результаты могут быть использованы на этапе предварительного проектирования систем управления ориентацией спутника.
Список литературы
Бажинов И.К., Гаврилов В.П., Ястребов В.Д. и др. Навигационное обеспечение полета орбитального комплекса “Салют-6”–“Союз”–“Прогресс”. М.: Наука, 1985.
Белецкий В.В. Движение искусственного спутника относительно центра масс. М.: Наука, 1965.
Белецкий В.В., Яншин А.М. Влияние аэродинамических сил на вращательное движение искусственных спутников. Киев: Наук. думка, 1984.
Барбашин Е.А. Функции Ляпунова. М.: Наука, 1970.
Малкин И.Г. Теория устойчивости движения. М.: Наука, 1966.
Меес Ж. Астрономические формулы для калькуляторов. М.: Мир, 1988.
Игнатов А.И., Сазонов В.В. Оценка остаточных микроускорений на борту ИСЗ в режиме одноосной солнечной ориентации // Космич. исслед. 2013. Т. 51. № 5. С. 380–388.
Игнатов А.И., Сазонов В.В. Реализация режима орбитальной ориентации искусственного спутника Земли без накопления кинетического момента гиросистемы // Изв. РАН. ТиСУ. 2020. № 1. С. 129–142.
Игнатов А.И., Сазонов В.В. Реализация режимов вращательного движения ИСЗ с малым уровнем микроускорений электромеханическими исполнительными органами // Космич. исслед. 2012. Т. 50. № 5. С. 380–393.
Зубов Н.Е., Микрин Е.А., Мисриханов М.Ш., Рябченко В.Н. Стабилизация орбитальной ориентации космического аппарата с одновременной разгрузкой кинетического момента инерционных исполнительных органов // Изв. РАН. ТиСУ. 2015. № 4. С. 124–131.
Mashtakov Y., Tkachev S., Ovchinnikov M. Use of External Torques for Desaturation of Reaction Wheels // Guidance, Control and Dynamics. 2018. V. 41. № 8. P. 1663–1674.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления