Известия РАН. Теория и системы управления, 2020, № 3, стр. 39-49
АНАЛИТИЧЕСКОЕ КВАЗИОПТИМАЛЬНОЕ РЕШЕНИЕ ЗАДАЧИ ПОВОРОТА ОСЕСИММЕТРИЧНОГО ТВЕРДОГО ТЕЛА С КОМБИНИРОВАННЫМ ФУНКЦИОНАЛОМ
А. В. Молоденков a, *, Я. Г. Сапунков a
a Институт проблем точной механики и управления РАН
Саратов, Россия
* E-mail: molalexei@yandex.ru
Поступила в редакцию 04.06.2019
После доработки 10.01.2020
Принята к публикации 27.01.2020
Аннотация
Представлены результаты аналитического и численного решения задачи управления вращательным движением осесимметричного твердого тела с комбинированным критерием качества процесса управления и использованием кватернионов. Критерий оптимизации учитывает продолжительность процесса управления, суммарные импульсы квадрата кинетического момента твердого тела и модуля управляющего момента, приложенного к телу. Управляемое движение осесимметричного твердого тела совершается из состояния покоя в состояние покоя.
Введение. С помощью замены переменных задача об оптимальном повороте осесимметричного твердого тела из состояния покоя в заданное состояние покоя сведена к решению аналогичной задачи со сферической симметрией тела, для которой построено квазиоптимальное аналитическое решение, близкое к оптимальному. В разд. 1 в кватернионных переменных ставится задача об оптимальном развороте тела с осевой симметрией. Функционал, определяющий качество процесса управления, представляет собой линейную комбинацию с весовыми множителями трех критериев: времени процесса управления, импульса квадрата кинетического момента тела и импульса модуля управляющего момента. В разд. 2 производится переход к безразмерным переменным. В разд. 3 с помощью замены переменных делается переход к задаче об оптимальном развороте тела со сферической симметрией. При этом возникает дополнительная фазовая переменная. В результате задача становится задачей оптимального управления с подвижным правым концом траектории. В разд. 4 с помощью принципа максимума Понтрягина решение задачи сводится к решению краевой задачи для системы дифференциальных уравнений по определению фазовых и сопряженных переменных. В разд. 5 для этой задачи строится аналитическое квазиоптимальное решение, так как при этом делается одно предположение о значении сопряженной переменной дополнительной фазовой координаты, которое позволяет упростить решение задачи. В разд. 6 приводятся примеры аналитического квазиоптимального решения задачи и проводится сравнение этого решения с численным решением задачи об оптимальном развороте тела с осевой симметрией. Сравнение показывает, что построенное аналитическое квазиоптимальное решение задачи с большой точностью аппроксимирует численное решение, построенное без каких-либо предположений. Отметим, что среди численных примеров приводятся развороты космического аппарата (КА) “Спейс Шаттл”, рассматриваемого как твердое тело [1]. Следует отметить, что ранее в динамической постановке были исследованы задачи оптимальных разворотов твердого тела (КА) различных динамических конфигураций с классическими критериями качества переходных процессов (быстродействие, минимум энергетических затрат и их свертка, суммарный импульс и т.д.) [1–9], не включающими в виде линейной комбинации квадрат модуля кинетического момента твердого тела. В [10] рассматривалась задача оптимального управления пространственной переориентацией КА из произвольного начального в заданное конечное угловое положение. Исследовался случай, когда минимизируемый функционал объединяет в заданной пропорции расход времени и интеграл от квадрата модуля кинетического момента на переориентацию КА. Задача решалась в кинематической постановке.
1. Постановка задачи. Движение твердого тела с одной осью симметрии вокруг неподвижной точки под действием управляющего момента M описывается системой уравнений [2]:
(1.1)
$\frac{{d{\mathbf{L}}}}{{dt}} = \frac{1}{2}{\mathbf{L}} \circ {\mathbf{w}},\quad \frac{{d{\mathbf{w}}}}{{dt}} = {{R}^{{ - 1}}}{\mathbf{M}} - {{R}^{{ - 1}}}\left[ {{\mathbf{w}},R{\mathbf{w}}} \right],$(1.2)
$R = \left\| {\begin{array}{*{20}{c}} {{{I}_{1}}}&0&0 \\ 0&{{{I}_{2}}}&0 \\ 0&0&{{{I}_{2}}} \end{array}} \right\|.$На управляющий момент наложено ограничение
Начальное состояние тела при t = 0 определяется соотношениями Конечное состояние тела при tk, которое не фиксировано, задается соотношениямиКомбинированный функционал, определяющий качество процесса управления, включает в себя с весовыми множителями ${{\alpha }_{i}} \geqslant 0$, $i = 1,2,3$, время процесса, импульс квадрата величины кинетического момента и импульс модуля управляющего момента:
(1.6)
$J = \int\limits_0^{{{t}_{k}}} {({{\alpha }_{1}} + {{\alpha }_{2}}(I_{1}^{2}w_{1}^{2} + I_{2}^{2}(w_{2}^{2} + w_{3}^{2})) + {{\alpha }_{3}}\left| {\mathbf{M}} \right|)} dt = \int\limits_0^{{{t}_{k}}} {({{\alpha }_{1}} + {{\alpha }_{2}}{{{(R{\mathbf{w}})}}^{2}} + {{\alpha }_{3}}\left| {\mathbf{M}} \right|)} dt.$Требуется найти оптимальное управление, удовлетворяющее ограничению (1.3), которое переводит управляемую систему (1.1) из начального состояния (1.4) в конечное (1.5) и сообщает минимальное значение функционалу (1.6).
Решение задачи оптимального управления зависит не от каждого весового множителя, а от отношения двух весовых множителей к третьему ненулевому, который может быть приравнен 1. В поставленной задаче безразмерный весовой множитель ${{\alpha }_{1}}$ будем полагать равным 1.
2. Переход к безразмерным переменным. Для перехода к безразмерным переменным вводится масштаб управляющего момента ${{M}_{*}}$, масштаб момента инерции I1 и масштаб времени T = = ${{({{I}_{1}}{\text{/}}{{M}_{*}})}^{{1/2}}}$. Безразмерные переменные t*, w*, M*, $I_{2}^{*}$, J*, $\alpha _{2}^{*}$, $\alpha _{3}^{*}$ связаны с размерными переменными по формулам
(2.1)
$\begin{gathered} t* = t{\text{/}}T,\quad {\mathbf{w}}* = {\mathbf{w}}T,\quad {\mathbf{M}}* = {\mathbf{M}}{\text{/}}{{M}_{*}},\quad I_{2}^{*} = {{I}_{2}}{\text{/}}{{I}_{1}} = {{b}_{1}}, \\ J* = J{\text{/}}T,\quad \alpha _{2}^{*} = {{\alpha }_{2}}I_{1}^{2}{{T}^{{ - 2}}},\quad \alpha _{3}^{*} = {{\alpha }_{3}}{{M}_{*}}. \\ \end{gathered} $Далее будут использоваться только безразмерные переменные, верхний индекс “*” у безразмерных величин будет опущен. Уравнения движения (1.1), граничные условия (1.4), (1.5) сохраняют свою форму в безразмерных переменных, а тензор инерции и ограничение на управляющий момент в безразмерных переменных принимают следующий вид:
(2.2)
$R = \left\| {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{{{b}_{1}}}&0 \\ 0&0&{{{b}_{{_{1}}}}} \end{array}} \right\|,\quad \left| {\mathbf{M}} \right| \leqslant 1.$Функционал (1.6) в безразмерных переменных запишется как
(2.3)
$J = \int\limits_0^{{{t}_{k}}} {(1 + {{\alpha }_{2}}(w_{1}^{2} + b_{1}^{2}(w_{2}^{2} + w_{3}^{2})) + {{\alpha }_{3}}\left| {\mathbf{M}} \right|)} dt.$Второе уравнение системы (1.1) в безразмерных переменных в проекциях на оси подвижной системы координат представим так:
(2.4)
$\frac{{d{{w}_{1}}}}{{dt}} = {{M}_{1}},\quad \frac{{d{{w}_{2}}}}{{dt}} = {{b}_{2}}{{M}_{2}} - ({{b}_{2}} - 1){{w}_{1}}{{w}_{3}},\quad \frac{{d{{w}_{3}}}}{{dt}} = {{b}_{2}}{{M}_{3}} + ({{b}_{2}} - 1){{w}_{1}}{{w}_{2}},\quad {{b}_{2}} = b_{1}^{{ - 1}}.$3. Замены переменных. Следуя подходу [3, 4] вводится вспомогательный кватернион ${\mathbf{B}}\left( {\theta (t)} \right)$ по формуле
(3.1)
${\mathbf{B}} = {\mathbf{B}}\left( {\theta (t)} \right) = \exp \left( {\frac{{{{{\mathbf{i}}}_{1}}}}{2}\theta (t)} \right),\quad \theta (t) = {{b}_{3}}\int\limits_0^t {{{\omega }_{1}}} (\tau )d\tau ,$(3.2)
${\mathbf{w}} = {\mathbf{B}} \circ \omega \circ {\mathbf{\tilde {B}}} - {{{\mathbf{i}}}_{1}}{{b}_{3}}{{\omega }_{1}},$(3.3)
$\frac{{d\omega }}{{dt}} = {\mathbf{\tilde {B}}} \circ {{b}_{2}}{\mathbf{M}} \circ {\mathbf{B}}.$Кватернион L выражается через другой вспомогательный кватернион Λ:
Если (3.2) и (3.4) подставить в первое уравнение (1.1) , то оно примет вид
Согласно (3.3), вместо управляющего параметра M вводится новый управляющий параметр u:
который, согласно (2.2), должен удовлетворять ограничениюТогда уравнение (3.3) запишется в виде
Из граничных условий (1.4), (1.5) с учетом замен (3.2), (3.4) следуют граничные условия для Λ и $\omega $:
(3.10)
$\Lambda ({{t}_{k}}) = {{{\mathbf{L}}}_{k}} \circ {\mathbf{B}}(\theta ({{t}_{k}})) = {{\Lambda }_{k}},\quad \omega ({{t}_{k}}) = 0.$Система уравнений (3.5), (3.8) описывает вращательное движение твердого тела со сферической симметрией. Согласно (3.6), управляющий момент M выражается через вспомогательный управляющий момент u по формуле
Если (3.2) и (3.11) подставить в функционал (2.3), то он примет вид
(3.12)
$J = \int\limits_0^{{{t}_{k}}} {(1 + {{\beta }_{2}}{{\omega }^{2}} + {{\beta }_{3}}\left| {\mathbf{u}} \right|)} dt,\quad {{\beta }_{2}} = {{\alpha }_{2}}b_{1}^{2},\quad {{\beta }_{3}} = {{\alpha }_{3}}{{b}_{1}}.$Вспомогательная переменная $\theta $, согласно (3.1), удовлетворяет уравнению
с начальным условиемВ результате перехода к безразмерным переменным и замены переменных задача оптимального управления, поставленная в первом разделе, сводится к задаче, в которой требуется найти оптимальное управление u(t), удовлетворяющее ограничению (3.7), которое переводит управляемую систему (3.5), (3.8), (3.13) из начального состояния (3.9), (3.14) на многообразие (3.10) и сообщает минимальное значение функционалу (3.12).
После решения этой вспомогательной задачи оптимального управления по формулам (3.2), (3.4) и (3.11) можно записать решение для задачи, поставленной в безразмерных переменных в разд. 2.
4. Краевая задача оптимального управления. Функция Гамильтона–Понтрягина [11] для системы (3.5), (3.8), (3.13) имеет вид
(4.1)
$H = - (1 + {{\beta }_{2}}{{\omega }^{2}} + {{\beta }_{3}}\left| {\mathbf{u}} \right|) + \frac{1}{2}(\psi ,\Lambda \circ \omega ) + (\nu ,{\mathbf{u}}) + \eta b{}_{3}{{\omega }_{1}},$(4.2)
$\frac{{d\psi }}{{dt}} = \frac{1}{2}\psi \circ \omega ,\quad \frac{{d\nu }}{{dt}} = 2{{\beta }_{2}}\omega - \frac{1}{2}{\text{vect}}(\tilde {\Lambda } \circ \psi ) - {{{\mathbf{i}}}_{1}}{{b}_{3}}\eta ,\quad \frac{{d\eta }}{{dt}} = 0,$Если ввести новую сопряженную векторную переменную p по формуле p = ${\text{vect}}(\tilde {\Lambda } \circ \psi )$ [2], то функция H и система уравнений (4.2) запишутся как
(4.3)
$H = - (1 + {{\beta }_{2}}{{\omega }^{2}} + {{\beta }_{3}}\left| {\mathbf{u}} \right|) + \frac{1}{2}({\mathbf{p}},\omega ) + (\nu ,{\mathbf{u}}) + \eta b{}_{3}{{\omega }_{1}},$(4.4)
 $\frac{{d{\mathbf{p}}}}{{dt}} = [{\mathbf{p}},\omega ],\quad \frac{{d\nu }}{{dt}} = 2{{\beta }_{2}}\omega - \frac{1}{2}{\mathbf{p}} - {{{\mathbf{i}}}_{1}}{{b}_{3}}\eta ,\quad \frac{{d\eta }}{{dt}} = 0.$
$\frac{{d{\mathbf{p}}}}{{dt}} = [{\mathbf{p}},\omega ],\quad \frac{{d\nu }}{{dt}} = 2{{\beta }_{2}}\omega - \frac{1}{2}{\mathbf{p}} - {{{\mathbf{i}}}_{1}}{{b}_{3}}\eta ,\quad \frac{{d\eta }}{{dt}} = 0.$Так как правый конец траектории в фазовом пространстве $\Lambda \times \omega \times \theta $ находится на многообразии (3.10), т.е. является подвижным, то на правом конце траектории должно выполняться соответствующее условие трансверсальности, которое, как показано в [3, 4], можно получить методом неопределенных множителей Лагранжа. После исключения множителей Лагранжа условие трансверсальности на правом конце траектории принимает вид
Из условия максимума для функции H следует, что оптимальное управление определяется по формулам
(4.6)
$\begin{gathered} {\mathbf{u}} = {{b}_{2}}\frac{\nu }{{\left| \nu \right|}},\quad {\text{если}}\quad \left| \nu \right| \geqslant {{\beta }_{3}}; \\ {\mathbf{u}} = 0,\quad {\text{если}}\quad \left| \nu \right| < {{\beta }_{3}}. \\ \end{gathered} $В конце процесса должно выполняться условие
Таким образом, решение задачи оптимального управления сводится к решению краевой задачи для системы дифференциальных уравнений (3.5), (3.7), (3.13), (4.4) с граничными условиями (3.9), (3.14) в начальный момент времени и условиями (3.10), (4.5), (4.7) в конце процесса, при этом управление определяется, согласно (4.6).
Полученная краевая задача оптимального управления похожа на краевую задачу работы [6], в которой рассматривалась задача об оптимальном развороте тела со сферической симметрией с тем же функционалом (3.12). Отличие новой задачи состоит в том, что добавилась дополнительная фазовая координата θ, правый конец траектории стал подвижным и изменилось ограничение на управляющий параметр (3.7). В [6] тело со сферической симметрией вращалось вокруг неподвижной оси, что позволило построить аналитическое решение краевой задачи оптимального управления. Наличие во втором уравнении системы (4.4) последнего слагаемого в правой части уравнения усложняет решение задачи. Для упрощения решения вспомогательной краевой задачи для тела со сферической симметрией, поставленной в разд. 3, положим, что сопряженная переменная $\eta $ (которая, согласно последнему уравнению (4.4), является константой) равняется нулю ($\eta (t) \equiv 0$). Это позволит с учетом нулевых граничных условий для угловой скорости полагать, что вспомогательное тело со сферической симметрией вращается вокруг неподвижной оси. В результате будут выполнены все уравнения и граничные условия краевой задачи оптимального управления, поставленные в разд. 4, кроме граничного условия трансверсальности (4.5) в конце движения. Можно надеяться, что решение квазиоптимальной задачи будет близко к решению задачи оптимального управления без предположения относительно $\eta $. Построенное в следующем разделе аналитическое решение для тела с осевой симметрией с учетом предположения для переменной $\eta $ сравним с численным решением задачи для тела с осевой симметрией, поставленной в разд. 2, для оценки аналитического решения.
5. Приближенное решение краевой задачи оптимального управления. Как сказано выше, вспомогательное тело со сферической симметрией с учетом предположения для переменной $\eta $ будет вращаться вокруг неподвижной оси, направление которой, согласно граничным условиям (3.9), (3.10), определяется единичным вектором е:
(5.1)
${\mathbf{e}} = \frac{{{\text{vect}}{\mathbf{N}}}}{{\left| {{\text{vect}}{\mathbf{N}}} \right|}},\quad {\mathbf{N}} = {{\tilde {\Lambda }}_{n}} \circ {{\Lambda }_{k}},$(5.2)
${{\varphi }_{k}} = 2{\text{arctg}}\frac{{\left| {{\text{vect}}\,{\mathbf{N}}} \right|}}{{\left| {{\text{scal}}\,{\mathbf{N}}} \right|}},$Вектор угловой скорости $\omega $, управляющий параметр u, сопряженные переменные p, $\nu $ будут параллельны вектору е, при этом, согласно первому уравнению системы (4.4), вектор p во все время движения будет оставаться постоянным. Надо заметить, что вектор ${\mathbf{e}} = {{{\mathbf{i}}}_{1}}{{e}_{1}} + {{{\mathbf{i}}}_{2}}e{}_{2} + {{{\mathbf{i}}}_{3}}{{e}_{3}}$ и угол поворота ${{\varphi }_{k}}$ зависят, согласно (3.10), (5.1), (5.2), от $\theta ({{t}_{k}})$, которое определится при решении задачи.
Оптимальное управление состоит из трех этапов, из которых первый и третий будут активными, на которых управляющий параметр принимал максимальное значение по величине, а второй – пассивный с нулевым значением параметра u, происходило движение по инерции.
На первом этапе ($0 \leqslant t < {{t}_{{p1}}}$, где ${{t}_{{p1}}}$ – неизвестный пока момент времени) фазовые и сопряженные переменные и управляющий параметр определяются по формулам
(5.3)
$\begin{gathered} \Lambda = {{\Lambda }_{n}} \circ (\cos (0.25{{b}_{2}}{{t}^{2}}) + {\mathbf{e}}\sin (0.25{{b}_{2}}{{t}^{2}})),\quad \omega = {\mathbf{e}}{{b}_{2}}t,\quad {\mathbf{u}} = {\mathbf{e}}{{b}_{2}}, \\ {\mathbf{p}} = {\mathbf{e}}2c,\quad \nu = {\mathbf{e}}(\beta + {{\beta }_{2}}{{b}_{2}}{{t}^{2}} - ct),\quad \theta = 0.5{{e}_{1}}{{b}_{2}}{{b}_{3}}{{t}^{2}}. \\ \end{gathered} $На втором этапе (${{t}_{{p1}}} \leqslant t < {{t}_{{p2}}}$, где tp2 неизвестный пока момент времени)
(5.4)
$\begin{gathered} \Lambda = {{\Lambda }_{n}} \circ \left( {\cos {{\varphi }_{2}}(t) + {\mathbf{e}}\sin {{\varphi }_{2}}(t)} \right),\quad {{\varphi }_{2}}(t) = 0.5{{b}_{2}}(t - 0.5{{t}_{{p1}}}){{t}_{{p1}}}, \\ \omega = {\mathbf{e}}{{b}_{2}}{{t}_{{p1}}},\quad {\mathbf{u}} = 0,\quad {\mathbf{p}} = {\mathbf{e}}2c,\quad \nu = {\mathbf{e}}(\beta - \beta {}_{2}{{b}_{2}}t_{{p1}}^{2} + (2{{\beta }_{2}}{{b}_{2}}{{t}_{{p1}}} - c)t), \\ \theta = {{e}_{1}}{{b}_{2}}{{b}_{3}}{{t}_{{p1}}}(t - 0.5{{t}_{{p1}}}). \\ \end{gathered} $На третьем этапе (${{t}_{{p2}}} \leqslant t \leqslant {{t}_{k}}$):
(5.5)
$\begin{gathered} \Lambda = {{\Lambda }_{n}} \circ \left( {\cos {{\varphi }_{3}}(t) + {\mathbf{e}}\sin {{\varphi }_{3}}(t)} \right),\quad {{\varphi }_{3}}(t) = 0.25{{b}_{2}}(2({{t}_{{p1}}} + {{t}_{{p2}}})t - {{t}^{2}} - t_{{p1}}^{2} - t_{{p2}}^{2}), \\ \omega = {\mathbf{e}}{{b}_{2}}({{t}_{k}} - t),\quad {\mathbf{u}} = - {\mathbf{e}}{{b}_{2}},\quad {\mathbf{p}} = {\mathbf{e}}2c, \\ \end{gathered} $Значение $\theta ({{t}_{k}})$, входящее в выражение для Λk, запишем по формуле
(5.6)
$\theta ({{t}_{k}}) = {{e}_{1}}{{b}_{2}}{{b}_{3}}(0.5t_{k}^{2} + {{t}_{{p1}}}({{t}_{{p2}}} - 0.5{{t}_{{p1}}}) - {{t}_{{p2}}}({{t}_{k}} - 0.5{{t}_{{p2}}})).$Постоянные величины $\beta $, c, ${{t}_{{p1}}}$, ${{t}_{{p2}}}$, tk, которые входят в выражения (5.3)–(5.6), определяются из выполнения граничных условий краевой задачи:
(5.7)
$\beta = {{b}_{1}} + {{\beta }_{3}},\quad c = {{b}_{1}}t_{{p1}}^{{ - 1}} + \beta {}_{2}{{b}_{2}}{{t}_{{p1}}},\quad {{t}_{{p2}}} = {{\varphi }_{k}}{{b}_{1}}t_{{p1}}^{{ - 1}},\quad {{t}_{k}} = {{t}_{{p1}}} + {{t}_{{p2}}},$(5.8)
${{\beta }_{2}}{{b}_{2}}t_{{p1}}^{4} - ({{b}_{1}} + {{\beta }_{2}}{{\varphi }_{k}} + 2{{\beta }_{3}})t_{{p1}}^{2} + \varphi {}_{k}b_{1}^{2} = 0$(5.9)
${{t}_{{p1}}} = \sqrt {({{b}_{1}} + {{\beta }_{2}}{{\varphi }_{k}} + 2{{\beta }_{3}} - \sqrt {{{{({{b}_{1}} + {{\beta }_{2}}{{\varphi }_{k}} + 2{{\beta }_{3}})}}^{2}} - 4{{\beta }_{2}}{{b}_{1}}{{\varphi }_{k}}} ){{{(2{{\beta }_{2}}{{b}_{2}})}}^{{ - 1}}}} .$Надо отметить, что ${{\varphi }_{k}}$, входящая в формулы (5.7), (5.9), согласно (5.1), зависит $\theta ({{t}_{k}})$, которое вместе с другими константами определяется по следующему алгоритму. Задается $\theta ({{t}_{k}})$, по формуле (3.1) находится ${{\Lambda }_{k}}$, из (5.1) и (5.2) вычисляется единичный вектор е и ${{\varphi }_{k}}$, из (5.9) – ${{t}_{{p1}}}$, а по формулам (5.7) рассчитываются ${{t}_{{p2}}}$ и tk. Затем по формуле (5.6) через полученные величины вычисляется $\theta ({{t}_{k}})$ и сравнивается с заданным значением $\theta ({{t}_{k}})$. Разность между заданным и вычисленным значением $\theta ({{t}_{k}})$ определяет невязку. Методом Ньютона уточняется значение $\theta ({{t}_{k}})$. В проведенных расчетах процесс сходился за три–четыре итерации.
Из последней формулы системы (5.7) следует, что длительности первого и третьего этапов совпадают.
Соотношения (5.3)–(5.5) с учетом формул преобразования переменных (3.2), (3.4), (3.11) определяют решение задачи о квазиоптимальном управлении разворота тела с осевой симметрией в безразмерных переменных из начального состояния покоя (1.4) в заданное состояние покоя (1.5). Значение функционала для оптимального процесса через вычисленные константы находится по формуле
(5.10)
$J = {{t}_{k}} + {{\alpha }_{2}}t_{{p1}}^{2}({{t}_{{p2}}} - {{t}_{{p1}}}{\text{/}}3) + 2{{\alpha }_{3}}{{t}_{{p1}}}.$В частном случае, когда α2 = 0, уравнение (5.8) для определения ${{t}_{{p1}}}$ упрощается, так как β2 = 0, и принимает вид $({{b}_{1}} + 2{{\beta }_{3}})t_{{p1}}^{2} = {{\varphi }_{k}}b_{1}^{2}$. Тогда длительность первого этапа вычисляется по формуле
Приведенные выше формулы (5.7) сохраняют свою силу при α2 = 0.
Задача об оптимальном развороте тела с осевой симметрией с тем же функционалом качества (2.3) решалась и в другой постановке. Начальное состояние тела определялось соотношениями (1.4), а конечное состояние – только положением тела
угловая скорость в конце движения оставалась произвольной. Рассматривалась задача об оптимальном развороте тела с подвижным правым концом траектории. В этом случае управление состояло из двух этапов: активный, на котором управляющий момент принимал максимально допустимое значение по величине, и пассивный с нулевым значением момента. Решение вспомогательной задачи на первом этапе определяется соотношениями (5.3), а на втором этапе – (5.4), но в них надо заменить ${{t}_{{p1}}}$ на tp, а ${{t}_{{p2}}}$ на tk.Значение $\theta ({{t}_{k}})$ вычисляется по формуле
Константы $\beta $, c, tk определяются по формулам
(5.14)
$\beta = {{b}_{1}} + {{\beta }_{3}},\quad c = {{b}_{1}}t_{p}^{{ - 1}} + {{\beta }_{3}}{{b}_{2}}{{t}_{p}},\quad {{t}_{k}} = {{\varphi }_{k}}{{b}_{1}}t_{p}^{{ - 1}} + 0.5{{t}_{p}},$(5.15)
${{\beta }_{2}}{{b}_{2}}t_{p}^{4} - ({{b}_{1}} + 2{{\beta }_{2}}{{\varphi }_{k}} + 2{{\beta }_{3}})t_{p}^{2} + 2{{\varphi }_{k}} = 0$(5.16)
${{t}_{p}} = \sqrt {(0.5{{b}_{1}} + {{\beta }_{2}}{{\varphi }_{k}} + {{\beta }_{3}} - \sqrt {{{{(0.5{{b}_{1}} + {{\beta }_{2}}{{\varphi }_{k}} + {{\beta }_{3}})}}^{2}} - 2{{\beta }_{2}}{{b}_{1}}{{\varphi }_{k}}} ){{b}_{1}}\beta _{2}^{{ - 1}}} .$Соотношения (5.3), (5.4) с учетом выражений преобразования переменных (3.2), (3.4), (3.11) определяют решение задачи о квазиоптимальном управлении разворота тела с осевой симметрией в безразмерных переменных с подвижным правым концом траектории из начального состояния покоя (1.4) в заданное положение (5.12). Значение функционала для оптимального процесса через вычисленные константы находится по формуле
(5.17)
$J = {{t}_{k}} + {{\alpha }_{2}}t_{p}^{2}({{t}_{k}} - 2{{t}_{p}}{\text{/}}3) + {{\alpha }_{3}}{{t}_{p}}.$В частном случае, когда α2 = 0, уравнение (5.15) для определения tp упрощается, так как β2 = 0, и принимает вид $({{b}_{1}} + 2{{\beta }_{3}})t_{{p1}}^{2} = 2{{\varphi }_{k}}b_{1}^{2}$. Тогда длительность первого этапа следует из выражения
Приведенные выше формулы (5.14) сохраняют свою силу и при α2 = 0.
6. Результаты расчетов. По методу построения квазиоптимального решения задачи об оптимальном развороте тела с осевой симметрией, изложенному в статье, проводились расчеты для четырех тел с осевой симметрией с различными отношениями главных моментов инерции.
Тело 1: I1 = 1.0, ${{I}_{2}} = {{I}_{3}} = 0.5$, ${{b}_{1}} = 0.5$. Тело 2: ${{I}_{1}} = 1.0$, ${{I}_{2}} = {{I}_{3}} = 1.0$, ${{b}_{1}} = 1.0$. Тело 3: I1 = 1.0, ${{I}_{2}} = {{I}_{3}} = 1.5$, ${{b}_{1}} = 1.5$. Тело 4 (КА “Спейс Шаттл”) [1, 12]: ${{I}_{1}} = 3400648$ кг ⋅ м2, ${{I}_{2}}$= 21041672 кг ⋅ м2, ${{I}_{3}} \approx \,{{I}_{2}}$ (размерные моменты инерции) или $\,{{b}_{1}} = 6.18755$; динамические характеристики КА “Спейс Шаттл” такие же, как у почти осесимметричного твердого тела.
Тело 2, которое является телом со сферической симметрией, включено по той причине, что изложенный метод дает для него точное решение. Для тел 2 и 4 наряду с расчетами по приведенному методу проводились расчеты по численному решению задачи об оптимальном развороте тела, поставленной в разд. 2, без преобразований, описанных в разд. 3.
Расчеты проводились для двух наборов весовых множителей в функционале качества процесса управления (2.3):
Начальное состояние для всех расчетов одно и то же:
(6.3)
${{L}_{{n0}}} = 0.79505,\quad {{L}_{{n1}}} = 0.29814,\quad {{L}_{{n2}}} = - 0.39752,\quad {{L}_{{n3}}} = 0.34783,\quad {{{\mathbf{w}}}_{n}} = 0.$Для задачи с закрепленным правым концом траектории проводились расчеты для двух наборов конечных состояний тела:
(6.4)
${{L}_{{k0}}} = 0.69804,\quad {{L}_{{k1}}} = 0.28997,\quad {{L}_{{k2}}} = - 0.20674,\quad {{L}_{{k3}}} = 0.62122,\quad {{{\mathbf{w}}}_{k}} = 0,$(6.5)
${{L}_{{k0}}} = 0.51684,\quad {{L}_{{k1}}} = 0.24683,\quad {{L}_{{k2}}} = 0.00898,\quad {{L}_{{k3}}} = 0.81968,\quad {{{\mathbf{w}}}_{k}} = 0.$В случае конечного условия (6.4) тело совершает поворот на угол 40.0°, а в случае условия (6.5) – на угол 80.0°.
В табл. 1 (первые четыре строки) приводятся результаты расчетов (моменты окончания трех этапов и значение функционала) для четырех перечисленных тел по изложенному в статье методу, т.е. по формулам (5.3)–(5.5), (3.2), (3.4), (3.11), для набора весовых множителей (6.1) для перевода тела из начального состояния (6.3) в конечное состояние (6.4). Оптимальное управление состоит из трех этапов: первый и третий активные, тело разворачивается под действием управляющего момента; второй этап пассивный, тело продолжает движение по инерции.
Таблица 1
| Тело | b1 | ${{t}_{{p1}}}$ | ${{t}_{{p2}}}$ | tk | J |
|---|---|---|---|---|---|
| 1 | 0.5 | 0.44809 | 1.08931 | 1.53740 | 2.26859 |
| 2 | 1.0 | 0.51304 | 1.36078 | 1.87382 | 2.85659 |
| 3 | 1.5 | 0.56728 | 1.66390 | 2.23118 | 3.51036 |
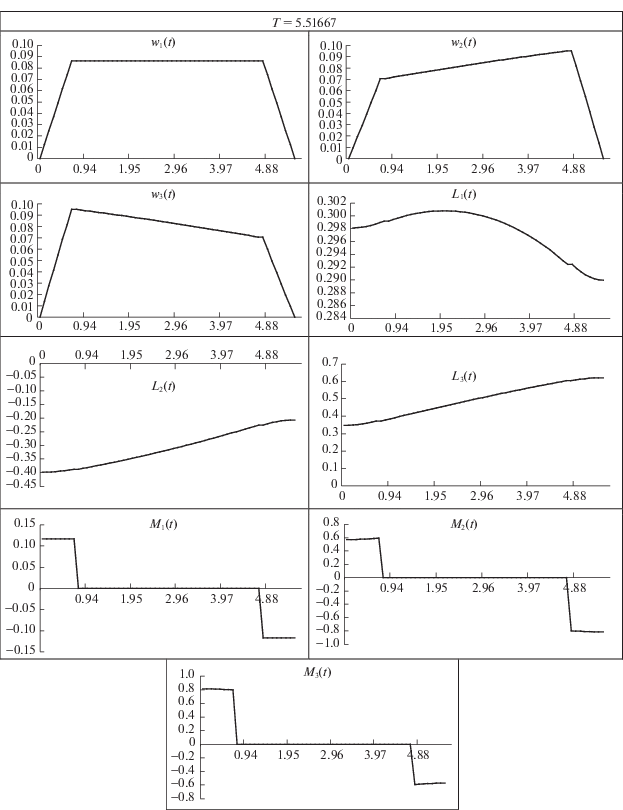
| 4 | 6.18755 | 0.73815 | 4.77821 | 5.51668 | 9.95924 |
| 4 | 6.18755 | 0.73826 | 4.77814 | 5.51640 | 9.95909 |
В табл. 1, как и в остальных таблицах, для оценки точности квазиоптимального решения задачи о развороте тела 4 в нижней строке приведены результаты численного решения задачи оптимального разворота КА “Спейс Шаттл”, построенного на основе принципа максимума с помощью универсальной программы [7]. Из сравнения результатов, представленных в четвертой и пятой строках табл. 1, видно, что аналитическое решение для квазиоптимального управления (четвертая строка) с большой точностью аппроксимирует численное решение задачи оптимального управления. Погрешность по величине функционала составляет 0.003%. Сравнение аналитического решения для тела 2 (тело со сферической симметрией) с численным решением задачи оптимального управления показало их полное совпадение всех знаков, приведенных в табл. 1. Из табл. 1 видно, что с увеличением величины ${{b}_{1}}$ для тела увеличивается длительность второго этапа (движения по инерции).
На рис. 1 приводятся графики изменения во времени компонент кватерниона положения, вектора угловой скорости и управляющего момента для оптимального разворота КА “Спейс Шаттл”, описанного в табл. 1. На втором (пассивном) этапе первая компонента угловой скорости ${{w}_{1}}$, согласно первому уравнению системы (2.4), сохраняет постоянное значение, две другие компоненты остаются переменными и на пассивном этапе.
В табл. 2 приводятся результаты расчетов для четырех тел для набора весовых множителей (6.1) и для перевода тела из начального состояния (6.3) в конечное состояние (6.5). Из сравнения данных табл. 1 и 2 видно, что с увеличением угла поворота между начальным и конечным положением тела незначительно увеличиваются длительности активных этапов (первого и третьего), но существенно увеличивается длительность пассивного (второго) этапа.
Таблица 2
| Тело | b1 | ${{t}_{{p1}}}$ | ${{t}_{{p2}}}$ | tk | J |
|---|---|---|---|---|---|
| 1 | 0.5 | 0.56731 | 1.66412 | 2.23142 | 3.51082 |
| 2 | 1.0 | 0.63205 | 2.20911 | 2.84116 | 4.67072 |
| 3 | 1.5 | 0.67392 | 2.78810 | 3.46202 | 5.88227 |
| 4 | 6.18755 | 0.77644 | 8.88830 | 9.66473 | 18.24467 |
| 4 | 6.18755 | 0.77705 | 8.88582 | 9.66288 | 18.24371 |
В табл. 3, 4 приводятся результаты расчетов для тех же тел для набора весовых множителей (6.2) при их переводе из начального состояния (6.3) в конечные состояния (6.4) или (6.5) соответственно. Второй набор весовых множителей характерен отсутствием квадрата величины кинетического момента в подынтегральной функции в функционале (2.3). Из сравнения данных табл. 1 и 3 и 2 и 4 между собой видно, отсутствие кинетического момента в (2.3) привело к увеличению длительности активных этапов и уменьшению длительности пассивного этапа, а также к уменьшению длительности всего процесса. При этом указанный эффект усиливается с увеличением отношения моментов инерции ${{b}_{1}}$.
Таблица 3
| Тело | b1 | ${{t}_{{p1}}}$ | ${{t}_{{p2}}}$ | tk | J |
|---|---|---|---|---|---|
| 1 | 0.5 | 0.49402 | 0.98804 | 1.48206 | 1.97608 |
| 2 | 1.0 | 0.59082 | 1.18164 | 1.77245 | 2.36327 |
| 3 | 1.5 | 0.68698 | 1.37397 | 2.06095 | 2.74794 |
| 4 | 6.18755 | 1.32802 | 2.65604 | 3.98406 | 5.31208 |
| 4 | 6.18755 | 1.32806 | 2.65589 | 3.98396 | 5.31202 |
Таблица 4
| Тело | b1 | ${{t}_{{p1}}}$ | ${{t}_{{p2}}}$ | tk | J |
|---|---|---|---|---|---|
| 1 | 0.5 | 0.68705 | 1.37410 | 2.06115 | 2.74819 |
| 2 | 1.0 | 0.83554 | 1.67109 | 2.50663 | 3.34217 |
| 3 | 1.5 | 0.96926 | 1.93853 | 2.90779 | 3.87705 |
| 4 | 6.18755 | 1.85758 | 3.71516 | 5.51668 | 7.43032 |
| 4 | 6.18755 | 1.85788 | 3.71405 | 5.51640 | 7.42981 |
Для задачи с подвижным правым концом траектории, в которой оптимальное управление состоит из двух этапов (первый этап активный, второй пассивный), проводились расчеты для двух конечных положений тела:
(6.6)
${{L}_{{k0}}} = 0.69804,\quad {{L}_{{k1}}} = 0.28997,\quad {{L}_{{k2}}} = - 0.20674,\quad {{L}_{{k3}}} = 0.62122,$(6.7)
${{L}_{{k0}}} = 0.51684,\quad {{L}_{{k1}}} = 0.24683,\quad {{L}_{{k2}}} = 0.00898,\quad {{L}_{{k3}}} = 0.81968.$Соотношение (6.6) указывает, что тело из состояния (6.3) разворачивается на угол 40°, а соотношение (6.7) – на 80°.
В табл. 5, 6 приводятся результаты расчетов (моменты окончания двух этапов и значение функционала) для четырех перечисленных выше тел по изложенному в статье методу для набора весовых множителей (6.1) для перевода тела из начального состояния (6.3) в конечное положение (6.6) и (6.7) соответственно. Из сравнения данных табл. 5 и 6 видно, что с увеличением угла поворота между начальным и конечным положениями тел незначительно увеличивается длительность активного (первого) этапа. Увеличение длительности активного этапа ослабляется по мере увеличения отношения моментов инерции ${{b}_{1}}$. В то же время с увеличением угла поворота между начальным и конечным положениями тел значительно увеличивается длительность пассивного (второго) этапа. При этом длительность пассивного этапа усиливается с увеличением ${{b}_{1}}$.
Таблица 5
| Тело | b1 | tp | tk | J |
|---|---|---|---|---|
| 1 | 0.5 | 0.57317 | 1.13819 | 1.79735 |
| 2 | 1.0 | 0.63205 | 1.42058 | 2.33536 |
| 3 | 1.5 | 0.67452 | 1.73662 | 2.95217 |
| 4 | 6.18755 | 0.77732 | 4.92643 | 9.31038 |
| 4 | 6.18755 | 0.77743 | 4.92627 | 9.31031 |
Таблица 6
| Тело | b1 | ${{t}_{p}}$ | ${{t}_{k}}$ | J |
|---|---|---|---|---|
| 1 | 0.5 | 0.67454 | 1.73684 | 2.95261 |
| 2 | 1.0 | 0.71811 | 2.30342 | 4.07390 |
| 3 | 1.5 | 0.74290 | 2.90065 | 5.26340 |
| 4 | 6.18755 | 0.79658 | 9.06183 | 17.57981 |
| 4 | 6.18755 | 0.79720 | 9.06080 | 17.57939 |
В табл. 7, 8 приводятся результаты расчетов для четырех тел по изложенному в статье методу для набора весовых множителей (6.2) для перевода тела из начального состояния (6.3) в конечное положение (6.6) и (6.7) соответственно. Из сравнения данных табл. 5, 7 и 6, 8 между собой видно, отсутствие кинетического момента в функционале (2.3), так как весовой множитель α2 = 0 для данных табл. 7, 8, привело к увеличению длительности активного этапа и уменьшению длительности пассивного этапа, а также к уменьшению длительности всего процесса. При этом указанный эффект усиливается с увеличением отношения моментов инерции b1. Из сравнения данных в четвертых и пятых строках всех таблиц, в которых приводятся результаты расчетов по аналитическому решению (четвертая строка) и численному решению (пятая строка), видно квазиоптимальное решение близко численному оптимальному решению задачи. Погрешность по величине функционала не превышает 0.01%.
Таблица 7
| Тело | b1 | tp | tk | J |
|---|---|---|---|---|
| 1 | 0.5 | 0.69865 | 1.04798 | 1.39730 |
| 2 | 1.0 | 0.83554 | 1.25331 | 1.67108 |
| 3 | 1.5 | 0.97154 | 1.45731 | 1.94308 |
| 4 | 6.18755 | 1.87811 | 2.81716 | 3.75621 |
| 4 | 6.18755 | 1.87814 | 2.81711 | 3.75618 |
Таблица 8
| Тело | b1 | tp | tk | J |
|---|---|---|---|---|
| 1 | 0.5 | 0.97163 | 1.45745 | 1.94327 |
| 2 | 1.0 | 1.18164 | 1.77245 | 2.36327 |
| 3 | 1.5 | 1.37074 | 2.05612 | 2.74149 |
| 4 | 6.18755 | 2.62701 | 3.94052 | 5.25403 |
| 4 | 6.18755 | 2.62723 | 3.94016 | 5.25377 |
Заключение. Представленное в статье аналитическое квазиоптимальное решение задачи управления вращательным движением осесимметричного твердого тела с комбинированным критерием качества процесса управления может найти свое применение при построении систем управления КА, как и известные аналитические решения задачи оптимального разворота сферически-симметричного и осесимметричного твердого тела, полученные для классических функционалов оптимизации [2, 8].
Список литературы
Li F., Bainum P.M. Numerical Approach for Solving Rigid Spacecraft Minimum Time Attitude Maneuvers // J. Guidance, Contr., and Dynamics. 1990. V. 13. № 1.
Бранец В.Н., Шмыглевский И.П. Применение кватернионов в задачах ориентации твердого тела. М.: Наука, 1973.
Молоденков А.В., Сапунков Я.Г. Аналитическое решение задачи оптимального разворота осесимметричного космического аппарата в классе конических движений // Изв. РАН. ТиСУ. 2016. № 6.
Молоденков А.В., Сапунков Я.Г. Аналитическое решение задачи оптимального по быстродействию разворота осесимметричного космического аппарата в классе конических движений // Изв. РАН. ТиСУ. 2018. № 2.
Левский М.В. Применение принципа максимума Л.С. Понтрягина к задачам оптимального управления ориентацией космического аппарата // Изв. РАН. ТиСУ. 2008. № 6.
Молоденков А.В., Сапунков Я.Г. Оптимальное управление вращательным движением твердого тела с комбинированным критерием качества // Изв. РАН. ТиСУ. 2019. № 3.
Сапунков Я.Г., Молоденков А.В. Численное решение задачи оптимальной переориентации вращающегося космического аппарата // Мехатроника, автоматизация, управление. 2008. № 6.
Бранец В.Н., Черток М.Б., Казначеев Ю.В. Оптимальный разворот твердого тела с одной осью симметрии // Космич. исслед. 1984. Т. 22. Вып. 3.
Левский М.В. Квадратично оптимальное управление переориентацией космического аппарата за фиксированное время в динамической постановке // Изв. РАН. ТиСУ. 2018. № 1.
Левский М.В. Аналитическое управление переориентацией космического аппарата с использованием комбинированного критерия оптимальности // Изв. РАН. ТиСУ. 2018. № 2.
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: Наука, 1961.
Griffin M.D., French J.R. Space Vehicle Design. AIAA Education Series. Reston, Virginia, 2004.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления