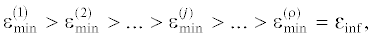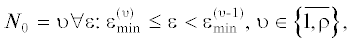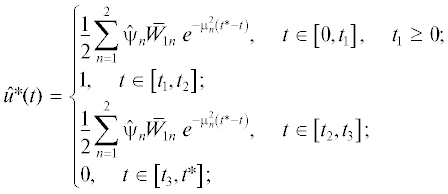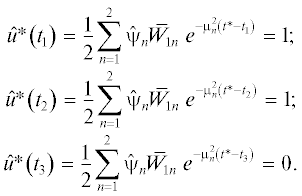Известия РАН. Теория и системы управления, 2020, № 4, стр. 42-57
ПРОГРАММНОЕ УПРАВЛЕНИЕ С МИНИМАЛЬНЫМ ЭНЕРГОПОТРЕБЛЕНИЕМ В СИСТЕМАХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
Ю. Э. Плешивцева a, Э. Я. Рапопорт a, *
a Самарский государственный технический ун-т
Самара, Россия
* E-mail: edgar.rapoport@mail.ru
Поступила в редакцию 07.10.2019
После доработки 15.01.2020
Принята к публикации 27.01.2020
Аннотация
Предлагается конструктивная технология решения задачи оптимального по расходу энергии программного управления системами с распределенными параметрами в условиях заданной точности равномерного приближения результирующего пространственного распределения управляемой величины к требуемому состоянию. Разработанный вычислительный алгоритм использует специальную процедуру предварительной параметризации управляющих воздействий на конечномерных подмножествах финишных значений сопряженных переменных в краевой задаче принципа максимума Понтрягина и последующую редукцию к задаче полубесконечной оптимизации, разрешаемой относительно искомого вектора параметров по схеме предложенного ранее альтернансного метода. Приводится представляющий самостоятельный интерес пример энергосберегающего управления процессом нестационарной теплопроводности.
Введение. Решение задач оптимального управления (ЗОУ) динамическими объектами в классической двухточечной формулировке с фиксированными концами траекторий движения управляемой системы в фазовом пространстве связано с известными трудностями, возрастающими с повышением порядка дифференциальных уравнений модели объекта и приобретающими принципиальный характер применительно к бесконечномерным системам с распределенными параметрами (СРП) [1–3]. Решения таких ЗОУ СРП во многих случаях либо не существуют ввиду неуправляемости СРП относительно наиболее характерных требуемых конечных состояний объекта из-за их несогласованности с типичными граничными условиями исследуемых начально-краевых задач, либо относятся к классу технически нереализуемых управляющих воздействий [1–5].
В подобной ситуации конструктивный подход к ЗОУ СРП состоит в переходе к заведомо разрешимой с реализуемыми результатами задаче управления с заданным целевым множеством результирующих пространственных распределений управляемой величины, которое отвечает достижимым значениям всегда существующих в технических приложениях допусков $\varepsilon $ на отклонение от требуемого в исходной двухточечной схеме конечного состояния объекта, оцениваемых в равномерной метрике, согласно типичным для приложений требованиям [5–7].
После предварительной процедуры последовательной параметризации управляющих воздействий с использованием аналитических условий оптимальности ЗОУ СРП в описанной формулировке сводятся к параметрической задаче полубесконечной оптимизации, технически реализуемое решение которой может быть получено с помощью конструктивной технологии альтернансного метода [5–7].
В настоящей работе эта технология применяется для получения алгоритмически точного решения рассматриваемой в указанной постановке типичной частной задачи минимизации энергопотребления в процессе управления СРП параболического типа [3].
В двухточечной интерпретации этой задачи возникает сложная проблема существования ее решений, формально представляемых в нереализуемой инженерными средствами форме суммы бесконечного числа экспонент [3]. Показывается, что в данном случае аппарат принципа максимума Понтрягина непосредственно, без каких-либо дополнительных преобразований приводит для линейных моделей СРП к линейной параметризованной форме искомых управляющих воздействий, определяемых с точностью до выбора зависящего от величины $\varepsilon $ конечного числа финишных значений сопряженных переменных [7].
При этом базовая система соотношений альтернансного метода с существенным использованием закономерностей конкретной предметной области сводится к линейной системе конечного числа алгебраических уравнений, аналитически разрешаемой на каждом этапе последовательной параметризации относительно вектора параметрического представления искомых управлений. В итоге оптимальные управляющие воздействия определяются в технически осуществимом виде суммы экспоненциальных составляющих, конечное число которых однозначно определяется заданной величиной допустимого отклонения результирующего состояния объекта от требуемого.
Возможности применения полученных результатов иллюстрируются на представляющем самостоятельный интерес примере оптимального по энергозатратам управления нестационарным процессом теплопроводности.
1. Постановка задачи. Пусть управляемая величина Q(x, t) объекта с распределенными параметрами описывается в зависимости от пространственной координаты $x \in \left[ {{{x}_{0}},{{x}_{1}}} \right]$ и времени $t \in \left[ {0,t{\text{*}}} \right]$ линейным уравнением в частных производных параболического типа с самосопряженным дифференциальным оператором в его правой части [2, 5]:
(1.1)
$\frac{{\partial Q\left( {x,t} \right)}}{{\partial t}} = B\left( x \right)\frac{{\partial Q\left( {x,t} \right)}}{{\partial x}} + C\left( x \right)\frac{{{{\partial }^{2}}Q\left( {x,t} \right)}}{{\partial {{x}^{2}}}} + D\left( x \right)Q\left( {x,t} \right) + {{f}_{{\text{v}}}}\left( x \right){{u}_{{\text{v}}}}\left( t \right)$(1.2)
$Q\left( {x,0} \right) = {{Q}_{0}}\left( x \right) = {{Q}_{0}} = {\text{const}},\quad {{x}_{0}} \leqslant x \leqslant {{x}_{1}},$(1.3)
${{\alpha }_{0}}Q\left( {{{x}_{0}},t} \right) + {{\beta }_{0}}\frac{{\partial Q\left( {{{x}_{0}},t} \right)}}{{\partial x}} = 0;\quad {{\alpha }_{1}}Q\left( {{{x}_{1}},t} \right) + {{\beta }_{1}}\frac{{\partial Q\left( {{{x}_{1}},t} \right)}}{{\partial x}} = {{u}_{s}}(t),\quad 0 \leqslant t \leqslant t{\text{*}},$Управляющие воздействия стесняются ограничениями
с известными предельно допустимыми величинами umin и umax, где здесь и всюду далее $u\left( t \right) = {{u}_{{\text{v}}}}\left( t \right)$ или $u\left( t \right) = {{u}_{s}}\left( t \right)$.Пусть требуется обеспечить в конце процесса управления заданной продолжительности t* необходимую точность ε > 0 равномерного приближения конечного пространственного распределения управляемой величины $Q\left( {x,t{\text{*}}} \right)$ к требуемому Q**(x), определяющую оцениваемое в равномерной метрике целевое множество конечных состояний объекта (1.1)–(1.4) [5–7]:
(1.5)
$\mathop {{\text{max}}}\limits_{x \in \left[ {{{x}_{0}},{{x}_{1}}} \right]} \left| {Q\left( {x,t{\text{*}}} \right) - Q{\text{**}}\left( x \right)} \right| \leqslant \varepsilon ,\quad \varepsilon > 0,$Применение к уравнениям объекта конечного интегрального преобразования по пространственному аргументу х с ядром, равным собственным функциям ${{\varphi }_{n}}\left( {{{\mu }_{n}},x} \right),$ $n = 1,2,...,$ начально-краевой задачи (1.1)–(1.3), где $\mu _{n}^{2}$ – собственные числа, приводит к описанию рассматриваемой СРП бесконечной системой обыкновенных дифференциальных уравнений для временных мод ${{\bar {Q}}_{n}}\left( {{{\mu }_{n}},t} \right)$ разложения Q(x, t) в сходящийся в среднем ряд по ${{\varphi }_{n}}\left( {{{\mu }_{n}},x} \right)$ [8]:
(1.6)
$\begin{gathered} \frac{{d{{{\bar {Q}}}_{n}}\left( {{{\mu }_{n}},t} \right)}}{{dt}} = - \mu _{n}^{2}{{{\bar {Q}}}_{n}}\left( {{{\mu }_{n}},t} \right) + {{K}_{{{\text{v}}n}}}{{u}_{{\text{v}}}}\left( t \right) + {{K}_{{sn}}}{{u}_{s}}\left( t \right), \\ {{{\bar {Q}}}_{n}}\left( {{{\mu }_{n}},0} \right) = \bar {Q}_{{}}^{0}\left( {{{\mu }_{n}}} \right),\quad n = 1,2,..., \\ \end{gathered} $(1.7)
$Q\left( {x,t} \right) = \sum\limits_{n = 1}^\infty {\bar {Q}_{n}^{{}}\left( {{{\mu }_{n}},t} \right)\,{{\varphi }_{n}}\left( {{{\mu }_{n}},x} \right).} $Здесь ${{K}_{{{\text{v}}n}}}$, $\bar {Q}_{{}}^{0}\left( {{{\mu }_{n}}} \right)$ – моды конечных интегральных преобразований функций ${{f}_{{\text{v}}}}\left( x \right)$ и ${{Q}_{0}}\left( x \right);$ ${{K}_{{sn}}}$ – известные коэффициенты [8]. Применительно к модальному представлению объекта (1.6), (1.7) требования (1.5) к его конечному состоянию предъявляются в форме соотношения
(1.8)
$\mathop {{\text{max}}}\limits_{x \in \left[ {{{x}_{0}},{{x}_{1}}} \right]} \left| {\sum\limits_{n = 1}^\infty {{{{\bar {Q}}}_{n}}\left( {{{\mu }_{n}},t{\text{*}}} \right){{\varphi }_{n}}\left( {{{\mu }_{n}},x} \right) - Q{\text{**}}\left( x \right)} } \right| \leqslant \varepsilon .$Пусть качество процесса управления оценивается интегральным функционалом
(1.9)
$I = \int\limits_0^{t*} {{{u}^{2}}\left( t \right)dt} \to \mathop {{\text{min}}}\limits_{u\left( t \right)} ,$Рассмотрим следующую задачу оптимального управления. Необходимо определить стесненное ограничением (1.4) оптимальное программное управление $u{\text{*}}\left( t \right)$, которое переводит объект управления (1.6), (1.7) из заданного начального состояния (1.2) в требуемое конечное, согласно (1.8), при минимальном значении критерия оптимальности (1.9).
2. Оптимальное программное управление. На сформулированную бесконечномерную задачу оптимизации распространяется принцип максимума Понтрягина [5]. Функция Понтрягина $H\left( {\bar {Q}\left( t \right),u\left( t \right),\psi \left( t \right)} \right)$ для рассматриваемой задачи оптимизации принимает следующий вид [12]:
(2.1)
$H\left( {\bar {Q}\left( t \right),u\left( t \right),\psi \left( t \right)} \right) = - {{u}^{2}}(t) + \sum\limits_{n = 1}^\infty {{{\psi }_{n}}\left( t \right)\left( { - \mu _{n}^{2}{{{\bar {Q}}}_{n}}\left( {{{\mu }_{n}},t} \right) + {{K}_{n}}u\left( t \right)} \right)} ,$(2.2)
$\frac{{d{{\psi }_{i}}}}{{dt}} = - \frac{{\partial H}}{{\partial {{{\bar {Q}}}_{i}}}} = \mu _{i}^{2}\psi _{i}^{{}},\quad i = 1,2,...,$(2.3)
${{\psi }_{n}}\left( t \right) = {{\psi }_{n}}\left( {t{\text{*}}} \right)e_{{}}^{{ - \mu _{n}^{2}\left( {t{\text{*}} - t} \right)}},\quad n = 1,2,...$Базовое условие
(2.4)
$H\left( {\bar {Q}{\text{*}}(t),u{\text{*}}(t),\psi {\text{*}}(t)} \right) = \mathop {\max }\limits_{u \in \left[ {{{u}_{{\min }}},{{u}_{{\max }}}} \right]} H\left( {\bar {Q}{\text{*}}(t),u,\psi {\text{*}}(t)} \right),\quad t \in \left( {0,t{\text{*}}} \right)$(2.5)
$u{\text{*}}\left( t \right) = \left\{ \begin{gathered} {{u}_{{{\text{max}}}}},\quad {\text{если}}\quad \frac{1}{2}\sum\limits_{n = 1}^\infty {{{K}_{n}}\psi _{n}^{*}\left( {t{\text{*}}} \right)\,{{e}^{{ - \mu _{n}^{2}\left( {t{\text{*}} - t} \right)}}} \geqslant {{u}_{{{\text{max}}}}};} \hfill \\ \frac{1}{2}\sum\limits_{n = 1}^\infty {{{K}_{n}}\psi _{n}^{*}\left( {t{\text{*}}} \right){{e}^{{ - \mu _{n}^{2}\left( {t{\text{*}} - t} \right)}}}{\text{,}}\quad {\text{если}}\quad {{u}_{{{\text{min}}}}} \leqslant \frac{1}{2}} \sum\limits_{n = 1}^\infty {{{K}_{n}}\psi _{n}^{*}\left( {t{\text{*}}} \right){{e}^{{ - \mu _{n}^{2}\left( {t{\text{*}} - t} \right)}}} \leqslant {{u}_{{{\text{max}}}}};} \hfill \\ {{u}_{{{\text{min}}}}}{\text{,}}\quad {\text{если}}\quad \frac{1}{2}\sum\limits_{n = 1}^\infty {{{K}_{n}}\psi _{n}^{*}\left( {t{\text{*}}} \right){{e}^{{ - \mu _{n}^{2}\left( {t{\text{*}} - t} \right)}}} \leqslant {{u}_{{{\text{min}}}}}.} \hfill \\ \end{gathered} \right.$Вектор $\psi {\text{*}}(t{\text{*}}) = (\psi _{n}^{*}(t{\text{*}})),$ n = 1, 2, … результирующих состояний сопряженной системы (2.2) должен быть найден из условий достижения целевого множества (1.8). Именно бесконечная размерность этого вектора приводит в двухточечной схеме, соответствующей значению ε = 0 в (1.8), к трудноразрешимой проблеме определения алгоритма оптимального управления вида (2.5) [3].
Заметим, что непосредственное использование в целях отыскания $\psi {\text{*}}(t{\text{*}})$ классических условий трансверсальности [12] становится невозможным в условиях негладкой границы целевого множества (1.8) в конечной точке оптимального процесса [5].
3. Последовательная параметризация управляющих воздействий. В [7] предложена процедура последовательной параметризации управляющих воздействий в ЗОУ СРП на конечномерных подмножествах величин $\psi \left( {t{\text{*}}} \right)$, формируемых в виде N-мерных векторов ${{\psi }^{{\left( N \right)}}} = (\tilde {\psi }_{n}^{{}}),$ $n = \overline {1,N} $, финишных значений ${{\tilde {\psi }}_{n}} = {{\psi }_{n}}\left( {t{\text{*}}} \right)N$ первых сопряженных функций (2.2) при равных нулю остальных величинах ${{\psi }_{n}}\left( {t{\text{*}}} \right)$ для всех n > N:
(3.1)
${{\psi }^{{\left( N \right)}}} = \left( {{{\psi }_{n}}\left( {t{\text{*}}} \right)} \right) = \left( {{{{\tilde {\psi }}}_{n}}} \right),\quad n = \overline {1,N} ,\quad N \geqslant 1;\quad {{\psi }_{n}}\left( {t{\text{*}}} \right) = 0,\quad n > N.$Параметризуемое подобным образом оптимальное управление (2.5) описывается конечной суммой N экспонент:
Ограничимся сначала типичным случаем линейной зависимости $u{\text{*}}\left( t \right)$ от вектора параметров ${{\tilde {\psi }}_{n}}$ в (3.3), считая, что ограничения (1.4) не достигаются на всем протяжении оптимального процесса.
Очевидно, что такой вариант возможен лишь при выборе достаточной величины t*, превышающей длительность оптимального по быстродействию процесса перевода объекта в требуемое, согласно (1.8), конечное состояние, при котором $u{\text{*}}\left( t \right)$ попеременно принимает лишь предельно допустимые значения ${{u}_{{{\text{max}}}}}$ и ${{u}_{{{\text{min}}}}}$ в (2.5) [2, 5]. Всюду далее предполагается, что это условие выполнено.
Согласно (3.1), ${{\psi }^{{\left( {{{N}_{1}}} \right)}}} = {{\psi }^{{\left( {{{N}_{2}}} \right)}}}$ при ${{N}_{2}} > {{N}_{1}}$, ${{\psi }_{n}}\left( {t{\text{*}}} \right) = 0$ для всех $n = \overline {{{N}_{1}} + 1,{{N}_{2}}} $. Отсюда следует, что в условиях (3.1) минимально достижимые в классе управлений (3.3) значения
(3.5)
$\varepsilon _{{{\text{min}}}}^{{\left( N \right)}} = \mathop {{\text{min}}}\limits_{{{\psi }^{{\left( N \right)}}}} [\mathop {{\text{max}}}\limits_{x \in [{{x}_{0}},{{x}_{1}}]} \left| {Q\left( {x,t{\text{*}}} \right) - Q{\text{**}}\left( x \right)} \right|]$Здесь точная нижняя грань εinf достижимых по условию (1.8) значений ε в цепочке неравенств (3.6) оказывается равной
минимаксу 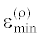 , где $\rho = \infty $ при ${{\varepsilon }_{{{\text{inf}}}}} = 0$ и $\rho < \infty $ при ${{\varepsilon }_{{{\text{inf}}}}} > 0$ соответственно для управляемых и неуправляемых относительно Q**(x) объектов [6]. Неравенства (3.6) как раз создают возможность обеспечения требуемой точности $\varepsilon $ достижения Q**(x) в случае $\varepsilon \geqslant {{\varepsilon }_{{{\text{inf}}}}}$ при конечном числе N, принципиально упрощая тем самым рассматриваемую ЗОУ СРП. В случае $\varepsilon < {{\varepsilon }_{{{\text{inf}}}}}$ решение этой задачи не существует. Согласно установленному в [7] принципу минимальной сложности $\psi _{{}}^{{\left( N \right)}}$-параметризуемых в соответствии с (3.1) структур оптимальных программных управлений,
размерность N = N0 вектора ${{\psi }^{{\left( {{{N}_{0}}} \right)}}}$, характеризующего $u{\text{*}}\left( t \right)$ в (3.3), определяется местом заданного достижимого значения $\varepsilon \geqslant {{\varepsilon }_{{{\text{inf}}}}}$ в (1.8) в цепочке неравенств (3.6) в соответствии с простым правилом:
, где $\rho = \infty $ при ${{\varepsilon }_{{{\text{inf}}}}} = 0$ и $\rho < \infty $ при ${{\varepsilon }_{{{\text{inf}}}}} > 0$ соответственно для управляемых и неуправляемых относительно Q**(x) объектов [6]. Неравенства (3.6) как раз создают возможность обеспечения требуемой точности $\varepsilon $ достижения Q**(x) в случае $\varepsilon \geqslant {{\varepsilon }_{{{\text{inf}}}}}$ при конечном числе N, принципиально упрощая тем самым рассматриваемую ЗОУ СРП. В случае $\varepsilon < {{\varepsilon }_{{{\text{inf}}}}}$ решение этой задачи не существует. Согласно установленному в [7] принципу минимальной сложности $\psi _{{}}^{{\left( N \right)}}$-параметризуемых в соответствии с (3.1) структур оптимальных программных управлений,
размерность N = N0 вектора ${{\psi }^{{\left( {{{N}_{0}}} \right)}}}$, характеризующего $u{\text{*}}\left( t \right)$ в (3.3), определяется местом заданного достижимого значения $\varepsilon \geqslant {{\varepsilon }_{{{\text{inf}}}}}$ в (1.8) в цепочке неравенств (3.6) в соответствии с простым правилом:
Дальнейшая проблема сводится к фактическому определению однозначно характеризующего оптимальное управление при N = N0 в (3.3) вектора параметров ${{\psi }^{{\left( {{{N}_{0}}} \right)}}}$ по числу N0 и величинам ${{\tilde {\psi }}_{n}}$, n = $\overline {1,{{N}_{0}}} ,$ его компонент из условий достижения заданной величины $\varepsilon $ в (1.8).
4. Редукция к задаче полубесконечной оптимизации. Интегрирование уравнений модели объекта (1.6) с ${{\psi }^{{\left( N \right)}}}$-параметризованным управлением (3.3) и подстановка $u{\text{*}}\left( t \right)$ в форме (3.3) в (1.9) приводят к представлению конечного состояния $Q\left( {x,t{\text{*}}} \right)$, описываемого его разложением в ряд (1.7), и критерия оптимальности (1.9) в форме явных зависимостей соответственно $Q(x,{{\psi }^{{\left( N \right)}}})$ и $I({{\psi }^{{\left( N \right)}}})$ от своих аргументов.
В результате осуществляется точная редукция исходной задачи оптимального управления (1.4), (1.6)–(1.9) к задаче полубесконечной оптимизации (ЗПО) [5–7]:
(4.1)
$I({{\psi }^{{\left( N \right)}}}) \to \mathop {{\text{min}}}\limits_{{{\psi }^{{\left( N \right)}}}} ;$(4.2)
$\Phi ({{\psi }^{{\left( N \right)}}}) = \mathop {{\text{max}}}\limits_{x \in \left[ {{{x}_{0}},{{x}_{1}}} \right]} \left| {Q(x,{{\psi }^{{\left( N \right)}}}) - Q{\text{**}}\left( x \right)} \right| \leqslant \varepsilon $Существенной особенностью рассматриваемой задачи минимизации энергозатрат является линейный характер зависимостей $Q(x,{{\psi }^{{\left( N \right)}}})$ от ${{\psi }^{{\left( N \right)}}}$ в (4.2) в силу линейности по ${{\psi }^{{\left( N \right)}}}$ алгоритма $u{\text{*}}({{\psi }^{{(N)}}}$, t) в (3.3).
Решение $\psi _{*}^{{\left( {{{N}_{0}}} \right)}}$ ЗПО (4.1), (4.2), где N0 выбирается по правилу (3.5), может быть получено по схеме альтернансного метода [5–7], базирующегося на специальных альтернансных свойствах $\psi _{*}^{{\left( {{{N}_{0}}} \right)}}$, согласно которым в условиях малостеснительных допущений в некоторых точках $x_{j}^{0} \in [{{x}_{0}}$, x1], $j = \overline {1,R} $ достигаются предельно допустимые значения $\Phi (\psi _{*}^{{\left( {{{N}_{0}}} \right)}})$, равные $\varepsilon $:
(4.3)
$\left| {Q(x_{j}^{0},\psi _{*}^{{\left( {{{N}_{0}}} \right)}}) - Q{\text{**}}(x_{j}^{0})} \right| = \varepsilon ,\quad j = \overline {1,R} .$Число R этих точек оказывается равным числу всех искомых параметров оптимального процесса, включая все компоненты $\tilde {\psi }_{i}^{*},\;i = \overline {1,{{N}_{0}},} $ вектора $\psi _{*}^{{\left( {{{N}_{0}}} \right)}}$ при заданной величине $\varepsilon $ в случае ε > $\varepsilon _{{{\text{min}}}}^{{{\text{(}}{{N}_{{\text{0}}}}{\text{)}}}}$ в (3.7) и наряду с ними априори неизвестную величину минимакса $\varepsilon _{{{\text{min}}}}^{{{\text{(}}{{N}_{{\text{0}}}}{\text{)}}}}$, определяемую, согласно (3.5), если $\varepsilon = \varepsilon _{{{\text{min}}}}^{{{\text{(}}{{N}_{{\text{0}}}}{\text{)}}}}$:
(4.4)
$R = \left\{ \begin{gathered} {{N}_{0}},\quad \varepsilon _{{{\text{min}}}}^{{{\text{(}}{{N}_{{\text{0}}}}{\text{)}}}} < \varepsilon < \varepsilon _{{{\text{min}}}}^{{{\text{(}}{{N}_{{\text{0}}}} - {\text{1)}}}}; \hfill \\ {{N}_{0}} + 1,\quad \varepsilon _{{{\text{min}}}}^{{{\text{(}}{{N}_{{\text{0}}}}{\text{)}}}} = \varepsilon . \hfill \\ \end{gathered} \right.$При наличии диктуемой закономерностями предметной области необходимой дополнительной информации о характере зависимости $Q(x,\psi _{*}^{{\left( {{{N}_{0}}} \right)}}) - Q{\text{**}}\left( x \right)$ от пространственной переменной х на интервале $\left[ {{{x}_{0}},{{x}_{1}}} \right]$, позволяющей идентифицировать значения $x_{j}^{0} \in \left[ {{{x}_{0}},{{x}_{1}}} \right]$ для всех $j = \overline {1,R} $ и знаки отклонений $Q(x_{j}^{0},\psi _{*}^{{\left( {{{N}_{0}}} \right)}}) - Q{\text{**}}(x_{j}^{0})$ в этих точках, обеспечивается редукция равенств (4.3), составляемых для абсолютных величин указанных отклонений, к разрешаемой стандартными методами замкнутой линейной по $\psi _{*}^{{\left( {{{N}_{0}}} \right)}}$ системе R + R1 уравнений для самих разностей:
(4.5)
$Q(x_{j}^{0},\psi _{*}^{{\left( {{{N}_{0}}} \right)}}) - Q{\text{**}}(x_{j}^{0}) = \pm \varepsilon ,\quad j = \overline {1,R} ;$(4.6)
$\frac{{\partial Q(x_{{jv}}^{0},\psi _{*}^{{\left( {{{N}_{0}}} \right)}})}}{{\partial x}} = 0;\quad x_{{jv}}^{0} \in {\text{int}}\left[ {{{x}_{0}},{{x}_{1}}} \right];\quad v = \overline {1,{{R}_{1}}} ;\quad {{R}_{1}} \leqslant R;\quad x_{{jv}}^{0} \in \{ x_{j}^{0}\} $В итоге предлагается следующая методика решения рассматриваемой задачи полубесконечной оптимизации (4.1), (4.2).
1. На первом этапе, полагая в (4.2) $\varepsilon = \varepsilon _{{{\text{min}}}}^{{{\text{(}}r{\text{)}}}},R = r + 1$, согласно (4.4), конструируется с использованием фундаментальных закономерностей оптимизируемых процессов система уравнений (4.5), (4.6) и находится ее решение, которое позволяет установить для последовательно возрастающих значений $r = 1,2,...,$ $\upsilon $ величины $\psi _{*}^{{\left( r \right)}}$ вместе с $\varepsilon _{{{\text{min}}}}^{{{\text{(}}r{\text{)}}}}$, определяя тем самым первые $\upsilon $ составляющих в цепочке неравенств (3.6).
2. Сравнение заданного в (4.5) значения $\varepsilon = {{\varepsilon }_{0}}$ с $\varepsilon _{{{\text{min}}}}^{{{\text{(}}r{\text{)}}}}$ на каждом шаге этого процесса определяет $\upsilon $ из условия 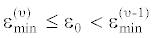 , откуда следует, что ${{N}_{0}} = \upsilon $ в соответствии с правилом (3.7), если $\upsilon \leqslant \rho $.
, откуда следует, что ${{N}_{0}} = \upsilon $ в соответствии с правилом (3.7), если $\upsilon \leqslant \rho $.
3. В случае ${{\varepsilon }_{0}} = \varepsilon _{{{\text{min}}}}^{{{\text{(}}{{N}_{{\text{0}}}}{\text{)}}}}$ задача оказывается уже решенной на первом этапе. Если исходные требования предусматривают
необходимость достижения заранее неизвестной величины ε в (1.5), (1.8), которая должна
совпадать с минимаксом $\varepsilon _{{{\text{min}}}}^{{{\text{(}}{{N}_{{\text{0}}}}{\text{)}}}}$ при некотором заранее выбираемом ${{N}_{0}} \leqslant \rho $, то $\psi _{*}^{{\left( {{{N}_{0}}} \right)}}$ вместе с $\varepsilon _{{{\text{min}}}}^{{{\text{(}}{{N}_{{\text{0}}}}{\text{)}}}}$ сразу находятся решением системы (4.5), (4.6) при ${{\varepsilon }_{0}} = \varepsilon _{{{\text{min}}}}^{{{\text{(}}{{N}_{{\text{0}}}}{\text{)}}}},\,\,R = {{N}_{0}} + 1$. При 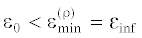 рассматриваемая задача оптимального управления не имеет решения.
рассматриваемая задача оптимального управления не имеет решения.
4. При выполнении строгого неравенства $\varepsilon _{{{\text{min}}}}^{{{\text{(}}{{N}_{{\text{0}}}}{\text{)}}}} < {{\varepsilon }_{0}} < \varepsilon _{{{\text{min}}}}^{{{\text{(}}{{N}_{{\text{0}}}}{\text{ - 1)}}}}$ остается решить систему (4.5), (4.6) с найденным на втором этапе значением N0 при $\varepsilon = {{\varepsilon }_{0}},$ $R = {{N}_{0}}$.
Учет ограничений на управляющие воздействия. Равенства (3.2), (3.4) для u*(t) могут достигаться в различные моменты времени на протяжении процесса управления, образуя в общем случае многочисленные варианты построения оптимальной программы $\hat {u}{\text{*}}\left( t \right)$, согласно (3.2)–(3.4). Ограничимся далее наиболее характерной ситуацией с выходом на ограничения (3.2), (3.4) только на начальной и конечной стадиях оптимизируемого процесса. В таком случае, характерном, например, для задач управления температурными режимами нагрева металла под обработку давлением, программное управление u*(t) должно дополняться, согласно (1.4), (3.2)–(3.4), участками поддержания максимально и минимально допустимых величин ${{u}_{{\max }}}$ и ${{u}_{{\min }}}$ соответственно на интервалах $[{{t}_{1}},{{t}_{2}}] \subset [0,t{\text{*}}],$ $[{{t}_{3}},t{\text{*}}] \subset [0,t{\text{*}}]$ [12] с параметрическим представлением $\hat {u}{\text{*}}\left( t \right)$ в следующем виде:
(4.7)
$\hat {u}{\text{*}}\left( t \right) = \left\{ \begin{gathered} \frac{1}{2}\sum\limits_{n = 1}^N {{{{\hat {\psi }}}_{n}}{{K}_{n}}{{e}^{{ - \mu _{n}^{2}\left( {t{\text{*}} - t} \right)}}},\quad t \in \left[ {0,{{t}_{1}}} \right],\quad {{t}_{1}} \geqslant 0;} \hfill \\ {{u}_{{{\text{max}}}}},\quad t \in \left[ {{{t}_{1}},{{t}_{2}}} \right]; \hfill \\ \frac{1}{2}\sum\limits_{n = 1}^N {{{{\hat {\psi }}}_{n}}{{K}_{n}}{{e}^{{ - \mu _{n}^{2}(t{\text{*}} - t)}}},\quad t \in \left[ {{{t}_{2}},{{t}_{3}}} \right];} \hfill \\ {{u}_{{{\text{min}}}}}{\text{,}}\quad t \in \left[ {{{t}_{3}},t{\text{*}}} \right]. \hfill \\ \end{gathered} \right.$Здесь компоненты ${{\hat {\psi }}_{n}}$ вектора параметров $\hat {\psi }_{{}}^{{\left( N \right)}} = \left( {{{{\hat {\psi }}}_{n}}} \right),$ $n = \overline {1,N} ,$ в (4.7) отличаются от ${{\tilde {\psi }}_{n}}$ в (3.3), а моменты ${{t}_{1}},{{t}_{2}},{{t}_{3}}$ схода и выхода на ограничения (1.4) фиксируются равенствами
(4.8)
$\begin{gathered} \hat {u}{\text{*}}\left( {{{t}_{i}}} \right) = \frac{1}{2}\sum\limits_{n = 1}^N {\hat {\psi }_{n}^{{}}} {{K}_{n}}{{e}^{{ - \mu _{n}^{2}\left( {t{\text{*}} - {{t}_{i}}} \right)}}} = {{u}_{{{\text{max}}}}},\quad i = 1,2; \\ \hat {u}{\text{*}}\left( {{{t}_{3}}} \right) = \frac{1}{2}\hat {\psi }_{n}^{{}}{{K}_{n}}{{e}^{{ - \mu _{n}^{2}\left( {t{\text{*}} - {{t}_{3}}} \right)}}} = {{u}_{{{\text{min}}}}}. \\ \end{gathered} $В результате после интегрирования уравнений модели объекта с параметризованным управляющим воздействием (4.7) аналогично задаче с управлением u*(t) осуществляется переход к ЗПО вида (4.1), (4.2) с заменой $\psi _{{}}^{{\left( N \right)}}$ на $\hat {\psi }_{{}}^{{\left( N \right)}}$, что приводит к отличающейся от $Q(x,\psi _{{}}^{{\left( N \right)}})$ параметрической зависимости конечного состояния объекта $Q(x,\hat {\psi }_{{}}^{{\left( N \right)}})$ от своих аргументов за счет разницы в структурах программных управлений u*(t) в (3.3) и $\hat {u}{\text{*}}\left( t \right)$ в (4.7). Важно подчеркнуть, что в итоге сохраняется линейная зависимость $Q(x,\hat {\psi }_{{}}^{{\left( N \right)}})$ от $\hat {\psi }_{{}}^{{\left( N \right)}}$.
На следующем этапе задача полубесконечной оптимизации сводится к решению по описанной выше схеме линейной системы уравнений вида (4.5), (4.6), дополняемой равенствами (4.8), где искомый вектор параметров $\psi _{*}^{{\left( {{{N}_{0}}} \right)}}$ надо заменить на $\hat {\psi }_{*}^{{\left( {{{N}_{0}}} \right)}} = (\hat {\psi }_{n}^{*}),$ $n = \overline {1,{{N}_{0}}} $.
Аналогичным образом могут быть рассмотрены и другие варианты компоновки $\hat {u}{\text{*}}\left( t \right)$ из различных участков алгоритма (3.2)–(3.4).
5. Минимизация энергопотребления в задачах с распределенными управляющими воздействиями. Пространственно-временное внутреннее управляющее воздействие u(x, t) в уравнении (1.1) объекта рассматривалось в разд. 1–4 в типовом для приложений варианте предварительной фиксации его пространственного распределения ${{f}_{{\text{v}}}}(x)$, т.е. в условиях $u\left( {x,t} \right) = {{f}_{{\text{v}}}}\left( x \right)\,{{u}_{{\text{v}}}}\left( t \right)$ перехода к поиску сосредоточенного управления ${{u}_{{\text{v}}}}(t)$. В более общем случае возникает задача оптимального по критерию энергопотребления распределенного управления u(x, t) с заведомо неизвестным характером его зависимости от пространственного и временного аргументов.
В этом случае модальное описание СРП принимает вместо (1.6) следующий вид при ${{u}_{s}}(t) = 0$:
(5.1)
$\begin{gathered} \frac{{d\bar {Q}_{n}^{{}}(\mu _{n}^{{}},t)}}{{dt}} = - \mu _{n}^{2}{{{\bar {Q}}}_{n}}(\mu _{n}^{{}},t) + {{{\bar {u}}}_{n}}\left( t \right),\quad n = 1,2,..., \\ {{{\bar {Q}}}_{n}}(\mu _{n}^{{}},0) = \bar {Q}_{{}}^{0}\left( {{{\mu }_{n}}} \right), \\ \end{gathered} $(5.2)
$u\left( {x,t} \right) = \sum\limits_{n = 1}^\infty {{{{\bar {u}}}_{n}}\left( t \right){{\varphi }_{n}}\left( {{{\mu }_{n}},x} \right)} .$Критерий оптимальности (1.9) заменяется двойным интегралом:
(5.3)
${{I}_{1}} = \int\limits_0^{t{\text{*}}} {\int\limits_{{{x}_{0}}}^{{{x}_{1}}} {{{u}^{2}}\left( {x,t} \right)\,dx\,dt} } \to \mathop {{\text{min}}}\limits_{u\left( {x,t} \right)} ,$(5.4)
${{I}_{1}} = \int\limits_0^{t{\text{*}}} {\left[ {\sum\limits_{n = 1}^\infty {\bar {u}_{n}^{2}\left( t \right)} } \right]} \,dt$Требования к конечному состоянию объекта управления сохраняются в форме (1.8).
Рассмотрим задачу определения не стесняемых ограничениями оптимальных модальных управляющих воздействий $\bar {u}_{n}^{*}\left( t \right),$ n = 1, 2, …, обеспечивающих перевод объекта (5.1) из заданного начального состояния в требуемое конечное, согласно (1.8), с минимальным значением критерия оптимальности (5.4).
Аналогично (2.1)–(2.5) стандартная процедура принципа максимума Понтрягина приводит в такой задаче к экспоненциальной форме представления всех $\bar {u}_{n}^{*}\left( t \right)$ с точностью до выбора вектора $\psi {\text{*}}\left( {t{\text{*}}} \right) = (\psi _{n}^{*}\left( {t{\text{*}}} \right)),$ $n = 1,2,...,$ конечных значений сопряженных переменных
(5.5)
$\bar {u}_{n}^{*}\left( t \right) = \frac{1}{2}\psi _{n}^{*}\left( {t{\text{*}}} \right){{e}^{{ - \mu _{n}^{2}\left( {t{\text{*}} - t} \right)}}},\quad n = 1,2,...$(5.6)
$u{\text{*}}\left( {x,t} \right) = \frac{1}{2}\sum\limits_{n = 1}^\infty {\psi _{n}^{*}\left( {t{\text{*}}} \right)\,{{e}^{{ - \mu _{n}^{2}\left( {t{\text{*}} - t} \right)}}}\varphi \left( {{{\mu }_{n}},x} \right)} $.Так же, как в (3.1), (3.3), укороченная сумма N первых членов ряда в (5.6) представляет собой ${{\psi }^{{(N)}}}$-параметризованную структуру искомого оптимального пространственно-временного управления
(5.7)
$u{\text{*}}\left( {x,t} \right) = \frac{1}{2}\sum\limits_{n = 1}^N {\tilde {\psi }_{n}^{{}}\,{{e}^{{ - \mu _{n}^{2}\left( {t{\text{*}} - t} \right)}}}\varphi \left( {{{\mu }_{n}},x} \right)} $Техническая реализация алгоритма (5.7) может оказаться затруднительной ввиду сложного характера его распределения по пространственной координате.
В такой ситуации u(x, t) представляется в форме взвешенной суммы заранее фиксируемых проектными решениями объекта и заведомо реализуемых (чаще всего кусочно-постоянных) зависимостей от пространственной координаты Fm(x) с весовыми коэффициентами, в роли которых выступают искомые сосредоточенные управляющие воздействия ${{\upsilon }_{m}}\left( t \right)$ [4]:
(5.8)
$u\left( {x,t} \right) = \sum\limits_{m = 1}^s {{{F}_{m}}\left( x \right){{\upsilon }_{m}}\left( t \right),\quad s \geqslant 1.} $При этом в (5.1)
(5.9)
${{\bar {u}}_{n}}\left( t \right) = \sum\limits_{m = 1}^s {\bar {F}_{{mn}}^{{}}{{\upsilon }_{m}}\left( t \right),\quad n = 1,2,...,} $Критерий оптимальности, суммирующий расход энергии по всем управлениям ${{\upsilon }_{m}}\left( t \right)$, записывается в виде
(5.10)
${{I}_{2}} = \sum\limits_{m = 1}^s {\int\limits_0^{t{\text{*}}} {\upsilon _{m}^{2}\left( t \right)dt \to \mathop {{\text{min}}}\limits_{{{\upsilon }_{m}}\left( t \right)} } } .$Исследуемая задача оптимального управления объектом (5.1) с подстановкой (5.9) и критерием оптимальности (5.10) сводится к рассмотренной в разд. 1–4 при s = 1 и является ее обобщением на случай использования многоканальных сосредоточенных управляющих воздействий при s > 1. В последнем случае задача опять может быть решена по схеме альтернансного метода, модифицированной применительно к векторному управлению $\upsilon \left( t \right) = \left( {{{\upsilon }_{m}}\left( t \right)} \right),$ $m = \overline {1,s} $ [13].
Если можно ограничиться учетом только $N$ мод при $n = \overline {1,N} $ в (5.1) и если возможен выбор s = N в (5.7), (5.8), то равенства (5.9) при $n = \overline {1,N} $ образуют линейную систему уравнений относительно ${{\upsilon }_{m}}\left( t \right),$ $m = \overline {1,s} $ , для заданных значений ${{\bar {u}}_{n}}\left( t \right)$, решение которой определяется по формулам Крамера:
(5.11)
${{\upsilon }_{m}}\left( t \right) = \sum\limits_{n = 1}^s {\frac{{D_{{nm}}^{{}}}}{D}{{{\bar {u}}}_{n}}\left( t \right),\quad m = \overrightarrow {1,s} ,} $По формулам (5.11) можно вычислить все искомые сосредоточенные воздействия, $\upsilon _{m}^{*}\left( t \right),$ $m = \overline {1,s} $, обеспечивающие оптимальное поведение всех учитываемых в (5.7) модальных управлений $\bar {u}_{n}^{*}\left( t \right),$ $n = \overline {1,N} $, заданное в форме (5.5). В итоге $u{\text{*}}\left( {x,t} \right)$ восстанавливается в заведомо реализуемом виде (5.8) с подстановками (5.5), (5.11):
(5.12)
$u{\text{*}}\left( {x,t} \right) = \frac{1}{2}\sum\limits_{m = 1}^s {{{F}_{m}}\left( x \right)\sum\limits_{n = 1}^s {\frac{{{{D}_{{nm}}}}}{D}\tilde {\psi }_{n}^{*}{{e}^{{ - \mu _{n}^{2}\left( {t{\text{*}} - t} \right)}}}} } $.5.1. Оптимизация проектных решений. В частном варианте $u\left( {x,t} \right) = F\left( t \right)\upsilon \left( x \right)$ с заданным характером зависимости F(t) и неизменным во времени пространственным управляющим воздействием $\upsilon (x)$, в роли которого рассматриваются искомые проектные решения объекта [14], следует принять в (5.1)
где $\bar {\upsilon }_{n}^{{}}$ – моды управления $\upsilon (x)$, восстанавливаемого по известным значениям $\bar {\upsilon }_{n}^{{}}$ подобно (5.2):(5.14)
$\upsilon \left( x \right) = \sum\limits_{n = 1}^\infty {\bar {\upsilon }_{n}^{{}}{{\varphi }_{n}}\left( {{{\mu }_{n}},x} \right)} $.Критерий оптимальности (5.4) превращается здесь в сумму квадратов $\bar {\upsilon }_{n}^{{}}$:
Нетрудно показать, что аналогично (5.7) укороченная сумма N первых слагаемых в (5.14) представляет собой параметризуемую на конечномерном подмножестве векторов $\bar {\upsilon }_{{}}^{{\left( N \right)}}$ структуру распределенного управления
(5.16)
$\begin{gathered} \upsilon \left( x \right) = \sum\limits_{n = 1}^N {\tilde {\upsilon }_{n}^{{}}\varphi _{n}^{{}}\left( {{{\mu }_{n}},x} \right);} \\ \bar {\upsilon }_{{}}^{{\left( N \right)}} = (\bar {\upsilon }_{n}^{{\left( N \right)}}){\text{:}}\quad \bar {\upsilon }_{n}^{{\left( N \right)}} = \tilde {\upsilon }_{n}^{{}},\quad n = \overline {1,N} ;\quad \bar {\upsilon }_{n}^{{\left( N \right)}} = 0,\quad n > N, \\ \end{gathered} $Рассматриваемая задача оптимизации проектных решений с учетом требований (1.8) редуцируется к параметрической задаче полубесконечной оптимизации:
(5.17)
$\begin{gathered} {{I}_{{2N}}} = \sum\limits_{n = 1}^N {\tilde {\upsilon }_{n}^{2} \to \mathop {{\text{min}}}\limits_{{{{\bar {\upsilon }}}^{{\left( N \right)}}}} ;} \\ \Phi (\bar {\upsilon }_{{}}^{{\left( N \right)}}) = \mathop {{\text{max}}}\limits_{x \in \left[ {{{x}_{0}},{{x}_{1}}} \right]} {\text{|}}Q(x,\bar {\upsilon }_{{}}^{{\left( N \right)}}) - Q{\text{**}}(x){\text{|}} \leqslant \varepsilon \\ \end{gathered} $(5.18)
$\begin{gathered} Q_{n}^{{}}\left( {{{\mu }_{n}},t{\text{*}}} \right) = \bar {Q}_{{}}^{{\left( 0 \right)}}\left( {{{\mu }_{n}}} \right){{e}^{{ - \mu _{n}^{2}t{\text{*}}}}} + K_{n}^{{}}\left( {t{\text{*}}} \right)\bar {\upsilon }_{n}^{{\left( N \right)}};\quad n = 1,2,..., \\ K_{n}^{{}}\left( {t{\text{*}}} \right) = \int\limits_0^{t{\text{*}}} {F\left( t \right){{e}^{{ - \mu _{n}^{2}\left( {t{\text{*}} - t} \right)}}}dt} . \\ \end{gathered} $Задача (5.17) может быть решена по схеме альтернансного метода.
Если аналогично (5.7) техническая реализация управления, представляемого укороченной суммой N слагаемых в (5.14), оказывается затруднительной, то подобно (5.8) поиск $\upsilon \left( x \right)$ производится в классе заведомо реализуемых функций ${{F}_{m}}\left( x \right)$, сумммируемых с весовыми коэффициентами hm:
Тогда вместо (5.13)
(5.20)
$\bar {\upsilon }_{n}^{{}} = \sum\limits_{m = 1}^s {{{h}_{m}}{{{\bar {F}}}_{{mn}}},\quad n = \overline {1,N} .} $Здесь требуемые значения $\bar {\upsilon }_{{}}^{{\left( N \right)}}$ в задаче (5.16), (5.17) могут быть обеспечены только при $N \leqslant s$ в (5.20) путем определения искомых коэффициентов hm в подобной (5.11) форме решения относительно hm линейной системы уравнений (5.20) для заданных $\bar {\upsilon }_{n}^{{}}$, и, следовательно, достижимые величины $\varepsilon $ в (5.17) ограничиваются в данном случае реализуемыми числами s в (5.19).
6. Оптимальное управление процессом нестационарной теплопроводности. В качестве примера, представляющего самостоятельный интерес, рассмотрим задачу оптимального управления процессом индукционного нагрева по критерию качества (1.9).
Пусть температурное поле Q(x, t) неограниченной пластины в процессе индукционного нагрева описывается линейным неоднородным уравнением теплопроводности вида (1.1)–(1.3) в относительных единицах [15–17]:
(6.1)
$\frac{{\partial Q\left( {x,t} \right)}}{{\partial t}} = \frac{{{{\partial }^{2}}Q\left( {x,t} \right)}}{{\partial {{x}^{2}}}} + {{W}_{1}}\left( x \right)u\left( t \right),\quad x \in \left[ {0,1} \right],\quad t \in \left[ {0,t{\text{*}}} \right]$(6.3)
$\frac{{\partial Q\left( {0,t} \right)}}{{\partial x}} = 0;\quad \frac{{\partial Q\left( {1,t} \right)}}{{\partial x}} + \alpha Q\left( {1,t} \right) = 0,$В пространстве модальных переменных ${{\bar {Q}}_{n}}\left( {{{\mu }_{n}},t} \right)$ объект управления (6.1)–(6.3) описывается бесконечной системой уравнений вида (1.6) [15]:
(6.5)
$\begin{gathered} \frac{{d{{{\bar {Q}}}_{n}}\left( {{{\mu }_{n}},t} \right)}}{{dt}} = - \mu _{n}^{2}{{{\bar {Q}}}_{n}}\left( {{{\mu }_{n}},t} \right) + {{{\bar {W}}}_{{1n}}}u\left( t \right),\quad n = 1,2,..., \\ {{{\bar {Q}}}_{n}}\left( {{{\mu }_{n}},0} \right) = 0, \\ \end{gathered} $Температурное поле Q(x, t) представляется его разложением в ряд вида (1.7) по собственным функциям ${\text{cos}}\,\left( {{{\mu }_{n}}x} \right)\,$ [15, 16]:
(6.6)
$Q\left( {x,t} \right) = \sum\limits_{n = 1}^\infty {\frac{{2{{\alpha }^{2}}\cos \left( {{{\mu }_{n}}x} \right)}}{{(\mu _{n}^{2} + {{\alpha }^{2}} + \alpha ){{{\sin }}^{2}}{{\mu }_{n}}}}\,{{{\bar {Q}}}_{n}}\left( {{{\mu }_{n}},t} \right)} .$Здесь ${{\mu }_{n}}$, n = 1, 2, …, – бесконечно возрастающая последовательность корней трансцендентного уравнения
В формуле (6.5)Пусть к конечному температурному состоянию Q(x, t*) при выборе достаточной заранее фиксируемой продолжительности t* оптимального процесса предъявляется требование (1.5) равномерного нагрева до заданной температуры $Q{\text{**}}\left( x \right) = Q{\text{**}} = {\text{const}} > 0$ с допустимой погрешностью $\varepsilon $:
(6.7)
$\mathop {{\text{max}}}\limits_{x \in \left[ {0,1} \right]} \left| {Q\left( {x,t{\text{*}}} \right) - Q{\text{**}}} \right| \leqslant \varepsilon $.Рассмотрим далее следующую задачу оптимального управления. Необходимо найти не стесняемое ограничениями (6.4) программное управляющее воздействие $u{\text{*}}\left( t \right)$, которое переводит объект управления (6.5) из заданного начального в требуемое, согласно (6.7), конечное состояние с минимальным значением критерия оптимальности (1.9).
Решение этой задачи позволяет оценить максимальный эффект, достигаемый по критерию (1.9) в условиях свободы выбора u(t) в (6.4), если при этом $u{\text{*}}\left( t \right) \geqslant 0$ для всех $t \in \left[ {0,t{\text{*}}} \right]$. В рассматриваемом случае искомое ${{\psi }^{{\left( N \right)}}}$-параметризованное управление u*(t) определяется в форме вида (3.3):
(6.8)
$u{\text{*}}\left( t \right) = \frac{1}{2}\sum\limits_{n = 1}^N {\tilde {\psi }_{n}^{{}}\bar {W}_{{1n}}^{{}}{{e}^{{ - \mu _{n}^{2}\left( {t{\text{*}} - t} \right)}}}} .$Интегрирование системы уравнений (6.5) с управляющим воздействием (6.8) приводит к линейной зависимости модальных переменных от $\psi _{{}}^{{\left( N \right)}} = \left( {{{{\tilde {\psi }}}_{n}}} \right),$ $n = \overline {1,N} $:
(6.9)
${{\bar {Q}}_{n}}(\psi _{{}}^{{(N)}},t) = \frac{{{{{\bar {W}}}_{{1n}}}}}{2}\sum\limits_{i = 1}^N {\frac{{{{{\tilde {\psi }}}_{i}}{{{\bar {W}}}_{{1i}}}}}{{\mu _{n}^{2} + \mu _{i}^{2}}}\,{{e}^{{ - \mu _{i}^{2}t{\text{*}}}}}({{e}^{{\mu _{i}^{2}t}}} - {{e}^{{ - \mu _{n}^{2}t}}})} ,\quad n = 1,2,...$Последующая подстановка этого результата в (6.6) для $t = t{\text{*}}$ определяет в явной форме линейную по $\psi _{{}}^{{\left( N \right)}}$ – параметризованную зависимость $Q\left( {x,t{\text{*}}} \right)$:
(6.10)
$Q(x,{{\psi }^{{\left( N \right)}}}) = \sum\limits_{n = 1}^\infty {\frac{{2{{\alpha }^{2}}\,{\text{cos}}\left( {{{\mu }_{n}}x} \right)}}{{(\mu _{n}^{2} + {{\alpha }^{2}} + \alpha )\,{\text{si}}{{{\text{n}}}^{2}}{{\mu }_{n}}}}} \,{{\bar {Q}}_{n}}({{\psi }^{{\left( N \right)}}},t{\text{*}})$Типичные технологические требования в рассматриваемой задаче сводятся к достижению удовлетворительной по величине $\varepsilon $ в (6.7) точности нагрева с помощью управляющих воздействий самой простой из возможных в этих условиях (и, следовательно, легче всего реализуемой) структуры. Применительно к параметрическому представлению $u{\text{*}}(t)$ в форме (6.8) это означает желательность выбора вектора ${{\psi }^{{(N)}}}$ минимальной размерности.
Так, например, легко реализуемый в режиме “включить $(u(t) = {{u}_{{\max }}})$ – выключить $(u(t) = 0)$” процесс оптимального по быстродействию управления объектом (6.1)–(6.4) с управляющим воздействием релейной формы, которое характеризуется всего двумя параметрами – длительностями интервалов его постоянства, как правило, оказывается удовлетворительным при максимально достижимой точности нагрева в этом классе программных управлений [15–17].
Ограничимся далее аналогичным типичным случаем N = 2 в (6.8) с двумя искомыми параметрами $\psi _{*}^{{{\text{(2)}}}} = (\tilde {\psi }_{1}^{*},\tilde {\psi }_{2}^{*})$, полагая $\varepsilon = \varepsilon _{{{\text{min}}}}^{{{\text{(2)}}}}$ в (6.7) по определению (3.5). В такой ситуации, согласно п. 1 предлагаемой в разд. 4 методики, достаточно составить и решить систему уравнений (4.5), (4.6) при $\varepsilon = \varepsilon _{{\min }}^{{(2)}},$ N0 = 2, R = 3.
Физические закономерности процесса индукционного нагрева приводят в данном случае, подобно [15–17], к показанному на рис. 1 характеру изменения $u{\text{*}}\left( t \right)$ во времени в условиях $u{\text{*}}\left( t \right) \geqslant 0$ $\forall t \in \left[ {0,t{\text{*}}} \right]$ и к соответствующей форме кривой пространственного распределения $Q(x,\psi _{*}^{{{\text{(2)}}}})$ на отрезке $\left[ {0,1} \right] \ni x$ при R = 3 (рис. 2), непосредственно фиксирующей систему четырех уравнений (4.5), (4.6) в следующем однозначно устанавливаемом виде:
(6.11)
$\begin{gathered} Q(0,\psi _{*}^{{{\text{(2)}}}}) - Q{\text{**}} = - \varepsilon _{{{\text{min}}}}^{{{\text{(2)}}}}; \\ Q(x_{2}^{0},\psi _{*}^{{{\text{(2)}}}}) - Q{\text{**}} = \varepsilon _{{{\text{min}}}}^{{{\text{(2)}}}}; \\ Q(1,\psi _{*}^{{{\text{(2)}}}}) - Q{\text{**}} = - \varepsilon _{{{\text{min}}}}^{{{\text{(2)}}}}; \\ \frac{{\partial Q(x_{2}^{0},\psi _{*}^{{{\text{(2)}}}})}}{{\partial x}} = 0. \\ \end{gathered} $Рис. 1.
Программное оптимальное управление без учета ограничений на управляющее воздействие (1 – для $\mathop {\max }\limits_t u{\text{*}}\left( t \right) > 1$: $\tilde {\psi }_{1}^{*} = 3.09,$ $\tilde {\psi }_{2}^{*} = 2.84,$ $t_{1}^{*} = 0.95;$ 2 – для $\mathop {\max }\limits_t u{\text{*}}\left( t \right) < 1$: $\tilde {\psi }_{1}^{*} = 2.26,$ $\tilde {\psi }_{2}^{*} = 2.01$, $t_{2}^{*} = 1.20$)
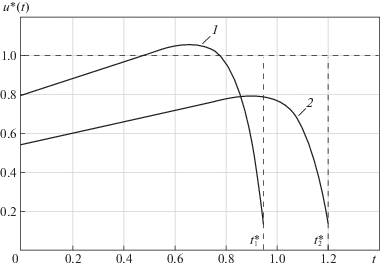
Рис. 2.
Температурное распределение в конце оптимального процесса без ограничений на управляющее воздействие для случая $t{\text{*}} = 0.95$ $(\varepsilon _{{\min }}^{{(2)}} = 0.0155;\;x_{2}^{0} = 0.71)$
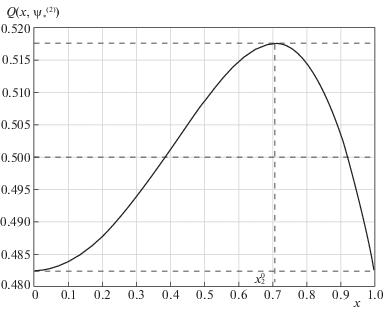
Решение этой линейной по $\psi _{*}^{{{\text{(2)}}}}$ системы известными методами с подстановками (6.9), (6.10) относительно $\tilde {\psi }_{1}^{*},\;\tilde {\psi }_{2}^{*},\;\varepsilon _{{{\text{min}}}}^{{{\text{(2)}}}}$ и $x_{2}^{0}$ при учете достаточно большого числа ${{N}_{1}}$ членов сходящегося ряда в (6.10) исчерпывает решение исходной задачи оптимального управления с требуемой точностью.
Если в том же классе управляющих воздействий при N0 = 2 оказывается допустимой задаваемая конкретным значением величина $\varepsilon $ в (6.7), превышающая найденное значение $\varepsilon _{{\min }}^{{(2)}}$ при $\varepsilon _{{\min }}^{{(2)}} < \varepsilon < \varepsilon _{{\min }}^{{(1)}}$, то, согласно п. 4 общей методики, остается составить и решить систему уравнений (4.5), (4.6) при ${{N}_{0}} = R = 2$. Тогда вместо (6.11) получаем аналогичным путем (опять исходя из фундаментальных свойств температурных полей при индукционном нагреве) систему теперь уже трех уравнений [15–17]:
Учет ограничений на управляющее воздействие. Заранее фиксируемые требования (6.4) могут быть нарушены при оптимальном управлении $u{\text{*}}\left( t \right)$, найденном без их учета (рис. 1, 3).
Рис. 3.
Программное оптимальное управление с учетом ограничений на управляющее воздействие (1 – для $\hat {u}{\text{*}}\left( t \right)$ при $\hat {\psi }_{1}^{*} = 2.85,$ $\hat {\psi }_{2}^{*} = 3.69,$ ${{t}_{1}} = 0.48,$ ${{t}_{2}} = 0.58,$ ${{t}_{3}} = 0.82,$ $t{\text{*}} = 0.85;$ 2 – для $u{\text{*}}\left( t \right)$)
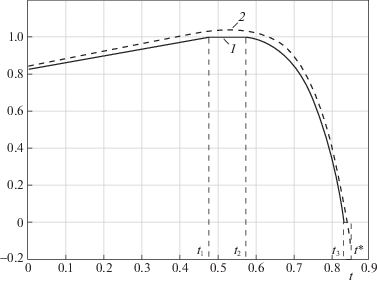
В частности, реализация формально допустимого в этих условиях неравенства $u{\text{*}}\left( {t{\text{*}}} \right) < 0$ при некоторых величинах t* приводит к физически неприемлемому требованию создания отрицательной мощности внутреннего тепловыделения на заключительной стадии оптимального процесса (рис. 3, кривая 2). В соответствии с формой $u{\text{*}}\left( t \right)$, показанной на рис. 3, алгоритм $\hat {u}{\text{*}}\left( t \right)$ программного управления с учетом ограничений (6.4) принимает вид (4.7), (4.8) при N = 2, $\varepsilon = \varepsilon _{{{\text{min}}}}^{{{\text{(2)}}}}$:
Интегрирование системы уравнений (6.5) с управляющим воздействием (6.12) приводит в отличие от (6.9) к выражению для ${{\bar {Q}}_{n}}({{\hat {\psi }}^{{(2)}}},t{\text{*}})$:
(6.14)
$\begin{gathered} {{{\bar {Q}}}_{n}}(\hat {\psi }_{{}}^{{{\text{(2)}}}},t{\text{*}}) = \frac{{{{{\bar {W}}}_{{1n}}}}}{2}\left\{ {\sum\limits_{i = 1}^2 {\frac{{{{{\hat {\psi }}}_{i}}{{{\bar {W}}}_{{1i}}}}}{{\mu _{n}^{2} + \mu _{i}^{2}}}{{e}^{{ - (\mu _{n}^{2} + \mu _{i}^{2})t{\text{*}}}}}} } \right.[({{e}^{{(\mu _{n}^{2} + \mu _{i}^{2}){{t}_{1}}}}} - 1) + ({{e}^{{(\mu _{n}^{2} + \mu _{i}^{2}){{t}_{3}}}}} - {{e}^{{(\mu _{n}^{2} + \mu _{i}^{2}){{t}_{2}}}}})] + \\ \, + \left. {\frac{2}{{\mu _{n}^{2}}}({{e}^{{ - \mu _{n}^{2}\left( {t{\text{*}} - {{t}_{2}}} \right)}}} - {{e}^{{ - \mu _{n}^{2}\left( {t{\text{*}} - {{t}_{1}}} \right)}}})} \right\} \\ \end{gathered} $Теперь задача (4.1), (4.2) для $Q(x,\hat {\psi }_{{}}^{{{\text{(2)}}}})$ опять редуцируется к системе уравнений вида (6.11), которую следует дополнить равенствами (6.13), фиксирующими значения ${{t}_{1}},\;{{t}_{2}},\;{{t}_{3}}$ в роли дополнительных искомых величин, при сохранении аналогичной рис. 2 формы кривой зависимости $Q(x,\hat {\psi }_{{}}^{{{\text{(2)}}}})$ от $x \in \left[ {0,1} \right]$ (рис. 4).
Рис. 4.
Температурное распределение в конце оптимального процесса с ограничением на управляющее воздействие $(\varepsilon _{{\min }}^{{(2)}} = 0.0158;\;x_{2}^{0} = 0.7)$
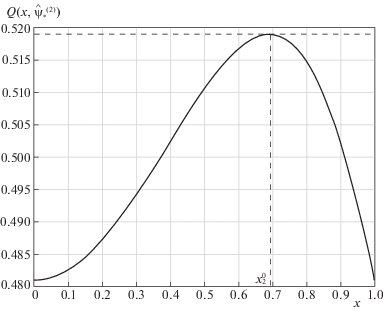
Решение этой системы теперь уже семи уравнений относительно всех семи неизвестных $\hat {\psi }_{1}^{*},\;\hat {\psi }_{2}^{*},\;\varepsilon _{{{\text{min}}}}^{{{\text{(2)}}}},\;x_{2}^{0}$ и ${{t}_{1}},\;{{t}_{2}},\;{{t}_{3}}$ завершает решение рассматриваемой задачи оптимального управления с учетом ограничений (6.4).
Некоторые расчетные результаты22, полученные при индукционном нагреве пластины из титановых сплавов для значений $\alpha = 0,5;$ $Q{\text{**}} = 0,5;$ $\varepsilon = \varepsilon _{{\min }}^{{\left( 2 \right)}}$ представлены на рис. 1, 2 и рис. 3, 4 соответственно в задачах без учета и с учетом ограничений (6.4) на управляющее воздействие. Приведенные зависимости построены по найденным для указанных исходных данных решениям систем уравнений соответственно (6.11) и (6.11), (6.13) при управлениях вида (6.8) и (6.12).
Заключение. Разработана конструктивная технология решения краевых задач оптимального по расходу энергии управления линейными системами с распределенными параметрами параболического типа в условиях оценки в равномерной метрике ограничений на конечные состояния объекта. Предлагаемый подход базируется на специальной процедуре последовательной параметризации управляющих воздействий на множествах конечного числа финишных значений сопряженных переменных принципа максимума Понтрягина и последующей редукции к задаче полубесконечной оптимизации, разрешаемой относительно искомого вектора параметров по схеме альтернансного метода. Получаемые результаты могут быть использованы для решения достаточно широкого круга актуальных проблем разработки энергосберегающих алгоритмов управления, в том числе применительно к представляющим самостоятельный интерес задачам оптимизации по энергопотреблению объектов технологической теплофизики.
Список литературы
Бутковский А.Г. Теория оптимального управления системами с распределенными параметрами. М.: Наука, 1965.
Бутковский А.Г. Методы управления системами с распределенными параметрами. М.: Наука, 1975.
Егоров А.И. Оптимальное управление тепловыми и диффузионными процессами. М.: Наука, 1978.
Рапопорт Э.Я. Анализ и синтез систем управления с распределенными параметрами. М.: Высш. шк., 2005.
Рапопорт Э.Я. Оптимальное управление системами с распределенными параметрами. М.: Высш. шк., 2009.
Рапопорт Э.Я. Альтернансный метод в прикладных задачах оптимизации. М.: Наука, 2000.
Плешивцева Ю.Э., Рапопорт Э.Я. Метод последовательной параметризации управляющих воздействий в краевых задачах оптимального управления системами с распределенными параметрами // Изв. РАН. ТиСУ. 2009. № 3. С. 22–33.
Рапопорт Э.Я. Структурное моделирование объектов и систем управления с распределенными параметрами. М.: Высш. шк., 2003.
Красовский Н.Н. Теория управления движением. М.: Наука, 1968.
Атанс М., Фалб П. Оптимальное управление. М.: Машиностроение, 1968.
Душин С.Е., Зотов Н.С., Имаев В.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления. М.: Высш. шк., 2003.
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: Наука, 1983.
Рапопорт Э.Я. Метод параметрической оптимизации в задачах многоканального управления системами с распределенными параметрами // Изв. РАН. ТиСУ. 2019. № 4. С. 47–61.
Рапопорт Э.Я., Плешивцева Ю.Э. Технология оптимального проектирования сложноструктурированных систем с распределенными параметрами: программные стратегии принятия решений // Онтология проектирования. 2017. Т. 7. № 2(24). С. 172–190.
Рапопорт Э.Я. Оптимизация процессов индукционного нагрева металла. М.: Металлургия, 1993.
Rapoport E., Pleshivtseva Yu. Optimal Control of Induction Heating Processes. London, New York : CRC Press, Taylor & Francis Group, Boca Raton, 2007.
Рапопорт Э.Я., Плешивцева Ю.Э. Оптимальное управление температурными режимами индукционного нагрева. М.: Наука, 2012.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления