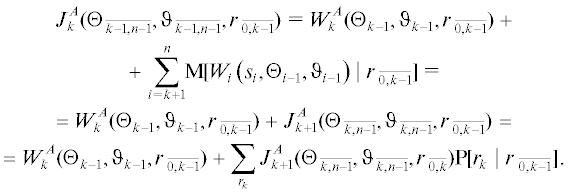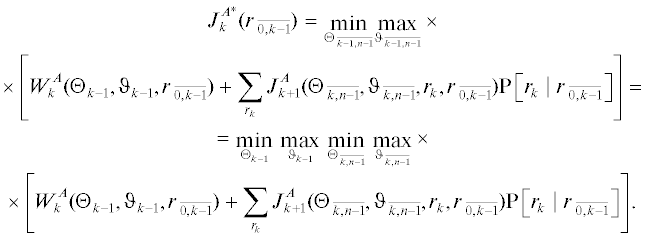Известия РАН. Теория и системы управления, 2020, № 4, стр. 18-27
ИГРОВОЕ УПРАВЛЕНИЕ СЛУЧАЙНОЙ СКАЧКООБРАЗНОЙ СТРУКТУРОЙ ОБЪЕКТА В ЧИСТЫХ СТРАТЕГИЯХ
В. А. Болдинов a, *, В. А. Бухалёв a, А. А. Скрынников a
a Московский научно-исследовательский телевизионный ин-т,
МАИ (национальный исследовательский ун-т), ФГУП “ГосНИИАС”
Москва, Россия
* E-mail: victorboldinov@mail.ru
Поступила в редакцию 26.11.2019
После доработки 10.02.2020
Принята к публикации 30.03.2020
Аннотация
Рассматривается задача оптимального управления случайной скачкообразной структурой объекта в условиях противодействия. Смена состояний структуры объекта наблюдается противоборствующими сторонами с помощью индикаторов, работающих с ошибками. Критерием оптимальности управлений является некоторый функционал состояния объекта, который один из противников стремится минимизировать, а другой – максимизировать. Игроки управляют структурой объекта в чистых стратегиях, применяя конечное число возможных стратегий. Оптимальные управления находятся в классе детерминированных зависимостей от результатов наблюдений, предшествующих текущему моменту. Приводится пример решения задачи оптимизации управления структурой объекта с двумя состояниями методами теории систем со случайной скачкообразной структурой в игровой постановке.
Введение. В настоящей статье приводится динамическая стохастическая система со случайной скачкообразной структурой (ССС) [1–6], имеющей конечное число возможных состояний. Переходы из одного состояния в другое происходят в случайные моменты времени и управляются двумя противоборствующими сторонами (военными противниками, экономическими или политическими конкурентами), преследующими строго противоположные интересы [1, 3]. При этом каждый из противников располагает конечным числом возможных стратегий (управлений) и руководствуется некоторым своим априорным представлением об управляемом объекте и информацией, которую он получает от своего индикатора структуры, регистрирующего с ошибками текущее состояние структуры объекта.
Ставится задача построения алгоритмов управления противников (“игроков”), состоящая в нахождении оптимальных управлений с обратной связью по состоянию объекта в каждый момент времени k в классе детерминированных зависимостей от показаний индикаторов структуры – на отрезке времени от начального момента до текущего k.
Для решения задачи используется теория стохастического динамического программирования на основе метода динамического программирования Беллмана, байесовская обработка информации и марковские математические модели [1, 3, 7–12]. Применение этих методов позволяет построить алгоритмы, сочетающие точность решения с простотой реализации. Их достоинствами являются: обратная связь управлений с состоянием объекта, комплексирование априорной и апостериорной информации о состоянии объекта и рекуррентная форма алгоритмов, не требующая запоминания всей совокупности наблюдений на отрезке времени, который предшествует текущему моменту. Это особенно важно, например, для реализации в системах управления, навигации и наведения летательных аппаратов при существующих ограничениях по памяти в бортовых цифровых вычислительных машинах [13].
1. Постановка задачи. Дано: рассматривается объект ССС, управляемый двумя игроками, которые преследуют строго противоположные интересы. Структура sk описывается марковской цепью с конечным числом возможных состояний ${{s}_{k}} = \overline {1,{{n}^{{(s)}}}} $ , где k – текущий момент времени: $k = \overline {0,n} $.
Информация, которой располагают игроки о вероятностях переходов из состояния sk в состояние ${{s}_{{k + 1}}}$, неодинакова:
(1.1)
$q_{k}^{A}\left( {{{s}_{{k + 1}}}{\text{|}}{{s}_{k}},{{\Theta }_{k}},{{\vartheta }_{k}}} \right)\quad {\text{и}}\quad q_{k}^{B}\left( {{{s}_{{k + 1}}}{\text{|}}{{s}_{k}},{{\Theta }_{k}},{{\vartheta }_{k}}} \right),$Состояние структуры регистрируется индикаторами с ошибками. Измерения состояния структуры описываются условно-марковскими цепями с конечным числом возможных состояний ${{r}_{k}} = \overline {1,{{n}^{r}}} $ и ${{\rho }_{k}} = \overline {1,{{n}^{\rho }}} $. Условно-марковские цепи заданы условными вероятностями переходов из rk в ${{r}_{{k + 1}}}$ и из ${{\rho }_{k}}$ в ${{\rho }_{{k + 1}}}$ при фиксированных ${{s}_{{k + 1}}}$, ${{\Theta }_{k}}$, ${{\vartheta }_{k}}$:
(1.2)
$\pi _{{k + 1}}^{A}\left( {{{r}_{{k + 1}}}{\text{|}}{{r}_{k}},{{s}_{{k + 1}}},{{\Theta }_{k}},{{\vartheta }_{k}}} \right)\quad {\text{и}}\quad \pi _{{k + 1}}^{B}\left( {{{\rho }_{{k + 1}}}{\text{|}}{{\rho }_{k}},{{s}_{{k + 1}}},{{\Theta }_{k}},{{\vartheta }_{k}}} \right).$Зависимость $\pi _{{k + 1}}^{A}( \cdot )$ от ${{\Theta }_{k}}$ означает, что игрок A может управлять как структурой объекта, так и характеристикой индикатора структуры. Зависимость $\pi _{{k + 1}}^{A}( \cdot )$ от ${{\vartheta }_{k}}$ означает, что игрок B может управлять не только структурой объекта sk, но и осуществлять информационное противодействие игроку A. Аналогичный смысл имеет зависимость $\pi _{{k + 1}}^{B}( \cdot )$ от ${{\vartheta }_{k}}$ и ${{\Theta }_{k}}$.
Так как интересы игроков строго противоположны, то показатели качества (эффективности) игры для обоих аналогичны:
(1.3)
$\begin{gathered} {{J}^{A}}(\Theta {{}_{{\overline {0,n - 1} }}},\vartheta {{}_{{\overline {0,n - 1} }}},r{{{\kern 1pt} }_{{\overline {0,n - 1} }}})\mathop = \limits^\Delta \sum\limits_{k = 1}^n {\text{M}}[{{W}_{k}}({{s}_{k}},{{\Theta }_{{k - 1}}},{{\vartheta }_{{k - 1}}})|r{{{\kern 1pt} }_{{\overline {0,k - 1} }}}] = \\ = \;\mathop \sum \limits_{k = 1}^n \sum\limits_{{{s}_{k}}} {\sum\limits_{{{\Theta }_{{k - 1}}}} {\sum\limits_{{{\vartheta }_{{k - 1}}}} {{{W}_{k}}({{s}_{k}},{{\Theta }_{{k - 1}}},{{\vartheta }_{{k - 1}}}){\text{P}}[{{s}_{k}},{{\Theta }_{{k - 1}}},{{\vartheta }_{{k - 1}}}|r{{{\kern 1pt} }_{{\overline {0,k - 1} }}}] = } } } \\ = \;\mathop \sum \limits_{k = 1}^n \sum\limits_{{{s}_{k}}} {{{W}_{k}}({{s}_{k}},{{\Theta }_{{k - 1}}},{{\vartheta }_{{k - 1}}}){\text{P}}[{{s}_{k}}|r{{{\kern 1pt} }_{{\overline {0,k - 1} }}}]} , \\ \end{gathered} $(1.4)
$\begin{gathered} {{J}^{B}}(\Theta {{{\kern 1pt} }_{{\overline {0,n - 1} }}},\vartheta {{{\kern 1pt} }_{{\overline {0,n - 1} }}},\rho {{{\kern 1pt} }_{{\overline {0,n - 1} }}})\mathop = \limits^\Delta \sum\limits_{k = 1}^n {\text{M}}[{{W}_{k}}({{s}_{k}},{{\Theta }_{{k - 1}}},{{\vartheta }_{{k - 1}}})|\rho {{{\kern 1pt} }_{{\overline {0,k - 1} }}}] = \\ = \;\sum\limits_{k = 1}^n {\sum\limits_{{{s}_{k}}} {{{W}_{k}}\left( {{{s}_{k}},{{\Theta }_{{k - 1}}},{{\vartheta }_{{k - 1}}}} \right){\text{P}}[{{s}_{k}}|\rho {{{\kern 1pt} }_{{\overline {0,k - 1} }}}]} } , \\ \end{gathered} $Поскольку рассматривается задача игрового управления, в которой показатели эффективности игроков (1.3), (1.4) различны, так как основываются на различной информации – rk и ρk, то для того, чтобы подчеркнуть это обстоятельство, в качестве показателя выбраны суммы условных математических ожиданий текущей функции потерь ${{W}_{k}}\left( {{{s}_{k}},{{\Theta }_{{k - 1}}},{{\vartheta }_{{k - 1}}}} \right)$ при фиксированных наблюдениях $r{{{\kern 1pt} }_{{\overline {0,k - 1} }}}$, $\rho {{{\kern 1pt} }_{{\overline {0,k - 1} }}}$ соответственно.
Как следует из (1.3), (1.4), критерии оптимальности ${{J}^{{A*}}},$ ${{J}^{{B*}}}$ определяются выражениями
(1.5)
${{J}^{{A*}}}(r{{{\kern 1pt} }_{{\overline {0,n - 1} }}})\mathop = \limits^\Delta \mathop {\min }\limits_{\Theta {{{\kern 1pt} }_{{\overline {0,n - 1} }}}} \mathop {\max }\limits_{\vartheta {{{\kern 1pt} }_{{\overline {0,n - 1} }}}} {{J}^{A}}(\Theta {{{\kern 1pt} }_{{\overline {0,n - 1} }}},\vartheta {{{\kern 1pt} }_{{\overline {0,n - 1} }}},r{{{\kern 1pt} }_{{\overline {0,n - 1} }}}),$(1.6)
${{J}^{{B*}}}(\rho {{{\kern 1pt} }_{{\overline {0,n - 1} }}}) = \mathop {\max }\limits_{\vartheta {{{\kern 1pt} }_{{\overline {0,n - 1} }}}} \mathop {\min }\limits_{\Theta {{{\kern 1pt} }_{{\overline {0,n - 1} }}}} {{J}^{B}}(\Theta {{{\kern 1pt} }_{{\overline {0,n - 1} }}},\vartheta {{{\kern 1pt} }_{{\overline {0,n - 1} }}},\rho {{{\kern 1pt} }_{{\overline {0,n - 1} }}}),$Априорные сведения о начальных значениях вероятностей состояний структуры, которыми располагают игроки, различны: $p_{0}^{A}({{s}_{0}})$ и $p_{0}^{B}({{s}_{0}})$.
Требуется найти: оптимальные управления $\Theta _{k}^{*}(r{{{\kern 1pt} }_{{\overline {0,k} }}},\rho {{{\kern 1pt} }_{{\overline {0,k} }}})$, $\vartheta _{k}^{*}\left( {r{{{\kern 1pt} }_{{\overline {0,k} }}},\rho {{{\kern 1pt} }_{{\overline {0,k} }}}} \right)$ с обратной связью по состоянию объекта в классе детерминированных зависимостей от наблюдений $r{{{\kern 1pt} }_{{\overline {0,k} }}}$, $\rho {{{\kern 1pt} }_{{\overline {0,k} }}}$.
2. Алгоритм игрока A. 2.1. Регулятор структуры. Найдем уравнения регулятора структуры (блока управления), связывающие оптимальное управление с вероятностью состояния структуры.
С учетом специфики поставленной задачи применим подход, разработанный Р. Беллманом и известный как метод динамического программирования [7]. Его обобщения и модификации широко используются для синтеза оптимальных управлений с обратной связью в стохастических системах [8–11].
Обозначим
(2.1)
$J_{k}^{A}(\Theta {{{\kern 1pt} }_{{\overline {k - 1,n} }}},\vartheta {{{\kern 1pt} }_{{\overline {k - 1,n} }}},r{{{\kern 1pt} }_{{\overline {0,k - 1} }}})\mathop = \limits^\Delta \sum\limits_{i = k}^n W_{i}^{A}({{\Theta }_{{i - 1}}},{{\vartheta }_{{i - 1}}},r{{{\kern 1pt} }_{{\overline {0,k - 1} }}}),$(2.2)
$W_{i}^{A}( \cdot )\mathop = \limits^\Delta {\text{M}}[{{W}_{i}}({{s}_{i}},{{\Theta }_{{i - 1}}},{{\vartheta }_{{i - 1}}})|r{{{\kern 1pt} }_{{\overline {0,k - 1} }}}] = \sum\limits_{{{s}_{i}}} {{{W}_{i}}({{s}_{i}},{{\Theta }_{{i - 1}}},{{\vartheta }_{{i - 1}}}){\text{P}}[{{s}_{i}}|r{{{\kern 1pt} }_{{\overline {0,k - 1} }}}]} ,$Представим $J_{k}^{A}( \cdot )$ в виде суммы двух слагаемых: $W_{k}^{A}( \cdot )$ и оставшейся части суммы из (2.1). Тогда на основании (2.1), (2.2) получаем
Обозначив
Формула (2.4) отражает традиционный способ, разработанный Р. Беллманом [7] и используемый всеми авторами, применяющими теорию динамического программирования для оптимизации управления стохастическими системами, например, Р.А. Ховард [8], А.А. Фельдбаум [9], М. Аоки [10], А.Е. Брайсон и Хо Ю Ши [11].
Так как $W_{k}^{A}( \cdot )$ от $\Theta {{{\kern 1pt} }_{{\overline {k,n - 1} }}}$, $\vartheta {{{\kern 1pt} }_{{\overline {k,n - 1} }}}$ не зависит, а
(2.5)
$\begin{gathered} J_{k}^{{A*}} = \mathop {\min }\limits_{{{\Theta }_{{k - 1}}}} \mathop {\max }\limits_{{{\vartheta }_{{k - 1}}}} \left[ {W_{k}^{A}\left( {{{\Theta }_{{k - 1}}},{{\vartheta }_{{k - 1}}}} \right) + \sum\limits_{{{r}_{k}}} J_{{k + 1}}^{{A*}}\left( {{{\Theta }_{{k - 1}}},{{\vartheta }_{{k - 1}}},{{r}_{k}}} \right)\sigma _{k}^{A}({{r}_{k}})} \right] = \\ = \;\mathop {\min }\limits_{{{\Theta }_{{k - 1}}}} \mathop {\max }\limits_{{{\vartheta }_{{k - 1}}}} [W_{k}^{A}\left( {{{\Theta }_{{k - 1}}},{{\vartheta }_{{k - 1}}}} \right) + \tilde {J}_{{k + 1}}^{{A*}}\left( {{{\Theta }_{{k - 1}}},{{\vartheta }_{{k - 1}}}} \right)], \\ \end{gathered} $(2.6)
$\begin{gathered} \sigma _{k}^{A}({{r}_{k}})\mathop = \limits^\Delta {\text{P}}[{{r}_{k}}|r{{{\kern 1pt} }_{{\overline {0,k - 1} }}}]; \\ \tilde {J}_{{k + 1}}^{{A*}}\left( {{{\Theta }_{{k - 1}}},{{\vartheta }_{{k - 1}}}} \right)\mathop = \limits^\Delta \sum\limits_{{{r}_{k}}} J_{{k + 1}}^{{A*}}({{\Theta }_{{k - 1}}},{{\vartheta }_{{k - 1}}},{{r}_{k}})\sigma _{k}^{A}({{r}_{k}}). \\ \end{gathered} $Аргумент $r{{{\kern 1pt} }_{{\overline {0,k - 1} }}}$ у всех функций здесь и далее опущен для простоты записи. Его наличие обозначено символами “$\widehat {}$”, “$\widetilde {}$” и пр.
Вероятность $\sigma _{k}^{A}({{r}_{k}})$ находится по формуле полной вероятности
(2.7)
$\sigma _{k}^{A}({{r}_{k}}) = \sum\limits_{{{s}_{k}}} \pi _{k}^{A}\left( {{{r}_{k}}|{{r}_{{k - 1}}},{{s}_{k}},{{\Theta }_{{k - 1}}},{{\vartheta }_{{k - 1}}}} \right)\tilde {p}_{k}^{A}({{s}_{k}}),$(2.8)
$W_{k}^{A}\left( {{{\Theta }_{{k - 1}}},{{\vartheta }_{{k - 1}}}} \right) = \sum\limits_{{{s}_{k}}} {{W}_{k}}({{s}_{k}},{{\Theta }_{{k - 1}}},{{\vartheta }_{{k - 1}}})\tilde {p}_{k}^{A}({{s}_{k}}),$(2.9)
$\tilde {p}_{k}^{A}({{s}_{k}}) = \sum\limits_{{{s}_{{k - 1}}}} q_{{k - 1}}^{A}\left( {{{s}_{k}}|{{s}_{{k - 1}}},{{\Theta }_{{k - 1}}},{{\vartheta }_{{k - 1}}}} \right)\hat {p}_{{k - 1}}^{A}({{s}_{{k - 1}}}),$Пара минимаксных управлений, согласно (2.5), (2.8), (2.9), определяется формулой
(2.10)
$(\Theta _{{k - 1}}^{*},\vartheta _{{k - 1}}^{A}) = \arg \mathop {\min }\limits_{{{\Theta }_{{k - 1}}}} \mathop {\max }\limits_{{{\vartheta }_{{k - 1}}}} [W_{k}^{A}(\hat {p}_{{k - 1}}^{A}({{s}_{{k - 1}}}),{{\Theta }_{{k - 1}}},{{\vartheta }_{{k - 1}}}) + \tilde {J}_{{k + 1}}^{{A*}}(\hat {p}_{{k - 1}}^{A}({{s}_{{k - 1}}}),{{\Theta }_{{k - 1}}},{{\vartheta }_{{k - 1}}})],$Рекуррентные уравнения (2.5)–(2.10) описывают алгоритм регулятора структуры игрока A. Выходными сигналами регулятора являются управления $\Theta _{k}^{*}$, $\vartheta _{k}^{A}$, входным сигналом – апостериорная вероятность $\hat {p}_{k}^{A}({{s}_{k}})$, которая определяется алгоритмом классификатора структуры (в блоке обработки информации).
2.2. Классификатор структуры. Апостериорная вероятность состояния структуры $\hat {p}_{k}^{A}({{s}_{k}})$, согласно формуле Байеса, обобщенной на класс ССС [1, 2], и формуле полной вероятности, определяется рекуррентными уравнениями
(2.11)
$\hat {p}_{{k + 1}}^{A}({{s}_{{k + 1}}}) = \frac{{\pi _{{k + 1}}^{A}({{r}_{{k + 1}}}|{{r}_{k}},{{s}_{{k + 1}}},\Theta _{k}^{*},\vartheta _{k}^{A})\tilde {p}_{{k + 1}}^{A}({{s}_{{k + 1}}})}}{{\sum\limits_{{{s}_{{k + 1}}}} \pi _{{k + 1}}^{A}({{r}_{{k + 1}}}|{{r}_{k}},{{s}_{{k + 1}}},\Theta _{k}^{*},\vartheta _{k}^{A})\tilde {p}_{{k + 1}}^{A}({{s}_{{k + 1}}})}},$(2.12)
$\tilde {p}_{{k + 1}}^{A}({{s}_{{k + 1}}}) = \sum\limits_{{{s}_{k}}} q_{k}^{A}({{s}_{{k + 1}}}|{{s}_{k}},\Theta _{k}^{*},\vartheta _{k}^{A})\hat {p}_{k}^{A}({{s}_{k}}),$В целом, оптимальный минимаксный информационно-управляющий алгоритм игрока A описывается замкнутой системой рекуррентных уравнений (2.5)–(2.12), в которой уравнения регулятора (2.5)–(2.10) решаются в “обратном времени” ($k = n,n - 1,\; \ldots ,\;1$) при “начальных” условиях $\tilde {J}_{{n + 1}}^{{A*}} \equiv 0$, а уравнения классификатора (2.11)–(2.12) – в “прямом времени” ($k = 0,1,\; \ldots ,\;n - 1$) при начальных условиях $\tilde {p}_{0}^{A} = p_{0}^{A}({{s}_{0}})$.
3. Алгоритм игрока B. Аналогичный информационно-управляющий максиминный алгоритм игрока B описывается уравнениями (2.5)–(2.12), в которых производятся следующие замены:
3.1. Регулятор структуры. С учетом выполненных преобразований алгоритм регулятора структуры игрока B будет иметь вид:
(3.1)
$J_{k}^{{B*}} = \mathop {\max }\limits_{{{\vartheta }_{{k - 1}}}} \mathop {\min }\limits_{{{\Theta }_{{k - 1}}}} [W_{k}^{B}\left( {{{\Theta }_{{k - 1}}},{{\vartheta }_{{k - 1}}}} \right) + \tilde {J}_{{k + 1}}^{{B*}}\left( {{{\Theta }_{{k - 1}}},{{\vartheta }_{{k - 1}}}} \right)],$(3.2)
$\tilde {J}_{{k + 1}}^{{B*}}\left( {{{\Theta }_{{k - 1}}},{{\vartheta }_{{k - 1}}}} \right)\mathop = \limits^\Delta \sum\limits_{{{\rho }_{k}}} J_{{k + 1}}^{{B*}}\left( {{{\Theta }_{{k - 1}}},{{\vartheta }_{{k - 1}}},{{\rho }_{k}}} \right)\sigma _{k}^{B}({{\rho }_{k}}),$(3.3)
$\sigma _{k}^{B}({{\rho }_{k}}) = \sum\limits_{{{s}_{k}}} \pi _{k}^{B}\left( {{{\rho }_{k}}|{{\rho }_{{k - 1}}},{{s}_{k}},{{\Theta }_{{k - 1}}},{{\vartheta }_{{k - 1}}}} \right)\tilde {p}_{k}^{B}({{s}_{k}}),$(3.4)
$W_{k}^{B}\left( {{{\Theta }_{{k - 1}}},{{\vartheta }_{{k - 1}}}} \right) = \sum\limits_{{{s}_{k}}} {{W}_{k}}({{s}_{k}},{{\Theta }_{{k - 1}}},{{\vartheta }_{{k - 1}}})\tilde {p}_{k}^{B}({{s}_{k}}),$(3.5)
$\tilde {p}_{k}^{B}({{s}_{k}}) = \sum\limits_{{{s}_{{k - 1}}}} q_{{k - 1}}^{B}\left( {{{s}_{k}}|{{s}_{{k - 1}}},{{\Theta }_{{k - 1}}},{{\vartheta }_{{k - 1}}}} \right)\hat {p}_{{k - 1}}^{B}({{s}_{{k - 1}}}),$(3.6)
$(\vartheta _{{k - 1}}^{*},\Theta _{{k - 1}}^{B}) = \arg \mathop {\max }\limits_{{{\vartheta }_{{k - 1}}}} \mathop {\min }\limits_{{{\Theta }_{{k - 1}}}} [W_{k}^{B}( \cdot ) + \tilde {J}_{{k + 1}}^{{B*}}( \cdot )],$3.2. Классификатор структуры. Алгоритм классификатора структуры игрока $B$ описывается уравнениями:
(3.7)
$\hat {p}_{{k + 1}}^{B}({{s}_{{k + 1}}}) = \frac{{\pi _{{k + 1}}^{B}({{\rho }_{{k + 1}}}|{{\rho }_{k}},{{s}_{{k + 1}}},\Theta _{k}^{B},\vartheta _{k}^{*})\tilde {p}_{{k + 1}}^{B}({{s}_{{k + 1}}})}}{{\sum\limits_{{{s}_{{k + 1}}}} \pi _{{k + 1}}^{B}({{\rho }_{{k + 1}}}|{{\rho }_{k}},{{s}_{{k + 1}}},\Theta _{k}^{B},\vartheta _{k}^{*})\tilde {p}_{{k + 1}}^{B}({{s}_{{k + 1}}})}},$(3.8)
$\tilde {p}_{{k + 1}}^{B}({{s}_{{k + 1}}}) = \sum\limits_{{{s}_{k}}} q_{k}^{B}({{s}_{{k + 1}}}|{{s}_{k}},\Theta _{k}^{B},\vartheta _{k}^{*})\hat {p}_{k}^{B}({{s}_{k}}),$4. Пример. Рассмотрим задачу оптимизации управления ССС объекта с двумя состояниями как частный случай общей постановки задачи из разд. 1.
Дано: структура объекта, индикаторы структуры и критерии оптимальности описываются следующими выражениями:
1) для игрока A:
(4.1)
$q_{k}^{A}({{s}_{{k + 1}}}|{{s}_{k}}) = {{q}_{k}}({{s}_{{k + 1}}}|{{s}_{k}}),\quad {{s}_{k}} = 1,2,$(4.2)
$\pi _{{k + 1}}^{A}\left( {{{r}_{{k + 1}}}|{{r}_{k}},{{s}_{{k + 1}}}} \right),\quad {{r}_{k}} = 1,2,$(4.3)
$J_{k}^{{A*}} = \mathop {\min }\limits_{q{{{\kern 1pt} }_{{\overline {0,n - 1} }}}} \mathop {\max }\limits_{g{{{\kern 1pt} }_{{\overline {0,n - 1} }}}} \sum\limits_{k = 1}^n {{\text{M}}[{{W}_{k}}({{s}_{k}},{{q}_{{k - 1}}},{{g}_{{k - 1}}})|r{{{\kern 1pt} }_{{\overline {0,k - 1} }}}]} ;$2) для игрока B:
(4.4)
$q_{k}^{B}({{s}_{{k + 1}}}|{{s}_{k}}) = {{q}_{k}}({{s}_{{k + 1}}}|{{s}_{k}}),\quad \tilde {p}_{0}^{B}({{s}_{0}}) = \tilde {p}_{0}^{A}({{s}_{0}}),$(4.5)
$\pi _{{k + 1}}^{B}({{\rho }_{{k + 1}}}|{{\rho }_{k}},{{s}_{{k + 1}}}),\quad {{\rho }_{k}} = 1,2,$(4.6)
$J_{k}^{{B*}} = \mathop {\max }\limits_{g{{{\kern 1pt} }_{{\overline {0,n - 1} }}}} \mathop {\min }\limits_{q{{{\kern 1pt} }_{{\overline {0,n - 1} }}}} \sum\limits_{k = 1}^n {{\text{M}}[{{W}_{k}}({{s}_{k}},{{q}_{{k - 1}}},{{g}_{{k - 1}}})|\rho {{{\kern 1pt} }_{{\overline {0,k - 1} }}}]} ,$(4.7)
${{W}_{k}}({{s}_{k}},{{q}_{{k - 1}}},{{g}_{{k - 1}}}) = \delta ({{s}_{k}},1) + \lambda {{q}_{{k - 1}}} - \mu {{g}_{{k - 1}}},$Вероятностью перехода ${{q}_{k}}$ управляет игрок A, а вероятностью ${{g}_{k}}$ – игрок B.
Согласно (2.2), (2.8), (4.7),
откуда следует содержательный смысл критериев оптимальности (4.3), (4.6): игрок A минимизирует вероятность первого состояния структуры, ограничивая свои усилия по переводу структуры из первого состояния во второе и предполагая, что противник будет максимизировать эту вероятность; игрок B максимизирует ту же самую вероятность, предполагая, что игрок A будет ее минимизировать. При этом игрок B также старается ограничить свои усилия по переводу структуры из второго состояния в первое (так как $max( - \mu {{g}_{{k - 1}}}) = min(\mu {{g}_{{k - 1}}})$). Весовые коэффициенты $\lambda $ и $\mu $ характеризуют приоритетность соответствующих частных показателей в общем показателе качества.Как видно из (4.1), каждый из игроков располагает двумя возможными режимами управления: “экономный” – ${{q}_{{min}}}$, ${{g}_{{min}}}$ и “энергичный” – ${{q}_{{max}}}$, ${{g}_{{max}}}$.
Требуется найти: оптимальные алгоритмы управления игроков в виде детерминированных зависимостей от показаний их индикаторов структуры $r{{{\kern 1pt} }_{{\overline {0,k} }}}$ и $\rho {{{\kern 1pt} }_{{\overline {0,k} }}}$.
Решение. Синтез оптимальных информационно-управляющих алгоритмов игроков A и B осуществляется методом игрового оптимального управления системами ССС.
Информационно-управляющий алгоритм игрока A.
Алгоритм управления игрока A состоит из регулятора и классификатора структуры.
Регулятор структуры игрока A. На основании (2.9), (4.8) получаем
(4.9)
$\begin{gathered} W_{k}^{A} = (1 - {{q}_{{k - 1}}} - {{g}_{{k - 1}}})\hat {p}_{{k - 1}}^{A}(1) + {{g}_{{k - 1}}} + \lambda {{q}_{{k - 1}}} - \mu {{g}_{{k - 1}}} = \\ = {{h}_{{k - 1}}}\hat {p}_{{k - 1}}^{A}(1) + \lambda {{q}_{{k - 1}}} + (1 - \mu ){{g}_{{k - 1}}}, \\ \end{gathered} $Будем искать решение уравнения (2.5) в виде
где $\psi _{k}^{A}$, $m_{k}^{A}$ – неопределенные параметры.Из (2.6), (2.9), (4.10), (4.11) следует
(4.12)
$\tilde {J}_{{k + 1}}^{{A*}} = \psi _{k}^{A}\tilde {p}_{k}^{A}(1) + m_{k}^{A} = \psi _{k}^{A}\left[ {{{h}_{{k - 1}}}{{{\hat {p}}}_{{k - 1}}}(1) + {{g}_{{k - 1}}}} \right] + m_{k}^{A}.$Оптимальные значения ${{q}_{{k - 1}}}$, ${{g}_{{k - 1}}}$, согласно (2.10), (4.9)–(4.11), определяются формулой
(4.13)
$(q_{{k - 1}}^{*},\hat {g}_{{k - 1}}^{A}) = \arg \mathop {\min }\limits_{{{q}_{{k - 1}}}} \mathop {\max }\limits_{{{g}_{{k - 1}}}} [W_{k}^{A} + \tilde {J}_{{k + 1}}^{{A*}}] = $(4.14)
$\lambda _{{k - 1}}^{A}\mathop = \limits^\Delta \lambda {{(1 + \psi _{k}^{A})}^{{ - 1}}};\quad \mu _{{k - 1}}^{A}\mathop = \limits^\Delta \mu {{(1 + \psi _{k}^{A})}^{{ - 1}}}.$Из (4.13), (4.14) следует
(4.15)
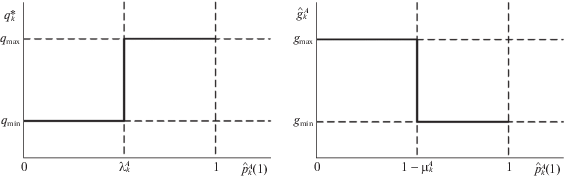
$q_{{k - 1}}^{*} = \left( \begin{gathered} {{q}_{{min}}}\quad {\text{при}}\quad \hat {p}_{{k - 1}}^{A}(1) \leqslant \lambda _{{k - 1}}^{A}, \hfill \\ {{q}_{{max}}}\quad {\text{при}}\quad \hat {p}_{{k - 1}}^{A}(1) > \lambda _{{k - 1}}^{A}, \hfill \\ \end{gathered} \right.$(4.16)
$\hat {g}_{{k - 1}}^{A} = \left( \begin{gathered} {{g}_{{min}}}\quad {\text{при}}\quad \hat {p}_{{k - 1}}^{A}(2) \leqslant \mu _{{k - 1}}^{A}, \hfill \\ {{g}_{{max}}}\quad {\text{при}}\quad \hat {p}_{{k - 1}}^{A}(2) > \mu _{{k - 1}}^{A}. \hfill \\ \end{gathered} \right.$Подставив (4.11)–(4.13) в (2.5), получаем
Приравнивая коэффициенты при $\hat {p}_{{k - 1}}^{A}(1)$ в левой и правой частях уравнения (4.17), получаем рекуррентное уравнение для ψk:
откуда следует и с учетом (4.14), (4.18) получаем рекуррентное уравнение для $\varepsilon _{k}^{A}\mathop = \limits^\Delta \lambda {\text{/}}\lambda _{k}^{A} = \mu {\text{/}}\mu _{k}^{A}$:(4.19)
$\varepsilon _{{k - 1}}^{A} = 1 + (1 - q_{k}^{*} - \hat {g}_{k}^{A})\varepsilon _{k}^{A},\quad \varepsilon _{n}^{A} = 1,\quad k = n,n - 1, \ldots ,1.$Пороговые значения $\lambda _{k}^{A}$, $\mu _{k}^{A}$ вычисляются по формулам
(4.20)
$\lambda _{k}^{A} = \lambda {\text{/}}\varepsilon _{k}^{A};\quad \mu _{k}^{A} = \mu {\text{/}}\varepsilon _{k}^{A}.$Учитывая, что $\hat {p}_{k}^{A}(2) = 1 - \hat {p}_{k}^{A}(1)$, алгоритм (4.16) удобно записать в виде
(4.21)
$\hat {g}_{{k - 1}}^{A} = \left( \begin{gathered} {{g}_{{min}}}\quad {\text{при}}\quad \hat {p}_{{k - 1}}^{A}(1) \geqslant 1 - \mu _{{k - 1}}^{A}, \hfill \\ {{g}_{{max}}}\quad {\text{при}}\quad \hat {p}_{{k - 1}}^{A}(1) < 1 - \mu _{{k - 1}}^{A}. \hfill \\ \end{gathered} \right.$Алгоритм регулятора игрока A изображен на рис. 1.
Классификатор структуры игрока A. Апостериорные вероятности $\hat {p}_{k}^{A}(1)$, $\hat {p}_{k}^{A}(2)$ вычисляются в классификаторе структуры, уравнения которого (2.11), (2.12) принимают вид
(4.22)
$\begin{gathered} \hat {p}_{{k + 1}}^{A}(1) = {{\left[ {1 + \frac{{\pi _{{k + 1}}^{A}\left( {{{r}_{{k + 1}}}|{{r}_{k}},2} \right)\tilde {p}_{{k + 1}}^{A}(2)}}{{\pi _{{k + 1}}^{A}\left( {{{r}_{{k + 1}}}|{{r}_{k}},1} \right)\tilde {p}_{{k + 1}}^{A}(1)}}} \right]}^{{ - 1}}}, \\ \hat {p}_{{k + 1}}^{A}(2) = 1 - \hat {p}_{{k + 1}}^{A}(1), \\ \tilde {p}_{{k + 1}}^{A}(1) = (1 - q_{k}^{*})\hat {p}_{k}^{A}(1) + \hat {g}_{k}^{A}\hat {p}_{k}^{A}(2), \\ \tilde {p}_{k}^{A}(2) = 1 - \tilde {p}_{k}^{A}(1), \\ k = 0,1,2,\; \ldots ,\;n - 1;\quad \tilde {p}_{0}^{A} = p_{0}^{A}(1). \\ \end{gathered} $Информационно-управляющий алгоритм игрока B. Алгоритм описывается уравнениями, подобными уравнениям алгоритма игрока A, в которых произведены изменения, соответствующие замене минимакса на максимин:
(4.23)
$\begin{gathered} \hat {q}_{{k - 1}}^{B} = \left( \begin{gathered} {{q}_{{min}}}\quad {\text{при}}\quad \hat {p}_{{k - 1}}^{B}(1) \leqslant \lambda _{{k - 1}}^{B}, \hfill \\ {{q}_{{max}}}\quad {\text{при}}\quad \hat {p}_{{k - 1}}^{B}(1) > \lambda _{{k - 1}}^{B}, \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \end{gathered} $(4.24)
$\lambda _{k}^{B} = \lambda {\text{/}}\varepsilon _{k}^{B};\quad \mu _{k}^{B} = \mu {\text{/}}\varepsilon _{k}^{B};$(4.25)
$\varepsilon _{{k - 1}}^{B} = 1 + (1 - \hat {q}_{k}^{B} - g_{k}^{*})\varepsilon _{k}^{B},\quad \varepsilon _{n}^{B} = 1,\quad k = n,n - 1, \ldots ,1,$(4.26)
$\begin{gathered} \hat {p}_{{k + 1}}^{B}(1) = {{\left[ {1 + \frac{{\pi _{{k + 1}}^{B}({{\rho }_{{k + 1}}}|{{\rho }_{k}},2)\tilde {p}_{{k + 1}}^{B}(2)}}{{\pi _{{k + 1}}^{B}({{\rho }_{{k + 1}}}|{{\rho }_{k}},1)\tilde {p}_{{k + 1}}^{B}(1)}}} \right]}^{{ - 1}}}, \\ \hat {p}_{{k + 1}}^{B}(2) = 1 - \hat {p}_{{k + 1}}^{B}(1), \\ \tilde {p}_{{k + 1}}^{B}(1) = (1 - \hat {q}_{k}^{B})\hat {p}_{k}^{B}(1) + g_{k}^{*}\hat {p}_{k}^{B}(2), \\ \tilde {p}_{k}^{B}(2) = 1 - \tilde {p}_{k}^{B}(1), \\ k = 0,1,2,\; \ldots ,\;n - 1;\quad \tilde {p}_{0}^{B} = p_{0}^{B}(1). \\ \end{gathered} $Физический смысл полученных оптимальных регуляторов структуры: если вероятность состояния структуры, нежелательного для игрока (sk = 1 – для игрока A и ${{s}_{k}} = 2$ – для игрока B), превышает некоторый порог ($\lambda _{k}^{*}$ – для игрока A и $\mu _{k}^{*}$ – для игрока B), то включается “энергичный” режим управления (${{q}_{{max}}}$ – для игрока A и ${{g}_{{max}}}$ – для игрока B), повышающий вероятность перехода в желаемое для данного игрока состояние структуры (${{s}_{k}} = 2$ – для игрока A и ${{s}_{k}} = 1$ – для игрока B).
Если же вероятность нежелательного состояния структуры меньше указанного порога, то включается “экономный” режим управления, при котором вероятность переходов минимальна (${{q}_{{min}}}$ – для игрока A и ${{g}_{{min}}}$ – для игрока B).
Кроме оптимальных управлений $q_{k}^{*}$ и $g_{k}^{*}$ каждый игрок определяет предполагаемое оптимальное управление своего противника ($\hat {g}_{k}^{A}$ или $\hat {q}_{k}^{B}$) на основании показаний своего индикатора структуры ($r{{{\kern 1pt} }_{{\overline {0,k} }}}$ или $\rho {{{\kern 1pt} }_{{\overline {0,k} }}}$). Эти оценки необходимы в качестве входных данных для классификаторов структуры.
Приближенно-оптимальные регуляторы структуры. Полученные алгоритмы можно существенно упростить, если в уравнениях (4.19), (4.25) приближенно заменить $q_{k}^{*}$, $\hat {q}_{k}^{B}$, $g_{k}^{*}$, $\hat {g}_{k}^{A}$ их некоторыми средневзвешенными значениями:
(4.27)
$\begin{gathered} q_{k}^{*} = \hat {q}_{k}^{B} = {{{\tilde {\lambda }}}_{k}}{{q}_{{min}}} + (1 - {{{\tilde {\lambda }}}_{k}}){{q}_{{max}}}, \\ g_{k}^{*} = \hat {g}_{k}^{A} = {{{\tilde {\mu }}}_{k}}{{g}_{{min}}} + (1 - {{{\tilde {\mu }}}_{k}}){{g}_{{max}}}, \\ \end{gathered} $Подставив (4.27) в (4.19), (4.25), получаем рекуррентное уравнение
(4.28)
${{\varepsilon }_{{k - 1}}} = (1 - {{q}_{{max}}} - {{g}_{{max}}}){{\varepsilon }_{k}} + \lambda ({{q}_{{max}}} - {{q}_{{min}}}) + \mu ({{g}_{{max}}} - {{g}_{{min}}}) + 1,$В установившемся режиме из (4.28) следует
(4.29)
${{\varepsilon }_{{k - 1}}} = {{\varepsilon }_{k}} = \varepsilon = \frac{{1 + \lambda ({{q}_{{max}}} - {{q}_{{min}}}) + \mu ({{g}_{{max}}} - {{g}_{{min}}})}}{{{{q}_{{max}}} + {{g}_{{max}}}}},$(4.30)
$\tilde {\lambda } = \lambda {\text{/}}\varepsilon ;\quad \tilde {\mu } = \mu {\text{/}}\varepsilon .$Как видно из (4.28)–(4.30), приближенные пороговые значения ${{\tilde {\lambda }}_{k}}$, ${{\tilde {\mu }}_{k}}$ вычисляются на основании только априорных данных и не зависят от показаний индикаторов структуры, что значительно упрощает практическую реализацию алгоритмов.
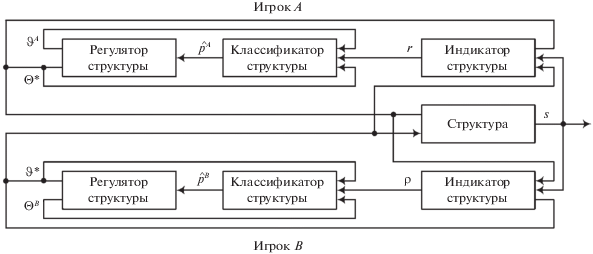
Заключение. Каждый из игровых информационно-управляющих алгоритмов противоборствующих сторон состоит из двух взаимосвязанных блоков: регулятора структуры и классификатора структуры (рис. 2).
Рассмотренная задача представляет собой игру с неполной информацией и ненулевой суммой и не имеет седловой точки вследствие различной информированности игроков о результатах игры. Прежде всего это объясняется различными показаниями индикаторов структуры ${{r}_{k}} \ne {{\rho }_{k}}$, откуда следует $\hat {p}_{k}^{A}({{s}_{k}}) \ne \hat {p}_{k}^{B}({{s}_{k}})$, $\Theta _{k}^{*} \ne \Theta _{k}^{B}$, $\vartheta _{k}^{*} \ne \vartheta _{k}^{A}$. Поэтому седловая точка игры отсутствует даже в том случае, когда противники располагают одинаковой априорной информацией (${{q}^{A}}( \cdot ) = {{q}^{B}}( \cdot )$, $\tilde {p}_{0}^{A}({{s}_{0}}) = \tilde {p}_{0}^{B}({{s}_{0}})$), а текущая функция потерь ${{W}_{k}}( \cdot )$ сепарабельна относительно управлений игроков qk, gk.
Список литературы
Бухалёв В.А. Распознавание, оценивание и управление в системах со случайной скачкообразной структурой. М.: Физматлит, 1996. 287 с.
Бухалёв В.А. Оптимальное сглаживание в системах со случайной скачкообразной структурой. М.: Физматлит, 2013. 188 с.
Бухалёв В.А., Скрынников А.А., Болдинов В.А. Алгоритмическая помехозащита беспилотных летательных аппаратов. М.: Физматлит, 2018. 192 с.
Артемьев В.М. Теория динамических систем со случайными изменениями структуры. Минск: Высш. шк., 1979. 160 с.
Пакшин П.В. Дискретные системы со случайными параметрами и структурой. М.: Наука, 1994. 304 с.
Скляревич А.Н. Линейные системы с возможными нарушениями. М.: Наука, 1975. 352 с.
Беллман Р. Динамическое программирование. М.: Изд-во иностр. лит., 1960. 400 с.
Ховард Р.А. Динамическое программирование и марковские процессы. М.: Сов. радио, 1964.
Фельдбаум А.А. Основы теории оптимальных автоматических систем. М.: Наука, 1966. 623 с.
Аоки М. Оптимизация стохастических систем. М.: Наука, 1971. 424 с.
Брайсон А.Е., Хо Ю Ши. Прикладная теория оптимального управления. М.: Мир, 1972. 544 с.
Стратонович Р.Л. Условные процессы Маркова // Теория вероятностей и ее применения. 1960. Т. 5. Вып. 2. С. 172–195.
Себряков Г.Г., Красильщиков М.Н. Управление и наведение беспилотных маневренных летательных аппаратов на основе современных информационных технологий. М.: Физматлит, 2003. 280 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления