Известия РАН. Теория и системы управления, 2020, № 4, стр. 160-168

Введение. В современной литературе можно выделить достаточно представительную ветвь исследований по динамике ветротурбин, работающих на основе эффекта Магнуса. Как правило, речь идет о горизонтально-осевых турбинах с цилиндрическими или с коническими лопастями, приводимыми во вращение посредством специальных моторов [1–4]. Затраты энергии, необходимые для работы моторов, с избытком покрываются за счет отбора энергии от потока (при плановом режиме функционирования турбины). В то же время известна конструкция, позволяющая реализовать авторотацию каждой лопасти без применения моторов: в качестве лопастей используются роторы Савониуса (далее “S-роторы”) [5, 6]. Возможность обойтись без дополнительных моторов радикально упрощает конструкцию. В результате интерес к турбинам, в которых для формирования силы Магнуса применяются S-роторы, вполне оправдан, несмотря на то, что они не развивают столь высоких значений крутящего момента, как турбины с принудительно раскрученными лопастями.

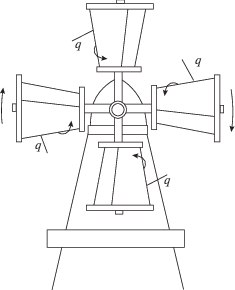
В [5] отмечена целесообразность использования авторотирующих лопастей не цилиндрической, а конической формы: каждая лопасть расширяется по направлению к внешней окружности основной турбины. Соответствующая схема, предложенная в патенте [5], представлена на рис. 1, символом q обозначена сила Магнуса, действующая на каждую лопасть. Отметим, что для турбин с принудительно вращающимися лопастями известны результаты сравнительного анализа [1], показывающие, что применение лопастей в форме усеченного конуса приводит (по сравнению с цилиндрическими лопастями) к увеличению механической мощности турбины в широком диапазоне параметров модели.

В то же время известные в литературе исследования динамики турбин с авторотирующими лопастями в форме S-роторов ограничены случаем лопастей цилиндрического сечения [6–8]. В настоящей работе для турбины, использующей в качестве лопастей S-роторы конического сечения, предложена малопараметрическая математическая модель, основанная на гипотезе квазистатического обтекания.

Для упрощения описания аэродинамики конических лопастей каждая лопасть в модели “заменена” парой цилиндрических S-роторов различного радиуса. Разбиение лопасти на пару роторов позволяет использовать экспериментальные данные о силомоментных характеристиках ротора в однородном потоке (именно такие данные доступны в литературе). Подобный подход разбиения лопасти с целью учета изменения характеристик обтекания вдоль радиуса применен в работе [9] для классической ветротурбины.

Относительная простота модели позволяет провести эффективный параметрический анализ и описать качественные особенности движения системы, не привлекая средства вычислительной аэродинамики. В частности, в настоящей статье проанализировано влияние внешнего электрического сопротивления в локальной цепи генератора ветроустановки на величину механической мощности на рабочем режиме. Построена стратегия управления, основанная на изменении внешнего электрического сопротивления в цепи генератора, позволяющая перевести систему на рабочий режим, характеризующийся максимальной величиной механической мощности.

1. Описание механической системы и постановка задачи. Рассмотрим механическую систему, состоящую из центрального вала и из n идентичных друг другу лопастей, установленных на центральном валу в цилиндрических шарнирах. Оси цилиндрических шарниров лежат в плоскости, перпендикулярной оси центрального вала.

Центральный вал жестко соединен с ротором электрогенератора. Генератор включен в локальную электрическую цепь. Величина внешнего сопротивления в цепи генератора рассматривается как управляющее воздействие на систему: она может быть изменена с целью достижения максимальной мощности или для того, чтобы перевести систему из начального состояния в окрестность программного рабочего режима.

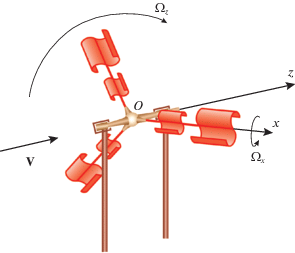
Центральный вал может вращаться вокруг неподвижной оси Oz, параллельной вектору V скорости потока (считаем, что величина и направление скорости потока постоянны). Ось одного из цилиндрических шарниров обозначим как Ox. Далее будем описывать одну из лопастей, предполагая, что все лопасти идентичны и начинают движение с одинаковыми начальными условиями.

Будем считать, что лопасть состоит из двух цилиндрических S-роторов различных радиусов (упрощенная “модель” конической лопасти). Ротор малого радиуса расположен ближе к оси Oz, ротор большого радиуса – дальше от оси Oz (рис. 2). Будем считать, что радиус ${{b}_{i}}$, $i = 1,2$, S-ротора пропорционален расстоянию от центра ротора до оси Oz (здесь и далее индексом “1” обозначены величины, характеризующие большой ротор, индексом “2” – малый). Пусть расстояние от оси Oz до центра большого ротора равно ${{r}_{1}}$, а до центра малого ротора – ${{r}_{2}}$. При этом предположим, что “высота” каждого ротора Савониуса вдоль его собственной центральной оси равна диаметру ротора и составляет $2{{b}_{i}}$ для большого и малого роторов соответственно. Это предположение обусловлено тем, что в литературе доступны экспериментальные данные о силе Магнуса, действующей на ротор Савониуса именно для роторов квадратного сечения [10].

Массу большого S-ротора обозначим ${{m}_{1}}$, малого – ${{m}_{2}}$. Вал, направленный вдоль оси Ox, на котором закреплены роторы, невесомый. Считаем лопасти однородными. Таким образом, центр масс лопасти удален от оси Oz на расстояние:

Лопасть (пара S-роторов) может вращаться вокруг оси Ox, являющейся ее осью геометрической симметрии и одной из главных центральных осей инерции. Пусть ${{J}_{x}}$ – момент инерции лопасти относительно оси $Ox$. Другие два главных момента инерции лопасти будем считать одинаковыми и обозначим через ${{J}_{S}}$. Тогда момент инерции S-ротора относительно любой оси, перпендикулярной оси Ox, в том числе относительно оси Oz, равен ${{J}_{S}}$ (не зависит от текущего угла поворота S-ротора относительно оси Ox). Пусть ${{J}_{z}}$ – момент инерции относительно оси Oz центрального вала вместе с закрепленным на нем ротором генератора, ${{\Omega }_{x}}$ – угловая скорость вращения лопасти вокруг оси Ox, ${{{\Omega }}_{z}}$ – угловая скорость вращения центрального вала вокруг оси Oz.

Кинетическая энергия одной лопасти имеет вид

Кинетическая энергия всей турбины, включая ротор генератора, жестко закрепленный на центральном валу, выражается формулой

где $J = n({{m}_{1}} + {{m}_{2}}){{r}^{2}} + n{{J}_{S}} + {{J}_{z}}$ – суммарный момент инерции всей системы относительно оси Oz.

Опишем силы, действующие на систему. Для каждого S-ротора будем считать, что центр давления (точка приложения аэродинамических сил) расположен в геометрическом центре C_i ротора. Таким образом, замена “конической” лопасти на лопасть, составленную из двух цилиндрических роторов, по сути, подразумевает использование модели аэродинамического воздействия с двумя центрами давления.

Будем считать, что аэродинамическое воздействие на отдельный S-ротор описывается аэродинамическим моментом ${{M}_{i}}$ относительно оси Ox и силами ${{{\mathbf{D}}}_{{\mathbf{i}}}}$ и ${{{\mathbf{L}}}_{{\mathbf{i}}}}$, приложенными в геометрическом центре C_i ротора. Здесь ${{{\mathbf{D}}}_{{\mathbf{i}}}}$ – сила лобового сопротивления, направленная противоположно вектору воздушной скорости точки C_i; ${{{\mathbf{L}}}_{{\mathbf{i}}}}$ – боковая сила, включающая в себя силу Магнуса; вектор ${{{\mathbf{L}}}_{{\mathbf{i}}}}$ направлен ортогонально вектору воздушной скорости точки C_i. Вектор ${{{\mathbf{U}}}_{i}}$ воздушной скорости точки C_i есть разность между вектором ее абсолютной скорости и вектором V скорости потока. Аэродинамическое воздействие на ротор будем описывать на базе квазистатического подхода, предполагая при этом, что аэродинамические силы и моменты зависят от мгновенной воздушной скорости точки ${{C}_{i}}$ и от угловой скорости S-ротора (подобно работам [7, 8, 10, 11]). Для описания вращения тела в среде можно использовать и альтернативные модификации квазистатической модели: например, как в работе [12] (более того, в [12] рассматриваются вопросы влияния на вращающийся управляемый объект дополнительных возмущений сложной структуры). Отметим, что во многих ситуациях значительно предпочтительнее модели, учитывающие зависимость аэродинамических характеристик S-ротора не только от угловой скорости, но и от угла поворота (например, такие модели необходимы для исследования положений равновесия рассматриваемой системы). Однако в настоящей работе ограничимся аэродинамическими функциями, усредненными по углу поворота, поскольку построение малопараметрической модели, описывающей зависимость аэродинамики S-ротора от угла поворота, является открытой задачей (что видно, например, из [13–15]), которая значительно выходит за рамки настоящей работы. Итак, используем следующую модель, которую можно считать относительно точной, при условии, что угловая скорость S-ротора не близка к нулевой:

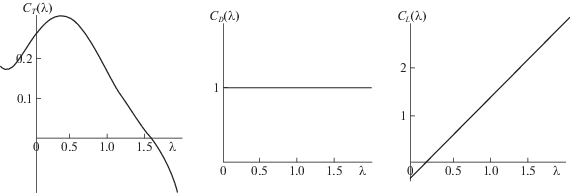
Здесь ρ – плотность воздуха, ${{S}_{i}} = 4b_{i}^{2}$ – характерная площадь одного S-ротора. Быстроходность ротора Савониуса (отношение линейной скорости точки, расположенной на краю ротора, к воздушной скорости точки C_i) обозначена ${{\lambda }_{i}}$. Функции ${{C}_{T}}\left( {{{\lambda }_{i}}} \right)$, ${{C}_{D}}\left( {{{\lambda }_{i}}} \right)$, ${{C}_{L}}\left( {{{\lambda }_{i}}} \right)$ – безразмерные коэффициенты момента M_i, силы D_i лобового сопротивления и боковой силы L_i соответственно. Эти функции строятся по результатам экспериментов. В данной работе эти функции аппроксимируются многочленами на основе экспериментальных данных для ротора Савониуса, приведенных в [10], при этом получены следующие зависимости (рис. 3):

Аэродинамические силы ${{{\mathbf{D}}}_{{\mathbf{i}}}}$ и ${{{\mathbf{L}}}_{{\mathbf{i}}}}$, приложенные в точках ${{С}_{1}}$ и ${{С}_{2}}$, создают момент относительно оси Oz. Суммарный аэродинамический момент M_a относительно оси Oz, действующий на центральный вал турбины (формируемый за счет $2n$ S-роторов), определяется выражением

Помимо аэродинамического момента M_a на центральный вал действует электромеханический момент M_e, отвечающий за нагрузку со стороны потребителей в локальной цепи электрогенератора ветроустановки. Будем считать, что он пропорционален угловой скорости вращения вала:

Здесь $\beta $ – коэффициент электромеханического взаимодействия (константа), $\sigma $ – внутреннее сопротивление генератора (константа), R – внешнее сопротивление в локальной цепи генератора. Данная модель электромеханического момента, действующего на ротор генератора, основана на работах [16, 17], где построена и проанализирована динамическая система, включающая уравнение изменения тока в локальной цепи генератора ветроустановки.

В настоящей работе величина R будет выступать в качестве варьируемого параметра, в том числе в качестве управления.

Рабочему режиму ветротурбины соответствует притягивающий стационарный режим движения механической системы. Требуется описать зависимость механической мощности ветроустановки от внешнего сопротивления в цепи генератора и от других параметров модели и предложить стратегию управления величиной внешнего сопротивления, позволяющую перевести систему на рабочий режим, характеризующийся максимальной мощностью.

2. Уравнения движения. Составляя уравнения движения системы в форме уравнений Лагранжа второго рода и проводя процедуру обезразмеривания, получаем уравнения движения в следующем виде:

Здесь точка обозначает производную по безразмерному времени $\tau = 0.5{{J}^{{ - 1}}}n\rho {{S}_{1}}r_{1}^{2}Vt$; переменные ${{\omega }_{x}} = {{V}^{{ - 1}}}{{b}_{1}}{{{\Omega }}_{x}}$, $~{{\omega }_{z}} = {{V}^{{ - 1}}}{{r}_{1}}{{{\Omega }}_{z}}$ – безразмерные угловые скорости, a – параметр, характеризующий инерционные свойства системы, k – коэффициент, описывающий внешнюю электрическую нагрузку.

Замечание 1. Следует отметить, что система (2.1) заведомо не может отражать поведение реальной турбины в окрестности положений равновесия последней, поскольку при построении модели были использованы функции аэродинамических коэффициентов, усредненные по углу. На практике, чтобы избежать остановки турбины, может потребоваться небольшая начальная принудительная раскрутка. Помимо этого, можно использовать лопасти, закрученные вдоль оси Ox, что может полностью “убрать” положения равновесия S-роторов (как показано, например, в [18, 19]). В настоящей модели можно рассмотреть ротор с закруткой: это соответствует тому, что S-образная поверхность малого S-ротора повернута (вокруг оси Ox) на 90° по отношению к большому S-ротору.

Замечание 2. Предположим, что известна зависимость аэродинамических коэффициентов не только от быстроходностей λ_i, но и от угла поворота S-роторов вокруг оси Ox (считаем, что все n лопастей совершают одинаковое движение, так что повороты всех S-роторов описываются одним значением угла). Тогда в области, где отделена от нуля угловая скорость Ω_x, можно принять угол поворота S-роторов за новое время. В случае малых значений величины ${{J}^{{ - 1}}}\rho {{S}_{1}}r_{1}^{3}$ можно считать безразмерные угловые скорости ω_x, ω_z медленными переменными и применить классическую теорему об усреднении, приведенную в монографии [20]. Усредненная по углу поворота S-роторов система имеет вид (2.1). Соответствие между решениями системы (2.1) и решениями неусредненной по углу системы, в том числе между асимптотически устойчивыми неподвижными точками системы (2.1) и аттракторами неусредненной системы, описывается теоремами работы [20].

3. Стационарные режимы. Устойчивая неподвижная точка $(\omega _{x}^{*};\omega _{z}^{*})$ системы (2.1) соответствует рабочему режиму ветроустановки (при $\omega _{x}^{*} \ne 0$, $\omega _{z}^{*} \ne 0$).

Неподвижная точка удовлетворяет следующим уравнениям:

Здесь $\lambda _{i}^{*}$ – значения быстроходностей S-роторов, соответствующие неподвижным точкам системы (2.1). Далее зафиксируем значения параметров, отвечающих за геометрические и массовые характеристики системы: ${{r}_{1}}{\text{/}}{{r}_{2}} = 2$, ${{b}_{1}}{\text{/}}{{b}_{2}} = 2$, a = 10. Построим численно зависимости ($\omega _{x}^{*}$; $\omega _{z}^{*}$) от параметра k, характеризующего управление внешней электрической нагрузкой. Для всех неподвижных точек, найденных путем численного решения системы (3.1), выполним численно проверку устойчивости, вычисляя максимальную вещественную часть собственных значений системы (2.1), линеаризованной вблизи соответствующей точки.

В результате численного анализа установлено, что при каждом рассмотренном значении k из диапазона k ∈ [0, 15] неподвижная точка системы (2.1) является единственной и асимптотически устойчивой. При дальнейшем увеличении параметра k значения $\omega _{x}^{*}$, $\omega _{z}^{*}$ практически перестают меняться: выходят на асимптоты.

Бифуркационные диаграммы, описывающие зависимости между коэффициентом k полезной нагрузки и безразмерными угловыми скоростями $\omega _{z}^{*}$ центрального вала и $\omega _{x}^{*}$ S-роторов на стационарных режимах, представлены на рис. 4.

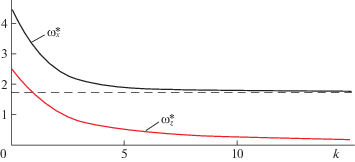
На рис. 4 пунктиром обозначена асимптота, к которой стремится значение $\omega _{x}^{*}$ при $k \to \infty $ ($\omega _{z}^{*}$ при этом стремится к нулю). На рис. 5 показаны значения $\lambda _{1}^{*}$, $\lambda _{2}^{*}$ быстроходностей ${{\lambda }_{i}}$ S-роторов на рабочих режимах, отвечающих неподвижным точкам системы (2.1).

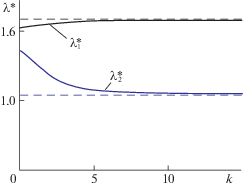
Из рис. 5 видно, что на рабочих режимах выполнены неравенства $\lambda _{1}^{*} > {{\lambda }_{0}}$, $\lambda _{2}^{*} < {{\lambda }_{0}}$, где ${{\lambda }_{0}} \approx 1.6$ – корень функции ${{C}_{T}}(\lambda )$ аэродинамического момента, действующего на S-ротор. Таким образом, аэродинамический момент относительно оси Ox, действующий на большой S-ротор, является тормозящим (${{C}_{T}}(\lambda _{1}^{*}) < 0$), а на малый – разгоняющим (${{C}_{T}}(\lambda _{2}^{*}) > 0$), т.е. малый ротор позволяет большому развить более высокую угловую скорость, чем скорость свободной авторотации в потоке, что увеличивает силу Магнуса, формируемую большим S-ротором (рис. 3).

Можно рассмотреть вопрос о существовании установившихся режимов, которым соответствуют замкнутые траектории (циклы) системы (2.1). При численном исследовании системы (2.1) не выявлено циклов. Однако можно показать, что добавление слагаемых, моделирующих сухое трение в шарнирах конструкции, может привести к возникновению неустойчивого цикла. Более детальное исследование вопроса о наличии периодических движений моделируемой ветроустановки может быть выполнено в усложненной модели, учитывающей трение в шарнирах, при помощи численно-аналитических методов поиска периодических решений. В частности, можно после замены переменных использовать метод, предложенный в [21].

4. Зависимость коэффициента мощности от коэффициента электрической нагрузки. Для найденных стационарных режимов построим зависимость коэффициента механической мощности от коэффициента k внешней электрической нагрузки. Значение коэффициента c_p механической мощности определяется по формуле (подобно работам [7, 9])

где s – отношение суммарной площади лопастей к площади поперечного сечения турбины. Далее считаем s = 0.1.

Для выбранного ранее набора геометрических и массовых параметров системы график зависимости c_p от параметра k приведен на рис. 6.

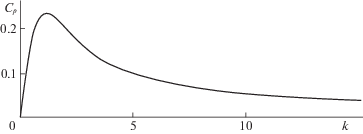
Максимальное значение c_p достигается при $k = {{k}_{{opt}}} \approx 1.2$ и составляет ${{c}_{p}} = {{c}_{{p\max }}} \approx 0.23$.

Естественно сравнить максимальное значение коэффициента мощности, достижимое для рассмотренной системы, с аналогичным значением для классического S-ротора, аэродинамика которого использовалась при описании лопастей. Согласно работе [10], последнее составляет примерно 0.2.

Помимо этого, сравним полученные результаты с моделью, в которой каждая лопасть представлена одним S-ротором, а не парой. Такая модель рассмотрена в [7]. В системе (2.1) это соответствует отсутствию одного из роторов (например, b₂ = 0) при расположении оставшегося ротора на некотором “эффективном” расстоянии $c{{r}_{1}}$, c < 1, и сохранении отношения суммарной площади лопастей к площади поперечного сечения турбины (s = 0.1). При выбранных ранее соотношениях на параметры модели (${{b}_{1}} = 2{{b}_{2}}$, ${{r}_{1}} = 2{{r}_{2}}$) существует такое значение эффективного радиуса в “однороторной” модели (а именно c = 0.8), при котором зависимости коэффициента c_p мощности от коэффициента k внешней нагрузки для двух моделей совпадают. Существование такого радиуса обосновано тем, что для функций ${{C}_{D}}(\lambda )$, ${{C}_{L}}(\lambda )$ было принято линейное приближение. С учетом нелинейности зависимостей ${{C}_{D}}(\lambda )$, ${{C}_{L}}(\lambda )$ (более точное приближение) в общем случае ни при каком r не будет полного совпадения графиков мощности в двух моделях. Итак, “двухроторная” модель лопасти, рассмотренная в настоящей работе, может быть приближена упрощенной моделью, предложенной в [7], при определенном выборе в последней параметра, определяющего эффективный радиус турбины. В то же время, для определения этого значения радиуса требуется использовать результаты, полученные в “двухроторной” модели.

5. Стратегия управления величиной внешнего электрического сопротивления. Предложим стратегию параметрического управления внешним сопротивлением R. При изменении скорости V ветра требуется изменять величину R таким образом, чтобы значение k оставалось равным ${{k}_{{opt}}}$:

Чем выше скорость ветра, тем меньше оптимальное значение внешнего сопротивления (т.е. больше потребителей в цепи генератора). Отметим, что если скорость ветра превышает некоторое критическое значение ${{V}_{{cr}}}$, то реализовать режим, характеризующийся максимальным коэффициентом мощности ${{c}_{p}} = {{c}_{{p\max }}}$, невозможно (поскольку значение R всегда положительно). Эта критическая скорость ветра определяется следующим образом:

Итак, найдено значение ${{k}_{{opt}}}$ варьируемого коэффициента k, при котором достигается максимальная механическая мощность на рабочем режиме, предложена стратегия управления внешним сопротивлением R в цепи генератора, позволяющая перейти в окрестность режима, который характеризуется максимальной мощностью.

Заключение. В работе построена математическая модель горизонтально-осевой ветроустановки класса “Савониус-Магнус”, учитывающая изменение ширины лопасти вдоль радиуса. Предложенная новая модель представляет собой существенное развитие модели из [7]. Описание аэродинамического воздействия основано на гипотезе квазистатического обтекания (аналогично работе [11]) с применением экспериментальных данных о силомоментных аэродинамических характеристиках ротора Савониуса, приведенных в [10]. Для моделирования электромеханической нагрузки используются результаты, полученные в [17], при этом предполагается возможность управления величиной внешнего сопротивления в локальной цепи генератора установки с целью максимизации механической мощности на рабочем режиме.

Определены характеристики рабочих режимов ветроустановки, отвечающих асимптотически устойчивым неподвижным точкам динамических уравнений модели. Построены бифуркационные диаграммы, описывающие зависимость механической мощности устройства и угловых скоростей его элементов от параметра, который характеризует внешнюю электрическую нагрузку. Предложена стратегия управления величиной внешнего сопротивления, позволяющая при изменении скорости ветра поддерживать максимально возможное значение механической мощности на рабочем режиме.