Известия РАН. Теория и системы управления, 2020, № 4, стр. 151-159

Введение. В подавляющем большинстве способных к перемещению в земных условиях технических устройств есть специальные движущиеся части, непосредственно взаимодействующие с окружающей средой: колеса, гусеницы, пропеллеры, ноги и т.д. Они располагаются вне корпуса, что влечет разного рода сложности. В случае, если внешняя среда агрессивна, эти элементы конструкции подвергаются повышенному риску повреждения, а усиление их устойчивости к внешним воздействиям ведет к росту как стоимости самого изделия, так и затрат на его эксплуатацию. В случае, если движение должно происходить в ранимой среде (например, внутри человеческого организма), указанные части представляют собой повышенную опасность. Поэтому желательно создание устройств с движителями, заключенными внутри герметичного корпуса, поверхность которого значительно легче адаптировать к внешним условиям.

Проблемы иного рода возникают при создании космических аппаратов (см., например, [1, 2]). Последние, как правило, используют реактивные двигатели для изменения ориентации в пространстве. Эти двигатели нуждаются в топливе, доставка которого в космос требует больших затрат. Заметим, что трудность состоит не столько в обеспечении необходимой для переориентации энергии, сколько в значительной массе требующегося рабочего тела. Энергия может быть получена от солнечных батарей или, скажем, от бортового атомного реактора, а рабочее тело, например, для функционирующих продолжительное время спутников нужно доставить на орбиту при запуске. Альтернативные способы решения проблемы ориентации основаны, в частности, на применении гиростабилизаторов. Однако для их использования необходимо доставлять на орбиту тяжелые конструкции и годами обеспечивать постоянное вращение с высокой скоростью массивных элементов. Поэтому представляет интерес разработка новых способов изменения ориентации космических аппаратов без использования реактивной тяги и непрерывно движущихся частей.

Оба комплекса проблем – относящихся как к робототехнике, так и к строительству космических аппаратов – могут быть решены путем использования подвижных масс [3–5]. В первом случае массы должны находиться внутри корпуса робота, а во втором это не обязательно, поскольку в безвоздушном пространстве механическую связь спутника и управляемой подвижной массы можно обеспечить разными способами. В обеих областях применения можно для определенных интервалов времени с приемлемой точностью пренебречь внешними воздействиями, поскольку процесс переориентации робота может происходить быстро, а космические аппараты в значительной мере изолированы.

В [6–8] были рассмотрены вопросы, касающиеся двумерного случая, а в данной работе обобщаются и анализируются кратко изложенные в работе [9] результаты.

1. Постановка задачи. Если в рамках задачи об изменении ориентации объекта не требуется перемещать центр масс твердого тела, то, как правило, предполагают, что этот центр в процессе переориентации должен быть неподвижен. Но такое невозможно при управлении с помощью подвижной массы, поскольку любое ее смещение приводит к смещению центра масс твердого тела, несмотря на то, что последний в конце процесса может вернуться в исходное положение относительно неподвижной системы координат, если подвижная масса сделает то же самое. Поэтому в рамках рассматриваемого подхода удобно описывать последовательность положений объекта в осях Кёнига [10], т.е. в поступательно перемещающейся системе координат с началом в центре масс тела.

Известно, что в задачах о переориентации важным является случай, когда вектор угловой скорости твердого тела не меняет своего направления [2]. Действительно, любая последовательность вращений этого тела может быть сведена к единственному повороту вокруг некоторой оси [11]. Поэтому интуитивно понятно, что если, скажем, требуется изменить ориентацию объекта за минимальное время, то нужно осуществлять указанное вращение с максимально возможной угловой скоростью. Этот факт нетрудно доказать строго, что мы и сделаем для удобства дальнейшего анализа.

Будем описывать движение твердого тела относительно его центра масс с помощью ортогональной матрицы A. Предположим, что вектор угловой скорости $\omega $ служит вектором управления, принадлежащим некоторой заданной выпуклой области W, и необходимо перевести твердое тело из начальной ориентации, заданной матрицей ${{{\mathbf{A}}}_{0}}$, в конечную, заданную матрицей A_T, за кратчайшее время T. В дальнейшем всюду будем обозначать точкой над символом полную производную соответствующей функции по времени в неподвижной системе координат. Функция ${\mathbf{A}} = {\mathbf{A}}(t)$ удовлетворяет дифференциальному уравнению ${\mathbf{\dot {A}}} = {\mathbf{A}}\Omega $, причем кососимметрическая матрица $\Omega $ состоит из компонентов вектора угловой скорости $\omega $ в системе координат, жестко связанной с телом (см., например, [11]). Согласно принципу максимума Понтрягина [12], гамильтониан в данном случае имеет вид $H = {\text{tr}}({\mathbf{{\rm A}}}\Omega {{{\mathbf{P}}}^{{\text{T}}}})$, где матрица P является сопряженной, а символ $^{{\text{T}}}$ означает транспонирование. Понятно, что

Воспользуемся известными соотношениями (см., например, [13]) и с учетом свойств матрицы $\Omega $ получим

Как известно [11], решения уравнений ${\mathbf{\dot {{\rm A}}}} = {\mathbf{{\rm A}}}\Omega $ и ${\mathbf{\dot {P}}} = {\mathbf{P}}\Omega $ отличаются произвольным постоянным множителем, т.е. ${\mathbf{P}} = {\mathbf{C{\rm A}}}$, где C – произвольная постоянная ортогональная матрица. Тогда

где ${\mathbf{{\rm A}}}\Omega {{{\mathbf{{\rm A}}}}^{{\text{T}}}}$ – матрица угловой скорости в неподвижной системе координат. Пусть ${{\omega }_{x}}$, ${{\omega }_{y}}$ и ${{\omega }_{z}}$ – соответствующие компоненты вектора угловой скорости, а c_ij – элементы матрицы C, причем $i = 1,2,3$ и $j = 1,2,3$. Следовательно,

Для наглядности запишем H в еще более простом виде. Матрице C соответствует кватернион [11] с компонентами q_i, $i = 0, \ldots ,3$, причем

где

Тогда

где через (⋅, ⋅) обозначено скалярное произведение, а вектор c имеет компоненты $ - 4{{q}_{0}}{{q}_{1}}$, $ - 4{{q}_{0}}{{q}_{2}}$ и $ - 4{{q}_{0}}{{q}_{3}}$, т.е. является произвольным постоянным вектором. Следовательно, для достижения максимума функции H на множестве $\omega \in W$ вектор $\omega $ должен быть постоянным в течение всего времени движения. Из теоремы Эйлера о конечном повороте [11] известно, что существует единственная постоянная ось вращения, позволяющая перевести твердое тело из начальной ориентации, заданной матрицей A₀, в конечную, заданную матрицей A_T, что и решает поставленную задачу.

Таким образом, случай, когда вектор угловой скорости не меняет своего направления, имеет существенное практическое значение, а потому требует особого внимания.

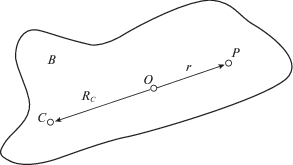
Предположим, что исследуемая механическая система состоит из показанных на рис. 1 материальной точки P с массой m и твердого тела B с массой M и центром масс в точке C, взаимодействующих друг с другом с помощью произвольных сил, внутренних по отношению к системе. Кроме того, исключим из рассмотрения все внешние силы, так что механическую систему можно полагать замкнутой, и пусть в начальный момент времени как материальная точка, так и твердое тело находятся в состоянии покоя. Тогда в процессе движения постоянно покоится и общий центр масс O всей механической системы. Кроме того, для системы в целом выполняются законы сохранения углового момента и количества движения.

Из того, что центр масс всей системы O покоится, а также из законов сохранения количества движения и углового момента для системы в целом, вытекают три соотношения в неподвижной системе координат с началом в точке O. Для радиус-вектора ${{{\mathbf{R}}}_{C}}$ центра масс тела имеем [6]

где r – радиус-вектор материальной точки относительно точки C, так что радиус-вектор материальной точки относительно общего центра масс O равен сумме ${{{\mathbf{R}}}_{C}} + {\mathbf{r}}$. Для абсолютной скорости ${{{\mathbf{v}}}_{C}}$ центра масс тела запишем [6] где $\omega $ – угловая скорость вращения твердого тела и v – скорость материальной точки относительно некоторой жестко связанной с телом подвижной системы координат с началом в центре масс C тела, а символ $ \times $ означает векторное произведение. Кроме того, получено [6] где J – тензор инерции твердого тела относительно своего центра масс.

Подставим в уравнение (1.3) функцию для r из (1.1) и соотношение для $\omega \times {\mathbf{r}} + {\mathbf{v}}$ из (1.2). Тогда

и уравнению (1.4) можно придать вид

Цель данного исследования состоит в реализации заданного вектором $\xi = \xi (t)$ движения твердого тела в осях Кёнига [10] путем перемещения материальной точки. Следовательно, требуется по компонентам вектора $\xi $ в неподвижной системе координат с началом в центре масс системы O найти вектор 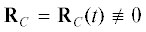, удовлетворяющий уравнению (1.5).

Способ задания требуемой последовательности ориентаций твердого тела с помощью вектора $\xi = \xi (t)$ в неподвижной системе координат представляется нестандартным, но он следует из структуры уравнения (1.5). При невырожденной матрице J этот вектор позволяет восстановить ориентацию твердого тела в любой момент времени по начальным данным. Действительно, можно проинтегрировать систему дифференциальных уравнений для соответствующей ортогональной матрицы ${\mathbf{{\rm A}}} = {\mathbf{{\rm A}}}(t)$ с начальным значением A₀:

где тензор J и вектор $\omega $ заданы в жестко связанной с телом системе координат, а кососимметрическая матрица $\Omega $ по-прежнему состоит из компонентов вектора $\omega $.

Заметим, что в случае $\xi (t) \equiv 0$ из соотношения (1.5) вытекает коллинеарность векторов ${{{\mathbf{R}}}_{C}}$ и ${{{\mathbf{\dot {R}}}}_{C}}$. Другими словами, центр масс твердого тела должен двигаться по прямой, проходящей через общий центр масс механической системы O. Однако никаких иных ограничений на вид функции ${{{\mathbf{R}}}_{C}} = {{{\mathbf{R}}}_{C}}(t)$, помимо дифференцируемости, условие (1.5) не накладывает. Далее будем рассматривать исключительно нетривиальные случаи, когда $\xi \ne 0$.

2. Решение задачи. Поскольку компоненты вектора ${{{\mathbf{\dot {R}}}}_{C}}$ не могут быть явно выражены из системы уравнений (1.5), обратим внимание на то, что искомый вектор R_C всегда ортогонален вектору ξ. Действительно, если умножить обе части соотношения (1.5) скалярно на вектор R_C, то получим равенство $({{{\mathbf{R}}}_{C}},\xi ) = 0$. Поэтому будем искать R_C в форме

где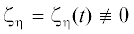 – неизвестная дифференцируемая скалярная функция, а 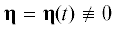– неизвестный дифференцируемый вектор, причем свойство дифференцируемости необходимо для существования скорости ${{{\mathbf{\dot {R}}}}_{C}}$.

Из (2.1) получаем

Тогда из (2.1) и (2.2) имеем

Преобразуем двойное векторное произведение

Аналогично получаем

где через $( \cdot , \cdot , \cdot )$ обозначено смешанное произведение векторов. Подставим (2.3) в (1.4), приняв во внимание (2.4) и (2.5). Тогда в каждый момент времени должно выполняться соотношение

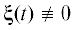Вектор не может быть коллинеарен вектору 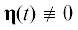, поскольку иначе из (2.1) вытекает, что ${{{\mathbf{R}}}_{C}} = {{{\mathbf{R}}}_{C}}(t) \equiv 0$, а это противоречит условию, наложенному при постановке задачи. Следовательно, должны обращаться в нуль множители, стоящие в (2.6) перед векторами ξ и η. Смешанное произведение $(\xi ,\eta ,\dot {\xi })$ равно нулю, если коллинеарны либо векторы ξ и $\dot {\xi }$, либо векторы η и $\dot {\xi }$. Поскольку нас больше интересует случай, когда вектор угловой скорости $\omega $ не меняет своего направления, то сначала рассмотрим вариант, когда коллинеарны векторы ξ и $\dot {\xi }$. Тогда из равенства нулю множителя перед ξ в (2.6) имеем

Подставив (2.7) в (2.1), получаем искомый вектор в случае коллинеарных векторов ξ и $\dot {\xi }$:

Представим векторы $\eta $ и $\dot {\eta }$ в виде следующих сумм векторов:

Другими словами, разложим каждый из векторов η и $\dot {\eta }$ на два вектора, один из которых коллинеарен вектору ξ, а другой лежит в плоскости, ортогональной этому вектору. Коллинеарные составляющие отмечены индексом $\parallel $, а ортогональные – индексом $ \bot $. При разложении вектора $\dot {\eta }$ использованы верхние индексы, чтобы не возникло ошибочного представления, например, о равенстве в общем случае вектора ${{\dot {\eta }}^{\parallel }}$ производной по времени от вектора ${{\eta }_{\parallel }}$.

Из (2.9) следует, что

и выражение (2.8) можно записать в форме

Следовательно, искомый вектор R_C зависит только от тех составляющих векторов η и $\dot {\eta }$, которые лежат в плоскости, перпендикулярной вектору ξ. Тогда можно выбирать вектор η так, чтобы он всегда лежал в этой плоскости.

Теперь докажем, что указанный вектор можно всегда полагать единичным без ограничения общности. Пусть

где $\rho = \rho (t)$ – некоторый дважды дифференцируемый единичный вектор. Приняв во внимание (2.10), получим

Поскольку смешанное произведение векторов $(\xi ,\varrho \rho ,\dot {\varrho }\rho )$ равно нулю, имеем

Подставим (2.10) и (2.12) в (2.8). Тогда

Таким образом, при коллинеарных векторах ξ и $\dot {\xi }$ можно ограничиться случаем, когда вектор η лежит в плоскости, ортогональной этим векторам и является единичным. Тогда в рассматриваемом варианте искомый вектор R_C зависит от единственной произвольной скалярной функции времени. Например, ею может быть функция $\beta = \beta (t)$, представляющая собой полярный угол для вектора η в некоторой неподвижной двумерной системе координат, лежащей в плоскости, ортогональной вектору ξ, с началом в центре масс O исследуемой механической системы.

Так как вектор η единичный, то векторы η и $\dot {\eta }$ всегда ортогональны. Их векторное произведение коллинеарно вектору ξ. Тогда смешанное произведение $(\xi ,\eta ,\dot {\eta }) = \pm {\text{|}}\xi {\text{|}}\,{\text{|}}\dot {\beta }{\text{|}}$. В этом выражении, как следует из (2.8), необходимо выбрать знак “минус”, т.е. векторы ξ, η и $\dot {\eta }$ должны составлять левую тройку. Механическую причину этого легче всего понять, если представить себе твердое тело в виде однородного шара. Тогда движущаяся в плоскости материальная точка и сечение шара этой же плоскостью должны вращаться в противоположные стороны для того, чтобы суммарный угловой момент механической системы в целом был равен нулю. Окончательно получаем

Зависимость ${\text{|}}{{{\mathbf{R}}}_{C}}{\text{|}} = {\text{|}}{{{\mathbf{R}}}_{C}}(t){\text{|}}$ может быть следствием конкретной технической реализации рассматриваемой упрощенной механической системы. В частности, форма возможных траекторий движения материальной точки может быть раз и навсегда определена. Тогда из соотношения (2.13) вытекает, что

Выражение (2.14) дает модуль скорости изменения полярного угла материальной точки при движении по заданной траектории для получения требуемой реализации вектора ξ в случае, когда его направление не меняется. Если траектории представляют собой, например, произвольные дуги, лежащие на фиксированной сфере с центром в общем центре масс устройства, то формула (2.14) приобретает особенно ясный механический смысл.

3. Общий случай. В случае, если векторы ξ и $\dot {\xi }$ неколлинеарны, векторы η и $\dot {\xi }$ должны быть, наоборот, коллинеарны, как это было отмечено выше при анализе соотношения (2.6). Тогда в (2.1) следует взять $\eta = {{\zeta }_{{\mathbf{\xi }}}}\dot {\xi }$, где ${{\zeta }_{{\mathbf{\xi }}}} = {{\zeta }_{{\mathbf{\xi }}}}(t)$ – некоторая дифференцируемая скалярная функция. Но в этом случае можно в (2.1) заменить произведение ${{\zeta }_{\eta }}{{\zeta }_{\xi }}$ двух неизвестных скалярных функций на единственную, оставив за ней прежнее обозначение ${{\zeta }_{\eta }}$, и просто выбрать $\eta = \dot {\xi }$. Следовательно, при неколлинеарных векторах ξ и $\dot {\xi }$ искомый вектор, согласно (2.8), имеет вид

В формуле (3.1) векторы $\xi $, $\dot {\xi }$ и $\ddot {\xi }$ должны образовывать левую тройку по тем же самым механическим причинам, которые были очевидны в описанном выше упрощенном случае. Заметим, что для существования вектора ${{{\mathbf{\dot {R}}}}_{C}}$ из соотношения (3.1) следует необходимость наличия третьей производной по времени вектора $\xi = \xi (t)$.

Обратим внимание на интересную интерпретацию формулы (3.1), связывающую ее с дифференциальной геометрией [14]. Запишем (3.1) в форме

где единичный вектор b – бинормаль, а величина $\varkappa $ – кручение кривой, задаваемой вектором χ. Оказывается, что заданное для рассматриваемой механической системы движение в осях Кёнига может быть реализовано только тогда, когда кручение $\varkappa $ кривой, описанной в (3.2) с помощью радиус-вектора $\chi = \chi (t)$, отрицательно.

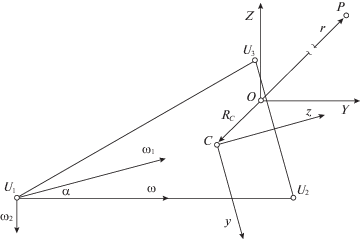
4. Пример для случая регулярной прецессии. Поскольку применение соотношения (3.1) может оказаться неочевидным, рассмотрим конкретный простой пример. Выберем классическую задачу о качении однородного кругового конуса по плоскости. Пусть масса конуса равна M, высота – h, а угол при вершине составляет $2\alpha $. Обозначим через J_A и J_C экваториальный и полярный моменты инерции соответственно. Следуя [10], предположим, что при качении нет проскальзывания, а плоскость, по которой оно происходит, является горизонтальной и неподвижной. Рассмотрим сечение конуса в начальный момент времени ${{t}_{0}} = 0$ вертикальной плоскостью. На рис. 2 оно обозначено точками ${{U}_{1}}$, ${{U}_{2}}$ и ${{U}_{3}}$. Вершина конуса ${{U}_{1}}$ закреплена неподвижно. Пусть, согласно [10],  в начальный момент времени центру основания конуса придана горизонтальная скорость ${v}$. Тогда наличие момента внешних сил заставляет конус осуществлять регулярную прецессию. Представим мгновенную угловую скорость $\omega $ в виде суммы угловой скорости собственного вращения ${{\omega }_{1}}$ и угловой скорости прецессии ${{\omega }_{2}}$, причем вектор ${{\omega }_{1}}$ направлен коллинеарно оси симметрии тела, а вектор ${{\omega }_{2}}$ – вертикально вниз.

Введем подвижную систему координат Cxy, жестко связанную с конусом и имеющую центр в точке C, являющейся центром масс конуса. Пусть ее оси Cx и Cy параллельны основанию. Тогда ось Cz будет направлена вдоль оси симметрии тела. Без ограничения общности предположим, что в начальный момент времени ось абсцисс этой системы направлена на читателя и, следовательно, перпендикулярна плоскости рисунка. В этой системе, согласно [10], проекции вектора кинетического момента ${\mathbf{K}} = {\mathbf{J}}\omega $ можно выразить с помощью углов Эйлера следующим образом:

где $\theta = \pi {\text{/}}2 + \alpha $ – постоянный угол нутации, образованный векторами ${{\omega }_{1}}$ и ${{\omega }_{2}}$. В соотношениях (4.1) функция $\varphi = \varphi (t)$ представляет собой угол собственного вращения конуса и в начальный момент времени $\varphi (0) = 0$. Заметим, что $\dot {\varphi } = {{\omega }_{1}} = \omega {\text{/}}cos\alpha $, ${{\omega }_{2}} = \omega {\text{tg}}\alpha $ и $\omega = v{\text{/}}(hsin\alpha )$.

Однако выражение (3.1) получено при условии, что компоненты вектора $\xi $ заданы в неподвижной системе координат. Поэтому рассмотрим показанную на рис. 2 неподвижную систему координат OXY. Ее ось абсцисс в начальный момент времени сонаправлена оси абсцисс подвижной системы координат Cxy, ось OZ вертикальна, а ось OY горизонтальна и дополняет оси OX и OZ до правой тройки векторов. В этой системе вектор кинетического момента K имеет следующие проекции:

причем $\sigma = 3co{{s}^{2}}\alpha + 1$. Выражения (4.2) определяют соответствующие компоненты вектора $\xi $ в соотношении (3.1).

Как видно из (4.2), вектор $\xi = \xi (t)$ имеет третью производную по времени. Помимо этого, для возможности реализации заданного движения, согласно формуле (3.1), необходимо, чтобы входящее в него смешанное произведение векторов было отрицательно. Действительно, если подставить выражения (4.2) в соотношение (3.1), получим

Следовательно, заданное формулами (4.2) движение можно реализовать в осях Кёнига.

Основываясь на соотношениях (3.1) и (1.1), можно выразить описывающий относительное движение материальной точки вектор r с компонентами в подвижной системе координат Cxy, равными

причем ${{r}_{{xy}}} = \sqrt {30} hsin\alpha {\text{/}}(10\sqrt \mu )$. Соотношения (4.3) означают, что для реализации заданного движения материальная точка должна вращаться с постоянной угловой скоростью вокруг оси симметрии конуса, всегда оставаясь в плоскости, перпендикулярной этой оси и находящейся на расстоянии ${{r}_{z}}$ от центра масс конуса. Траектория материальной точки при этом должна представлять собой окружность радиуса r_xy, а частота вращения должна быть равна частоте собственного вращения конуса. Понятно, что последний не будет катиться по некоторой неподвижной плоскости, как это происходит при регулярной прецессии, описанной в [10], но движение в осях Кёнига будет тем же самым.

Обратим внимание на то, что расстояние r_z между центром масс конуса и плоскостью, в которой должна вращаться материальная точка, может оказаться весьма большим, из-за чего на рис. 2 центр масс O системы в целом показан существенно смещенным относительно центра масс C конуса, а положение материальной точки, описываемое радиус-вектором r, показано с учетом разрыва этого вектора. Действительно, пусть $\alpha = \pi {\text{/}}12$, m = 0.01 кг, $M = 0.05$ кг и h = 0.1 м. Тогда из соотношений (4.3) имеем ${{r}_{{xy}}} \approx 0.035$ м и расстояние ${{r}_{z}} \approx 0.26$ м.

Заключение. Для изменения ориентации твердого тела с помощью перемещающейся массы необходимо сделать следующее. Сперва следует задать требуемое движение объекта в некоторой системе координат с началом в центре масс тела и осями, перемещающимися поступательно, причем движение самой этой системы относительно какой-либо инерциальной системы координат роли не играет. Далее нужно найти компоненты вектора $\xi = {\mathbf{J}}\omega $ как функции времени в неподвижной системе координат и определить, существуют ли интервалы времени, на которых векторы ξ и $\dot {\xi }$ коллинеарны. Если такие интервалы есть, то на них требуемое движение материальной точки всегда существует и может быть найдено по формуле (2.8), куда входит произвольный дважды дифференцируемый вектор $\eta = \eta (t)$, причем смешанное произведение векторов $(\xi ,\eta ,\dot {\eta })$ должно быть отрицательным. Из соотношения (2.8) вытекает, что материальная точка должна двигаться в плоскости, ортогональной векторам ξ и $\dot {\xi }$. Без ограничения общности вектор η можно выбирать единичным и лежащим в той же плоскости. Следовательно, вектор η фактически определен с точностью до произвольной дифференцируемой скалярной функции времени, обеспечивающей отрицательный знак указанного смешанного произведения. В качестве таковой функции может выступать, скажем, полярный угол этого вектора в некоторой двумерной системе координат, находящейся в плоскости, ортогональной векторам ξ и $\dot {\xi }$. Данное свойство позволяет, например, обеспечить требуемое движение при произвольно выбранной траектории движения материальной точки в указанной плоскости.

На тех интервалах времени, где векторы ξ и $\dot {\xi }$ неколлинеарны, движение материальной точки определяется однозначно формулой (3.1), а потому существует лишь тогда, когда существует третья производная вектора ξ как функции времени, причем смешанное произведение векторов $(\xi ,\dot {\xi },\ddot {\xi })$ должно быть отрицательно. Это накладывает ограничения на алгоритмы переориентации объекта.

Итоговые соотношения (2.8) и (3.1) могут быть использованы как для изменения ориентации капсульных роботов, так и при эксплуатации космических аппаратов.