Известия РАН. Теория и системы управления, 2020, № 4, стр. 92-102
МЕТОД ФУНКЦИОНАЛЬНОГО ДИАГНОСТИРОВАНИЯ НЕДЕТЕРМИНИРОВАННЫХ КОНЕЧНЫХ АВТОМАТОВ
А. Н. Жирабок a, *, Н. А. Калинина a, А. Е. Шумский a
a Дальневосточный федеральный ун-т, Институт проблем морских технологий ДВО РАН
Владивосток, Россия
* E-mail: zhirabok@mail.ru
Поступила в редакцию 05.06.2019
После доработки 10.12.2019
Принята к публикации 27.01.2020
Аннотация
Рассматривается задача функционального диагностирования систем ответственного назначения, описываемых моделью недетерминированного конечного автомата. Предлагается новый метод решения задачи, отличительной особенностью которого является использование математического аппарата алгебры покрытий. Особенности и преимущества метода иллюстрируются на примере задачи мониторинга ошибок операторов IT-системы.
Введение. Модель конечного автомата (КА) широко используется для описания технических объектов и их подсистем, поведение которых характеризуется, во-первых, наличием конечного числа состояний и, во-вторых, переходами между этими состояниями, инициируемыми внешними воздействиями и/или условиями функционирования; эти воздействия и условия ниже рассматриваются как входы автомата. В зависимости от полноты знаний об объекте диагностирования (ОД) и степени определенности окружающей среды могут быть использованы различные виды этой модели, включая модель детерминированного конечного автомата (ниже также КА) и модель недетерминированного конечного автомата (НДКА). Отличительной особенностью последней модели является то, что она допускает возможность существования для некоторых состояний автомата переходов в различные состояния, инициируемых одним и тем же входом автомата.
Ряд решений диагностических задач на основе моделей КА в различной постановке был получен с использованием математического аппарата парной алгебры разбиений [1], см., например, [2–4]. В работах [5–7] аппарат парной алгебры разбиений был также использован для случая моделей НДКА в приложении к задачам обнаружения и диагностирования ошибок человека-оператора на рельсовом транспорте и в IT-системах соответственно.
Заметим, что задача диагностирования ошибок человека-оператора представляет самостоятельный интерес, что подтверждается значительным числом публикаций на эту тему в зарубежной литературе. Так в работе [8] рассматривалась задача обнаружения и классификации ситуаций, приводящих к ошибкам человека-оператора на рельсовом транспорте. В [9] изучалась задача обработки последствий возникновения непредвиденных ситуаций, в [10] – задача оперативного обнаружения и предотвращения непредвиденных ситуаций, в основе решения которой лежала прямая оценка эмоционального и психологического состояния человека-оператора.
Подход работы [10] ориентирован на непосредственное выявление пограничных состояний (потеря внимания, перевозбуждение и т.п.) человека-оператора, которые могут привести к фатальным последствиям. Недостаток такого подхода – необходимость использования датчиков (часть из которых непосредственно контактирует с человеком-оператором), стоимость которых достаточно высока и надежность работы которых не гарантирована. Поэтому в некритических ситуациях, не связанных с непосредственной угрозой жизни и здоровью человека либо значительными материальными потерями, целесообразно применение поведенческого подхода, предполагающего использование математических моделей, в частности, модели конечного автомата для описания поведения человека-оператора [11].
В настоящей статье предлагается новый метод решения задачи диагностирования НДКА, отличительной особенностью которого является использование математического аппарата парной алгебры покрытий. Преимущество нового метода (по сравнению с известными) состоит в том, что с его помощью в ряде случаев можно увеличить глубину диагностирования. Результаты применения полученных результатов иллюстрируются на примере задачи мониторинга ошибок операторов IT-системы, ранее описанной в [7].
1. Постановка задачи. Пусть ОД в исправном состоянии описывается моделью НДКА следующего вида:
где $I = \{ {{i}_{1}},~{{i}_{2}}, \ldots ,~{{i}_{q}}\} ,S = \{ {{s}_{1}},~{{s}_{2}},~ \ldots ,~{{s}_{n}}\} $ и $O = \{ o,~{{o}_{2}},~ \ldots ,~{{o}_{l}}\} $ – конечные множества входов, состояний и выходов автомата, δ – функция переходов из одного состояния в другое: λ – функция выхода:В (1.2) и (1.3) ${{s}^{ + }} \in S_{{\left( {s,~i} \right)}}^{ + }$ – состояние, имеющее место после перехода из состояния s ∈ S под воздействием входа i ∈ I, $S_{{\left( {s,~i} \right)~}}^{ + } \subseteq S~$– множество всех состояний, достижимых из состояния s ∈ S под воздействием входа i ∈ I, и o ∈ O – выход, формируемый автоматом в состоянии s ∈ S. Для удобства ниже используется табличное задание функций переходов и выходов. Исходная модель (1.1) может также быть не полностью определенной, т.е. допускать не совместимые (невозможные, не приводящие к переходу) пары $\left( {s,~i} \right),~s \in S,~i \in I$.
Неисправности в ОД могут приводить к реализации не предусмотренных в (1.2) переходов. Пусть вследствие неисправности имеет место ошибка перехода ${{e}_{p}}:{\text{\;}}{{(s{\kern 1pt} ' \to s{\kern 1pt} '')}_{{({{s}_{k}},~{{i}_{g}})~}}}$ (номер ошибки p соответствует номеру неисправности), при которой вместо перехода из состояния sk под воздействием входа ig в состояние $s{\kern 1pt} ' \in S_{{({{s}_{k}},~{{i}_{g}})~}}^{ + }$ происходит переход в состояние $s{\kern 1pt} '' \notin S_{{({{s}_{k}},~{{i}_{g}})~}}^{ + }$. Ниже рассматриваются только однократные ошибки и предполагается, что список всех ошибок E = = $\{ {{e}_{1}},{{e}_{2}},~ \ldots ,{{e}_{N}}\} $, к которым могут приводить возможные в ОД неисправности, известен.
Цель статьи состоит в изложении метода синтеза схемы диагностирования, позволяющей осуществлять обнаружение факта возникновения ошибки и определение вида этой ошибки.
Введем автомат Ap:
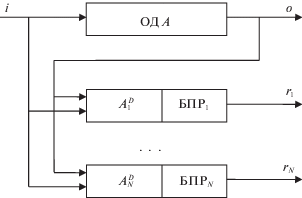
функция переходов δp которого получается дополнением функции переходов δ автомата A переходом, соответствующим ошибке ep. Следуя [7], рассмотрим схему диагностирования, представленную на рисунке. Здесь $A_{p}^{D}~$–КА, описываемый моделью получаемый путем детерминизации автомата Ap. Функция переходов автомата $A_{p}^{D}$ задается в виде ${\delta }_{p}^{D}:I \times O \times S_{p}^{D} \to S_{p}^{D}$, где $S_{d}^{D} = \{ s_{{p,~1}}^{D},~s_{{p,~2}}^{D},~ \ldots ,s_{{p,~{{n}_{p}}}}^{D}\} ~$– конечное множество состояний этого автомата и np – число его состояний, ${{n}_{p}} \leqslant n$.Для согласованного функционирования КА, описываемых моделями (1.4) и (1.5), их состояния должны удовлетворять определенным условиям. Так, в работе [7] предполагалось существование отображения ${{{\varphi }}_{p}}:{{S}_{p}} \to S_{p}^{D}$, такого, что в случае ошибки ep выполняется равенство
Известно, что отображение ${{{\varphi }}_{p}}:{{S}_{p}} \to S_{p}^{D}$ задает на множестве Sp разбиение, так что использование отображений вида (1.6) с необходимостью приводит к алгебре разбиений. Поскольку целью работы является применение более общей алгебры покрытий, отображение ${{{\varphi }}_{p}}:{{S}_{p}} \to S_{p}^{D}$ следует заменить также более общим понятием отношения и предполагать, что в случае ошибки ep пара $(s_{p}^{D},~s)$ удовлетворяет некоторому отношению
Принимая во внимание (1.3), можно также ввести отношение
справедливое для всех пар $(s_{p}^{D},~o)$, для которых одновременно выполняется (1.3) и (1.7).Заметим, что поскольку все переходы, задаваемые функцией δ, включаются во множество переходов, задаваемых функцией δp, отношения (1.7) и (1.8) будут также справедливы и в случае исправного функционирования ОД. Заметим также, что снятие требования существования отображения φp, удовлетворяющего (1.6), и замена его отношением Φp позволяет обеспечить преимущество предлагаемого метода. Отношение Φp (наряду с Ψp) будет основной конструкцией, используемой при синтезе схемы диагностирования.
Блок принятия решений (БПР) осуществляет проверку выполнения отношения (1.8). При этом в случае отсутствия ошибок, а также при возникновении ошибки ep БПР формирует невязку rp = 0. Для обнаружения ошибки ${{e}_{j}},~j \ne p,$ БПР формирует невязку rp = 1, что предполагает нарушение отношения (1.8).
Синтез схемы диагностирования включает решение следующих задач:
1) синтез КА $A_{p}^{D},~1 \leqslant p \leqslant N~$(предполагает нахождение отношений Φp, $1 \leqslant p \leqslant N)$;
2) синтез БПР (предполагает формирование отношений Ψp, $~1 \leqslant p$ ≤ N);
3) оценку возможности обнаружения и диагностики ошибок на основе получаемой схемы диагностирования.
2. Математические конструкции. В настоящем разделе дается краткое изложение конструкций парной алгебры покрытий как более общего случая конструкций парной алгебры разбиений в приложении к НДКА. Основными конструкциями рассматриваемой алгебры являются покрытия множества S. Напомним, что покрытием π множества S называется множество его подмножеств (блоков покрытия) $\{ {{B}_{{{{{\pi }}_{1}}}}},{{B}_{{{{{\pi }}_{2}}}}},~ \ldots ,~{{B}_{{{{{\pi }}_{{\nu }}}}}}\} $, таких, что
Заметим, что в случае выполнения дополнительного требования
приведенная выше конструкция определяет разбиение множества S. Таким образом, разбиение некоторого множества является частным случаем покрытия этого множества. Отметим, что, воспользовавшись правилом(2.1)
$s \equiv s{\kern 1pt} '({{{\pi }}_{{\varphi }}}) \Leftrightarrow {\varphi }(s) = {\varphi }(s{\kern 1pt} '),~\quad s,~s{\kern 1pt} ' \in S,$Пусть π и σ – некоторые покрытия множества S. Будем говорить, что покрытие π меньше или равно покрытию σ и обозначать ${\pi } \leqslant {\sigma }$, если для некоторого блока ${{B}_{{{{{\pi }}_{j}}}}}$ покрытия π всегда найдется блок ${{B}_{{{{{\sigma }}_{k}}}}}$ покрытия σ, такой, что ${{B}_{{{{{\pi }}_{j}}}}} \subseteq {{B}_{{{{{\sigma }}_{k}}}}}$.
Существует два специальных покрытия, обозначаемые как 0 и 1, которые являются разбиениями, такими, что каждый блок разбиения 0 содержит только один элемент множества S, в то время как разбиение 1 включает только один блок, содержащий все элементы множества S. Для произвольного покрытия π множества S выполняется
Известно [1], что множество всех покрытий множества S с отношением частичного порядка образует решетку. Следовательно, для каждой пары покрытий (π, σ) множества S можно найти два покрытия inf(π, σ) и sup(π, σ) Принято обозначать эти покрытия π × σ и π + σ – соответственно произведение и сумма покрытий. Для вычисления результата операций × можно использовать следующее простое правило [1]: каждый блок покрытия π × σ представляет собой пересечение некоторых блоков покрытий π и σ. В то же время правило вычисления операции π + σ отличается от предложенного в [1] правила, результатом применения которого обязательно будет разбиение. Новое правило выглядит следующим образом: каждый блок покрытия π + σ представляет собой объединение пересекающихся блоков покрытий π и σ. При этом результатом применения нового правила будет покрытие, не превышающее разбиения, получаемого правилом работы [1].
Пример 1. Пусть $S = \left\{ {{{s}_{1}},{{s}_{2}},{{s}_{3}},{{s}_{4}},{{s}_{5}},{{s}_{6}}} \right\}$, ${\pi } = \{ ({{s}_{1}});({{s}_{3}});({{s}_{2}},~{{s}_{4}});({{s}_{2}},~{{s}_{5}},~{{s}_{6}})\} $, σ = {(s1); (s2, s5); (s3); $({{s}_{4}});({{s}_{6}})\} $. В этом случае ${\pi } \times {\sigma } = \left\{ {({{s}_{1}});({{s}_{2}},~{{s}_{5}});({{s}_{3}});({{s}_{4}});({{s}_{6}})} \right\}$. Для вычисления покрытия π + σ найдем объединение всех пересекающихся блоков покрытий π и σ: ${\rho } = \left\{ {({{s}_{1}});({{s}_{3}});({{s}_{2}},~{{s}_{4}},~{{s}_{5}});({{s}_{2}},~{{s}_{5}},~{{s}_{6}})} \right\}$.
Покрытиям можно дать информационную трактовку: возможность вычисления покрытия π будем трактовать как возможность получения информации о состоянии автомата с точностью до блоков покрытия π$.$ Если π ≤ σ, то покрытие π содержит не меньше информации о состоянии автомата, чем покрытие σ. Очевидно, что покрытие π × σ содержит не меньше информации о состоянии автомата, чем каждое из покрытий π и σ. Также каждое из покрытий π и σ содержит не меньше информации о состоянии автомата, чем покрытие π + σ. Покрытие 0 содержит полную информацию о состоянии автомата, в то время как покрытие 1 не содержит информации о состоянии автомата.
Для учета динамики автомата вводится отношение Δ. Пусть π и σ – некоторые покрытия множества S. Отношение Δ включает все пары (π, σ), удовлетворяющие следующему условию:
Для заданного покрытия π могут существовать несколько покрытий, удовлетворяющих отношению $({\pi },{\sigma }) \in \Delta $. В частности, $\left( {{\pi },{\text{\;}}1} \right) \in \Delta $ справедливо для любого покрытия π. Введем оператор m, ставящий в однозначное соответствие покрытию π покрытие m(π) следующим образом:
Способ вычисления покрытия m(π) отличается от способа вычисления соответствующего разбиения, описанного в [1] (по тем же причинам, что и в случае операции +), и предполагает выполнение следующих действий.
Алгоритм 1 (вычисление оператора m).
Шаг 1. Для каждого i ∈ I и каждого $j,~\;1 \leqslant j \leqslant L,$ где L – число блоков покрытия π, найти подмножество Bi,j такое, что $s,~s{\kern 1pt} ' \in {{B}_{{\pi ,~j}}} \Rightarrow \delta (s,~i),~\delta (s{\kern 1pt} ',~i) \in {{B}_{{i,j}}}$.
Шаг 2. Записать множество подмножеств $Q = \{ {{B}_{{i,j}}},i \in I,1 \leqslant j \leqslant L\} .$
Шаг 3. Сформировать покрытие m(π) из Q путем удаления тех подмножеств, которые включаются в оставшиеся.
Пример 2. Рассмотрим НДКА из табл. 1 и положим ${\pi } = \left\{ {\left( {{{s}_{1}},~{{s}_{5}}} \right);~\left( {{{s}_{2}},~{{s}_{3}}} \right);~} \right.$ (s3, s4)}. В таблице символом “–” обозначены несовместимые значения состояний и входов. На шаге 1 алгоритма 1 получим: ${{B}_{{1,~1}}} = \left\{ {{{s}_{2}},~{{s}_{3}}} \right\}$, ${{B}_{{1,~2}}} = \left\{ \emptyset \right\},~{{B}_{{1,~3}}} = \left\{ \emptyset \right\}$, ${{B}_{{2,~1}}} = \left\{ {{{s}_{2}}} \right\}$, ${{B}_{{2,~2}}} = \left\{ {{{s}_{2}},~{{s}_{3}},~{{s}_{4}}} \right\}$, ${{B}_{{2,~3}}} = \left\{ {{{s}_{2}},~{{s}_{3}}} \right\}$, ${{B}_{{3,~1}}} = \left\{ {{{s}_{3}},~{{s}_{4}}} \right\}$, ${{B}_{{3,~2}}}$ = {s1, s2}, ${{B}_{{3,~3}}} = \left\{ {{{s}_{2}},~{{s}_{5}}} \right\}$. Как следствие, выполнение шага 2 приводит к Q = {(s2, s3); (s2); (s2, ${{s}_{3}},~{{s}_{4}});({{s}_{3}},$ ${{s}_{4}});({{s}_{1}},~{{s}_{2}});({{s}_{2}},~{{s}_{5}})\} $. Теперь учтем, что $\left( {{{s}_{2}}} \right) \in \left( {{{s}_{2}},~{{s}_{3}}} \right) \in \left( {{{s}_{2}},~{{s}_{3}},~{{s}_{4}}} \right)$ и, как следствие, подмножества (s2) и (s2, s3) на шаге 3 должны быть исключены из множества Q. В результате получим m(π) = $\left\{ {({{s}_{1}},~{{s}_{2}});({{s}_{2}},~{{s}_{3}},~{{s}_{4}});({{s}_{2}},~{{s}_{5}})} \right\}$.
Таблица 1.
Таблица переходов НДКА
| s | i1 | i2 | i3 |
|---|---|---|---|
| s1 | s2 | s2 | s3 |
| s2 | – | s3, s4 | s1 |
| s3 | – | s2, s3 | s2 |
| s4 | – | – | s5 |
| s5 | s3 | – | s4 |
Заметим, что для НДКА (в отличие от КА) всегда выполняется соотношение
Это связано с тем, что в случае НДКА по крайней мере одно из подмножеств Bi,j содержит более, чем одно состояние, что с неизбежностью приводит к вышеприведенному неравенству. Например, для НДКА из приведенного выше примера имеем ${\mathbf{m}}\left( 0 \right) = \left\{ {\left( {{{s}_{1}}} \right);~\left( {{{s}_{2}},~{{s}_{3}}} \right);~\left( {{{s}_{3}},~{{s}_{4}}} \right);~\left( {{{s}_{5}}} \right)} \right\}$.
3. Синтез КА $A_{p}^{D}$. Отметим, что описываемый ниже синтез сводится к детерминизации автомата Ap. Сформулируем требование к отношению Φp, выполнение которого будет гарантировать существование КА $A_{p}^{D}$ вида (1.5). Пусть ${{\pi }_{{{{{\varphi }}_{p}}}}}~$ – покрытие, удовлетворяющее неравенству
(3.1)
${\mathbf{m}}({{{\pi }}_{{\lambda }}} \times {{{\pi }}_{{{{{\varphi }}_{p}}}}}) \leqslant {{{\pi }}_{{{{{\varphi }}_{p}}}}},$Теорема 1. Пусть ${\pi }_{{{{{\varphi }}_{p}}}}^{{\left( j \right)}},~j \geqslant 1,$ – покрытие, определяемое соотношением
(3.2)
${\pi }_{{{{{\varphi }}_{p}}}}^{{\left( j \right)}} = {\pi }_{{{{{\varphi }}_{p}}}}^{{\left( {j - 1} \right)}} + {\mathbf{m}}({{{\pi }}_{{\lambda }}} \times {\pi }_{{{{{\varphi }}_{p}}}}^{{\left( {j - 1} \right)}}),\quad {\pi }_{{{{{\varphi }}_{p}}}}^{{\left( 0 \right)}} = 0,~$(3.3)
${\pi }_{{{{{\varphi }}_{p}}}}^{{\left( j \right)}} = {\pi }_{{{{{\varphi }}_{p}}}}^{{\left( {j - 1} \right)}}.~$Тогда ${{{\pi }}_{{{{{\varphi }}_{p}}}}} = {\pi }_{{{{{\varphi }}_{p}}}}^{{\left( j \right)}}~$ – минимальное покрытие, удовлетворяющее (3.1).
Доказательство теоремы опускается, так как оно совпадает с доказательством аналогичной теоремы, ранее сформулированной для случая разбиений (см., например, [4, 6]).
Заметим, что если ${{{\pi }}_{{{{{\varphi }}_{p}}}}}$ – разбиение, то при синтезе КА $A_{p}^{D}$ каждому блоку этого разбиения ставится в соответствие состояние КА $A_{p}^{D}$, определяемое функцией φp следующим образом: если блоку ${{B}_{{{{{\pi }}_{{{{{\varphi }}_{p}}}}},~k}}}$ соответствует состояние $s_{{p,k}}^{D}$ автомата $A_{p}^{D}$, то ${{{\varphi }}_{p}}\left( s \right) = s_{{p,k}}^{D}$ для всех $s \in {{B}_{{{{{\pi }}_{{{{{\varphi }}_{p}}}}},~k}}}$, где индекс k соответствует номеру состояния КА (1.5), ${{B}_{{{{{\pi }}_{{{{{\varphi }}_{p}}}}},~k}}}$ – блок покрытия ${{{\pi }}_{{{{{\varphi }}_{p}}}}}$ с номером k.
Распространяя это правило на случай покрытия ${{{\pi }}_{{{{{\varphi }}_{p}}}}}$, построим отношение Φp следующим образом: если блоку ${{B}_{{{{{\pi }}_{{{{{\varphi }}_{p}}}}},~k}}}$ покрытия ${{{\pi }}_{{{{{\varphi }}_{p}}}}}$ соответствует состояние $s_{p}^{D}$ автомата $A_{p}^{D}$, то
(3.4)
$(s_{{p,~k}}^{D},~s) \in {{{\Phi }}_{p}} \Leftrightarrow s \in {{B}_{{{{{\pi }}_{{{{{\varphi }}_{p}}}}},~k}}}.$Отметим, что здесь некоторому состоянию s автомата A может соответствовать несколько состояний $s_{{p,k}}^{D}$ автомата $A_{p}^{D}$.
Теорема 2. Для НДКА (1.4) отношение Φp, определяемое соотношением (3.4), обеспечивает существование КА (1.5).
Доказательство. Отметим сначала, что в силу (3.1) для каждого входа i ∈ I из знания состояния НДКА Ap с точностью до блока разбиения ${{{\pi }}_{{\lambda }}} \times {{\pi }_{{{{{\varphi }}_{p}}}}}$ следует возможность вычисления состояния, в которое переходит Ap под воздействием этого входа, с точностью до блока покрытия ${{{\pi }}_{{{{{\varphi }}_{p}}}}}$. Дальнейшее доказательство теоремы конструктивно и сводится к описанию алгоритма построения таблицы переходов КА (1.5).
Алгоритм 2 (построение таблицы переходов КА $A_{p}^{D}$).
Шаг 1. Вычислить ${{{\pi }}_{{\lambda }}} \times {{{\pi }}_{{{{{\varphi }}_{p}}}}}$; отметим, что поскольку πλ – разбиение, то ${{{\pi }}_{{\lambda }}} \times {{{\pi }}_{{{{{\varphi }}_{p}}}}}$ – также разбиение.
Шаг 2. Объединить те строки таблицы переходов автомата Ap, в крайней левой позиции которых находятся состояния, принадлежащие одному и тому же блоку разбиения ${{{\pi }}_{{\lambda }}} \times {{{\pi }}_{{{{{\varphi }}_{p}}}}}$, в одну строку. Заменить состояния в крайнем левом столбце символами соответствующих блоков.
Шаг 3. Заменить содержимое ячеек полученной таблицы блоками покрытия ${{{\pi }}_{{{{{\varphi }}_{p}}}}}$. Поскольку ${{{\pi }}_{{\lambda }}} \times {{{\pi }}_{{{{{\varphi }}_{p}}}}} \leqslant {{{\pi }}_{{\lambda }}}$, блоки разбиения ${{{\pi }}_{{\lambda }}} \times {{{\pi }}_{{{{{\varphi }}_{p}}}}}$ в крайнем левом столбце заменить блоками разбиения πλ.
Шаг 4. Поставить в соответствие каждому блоку ${{B}_{{{{{\pi }}_{{{{{\varphi }}_{p}}}}},~k}}}$ покрытия ${{{\pi }}_{{{{{\varphi }}_{p}}}}}$ состояние $s_{{p,~k}}^{D}$ автомата $A_{p}^{D}$.
Шаг 5. Получить таблицу переходов автомата $A_{p}^{D}$ заменой в ранее полученной таблице блоков покрытия ${{{\pi }}_{{{{{\varphi }}_{p}}}}}$ соответствующими состояниями автомата $A_{d}^{p}$, а блоков разбиения πλ – соответствующими выходами автомата Ap.
Сделаем два важных замечания. Во-первых, в силу (2.2) всегда выполняется ${{{\pi }}_{{{{{\varphi }}_{p}}}}} \ne 0,$ т.е. синтез КА $A_{p}^{D}$ всегда сопровождается потерей информации о состоянии НДКА Ap. Во-вторых, в силу минимальности покрытия ${{\pi }_{{{{\varphi }_{p}}}}}$, КА $A_{p}^{D}$ позволяет извлечь максимум информации о состоянии НДКА Ap в результате детерминизации последнего.
4. Отношение Ψpи глубина диагностирования. Имея в виду общую конструкцию (1.8), отношение Ψp введем следующим образом
(4.1)
$(s_{{p,~k}}^{D},~{{o}_{j}}) \in {{{\Psi }}_{p}} \Leftrightarrow {{B}_{{{{\pi }_{{{{\varphi }_{p}}}}},~k}}} \cap {{B}_{{{{\pi }_{{\lambda ~,j}}}}}} \ne \emptyset ,~$По определению отношения Φp и построению покрытия ${{{\pi }}_{{{{{\varphi }}_{p}}}}}$ отношение Ψp справедливо как в случае исправного функционирования ОД, так и при возникновении в ОД ошибки ep, что дает нулевое значение невязки rp. Для обнаружения ошибок ${{e}_{j}}:{{{\text{(}}s{\kern 1pt} ' \to s{\kern 1pt} ''{\text{)}}}_{{({{s}_{{v}}},~{{i}_{g}})}}},j \ne p,$ по единичному значению невязки rp отношение Ψp не должно содержать пар $(s_{{p,~k}}^{D},~o{\kern 1pt} '')~$, где $s{\kern 1pt} '$ ∈ ${{B}_{{{{{\pi }}_{{{{{\varphi }}_{p}}}}},~k}}}~$ и $o{\kern 1pt} '' = \lambda (s{\kern 1pt} '')$. Это условие выполняется, если при $s{\kern 1pt} '$ ∈ ${{B}_{{{{{\pi }}_{{{{{\varphi }}_{p}}}}},~k}}}$ и $s{\kern 1pt} '' \in {{B}_{{{{{\pi }}_{{{\lambda \;},{v}}}}}}}$ для некоторого ${v}$ имеет место условие
(4.2)
${{B}_{{{{{\pi }}_{{{{{\varphi }}_{p}}}}},~k}}} \cap {{B}_{{{{{\pi }}_{{{\lambda \;},{v}}}}}}} = \emptyset .~$Таким образом, возможность обнаружения некоторой ошибки по значению невязки rp может быть установлена путем проведения проверок на основе соотношения (4.2) для $1 \leqslant k \leqslant {{n}_{p}}~$ и $1 \leqslant {v} \leqslant l$. При этом связь между ошибками в ОД и значениями невязок может быть представлена матрицей синдромов ошибок (табл. 2).
На пересечении p-й строки и j-го столбца матрицы ставится единица, если ошибка ej обнаруживается по невязке rp (т.е. выполняется условие (4.2)), и ноль в противном случае. Ошибки ei и ej различимы, если соответствующие столбцы матрицы содержат различные комбинации нулей и единиц. Из табл. 2, например, следует, что ошибки e1 и e3 неразличимы. При этом схема диагностирования может быть упрощена за счет исключения одного из КА ($A_{1}^{D}$ или $A_{3}^{D}$) и соответствующего БПР.
5. Иллюстративный пример. Рассмотрим на примере основные этапы синтеза схемы диагностирования НДКА, а также покажем преимущества предлагаемого подхода перед традиционным, использующим математический аппарат алгебры разбиений. Для этого воспользуемся модифицированной моделью процесса управления изменениями в IT-системе; подробное описание модели и способа ее получения приведено в работе [7]. Исходная модель в виде НДКА, соответствующая безошибочной работе участников процесса (инициатор, исполнитель и менеджер), имеет вид табл. 3.
Таблица 3.
Таблица переходов НДКА А
| s | i1 | i2 | i3 | i4 | i5 | i6 | i7 | λ |
|---|---|---|---|---|---|---|---|---|
| s1 | s2 | – | – | – | – | – | – | o1 |
| s2 | – | s3 | s1 | – | – | – | – | o2 |
| s3 | – | – | – | s2, s4 | – | – | – | o3 |
| s4 | – | – | – | – | s2, s5 | – | – | o4 |
| s5 | – | – | – | – | – | s6 | s1 | o2 |
| s6 | – | – | – | – | – | – | – | o5 |
Будем учитывать ошибки инициатора, исполнителя и менеджера процесса – ${{e}_{1}}:{{({{s}_{2}} \to {{s}_{3}})}_{{\left( {{{s}_{1}},~{{i}_{1}}} \right)}}}$, ${{e}_{2}}:{{\left( {{{s}_{5}} \to {{s}_{6}}} \right)}_{{\left( {{{s}_{4}},~{{i}_{5}}} \right)}}}$ и ${{e}_{3}}:{{\left( {{{s}_{3}} \to {{s}_{4}}} \right)}_{{\left( {{{s}_{2}},~{{i}_{2}}} \right)}}}$ соответственно. Табл. 4–6 переходов автоматов, соответствующих этим ошибкам, представлены ниже.
Таблица 4.
Таблица переходов НДКА A1
| s | i1 | i2 | i3 | i4 | i5 | i6 | i7 |
|---|---|---|---|---|---|---|---|
| s1 | s2, s3 | – | – | – | – | – | – |
| s2 | – | s3 | s1 | – | – | – | – |
| s3 | – | – | – | s2, s4 | – | – | – |
| s4 | – | – | – | – | s2, s5 | – | – |
| s5 | – | – | – | – | – | s6 | s1 |
| s6 | – | – | – | – | – | – | – |
Таблица 5.
Таблица переходов НДКА A2
| s | i1 | i2 | i3 | i4 | i5 | i6 | i7 |
|---|---|---|---|---|---|---|---|
| s1 | s2 | – | – | – | – | – | – |
| s2 | – | s3 | s1 | – | – | – | – |
| s3 | – | – | – | s2, s4 | – | – | – |
| s4 | – | – | – | – | s2, s5, s6 | – | – |
| s5 | – | – | – | – | – | s6 | s1 |
| s6 | – | – | – | – | – | – | – |
Таблица 6.
Таблица переходов НДКА A3
| s | i1 | i2 | i3 | i4 | i5 | i6 | i7 |
|---|---|---|---|---|---|---|---|
| s1 | s2 | – | – | – | – | – | – |
| s2 | – | s3, s4 | s1 | – | – | – | – |
| s3 | – | – | – | s2, s4 | – | – | – |
| s4 | – | – | – | – | s2, s5 | – | – |
| s5 | – | – | – | – | – | s6 | s1 |
| s6 | – | – | – | – | – | – | – |
Проиллюстрируем синтез КА $A_{1}^{D}$ на основе НДКА A1 (табл. 4). Для этого, используя процедуру теоремы 2, найдем покрытие ${{{\pi }}_{{{{{\varphi }}_{1}}}}}$. Согласно (3.3), имеем ${\pi }_{{{{{\varphi }}_{1}}}}^{{\left( 1 \right)}} = 0 + {\mathbf{m}}(0)$ = {(s1); (s2, s3); $({{s}_{2}},~{{s}_{4}})$; (s2, s5); (s6)}. Далее, ${{{\pi }}_{{\lambda }}} \times {\pi }_{{{{{\varphi }}_{1}}}}^{{\left( 1 \right)}}$ = $\left\{ {\left( {{{s}_{1}}} \right);~\;\left( {{{s}_{2}},~{{s}_{5}}} \right);\;~\left( {{{s}_{3}}} \right);\;\left( {{{s}_{4}}} \right);\;\left( {{{s}_{6}}} \right)} \right\}$ и, поскольку ${\mathbf{m}}({{{\pi }}_{{\lambda }}} \times {\pi }_{{{{{\varphi }}_{1}}}}^{{(1)}})$ = m({(s1); $({{s}_{2}},~{{s}_{5}});\;({{s}_{3}});\;({{s}_{4}});\;({{s}_{6}})\} )$ = ${\pi }_{{{{{\varphi }}_{1}}}}^{{(1)}}$, получаем ${\pi }_{{{{{\varphi }}_{1}}}}^{{\left( 1 \right)}} = {\pi }_{{{{{\varphi }}_{1}}}}^{{\left( 2 \right)}} = {{{\pi }}_{{{{{\varphi }}_{1}}}}}$. Дальнейший синтез осуществляется в соответствии с алгоритмом 2. Выполняя шаг 1 алгоритма 2, запишем разбиение ${{{\pi }}_{{\lambda }}} \times {{{\pi }}_{{{{{\varphi }}_{1}}}}}$ = = $\left\{ {\left( {{{s}_{1}}} \right);\;~\left( {{{s}_{2}},~{{s}_{5}}} \right);~\;\left( {{{s}_{3}}} \right);\;\left( {{{s}_{4}}} \right);\;\left( {{{s}_{6}}} \right)} \right\}.$ Объединим строки табл. 4, которые соответствуют состояниям, принадлежащим одному и тому же блоку разбиения ${{{\pi }}_{{\lambda }}} \times {{{\pi }}_{{{{{\varphi }}_{1}}}}}$, в соответствии с шагом 2 алгоритма 2, заменим их соответствующими блоками и получим следующую таблицу (табл. 7). Выполняя затем шаг 3 с учетом ${{B}_{{{{{\pi }}_{{\lambda }}} \times {{{\pi }}_{{{{{\varphi }}_{1}}}}}{{,}_{j}}}}} = {{B}_{{{{{\pi }}_{{\lambda }}}{{,}_{j}}}}}~$, $1 \leqslant j \leqslant 5,~$ перепишем предыдущую таблицу в следующем виде (табл. 8). Последовательно выполняя шаги 4 и 5 алгоритма 2, окончательно получим таблицу переходов КА $A_{1}^{D}$ (табл. 9). В этой таблице состояния $s_{{1,~k}}^{D}$ автомата $A_{1}^{D}$ соответствуют блокам ${{B}_{{{{{\pi }}_{{{{{\varphi }}_{1}}}}},~k}}}$, $1 \leqslant k \leqslant 5,$ покрытия ${{{\pi }}_{{{{{\varphi }}_{1}}}}},$ а выходы oj соответствуют блокам ${{B}_{{{{{\pi }}_{{\lambda }}}{{,}_{j}}}}},\;{\kern 1pt} 1 \leqslant j \leqslant 5,$ разбиения πλ.
Таблица 7.
Модифицированная таблица переходов НДКА A1
| Блоки разбиения | i1 | i2 | i3 | i4 | i5 | i6 | i7 |
|---|---|---|---|---|---|---|---|
| ${{B}_{{{{{\pi }}_{{\lambda }}} \times {\varphi }{{,}_{1}}}}}$ | s2, s3 | – | – | – | – | – | – |
| ${{B}_{{{{\pi }_{\lambda }} \times \varphi {{,}_{2}}}}}~$ | – | s3 | s1 | – | – | s6 | s1 |
| ${{B}_{{{{{\pi }}_{{\lambda }}} \times {\varphi }{{,}_{3}}}}}$ | – | – | – | s2, s4 | – | – | – |
| ${{B}_{{{{{\pi }}_{{\lambda }}} \times {\varphi }{{,}_{4}}}}}$ | – | – | – | – | s2, s5 | – | – |
| ${{B}_{{{{{\pi }}_{{\lambda }}} \times {\varphi }{{,}_{5}}}}}$ | – | – | – | – | – | – | – |
Таблица 8.
Таблица переходов в символах блоков покрытия ${\text{\;}}{{{\pi }}_{{{{{\varphi }}_{1}}}}}$ и разбиения πλ
| Блоки разбиения | i1 | i2 | i3 | i4 | i5 | i6 | i7 |
|---|---|---|---|---|---|---|---|
| ${{B}_{{{{{\pi }}_{{\lambda }}}{{,}_{1}}}}}$ | ${{B}_{{{{{\pi }}_{{{{{\varphi }}_{1}}}}},~2}}}$ | – | – | – | – | – | – |
| ${{B}_{{{{\pi }_{\lambda }}{{,}_{2}}}}}~$ | – | ${{B}_{{{{{\pi }}_{{{{{\varphi }}_{1}}}}},~2}}}$ | ${{B}_{{{{{\pi }}_{{{{{\varphi }}_{1}}}}},~1}}}$ | – | – | ${{B}_{{{{{\pi }}_{{{{{\varphi }}_{1}}}}},~5}}}$ | ${{B}_{{{{{\pi }}_{{{{{\varphi }}_{1}}}}},~1}}}$ |
| ${{B}_{{{{{\pi }}_{{\lambda }}}{{,}_{3}}}}}$ | – | – | – | ${{B}_{{{{{\pi }}_{{{{{\varphi }}_{1}}}}},~3}}}$ | – | – | – |
| ${{B}_{{{{{\pi }}_{{\lambda }}}{{,}_{4}}}}}$ | – | – | – | – | ${{B}_{{{{{\pi }}_{{{{{\varphi }}_{1}}}}},~4}}}$ | – | – |
| ${{B}_{{{{{\pi }}_{{\lambda }}}{{,}_{5}}}}}$ | – | – | – | – | – | – | – |
Таблица 9.
Таблица переходов ДКА $A_{1}^{D}$
| o | i1 | i2 | i3 | i4 | i5 | i6 | i7 |
|---|---|---|---|---|---|---|---|
| o1 | $s_{{1,~2}}^{D}$ | – | – | – | – | – | – |
| o2 | – | $s_{{1,~2}}^{D}$ | $s_{{1,~1}}^{D}$ | – | – | $s_{{1,~5}}^{D}$ | $s_{{1,~1}}^{D}$ |
| o3 | – | – | – | $s_{{1,~3}}^{D}$ | – | – | – |
| o4 | – | – | – | – | $s_{{1,~4}}^{D}$ | – | – |
| o5 | – | – | – | – | – | – | – |
Следуя (4.1) с учетом ${{B}_{{{{{\pi }}_{{{{{\varphi }}_{1}}}}},~1}}} = \left\{ {{{s}_{1}}} \right\}$, ${{B}_{{{{{\pi }}_{{{{{\varphi }}_{1}}}}},~2}}} = \left\{ {{{s}_{2}},~{{s}_{3}}} \right\}$, ${{B}_{{{{{\pi }}_{{{{{\varphi }}_{1}}}}},~3}}} = \left\{ {{{s}_{2}},~{{s}_{4}}} \right\},$ ${{B}_{{{{{\pi }}_{{{{{\varphi }}_{1}}}}},~4}}} = \left\{ {{{s}_{2}},~{{s}_{5}}} \right\},{\text{\;}}{{B}_{{{{{\pi }}_{{{{{\varphi }}_{1}}}}},~5}}} = \left\{ {{{s}_{6}}} \right\}$, ${{B}_{{{{{\pi }}_{{\lambda }}},~1}}} = \left\{ {{{s}_{1}}} \right\},{\text{\;}}~{{B}_{{{{{\pi }}_{{\lambda }}},~2}}} = \left\{ {{{s}_{2}},~{{s}_{5}}} \right\},$ ${{B}_{{{{\pi }_{\lambda }},~3}}} = \left\{ {{{s}_{3}}} \right\},$ $~{{B}_{{{{\pi }_{\lambda }},~4}}} = \left\{ {{{s}_{4}}} \right\}$, ${{B}_{{{{{\pi }}_{{\lambda }}},~5}}} = {\text{\;}}\left\{ {{{s}_{6}}} \right\}$, построим отношение Ψ1 (табл. 10).
Таблица 10.
Отношение ${{{\Psi }}_{1}}$
| s | o1 | o2 | o3 | o4 | o5 |
|---|---|---|---|---|---|
| $s_{{d,~1}}^{1}$ | + | – | – | – | – |
| $s_{{d,~2}}^{1}$ | – | + | + | – | – |
| $s_{{d,~3}}^{1}$ | – | + | – | + | – |
| $s_{{d,~4}}^{1}$ | – | + | – | – | – |
| $s_{{d,~5}}^{1}$ | – | – | – | – | + |
В табл. 10 символом “+” помечены пары, связанные отношением Ψ1 и, соответственно символом “–” помечены пары, не удовлетворяющие этому отношению.
Проверим возможность обнаружения ошибок e2 и e3 на основе анализа невязки r1. Напомним, что ошибка e2 имеет вид ${{e}_{2}}:{{\left( {{{s}_{5}} \to {{s}_{6}}} \right)}_{{\left( {{{s}_{4}},~{{i}_{5}}} \right)}}}$. Прежде всего отметим, что в силу ${{s}_{5}} \in {{B}_{{{{\varphi }_{1}},~4}}}$, ${{s}_{6}} \in {{B}_{{{{\pi }_{\lambda }},~5}}}$ ошибка e2 приведет к формированию пары $(s_{{1,~4}}^{D},{{o}_{5}})$, которая не удовлетворяет отношению Ψ1, поскольку ${{B}_{{{{{\pi }}_{{{{{\varphi }}_{1}}}}},~4}}} \cap {{B}_{{{{\pi }_{\lambda }},~5}}} = \emptyset $, т.е. выполняется условие (4.2). Таким образом, ошибка e2 приведет к r1 = 1 и будет обнаружена. Аналогично можно показать, что ошибке e3 соответствует пара $(s_{{1,~2}}^{D},{{o}_{4}})$, которая не удовлетворяет отношению Ψ1 (проверка условия (4.2) показывает, что ${{B}_{{{{{\pi }}_{{{{{\varphi }}_{1}}}}},~2}}} \cap {{B}_{{{{\pi }_{\lambda }},~4}}} = \emptyset $). Следовательно, ошибка e3 также приведет к r1 = 1 и будет обнаружена.
Для оценки глубины диагностирования, применяя условие теоремы 2 к НДКА A2 и A3, найдем покрытия ${{{\pi }}_{{{{{\varphi }}_{2}}}}} = \left\{ {\left( {{{s}_{1}}} \right);~\left( {{{s}_{2}},~{{s}_{4}}} \right);~\left( {{{s}_{3}}} \right);~\left( {{{s}_{2}},~{{s}_{5}},~{{s}_{6}}} \right)} \right\}$ и ${{{\pi }}_{{{{{\varphi }}_{3}}}}} = \left\{ {\left( {{{s}_{1}}} \right);~\left( {{{s}_{2}},~{{s}_{4}}} \right);} \right.$ $\left( {{{s}_{2}},~{{s}_{5}}} \right);~\left. {\left( {{{s}_{3}},~{{s}_{4}}} \right);~\left( {{{s}_{6}}} \right)} \right\}$, соответствующие ДКА $A_{2}^{D}$ и $A_{3}^{D}$. Можно показать, что в случае $A_{2}^{D}$ ошибкам e1 и e3 соответствуют пары $(s_{{2,2}}^{D},{{o}_{3}})$, $(s_{{2,3}}^{D},{{o}_{3}})$ и $(s_{{2,2}}^{D},{{o}_{4}})$. Так как при этом проверка (4.2) показывает, что ${{B}_{{{{{\pi }}_{{{{{\varphi }}_{2}}}}},~2}}} \cap {{B}_{{{{\pi }_{\lambda }},~3}}} = \emptyset $, ${{B}_{{{{{\pi }}_{{{{{\varphi }}_{3}}}}},~3}}} \cap {{B}_{{{{\pi }_{\lambda }},~3}}} = \emptyset $ и ${{B}_{{{{{\pi }}_{{{{{\varphi }}_{2}}}}},~2}}} \cap {{B}_{{{{\pi }_{\lambda }},~4}}} = \emptyset $, ошибки e1 и e3 обнаруживаются по невязке r2 = 1. Поскольку в случае $A_{3}^{D}$ ошибкам e1 и e2 соответствуют пары $(s_{{3,2}}^{D},{{o}_{3}})$, $(s_{{3,3}}^{D},{{o}_{3}})$ и $(s_{{3,3}}^{D},{{o}_{5}})$, а результаты проверки (4.2) дают ${{B}_{{{{{\pi }}_{{{{{\varphi }}_{3}}}}},~2}}} \cap {{B}_{{{{\pi }_{\lambda }},~3}}} = \emptyset $, ${{B}_{{{{{\pi }}_{{{{{\varphi }}_{3}}}}},~3}}} \cap {{B}_{{{{\pi }_{\lambda }},~3}}} = \emptyset $, ${{B}_{{{{{\pi }}_{{{{{\varphi }}_{3}}}}},~3}}} \cap {{B}_{{{{\pi }_{\lambda }},~5}}} = \emptyset $, ошибки e1 и e2 обнаруживаются по невязке r3 = 1. Из изложенного выше получаем матрицу синдромов ошибок (табл. 11). Несложно видеть, что полученная матрица гарантирует локализацию всех ошибок в ОД.
Покажем теперь преимущество предлагаемого метода перед традиционным [2–7], использующим математический аппарат алгебры разбиений. Заметим, что разбиения, соответствующие ДКА $A_{1}^{D}$ – $A_{3}^{D}$, могут быть получены объединением пересекающихся блоков ранее найденных покрытий; имеем соответственно: ${{{\pi }}_{{{{{\varphi }}_{1}}}}} = \left\{ {\left( {{{s}_{1}}} \right);~\left( {{{s}_{2}},~{{s}_{3}},~{{s}_{4}},~{{s}_{5}}} \right);~\left( {{{s}_{6}}} \right)} \right\}$ ($A_{1}^{D}$), ${{{\pi }}_{{{{{\varphi }}_{2}}}}} = \left\{ {\left( {{{s}_{1}}} \right);~\left( {{{s}_{2}},~{{s}_{4}},~{{s}_{5}},~{{s}_{6}}} \right);~\left( {{{s}_{3}}} \right)} \right\}$ ($A_{2}^{D}$) и ${{{\pi }}_{{{{{\varphi }}_{2}}}}} = \left\{ {\left( {{{s}_{1}}} \right);~\left( {{{s}_{2}},~{{s}_{3}},~{{s}_{4}},~{{s}_{5}}} \right);~\left( {{{s}_{6}}} \right)} \right\}$ ($A_{3}^{D}$). Проверка диагностируемости ошибок приводит к следующим результатам. Для первого автомата и ошибки e3 проверка условия (4.2) приводит к ${{B}_{{{{{\pi }}_{{{{{\varphi }}_{1}}}}},~2}}} \cap {{B}_{{{{\pi }_{\lambda }},~4}}} \ne \emptyset $, т.е. ошибка e3 не будет обнаружена по значению невязки r1. Для второго автомата и ошибок e1 и e3 проверка условия (4.2) дает положительные результаты. И, наконец, для третьего автомата и ошибки e1 имеем ${{B}_{{{{{\pi }}_{{{{{\varphi }}_{3}}}}},~2}}} \cap {{B}_{{{{\pi }_{\lambda }},~3}}} \ne \emptyset $, т.е. ошибка e1 не будет обнаружена по значению невязки r3. Таким образом, для случая использования алгебры разбиений имеем матрицу синдромов ошибок табл. 2. Как отмечалось выше, использование такой матрицы не позволяет различать ошибки e1 и e3.
Заключение. В настоящей статье в рамках разработки нового метода диагностирования недетерминированных конечных автоматов были решены следующие задачи.
1. Осуществлено развитие математического аппарата парной алгебры на случай покрытий, задаваемых на множестве состояний недетерминированного конечного автомата, что потребовало: 1) модификации правила вычисления операции суммы покрытий и 2) разработки нового способа вычисления оператора m.
2. Предложен новый метод синтеза схем диагностирования недетерминированных конечных автоматов, в основе которого лежит процедура детерминизации, позволяющая сохранять максимум информации о недетерминированном автомате, подвергаемом детерминизации. Это потребовало замены отображений, связывающих состояния недетерминированного и соответствующего ему детерминированного автоматов (случай использования алгебры разбиений), отношениями.
3. Предложен способ принятия решения о наличии ошибки в недетерминированном конечном автомате и о виде этой ошибки путем проверки некоторых отношений, существующих между выходом диагностируемого автомата и состоянием соответствующего ему детерминированного конечного автомата, входящего в схему диагностирования.
4. Разработана методика анализа глубины диагностирования и показано, что по сравнению с известными методами, в основе которых лежит использование математического аппарата алгебры разбиений, применение алгебры покрытий может позволить повысить глубину диагностирования.
5. Показана возможность использования полученных результатов для решения задачи диагностирования ошибок человека-оператора в человеко-машинных системах.
Список литературы
Hartmanis J., Stearns R. The Algebraic Structure Theory of Sequential Machines. N.Y.: Prentice-Hall Inc, 1966.
Данилов В.В., Колесов Н.В., Подкопаев Б.П. Алгебраическая модель аппаратного контроля автоматов // АиТ. 1975. № 6. С. 118–125.
Щербаков Н.С., Подкопаев Б.П. Структурная теория аппаратного контроля цифровых автоматов // М.: Машиностроение, 1982. 191 с.
Zhirabok A., Shumsky A. Fault Accommodation in Discrete-Event Robots // Discrete event Robots / Ed. C. Ciufudean. Hong Kong: iConcept Press, 2012. P. 323–339.
Berdjag D., Vanderhagen F., Shumsky A., Zhirabok A. Unexpected Situation Diagnosis: a Model-based Approach for Human Machine Systems // Proc. 19th IFAC Congress. Cape Town, South Africa, 2014. P. 3545–3550
Berdjag D., Vanderhaegen F., Shumsky A., Zhirabok A. Abnormal Operation Diagnosis in Human-Machine Systems // Proc. 10th Asian Control Conf. Kota-Kinabalu, Malayzia, 2015.
Жирабок А.Н., Калинина Н.А., Шумский А.Е. Метод мониторинга поведения человека-оператора в человеко-машинных системах // Изв. РАН. ТиСУ. 2018. № 3. С. 1–10.
Wilson J.R., Norris B.J. Rail Human Factors: Past, Present and Future // Applied Ergonomics. 2005. V. 36. P. 649–660.
Ouedraogo K.A., Enjalbert S., Vanderhaegen F. A State of the Art in Feedforward-feedback Learning Control Systems for Human Errors Prediction // Preprints of the 18th IFAC World Congress. Milano, Italy, 2011.
Woods D. Behind Human Error. Berlin: Ashgate Publishing Company, 2010.
Jagacinski R.J., Flach J.M. Control Theory for Humans: Quantitative Approaches to Modeling Performance. N.J.: Lawrence Erlbaum, 2003.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления