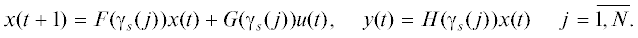Известия РАН. Теория и системы управления, 2020, № 5, стр. 44-55

Введение. Проблемы диагностирования и отказоустойчивости занимают важное место в процессе разработки систем управления и обработки информации. Несмотря на то, что исследования в этой области проводятся в течение нескольких десятилетий и их результаты отражены в многочисленных публикациях, практика выдвигает новые задачи, требующие углубленного изучения. При этом одними из наиболее существенных факторов, побуждающих к новым исследованиям, являются непрерывный рост сложности систем и множественность причин возникновения нарушений, среди которых – отказы и сбои аппаратуры, а также ошибки в программном обеспечении. Проблема высокой размерности задачи преодолевается на практике путем ее декомпозиции на основе иерархического подхода, при котором компоненты системы размещаются по уровням сложности. Далее для каждого уровня разрабатываются свои средства диагностирования (СД), обнаруживающие нарушения в информационных связях между компонентами. Основу решений, применяемых на практике при синтезе СД, составляют техники функционального и тестового диагностирования [1–6]. При этом в качестве математической модели диагностируемого объекта обычно используются сеть Петри, динамическая система, конечный автомат. Известно, что решение задачи диагностирования всегда связано с применением в системе аппаратурной, информационной или временной избыточности. Сами СД есть пример такой избыточности. Кроме того, перед синтезом СД в систему может вводиться избыточность с целью упрощения процесса диагностирования. В частности, это могут быть шаги по увеличению числа входов или выходов системы, введение в систему специальных средств анализа и т.п. Вводимая избыточность формально может быть отнесена как к системе, так и к СД, что несущественно. Именно этому направлению, предполагающему введение избыточности для упрощения диагностирования, и принадлежит подход, предложенный ранее [7–10] и развиваемый авторами в данной работе.

В статье рассматриваются распределенные вычислительные системы (РВС) реального времени, составляющие ядро современных систем управления и обработки информации, характерной особенностью которых является периодический поток входных данных. При этом обсуждение фокусируется на формировании для них диагностических моделей верхнего уровня, на котором распределенная система представляется композицией программных модулей (ПМ), составляющих программное обеспечение системы, а в рассматриваемый класс отказов включает всевозможные нарушения в адресации обменов между ПМ, размещенными на процессорах РВС и обменивающимися необходимой информацией асинхронно, т.е. по ее готовности. Исследуемая диагностическая модель, ориентирована на решение проблемы тестового диагностирования и представляет собой линейный конечный автомат (двоичную линейную динамическую систему). Особенностью рассматриваемого подхода является то, что диагностическая модель встраивается в систему, исполняется параллельно с основным программным обеспечением системы и позволяет упрощать процесс ее тестового диагностирования. В силу указанной особенности подход назван диагностированием с параллельной моделью. Данную диагностическую модель с точки зрения класса отказов можно отнести к дискретно-событийным системам [11], когда работа системы представляется на языке последовательностей некоторых событий. В данном случае это события информационных обменов между ПМ. Подобные модели широко применяются при анализе и тестировании сложных систем [12]. Основной вклад настоящей статьи состоит в формулировке достаточных условий наблюдаемости и управляемости для усовершенствованных диагностических моделей более общего вида, нежели в предшествующих работах [7, 8]. Свойства наблюдаемости и управляемости модели существенным образом влияют на сложность процедур построения тестов. При этом в наблюдаемой модели существует возможность оценивания текущего состояния модели по виду наблюдаемой выходной последовательности, а для управляемой модели существуют входные последовательности, переводящие систему между парой ее любых состояний. Использование усовершенствованных моделей позволяет сокращать объем диагностической информации, передаваемой между ПМ. Основным содержанием работ [9, 10] является синтез и исследование процедур построения тестов по предлагаемым моделям.

Апробация обсуждаемого подхода в реальных системах показала, что сложность встраиваемых моделей относительно рабочего программного обеспечения составляет единицы процентов.

Кратко опишем подход к тестированию РВС с параллельной моделью [7–10], иллюстрируя его на простом примере (рис. 1, а). Здесь представлен граф межмодульных связей системы S реального времени. В системе реализуются три функционально связанных программных модуля (ПМ): ПМ₁, ПМ₂ и ПМ₃, которые могут быть размещены как на разных процессорах системы, так и на одном. Каждый из ПМ на основе входных данных (${{u}_{1}}$ – для ПМ₁, ${{u}_{2}}$ и ${{y}_{3}}$ – для ПМ₂, ${{y}_{1}}$, и y₂ – для ${\text{П}}{{{\text{М}}}_{{\text{3}}}}$) формирует выходные (${{y}_{1}}$,${{y}_{2}}$ и y₃ соответственно). Входные данные поступают и обрабатываются в реальном времени с некоторым заданным периодом. В системе все входные потоки конкретного ПМ являются аргументами реализуемой им функции, необходимыми для ее вычисления. На рис. 1, б система S приведена совместно с СД. В систему уже введена избыточность, представленная алгоритмами ${{\pi }_{{d1}}}$, ${{\pi }_{{d2}}}$ и ${{\pi }_{{d3}}}$. СД состоят из генератора тестов (ГТ), генератора эталонных реакций (ГЭР) и компаратора (К).

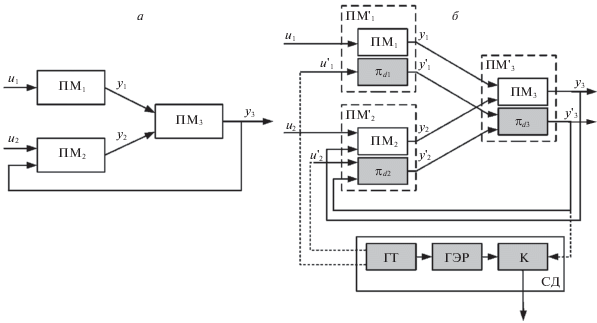
СД формируют для системы тестовые данные, дополняя ими входные данные для ПМ₁ и ПМ₂, и анализируют выходную реакцию S (ПМ₃). В каждый ПМ (ПМ₁, ПМ₂ и ПМ₃) по каналам обмена поступает информация, которая обрабатывается штатными алгоритмами. Параллельно с этим тестовые информационные слова обрабатываются специальными алгоритмами ${{\pi }_{{d1}}}$, ${{\pi }_{{d2}}}$ и ${{\pi }_{{d3}}}$, реагирующими на события приема/выдачи информации, а результаты их обработки выдаются в составе выходных данных. Поскольку механизм обмена реальными и тестовыми данными в системе является общим, возникает возможность по наблюдаемым в процессе работы тестовым результатам делать вывод о наличии или отсутствии нарушений в адресации обменов. Заметим, что искажения реальных данных в процессе обмена при сохранении графа информационных связей не входят в этот класс нарушений. Таким образом, при тестировании с параллельной моделью проблема состоит в построении алгоритмов обработки тестов в ПМ, а также в построении по виду этих алгоритмов самих тестов.

Целесообразность рассматриваемого подхода, по мнению авторов, диктуется следующими простыми соображениями. Прежде всего, необходимо отметить, что диагностирование РВС на верхнем уровне можно было бы реализовать, не используя параллельную модель, а опираясь на штатное программное обеспечение (ПО). Очевидно, что такое решение окажется существенно более сложным как на этапе построения теста, так и на этапе его использования. В этом случае разработчик вынужден будет формировать тест для нелинейной динамической системы, представляющей реальное программное обеспечение. Понятно, что эта процедура будет характеризоваться экспоненциальной зависимостью от размерности системы, поскольку такая сложность характерна для процессов тестирования конечных автоматов общего вида [5, 6]. Кроме того, из-за очень большой длины теста этот шаг потребует выделения на временной диаграмме системы весьма значительного в отличие от случая с параллельной моделью временного интервала для выполнения теста. В случае использования параллельной модели разработчик сам выбирает вид этой модели, причем делает это так, чтобы упростить и процедуру построения теста, и сам тест, а именно выбирает линейную модель, характеризующуюся полиномиальной зависимостью процедур от размерности системы. Существенное влияние на снижение сложности построения теста оказывает относительная простота получения наблюдаемых и управляемых моделей в линейном случае, что крайне важно для построения эффективных тестов. Заметим, что для нелинейного штатного ПО эти свойства, как правило, весьма ограничены и с трудом поддаются анализу.

1. Предварительные сведения. Основу подхода к тестированию РВС с параллельной моделью составляет алгоритм синтеза диагностической модели с иерархической структурой, состоящий из двух этапов. На первом этапе построения модели на основе известных алгоритмов [13] формируется множество вычислительных путей (трасс), составляющих покрытие дуг графа межмодульных связей. При этом под вычислительным путем понимаем последовательность срабатывающих ПМ, соединяющую некоторый вход с выходом. Затем с каждым из полученных путей сопоставляется цепь из такого числа динамических звеньев, через сколько ПМ проходит данный путь. После описанных построений модель системы представляется совокупностью функционально независимых цепей, а задача диагностирования может быть сведена к диагностированию отдельных цепей.

При этом учитывается, что искомая динамическая модель системы далее используется для построения тестов и что процедура построения тестов упрощается, если модель системы, во-первых, линейна, а во-вторых, управляема и наблюдаема. Отсюда можно сформулировать требование к звеньям цепей модели. Они должны быть линейны, т.е.

где ${{x}_{i}}(t),\;{{u}_{i}}(t),\;{{y}_{i}}(t)$ – векторы состояния, входа и выхода, ${{f}_{i}},\;{{g}_{i}},\;{{h}_{i}}$ – матрицы динамики, входа и выхода соответственно для i-го звена цепи, $v$ – число звеньев в модели. Кроме того, звенья должны быть таковы, чтобы модель системы также была бы управляема и наблюдаема. Структура модели для рассматриваемого примера, состоящая из независимых цепей, приведена на рис. 2, а. Однако применение описанной модели РВС может в некоторых случаях потребовать передачи через каналы обмена большого количества диагностической информации, что не всегда допустимо. В примере эта информация включает $y_{1}^{'}$, $y_{2}^{'}$ и $y_{3}^{'}$. В подобных ситуациях целесообразно воспользоваться приемом, заключающимся в обработке нескольких массивов информации одним звеном (слияние вычислительных путей) [8]. Этот вариант иллюстрируется на рис. 2, б. Здесь выходные массивы информации звеньев ${{M}_{{11}}}$ и M₂₂ обрабатываются звеном ${{M}_{{31}}}$, а звено ${{M}_{{32}}}$ исключается. В результате сокращается размерность выходного вектора, а следовательно, и объем выдаваемой из ПМ в каждом такте диагностической информации. При этом, рассматривая цепь как частный случай иерархии, можно видеть, что структура модели как в случае с независимыми цепями, так и в случае со слиянием цепей является иерархической.

Динамическое описание цепи или модели со слиянием цепей получается по следующим правилам. Предположим, что в каждый момент времени в системе происходит лишь один обмен. Тогда формируется вектор состояния $x(t)$, составленный из векторов состояния звеньев ${{x}_{i}}(t),$ $i = \overline {1,v} $, входящих в эту модель, а с помощью матриц $F(t),\;G(t),\;H(t)$ описывается перенос информации между ПМ или ПМ и СД в каждом  j-м информационном обмене. Так будет, если выполняется предположение о единственности обмена в каждый момент времени. На практике это предположение не выполняется, однако, как показано в работах [7, 8], это не является препятствием для использования таких моделей при построении тестов. Для удобства описания свяжем с каждой последовательностью матриц на интервале, равном периоду, свою последовательность индексов, множество которых обозначим через $\Gamma = {\text{\{ }}{{\gamma }_{{\text{s}}}}\,{\text{|}}\,s = \overline {1,N} \} $, где N – общее число обменов в системе. Их начальные отрезки на интервале длительностью в период получаются в результате циклического сдвига последовательности индексов 1, 2, …, N. При N = 3 имеем три последовательности индексов: Γ = {1, 2, 3; 2, 3, 1; 3, 1, 2}. Тогда описание модели ${{S}^{{\text{m}}}}$ для системы S принимает вид

Матрицы в этих уравнениях зависят от номера такта (номера обмена), т.е. модель нестационарна. Более того, она периодически нестационарна, так как из-за периодичности входного потока процессы обработки данных в системе периодические. Напомним, что свойства наблюдаемости и управляемости для нестационарных систем зависят от используемых для наблюдения и управления интервалов ${{\gamma }_{{\text{s}}}}$, поэтому говорят о ${{\gamma }_{s}}$-наблюдаемости и ${{\gamma }_{s}}$-управляемости.

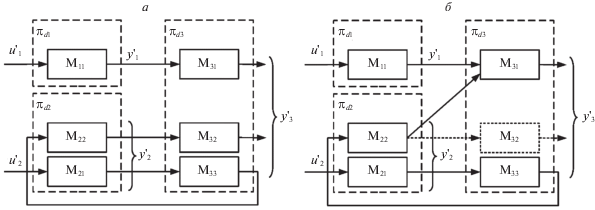
Пример 1. Проиллюстрируем формирование динамики модели на рассматриваемом примере слияния двух цепей (рис. 2, б). Введем следующую нумерацию для звеньев цепей и, как следствие, для описывающих их матриц и векторов: $1 - {{M}_{{11}}}$, $2 - {{M}_{{21}}}$, $3 - {{M}_{{33}}}$, $4 - {{M}_{{22}}}$, $0 - {{M}_{{31}}}$. Предполагая, что формат вектора состояния модели имеет вид 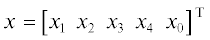, получаем следующую последовательность матриц обменов на периоде, заканчивающимся сеансом приема тестовой информации от СД (нулевые элементы матриц не показаны):

2. Постановка задачи. Приведем некоторые свойства исследуемой модели или особенности ее применения, сформулированные и использованные в предыдущих работах [7, 8] и которые будут полезны при дальнейшем обсуждении.

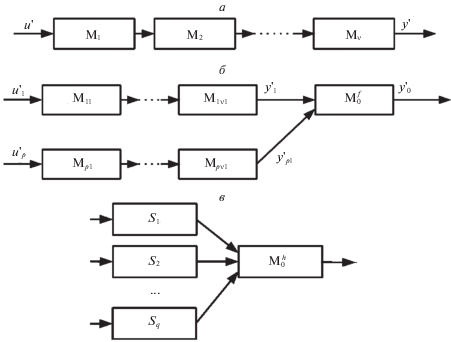
Свойство 1. Возможность применения для моделирования параллельного вычислительного процесса в распределенной системе и, как следствие, для составления тестов модели дискретной динамической системы, реализующей по определению последовательный вычислительный процесс с моделированием в каждый момент времени лишь одного сеанса обмена. При этом допускается различие во временном позиционировании внутренних и, как следствие, выходных событий процесса обработки информации, формируемых во встроенной модели и в модели, вычисляемой в СД для получения эталонной реакции. Различие возникает из-за отсутствия в СД при генерировании эталонной реакции информации о реальной длительности исполнения программных модулей, что не является препятствием для сопоставления реальных и эталонных событий при проведении диагностирования. Данная особенность дает определенную свободу в выборе модели. В частности, при моделировании цепи она позволяет считать, что разные порции информации обрабатываются не параллельно, а строго последовательно. Более того, в модели со слиянием цепей можно считать, что последовательно обрабатываются не только разные порции информации, но и одна и та же порция информации в разных цепях, подвергшихся слиянию. Этот прием поясняется на рис. 3.

Здесь представлен порядок вычислений в динамической модели. Сначала информация принимается (П) во все цепи одновременно. Далее информация обрабатывается (О1) в первой цепи, затем – во второй (О2) и, наконец, в последней p-й. Затем с выходов этих цепей информация принимается и обрабатывается (O0) в установленной последовательности нулевым звеном (звеном слияния), после чего результат выдается (В) в СД. Обращаем внимание на тот факт, что информация с выходов цепей всегда обрабатывается в звене слияния в одной и той же последовательности независимо от порядка ее поступления в звено, что всегда можно реализовать.

Свойство 2. Возможность сведения к стационарной модели $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} _{{}}^{m}$ любой периодически нестационарной модели ${{S}^{{\text{m}}}}$ системы S из рассматриваемого класса, т.е. имеющей на периоде один сеанс приема и один сеанс выдачи информации в СД. При этом нестационарная система с независимыми цепями переходит в стационарную систему с независимыми цепями, а нестационарная система со слиянием цепей – в стационарную систему со слиянием цепей.

Для любой периодически нестационарной системы ${{S}^{{\text{m}}}}$, которая описывается моделью

имеет на периоде функционирования один сеанс приема информации от СД, описываемый для некоторой последовательности ${{\gamma }_{{\text{r}}}}$ матрицами $F({{\gamma }_{r}}(N))$, $G({{\gamma }_{r}}(N))$, $H({{\gamma }_{r}}(N))$, и один сеанс выдачи информации в СД, описываемый матрицами $F({{\gamma }_{r}}(N - 1))$, $G({{\gamma }_{r}}(N - 1))$, $H({{\gamma }_{r}}(N - 1))$, существует стационарная система $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} _{{}}^{m}$: которая при любой входной последовательности формирует выходные последовательности, совпадающие с выходными последовательностями системы ${{S}^{{\text{m}}}}$ на ${{\gamma }_{{\text{r}}}}$. При этом k – периоды системы (2.1),

Итак, ниже рассматривается следующая задача. Предполагается, что для диагностируемой системы S задана иерархическая структура модели с произвольным числом точек слияния, которая может быть получена из модели с независимыми цепями путем введения некоторого набора точек слияния. Заметим, что при любом числе точек слияния структура модели будет оставаться иерархической. Необходимо сформулировать достаточные условия, которым должны удовлетворять звенья модели и при которых модель системы будет наблюдаема и управляема. Заметим, что в [8] подобные условия формулируются лишь для модели с одной точкой слияния.

Поиск условий осуществляется при следующих предположениях:

1) описание моделей S^m и ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} }^{m}}$ осуществляется в двоичном поле (двоичной арифметике);

2) система S^m включает только звенья со скалярными входами и выходами, что уменьшает количество передаваемой диагностической информации, но и максимально усложняет проблему обеспечения наблюдаемости и управляемости системы в целом.

Вывод достаточных условий наблюдаемости и управляемости рассматриваемой диагностической модели для случая, когда точек слияния более одной, будет произведен в следующей последовательности. Сначала осуществляется переход от периодически нестационарной модели к стационарной (свойство 2). Затем доказываются достаточные условия, которым должны удовлетворять звенья исходной нестационарной модели для того, чтобы стационарная модель была бы наблюдаема и управляема. После этого доказывается, что эти условия являются также достаточными для наблюдаемости и управляемости нестационарной модели.

3. Анализ стационарных моделей. Рассматриваемые далее иерархические стационарные модели ${{\hat {S}}^{m}}$ представляют собой композицию структурных элементов трех типов – цепь ${{\hat {S}}^{c}}$ (рис. 4, а), структура со слиянием цепей ${{\hat {S}}^{f}}$ (рис. 4, б) и иерархическая структуры ${{\hat {S}}^{h}}$ (рис. 4, в), в которой каждая из подмоделей S_i может также представлять из себя либо цепь, либо структуру со слиянием цепей, либо иерархическую структуру.

Поскольку условия наблюдаемости и управляемости рассматриваемых моделей формулируются в терминах их характеристических многочленов, важно располагать простыми правилами их вычисления, которые приводятся далее в первых трех утверждениях. При этом для упрощения анализа предполагается, что в составном векторе состояния модели ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} }^{m}}$ цепи вектора состояния звеньев пронумерованы в направлении от входа к выходу цепи.

Утверждение 1. Матрица динамики ${{A}^{c}}$ стационарной цепи ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} }^{c}}$ (рис. 4,а) из $v$ звеньев (1.1) является неособенной нижней блочно-треугольной с характеристическим многочленом

где ${{\varphi }_{i}}$ – характеристический многочлен i-го звена $i = \overline {1,v} $, и имеет вид где f_i – матрица динамики i-го звена $i = \overline {1,v} $, ${{R}_{{i,i + 1}}} = {{g}_{{i + 1}}}{{h}_{i}}$ – матрица связи между i-м и (i + 1)-м звеньями $i = \overline {1,v - 1} $.

Доказательство. Матрица сеанса в нестационарной модели по определению и в соответствии с предположением о нумерации звеньев является нижней блочно-треугольной с блоками f_i $i = \overline {1,v} $, и ${{R}_{{i,i + 1}}}$ $i = \overline {1,v - 1} $. Во всех ее блоках на главной диагонали, кроме одного, расположены единичные матрицы E (см. пример 1). Единственный “неединичный” блок, который описывает обмен информацией в данном сеансе между соседними звеньями M_i и ${{M}_{{i + 1}}}$, имеет вид

где ${{g}_{{i,i + 1}}}$ – матрица связи между i-м и (i + 1)-м звеньями.

В результате матрица A динамики стационарной модели также является нижней блочно-треугольной, поскольку она образуется как произведение матриц сеансов (см. свойство 2). При этом поскольку каждое звено срабатывает за период только один раз при приеме информации, то в главной диагонали матрицы A будут стоять матрицы динамики звеньев цепи в соответствии с упорядоченностью звеньев в цепи. Известно, что характеристический многочлен нижней блочно-треугольной матрицы равен произведению характеристических многочленов блоков главной диагонали. Поскольку матрицы динамики звеньев неособенные, то и матрица A^c будет также неособенной.

Утверждение 2. Матрица динамики A^f стационарной структуры ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} }^{f}}$ со слиянием p цепей (рис. 4, б) является неособенной нижней блочно-треугольной с характеристическим многочленом

где $\varphi _{0}^{p}$ – характеристический многочлен звена слияния $M_{0}^{f}$ в степени p, $\varphi _{j}^{c}$ – характеристический многочлен j-й цепи $j = \overline {1,p} $, и имеет вид: где $A_{{{{\gamma }_{{r,l}}}}}^{c}$ – матрица динамики l-й цепи, ${{R}_{{l,0}}}$ – матрица связи между l-й цепью $l = \overline {1,p} $ и звеном слияния.

Доказательство. Формирование матриц динамики цепей было рассмотрено при обсуждении предыдущего утверждения. Они располагаются вдоль главной диагонали A^f в соответствии с выбранным порядком. Поскольку все матрицы ${{A}_{{{{\gamma }_{{\text{r}}}},l}}}$, $l = \overline {1,p} $, а также матрица $f_{0}^{p}$ неособенные, то и матрица A^f также неособенная. Степень p вхождения матрицы f₀ в выражение для A^f объясняется тем, что звено слияния срабатывает p раз за период (p раз принимает информацию).

Утверждение 3. Матрица динамики A^h стационарной иерархической структуры ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} }^{h}}$ (рис. 4, в) является неособенной нижней блочно-треугольной с характеристическим многочленом

где $\varphi _{0}^{q}$ – характеристический многочлен звена слияния $M_{0}^{h}$ в степени q, $\varphi _{k}^{s}$ – характеристический многочлен подсистемы ${{S}_{k}}$ $k = \overline {1,q} $, и имеет вид где матрица динамики $A_{{{{\gamma }_{r}},l}}^{s}$ соответствует l-й подсистеме.

Нетрудно видеть, что в качестве доказательства для этого утверждения может быть использовано доказательство предыдущего. Действительно, любая подсистема в иерархической структуре может рассматриваться как некоторое звено. Таким образом, в данном случае мы имеем уже рассмотренную ситуацию со слиянием однозвенных цепей.

Проанализировав структуру матриц (3.1)–(3.3), можно прийти к следующим простым, но важным для дальнейшего изложения выводам в отношении стационарных моделей. Стационарная модель ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} }^{c}}$ цепи есть цепь, стационарная модель A^f структуры со слиянием p цепей также есть структура со слиянием p цепей и, наконец, стационарная модель ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} }^{h}}$ иерархической структуры с q подсистемами есть иерархическая структура с q подсистемами. Этот факт будет использован при доказательстве утверждения 4, где структура анализируется как композиция подсистем $\{ {{S}_{k}}\,{\text{|}}\,k = \overline {1,q} \} $ и звена слияния $M_{0}^{h}$. Причем процесс обработки в $M_{0}^{h}$ выходной информации цепей описывается с привлечением передаточных функций $\{ {{J}_{k}} = {{c}_{k}}(x){\text{/}}\varphi _{{f_{0}^{q}}}^{*}(x)\,{\text{|}}\,k = \overline {1,q} \} $с выхода k-й цепи на выход звена слияния.

Для цепей и моделей со слиянием цепей достаточные условия наблюдаемости и управляемости приведены в [7, 8], поэтому выведем их для иерархической структуры произвольного вида. При этом будем анализировать иерархическую стационарную структуру ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} }^{h}}$, представленную в развернутом виде с использованием структуры “цепь” и структуры с одной точкой слияния (рис. 3, а и б). При этом описание ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} }^{h}}$ будет содержать μ точек слияния.

4. Условия наблюдаемости и управляемости параллельной модели при наличии в ней более одной точки слияния.

Утверждение 4. Иерархическая стационарная структура ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} }^{h}}$, включающая $\mu $ точек слияния, наблюдаема и управляема, если для любой $\nu $-й точки слияния $\nu = \overline {1,\mu } $ в звене $M_{\nu }^{h}$ скалярных подсистем из множества $\{ {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} }_{k}}\,{\text{|}}\,k = \overline {1,{{q}_{\nu }}} \} $ выполняется:

− подсистемы $\{ {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} }_{k}}\,{\text{|}}\,k = \overline {1,{{q}_{\nu }}} \} $ наблюдаемы и управляемы,

− характеристические многочлены $\{ {{\varphi }_{k}}\,{\text{|}}\,k = \overline {1,{{q}_{\nu }}} \} $ подсистем, характеристический многочлен ${{\varphi }_{{{{f}_{\nu }}}}}$ и многочлены $\{ {{c}_{k}}\,{\text{|}}\,k = {{\overline {1,q} }_{\nu }}\} $ числителей передаточных функций $\{ {{J}_{k}}\,{\text{|}}\,k = \overline {1,{{q}_{\nu }}} \} $ звена слияния $M_{\nu }^{h}$ взаимно просты.

Доказательство. Покажем сначала наблюдаемость иерархической структуры ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} }^{h}}$. Базис пространства выходных последовательностей иерархической структуры ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} }^{h}}$в ν-й точке слияния, заданный на периоде T (T – период выходных последовательностей свободного движения иерархической структуры ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} }^{h}}$), при свободном движении складывается, во-первых, из базиса подпространства выходных последовательностей свободного движения звена слияния и, во-вторых, из базисов аналогичных подпространств объединяемых подсистем, переработанных звеном слияния и заданных на том же периоде.

Первый базис – базис подпространства ${{P}_{\nu }}$ выходных последовательностей свободного движения звена слияния $M_{\nu }^{h}$ – представляется воспроизводящей матрицей ${{V}_{\nu }}$ этого звена, повторенной ${T \mathord{\left/ {\vphantom {T {{{T}_{\nu }}}}} \right. \kern-0em} {{{T}_{\nu }}}}$ раз на периоде T, где ${{T}_{\nu }}$ – период выходной последовательности свободного движения звена слияния, т.е. базис имеет вид $\left[ {\begin{array}{*{20}{c}} {{{V}_{\nu }}}&{{{V}_{\nu }}}&{...}&{{{V}_{\nu }}} \end{array}} \right]$. Многочлен, описывающий первый вектор из этого базиса, вычисляется по формуле

Многочлен для второго вектора получается из (4.1) умножением на x, для третьего – на x² и т.д. для последнего – на ${{x}^{{{{m}_{\nu }} - 1}}}$ (${{m}_{\nu }}$ – размерность звена слияния).

Далее для описания остальных базисов – базисов подпространств выходных последовательностей свободного движения подсистем, переработанных звеном слияния – удобно воспользоваться известным [14] d-преобразованием для последовательностей над полями Галуа. В этом случае последовательности представляются в виде степенных многочленов, а для динамических систем вводится понятие передаточной функции. Запишем выражение для передаточной функции для линейного динамического звена слияния. Эта функция для каждой из объединяемых подсистем будет в общем случае своя, так как для разных подсистем входные матрицы объединяющего звена различны. С учетом правил вычислений в двоичном поле и при введении переменной x (не следует путать с вектором состояния) вместо d эта функция имеет вид

где ${{(xf_{\nu }^{q} + E)}^{П}}$ – матрица алгебраических дополнений, выраженных степенными многочленами, $\varphi _{{f_{\nu }^{q}}}^{*}(x)$ – многочлен, двойственный к характеристическому многочлену ${{\varphi }_{{f_{\nu }^{q}}}}(x)$.

Базис подпространства ${{P}_{k}}$ выходных последовательностей свободного движения k-й подсистемы представляется воспроизводящей матрицей ${{V}_{k}}$ этой подсистемы, повторенной $T{\text{/}}{{T}_{k}}$ раз на периоде T, где T_k – период выходной последовательности свободного движения k-й подсистемы, т.е. базис имеет вид $\left[ {\begin{array}{*{20}{c}} {{{V}_{k}}}&{{{V}_{k}}}&{...}&{{{V}_{k}}} \end{array}} \right]$. Следуя (4.1), но учитывая обработку (4.2) в звене слияния получаем многочлен, описывающий первый вектор из базиса k-й подсистемы:

Подставляя в (4.3) ${{J}_{k}} = {{c}_{k}}(x){\text{/}}\varphi _{{f_{\nu }^{q}}}^{*}(x)$, получаем

Покажем, что базисные векторы из подпространств P₀ и ${{P}_{k}}$ $k = \overline {1,q} $, линейно независимы. Предположив существование линейной зависимости, приходим к выражению

где $a(x)$ и ${{b}_{k}}(x)$ – многочлены, отражающие сдвиги базисных векторов, просуммированных в подпространствах ${{P}_{\nu }}$ и ${{P}_{k}}$, $k = \overline {1,q} $, соответственно.

Подставляя выражения для $\Psi {\kern 1pt} '$, $\Psi _{k}^{{''}}$ и J^k, получаем

а после преобразования имеем

Рассмотрим произвольное k-е слагаемое в правой части. Среди его сомножителей отсутствует φ_k. Однако это слагаемое должно делиться на φ_k, так как левая часть равенства и все остальные слагаемые правой части содержат этот сомножитель. Это не выполняется, поскольку по условию утверждения φ_k является взаимно простым по отношению к ${{\varphi }_{{\text{s}}}}$, $s \ne k$, к c_k и к ${{\varphi }_{{{{f}_{\nu }}}}}$, а значит, и к ${{\varphi }_{{f_{\nu }^{q}}}}$. Следовательно, сделанное предположение (4.5) о существовании линейной зависимости неверно и базисные векторы из подпространств ${{P}_{\nu }}$ и ${{P}_{k}}$, $k = \overline {1,q} $, линейно независимы.

Для доказательства полной управляемости достаточно повторить приведенные выше рассуждения относительно двойственной системы.

Утверждение 5. Если стационарная система (2.2) наблюдаема (управляема), то периодически нестационарная система (2.1) ${{\gamma }_{{\text{r}}}}$-наблюдаема (${{\gamma }_{{\text{r}}}}$-управляема).

Таким образом, условия наблюдаемости и управляемости (утверждение 4), сформулированные для стационарной системы, являются также и условиями ${{\gamma }_{{\text{r}}}}$-наблюдаемости и ${{\gamma }_{{\text{r}}}}$-управляемости для нестационарной.

Утверждение 6. Если периодически нестационарная система ${{S}^{{\text{f}}}}$ ${{\gamma }_{{\text{r}}}}$-наблюдаема и ${{\gamma }_{{\text{r}}}}$-управляема и все матрицы динамики этой цепи неособенные, то она полностью наблюдаема и управляема.

Действительно, ${{\gamma }_{{\text{r}}}}$-наблюдаемость цепи позволяет определить по ее выходу состояние x_i, в котором система находится в момент времени, совпадающий с началом последовательности ${{\gamma }_{{\text{r}}}}$. Однако благодаря неособенности всех матриц динамики можно, зная ${{x}_{i}}$, определить не только любое последующее, но и любое предшествующее ему состояние, что свидетельствует о полной наблюдаемости системы. Воспользовавшись принципом двойственности, к аналогичному выводу можно прийти и в отношении управляемости.

Пример 2. Продолжим пример 1, конкретизировав вид звеньев. Будем использовать однородные цепи, т.е. состоящие из одинаковых звеньев. Пусть описание звеньев имеет следующий вид (1 – M₁₁, $2 - {{M}_{{21}}}$, $3 - {{M}_{{33}}}$, $4 - {{M}_{{22}}}$, 0 – M₃₁):

– звенья нестационарных цепей

– звено слияния нестационарной модели – звенья стационарных цепей – звено слияния стационарной модели

Все эти звенья наблюдаемы и управляемы, а их характеристические многочлены взаимно просты (неприводимы), что гарантирует выполнение условий утверждения 4 и, как следствие, утверждений 5 и 6.

Заключение. Рассмотрены вопросы синтеза диагностической модели распределенной вычислительной системы реального времени. Она предназначена для использования при тестовом диагностировании с параллельной моделью, когда модель встраивается в систему и исполняется параллельно с основным программным обеспечением. Изложенные выше результаты дают возможность получения более рациональных версий модели с точки зрения объема передаваемой диагностической информации, нежели модели, получаемые с помощью известных алгоритмов синтеза. Для данных моделей формулируются достаточные условия наблюдаемости и управляемости.