1. На главную
  2. Электронные версии
  3. Известия РАН. Теория и системы управления
  4. № 5, 2020

Известия РАН. Теория и системы управления, 2020, № 5, стр. 5-27

ТЕОРИЯ СКРЫТЫХ КОЛЕБАНИЙ И УСТОЙЧИВОСТЬ СИСТЕМ УПРАВЛЕНИЯ

Н. В. Кузнецов *

Санкт-Петербургский государственный ун-т, Институт проблем машиноведения РАН
Санкт-Петербург, Россия

* E-mail: n.v.kuznetsov@spbu.ru

Поступила в редакцию 13.05.2019
После доработки 30.08.2019
Принята к публикации 25.05.2020

Полный текст (PDF)

Аннотация

Развитие теории устойчивости, теории бифуркаций, теории хаоса, теории робастного управления и новые вычислительные технологии позволили по-новому взглянуть на ряд известных научных проблем и практических задач анализа многомерных систем управления, что привело к появлению теории скрытых колебаний, ставшей современным этапом развития теории колебаний А.А. Андронова. Основой теории скрытых колебаний стала новая классификация колебаний как самовозбуждающихся или скрытых. В то время как самовозбуждение колебаний может быть эффективно исследовано численно, выявление скрытых колебаний требует применения специальных аналитико-численных методов. Анализ скрытых колебаний необходим для определения точных границ устойчивости, оценки зазора между необходимыми и достаточными условиями глобальной устойчивости и их сближения, а также выделения классов систем управления, для которых эти условия совпадают. Разработанные для анализа скрытых колебаний методы позволили определить границы устойчивости и обнаружить скрытые колебания в различных актуальных динамических моделях. В настоящем обзоре представлены известные теоретические и инженерные задачи, в которых скрытые колебания (их отсутствие или наличие и расположение) играют важную роль.

Введение. История создания теории скрытых колебаний. Математическое моделирование динамики и определение устойчивости в технических системах является актуальнейшим направлением в научном и технологическом развитии любого государства, которое стремится занять лидирующие позиции в современном мире. Изучение предельных динамических режимов (аттракторов) и устойчивости необходимо как в классических теоретических, так и в актуальных практических задачах. Одни из первых таких задач связаны с проектированием систем управления: автоматических регуляторов, в XVIII–XIX вв. Регуляторы должны были обеспечивать переход динамики объекта управления к рабочему режиму и устойчивость рабочего режима относительно начальных отклонений и внешних возмущений. Классическим примером является регулятор Уатта, использовавшийся для поддержания заданной постоянной скорости вращения вала турбины. Так, в одной только Великобритании в 1868 г. на промышленных предприятиях работало около 75 тыс. паровых машин, снабженных регуляторами Уатта [1]. Однако в середине XIX в. многие произведенные паровые машины оказались неработоспособными из-за явления самораскачивания, когда регулятор не справлялся с поддержанием выравнивания моментов. Высокая аварийность этих машин ставила новые инженерные требования к их проектированию и тем самым стимулировала развитие математической теории устойчивости систем управления.

Знаменитая работа И.А. Вышнеградского о регуляторе Уатта [2], опубликованная в 1877 г., является примером математической постановки и решения таких задач. В этой публикации исследовалась замкнутая динамическая модель “паровая машина – регулятор”, для которой явление самораскачивания было переформулировано на математический язык как свойство неустойчивости решения дифференциального уравнения. И.А. Вышнеградский определил условия устойчивости стационарного решения (тривиального аттрактора), соответствующего требуемому рабочему режиму, для приближенной линейной модели, без учета сухого трения.

После этой работы, однако, оставался открытым важный вопрос строгого доказательства глобальной устойчивости и допустимости проведения линеаризации модели путем отбрасывания сухого трения. В 1885 г. М. Леотэ впервые показал, что в инженерных системах регулирования c сухим трением могут возникать предельные периодические колебания – предельные циклы (периодические аттракторы) [3]. Это привело к критике подхода И.А. Вышнеградского и его выводов, в том числе выдающимся российским ученым Н.Е. Жуковским [4].

Систематическое изучение предельных циклов (периодических аттракторов) и критериев их отсутствия в прикладных динамических системах связано с работами научной школы А.А. Андронова, которым была создана математическая теория колебаний, объясняющая поведение многих прикладных систем. Эта теория соединила в себе математические идеи анализа локальной устойчивости А.М. Ляпунова [5] и предельных колебаний А. Пуанкаре [6] для гладких динамических систем с инженерными потребностями учета разрывных нелинейностей.

Теория колебаний Андронова позволила аналитически изучать возникновение предельных колебаний, а также получать необходимые и достаточные условия отсутствия колебаний и глобальной устойчивости для систем невысокого порядка. Основы этой теории изложены в знаменитой монографии “Теория колебаний”, первое издание которой было опубликовано в 1937 г. [7] и посвящено анализу двумерных математических моделей различных колебательных систем22.

Начиная с 1944 г., А.А. Андронов активно занимался применением теории колебаний к задачам автоматического регулирования и организовал знаменитый семинар в Институте автоматики и телемеханики (теперь Институт проблем управления) в Москве, где им была заложена всемирно известная научная школа по теории автоматического регулирования – разделу современной теории управления [10, 11]. Первыми результатами А.А. Андронова в этом направлении являются строгий нелокальный анализ нелинейной модели регулятора Уатта с сухим трением и доказательство достаточности условий Вышнеградского для отсутствия колебаний и глобальной устойчивости рабочего режима (существование отрезка покоя, притягивающего траектории из любых начальных данных) [12, 13]. Значимость этих результатов была отмечена при избрании А.А. Андронова в 1946 г. действительным членом АН СССР по Отделению технических наук, где он стал первым академиком по теории управления [14, с. 56]. В послевоенные годы участниками Андроновского семинара были М.А. Айзерман, В.В. Петров, Я.З. Цыпкин и многие другие ученые, ставшие яркими представителями Московской школы теории управления.

Дальнейшее развитие результатов Андронова–Вышнеградского и получение достаточных условий устойчивости и отсутствия колебаний для многомерных систем автоматического регулирования с разрывными характеристиками связано с работами А.Х. Гелига, Г.А. Леонова и их учеников [15–18]. Отметим, что такие задачи до сих пор остаются актуальными для современных регуляторов турбин, как показали недавняя авария на Саяно-Шушенской ГЭС и анализ ее возможных причин [19–22]. Мотивацией к дальнейшему развитию методов анализа систем регулирования с разрывными характеристиками является важность учета современных моделей трибологии [23–25] и управления [26–34].

В общем случае для практического использования регуляторов необходимо выявлять в замкнутой системе все устойчивые стационарные и колебательные режимы, а также области их притяжения (устойчивость в большом). В работах Л.И. Мандельштама, Н.Д. Папалекси и А.А. Андронова при описании колебательных систем устойчивый стационарный режим характеризуется как несамовозбужденное состояние, а переход от ставшего неустойчивым стационарного режима к периодическому колебательному режиму (предельному циклу) описывается как самовозбуждение автоколебаний33 [7, 35]. В 1963 г. американский метеоролог Э. Лоренц показал, что аналогичное самовозбуждение может приводить не только к периодическим, но и к хаотическим предельным режимам (хаотическим аттракторам) в гладких многомерных динамических системах [36]. Для гладких систем с периодическим возмущением аналогичный эффект был открыт японским ученым Й. Уеда в 1961 г., однако известность этот результат получил только в 70-е гг. [37]. Для кусочно-линейной системы самовозбуждение хаотических колебаний было впервые обнаружено в моделях электронных цепей Чуа в 1984 г. [38].

Задачи анализа многомерных систем управления и получения необходимых и достаточных условий глобальной устойчивости, в том числе гарантирующих отсутствие хаотических колебаний, показали необходимость дальнейшего развития теории колебаний А.А. Андронова и создания новых аналитических и численных методов анализа устойчивости и колебаний.

На современном этапе исследования колебаний инженерные понятия переходного процесса и удержания тесно связаны с возможностью численного анализа предельных колебаний. В общем случае колебание в динамической системе может быть выявлено численно, если начальные данные из его окрестности соответствуют притягиваемым к нему колебаниям. Таким притягивающим ограниченным колебаниям (или множествам колебаний) в фазовом пространстве динамической системы соответствуют аттракторы44. Классический инженерный анализ устойчивости и колебаний в системе заключается в определении стационарных режимов, аналитическом определении их локальной устойчивости и затем численном анализе поведения системы с начальными данными в окрестности неустойчивых стационарных режимов. Такой анализ позволяет показать притяжение траекторий из окрестности неустойчивых состояний равновесия к устойчивым состояниям равновесия: тривиальным аттракторам (как, например, притяжение траекторий к тривиальному аттрактору в модели математического маятника), или выявить нетривиальные (колебательные) аттракторы. Благодаря свойству самовозбуждения современные вычислительные средства позволили легко обнаружить аттракторы в моделях ван дер Поля55, Лоренца и Чуа при помощи численного интегрирования траекторий с начальными данными из окрестности неустойчивых состояний равновесия [39].

В рамках такого подхода оставалась открытой проблема существования в системе таких аттракторов, к которым не притягиваются траектории из окрестностей состояний равновесия. В 2009 г. Г.А. Леоновым и Н.В. Кузнецовым, автором этого обзора, была предложена новая классификация аттракторов динамических систем, ставшая основой теории скрытых колебаний: аттрактор называется скрытым, если область его притяжения не соприкасается с неустойчивыми состояниями равновесия, в противном случае аттрактор называется самовозбуждающимся [39–43]. Понятие аттрактора позволяет обобщить идеи А.А. Андронова о соответствии между установившимися периодическими колебаниями и предельными циклами динамических систем также и на случай установившихся непериодических колебаний (произвольные колебания в зависимости от их областей притяжения можно аналогично классифицировать как самовозбуждающиеся или скрытые относительно неустойчивых стационарных режимов). Так впервые были введены термины скрытый аттрактор и скрытое колебание и даны их математические определения. Предложенная классификация согласуется с экспериментальным подходом к анализу возникновения колебаний и численными процедурами поиска аттракторов, отражает трудности решения ряда актуальных инженерных задач и известных научных проблем, а также стала катализатором открытия новых аттракторов в известных системах. В то время как самовозбуждающиеся аттракторы (self-excited66 attractors) могут быть легко обнаружены и визуализированы траекториями в численных экспериментах с начальными данными из окрестностей неустойчивых состояний равновесия, скрытые аттракторы (hidden attractors) не связаны с состояниями равновесия и их области притяжения “скрыты” в фазовом пространстве системы. Поэтому численный поиск скрытых аттракторов и определение начальных данных для их визуализации в общем случае оказывается нетривиальной задачей, решением которой в настоящее время занимаются ученые разных стран77.

Теория скрытых колебаний [45–47] является современным этапом развития теории колебаний А.А. Андронова. Она востребована во многих теоретических и актуальных инженерных задачах, в которых скрытые аттракторы (их отсутствие или наличие и расположение) играют важную роль.

Важность выявления скрытых аттракторов для систем управления связана с классическими задачами определения точных границ глобальной устойчивости, анализа зазора между необходимыми и достаточными условиями глобальной устойчивости и их сближения, а также выделения классов систем управления, для которых эти условия совпадают. На практике переход состояния системы управления к скрытому аттрактору, вызванный внешними возмущениями, приводит к нежелательным режимам работы и часто является причиной аварий и катастроф.

Для анализа скрытых колебаний были разработаны эффективные аналитические и численные методы, которые позволяют определять границы устойчивости и обнаруживать скрытые колебания в различных актуальных задачах. Полученные в этом направлении основные результаты – предмет докторской диссертации автора данного обзора: “Аналитико-численные методы анализа скрытых колебаний”88 [43]. За последние годы теория скрытых колебаний получила признание научного сообщества как в России, так и за рубежом: первые основополагающие публикации по этой тематике вошли в 2016 г. в 1% самых цитируемых статей базы Web of Science, при этом две публикации [39, 41] стали наиболее цитируемыми статьями журналов99, в которых они были опубликованы.

Данный обзор подготовлен по материалам пленарных докладов на 11-й Российской мультиконференции по проблемам управления (Санкт-Петербург, 2018 г.) и 5th IFAC Conference on Analysis and Control of Chaotic Systems (Eindhoven, 2018 г.). В обзоре рассмотрены теоретические и инженерные задачи в рамках теории скрытых колебаний: задача Андронова-Вышнеградского о нелинейном анализе центробежного регулятора паровой машины, задача Келдыша о нелинейном анализе моделей подавления флаттера, гипотезы Айзермана и Калмана об абсолютной устойчивости систем управления в форме Лурье, 16-я проблема Гильберта, эффект Зоммерфельда застревания частоты, цепи Чуа, системы управления фазовой синхронизацией и гипотеза Капранова, выявление скрытых колебаний в динамических моделях буровых установок.

1. Скрытые колебания в контрпримерах к гипотезам Айзермана и Калмана. В середине прошлого века М.А. Айзерман и Р.Е. Калман изучали совпадение условия глобальной устойчивости в нелинейных системах управления с условием устойчивости линейных приближений для систем управления с единственным состоянием равновесия и нелинейностями из заданного сектора.

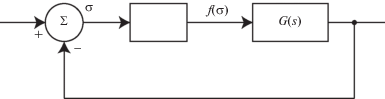
Начиная с 40-х гг. прошлого века стали разрабатываться критерии отсутствия колебаний в системах автоматического регулирования. В 1944 г. была опубликована знаменитая работа А.И. Лурье и В.Н. Постникова [48], в которой был впервые предложен эффективный прием получения достаточных условий отсутствия колебаний и глобальной устойчивости, основанный на рассмотрении специального класса функций Ляпунова1010, для математической модели системы управления следующего вида:

(1.1)
$\dot {z} = Pz + qf({{r}^{{\text{T}}}}z),$
где z – вектор состояний объекта, P – постоянная матрица, q и $r$ – постоянные векторы, $f( \cdot )$ – скалярная непрерывная нелинейность из заданного класса, ${\text{T}}$ – операция транспонирования. Такую систему управления в литературе часто называют системой Лурье. В том же году А.А. Андроновым и А.Г. Майером [12, 13] для модели регулятора Уатта из работы И.А. Вышнеградского [2] в форме системы Лурье (1.1) c разрывной нелинейностью:
(1.2)
$P = \left( {\begin{array}{*{20}{c}} 0&0&1 \\ { - 1}&0&0 \\ { - \alpha }&1&{ - \beta } \end{array}} \right),\quad q = \left( {\begin{array}{*{20}{c}} 0 \\ 0 \\ { - 1} \end{array}} \right),\quad r = \left( {\begin{array}{*{20}{c}} 0 \\ 0 \\ 1 \end{array}} \right),\quad f(\sigma ) = \frac{1}{2}{\text{sign}}(\sigma ),$
учитывающей сухое трение, было показано совпадение условий асимптотической устойчивости “линеаризованной” модели без сухого трения и глобальной устойчивости нелинейной модели при выполнении условий Вышнеградского: $\alpha > 0,\beta > 0$ и $\alpha \beta > 1$.

Эти работы привели к задаче выделения классов систем Лурье, для которых необходимые условия устойчивости и отсутствия самовозбуждающихся колебаний совпадают с достаточными условиями глобальной устойчивости. В 1957 г. Р.Е. Калманом был сформулирован следующий критерий [50]: “Если при замене $f(\sigma )$ на рис. 1 константами $k$, соответствующими всем возможным значениям $f{\kern 1pt} '(\sigma )$, замкнутая система устойчива для всех таких $k$, то интуитивно ясно, что система должна быть моноустойчивой, т.е. все переходные режимы будут стремиться к единственной устойчивой стационарной точке.” Из отсутствия самовозбуждающихся колебаний, необходимого условия устойчивости, здесь делается вывод о глобальной устойчивости. Интересно, что, обладая огромной инженерной интуицией, Р.Е. Калман сформулировал критерий, справедливый (как оказалось позже) в 3-мерном пространстве [51, 52], которое человек хорошо себе представляет. Однако в общем случае уже в 4-мерном пространстве1111 критерий Калмана неверен, и к нему были [39] построены контрпримеры. Например, система Лурье (1.1) c

(1.3)
$P = \left( {\begin{array}{*{20}{c}} 0&1&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \\ { - {{a}_{0}}}&{ - {{a}_{1}}}&{ - {{a}_{2}}}&{ - {{a}_{3}}} \end{array}} \right),\quad q = \left( {\begin{array}{*{20}{c}} 0 \\ 0 \\ 0 \\ 1 \end{array}} \right),\quad r = \left( {\begin{array}{*{20}{c}} 0 \\ 0 \\ { - 1} \\ 0 \end{array}} \right)$
и ${{a}_{0}} = (m_{1}^{2} + {{\beta }^{2}})(m_{2}^{2} + {{\beta }^{2}})$, ${{a}_{1}} = 2\beta (m_{1}^{2} + m_{2}^{2} + 2{{\beta }^{2}})$, ${{a}_{2}} = m_{1}^{2} + m_{2}^{2} + 6{{\beta }^{2}}$, ${{a}_{3}} = 4\beta $, ${{m}_{1}} = 0.9$, ${{m}_{2}} = 1.1$, $\beta \geqslant 0$ имеет бесконечный сектор линейной устойчивости, и для нелинейностей
$f(\sigma ) = {\text{tanh}}(100\sigma )\quad {\text{и}}\quad f(\sigma ) = {\text{sign}}(\sigma )$
в ней найдены [54, 55] скрытые колебания1212 (см. рис. 2, $z = ({{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}})$). К аналогичным контрпримерам к гипотезе Калмана и скрытым колебаниям приводит также учет динамики сервопривода $\dot {z} + z = x$ в модели регулирятора (1.2) (например, для α = 1.3, β = 1.2) при сглаживании нелинейности для аппроксимации решения разрывной системы в определении Айзермана–Пятницкого [57]. Отметим, что определять устойчивость и искать скрытые периодические колебания для кусочно-линейных нелинейностей и систем малой размерности можно методом точечных отображений Андронова, в то время как поиск хаотических скрытых колебаний в таких системах требует применения специальных аналитико-численных методов, разрабатываемых в теории скрытых колебаний.

Рис. 1.

G(s) – передаточная функция, $f(\sigma )$ – скалярная функция

Рис. 2.

а – $f(\sigma ) = tanh(\sigma )$, $\beta = 0.1$ (${{a}_{0}} = 1.0004$, ${{a}_{1}} = 0.408$, ${{a}_{2}} = 2.08$, ${{a}_{3}} = 0.4$): скрытый хаотический аттрактор и скрытый периодический аттрактор сосуществуют с устойчивым состоянием равновесия; б – $f(\sigma ) = {\text{sign}}(\sigma )$, $\beta = 0.03$ (${{a}_{0}} = 0.98191881$, ${{a}_{1}} = 0.121308$, ${{a}_{2}} = 2.0254$, ${{a}_{3}} = 0.12$): три сосуществующих периодических аттрактора: два симметричных скрытых периодических аттрактора и один самовозбуждающийся (относительно отрезка покоя) аттрактор

М.А. Айзерман, который в послевоенные годы был активным участником Андроновского семинара, в 1949 г. сформулировал проблему обоснования утверждения, аналогичного критерию Калмана, где требовалась принадлежность сектору линейной устойчивости только самой нелинейности, а не ее производной [58]. Контрпримеры к проблеме Айзермана существуют уже в 2-мерном пространстве1313 [60]. В 1960 г. Л. Маркус и Х. Ямабе, основываясь на работе М.А. Айзермана, высказали общую гипотезу о глобальной устойчивости произвольной гладкой динамической системы с одним состоянием равновесия и устойчивой всюду матрицей Якоби [61, 62]. К гипотезе Маркуса–Ямабе в 3-мерном пространстве существуют контрпримеры с неограниченными траекториями, а в 4-мерном пространстве были построены контрпримеры с периодическими и хаотическими скрытыми аттракторами (рис. 2) [39, 54].

Выдвижение гипотез Айзермана и Калмана можно объяснить также тем, что метод гармонического баланса и линеаризации, разработанный к тому времени в работах ван дер Поля [63], Н.М. Крылова и Н.Н. Боголюбова [64] и широко применяемый на практике [65, 66], показывал отсутствие колебаний при выполнении условий этих гипотез. Так, условия И.А. Вышнеградского для модели (1.2) соответствуют бесконечному сектору линейной устойчивости (т.е. система (1.2) c $f(\sigma ) = k\sigma $ устойчива при всех $k \in [0, + \infty )$), и поэтому метод гармонического баланса показывает отсутствие скрытых колебаний. В настоящее время, используя методы теории дифференциальных включений, которые были разработаны уже после исследований А.А. Андронова, условия И.А. Вышнеградского могут быть строго получены из рассмотрения специальной разрывной функции Ляпунова или частотных условий абсолютной устойчивости [18]. Однако в общем случае строгий анализ отсутствия и возникновения скрытых колебаний для получения необходимых и достаточных условий глобальной устойчивости систем управления является нетривиальной задачей [39, 41].

В 60-е гг., работая над обоснованием своего критерия, Р.Е. Калман пришел к строгим достаточным условиям глобальной устойчивости систем управления (которые гарантируют отсутствие скрытых аттракторов1414). Незадолго до этого аналогичные результаты были получены В.М. Поповым и В.А. Якубовичем [17, 68]. В дальнейшем эти результаты были распространены А.Х. Гелигом и Г.А. Леоновым на системы управления с разрывными нелинейностями (дифференциальные включения) [16–18].

Отметим, что для разрывных систем с кусочно-постоянной нелинейностью и гистерезисом результаты анализа периодических колебаний методом гармонического баланса в ряде случаев могут быть уточнены методом годографа Цыпкина [69, 70], однако к этому методу в общем случае также могут быть построены контрпримеры (например, в системе (1.3) при $\beta = 0.03$ траектории из н.д. $z = ( \pm 0.6252, \pm 3.7324,0.0, \pm 3.4754)$ притягиваются к скрытым периодическим колебаниям, которые не выявляются из анализа годографа Цыпкина).

Позже в развитие теории скрытых колебаний в [39, 41, 67, 71] был предложен эффективный аналитико-численный метод для построения контрпримеров к гипотезам Айзермана и Калмана для различных классов нелинейностей, в которых скрытые периодические и хаотические аттракторы сосуществуют с единственным устойчивым состоянием равновесия. Практическая значимость выявления скрытых колебаний для систем управления и построения контрпримеров связана с задачами определения точных границ глобальной устойчивости, анализом зазора между необходимыми и достаточными условиями глобальной устойчивости, а также выделения классов систем управления, для которых эти условия совпадают.

Отметим также, что для неавтономных систем управления и нестационарных линеаризаций даже гипотеза об определении локальной устойчивости по первому приближению не верна в общем случае: в работах [72–75] к ней были построены различные контрпримеры перроновского типа и предложены достаточные критерии устойчивости. Например [76, 74 ], для системы Лурье (1.1) с неавтономной линейной частью:

(1.4)
$\begin{gathered} P(t) = \left( {\begin{array}{*{20}{c}} { - a}&0 \\ 0&{(sin(ln(t + 1) + cos(ln(t + 1) - 2a)} \end{array}} \right), \\ q = \left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right),\quad r = \left( {\begin{array}{*{20}{c}} 1 \\ 0 \end{array}} \right),\quad f(\sigma ) = {{\sigma }^{2}}, \\ \end{gathered} $
при $1 < 2a < 1 + {{e}^{{ - \pi }}}{\text{/}}2$ ненулевые решения системы первого приближения имеют отрицательные ляпуновские показатели –a или $ - 2a + 1$ (т.е. нулевое решение устойчиво), а решения нелинейной системы с ненулевыми начальными данными имеют один положительный показатель $1 - 2a + {{e}^{{ - \pi }}}{\text{/}}2$ > 0 и стремятся к бесконечности (т.е. нулевое решение неустойчиво).

2. Скрытые колебания и устойчивость систем управления летательными аппаратами. В 1944 г. одновременно с работами Андронова–Майера [12] и Лурье–Постникова [48] в Трудах ЦАГИ была опубликована работа М.В. Келдыша [77], посвященная исследованию флаттера органов управления самолета. В ней М.В. Келдыш ставит задачу нелинейного анализа моделей подавления флаттера гидравлическим демпфером с сухим трением. Эти модели описываются системой Лурье (1.1) с разрывной нелинейностью. Для приближенного анализа возникновения колебаний и оценки области устойчивости отрезка покоя М.В. Келдыш использовал метод гармонического баланса и писал: “мы не даем строгого математического доказательства всех относящихся сюда положений, а ряд выводов построим на интуитивных соображениях”. Практическая значимость в то время работ М.В. Келдыша в области флаттера была отмечена в 1946 г. при его избрании действительным членом АН СССР по Отделению технических наук [14, с. 72]. Благодаря работам М.В. Келдыша и его школы в ЦАГИ в 30–40 гг. прошлого века в СССР удалось избежать многочисленных аварий, которые сопровождали развитие авиации за рубежом (так, например, известно, что в Германии за 1935–1943 гг. произошло более 150 аварий и катастроф опытных самолетов из-за флаттера).

Отметим, что в то время как в теории управления часто ставится задача полного подавления колебаний, М.В. Келдыш в своей работе допускал в силу конструктивных особенностей регулятора эксплуатацию системы регулирования в ограниченной области устойчивости рабочего режима (это означало возможность сосуществования нежелательных предельных режимов – скрытых аттракторов). Например, для двумерной модели (1.1) с

(2.1)
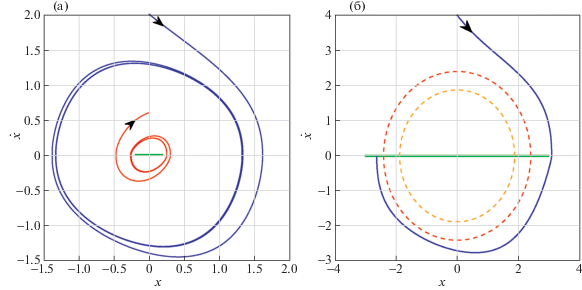
$P = \left( {\begin{array}{*{20}{c}} 0&{{{J}^{{ - 1}}}} \\ { - k}&{ - \mu {{J}^{{ - 1}}}} \end{array}} \right),\quad q = \left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right),\quad r = \left( {\begin{array}{*{20}{c}} 0 \\ {{{J}^{{ - 1}}}} \end{array}} \right),\quad f(\sigma ) = (\Phi + \kappa {{\sigma }^{2}}){\text{sign}}(\sigma )$
М.В. Келдыш, описывая поведение разрывной модели на плоскости (исходя из физических свойств сухого трения) и применяя метод гармонического баланса для поиска приближенных периодических решений, получил следующее утверждение: при $\mu < - {{\delta }_{{{\text{cr}}}}} = - (8{\text{/}}\pi )\sqrt {2\Phi \kappa {\text{/}}3} $ система имеет два периодических решения и область, ограниченная внутренним замкнутым решением, заполнена сворачивающимися с нее фазовыми траекториями, заканчивающимися в одном из возможных положений равновесия; в случае обратного неравенства система не имеет периодических решений и все движения стремятся к положениям равновесия.

В анализе М.В. Келдыша внешний предельный цикл соответствует устойчивому флаттеру и в рамках теории скрытых колебаний является скрытым аттрактором, так как его область притяжения не касается стационарного множества – отрезка покоя. Заметим, что в случае близкого расположения двух предельных циклов численный анализ из-за дискретизации может не обнаружить устойчивый предельный цикл – скрытый аттрактор и, проскакивая оба цикла, показывать стремление к отрезку покоя. Анализ М.В. Келдыша для определения границы области притяжения отрезка покоя в общем случае должен дополняться условиями непересечения циклов с отрезком покоя [78, 79], которые не учитываются в классическом методе гармонического баланса [65, 66]. На рис. 3 [78–80] показано качественное поведение траекторий ($z = (x,\dot {x}$)) на фазовой плоскости при наличии двух предельных циклов и их “разрушение” отрезком покоя. Последующее развитие теории дифференциальных включений, теории скрытых колебаний и аналитических и численных методов анализа, не доступных М.В. Келдышу во время его работы, позволили в настоящее время [78–80] провести строгий анализ устойчивости и возникновения скрытых колебаний в задаче Келдыша о нелинейном анализе моделей подавления флаттера (в том числе, для 2-мерной модели (2.1) установлена строгая оценка области глобальной устойчивости $\mu < - 2\sqrt {\Phi \kappa } $, которая уточняет условие Келдыша c μ < < $ - {{\delta }_{{{\text{cr}}}}} \approx - 2.08\sqrt {\Phi \kappa } $; а 4-мерная модель может быть сведена выбором параметров к модели (1.3) со скрытыми колебаниями).

Рис. 3.

Численный анализ модели Келдыша для $J = k = \kappa = 1$, когда выполнены условия Келдыша $\mu < - {{\delta }_{{{\text{cr}}}}}$ существования двух предельных циклов: а – при Φ = 0.2, $\mu = - 1.3967{{\delta }_{{{\text{cr}}}}} \approx - 1.2987$ внешняя траектория закручивается к устойчивому предельному циклу, а внутренняя траектория сматывается с неустойчивого предельного цикла, ограничивающего область притяжения отрезка покоя; б – при Φ = 3, $\mu = - 1.0076{{\delta }_{{{\text{cr}}}}}$ предельные циклы исчезли (метод гармонического баланса дает предельные циклы с амплитудами ${{a}_{ \pm }} = \tfrac{3}{8}\left( {\pi \mu \pm \sqrt {{{\pi }^{2}}{{\mu }^{2}} - \tfrac{{32}}{3}\Phi } } \right)$, показанные пунктиром) и наблюдается жесткость в поведении системы

Проблемы численного анализа возникновения скрытых колебаний и устойчивости систем управления остаются актуальными и при проектировании современных летательных аппаратов [81, 82]. Так, на ведущей конференции по управлению IEEE Conference on Decision and Control (California, США, 1997) был представлен доклад, посвященный моделированию систем управления и аварии многоцелевого истребителя 5-го поколения YF-22 Lockheed/Boeing из-за возникновения колебаний самолета при посадке. В нем делается вывод, что “поскольку устойчивость в моделировании не гарантирует устойчивость в физической системе управления, требуется более глубокое теоретическое изучение” [83]. Такое изучение в настоящее время является в том числе предметом теории скрытых колебаний и устойчивости систем управления. На необходимость валидации и дальнейшего совершенствования существующих аналитико-численных методов и их программных реализаций, используемых при проектировании летательных аппаратов, указывал директор ЦАГИ С.Л. Чернышев в пленарном докладе на Международной научной конференции по механике “VIII Поляховские чтения” в 2018 г. [84]. Вопросам анализа устойчивости и скрытых колебаний в системах управления летательными аппаратами посвящены также, напирмер, работы [85–89].

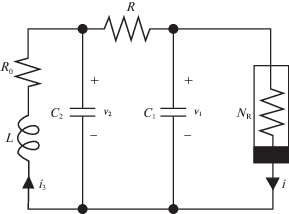
3. Скрытые хаотические колебания в электронном генераторе Чуа. В 80-е гг. прошлого века Л. Чуа (L. Chua, Университет Беркли, США) предложил первую электронную схему управления колебаниями, генерирующую хаотический сигнал [90] (рис. 4).

Рис. 4.

Цепь Чуа – электронный генератор хаотических колебаний

Математическая модель цепи может быть записана в виде трехмерной системы Лурье (1.1) с кусочно-линейной нелинейностью “насыщение” (которая является типичной нелинейностью для задач управления), где

(3.1)
$\begin{gathered} P = \left( {\begin{array}{*{20}{c}} { - \alpha ({{m}_{1}} + 1)}&\alpha &0 \\ 1&{ - 1}&1 \\ 0&{ - \beta }&{ - \gamma } \end{array}} \right),\quad q = \left( {\begin{array}{*{20}{c}} { - \alpha } \\ 0 \\ 0 \end{array}} \right),\quad r = \left( {\begin{array}{*{20}{c}} 1 \\ 0 \\ 0 \end{array}} \right), \\ f(\sigma ) = ({{m}_{0}} - {{m}_{1}}){\text{sat}}(\sigma ) = \frac{1}{2}({{m}_{0}} - {{m}_{1}})({\text{|}}\sigma + 1{\text{|}}\; - \;{\text{|}}\sigma - 1{\text{|}}). \\ \end{gathered} $

Здесь $z = ({{{\text{v}}}_{1}},{{{\text{v}}}_{2}},{\text{R}}{{{\text{i}}}_{3}})$, $\alpha = {{({\text{R}}{{{\text{C}}}_{1}})}^{{ - 1}}}$, $\beta = {\text{R}}{{{\text{L}}}^{{ - 1}}}$, $\gamma = {{{\text{R}}}_{0}}{{{\text{L}}}^{{ - 1}}}$, а RC2 = 1 и ${\text{i}}({{{\text{v}}}_{1}}) = ({{m}_{1}}{{c}^{{\text{T}}}}z + f({{c}^{{\text{T}}}}z)){{{\text{R}}}^{{ - 1}}}$ – вольт-амперная характеристика нелинейного резистора NR.

В физических экспериментах, где запуск электронной цепи происходил включением в цепь нелинейного резистора при нулевых начальных данных (начальном напряжении на конденсаторах и токе через катушку), соответствующих неустойчивому нулевому состоянию равновесия1515, можно было наблюдать только самовозбуждающиеся аттракторы. Сотни таких различных самовозбуждающихся аттракторов были обнаружены в цепи Чуа [91]. Сам Л. Чуа выдвинул гипотезу, что в его цепи могут быть только самовозбуждающиеся хаотические аттракторы [90].

В 2009 г. в рамках развития теории скрытых колебаний впервые была предложена идея построения скрытого хаотического аттрактора Чуа [40, 92, 93] и в 2011 г. открыт первый скрытый хаотический аттрактор в классической цепи Чуа1616 [94, 95]. Этот скрытый аттрактор имеет очень “тонкую” область притяжения и сосуществует с устойчивым нулевым состоянием равновесия, таким образом, оказываясь “скрытым” от стандартных физических экспериментов.

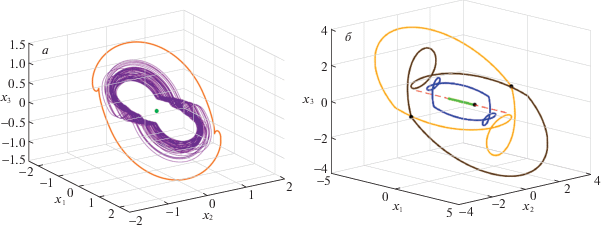
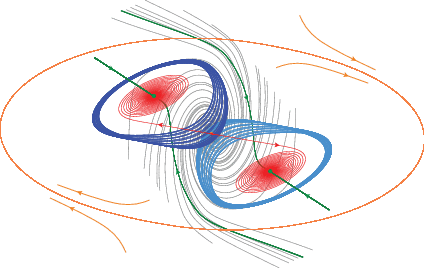
После открытия скрытого аттрактора Л. Чуа поставил задачу определения максимально возможного числа сосуществующих аттракторов в цепи, включая скрытые аттракторы. В настоящее время в цепи Чуа удалось впервые найти пять сосуществующих аттракторов, три из которых являются скрытыми [96, 97] (рис. 5)1717.

Рис. 5.

Пять сосуществующих аттракторов в трехмерном фазовом пространстве цепи Чуа для α = 8.4, $\beta = 12$, $\gamma = - 0.005$, ${{m}_{0}} = - 1.2$, ${{m}_{1}} = - 0.05$: два устойчивых состояния равновесия, скрытый периодический аттрактор, два симметричных скрытых хаотических аттрактора. Области притяжения скрытых аттракторов не соприкасаются с неустойчивым нулевым состоянием равновесия, из окрестности которого траектории притягиваются к двум симметричным устойчивым состояниям равновесия

Отметим, что системы передачи данных, использующие автоподстройку и синхронизацию хаотических сигналов (например, цепей Чуа), могут некорректно работать в случае наличия скрытых аттракторов, что было показано в публикациях [98, 99].

4. Скрытые колебания и устойчивость в электромеханических системах. Одним из ярких примеров скрытых колебаний в электромеханических системах является эффект застревания частоты вращения ротора при запуске электрической машины, установленной на упругом основании. В этой системе для некоторых параметров существенная часть энергии может переходить в колебания основания. При этом частота вращения ротора оказывается существенно меньше частоты при нормальном режиме работы. Этот эффект был впервые замечен в 1902 г. известным немецким ученым А. Зоммерфельдом [100], а затем аналитически описан в работе И.И. Блехмана [101]. В рамках теории скрытых колебаний [102, 103] показано, что этот эффект соответствует сосуществованию двух скрытых аттракторов в математической модели, описывающей динамику частоты вращения ротора, скорости и отклонения основания. При этом в физических экспериментах при естественном запуске мотора из нулевых начальных состояний (которые здесь не соответствуют стационарному режиму) наблюдается только один из аттракторов, соответствующий нежелательному рабочему режиму. Определение области притяжения второго (скрытого) аттрактора, соответствующего желаемому рабочему режиму, и дополнительное управление состоянием системы для перевода в область притяжения этого скрытого аттрактора является актуальной инженерной задачей [104, 105].

Аналогичный зоммерфельдовскому эффект был недавно описан в работах группы ученых из Технического университета Эйндховена (Нидерланды) о буровых установках, где энергия от электропривода расходовалась на возбуждение крутильных колебаний бура, что в итоге приводило к дорогостоящим поломкам бура [106]. В рамках теории скрытых колебаний в [107–109] показано, что такие нежелательные режимы бурильных установок соответствуют скрытым аттракторам, в область притяжения которых система переходит при резком изменении силы трения в процессе бурения. Здесь длинный бур, допускающий изгибно-крутильные колебания, играет роль упругого основания в эффекте Зоммерфельда.

5. Скрытые хаотические аттракторы в физических моделях. Развитие теории скрытых колебаний позволило обнаружить ранее неизвестные скрытые аттракторы в различных известных физических моделях. Многие физические системы имеют “встроенные” механизмы регулирования, реализующиеся в виде бассейнов притяжения – областей начальных состояний системы, для каждой из которых все соответствующие режимы притягиваются к одному аттрактору (устойчивому состоянию равновесия, периодическому, квазипериодическому или хаотическому аттрактору). Интерес к хаотическим аттракторам во многом был вызван попытками описания турбулентности в моделях динамики жидкости. Одним из ярких результатов в этом направлении является доказательство О.А. Ладыженской существования конечномерного глобального аттрактора для двумерных уравнений Навье–Стокса [110]. С точки зрения теории управления, в этом случае внутренние механизмы “регулирования” системы заставляют все траектории притягиваться к глобальному аттрактору. Первой книгой, посвященной аналитическим методам локализации глобальных аттракторов в конечномерных динамических системах, стала книга Г.А. Леонова и Ф. Райтманна, опубликованная на немецком языке в 1987 г. [111].

В общем случае глобальный аттрактор может содержать в себе несколько сосуществующих локальных аттракторов (самовозбуждающихся или скрытых аттракторов). Так, например, в знаменитой модели Лоренца [36] в зависимости от значений параметров глобальный аттрактор может содержать один или три локальных аттрактора: самовозбуждающийся хаотический аттрактор может сосуществовать с двумя тривиальными аттракторами (устойчивыми состояниями равновесия). В общем случае важной является задача определения всех сосуществующих локальных аттракторов [112]. Если самовозбуждающиеся аттракторы могут быть легко визуализированы в численных экспериментах траекториями с начальными данными из окрестности неустойчивых состояний равновесия (так и был открыт первый хаотический аттрактор Лоренца [36]), то поиск скрытых аттракторов требует специальных методов. Разработка и применение таких методов в рамках теории скрытых колебаний [39, 43] позволили впервые обнаружить скрытые аттракторы в известных физических моделях Рабиновича, Глуховского–Должанского, Рабиновича–Фабриканта и др. [42, 113–119].

Задачи управления состоянием системы и переводом состояния в область притяжения заданного аттрактора изучаются в кибернетической физике и в теории управления хаосом [120, 121]. Для модели Рёсслера [122] в форме системы Лурье (1.1) с

(5.1)
$P = \left( {\begin{array}{*{20}{c}} 0&{ - 1}&{ - 1} \\ 1&0&0 \\ 0&\alpha &{ - \beta } \end{array}} \right),\quad q = \left( {\begin{array}{*{20}{c}} 0 \\ 0 \\ { - a} \end{array}} \right),\quad r = \left( {\begin{array}{*{20}{c}} 0 \\ 1 \\ 0 \end{array}} \right),\quad f(\sigma ) = {{\sigma }^{2}},$
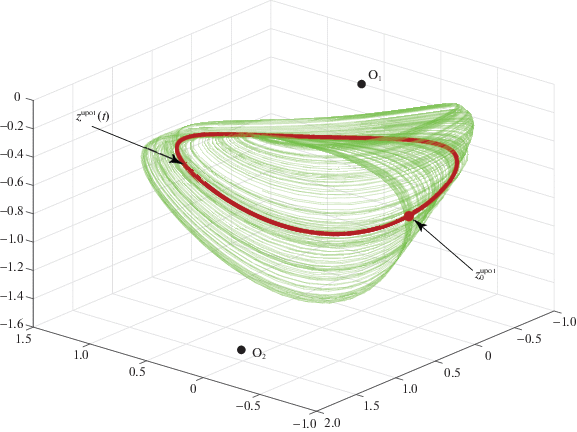
используя стабилизацию обратной связью с запаздыванием (метод Пирагаса):
(5.2)
$qf({{r}^{{\text{T}}}}z(t)) \to qf({{r}^{{\text{T}}}}z(t)) + 0.1r{{r}^{{\text{T}}}}(z(t - \tau ) - z(t)),$
удается [123, 124] (см. рис. 6) вычислить и стабилизировать неустойчивую периодическую траекторию c периодом T, встроенную в хаотический самовозбуждающийся аттрактор (для дискретных систем аналогичные идеи развиты, например, в [125]). Также в работах [126–129] представлены некоторые результаты в этих направлениях. Задачи выявления сложных колебательных режимов и скрытых аттракторов возникают в различных моделях децентрализованного и сетевого управления [113, 130–133]. Отметим, что стабилизация неустойчивых периодических траекторий позволила получать оценки снизу ляпуновской размерности и топологической энтропии в рамках изучения гипотезы Идена и различных ее уточнений [114, 124, 134–136], в том числе важных для задач оценивания интенсивности информационного обмена, необходимого и достаточного для наблюдения/стабилизации систем с нелинейной динамикой через каналы связи с ограниченной пропускной способностью [137].

Рис. 6.

Управление хаосом в модели Рёсслера с $\alpha = 0.386$, $\beta = 0.2$. Стабилизация и вычисление в модели (5.1) периодического колебания ${{z}^{{{\text{up}}{{{\text{o}}}_{1}}}}}(t) = {{z}^{{{\text{up}}{{{\text{o}}}_{1}}}}}(t,z_{0}^{{{\text{up}}{{{\text{o}}}_{1}}}})$ с начальными данными $z_{0}^{{{\text{up}}{{{\text{o}}}_{1}}}} \approx (0.9189,0.7152,0.5388)$ и периодом $\tau \approx 6.3245$, встроенного в самовозбуждающийся аттрактор, методом Пирагаса (стабилизации обратной связью с запаздыванием (5.2)). Конечно-временная ляпуновская размерность на траектории ${{z}^{{{\text{up}}{{{\text{o}}}_{1}}}}}(t,z_{0}^{{{\text{up}}{{{\text{o}}}_{1}}}})$ равна 2.3204 и на хаотической псевдотраектории $\tilde {z}(t,z_{0}^{{{\text{up}}{{{\text{o}}}_{1}}}})$, получаемой стандартным численным интегрированием модели (5.1) (без замены (5.2)) из точки $z_{0}^{{{\text{up}}{{{\text{o}}}_{1}}}}$ равна 2.2641; аналогичные значения для топологической энтропии: 0.1365 и 0.1035 соответственно

Отметим, что переход состояния системы из неустойчивого состояния равновесия при сколь угодно малом возмущении состояния системы к самовозбуждающемуся аттрактору (самопроизвольное возбуждение колебаний) соответствует мягкому режиму возбуждения колебаний, а переход из устойчивого состояния равновесия к скрытому аттрактору при некотором начальном отклонении состояния системы от состояния равновесия соответствует жесткому режиму возбуждения колебаний [7].

6. Трудности численного поиска скрытых колебаний и анализа устойчивости. Развитие концепции скрытых и самовозбуждающихся колебаний началось в научной школе Г.А. Леонова в 2008 г. в рамках исследования построений вложенных предельных циклов для двумерных полиномиальных систем в 16-й проблеме Гильберта. В ней внутренние вложенные циклы не “связаны” с состояниями равновесия и являются скрытыми колебаниями.

После работ А.А Андронова (со второй половины прошлого века) для изучения сценариев рождения колебаний и структурных изменений фазовых портретов динамических систем активно развивалась теория бифуркаций [138], которая позволила существенно продвинуться в исследовании сценариев потери устойчивости и рождения аттракторов, однако многие касающиеся этих вопросов известные задачи глобального анализа, в том числе 16-я проблема Гильберта, до сих пор остаются нерешенными и требуют дальнейшего развития теории и численных методов.

В середине прошлого века Н.Н. Баутин, развивая идеи А.А Андронова и Л.С. Понтрягина о грубости и структурной устойчивости систем [7, 139] и изучая опасные и безопасные границы линейной устойчивости, предложил метод теоретического построения систем с вложенными предельными циклами [140]. Однако метод Баутина, основанный на последовательных относительно малых возмущениях, позволял строить только вложенные циклы c очень малой амплитудой, которые не были видны в численных экспериментах [39, 141, 142]. В 2008 г. на защите автором этого обзора Ph.D. диссертации [74] в University of Jyväskylä (Финляндия) в рамках совместной российско-финской научно-образовательной программы и на пленарном докладе [143] международного семинара “Устойчивость и колебания нелинейных систем управления” им. Е.С. Пятницкого в Институте проблем управления РАН (Москва) обсуждались сложности вычисления таких малых предельных циклов: они оказываются “скрытыми” от стандартных вычислительных методов. Трудности выявления систем с предельными циклами и их вычисления хорошо иллюстрирует эксперимент А.Н. Колмогорова, описание которого приводит в своей книге В.И. Арнольд [144]: “Чтобы оценить число предельных циклов квадратичных векторных полей на плоскости, он раздал несколько сотен таких полей (со случайно выбранными коэффициентами многочленов второй степени) нескольким сотням студентов механико-математического факультета МГУ в качестве математического практикума. Каждый студент должен был найти число предельных циклов своего поля. Результат этого эксперимента был совершенно неожиданным: ни у одного поля не оказалось ни одного предельного цикла! При малом изменении коэффициентов поля предельный цикл сохраняется. Поэтому системы с одним, двумя, тремя (и даже, как стало известно позже, четырьмя) предельными циклами образуют в пространстве коэффициентов открытые множества, так что вероятности попасть в них при случайном выборе коэффициентов многочленов положительны.”

Создание специальных аналитико-численных процедур в теории скрытых колебаний для двумерных полиномиальных систем позволило в работах [39, 145] решить проблему Гильберта–Колмогорова: построить квадратичную систему и провести в ней визуализацию четырех предельных циклов (это наибольшее известное число сосуществующих циклов для двумерных квадратичных систем). Такие примеры с четырьмя предельными циклами являются контрпримерами к утверждению в известной работе И.Г. Петровского1818 и Е.М. Ландиса [146] о возможности существования только трех предельных циклов в двумерных полиномиальных квадратичных системах. Основные трудности численного анализа вложенных предельных циклов связаны с уплощением траекторий, бифуркациями слияния предельных циклов и рождения полуустойчивых циклов.

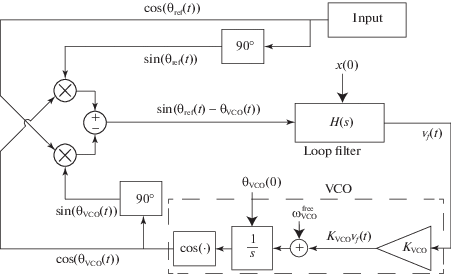
Трудности, связанные с наличием скрытых колебаний, возникают также при инженерном проектировании различных систем управления, например, классических систем управления фазовой синхронизацией (фазовой автоподстройки). Системы фазовой автоподстройки (ФАП, Phase-Locked Loop) были впервые использованы в начале прошлого века для подстройки фазы/частоты электрического сигнала локального генератора к входному сигналу (master-slave synchronization).

Важными инженерными характеристиками работы ФАП являются диапазоны разностей частот, для которых происходит подстройка генераторов, что соответствует устойчивости математических моделей ФАП в пространстве фаз сигналов, с требуемыми свойствами переходных процессов. Возможность эффективного нелинейного анализа математических моделей простейших систем ФАП была впервые показана в работе 1933 г. Ф. Трикоми [147], в которой исследовалось качественное поведение двумерных систем маятникового типа (описывающих динамику моделей ФАП и электрической машины при нагрузке) методом фазовой плоскости. Эти идеи затем развивались А.А. Андроновым и его последователями (см. [148–152] и др.). Так в 1956 г. М.В. Капрановым была опубликована работа, в которой он предполагал, что аналогично гипотезам Вышнеградского и Айзермана условия глобальной устойчивости двумерной модели ФАП в форме Лурье (1.1) с

(6.1)
$P = \left( {\begin{array}{*{20}{c}} {\frac{{ - 1}}{{{{\tau }_{1}} + {{\tau }_{2}}}}}&0 \\ {\frac{{ - {{K}_{{{\text{vco}}}}}{{\tau }_{2}}}}{{{{\tau }_{1}} + {{\tau }_{2}}}}}&0 \end{array}} \right),\quad q = \left( {\begin{array}{*{20}{c}} {\frac{1}{{{{\tau }_{1}} + {{\tau }_{2}}}}} \\ {\frac{{ - {{K}_{{{\text{vco}}}}}{{\tau }_{1}}}}{{{{\tau }_{1}} + {{\tau }_{2}}}}} \end{array}} \right),\quad r = \left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right),\quad f(\sigma ) = sin\sigma - \frac{{\omega _{e}^{{{\text{free}}}}}}{{{{K}_{{{\text{vco}}}}}}}$
определяются условиями отсутствия самовозбуждающихся колебаний [153] (тривиальная граница глобальной устойчивости, связанная с локальными бифуркациями потери устойчивости). Рассмотренная М.В. Капрановым модель описывает, например, динамику управления генератором в современной модели двухфазной ФАП [154] (см. рис. 7) относительно сдвинутого состояния фильтра и расфазировки $z(t) = (x(t) - ({{\tau }_{1}}\omega _{e}^{{{\text{free}}}}){\text{/}}K{\text{vco}}$, ${{\theta }_{{{\text{ref}}}}}(t) - {{\theta }_{{{\text{vco}}}}}(t))$ при постоянной частоте входного сигнала $\mathop {\dot {\theta }}\nolimits_{{\text{ref}}} (t) \equiv {{\omega }_{{{\text{ref}}}}}$, $\omega _{e}^{{{\text{free}}}} = {{\omega }_{{{\text{ref}}}}} - \omega _{{{\text{vco}}}}^{{{\text{free}}}}$ и передаточной функции фильтра H(s) = $(1 + {{\tau }_{1}}s){\text{/}}(1$ + (τ1 + τ2)s).

Рис. 7.

Система управление фазовой синхронизацией в двухфазной модели ФАП

Позднее гипотеза Капранова была опровергнута и были построены примеры, где условие потери глобальной устойчивости определялось нелокальным рождением скрытого колебания из уплощения траекторий [39, 149] (скрытая граница глобальной устойчивости, связанная с нелокальными бифуркациями). Отметим, что метод гармонического баланса не позволяет определить здесь точную границу устойчивости, предсказывая существование периодического решения внутри области глобальной устойчивости, и дает только консервативную оценку [155]. Так для модели (6.1) с ${{\tau }_{1}} = 0.0185$, ${{\tau }_{2}} = 0.0448$, ${{K}_{{{\text{vco}}}}} = 250$ оценка диапазона захвата (соответствующего притяжению всех траекторий к стационарному множеству), получаемая методом построения периодической функции Ляпунова: $\omega _{e}^{{{\text{free}}}} \in [0,126.3)$, а методом анализа рождения скрытого колебания: $\omega _{e}^{{{\text{free}}}} \in [0,178.1)$. При этом численная оценка диапазона быстрого захвата без проскальзывания циклов (проблема Ф. Гарднера): $\omega _{e}^{{{\text{free}}}} \in [0,101.5)$.

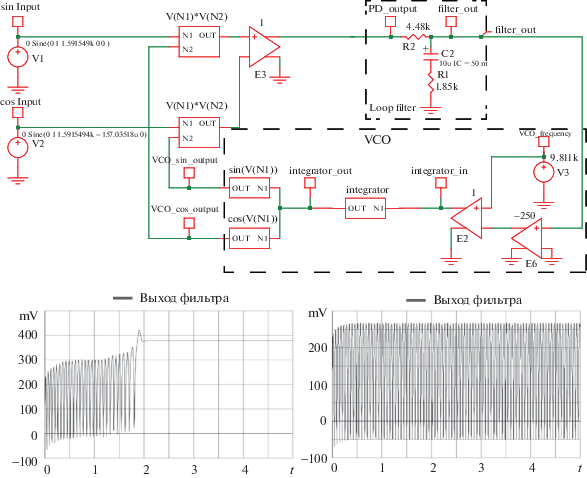
В работах [156–159] были реализованы специальные примеры моделирования систем ФАП в пакетах проектирования SPICE1919. Данные примеры демонстрируют трудности достоверного численного анализа ФАП при наличии скрытых колебаний (см. рис. 8), а также могут использоваться для валидации инженерных пакетов проектирования ФАП. Эта задача была поставлена известным американским инженером С. Голдманом (Texas Instruments, США) [160].

Рис. 8.

Пример моделирования в SIMetrix (SPICE) двухфазной системы ФАП: ${{\tau }_{1}} = {\text{R}}1{\text{C}}2 = 1.85 \times {{10}^{{ - 2}}}$, ${{\tau }_{2}} = {\text{R}}2{\text{C}}2 = 4.48 \times {{10}^{{ - 2}}}$, $\omega _{{{\text{vco}}}}^{{{\text{free}}}} = 2\pi 9.811 \times {{10}^{3}}$, ${{\omega }_{{{\text{ref}}}}} = 2\pi 1.5915494 \times {{10}^{3}}$, ${{K}_{{{\text{vco}}}}}$ = 250, x(0) = 0.5, ${{\theta }_{{{\text{vco}}}}}(0) = 0$ со скрытым аттрактором, ограничивающим область притяжения рабочего режима. При шаге дискретизации, установленном по умолчанию равным “10 m”, моделирование показывает достижение синхронного режима работы – управляющий сигнал ${{v}_{f}}(t)$ стабилизируется (нижний левый график); для уменьшенного шага дискретизации “1 m” при тех же начальных данных моделирование показывает режим биения и отсутствия синхронизации (нижний правый график)

Трудности численного анализа скрытых колебаний показали необходимость разработки и применения аналитических критериев устойчивости систем управления и отсутствия скрытых колебаний. Для систем фазовой автоподстройки такие математические методы нелинейного анализа были разработаны Г.А. Леоновым2020 и его учениками [161–165]. В этих работах были преодолены трудности, связанные с анализом многомерных моделей ФАП, и обобщены классические результаты теории управления на системы с периодическими непрерывными и разрывными нелинейностями в цилиндрическом фазовом пространстве (также аналогичные модели и трудности возникают при исследовании систем управления угловой ориентацией [166]). Так, например, критерии глобальной устойчивости Барбашина–Красовского и Ла-Салля требуют неограниченного возрастания функций Ляпунова по всем координатам, в то время как в цилиндрическом фазовом пространстве рассматриваются изменение фазы на периоде и периодические функции Ляпунова [167]. Эти принципиальные математические различия часто не принимаются во внимание на практике (см., например, [168]), что может приводить к неверным выводам.

В настоящее время различные схемы ФАП реализуются в виде компактных электронных схем и программных алгоритмов и получили широкое распространение в современном телекоммуникационном оборудовании, распределенных компьютерных архитектурах, глобальных навигационных системах (GPS, ГЛОНАСС), энергетике и электрических сетях, а также многих других приложениях [169–172]. Достаточно отметить, что синтезаторы частот, использующиеся в каждом современном компьютере, имеют в своей конструкции такие системы управления фазовой синхронизацией. В последние годы в связи с существенным повышением частот генераторов и требований к переходным режимам, а также развитием цифровых систем передачи данных на основе ФАП потребовалось и было реализовано [156, 173–183] дальнейшее развитие новых математических методов анализа и синтеза математических моделей систем управления фазовой синхронизацией.

Заключение. Данный обзор посвящен теории скрытых колебаний и ее актуальным приложениям, таким, как задача Андронова–Вышнеградского о нелинейном анализе центробежного регулятора паровой машины задача Келдыша о нелинейном анализе систем подавления флаттера, гипотезы Айзермана и Калмана об абсолютной устойчивости систем управления в форме Лурье, цепи Чуа, эффект Зоммерфельда застревания частоты, проблема Гильберта–Колмогорова, системы управления фазовой синхронизацией и гипотеза Капранова, выявление скрытых колебаний в динамических моделях буровых установок и систем управления летательными аппаратами.

Быстрое развитие современной вычислительной техники сделало легкодоступным математическое моделирование и численный анализ динамики и привело к созданию большого числа специализированных пакетов моделирования. Однако оказалось, что возможности таких пакетов и стандартных численных методов часто ограничены, а их применение может существенно искажать характеристики реальной динамики и приводить к неверным качественным выводам об устойчивости и колебательных режимах.

Для проведения достоверного математического моделирования технических систем важно обращать особое внимание на строгий вывод используемых математических моделей и учет границ их применимости, разработку эффективных аналитико-численных методов исследования динамики, учитывающих возможности и ограничения существующих аналитических методов исследования устойчивости и возникновения колебаний. Самовозбуждение колебаний может быть эффективно обнаружено аналитически и численно. Анализ же скрытых колебаний (их отсутствия или наличия и расположения) требует разработки специальных аналитико-численных методов и является ключевым для определения точных границ глобальной устойчивости, анализа зазора между необходимыми и достаточными условиями глобальной устойчивости и их сближения, а также выделения классов систем управления, для которых эти условия совпадают. На практике переход состояния системы управления к скрытому аттрактору, вызванный внешними возмущениями, приводит к нежелательным режимам работы и часто оказывается причиной аварий и катастроф.

Теория скрытых колебаний является современным этапом развития теории колебаний А.А. Андронова. Она востребована во многих теоретических и актуальных инженерных задачах, в которых скрытые аттракторы (их отсутствие или наличие и расположение) играют важную роль, и, в том числе, позволяет решать задачи устойчивости систем управления. За последние годы теория скрытых колебаний привлекла большое внимание мирового научного сообщества. В 2016 г. первые публикации по этой тематике вошли в 1% самых цитируемых статей базы Web of Science и стали наиболее цитируемыми статьями журнала [39] и переводной версии журнала [41]. В одном из престижных журналов – Physics Reports (A Review Section of Physics Letters) была опубликована обзорная статья по скрытым колебаниям, подготовленная специалистами из России совместно с коллегами из Польши, Ирана и Индии [113]. Задачами выявления скрытых аттракторов и определения границ устойчивости систем управления в настоящее время занимаются большое число ученых в разных странах.

Получение представленных в обзоре результатов было бы невозможно без подготовки и участия молодых специалистов Кафедры прикладной кибернетики Санкт-Петербургского государственного университета, коллектив которой неоднократно признавался Ведущей научной школой РФ2121. За последние годы более 10 диссертаций по теории скрытых колебаний были защищены на кафедре под руководством Г.А. Леонова и автора данного обзора, и многие из их учеников продолжают свою работу на кафедре: http://apcyb.spbu.ru/.

Материал этого обзора обсуждался на заседании Бюро Отделения энергетики, машиностроения, механики и процессов управления РАН (03.03.20)2222, семинарах акад. В.М. Фомина (ИТПМ СО РАН, 23.10.19), акад. Ф.Л. Черноусько (ИПМех РАН, 18.04.19), президента IFAC F. Allgöwer (Institute for System theory and Automatic Control, Stuttgart, 07.02.19), акад. Н.Ф. Морозова (ИПМаш РАН, 14.05.18) – всем участникам которых автор выражает искреннюю благодарность за интерес, жаркие обсуждения и ценные замечания. Также материалы данного обзора по теории скрытых колебаний и устойчивости систем управления были представлены и обсуждались на обзорных и пленарных докладах ряда ведущих российских и международных конференций, в том числе конференций Международной федерации автоматического регулирования (IFAC) [45–47, 184–188].

Список литературы

  1. Denny M. Watt Steam Governor Stability // European J. of Physics. 2002. V. 23 (3). P. 339–351.

  2. Вышнеградский И.А. О регуляторах прямого действия // Изв. Санкт-Петербургского технологического ин-та. 1877. Т. 1. С. 21–62.

  3. Léauté M.H. Mémoire sur les Oscillations à Longue Période Dans les Machines Actionnées par des Moteurs Hydrauliques et sur les Moyens de Prévenir ces Oscillations // J. de l’êcole Polytechnique. 1885. V. 55. P. 1–126.

  4. Жуковский Н.Е. Теория регулирования хода машин. Ч. 1. М.: Типо-литография Товарищества И.Н. Кушнерев и Ко., 1909.

  5. Ляпунов А.М. Общая задача об устойчивости движения. Харьков: Типография Зильберта. Издание Харьковского математического общества, 1892.

  6. Poincare H. Mémoire sur les courbes définies par une équations différentielle (II) // J. de Mathématiques. 1882. V. 8. P. 251–296.

  7. Андронов А.А., Хайкин С.Э. Теория колебаний. М.–Л.: ОНТИ, 1937.

  8. Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний. 2-е изд. М.: Физматлит, 1959.

  9. Rocard Y. Théorie des Oscillateurs. Paris: Revue scientifique, 1941.

  10. Цыпкин Я.З. А.А. Андронов и теория автоматического управления // АиТ. 1974. Т. 5. С. 5–10.

  11. Bissel C. A.A. Andronov and the Development of Soviet Control Engineering // IEEE Control Systems Magazine. 1998. V. 18. P. 56–62.

  12. Андронов А.А., Майер А.Г. Задача Мизеса в теории прямого регулирования и теория точечных преобразований поверхностей // Докл. АН СССР. 1944. Т. 43 (2). С. 58–60.

  13. Андронов А.А., Майер А.Г. Задача Вышнеградского в теории прямого регулирования // Докл. АН СССР. 1945. Т. 47 (5). С. 345–348.

  14. Академики, избранные Общим собранием АН СССР 30 ноября 1946 года // Вестн. АН СССР. 1947. Т. 1. С. 83.

  15. Гелиг А.Х. Об устойчивости движения систем с неединственным положением равновесия // Докл. АН СССР. 1962. Т. 147 (3). С. 526–528.

  16. Леонов Г.А. Об устойчивости нелинейных регулируемых систем с неединственным положением равновесия // АиТ. 1971. Т. 10. С. 23–28.

  17. Гелиг А.Х., Леонов Г.А., Якубович В.А. Устойчивость нелинейных систем с неединственным состоянием равновесия. М.: Наука, 1978.

  18. Леонов Г.А., Кузнецов Н.В., Киселева М.А., Мокаев Р.Н. Глобальные задачи дифференциальных включений: проблемы Калмана и Вышнеградского, цепи Чуа // Дифференциальные уравнения и процессы управления. 2017. Т. 4. С. 1–52.

  19. Фортов В.Е., Федоров М.П. Авария на Саяно-Шушенской ГЭС и научно-техническое сопровождение ее восстановления // Заседание Президиума Российской академии наук / 29.06.2010. http://www.ras.ru/FStorage/Download.aspx?id431c54-8c18-42c4-aeff-6dfc9ea18aa4.

  20. Ганиев Р.Ф. Нелинейные резонансы и катастрофы. Надежность, безопасность и бесшумность. М., Ижевск: РХД, 2013.

  21. Leonov G.A., Kuznetsov N.V., Solovyeva E.P. A Simple Dynamical Model of Hydropower Plant: Stability and Oscillations // IFAC-PapersOnLine. 2015. V. 48 (11). P. 656–661.

  22. Леонов Г.А., Кузнецов Н.В., Соловьева Е.П. Математическое моделирование вибраций в турбогенераторах Саяно-Шушенской ГЭС // ДАН. 2016. Т. 466 (6). С. 654–659.

  23. Журавлев В.Ф., Климов Д.М. О некоторых задачах динамики твердого тела с сухим трением // Вестн. Нижегородского ун-та им. Н.И. Лобачевского. 2011. Т. 4–2. С. 133–134.

  24. Горячева И.Г. Механика фрикционного взаимодействия. М.: Наука, 2001.

  25. Колесников В.И., Иваночкин П.Г., Челохьян А.В., Луговой Е.А. Трение и изнашивание узлов машин и механизмов. Ростов-на-Дону: Ростовский государственный ун-т путей сообщения, 2000.

  26. Федосов Е.А., Колесников К.С., Себряков Г.Г. Машиностроение, энциклопедия. Т. 1–4. Автоматическое управление. М.: Машиностроение, 2000.

  27. Васильев С.Н., Жерлов А.К., Федосов Е.А., Федунов Б.Е. Интеллектное управление динамическими системами. М.: Физматлит, 2000.

  28. Черноусько Ф.Л., Ананьевский И.М., Решмин С.А. Методы управления нелинейными механическими системами. М.: Физматлит, 2006.

  29. Деменков Н.П., Микрин Е.А. Управление в технических системах. М.: МГТУ им. Н.Э. Баумана, 2017.

  30. Utkin V., Guldner J., Shi J. Sliding Mode Control in Electro-Mechanical Systems. Boca Raton: CRC Press, 2017.

  31. Андриевский Б.Р., Бобцов А.А., Фрадков А.Л. Методы анализа и синтеза нелинейных систем управления. М.–Ижевск: ИКИ, 2018.

  32. Поляк Б.Т., Хлебников М.В., Рапопорт Л.Б. Математическая теория автоматического управления. М.: ЛЕНАНД, 2019.

  33. Новиков Д.А. Теория управления (дополнительные главы). М.: ЛЕНАНД, 2019.

  34. Kurzhanski A.B., Daryin A.N. Dynamic Programming for Impulse Feedback and Fast Controls: The Linear Systems Case. London: Springer, 2020.

  35. Мандельштам Л.И., Папалекси Н.Д. О явлениях резонанса n-го рода // Журн. техн. физики. 1932. Т. 2. С. 775–811.

  36. Lorenz E.N. Deterministic Nonperiodic Flow // J. Atmos. Sci. 1963. V. 20 . P. 130–141.

  37. Ueda Y., Akamatsu N., Hayashi C. Computer Simulations and Non-Periodic Oscillations // Trans. IEICE Japan. 1973. V. 56A (4). P. 218–255.

  38. Matsumoto T., Chua L., Komuro M. The Double Scroll // IEEE Transactions on Circuits and Systems. 1985. V. 32 (8). P. 797–818.

  39. Leonov G.A., Kuznetsov N.V. Hidden Attractors in Dynamical Systems. From Hidden Oscillations in Hilbert-Kolmogorov, Aizerman, and Kalman Problems to Hidden Chaotic Attractors in Chua Circuits // Intern. J. of Bifurcation and Chaos in Applied Sciences and Engineering. 2013. V. 23(1). Art. no. 1330002.

  40. Kuznetsov N.V., Leonov G.A., Vagaitsev V.I. Analytical-numerical Method for Attractor Localization of Generalized Chua’s System // IFAC Proceedings Volumes. 2010. V. 43 (11). P. 29–33.

  41. Брагин В.О., Вагайцев В.И., Кузнецов Н.В., Леонов Г.А. Алгоритмы поиска скрытых колебаний в нелинейных системах. Проблемы Айзермана, Калмана и цепи Чуа // Изв. РАН. ТиСУ. 2011. Т. 4. С. 3–36.

  42. Leonov G.A., Kuznetsov N.V., Mokaev T.N. Homoclinic Orbits, and Self-excited and Hidden Attractors in a Lorenz-like System Describing Convective Fluid Motion // The European Physical J. Special Topics. 2015. V. 224. P. 1421–1458.

  43. Кузнецов Н.В. Аналитико-численные методы анализа скрытых колебаний: Дис. докт. физ.-мат. наук. Отзывы: И.М. Буркин, Н.Г. Кузнецов, Г.А. Леонов, Е.А. Микрин, В.Г. Пешехонов, Р.М. Юсупов, В.И. Некоркин и А.М. Сергеев – ведущая организация, ИПФ РАН. Санкт-Петербургский гос. ун-т. 2016.

  44. Barkhausen H. Textbook of Electron Tubes and their Technical Applications. German: S. Hirzel, 1935.

  45. Kuznetsov N.V. Plenary lecture “Theory of Hidden Oscillations” // 11th Russian Multiconference on Control Problems. St. Petersburg, 2018.

  46. Kuznetsov N.V. Plenary lecture “Theory of Hidden Oscillations” // 5th IFAC Conference on Analysis and Control of Chaotic Systems. Eindhoven, 2018.

  47. Кузнецов Н.В. Теория скрытых колебаний // Тр. XIII Всероссийск. совещ. по проблемам управления ВСПУ-2019. М.: ИПУ, 2019. С. 103–107.

  48. Лурье А.И., Постников В.Н. К теории устойчивости регулируемых систем // ПММ. 1944. Т. 8. № 3. С. 246–248.

  49. Барбашин Е.А., Красовский Н.Н. Об устойчивости движения в целом // Докл. АН СССР. 1952. Т. 86 (3). С. 453–459.

  50. Kalman R.E. Physical and Mathematical Mechanisms of Instability in Nonlinear Automatic Control Systems // Transactions of ASME. 1957. V. 79 (3). P. 553–566.

  51. Leonov G.A., Ponomarenko D.V., Smirnova V.B. Frequency-Domain Methods for Nonlinear Analysis. Theory and Applications. Singapore: World Scientific, 1996.

  52. Барабанов Н.Е. О проблеме Калмана // Сиб. мат. журн. 1988. Т. XXIX. С. 3–11.

  53. Heath W.P., Carrasco J., de la Sen M. Second-order Counterexamples to the Discrete-time Kalman Conjecture // Automatica. 2015. V. 60. P. 140–144.

  54. Kuznetsov N.V., Kuznetsova O.A., Koznov D.V., Mokaev R.N., Andrievsky B.R. Counterexamples to the Kalman Conjectures. IFAC-PapersOnLine. 2018. V. 51 (33). P. 138–143.

  55. Kuznetsov N.V., Kuznetsova O.A., Mokaev T.N., Mokaev R.N., Yuldashev M.V., Yuldashev R.V. Coexistence of Hidden Attractors and Multistability in Counterexamples to the Kalman Conjecture // IFAC-PapersOnLine. 2019. V. 52 (16). P. 7–12.

  56. Филиппов А.Ф. Дифференциальные уравнения с разрывной правой частью. М.: Наука, 1985.

  57. Айзерман М.А., Пятницкий Е.С. Основы теории разрывных систем. I // АиТ. 1974. Т. 7. С. 33–47.

  58. Айзерман М.А. Об одной проблеме, касающейся устойчивости в “большом” динамических систем // УМН. 1949. Т. 4. С. 187–188.

  59. Плисс В.А. Некоторые проблемы теории устойчивости движения. Л.: Изд-во ЛГУ, 1958.

  60. Красовский Н.Н. Теоремы об устойчивости движений, определяемых системой двух уравнений // ПММ. 1952. Т. 16 (5). С. 547–554.

  61. Markus L., Yamabe H. Global Stability Criteria for Differential Systems // Osaka Math. J. 1960. V. 12. P. 305–317.

  62. Meisters G. A Biography of the Markus-Yamabe Conjecture // http://www.math.unl.edu/ gmeisters1/papers/HK1996.pdf. 1996.

  63. Van der Pol B. On Relaxation-oscillations // Philosophical Magazine and J. of Science. 1926. V. 7. P. 978–992.

  64. Крылов Н.М., Боголюбов Н.Н. Введение в нелинейную механику. Киев: Изд-во АН УССР, 1937.

  65. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. М.: Физматлит, 1966.

  66. Khalil H.K. Nonlinear Systems. N.J.: Prentice Hall, 2002.

  67. Леонов Г.А., Кузнецов Н.В. Алгоритмы поиска скрытых колебаний в проблемах Айзермана и Калмана // ДАН. 2011. Т. 439 (2). С. 167–173.

  68. Barabanov N.E., Gelig A.Kh., Leonov G.A., Likhtarnikov A.L., Matveev A.S., Smirnova V.B., Fradkov A.L. The Frequency Theorem (the Yakubovich–Kalman Lemma) in Control Theory // Automatic Remote Control. 1996. V. 10 (9). P. 3–40.

  69. Цыпкин Я.З. Теория релейных систем автоматического регулирования. М.: Гостехиздат, 1955.

  70. Kuznetsov N.V., Mokaev R.N., Akimova E.D., Boiko I.M. Harmonic balance method, Tsypkin locus, and LPRS: comparison and counterexamples // Proc. of European Control Conf. St. Petersburg, 2020. P. 781–786.

  71. Леонов Г.А., Брагин В.О., Кузнецов Н.В. Алгоритм построения контрпримеров к проблеме Калмана // ДАН. 2010. Т. 433 (2). С. 163–166.

  72. Кузнецов Н.В., Леонов Г.А. Контрпример Перрона в дискретном случае // Изв. РАЕН. Дифференц. уравнения. 2001. Т. 5. С. 71.

  73. Leonov G.A., Kuznetsov N.V. Time-varying Linearization and the Perron Effects // Intern. J. Bifurcation and Chaos in Applied Sciences and Engineering. 2007. V. 17 (4). P. 1079–1107.

  74. Kuznetsov N.V. Stability and Oscillations of Dynamical Systems: Theory and Applications. Jyväskylä: Jyväskylä University Printing House, 2008.

  75. Kuznetsov N.V., Leonov G.A. Strange Attractors and Classical Stability Theory: Stability, Instability, Lyapunov Exponents and Chaos // Handbook of Applications of Chaos Theory / Eds Ch.H. Skiadas, C. Skiadas. Chapman and Hall/CRC, 2016. P. 105–134.

  76. Perron O. Die Stabilitatsfrage bei Differentialgleichungen // Mathematische Zeitschrift. 1930. V. 32 (5). P. 702–728.

  77. Келдыш М.В. О демпферах с нелинейной характеристикой // Тр. ЦАГИ. 1944. Т. 557. С. 26–37.

  78. Leonov G.A., Kuznetsov N.V. On the Keldysh Problem of Flutter Suppression // AIP Conf. Proceedings. 2018. V. 1959 (1). Art. num. 020002.

  79. Леонов Г.А., Кузнецов Н.В. О подавлении флаттера в модели Келдыша // ДАН. 2011. Т. 428 (1). С. 33–37.

  80. Kudryashova E.V., Kuznetsov N.V., Kuznetsova O.A., Leonov G.A., Mokaev R.N. Harmonic Balance Method and Stability of Discontinuous Systems // Dynamics and Control of Advanced Structures and Machines / Eds. V.P. Matveenko, M. Krommer, A. Belyaev, H. Irschik. Switzerland: Springer Nature, 2019. P. 99–107.

  81. Бюшгенс Г.С., Чернышев С.Л., Гоман М.Г. и др. Аэродинамика, устойчивость и управляемость сверхзвуковых самолетов. М.: Наука, 2016.

  82. Погосян М.А. Проектирование самолетов. М.: Инновационное машиностроение, 2008.

  83. Lauvdal T., Murray R.M., Fossen T.I. Stabilization of Integrator Chains in the Presence of Magnitude and Rate Saturations: a Gain Scheduling Approach // IEEE Control and Decision Conference. San Diego, 1997. V. 4. P. 4404–4005.

  84. Чернышев С.Л. Пленарный доклад ”Современные проблемы авиастроения в прикладных задачах аэрогидромеханики”// Междунар. научн. конф. по механике “VIII Поляховские чтения”. Санкт-Петербург, 2018. https://events.spbu.ru/eventsContent/events/2018/polyakhov/tsagi.pdf.

  85. Андриевский Б.Р., Кузнецов Н.В., Леонов Г.А. Методы подавления нелинейных колебаний в астатических системах автопилотирования летательных аппаратов // Изв. РАН. ТиСУ. 2017. Т. 3. С. 105–121.

  86. Леонов Г.А., Андриевский Б.Р., Кузнецов Н.В., Погромский А.Ю. Управление летательными аппаратами с AW-коррекцией // Дифференциальные уравнения и процессы управления. 2012. Т. 3. С. 1–36.

  87. Леонов Г.А., Кузнецов Н.В., Погромский А.Ю. Анализ области устойчивости системы управления с антивиндап для неустойчивого объекта // ДАН. 2012. Т. 445 (1). С. 28–31.

  88. Andrievsky B.R., Kuznetsov N.V., Leonov G.A., Pogromsky A.Yu. Hidden Oscillations in Aircraft Flight Control System with Input Saturation // IFAC Proceedings Volumes. 2013. V. 46 (12). P. 75–79.

  89. Andrievsky B.R., Kudryashova E.V., Kuznetsov N.V., Kuznetsova O.A. Aircraft wing rock oscillations suppression by simple adaptive control // Aerospace Science and Technology. 2020. https://doi.org/10.1016/j.ast.2020.106049

  90. Chua L.O. A Zoo of Strange Attractors from the Canonical Chua’s Circuits // Proc. IEEE 35th Midwest Sympos. on Circuits and Systems (Cat. No.92CH3099-9). Washington, 1992. V. 2. P. 916–926.

  91. Bilotta E., Pantano P. A Gallery of Chua Attractors. Singapore: World Scientific, 2008.

  92. Leonov G.A., Kuznetsov N.V. Plenary Lecture “Localization of Hidden Oscillations in Dynamical Systems” // 4th Int. Sci. Conf. on Physics and Control, Catania, 2009. http://www.math.spbu.ru/user/leonov/publications/2009-PhysCon-Leonov-plenary-hidden-oscillations.pdf#page!.

  93. Леонов Г.А., Вагайцев В.И., Кузнецов Н.В. Алгоритм локализации аттракторов Чуа на основе метода гармонической линеаризации // ДАН. 2010. Т. 433 (3). С. 323–326.

  94. Kuznetsov N.V., Kuznetsova O.A., Leonov G.A., Vagaytsev V.I. Hidden attractor in Chua’s circuits // ICINCO 2011 – Proc. of the 8th Intern. Conf. Informatics in Control, Automation and Robotics. 2011. V. 1. P. 279–283.

  95. Leonov G.A., Kuznetsov N.V., Vagaitsev V.I. Localization of Hidden Chua’s Attractors // Physics Letters A. 2011. V. 375 (23). P. 2230–2233.

  96. Kuznetsov N.V., Kuznetsova O.A., Leonov G.A., Mokaev T.N., Stankevich N.V. Hidden Attractors Localization in Chua Circuit via the Describing Function Method // IFAC-PapersOnLine. 2017. V. 50 (1). P. 2651–2656.

  97. Stankevich N.V., Kuznetsov N.V., Leonov G.A., Chua L. Scenario of the Birth of Hidden Attractors in the Chua Circuit // Intern. J. Bifurcation and Chaos in Applied Sciences and Engineering. 2017. V. 27 (12). Art. num. 1730038.

  98. Kuznetsov N.V., Leonov G.A. Hidden Attractors in Dynamical Systems: Systems with no Equilibria, Multistability and Coexisting Attractors // IFAC Proceedings Volumes (19th IFAC World Congress). 2014. V. 47. P. 5445–5454.

  99. Kiseleva M.A., Kudryashova E.V., Kuznetsov N.V., Kuznetsova O.A., Leonov G.A., Yuldashev M.V., Yuldashev R.V. Hidden and Self-excited Attractors in Chua Circuit: Synchronization and SPICE Simulation // Intern. J. Parallel, Emergent and Distributed Systems. 2018. V. 33 (5). P. 513–523.

  100. Sommerfeld A. Beitrage zum Dynamischen Ausbau der Festigkeitslehre // Zeitschrift des Vereins deutscher Ingenieure. 1902. V. 46. P. 391–394.

  101. Блехман И.И. Самосинхронизация вибраторов некоторых вибрационных машин // Инж. сб. 1953. Т. 16. С. 49–72.

  102. Kiseleva M.A., Kuznetsov N.V., Leonov G.A. Hidden Attractors in Electromechanical Systems with and without Equilibria // IFAC-PapersOnLine. 2016. V. 49 (14). P. 51–55.

  103. Kiseleva M., Kondratyeva N., Kuznetsov N., Leonov G. Hidden Oscillations in Electromechanical Systems // Dynamics and Control of Advanced Structures and Machines / Eds H. Irschik, A. Belyaev, M. Krommer. Cham: Springer, 2018. P. 119–124.

  104. Blekhman I.I., Indeitsev D.A., Fradkov A.L. Slow Motions in Systems with Inertially Excited Vibrations // IFAC Proceedings Volumes. 2007. V. 40 (14). P. 126–131.

  105. Fradkov A., Tomchina O., Tomchin D. Controlled Passage Through Resonance in Mechanical Systems // J. Sound and Vibration. 2011. V. 330 (6). P. 1065–1073.

  106. Mihajlovic N., van Veggel A.A., van de Wouw N., Nijmeijer H. Analysis of Friction-induced Limit Cycling in an Experimental Drill-string System // J. Dyn. Syst. Meas. Control. 2004. V. 126 (4). P. 709–720.

  107. Leonov G.A., Kuznetsov N.V., Kiseleva M.A., Solovyeva E.P., Zaretskiy A.M. Hidden Oscillations in Mathematical Model of Drilling System Actuated by Induction Motor with a Wound Rotor // Nonlinear Dynamics. 2014. V. 77 (1–2). P. 277–288.

  108. Kiseleva M.A., Kondratyeva N.V., Kuznetsov N.V., Leonov G.A., Solovyeva E.P. Hidden Periodic Oscillations in Drilling System Driven by Induction Motor // IFAC Proceedings Volumes. 2014. V. 47 (19). P. 5872–5877.

  109. Kiseleva M.A., Kondratyeva N.V., Kuznetsov N.V., Leonov G.A. Hidden Oscillations in Drilling Systems with Salient Pole Synchronous Motor // IFAC-PapersOnLine. 2015. V. 48 (11). P. 700–705.

  110. Ладыженская О.А. О нахождении минимальных глобальных аттракторов для уравнений Навье–Стокса и других уравнений с частными производными // УМН. 1987. Т. 42 (6). С. 25–60.

  111. Leonov G.A., Reitmann V. Attraktoreingrenzung für Nichtlineare Systeme. Stuttgart-Leipzig: Teubner, 1987.

  112. Leonov G.A., Kuznetsov N.V. On Differences and Similarities in the Analysis of Lorenz, Chen, and Lu Systems // Applied Mathematics and Computation. 2015. V. 256. P. 334–343.

  113. Dudkowski D., Jafari S., Kapitaniak T., Kuznetsov N.V., Leonov G.A., Prasad A. Hidden Attractors in Dynamical Systems // Physics Reports. 2016. V. 637. P. 1–50.

  114. Kuznetsov N.V., Leonov G.A., Mokaev T.N., Prasad A., Shrimali M.D. Finite-time Lyapunov Dimension and Hidden Attractor of the Rabinovich System // Nonlinear Dynamics. 2018. V. 92. P. 267–285.

  115. Chen G., Kuznetsov N.V., Leonov G.A., Mokaev T.N. Hidden Attractors on One Path: Glukhovsky-Dolzhansky, Lorenz, and Rabinovich Systems // Intern. J. Bifurcation and Chaos in Applied Sciences and Engineering. 2017. V. 27 (8). Art. num. 1750115.

  116. Leonov G.A., Kuznetsov N.V., Vagaitsev V.I. Hidden Attractor in Smooth Chua Systems // Physica D: Nonlinear Phenomena. 2012. V. 241 (18). P. 1482–1486.

  117. Danca M.-F., Kuznetsov N.V. Hidden Chaotic Sets in a Hopfield Neural System // Chaos, Solitons & Fractals. 2017. V. 103. P. 144–150.

  118. Danca M.-F., Kuznetsov N., Chen G. Unusual Dynamics and Hidden Attractors of the Rabinovich–Fabrikant System // Nonlinear Dynamics. 2017. V. 88. P. 791–805.

  119. Leonov G.A., Kuznetsov N.V., Mokaev T.N. Hidden Attractor and Homoclinic Orbit in Lorenz-like System Describing Convective Fluid Motion in Rotating Cavity // Communications in Nonlinear Science and Numerical Simulation. 2015. V. 28. P. 166–174.

  120. Fradkov A.L., Evans R.J. Control of Chaos: Methods and Applications in Engineering // Annual Reviews in Control. 2005. V. 29(1). P. 33–56.

  121. Фрадков А.Л. Кибернетическая физика: принципы и примеры. СПб.: Наука, 2003.

  122. Rössler O.E. Continuous Chaos – Four Prototype Equations // Annals of the New York Academy of Sciences. 1979. V. 316. P. 376–392.

  123. Kuznetsov N.V., Mokaev T.N. Numerical Analysis of Dynamical Systems: Unstable Periodic Orbits, Hidden Transient Chaotic Sets, Hidden Attractors, and Finite-time Lyapunov Dimension // J. Physics: Conf. Series. 2019. V. 1205 (1). Art. num. 012034.

  124. Kuznetsov N.V., Mokaev T.N., Kudryashova E.V., Kuznetsova O.A., Danca M.-F. On Lower-bound Estimates of the Lyapunov Dimension and Topological Entropy for the Rossler Systems // IFAC-PapersOnLine. 2019. V. 52 (18). P. 97–102.

  125. Поляк Б.Т. Стабилизация хаоса с помощью прогнозирующего управления // АиТ. 2005. Т. 11. С. 99–112.

  126. Sharma P.R., Shrimali M.D., Prasad A., Kuznetsov N.V., Leonov G.A. Control of Multistability in Hidden Attractors // The European Physical J. Special Topics. 2015. V. 224. P. 1485–1491.

  127. Sharma P.R., Shrimali M.D., Prasad A., Kuznetsov N.V., Leonov G.A. Controlling Dynamics of Hidden Attractors // Intern. J. Bifurcation and Chaos in Applied Sciences and Engineering. 2015. V. 25 (04). Art. num. 1550061.

  128. Leonov G.A., Shumafov M.M., Kuznetsov N.V. Delayed Feedback Stabilization of Unstable Equilibria // IFAC Proceedings Volumes (IFAC-PapersOnline). 2014. V. 19. P. 6818–6825.

  129. Leonov G.A., Shumafov M.M., Kuznetsov N.V. Delayed Feedback Stabilization and the Huijberts–Michiels–Nijmeijer problem // Differential Equations. 2016. V. 52(13). P. 1707–1731.

  130. Leonov G.A., Adan I., Andrievsky B.R., Kuznetsov N.V., Pogromsky A.Yu. Plenary lecture “Nonlinear Problems in Control of Manufacturing Systems”// IFAC Proceedings Volumes. 2013. V. 46 (9). P. 33–42.

  131. Андриевский Б.Р., Кузнецов Н.В., Леонов Г.А., Погромский А.Ю. Распределенное управление нелинейной производственной системой // Мехатроника, автоматизация, управление. 2014. Т. 5. С. 13–25.

  132. Фрадков А.Л. (ред.) Проблемы сетевого управления. М.–Ижевск: ИКИ, 2015.

  133. Dudkowski D., Kuznetsov N.V., Mokaev T.N. Chimera States and Hidden Attractors // Physics of Life Reviews. 2019. V. 28. P. 131–133.

  134. Kuznetsov N.V. The Lyapunov Dimension and its Estimation via the Leonov Method // Physics Letters A. 2016. V. 380 (25–26). P. 2142–2149.

  135. Kuznetsov N.V., Alexeeva T.A., Leonov G.A. Invariance of Lyapunov Exponents and Lyapunov Dimension for Regular and Irregular Linearizations // Nonlinear Dynamics. 2016. V. 85 (1.1). P. 195–201.

  136. Kuznetsov N.V., Reitmann V. Attractor Dimension Estimates for Dynamical Systems: Theory and Computation (Dedicated to Gennady Leonov). Cham: Springer, 2021.

  137. Matveev A.S., Pogromsky A.Yu. Observation of Nonlinear Systems via Finite Capacity Channels. Pt. II. Restoration Entropy and its Estimates // Automatica. 2019. V. 103. P. 189–199.

  138. Арнольд В.И., Афраймович В.С., Ильяшенко Ю.С., Шильников Л.П. Теория бифуркаций. М.: ВИНИТИ, 1986.

  139. Андронов A.A., Понтрягин Л.С. Грубые системы // Докл. АН СССР. 1937. Т. 14 (5). С. 247–250.

  140. Баутин Н.Н. О числе предельных циклов, появляющихся при изменении коэффициентов из состояния равновесия типа фокуса или центра // Мат. сб. 1952. Т. 30(72). С. 181–196.

  141. Kuznetsov N.V., Leonov G.A. Lyapunov Quantities, Limit Cycles and Strange Behavior of Trajectories in Two-dimensional Quadratic Systems // J. Vibroengineering. 2008. V. 10 (4). P. 460–467.

  142. Леонов Г.А., Кузнецов Н.В., Кудряшова Е.В. Прямой метод вычисления ляпуновских величин двумерных динамических систем // Тр. Института математики и механики УрО РАН. 2010. Т. 16 (1). С. 119–126.

  143. Leonov G.A., Kuznetsov N.V., Kudryashova E.V. Plenary Lecture “Local Methods for Dynamic System Cycle Investigation” // E.S. Pyatnitskiy X Intern. Workshop Stability and Oscillations of Nonlinear Control Systems. Moscow, 2008.

  144. Арнольд В.И. Экспериментальная математика. М.: ФАЗИС, 2005.

  145. Kuznetsov N.V., Kuznetsova O.A., Leonov G.A. Visualization of Four Normal Size Limit Cycles in Two-dimensional Polynomial Quadratic System // Differential Equations and Dynamical Systems. 2013. V. 21 (1–2). P. 29–34.

  146. Петровский И.Г., Ландис Е.М. О числе предельных циклов уравнения dy/dx=P(x,y)/Q(x,у), где Р и Q многочлены второй степени // Мат. сб. 1955. Т. 37 (79). С. 209–250.

  147. Tricomi F. Integrazione di Differeziale Presentasi in Electrotechnica // Annali della Roma Schuola Normale Superiore de Pisa. 1933. V. 2. P. 1–20.

  148. Барбашин Е.А., Табуева В.А. Динамические системы с цилиндрическим фазовым пространством. М.: Наука, 1969.

  149. Белюстина Л.Н., Быков В.В., Кивелева К.Г., Шалфеев В.Д. О величине полосы захвата системы ФАПЧ с пропорционально-интегрирующим фильтром // Изв. вузов. Радиофизика. 1970. Т. 13 (4). С. 561–567.

  150. Шахтарин Б.И. Анализ систем синхронизации методом усреднения. М.: Радио и связь, 1999.

  151. Матросов В.В., Шалфеев В.Д. Нелинейная динамика систем фазовой синхронизации. Н. Новгород: Изд-во Нижегородского ун-та, 2013.

  152. Aleksandrov K.D., Kuznetsov N.V., Leonov G.A., Neittaanmaki N., Yuldashev M.V., Yuldashev R.V. Computation of the Lock-in Ranges of Phase-locked Loops with PI Filter // IFAC-PapersOnLine. 2016. V. 49 (14). P. 36–41.

  153. Капранов М.В. Полоса захвата при фазовой автоподстройке частоты // Радиотехника. 1956. Т. 11 (12). С. 37–52.

  154. Best R.E., Kuznetsov N.V., Leonov G.A., Yuldashev M.V., Yuldashev R.V. Discontinuity and Complexity in Nonlinear Physical Systems. V. 6 // Chapter Nonlinear Analysis of Phase-locked Loop Based Circuits Cham: Springer, 2014. P. 169–192.

  155. Kudryashova E.V., Kuznetsov N.V., Leonov G.A., Yuldashev M.V., Yuldashev R.V. Nonlinear Analysis of PLL by the Harmonic Balance Method: Limitations of the Pull-in Range Estimation // IFAC-PapersOnLine. 2017. V. 50 (1). P. 1451–1456.

  156. Leonov G.A., Kuznetsov N.V., Yuldashev M.V., Yuldashev R.V. Hold-in, Pull-in, and Lock-in Ranges of PLL Circuits: Rigorous Mathematical Definitions and Limitations of Classical Theory // IEEE Trans. on Circuits and Systems–I: Regular Papers. 2015. V. 62 (10). P. 2454–2464.

  157. Leonov G.A., Kuznetsov N.V., Yuldashev M.V., Yuldashev R.V. Hidden Attractors in Dynamical Models of Phase-locked Loop Circuits: Limitations of Simulation in MATLAB and SPICE // Commun Nonlinear Sci Numer Simulat. 2017. V. 51. P. 39–49.

  158. Bianchi G., Kuznetsov N.V., Leonov G.A., Yuldashev M.V., Yuldashev R.V. Limitations of PLL Simulation: Hidden Oscillations in MATLAB and SPICE // Intern. Congr. on Ultra Modern Telecommunications and Control Systems and Workshops (ICUMT 2015). Brno, 2016. P. 79–84.

  159. Bianchi G., Kuznetsov N.V., Leonov G.A., Seledzhi S.M., Yuldashev M.V., Yuldashev R.V. Hidden Oscillations in SPICE Simulation of Two-phase Costas Loop with Non-linear VCO // IFAC-PapersOnLine. 2016. V. 49 (14). P. 45–50.

  160. Goldman S.J. Phase-Locked Loops Engineering Handbook for Integrated Circuits. Boston: Artech House, 2007.

  161. Leonov G.A., Reitmann V., Smirnova V.B. Nonlocal Methods for Pendulum-like Feedback Systems. Stuttgart-Leipzig: Teubner Verlagsgesselschaft, 1992.

  162. Leonov G.A., Burkin I.M., Shepelyavy A.I. Frequency Methods in Oscillation Theory. Dordretch: Kluwer, 1996.

  163. Леонов Г.А., Селеджи С.М. Системы фазовой синхронизации в аналоговой и цифровой схемотехнике. СПб.: Невский диалект, 2002.

  164. Leonov G.A., Kuznetsov N.V., Seledzhi S.M. Automation Control – Theory and Practice// Chapter Nonlinear Analysis and Design of Phase-Locked Loops. London: In-Tech, 2009. P. 89–114.

  165. Leonov G.A., Kuznetsov N.V. Nonlinear Mathematical Models of Phase-Locked Loops. Stability and Oscillations. Cottenham: Cambridge Scientific Publishers, 2014.

  166. Кузнецов Н.В. Развитие теории устойчивости для дифференциальных включений в работах Г.А. Леонова и ее применение для анализа устойчивости систем угловой ориентации // Королевские чтения. М., 2019.

  167. Kuznetsov N.V., Lobachev M.Y., Yuldashev M.V., Yuldashev R.V., Kudryashova E.V., Kuznetsova O.A., Rosenwasser E.N., Abramovich S.M. The Birth of the Global Stability Theory and the Theory of Hidden Oscillations // Proc. of European Control Conf. St. Petersburg, 2020. P. 769–774.

  168. Abramovitch D. Analysis and Design of a Third Order Phase-Lock Loop // 21st Century Military Communications – What’s Possible? Conf. Record. Military Communications Conf. San Diego, 1988. P. 455–459.

  169. Желтов С.Ю., Веремеенко К.К., Ким Н.В., Козорез Д.А., Красильщиков М.Н., Себряков Г.Г., Сыпало К.И., Черноморский А.И. Современные информационные технологии в задачах навигации и наведения беспилотных маневренных летательных аппаратов. М.: Физматлит, 2009.

  170. Kaplan E.D., Hegarty C.J. Understanding GPS: Principles and Applications. Boston: Artech House, 2006.

  171. Каляев И.А., Левин И.И., Семерников Е.А., Шмойлов В.И. Реконфигурируемые мультиконвейерные вычислительные структуры Ростов-на-Дону: ЮНЦ РАН, 2008.

  172. Вольский С.И., Кузнецов Н.В., Сорокин Д.А., Юлдашев М.В., Юлдашев Р.В. Выбор частоты выходного напряжения магнитоэлектрического генератора системы электроснабжения самолетов с электрической тягой // Междунар. научн. конф. по электротехническим комплексам и системам. Уфа, 2020. http://www.icoecs.com/.

  173. Leonov G.A., Kuznetsov N.V., Yuldashev M.V., Yuldashev R.V. Analytical Method for Computation of Phase-detector Characteristic // IEEE Trans. on Circuits and Systems - II: Express Briefs. 2012. V. 59 (10). P. 633–647.

  174. Leonov G.A., Kuznetsov N.V., Yuldashev M.V., Yuldashev R.V. Nonlinear Dynamical Model of Costas Loop and an Approach to the Analysis of its Stability in the Large // Signal Processing. 2015. V. 108. P. 124–135.

  175. Best R.E., Kuznetsov N.V., Leonov G.A., Yuldashev M.V., Yuldashev R.V. Simulation of Analog Costas Loop Circuits // Intern. J. Automation and Computing. 2014. V. 11 (6). P. 571–579.

  176. Best R.E., Kuznetsov N.V., Kuznetsova O.A. et al. A Short Survey on Nonlinear Models of the Classic Costas Loop: Rigorous Derivation and Limitations of the Classic Analysis // Proc. American Control Conf. IEEE. Chicago, 2015. P. 1296–1302. Art. num. 7170912.

  177. Леонов Г.А., Кузнецов Н.В., Юлдашев М.В., Юлдашев Р.В. Характеристика фазового детектора классической системы фазовой автоподстройки частоты // ДАН. 2015. Т. 461 (2). С. 151–154.

  178. Леонов Г.А., Кузнецов Н.В., Юлдашев М.В., Юлдашев Р.В. Математические модели схемы Костаса // ДАН. 2015. Т. 464 (6). С. 660–664.

  179. еонов Г.А., Кузнецов Н.В., Юлдашев М.В., Юлдашев Р.В. Вычисление характеристики фазового детектора для схемы Костаса с квадратурной фазовой манипуляцией // ДАН. 2016. Т. 468 (6). С. 624–629

  180. Kuznetsov N.V., Yuldashev M.V., Yuldashev R.V., Blagov M.V., Kudryashova E.V., Kuznetsova O.A., Mokaev T.N. Comments on van Paemel’s Mathematical Model of Charge-pump Phase-locked Loop // Differencialnie Uravnenia i Protsesy Upravlenia (Differential Equations and Control Processes). 2019. V. 1. P. 109–120. https://diffjournal.spbu.ru/pdf/19107-jdecp-kuznetsov.pdf

  181. Best R.E., Kuznetsov N.V., Leonov G.A., Yuldashev M.V., Yuldashev R.V. Tutorial on Dynamic Analysis of the Costas Loop // IFAC Annual Reviews in Control. 2016. V. 42. P. 27–49.

  182. Kuznetsov N.V., Kuznetsova O.A., Leonov G.A., Yuldashev M.V., Yuldashev R.V. A Short Survey on Nonlinear Models of QPSK Costas Loop // IFAC-PapersOnLine. 2017. V. 50 (1). P. 6525–6533.

  183. Кузнецов Н.В., Лобачев М.Ю., Юлдашев М.В., Юлдашев Р.В. О проблеме Гарднера для систем управления фазовой автоподстройкой частоты // ДАН. 2019. Т. 489 (6). С. 541–544.

  184. Leonov G.A., Kuznetsov N.V. Analytical-Numerical Methods for Investigation of Hidden Oscillations in Nonlinear Control Systems // IFAC Proceedings Volumes (18th IFAC World Congress). 2011. V. 44 (1). P. 2494–2505.

  185. Kuznetsov N.V. Plenary lecture “Hidden Attractors in Fundamental Problems and Engineering Models. A short survey”// Lecture Notes in Electrical Engineering (Conference on Advanced Engineering Theory and Applications). 2016. V. 371. P. 13–25.

  186. Kuznetsov N.V. Plenary lecture “Theory of Hidden Oscillations and Stability of Control Systems”// Intern. Conf. “Stability, Control, Differential Games” Devoted to the 95th Anniversary of Academician N.N. Krasovskii. Yekaterinburg, 2019. P. 201–204.

  187. Кузнецов Н.В. Приглашенный секционный доклад “Теория скрытых колебаний и устойчивость систем управления” (https://www.youtube.com/watch?v=843m-rI5nTM) // XII Всероссийский съезд по фундаментальным проблемам теоретической и прикладной механики: сб. трудов. Т. 1. Уфа, 2019. С. 46–48.

  188. Кузнецов Н.В. Пленарный доклад “Управление колебаниями в системах фазовой автоподстройки частоты” // 12-я мультиконф. по проблемам управления. Дивноморское, 2019. Т. 3. С. 21–26.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Теория и системы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал