Известия РАН. Теория и системы управления, 2020, № 5, стр. 60-72
ОПТИМИЗАЦИЯ ВСТРАИВАНИЯ КРИПТОГРАФИЧЕСКИХ КЛЮЧЕЙ В БИОМЕТРИЧЕСКИЕ ДАННЫЕ
Э. Т. Зайнулина a, *, И. А. Матвеев b, **
a МФТИ
МО, Долгопрудный, Россия
b Федеральный исследовательский центр “Информатика и управление” РАН
Москва, Россия
* E-mail: zaynulina.et@phystech.edu
** E-mail: matveev@ccas.ru
Поступила в редакцию 06.04.2020
После доработки 20.04.2020
Принята к публикации 25.05.2020
Аннотация
Двумя важными компонентами современных систем контроля и управления доступом являются криптография и биометрия. Криптографические системы сами по себе высоконадежны, но требуют точного воспроизведения ключей доступа, что человек не в состоянии сделать самостоятельно, а соответствующие устройства могут быть утеряны или похищены. Биометрические данные у человека всегда при себе, но они изменчивы: невозможно повторно получить те же значения признаков. В работе предлагается способ объединения криптографического ключа и биометрических признаков радужной оболочки глаза. При этом получается ключ, из которого нельзя извлечь ни одну из двух исходных компонент, пока не будут предъявлены близкие к исходным биометрические признаки, т.е. данные того же человека. Метод объединения (кодер) и извлечения (декодер) состоят из нескольких отдельных последовательно исполняемых шагов. Подбор параметров осуществляется с помощью решения задачи дискретной оптимизации, состоящей в том, чтобы при некотором заданном пороге коэффициента ложного допуска минимизировать значение коэффициента ложного отказа в допуске. При этом есть ограничения в виде минимального размера кодируемого ключа и максимального размера итогового ключа. Проведены численные эксперименты на базах данных, находящихся в открытом доступе.
Введение. В настоящее время повсеместно применяется защита информации, основанная на криптографических алгоритмах. Таких алгоритмов, равно как и способов их применения, изобретено большое количество [1]. Здесь мы ограничимся случаем симметричного шифрования, при котором на этапе кодирования из сообщения $M$ и секретного ключа $K$ функцией-кодером $\Phi $ вычисляется код $C = \Phi (M,K)$, а на этапе декодирования функция-декодер $\Psi $ восстанавливает сообщение: $M = \Psi (C,K)$. Из кода $C$ без ключа $K$ невозможно получить M, поэтому $C$ будет открытым, не секретным. Cвойством симметричного шифрования является то, что используемый ключ $K$ должен быть повторен совершенно точно, например, в случае двоичной последовательности должны совпадать все ее биты. Острая проблема при этом состоит в том, что такие ключи легко отчуждаются (передаются, похищаются, теряются). Столь же насущная проблема – слабая способность человека запоминать парольные последовательности. Если придуманный лично им пароль человек в состоянии запомнить и воспроизвести (хотя уже здесь появляются трудности), то для автоматически сгенерированной последовательности из нескольких десятков псевдослучайных символов это практически невозможно [2].
В то же время человек располагает легко извлекаемыми, сложно отчуждаемыми и имеющими значительный информационный объем биометрическими признаками. Речь идет прежде всего о радужной оболочке глаза (РОГ) [3] и, в меньшей степени, об изображениях лица [4], отпечатках пальцев [5], подписи [6]. Биометрия редко утрачивается, сложно подделывается, легко предъявляется при наличии специального оборудования. Недостатком биометрических признаков в данном приложении является их изменчивость: невозможно в точности повторить результаты измерения, можно лишь утверждать, что два набора признаков, полученные от одного человека, в некотором смысле различаются слабее,чем наборы, взятые от разных людей.
Представляет большой интерес объединение двух подходов, т.е. разработка методов точного воспроизведения (генерации) криптографического ключа из биометрических признаков, или замаскированного добавления существующего ключа к таким признакам, или иных методов и сценариев связывания строго определенных и имеющих необходимые статистические свойства данных, пригодных к использованию в криптографических протоколах, с наборами изменчивых биометрических признаков.
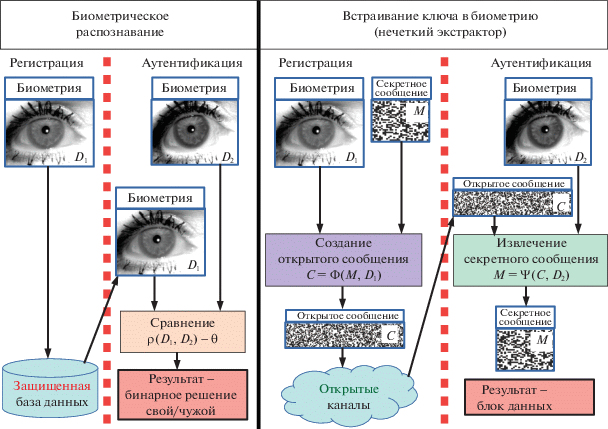
1. Выбор метода встраивания ключа в биометрию. Автоматическая биометрия уже достаточно долго используется для идентификации (поиска) и аутентификации (подтверждения) личности человека. Центральную задачу, решаемую такими системами, можно сформулировать как задачу создания оптимального классификатора: необходимо построить функцию расстояния между двумя наборами биометрических данных $\rho ({{D}_{1}},{{D}_{2}})$ и задать порог $\theta $ так, что как можно большее число пар ${{D}_{1}}$ и ${{D}_{2}}$, принадлежащих одному человеку, дает расстояние $\rho ({{D}_{1}},{{D}_{2}}) < \theta $, а как можно большее число от разных людей дает $\rho ({{D}_{1}},{{D}_{2}}) > \theta $. Функцию $\rho $ можно представить как суперпозицию двух этапов: вычисление биометрического эталона T по данным $T = T(D)$, т.е. выделение признаков, устойчиво близких для одного человека и различающихся для разных людей, и расчет собственно расстояния $\rho ({{T}_{1}},{{T}_{2}})$. Эталон T представляет собой набор данных размером от нескольких сотен байт до нескольких килобайт, хотя элементы этих данных (в отличие от криптографических ключей) сильно коррелированы. Тем не менее, информационная емкость (энтропия) биометрического эталона сравнима или превосходит таковую для используемых в настоящее время криптографических ключей [7]. Например, для РОГ существует оценка в 249 степеней свободы [8], для отпечатка пальца разработана система, выделяющая 80 некоррелированных параметров [9]. Это дает основания считать, что возможно внедрить криптографический ключ в биометрию, не снизив его стойкости.
Следует отметить, что основное количество работ, посвященных применению криптографических методов в биометрии, развивают схему отменяемой биометрии (cancelable biometrics) [10]. Суть ее состоит в преобразовании биометрических данных в формат, из которого их нельзя извлечь в исходном виде, но в котором их можно сравнивать в системе распознавания. Отменяемая биометрия – ни что иное как разновидность нечеткого хеширования [11], что можно формально представить как введение дополнительного шага в расчет функции расстояния $\rho $. В этой схеме вычисляется $\rho ({{H}_{1}},{{H}_{2}})$ (в некоторых вариантах $\rho ({{H}_{1}},{{T}_{2}})$), где $H$ – хэш-функция биометрического эталона $H = H(T)$. Очевидно, что по-прежнему решается задача распознавания.
Существует два подхода к тому, каким образом обрабатывать изменчивую биометрию, приводя ее к неизменному криптографическому ключу. В первом используются уже вычисленные биометрические признаки, которые исправляются различными вариантами избыточного кодирования с коррекцией ошибок. В русле данного подхода сделана и эта работа. Во втором подходе, развиваемом отечественными исследователями [12], биометрические признаки явно не вычисляются, вместо этого на “сырых” биометрических данных тренируется нейросеть, обучаемая выдавать тот или иной код [13]. Преимуществом этого подхода называется меньшая избыточность кодирования за счет использования на всех этапах непрерывных данных и квантования только в конце. Недостатки – непредсказуемость обучения нейросети, отсутствие гарантированного качества работы, в том числе отсутствие гарантии того, что результаты сохранят качество при работе с большим разнообразнем данных, чем использовалось при обучении.
Задача воспроизведения криптографического ключа решается биометрическими криптосистемами (biometric crypto system) [10], которые делятся на два класса, реализующих разные схемы работы: генерации ключа (key generation) и встраивания ключа (key binding).
В [14, 15] исследовались методы прямой генерации ключа из биометрических данных без использования какой-либо дополнительной информации. В этом случае при регистрации и распознавании вычисляется одна и та же функция, отображающая многообразие биометрических данных в пространство криптографических ключей (как правило, битовых строк): K(D): $D \to \mathop {\{ 0,1\} }\nolimits^n $, где n – битовая длина ключа. При этом должны выполняться условия
(1.1)
$\begin{gathered} {{D}_{1}},{{D}_{2}}\; - \;{\text{данные}}\;{\text{одного}}\;{\text{человека}}\;\; \Rightarrow \;\;{{K}_{1}} = {{K}_{2}}, \\ {{D}_{1}},{{D}_{2}}\; - \;{\text{данные}}\;{\text{разных}}\;{\text{людей}}\;\; \Rightarrow \;\;{{K}_{1}} \ne {{K}_{2}}, \\ \end{gathered} $Лучшие показатели имеет схема с использованием вспомогательного кода (helper code). В этом случае при регистрации кроме криптографического ключа ${{K}_{1}} = K({{D}_{1}})$, который применяется для шифрования сообщения M и немедленно после этого уничтожается, при помощи кодера вычисляется вспомогательный код $h = \Phi ({{D}_{1}})$. Он обладает следующими свойствами: (1) исходные данные D1 из него восстановить невозможно; (2) при предъявлении биометрии D2 с помощью декодера можно вычислить ключ ${{K}_{2}} = \Psi ({{D}_{2}},h)$, который удовлетворяет условиям (1.1). Таким образом, предъявив вспомогательный код h и биометрию, пользователь может получить ключ K1, а значит, и сообщение M, зашифрованное этим ключом при регистрации. Нарушитель, даже зная $h$, не сможет получить ${{K}_{1}}$ [17].
Если в качестве ключа использовать сами данные ${{K}_{1}} = {{D}_{1}}$, то восстанавливается исходная биометрия. Такая схема называется защищенным оттиском (secure sketch) [18]. С помощью вспомогательного кода можно работать даже с весьма изменчивыми биометрическими данными. Однако имеющиеся в печати работы показывают довольно скромные результаты. Например, в [19] делается предположение о внутриклассовой изменчивости в 10% признаков, хотя на практике она составляет больше 20%, что приводит к неработоспособности предлагаемого метода.
Схема встраивания ключа в заданных выше терминах выглядит как совокупность функций кодера $C = \Phi ({{K}_{1}},{{D}_{1}})$, декодера ${{K}_{2}} = \Psi (C,{{D}_{2}})$, удовлетворяющих условию (1.1). Ключ K1 задается извне, что является преимуществом, поскольку не нужно учитывать природу алгоритма шифрования. С этой точки зрения ключ K1 можно воспринимать как внешнее по отношению к системе кодирования сообщение M, что немедленно приводит к сценарию, сходному с симметричным шифрованием. Отличие состоит в том, что в симметричном шифровании секретный ключ $K$ не должен изменяться, а биометрические признаки (тоже секретные) отличаются при кодировании и декодировании: ${{D}_{1}} \ne {{D}_{2}}$. Такая схема называется нечетким экстрактором (fuzzy extractor) [18]. Схемы биометрической идентификации и нечеткого экстрактора приведены на рис. 1.
Если биометрические данные представляют собой набор действительных чисел $D \in {{\mathbb{R}}^{d}}$, а функции $\Phi $ и $\Psi $ обратны друг другу: $K = \Psi \left( {\Phi (K,D),D} \right)$, то полученная схема называется экранирующими функциями (shielding functions) [20]. В современных системах регистрации и распознавания РОГ признаками являются целые числа или даже биты, поэтому использование экранирующих функций затруднено.
Очень популярное направление развития схемы встраивания ключа – нечеткое хранилище (fuzzy vault) [7]. Данный подход по сути есть приложение схемы разделения секрета Шамира [21]. При этом получены достаточно низкие, имеющие практический смысл значения ошибок: в [22] при нулевом FAR достигнуто значение ${\text{FRR}} = 0.78\% $, в [23] ${\text{FRR}} = 4.8\% $. Однако каждый из этих результатов показан на одной небольшой (меньше 1000 изображений) базе.
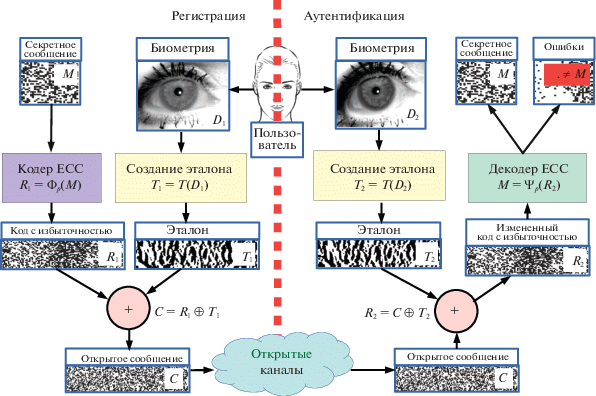
Наиболее перспективной для использования в системах биометрии РОГ является схема нечеткого связывания (fuzzy commitment) [24]. Для радужки можно построить простой метод, описанный в [25]. Эталон радужки в большинстве систем распознавания представляет собой битовое изображение (растр) определенных размеров, как правило, это $N = 256 * 8 = 2048$ бит, каждый бит – локальный признак, обычно знак свертки с фильтром в данной точке. Основой сравнения таких эталонов является нормированное расстояние Хэмминга – доля несовпадающих бит:
(1.2)
$\rho ({{T}_{1}},{{T}_{2}}) = \frac{1}{N}\sum\limits_{i = 1}^N \,{{T}_{1}}(i) \oplus {{T}_{2}}(i).$Если расстояние меньше некоторого порога p, который устанавливается разработчиками системы, то эталоны ${{T}_{1}}$ и ${{T}_{2}}$ признаются принадлежащими одному человеку.
Основная идея [25] состоит в использовании кодирования, исправляющего ошибки (error correcting code, ECC) [26]. Схема кодирования состоит из пары функций: кодера $R = {{\Phi }_{p}}(M)$, отображающего сообщение в больший по размеру код с избыточностью $R$, и декодера $M = {{\Psi }_{p}}(R)$, где p – доля ошибок в коде $R$, которая может быть исправлена декодером. Секретное сообщение M кодируется, причем вероятность “ошибки передачи данных” устанавливается равной порогу классификации. Код ${{R}_{1}} = {{\Phi }_{p}}(M)$ (в общем случае представляющий собой псевдослучайные числа) побитово складывается по модулю $2$ (исключающее или) с эталоном радужки $C = {{R}_{1}} \oplus {{T}_{1}}$. После вычисления C эталон и секретное сообщение уничтожаются. Полученные данные C также имеют вид случайных, из них нельзя извлечь ни эталон радужки ${{T}_{1}}$, ни сообщение M, их допустимо передавать по незащищенным каналам. Для декодирования регистрируется радужка и формируется новый эталон ${{T}_{2}}$, который, конечно, не совпадает с исходным. Однако если эталоны ${{T}_{1}}$ и ${{T}_{2}}$ принадлежат одному человеку, то они близки в смысле расстояния (1.2): $\rho ({{T}_{1}},{{T}_{2}}) \leqslant p$. Можно записать ${{R}_{2}} = C \oplus {{T}_{2}}$ $ = ({{R}_{1}} \oplus {{T}_{1}}) \oplus {{T}_{2}}$, откуда ${{R}_{1}} \oplus {{R}_{2}} = {{T}_{1}} \oplus {{T}_{2}}$, значит, справедливо $\rho ({{R}_{1}},{{R}_{2}}) \leqslant p$ и можно восстановить секретное сообщение $M = {{\Psi }_{p}}({{R}_{2}})$. Схема работы показана на рис. 2. Интересным развитием этого метода представляется обобщение операции сложения по модулю 2 до более широкого класса операторов поиска различия [27, 28].
В [25] используется каскад двух алгоритмов помехоустойчивого кодирования: Рида–Соломона [29] и Адамара [26]. Кодирование Рида–Соломона обрабатывает весь блок данных длины L, трактуя его как последовательность из L/s s-битовых символов, при этом любые как угодно расположенные символы (не биты!) могут отличаться, если их количество не больше pL. Это кодирование предназначено для того, чтобы компенсировать групповые ошибки, возникающие из-за наличия различных затенений (ресниц, бликов), закрывающих значительные области радужки. Кодирование Адамара исполняется для малых групп данных (несколько бит), и исправляет не более 25% ошибок в каждой группе. Другими словами, ошибки (различия эталонов ${{T}_{1}}$ и ${{T}_{2}}$) должны быть распределены равномерно по эталону с плотностью не выше 25%. Это кодирование предназначено для борьбы с точечными различиями, вызываемыми шумом камеры. Сообщение $M$ кодируется последовательно сначала кодом Рида–Соломона, потом результат – кодом Адамара.
Однако данный каскад алгоритмов может использоваться лишь, если доля различающихся бит в эталонах одного человека не превышает 25%. На реальных базах данных и в приложениях это не так, и такое ограничение приводит к неприемлемо высокой (более 50%) ошибке первого рода. Для преодоления этого затруднения в [30] дополнительно вводится маскирование эталона: каждый четвертый бит эталонов РОГ устанавливается в 0. За счет этого доля различающихся бит в эталонах одного человека снижается до 20%. Критика этого метода, с точки зрения неустойчивости ко взлому, приведена в [31]. Атака осуществляется путем постепенного восстановления исходного эталона (приближения к нему).
В данной работе предпринята попытка доработать схему [25] более разумным образом и построить практически пригодный метод встраивания ключа. На основе системы выделения признаков РОГ проведены численные эксперименты на нескольких открытых базах изображений, определено пороговое расстояние Хэмминга. Вводятся дополнительные два шага: простое мажоритарное кодирование и псевдослучайное перемешивание. Параметры полученных четырех последовательных шагов кодера (и соответствующих им шагов декодера) подбираются решением дискретной оптимизационной задачи.
2. Определение пороговой вероятности. Алгоритм биометрического распознавания можно разбить на функцию выделения признаков (построения эталона) $T = T(D)$ и функцию сравнения эталонов $\rho ({{T}_{1}},{{T}_{2}})$. Биометрические системы распознавания прошли большой путь и достигли очень хороших показателей точности классификации (малых значений ошибок), в том числе за счет оптимизации методов выделения признаков. Поэтому обосновано использование признаков, получаемых имеющимися методами. В работе применялось выделение области радужки на изображении [32] и вычисление признаков РОГ [33], которые в совокупности реализуют функцию $T = T(D)$.
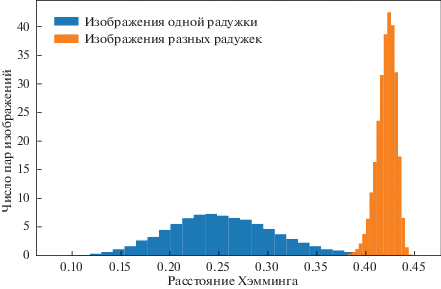
Согласно развиваемой в работе разновидности нечеткого экстрактора, предложенной в [25], для сравнения используется расстояние Хэмминга (1.2). В этой схеме если биометрический эталон ${{T}_{1}}$, использованный при регистрации, и предъявляемый эталон ${{T}_{2}}$ находятся на расстоянии меньше порога $p$, то зашифрованное сообщение $M$ восстанавливается, иначе – нет. Другими словами, порог $p$ разделяет “своих” и “нарушителей”. На рис. 3 показана типичная картина распределения сравнений по расстоянию $\rho ({{T}_{1}},{{T}_{2}})$. Левая группа соответствует случаю, когда ${{T}_{1}}$ и ${{T}_{2}}$ получены регистрацией одной радужки (“свои”). При этом исключены сравнения эталона с собой (дающие нулевое расстояние), как не встречающиеся на практике. Правая группа соответсвует случаю, когда ${{T}_{1}}$ и ${{T}_{2}}$ получены с разных радужек (“нарушители”). Необходимо определить величину порога.
Для экспериментов использованы базы данных (БД), находящиеся в открытом доступе: CASIA-4-Thousand [16], BATH [34], подмножество ICE базы NDIRIS [35], UBIRIS-1 [36]. Кроме того также участвовали базы изображений, собранных авторами [32, 33] на устройствах регистрации РОГ Panasonic BM-ET300 [37], LG IrisAccess-3000 [38] и Iritech Irishield MK2120U [39].
В табл. 1 приведен список семи использованных БД. Для каждой даны их собственные параметры (количество индивидуальных радужек и количество изображений) и значение порога, при котором ошибка второго рода равна 10–4, что соответствует вероятности угадать четырехзначный пин-код банкомата. Из таблицы видно, что, взяв порог $\theta = 0.35$, можно добиться того, чтобы, предъявив чужую биометрию, получить доступ к секрету лишь с вероятностью, меньшей 10–4.
Таблица 1.
Характеристики баз данных и пороги
| БД | Количество | θ при FAR = 10–4 | FAR при θ = 0.35, ×10–4 | FRR при θ = 0.35, ×10–2 | |
|---|---|---|---|---|---|
| радужек | изображений | ||||
| BATH | 1600 | 31 988 | 0.402 | 0.03 | 4.46 |
| CASIA | 2000 | 20 000 | 0.351 | 0.97 | 6.71 |
| ICE | 242 | 2953 | 0.395 | 0.011 | 7.13 |
| Iritech | 426 | 22 954 | 0.356 | 0.79 | 3.88 |
| LG | 265 | 2864 | 0.386 | 0.07 | 2.36 |
| Panasonic | 277 | 2890 | 0.389 | 0.2 | 4.74 |
| UBIRIS | 240 | 1207 | 0.401 | 0.001 | 5.18 |
Таким образом, значение $\theta = 0.35$ далее используется как базовое, т.е. трактуется как вероятность ошибки, которую должен исправлять код. В табл. 1 также приведены значения вероятностей ошибок первого и второго рода для этого порога. Очевидно, вероятность ошибки второго рода лишь убывает на каждой из баз и тем сильнее, чем собственное значение порога при FAR = 10–4 отличается от 0.35. При этом максимальное значение ошибки первого рода не превышает 8%.
3. Описание методов. Описывать применяемые методы будем в последовательности их исполнения декодером, что также соответствует переходу “от простого к сложному”, так как вначале единицей данных является один бит, а в конце – все сообщение.
Итак, необходимо сконструировать код, восстанавливающий исходное сообщение из блока данных, каждый бит которых может быть изменен со средней вероятностью не более $p = 0.35$. Во-первых, это значение существенно больше $p = 0.25$, являющегося пороговым для возможности применения популярных методов Уолша–Адамара или Рида–Мюллера [40]. Во-вторых, возникновение этих ошибок нельзя считать независимым. Напротив, ошибки в близких элементах сильно коррелированы (возникают блоками).
3.1. Декоррелирование псевдослучайным перемешиванием. Проектировать методы, исправляющие коррелированные ошибки, значительно труднее, и их показатели хуже, чем для случая некоррелированных ошибок. Значительная часть усилий в этом случае направлена именно на декорреляцию. В рассматриваемой системе весь блок данных доступен целиком (а не последовательно, как во многих системах, работающих с каналами передачи) и можно применить простой метод декорреляции – псевдослучайное перемешивание битов эталона радужки. Если ко всем эталонам применяется одинаковое перемешивание, то расстояние Хэмминга не изменяется и сохраняются все конструкции, основанные на нем. Но при этом соседние биты последовательностей, используемых в кодах на следующих этапах, берутся уже из разнесенных пикселей эталона и ошибки в них независимы.
3.2. Битовое мажоритарное кодирование. Уровень ошибок $p = 0.35$ слишком высок для большинства корректирующих кодов. Практически единственной возможностью здесь остается мажоритарное кодирование отдельных битов, исправляющее до 50% ошибок. При кодировании значение бита повторяется $n$ раз, при декодировании подсчитывается сумма принятых $n$ бит, и если она меньше n/2, то принимается значение 0, иначе 1. Если $p$ – вероятность ошибки в единичном бите и искажения битов независимы, то вероятность ошибки при приеме составляет
(3.1)
${{p}_{D}}(p) = 1 - \sum\limits_{l = 0}^{(n - 1)/2} \,C_{n}^{l}{{p}^{{n - l}}}{{(1 - p)}^{l}} = 1 - {{(1 - p)}^{n}}\sum\limits_{l = 0}^{(n - 1)/2} \,C_{n}^{l}\mathop {\left( {\frac{p}{{1 - p}}} \right)}\nolimits^l ,$На рис. 4 приведены графики функции (3.1) при некоторых n.
Рис. 4.
Графики ошибок мажоритарного кодирования для значений n = 1 (прямая линия), 3, 7, 13, 25, 101
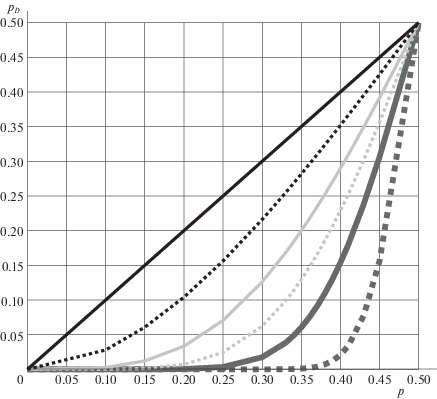
Видно, что если вероятность ошибки одного бита кода равна $p = 0.35$, то, семикратно продублировав бит сообщения, можно передать его с вероятностью ошибки ${{p}_{D}} = 0.2$, что позволяет использовать коды Адамара. Большая кратность дублирования также допустима, но приводит к большему размеру кода.
Параметром этого метода является кратность повтора бита $n$.
3.3. Блоковое кодирование Адамара. Обозначим через $\mathbb{B} = \{ 0,1\} $, ${{\mathbb{B}}^{l}}$ = {(b1, ..., ${{b}_{l}}){\kern 1pt} :\;{{b}_{i}} \in \mathbb{B}$ ${{b}_{l}}){\kern 1pt} :\;{{b}_{i}} \in \mathbb{B}$, $i = \overline {1,l} \} $ множество всех двоичных последовательностей длины l (l-мерный двоичный куб). Для любых двух элементов $u,v \in {{\mathbb{B}}^{l}}$ задано нормированное расстояние Хэмминга (1.2), равное отношению количества различающихся бит в последовательностях к их длине. Также обозначим через $b(u)$ число единичных бит в последовательности u.
Пусть $M$ – исходное сообщение (message) длиной k бит, $M \in {{\mathbb{B}}^{k}}$, т.е. единицей кодирования является блок из нескольких бит. Алгоритм кодирования Адамара отображает сообщение в избыточный код длиной $n$ бит из некоторого известного алфавита $\mathbb{H}$: $C{\kern 1pt} *(M) \in \mathbb{H} \subset {{\mathbb{B}}^{n}}$, $n > k$. Пусть $C \in {{\mathbb{B}}^{n}}$ – искаженный код, возникший при замене (инвертировании) некоторых бит исходного кода C*. Вероятность искажения одного бита равна pD (взята из предыдущего этапа (3.1)), искажения независимы. Далее в этом разделе для простоты переобозначим ${{p}_{D}} \to p$. Будем декодировать сообщение, предполагая, что исходный код искажен минимально, т.е. для $C$ будем искать ближайший в смысле расстояния Хэмминга код из алфавита $\mathbb{H}$. Назовем его аттрактором. Аттракторов может быть несколько (несколько кодов могут иметь одинаковое минимальное расстояние до C). Если аттракторов несколько, то выбирается случайный. Обозначим множество аттракторов $C$ как $A(C)$.
Известна простая оценка вероятности ошибки блокового кодирования Адамара, с длиной кодового слова $n$ используемая в так называемой границе Хэмминга:
(3.2)
${{p}_{H}} \leqslant 1 - {{P}_{{corr}}} = 1 - \mathop {\left( {1 - p} \right)}\nolimits^n \sum\limits_{l = 0}^{(n - 1)/4} \,C_{n}^{l}\mathop {\left( {\frac{p}{{1 - p}}} \right)}\nolimits^l ,$Но это довольно грубая оценка, ухудшающаяся с ростом $n$. Найдем точную формулу. Вероятность правильного декодирования
Без ограничения общности в силу симметричности кода Адамара [26] можно считать, что $C{\kern 1pt} *$ – нулевой код, т.е. последовательность нулевых бит соответствующей длины (так оно и есть при стандартном кодировании). Тогда вероятность получить определенный код $C$ из нулевого равна ${{p}^{{b(C)}}}{{(1 - p)}^{{n - b(C)}}}$ и
где $p(0|C)$ – вероятность получить нулевой код из $C$:(3.3)
$p(0\,{\text{|}}\,C) = \left\{ \begin{gathered} 0,\quad \exists C{\kern 1pt} ' \in \mathbb{H},\quad C{\kern 1pt} ' \ne 0{\kern 1pt} :\;\rho (C{\kern 1pt} ',C) < \rho (0,C) = b(C), \hfill \\ 1/{\text{|}}A(C){\text{|}},\quad A(C) = \left\{ {C{\kern 1pt} ' \in \mathbb{H}{\kern 1pt} :\;\rho (C{\kern 1pt} ',C) = b(C)} \right\}. \hfill \\ \end{gathered} \right.$Для небольших значений длины кода $n$ можно построить гистограмму распределения точек пространства кодов ${{\mathbb{B}}^{n}}$ в зависимости от расстояния до нулевого кода $b = b(C)$ и количества аттракторов $a = {\text{|}}A(C){\text{|}}$. Положим a = 0 в случае выполнения первого условия из (3.3). Тогда можно записать двумерное распределение
(3.4)
${{p}_{H}} = 1 - {{P}_{{corr}}} = 1 - {{(1 - p)}^{n}}\sum\limits_b \,h(b)\mathop {\left( {\frac{p}{{1 - p}}} \right)}\nolimits^b ,\quad h(b) = \sum\limits_{a \ne 0} \,\frac{{H(b,a)}}{a}.$Запись совпадает с (3.2) за исключением используемых коэффициентов и пределов суммирования (в (3.4) суммирование производится по всем b). Таблица значений $H(b,a)$ и h(b) для пополненного кода Адамара порядка 5 ($n = {{2}^{5}} - 1 = 31$, $k = 5 + 1 = 6$) дана ниже (табл. 2). Для сравнения приведены значения $C_{n}^{b}$. Также представлены средние значения вероятности выбора правильного аттрактора:
Таблица 2.
Значения $H(b,a)$, $h(b)$ и $\bar {a}(b)$ для кода Адамара k = 6, n = 31
| b | $H(b,1)$ | $H(b,2)$ | $H(b,3)$ | $H(b,4)$ | $H(b,6)$ | $h(b)$ | $C_{n}^{b}$ | $\bar {a}(b)$ |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1. |
| 1 | 31 | 0 | 0 | 0 | 0 | 31 | 31 | 1. |
| 2 | 465 | 0 | 0 | 0 | 0 | 465 | 465 | 1. |
| 3 | 4495 | 0 | 0 | 0 | 0 | 4495 | 4495 | 1. |
| 4 | 31 465 | 0 | 0 | 0 | 0 | 31 465 | 31 465 | 1. |
| 5 | 169 911 | 0 | 0 | 0 | 0 | 169 911 | 169 911 | 1. |
| 6 | 736 281 | 0 | 0 | 0 | 0 | 736 281 | 736 281 | 1. |
| 7 | 2 629 575 | 0 | 0 | 0 | 0 | 2 629 575 | 2 629 575 | 1. |
| 8 | 7 291 200 | 398 040 | 0 | 0 | 0 | 7 490 220 | 7 888 725 | 0.974 |
| 9 | 11 179 840 | 5 077 800 | 238 080 | 0 | 0 | 13 798 100 | 20 160 075 | 0.836 |
| 10 | 1 833 216 | 9 114 000 | 4 999 680 | 833 280 | 5208 | 8 265 964 | 44 352 165 | 0.492 |
| 11 | 0 | 0 | 0 | 624 960 | 1 630 104 | 427 924 | 84 672 315 | 0.190 |
Для этого кода значения b изменяются от 0 до 31, приведены первые 12. Остальные значения нулевые, все последовательности, отличающиеся от нулевой более чем на 11 бит, “притягиваются” к другим кодовым векторам. Из таблицы видно, что вплоть до значений $b = 7$ происходит выбор лишь одного аттрактора, т.е. при таком или меньшем расхождении сообщение восстанавливается всегда. Это соответствует границе Хэмминга. Однако и при больших расхождениях существует значительная вероятность правильного восстановления. Это существенно, поскольку кодов за границей Хэмминга существует гораздо больше, чем внутри. Таким образом, оценка по Хэммингу вероятности ошибки декодирования сильно завышена. Например, для пополненного кода Адамара k = 6, n = 31 и ошибке $p = 0.250$ оценка по (3.2) дает ${{p}_{H}} = 0.527$, что, казалось бы, исключает использование такого кода. Однако расчет по формуле (3.4) дает ${{p}_{H}} = 0.261$, что вполне пригодно для использования на следующем шаге – коировании Рида–Соломона. На рис. 5 приведены графики функции (3.2) и (3.4) для k = 6, n = 31.
Рис. 5.
Графики ошибки кодирования Адамара для n = 31, k = 6: оценка границей Хэмминга (3.2) (пунктирная линия) и точное значение (3.4) (сплошная линия)

Параметр кодирования Адамара – длина слова k.
3.4. Кодирование Рида–Соломона. Единицей кодирования для алгоритма Рида–Соломона является все сообщение, которое разбивается на слова фиксированного размера, s бит каждое. Одно такое слово – запись целого числа в диапазоне $[0;{{2}^{s}} - 1]$. Последовательность из $L$ бит разбивается на $k = \left\lceil {L{\text{/}}s} \right\rceil $ слов, т.е. чисел. Эти числа трактуются как коэффициенты полинома над полем Галуа $GF({{2}^{k}})$. Оказывается, что если определенным образом расширить полином с $k$ коэффициентами до полинома с $n > k$ коэффициентами, то можно среди полученных $n$ коэффициентов произвольно исказить любые $t \leqslant (n - k){\text{/}}2$ из них и из полученной записи восстановить исходные коэффициенты.
Обозначим: $L$ – длина сообщения (число кодируемых бит); $s$ – размер слова кода Рида–Соломона (РС); $k$ – число слов РС в сообщении, $k = \left\lceil {L{\text{/}}s} \right\rceil $; $n$ – число слов РС в коде; $N$ – длина кода (число бит в коде, полученном методом РС), $N = ns$; p – доля допустимых ошибочных слов в коде, при которой еще возможно восстановление сообщения. Код РС исправляет не более $t$ ошибок, где $t$ равно половине избыточных слов в коде, добавленных к исходному сообщению, т.е. $n = k + 2t$, обозначив $p = t{\text{/}}n$, получим
Вычисленная таким образом доля может служить оценкой допустимой вероятности ошибки слова кода. Также есть ограничение на максимальное число слов кода:
Зафиксировав длину сообщения $L$, выбрав длину слова $s$ и зная вероятность ошибки декодирования предыдущего шага $p = {{p}_{H}}$, можно построить код РС. Вероятность ${{p}_{H}}$ определяется извне, поэтому код РС параметризуется двумя величинами: размером слова $s$ и длиной сообщения $L$.
3.5. Добавочная ошибка восстановления кода. Расстояние Хэмминга задает функцию зависимости ошибки первого рода от ошибки второго рода. Для некоторой базы данных и фиксированного порога $\theta $ рассмотрим количества различных исходов. Существует всего четыре исхода: истинный допуск (обозначим число таких событий “true positive” ${{N}_{{TP}}}$), ложный отказ (“false positive” ${{N}_{{FR}}}$), истинный отказ (“true negative” ${{N}_{{TN}}}$) и ложный отказ (“false negative” ${{N}_{{FN}}}$). Вероятности ошибки первого (false reject) и второго (false accept) рода определяются как
(3.7)
${{p}_{{FR}}} = \frac{{{{N}_{{FN}}}}}{{{{N}_{{FN}}} + {{N}_{{TP}}}}},\quad {{p}_{{FA}}} = \frac{{{{N}_{{FP}}}}}{{{{N}_{{FP}}} + {{N}_{{TN}}}}}.$Следует отметить, что при работе с БД сумма ${{N}_{{FN}}} + {{N}_{{TP}}}$ постоянна и равна числу сравнений эталонов одного человека, а сумма ${{N}_{{FP}}} + {{N}_{{TN}}}$ постоянна и равна числу сравнений эталонов разных людей.
Восстановление сообщения из кода вносит дополнительную ошибку, оценим ее. Обозначим вероятность ошибки восстановления ${{p}_{R}}$. Соответственно вероятность правильного восстановления равна $1 - {{p}_{R}}$. Ожидаемое число событий истинного допуска в схеме с восстановлением уменьшается пропорционально этой вероятности: $N_{{TP}}^{'} = {{N}_{{TP}}}(1 - {{p}_{R}})$. Значит, увеличивается число ложных отказов: $N_{{FN}}^{'} = {{N}_{{FN}}} + {{N}_{{TP}}}{{p}_{R}}$. Аналогично число ложных допусков уменьшается: $N_{{FP}}^{'} = {{N}_{{FP}}}(1 - {{p}_{R}})$, число истинных отказов увеличивается: $N_{{TN}}^{'} = {{N}_{{TN}}} + {{N}_{{FP}}}{{p}_{R}}$. Рассчитывая новые вероятности ошибок первого и второго рода, получаем:
(3.8)
$\begin{gathered} p_{{FR}}^{'} = \frac{{{{N}_{{FN}}} + {{N}_{{TP}}}{{p}_{R}}}}{{{{N}_{{FN}}} + {{N}_{{TP}}}}} = {{p}_{{FR}}} + \frac{{{{N}_{{TP}}}}}{{{{N}_{{FN}}} + {{N}_{{TP}}}}}{{p}_{R}} = {{p}_{{FR}}} + \left( {1 - \frac{{{{N}_{{FN}}}}}{{{{N}_{{FN}}} + {{N}_{{TP}}}}}} \right){{p}_{R}} = \\ \, = {{p}_{{FR}}} + (1 - {{N}_{{FR}}}){{p}_{R}} = {{p}_{{FR}}}(1 - {{p}_{R}}) + {{p}_{R}}, \\ p_{{FA}}^{'} = \frac{{{{N}_{{FP}}}}}{{{{N}_{{FP}}} + {{N}_{{TN}}}}}(1 - {{p}_{R}}) = {{p}_{{FA}}}(1 - {{p}_{R}}). \\ \end{gathered} $Если ${{p}_{R}} \ll 1$, ${{p}_{{FR}}} \ll 1$, то можно приблизить: $p_{{FR}}^{'} \approx {{p}_{{FR}}} + {{p}_{R}}$, $p_{{FA}}^{'} \approx {{p}_{{FA}}}$. Таким образом, вероятность ошибки первого рода увеличивается на величину вероятности ошибки восстановления, вероятность ошибки второго рода можно считать неизменной.
4. Подбор параметров схемы кодирования. Описанные четыре последовательно исполняемых алгоритма имеют следующие параметры, влияющие на их характеристики: (1) псевдослучайное перемешивание не имеет таких параметров; (2) мажоритарное кодирование параметризуется кратностью повтора бита $n$; (3) кодирование Адамара – размером слова k, кодирование РС – размером слова $s$ и длиной сообщения $L$. Различные комбинации значений $(n,k,s,L)$ приводят к построению различных кодеков, имеющих разные отношения длины кода к длине сообщения. Можно формально записать зависимости ошибок первого и второго рода от этих параметров: $FRR(n,k,s,l)$ и $FFR(n,k,s,l)$. Фактически, эти значения находились экспериментально. Используемая биометрия [33] имеет размер $Z = 6656$ бит. Размер кода $C$ не может быть больше, дублирование и маскирование недопустимы, так как делают тривиальным взлом такого кода. Также следует учесть, что практически осмысленным является кодирование сообщения некоторой минимальной длины $Y$. Тогда можно записать задачу поиска оптимального кода:
(4.1)
$\begin{gathered} FRR(n,k,s,L) \to min, \\ s.t.\;FAR \leqslant {{10}^{{ - 4}}},\quad C \leqslant Z,\quad L \geqslant Y. \\ \end{gathered} $Для $Y = 64$ решение найдено: $n = 13$, $k = 5$, $s = 5$, $L = 65$, $FRR$ = 10.4%. Такой размер считается достаточным для “обычных” пользовательских ключей. Для Y = 128 и выше решение данной задачи не получено. Следует отметить, что без псевдослучайного перемешивания (явным образом не участвующего в (4.1)) задача не решается и при $Y = 64$.
Заключение. В парадигме нечеткого экстрактора построен метод внедрения криптографического ключа в биометрию радужной оболочки глаза. Успешно внедряется ключ размером до $65$ бит, для больших размеров решение не получено. Использование дополнительных шагов псевдослучайного перемешивания и мажоритарного битового кодирования позволило решить проблемы изменчивости и локальной коррелированности биометрических признаков. Метод протестирован на нескольких базах изображений радужной оболочки глаза. Требуется изучение криптостойкости представленного метода.
Список литературы
Алферов А.П., Зубов А.Ю., Кузьмин А.С., Черемушкин А.В. Основы криптографии. М.: Гелиос АРВ, 2005. 480 с.
Чмора А.Л. Маскировка ключа с помощью биометрии // Проблемы передачи информации. 2011. Т. 47. № 2. С. 28–143.
Daugman J.G. Information Theory and the IrisCode // IEEE Trans. Information Forensics and Security. 2016. V. 11. № 2. P. 400–409.
Gong S., Boddeti V.N., Jain A.K. On the Capacity of Face Representation // 2017. URL: https://arxiv.org/abs/1709.10433.
Yankov M.P., Olsen M.A., Stegmann M.B., Christensen S.S., Forchhammer S. Fingerprint Entropy and Identification Capacity Estimation Based on Pixel-Level Generative Modelling // IEEE Trans. Information Forensics and Security. 2020. V. 15. P. 56–65.
Иванов А.И., Ложников П.С., Сулавко А.Е. Оценка надежности верификации автографа на основе искусственных нейронных сетей, сетей многомерных функционалов Байеса и сетей квадратичных форм // Компьютерная оптика. 2017. V. 41. № 5. С. 765–774.
Juels A., Sudan M. A fuzzy vault scheme // Designs, Codes and Cryptography. 2006. V. 38. P. 237–257.
Daugman J. How Iris Recognition Works // Proc. Int. Conf. Image Processing. Lake Buena Vista, Orlando, USA, 2012. V. 1. P. 33–36.
Shekar B.H., Bharathi R.K., Kittler J., Vizilter Y.V., Mestestskiy L. Grid Structured Morphological Pattern Spectrum for Off-line Signature Verification // Proc. 2015 Int. Conf. Biometrics. Phuket, Thailand, 2015. V. 8. P. 430–435.
Rathgeb C. Uhl A. A Survey on Biometric Cryptosystems and Cancelable Biometrics // EURASIP J. Information Security. 2011. V. 3. P. 1–25.
Майоров А.В. Нейросетевая хеш-функция // Нейрокомпьютеры: разработка, применение. 2009. № 6. P. 45–48.
Иванов А.И., Сомкин С.А., Андреев Д.Ю., Малыгина Е.А. О многообразии метрик, позволяющих наблюдать реальные статистики распределения биометрических данных “нечетких экстракторов” при их защите наложением гаммы // Вестн. УрФО. Безопасность в информационной сфере. 2014. V. 2. № 12. С. 16–23.
Защита информации. Техника защиты информации. Автоматическое обучение нейросетевых преобразователей биометрия-код доступа. ГОСТР 52633.5-2011. М.: Стандартинформ, 2012.
Sutcu Y., Sencar H.T., Memon N. A Secure Biometric Authentication Scheme Based on Robust Hashing // Proc. 7th Workshop Multimedia and Security. N.Y., USA, 2005. P. 111–116.
Rathgeb C., Uhl A. Privacy Preserving Key Generation for Iris Biometrics // Communications and Multimedia Security. Eds. De Decker B., Schaumueller-Bichl I. Berlin, Heidelberg: Springer, 2010. P. 191–200.
CASIA Iris Image Database, Institute of Automation, Chinese Academy of Sciences. 2010. http:// biometrics.idealtest.org/ findTotalDbByMode.do?mode=Iris.
Davida G., Frankel Y., Matt B. On the Relation of Error Correction and Cryptography to an Offline Biometric Based Identification Scheme // Proc. Workshop on Coding and Cryptography. Paris, France, 1999. P. 129–138.
Dodis Y., Ostrovsky R., Reyzin L., Smith A. Fuzzy extractors: How to Generate Strong Keys from Biometrics and Other Noisy Data // SIAM J. Computing. 2008. V. 38. № 1. P. 97–139.
Yang S., Verbauwhede I. Secure Iris Verification // Proc IEEE Int. Conf. Acoustics, Speech and Signal Processing. Honolulu, USA, 2007. V. 2. P. 133–136.
Linnartz J.-P., Tuyls P. New Shielding Functions to Enhance Privacy and Prevent Misuse of Biometric Templates // Proc. 4th Int. Conf. Audio- and Video-Based Biometric Person Authentication. Guildford, UK, 2003. P. 393–402.
Shamir A. How to share a secret // Commun. ACM. 1979. V. 22. № 11. P. 612–613.
Lee Y.J., Bae K., Lee S.J., Park K.R., Kim J. Biometric Key Binding: Fuzzy Vault Based on Iris Images // Proc. 2nd Int. Conf. Biometrics. Seoul, Korea, 2007. P. 800–808.
Wu X., Qi N., Wang K., Zhang D. An Iris Cryptosystem for Information Security // Proc. Int. Conf. Intelligent Information Hiding and Multimedia Signal Processing. Harbin, China, 2008. P. 1533–1536.
Juels A., Wattenberg M. A Fauzzy Commitment Scheme // 6th ACM Conf. Computer and Communications Security. Singapore, 1999. P. 28–36.
Hao F., Anderson R., Daugman J. Combining Crypto with Biometrics Effectively // IEEE Trans. Computers. 2006. V. 55. № 9. P. 1081–1088.
Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение. М.: Техносфера, 2005.
Рубис А.Ю., Лебедев М.А., Визильтер Ю.В., Выголов О.В., Желтов С.Ю. Компаративная фильтрация изображений с использованием монотонных морфологических операторов // Компьютерная оптика. 2018. V. 42. № 2. С. 306–311.
Лебедев М.А., Рубис А.Ю., Визильтер Ю.В., Выголов О.В., Желтов С.Ю. Выделение отличий на изображениях с помощью референтных EMD-фильтров // Математические методы распознавания образов. 2017. V. 18. № 1. С. 116–117.
Reed I.S., Solomon G. Polynomial Codes over Certain Finite Fields // J. Society for Industrial and Applied Mathematics. 1960. V. 8. № 2. P. 300–304.
Kanade S., Camara D., Krichen E., Petrovska-Delacretaz D., Dorizzi B. Three Factor Scheme for Biometric-based Cryptographic Key Regeneration Using Iris // Proc. Biometrics Symposium. Tampa, FL, USA, 2008. P. 59–64.
Иванов А.И. Нечеткие экстракторы: проблема использования в биометрии и криптографии // Первая миля. 2015. № 1. С. 40.
Ганькин К.А., Гнеушев А.Н., Матвеев И.А. Сегментация изображения радужки глаза, основанная на приближенных методах с последующими уточнениями // Изв. РАН. ТиСУ. 2014. № 2. С. 80–94.
Novik V., Matveev I., Litvinchev I. Enhancing Iris Template Matching with the Optimal Path Method // Wireless Networks. 2018. P. 1–8.
Woodard D.L., Ricanek K. Iris Databases. Eds: Li S.Z., Jain A. Encyclopedia of Biometrics. Boston, MA, USA: Springer, 2009.
Phillips P., Scruggs W., O’Toole A. et al. Frvt 2006 and Ice 2006 Large-scale Experimental Results // IEEE PAMI. 2010. V. 5. № 32. P. 831–846.
Proenca H., Alexandre L. UBIRIS: A Noisy Iris Image Database // 13th Int. Conf. Image Analysis and Processing. Cagliari, Italy, 2005. P. 970–977.
https://www.sovereigncctv.com/panasonic-bm-et300-iris-reader.html Дата обращения 13.04.2020.
https://www.sourcesecurity.com/lg-iris-irisaccess-3000-technical-details.html Дата обращения 13.04.2020.
9 http://www.iritech.com/products/hardware/ Дата обращения 13.04.2020.
Reed I.S. A Class of Multiple-error-correcting Codes and the Decoding Scheme // Transactions IRE Professional Group on Information Theory. 1954. V. 4. № 4. P. 38–49.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления