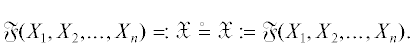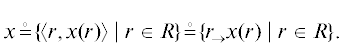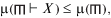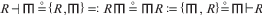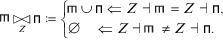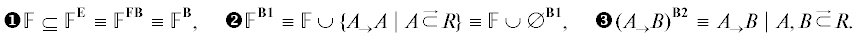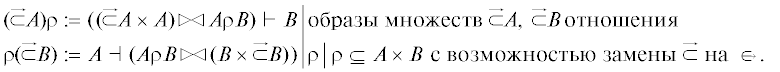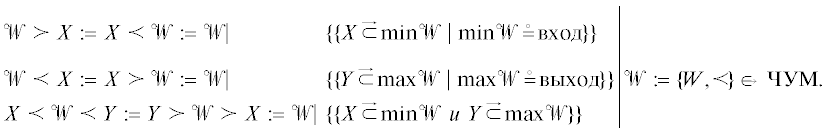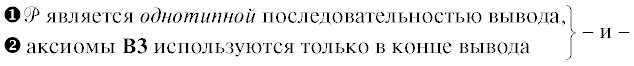Известия РАН. Теория и системы управления, 2020, № 6, стр. 152-176
СИНТЕЗ-АНАЛИЗ ПОСЛЕДОВАТЕЛЬНОСТЕЙ ВЫВОДА ФУНКЦИОНАЛЬНЫХ ЗАВИСИМОСТЕЙ ТАБЛИЦ
Л. А. Поморцев a, *, В. И. Цурков b, **
a МФТИ
Москва, Россия
b ФИЦ ИУ РАН
Москва, Россия
* E-mail: brickfactory.org@mail.ru
** E-mail: tsur@ccas.ru
Поступила в редакцию 14.01.2019
После доработки 17.12.2019
Принята к публикации 27.01.2020
Аннотация
Последовательности вывода функциональных зависимостей, как и все вычислительные программы, представляют собою дважды частично упорядоченные множества: по следованию команд в программе и по их исполнению во времени. Согласованность порядков достигается теоретико-множественным вложением одного в другой. Подобные множества далее называются каскадно упорядоченными и для них нет необходимости прибегать к терминологии теории реляционных баз данных. Имеется возможность представления последовательности вывода в виде специального объединения почти непересекающихся более простых подпоследовательностей, называющихся в статье острыми множествами. Оно достигается применением к ним операции $\unicode{230} $ склеивания. Процесс образования каскадно-упорядоченного множества из острых множеств отражен в заглавии термином “Синтез”2. Исследованию этого процесса посвящена предлагаемая статья. Завершающая часть статьи излагает принципы “Анализа”3, т.е. разложения заданного каскадно-упорядоченного множества на так называемые АР-конусы. Этот вопрос получит полное разрешение в последующих статьях.
Здесь для доказательств применяются логические схемы, которые предназначены для вычисления предикатов из заданных. Реже используются блок-схемы, обычные для алгоритмирования. Их совместное применение служит целям автоматизации математических доказательств. Логический инструментарий статьи является предпосылкой построения математической модели искусственного интеллекта.
Введение. Функциональные зависимости (ФЗ) – понятие, лежащее в основе вопросов, связанных с конструкцией таблиц, которые составляют так называемые реляционные базы данных (РБД). ФЗ представляются упорядоченными парами подмножеств имен колонок (то же, что полей) таблиц, которые в научной литературе называются атрибутами данного отношения. В совокупности атрибуты составляют схему R, играющую в быту роль шапки таблицы. Содержательная часть таблицы, с точки зрения алгебры, является отношением. Подробности можно почерпнуть в монографии [1], положившей начало нашим исследованиям. Необходимо все же иметь в виду, что она носит алгоритмический характер и далека от применения алгебры в теории РБД (ТРБД).
ФЗ заключают в себе семантические свойства таблицы, способные влиять на структуру РБД в соответствии с теоремой Хита (см. [2] и [3, п. 3.6.2, с. 70]), обеспечивающей декомпозицию таблиц без информационных потерь и избыточности. В совокупности с основополагающей в ТРБД операцией ⋈ соединения таблиц декомпозиция Хита позволяет понимать РБД как единую очень большую таблицу с приданной ей совокупностью тех функциональных зависимостей, которым надлежит разбить целое на требуемые части. Это означает, что ФЗ заключают в себе квинтэссенцию конструирования (проектирования) РБД. Заметим, пара операций ⋈ и декомпозиция, основанная на применении теоремы Хита к ФЗ, осуществляют СИНТЕЗ-АНАЛИЗ таблиц, который уместно назвать объектным, чтобы отличить его от целевого, фигурирующего в названии настоящей статьи.
Несмотря на то, что для заданной таблицы можно построить полное множество ее ФЗ (пока, увы, вручную), на практике РБД конструируют, исходя из заданных ФЗ, отражающих априорные знания об объекте автоматизации. Инверсный подход к созданию баз данных отчуждает ФЗ от отношений (таблиц). И те взаимосвязи между ФЗ, которые первоначально устанавливались на отношениях с помощью теоретико-множественной формалистики, основанной на данном ниже определении 9, в процессе проектирования РБД становятся правилами вывода одних ФЗ из других. Поскольку в этом случае в них надо верить, то их параллельно, называют также аксиомами вывода (АВ). АВ осуществляют разовые преобразования не более чем двух ФЗ в третью, но их можно применять последовательно и что в результате даст упорядоченную по времени исполнения цепочку АВ называемую последовательностью вывода. Для них ставятся следующие задачи:
1) СИНТЕЗ-АНАЛИЗ частично упорядоченных множеств (настоящая статья),
2) перестройка порядков каскадно упорядоченного множества (продолжение),
3) гигиена последовательностей вывода (ПВ) (продолжение),
4) алгебраизация ПВ (продолжение).
Решению поставленных задач посвящен цикл из четырех работ, поддерживающих научное направление алгебраизации алгоритмов средствами матлогики. Первая из них представлена настоящим исследованием. Обзор [4] служит общим введением к ним и охватывает весь цикл, завершающий исследования, начатые в [5, 6]. К сожалению, задача конструктивного преобразования алгоритмов (программ) в алгебраические выражения до сих пор ставилась слабо. По этой причине весьма узок список математической литературы, на которую можно было бы опереться. Однако мы надеемся, что настоящая публикация и последующие за ней три статьи привлекут внимание математической общественности к проблематике внедрения алгебраических методов в информатику и вовлечения области искусственного интеллекта в математическую логику.
В задачах 1) и 2) представленного выше списка тe же последовательности вывода ФЗ фигурируют в виде частично и, более того, каскадно-упорядоченных множеств (см. ниже определение 20) и для них примененяется исключительно терминология алгебры. Как видно, ПВ занимают основное место в списке задач, предстоящих для решения, а ФЗ находятся на магистральном пути конструирования РБД, что в свою очередь требует умения конструировать сами ФЗ. Однако ПВ, как и всякое программное обеспечение, являются дорогим удовольствием. Альтернативой им выступают алгебраические выражения в специально построенной ассоциативной алгебре, использующие в качестве аргументов те же ФЗ и дающие те же результаты. Они по сравнению с ПВ вербально однозначны, экономны и алгоритмически проще. Установка функциональной эквивалентности (ФЭ) ПВ (ФЭПВ) и соответствующих им алгебраических выражений достигается решением финальной задачи 4.
1. Инструментарий логических схем. 1.1. Субъекты текста.
Обозначения от 1 до 8 – символы логики.
1. Эквивалентность A PRIORI44, эмпирическое равенство, безапеляционное равенство:
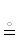 ← “то же, что” (см. также обозначение 25).
← “то же, что” (см. также обозначение 25).
2. := ← первоначальное равенство, заменяет фразу “пo определению есть” и используется для присвоения значения определяемому имени. Для правостороннего расположения определяемого субъекта55 $\mathfrak{X}$ будет использоваться знак =:, как показано ниже:
Внимание! Переопределения отменяют предыдущие определения субъекта.
3. Так называемый грамматор | заменяет фразы “такой(ие), что” или “при условии”. Сущность α, подчинящаяся условию $\mathcal{A}$(α), которое выражается предикатом $\mathcal{A}$, является решением уравнения $\mathcal{A}$(α) = ДА. То же самое записывается словом α|$\mathcal{A}$.
4. A $ \cup ^\circ $ B := A ∪ B | A ∪ B = ∅ ← разбиение множества A ∪ B на непересекающиеся подмножества A и B (сравни с обозначением 40).
5. {α|$\mathcal{A}$(α)} ← совокупность решений уравнения $\mathcal{A}$(α) = ДА,
{} ← оператор формирования множеств, в частности …
{a, …, z} ← конечное множество.
Множества типа {} не предполагаются упорядоченными. Для конечных множеств, упорядоченных в направлении чтения, будут использованы скобки 〈 〉, например 〈a, …, z〉. Такие множества будем называть списочными.
6. $ \in \to $ и $\overrightarrow \subset $ – символы произвольного выбора элемента и подмножества в множестве:
$ \in \to $ X и $\overrightarrow \subset $ X ← временные имена выбранных, но “безымянных” субъектов,
$\overrightarrow \supset $ X ← безымянное надмножество множества X,
Y $\overrightarrow \supset $ X ← Y есть некоторое расширение заданного множества X.
Примеры: {a $ \in \to $ A} = A; $ \in \to ${a} = a; a $ \in \to $ A := |a ∈ A; X $\overrightarrow \subset $ A := X|X ⊆ A.
Внимание! 1. Подвыражения $ \in \to $ M (или $\overrightarrow \subset $ M, или $\overrightarrow \supset $ M) имеют одно и то же значение в выражении, в котором они могут встретиться многажды.
2. В выборах ${v}$ $ \in \to $ w, ${v}$ $\overrightarrow \subset $ w, ${v}$ $\overrightarrow \supset $ w конец стрелки указывает на результат w действий $ \in \to $ $\overrightarrow \subset $ $\overrightarrow \supset $, исходящих из множества ${v}$ (см. ниже обозначение 14.3).
7. Кванторы существования – $\exists $ и всеобщности – $\forall $. Далее использование кванторов ограничивается. Взамен предлагаем следующие конструкции:
x $ \in \to $ X | $\mathcal{A}$(x) 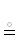 $\mathcal{A}$(x) | x $ \in \to $ X
$\mathcal{A}$(x) | x $ \in \to $ X 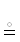 $\exists $x ∈ $\mathcal{A}$(x) для предиката $\mathcal{A}$(x) с переменной x.
$\exists $x ∈ $\mathcal{A}$(x) для предиката $\mathcal{A}$(x) с переменной x.
В то же время выражение x ∈ X|$\mathcal{A}$(x) по умолчанию использует $\forall $.
8. $\mathcal{A}$ ⇒ $\mathcal{B}$ 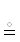 $\mathcal{B}$ ⇐ $\mathcal{A}$
$\mathcal{B}$ ⇐ $\mathcal{A}$  из $\mathcal{A}$ следует $\mathcal{B}$ | $\mathcal{A}$ и $\mathcal{B}$ – предикаты; $\mathcal{A}$ ⇒ $\mathcal{B}$ и $\mathcal{A}$ ⇐ $\mathcal{B}$
из $\mathcal{A}$ следует $\mathcal{B}$ | $\mathcal{A}$ и $\mathcal{B}$ – предикаты; $\mathcal{A}$ ⇒ $\mathcal{B}$ и $\mathcal{A}$ ⇐ $\mathcal{B}$ 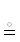 $\mathcal{A}$ ⇔ $\mathcal{B}$ ← логическая эвивалентность. Надо понимать, что: $\mathfrak{X}$ := $\mathfrak{Y}$ ⇒ $\mathfrak{X}$
$\mathcal{A}$ ⇔ $\mathcal{B}$ ← логическая эвивалентность. Надо понимать, что: $\mathfrak{X}$ := $\mathfrak{Y}$ ⇒ $\mathfrak{X}$  $\mathfrak{Y}$; ($\mathcal{A}$ ⇔ $\mathcal{B}$) ⇒ ($\mathcal{A}$
$\mathfrak{Y}$; ($\mathcal{A}$ ⇔ $\mathcal{B}$) ⇒ ($\mathcal{A}$ 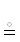 $\mathcal{B}$).
$\mathcal{B}$).
Внимание! Математические выражения, содержащие стрелки ← ← ↤ ⇐ ⇚, читаются справа-налево. Тоже относится к символу =:. Вертикальные стрелки ↑ ⇑ ⤊ задают чтение снизу-вверх. Стрелки ↓ ⇓ ⤋ ориентируют текст сверху-вниз.
Обозначения от 9 до 15 – символы сущностей.
9. μ(M) – мощность множества M.
10. $\mathbb{Z}$ – множество целых чисел; ${{\mathbb{Z}}^{ + }}$ – множество неотрицательных целых чисел;
$\mathbb{R}$ – все действительные числа; ${{\mathbb{R}}^{n}}$ | n ∈ ${{\mathbb{Z}}^{ + }}$ – n-мерное, векторное пространство.
11. Конечные, связные множества целых чисел: (см. 〈 〉 в обозначениях 5):
[n, m] – интервал целых чисел от n до m включительно в предположении n ≤ m;
Пустота полуинтервалов допускается. Квадратно-скобочная символика будет применяться к любым линейно-упорядоченным множествам в тех же целях.
12. Кортеж как средство выборки, хранения и именования данных.
12.1. Кортеж – это отображение x: R → X, где X, R | μ(R) < ∞ – некоторые множества; R называется схемой кортежа x. Условие μ(R) < ∞ конечности схемы существенно. Схема66 состоит из так называемых атрибутов. Область значений X кортежа x называется его доменом. Допускается dom(x) := X ≠ x(R), т.е. x(R) ⊂ dom(x). Кортеж можно представить в виде таблицы размером 2 × μ(R) (см. 〈 〉 и → в обозначениях 5 и 12.2)
Из нее видно, что атрибуты схемы R, представляя собою систему имен, разделяют одинаковые элементы множества экземпляров, выбранных из X отображением x: R → X.
12.2. 〈x0, x1, …, xn〉 – позиционный кортеж сущностей x0, …, xn | n ∈ ${{\mathbb{Z}}^{ + }}$ 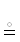 упорядоченный кортеж. Знаки препинания (ЗП) применяются для структуризации кортежа, угловые скобки – для
структуризации контекста. В случае их отсутствия кортеж имеет форму слова. В состав кортежа ЗП не входят. Они не обязательны в обозначениях или могут иметь
иные начертания, как, например, в определениях x := x0→x1→…→xn – 1 := 〈x0, x1, …, xn – 1〉 =: xn – 1←xn – 2←…←x0, в которых используется знак →, имеющий двойной смысл – разделитель между элементами кортежа и указатель их порядка.
упорядоченный кортеж. Знаки препинания (ЗП) применяются для структуризации кортежа, угловые скобки – для
структуризации контекста. В случае их отсутствия кортеж имеет форму слова. В состав кортежа ЗП не входят. Они не обязательны в обозначениях или могут иметь
иные начертания, как, например, в определениях x := x0→x1→…→xn – 1 := 〈x0, x1, …, xn – 1〉 =: xn – 1←xn – 2←…←x0, в которых используется знак →, имеющий двойной смысл – разделитель между элементами кортежа и указатель их порядка.
Пример. Если X := $\mathbb{R}$, то 〈x0, …, xn – 1〉 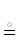 (x0, …, xn – 1) ∈ ${{\mathbb{R}}^{n}}$ ← n-мерный вектор.
(x0, …, xn – 1) ∈ ${{\mathbb{R}}^{n}}$ ← n-мерный вектор.
12.3. Нумерация элементов в упорядоченных кортежах и последовательностях:
${{\mathcal{V}}_{i}}$ | i ∈ [1, n] – член, стоящий на i-том месте кортежа или последовательности $\mathcal{V}$.
По умолчанию нумерацию элементов будем начинать с нуля. Это означает, что $\mathcal{V}$ ≡ 〈${{\mathcal{V}}_{0}}$, ${{\mathcal{V}}_{1}}$, …, ${{\mathcal{V}}_{{\mu (\mathcal{V}) - 1}}}$〉 и μ($\mathcal{V}$) – 1 – последний номер, используемый в $\mathcal{V}$.
Для перехода от упорядоченного кортежа $\mathcal{V}$ к общему необходимо воспользоваться отображением $\mathcal{V}$: [0, n[ → dom($\mathcal{V}$) | $ \in \to $ [0, n[ ${{\mathcal{V}}_{{ \in \,[0,n[ \to }}}$ ∈ dom($\mathcal{V}$).
Последовательность $\mathcal{V}$, в отличие от кортежа, не имеет определенного конца, который уходит в бесконечность ∞: $\mathcal{V}$ ≡ 〈${{\mathcal{V}}_{0}}$, ${{\mathcal{V}}_{1}}$, …〉 ≡ 〈${{\mathcal{V}}_{0}}$, ${{\mathcal{V}}_{1}}$, …, ∞〉.
12.4. Взаимоотношение кортежей: x: R → X и y: S → Y:
y ⊆ x 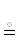 S → Y ⊆ R → X ⇔ {{R → X и Y ⊆ X}} ← подкортеж y кортежа x,
S → Y ⊆ R → X ⇔ {{R → X и Y ⊆ X}} ← подкортеж y кортежа x,
r $ \dashv $ x 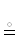 x $ \vdash $ r := r→x(r) ← проекция атрибута r на кортеж x,
x $ \vdash $ r := r→x(r) ← проекция атрибута r на кортеж x,
S $ \dashv $ x  x $ \vdash $ S := {r→x(r)|r ∈ R ∩ S} ← проекция подсхемы S на кортеж x,
x $ \vdash $ S := {r→x(r)|r ∈ R ∩ S} ← проекция подсхемы S на кортеж x,
x $ \dashv $ S 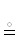 S $ \vdash $ x := R ∩ S ← VICE VERSA: проекция кортежа x на схему S.
S $ \vdash $ x := R ∩ S ← VICE VERSA: проекция кортежа x на схему S.
Свойства: (S $ \dashv $ x) $ \dashv $ R = R ∩ S; (x $ \dashv $ S) $ \dashv $ y = R ∩ S $ \dashv $ y; y ⊆ x ⇒ (x $ \dashv $ S) $ \dashv $ y = y.
12.5. Особый кортеж, не имеющий ни определенной схемы $\overrightarrow \subset $R, ни заполнения X, будем называть пустым и обозначать через ∅. Состав его схемы произволен. На атрибутах пустого кортежа (ПуК) значения представляют собой пустоту. ПуК обладает свойством пустого множества ($\overrightarrow \subset $x) ∪ ∅ = ($\overrightarrow \subset $x).
13. × – декартовое произведение (ДП) множеств X1, X2, …, Xn:
X×n := X1 × … × Xn | X := X1 = … = Xn ← декартовая степень n множества X.
Внимание! A × ∅ = ∅ = ∅ × A не коммутативно.
Формально: ∅ ≠ A ≠ B ≠ ∅ ⇒ A × B ≠ B × A.
14. ГЛАГОЛЫ-ПРЕДИКАТЫ77, ОТНОШЕНИЯ-ТАБЛИЦЫ
14.1. В бинарных предикатах глагол связывает две сущности и, грубо говоря (ниже будет дано уточнение), представляет собой плоское бинарное отношение88 между возможно различными множествами. Замена сущностей предиката другими предикатами,
называющаяся суперпозицией, приводит к образованию многоместных (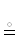 n-арных, где n – количество мест) предикатов, являющихся частными случаями предикатов, созданных
на основе таблиц общего вида (см. далее разд. 2). Суперпозиции для них реализуются
соединением ⋈ таблиц, как это описано далее. К сказанному добавим три замечания.
n-арных, где n – количество мест) предикатов, являющихся частными случаями предикатов, созданных
на основе таблиц общего вида (см. далее разд. 2). Суперпозиции для них реализуются
соединением ⋈ таблиц, как это описано далее. К сказанному добавим три замечания.
1. Предикат является математическим объектом в духе примечания 5, позволяющим генерировать
кортежи и таблицы из них. Имя и Шапка (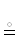 схема) таблицы с приданными им правилами ее заполнения образуют глагол, связывающий используемые в нем сущности. С языковой точки зрения глагол и присоединенный
к нему кортеж представляют высказывание, реализующее предикат. Глагол высказываний отождествляется с глаголом предиката,
если кортежи высказываний генерируются их предикатом. В смысле ТРБД и алгебры все
кортежи таблицы-предиката составляют отношение. Явное добавление к нему схемы превращает его в таблицу. Однако на практике максимально-предельное
заполнение таблицы кортежами вряд ли возможно. Поэтому предикат играет роль виртуальной
таблицы и далее становится самостоятельным объектом логики, в рамках которой логический
вывод осуществляется виртуальными операциями ⋈ соединения таблиц, а переход к выводимому
предикату обозначается символом ⇒. Заметим, что одноразовый шаг вывода ⇒ становится
невырожденным глаголом в силу того, что далеко не каждая ориентированная пара (тройка,
четверка и т.д.) утверждений (предикатов) может быть связана выводом и в то же время
такие пары существуют.
схема) таблицы с приданными им правилами ее заполнения образуют глагол, связывающий используемые в нем сущности. С языковой точки зрения глагол и присоединенный
к нему кортеж представляют высказывание, реализующее предикат. Глагол высказываний отождествляется с глаголом предиката,
если кортежи высказываний генерируются их предикатом. В смысле ТРБД и алгебры все
кортежи таблицы-предиката составляют отношение. Явное добавление к нему схемы превращает его в таблицу. Однако на практике максимально-предельное
заполнение таблицы кортежами вряд ли возможно. Поэтому предикат играет роль виртуальной
таблицы и далее становится самостоятельным объектом логики, в рамках которой логический
вывод осуществляется виртуальными операциями ⋈ соединения таблиц, а переход к выводимому
предикату обозначается символом ⇒. Заметим, что одноразовый шаг вывода ⇒ становится
невырожденным глаголом в силу того, что далеко не каждая ориентированная пара (тройка,
четверка и т.д.) утверждений (предикатов) может быть связана выводом и в то же время
такие пары существуют.
2. Приведем пример связи между предикатом и его таблицей. Рассмотрим высказывание “Мама мыла Милу мылом”. В нем глагол “мыть” можно рассматривать как схему {“Кто?Что?” “Кого? Что?” “Кем? Чем?”}99, образующую из сущностей “Мама”, “Мила”, “мыло” осмысленный кортеж, т.е. высказывание. Для большей наглядности заполним таблицу “мыть” тремя высказываниями:
3. Совокупность всех мыслимых предикатов назовем “Картиной Мира”. Во избежание противоречий, заключенных в этой конструкции, необходимо убрать из нее квантор “всех”. Картину Мира, ограниченную какими-либо обстоятельствами, будем называть “Частной (Частичной) Картиной Мира” (ЧКМ). Исходя из конструктивности ЧКМ, количество ее предикатов должно быть конечным. Но это означает, что каждая ЧКМ описывается одним предикатом, получающимся из заданных операцией соединения. Обратно, заданная ЧКМ, благодаря теореме Хита, может быть разложена его социоэлементом на составляющие, для чего требуются ФЗ, возникающие в сознании на интуитивном уровне или, быть может, являющиеся результатом вычислений или целеуказаний. Из них иной социоэлемент, привлекая предикаты третьего социоэлемента, может производить свою ЧКМ и передавать ее четвертому социоэлементу при наличии “взаимопонимания” между ними. Таким образом имеется возможность средствами ТРБД, как части Общей алгебры1010, формализовать понятие “взаимопонимание” на, основе получения непустых предикатов из заданных. В конкретных условиях соединение ⋈ предикатов и разложение Хита могут не быть взаимообратными, тем интереснее вопрос для дальнейших исследований.
14.2. Изъявительные предикаты в зависимости от обстоятельств могут быть в трех состояниях: ДА НЕТ Не
Знаю1111, последнее из которых характерно для предикатов, содержащих объекты. Для него можно
предложить другую форму: МожетБыть|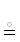 НеЗнаю. Изъявительные предикаты пассивны и внутренними источниками информации не располагают.
Их истинность устанавливается по соответствию свойствам окружения (контекста). В качестве
примера приведем символы следствия ⇒, ⇐ и ⇔, которые служат глаголами в изъявительных бинарных предикатах. То же относится и к глаголу = “равно” при его правильном применении.
НеЗнаю. Изъявительные предикаты пассивны и внутренними источниками информации не располагают.
Их истинность устанавливается по соответствию свойствам окружения (контекста). В качестве
примера приведем символы следствия ⇒, ⇐ и ⇔, которые служат глаголами в изъявительных бинарных предикатах. То же относится и к глаголу = “равно” при его правильном применении.
14.3. Повелительные предикаты выражают ДЕЙСТВИЯ и могут быть только в состоянии ДА безотносительно к их внутреннему устройству. Они предназначенны для формирования новых субъектов из существующих. В настоящей работе предусмотрено использование бинарных ДЕЙСТВИЙ, выражаемых глаголами :=, $ \in \to $, $\overrightarrow \subset $, !, {}. Из сказанного, в частности, следует, что достаточность и независимость предлагаемого состава действий требует специального расследования. Действия, как правило, приводят к потере информации об ее источниках, например 5 := 3 + 2 .
14.4. Глаголы совершенного вида1212 обладают $ \ulcorner {\text{внутренней}} \lrcorner $1313, информацией, позволяющей установить их истинность, выражающуюся логической величиной ДА. В этом качестве необходимо рассматривать глагол ≡ “равно тождественно”. К сожалению, во многих случаях в том же смысле используется глагол =, но это требует контекстной поддержки.
15. ! – символ гипотез. Изъявительные предикаты вида $\mathcal{A}$(α, …, ω) могут быть приведены в состояние ДА за счет решения уравнения $\mathcal{A}$(α, …, ω) = ДА, что неявно объявляет и инициализирует сущностные переменные α, …,
ω. С этой целью в математике используется повелительный глагол ПУСТЬ или его синоним
LET, которые будем заменять знаком !, скрывающим использование квантора $\exists $ существования: $\exists $α, …, ω|$\mathcal{A}$(α, …, ω)  !$\mathcal{A}$(α, …, ω). Надо понимать, что !a ∈ X
!$\mathcal{A}$(α, …, ω). Надо понимать, что !a ∈ X 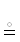 a $ \in \to $ X и $\exists $a ∈ X
a $ \in \to $ X и $\exists $a ∈ X 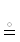 {{!a ∈ X ⇒ a ∈ A}}.
{{!a ∈ X ⇒ a ∈ A}}.
Определение 1. Двоичный предикат. Предикат $\mathcal{A}$ назовем двоичным, если его состояниями могут быть значения {ДА НЕТ}. Отрицание ¬$\mathcal{A}$ бинарно-двоичного предиката $\mathcal{A}$ воздействует на его глагол $\mathbb{V}$. Если $\mathcal{A}$ := $\mathfrak{X}\mathbb{V}\mathfrak{Y}$, то $\mathcal{A}$ 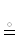 $\mathfrak{X}\neg \mathbb{V}\mathfrak{Y}$
$\mathfrak{X}\neg \mathbb{V}\mathfrak{Y}$ 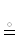 ${{\mathfrak{X}}_{ \to }}\mathfrak{Y}$ ∉ $\mathbb{V}$.
${{\mathfrak{X}}_{ \to }}\mathfrak{Y}$ ∉ $\mathbb{V}$.
Определение 2. $\mathcal{A}?$ := {0|¬$\mathcal{A}$ или 1|$\mathcal{A}$} – функция истинности (ФИ) двоичного предиката $\mathcal{A}$. Заметим, что двоичный – эпитет логики; бинарный – эпитет конструкции предиката, т.е. имеет место терминологическое расхождение:
двоичный предикат 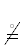 бинарный предикат.
бинарный предикат.
Определение 3. Множество M назовем нéмощным, если μ(M) ≤ 1. Прочие множества будут называться мощными.
1.2. Логические схемы (ЛС). Перейдем к логическим манипуляциям, основанным на жесткой структуризации текста. Ниже сущности текста, являющиеся предметом манипуляций, именованы буквами $\mathcal{A}\mathcal{B}\mathcal{C}$. Для ЛС ими должны быть некоторые предикаты из которых ЛС вычисляют иные предикаты. Данная проблематика заслуживает развития собственной теории, но ниже пространственное взаимодействие между сущностями, связанных логическим выводом, носит описательный характер, достаточный для нужд алгебраизации ПВ.
Во-первых. Каждое утверждение настоящей статьи начинается собственным заголовком. Следующий заголовок является одновременно концом предыдущего утверждения. Доказательства утверждений, следующих после этой договоренности, начинаются со слова “Доказательство”.
Во-вторых. См. обозначение 8.
В-третьих. Цепочка импликаций ${{\mathcal{A}}_{1}}$ ⇒ ${{\mathcal{A}}_{2}}$; ${{\mathcal{A}}_{2}}$ ⇒ ${{\mathcal{A}}_{3}}$; …; ${{\mathcal{A}}_{{k - 1}}}$ ⇒ ${{\mathcal{A}}_{k}}$, которую назовем потоком предикатов, записывается в виде ${{\mathcal{A}}_{1}}$ ⇒ ${{\mathcal{A}}_{2}}$; ⇒ ${{\mathcal{A}}_{3}}$; ⇒ …; ⇒${{\mathcal{A}}_{{k - 1}}}$ ⇒ ${{\mathcal{A}}_{k}}$. Вместо ‘;’ могут использоваться любые знаки препинания: точка, двоеточие и пр. Их присутствие в потоке существенно, так как импликация в логических выражениях не ассоциативна. Игнорирование делителей потока {; . : …} допускается, если возможно их контекстное восстановление. Для вертикального вывода используются $\ddot { \Downarrow }$, и $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\cdot\cdot}$}}{ \Uparrow } $.
В-четвертых. Точки входа-выхода в графах доказательств отмечаются иероглифами {$ \rtimes $ ⇒, ⇐$ \ltimes $} и {⇒$ \rtimes $, $ \ltimes $⇐} соответственно.
В-пятых. Направленность внешних импликаций задает направление чтения равенств в цепочке, так запись ⇒ a0 = a1 = … = ak – 1 = ak; ⇒ … должна пониматься как ⇒a0 = a1;⇒ a1 = a2; ⇒ …; ⇒ ak – 1 = ak; ⇒ … То же относится к противоположному направлению равенств в цепочке. В конструкции …$\left\{ \begin{gathered} \Rightarrow \\ \Leftarrow \\ \end{gathered} \right\}$a0 = a1 = … = ak – 1 = ak$\left\{ \begin{gathered} \Leftarrow \\ \Rightarrow \\ \end{gathered} \right\}$… возможно использование планарных внешних следований, что для общего случая объясняется ниже.
В-шестых. В заключение построим на примерах {{этого достаточно}} пространственный алгоритм (ПА) {{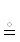 ЛС}} из отдельных СИЛЛОГИЗМОВ1414, известных со времен Аристотеля. Каждый из них имеет вид {{${{\mathcal{A}}_{1}}$ и ${{\mathcal{A}}_{2}}$ и … и ${{\mathcal{A}}_{k}}$}} ⇒ $\mathcal{A}$|k ∈ ${{\mathbb{Z}}^{ + }}$, что необходимо понимать в качестве развeтвителя в графах доказательств {{
ЛС}} из отдельных СИЛЛОГИЗМОВ1414, известных со времен Аристотеля. Каждый из них имеет вид {{${{\mathcal{A}}_{1}}$ и ${{\mathcal{A}}_{2}}$ и … и ${{\mathcal{A}}_{k}}$}} ⇒ $\mathcal{A}$|k ∈ ${{\mathbb{Z}}^{ + }}$, что необходимо понимать в качестве развeтвителя в графах доказательств {{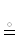 ПА
ПА 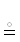 ЛС}} после придания ему геометрического вида
ЛС}} после придания ему геометрического вида 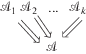 .
.
Три примера использования силлогизмов представлены ниже:
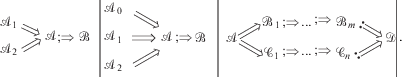 (1.1)
(1.1)
Кусты импликаций (1.1) эквивалентны предикатам {{${{\mathcal{A}}_{1}}$ и ${{\mathcal{A}}_{2}}$}} ⇒ $\mathcal{A}$; ⇒ $\mathcal{B}$, {{${{\mathcal{A}}_{0}}$ и ${{\mathcal{A}}_{1}}$ и ${{\mathcal{A}}_{2}}$}} ⇒ $\mathcal{A}$; ⇒ $\mathcal{B}$ и $\mathcal{A}$ ⇒ {{${{\mathcal{B}}_{1}}$; ⇒ …; ⇒ ${{\mathcal{B}}_{m}}$ и ${{\mathcal{C}}_{1}}$ ; ⇒ …; ⇒ ${{\mathcal{C}}_{n}}$}}; ⇒ $\mathcal{D}$ соответственно. В последнем примере начальный вывод силлогизмом не является. Его
нужно понимать в смысле {{${{\mathcal{B}}_{1}}$ ⇐ $\mathcal{A}$ ⇒ ${{\mathcal{B}}_{2}}$}} 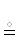
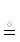 {{$\mathcal{A}$ ⇒ ${{\mathcal{B}}_{1}}$ и $\mathcal{A}$ ⇒ ${{\mathcal{B}}_{2}}$}}. Рекомендуется импликации ⇒ использовать в ЛС, соединяя ими глаголы предикатов,
поскольку глаголы имеют практически точечное изображение, например ∈ ⊆ $ \in \to $ $\overrightarrow \subset $ := и пр. Текстовые предикаты – леммы, теоремы, формулы и пр., заменяются именами.
Ввиду их компактности они также могут быть соединены графическими образами импликаций.
{{$\mathcal{A}$ ⇒ ${{\mathcal{B}}_{1}}$ и $\mathcal{A}$ ⇒ ${{\mathcal{B}}_{2}}$}}. Рекомендуется импликации ⇒ использовать в ЛС, соединяя ими глаголы предикатов,
поскольку глаголы имеют практически точечное изображение, например ∈ ⊆ $ \in \to $ $\overrightarrow \subset $ := и пр. Текстовые предикаты – леммы, теоремы, формулы и пр., заменяются именами.
Ввиду их компактности они также могут быть соединены графическими образами импликаций.
Доказательства строятся из ЛС типа (1.1). В общем виде они могут представляться изощренными графами, но относительно простые ЛС, вроде (1.1), можно упаковывать в строки с помощью скобок {{и}}, как показано ниже:
Общим назначением скобок {{}} является придание простого статуса сложным предикатам. Вход и/или выход в сложные предикаты, получивших статус простых, возможен только с помощью импликаций, примыкающих к скобкам {{}} с внутренних сторон.
В следствиях типа $\mathcal{A}$ ⇒ {{…}} и $\mathcal{A}$ ⇐ {{…}}, где скобки свободны от внутренних примыкающих импликаций, их содержимое, обозначенное точками, представляет собою единое целое. В этом случае скобки {{и}} всего лишь группируют заключенные в них сущности (в частности, предикаты).
Синонимы: логическая схема (ЛС), л. схема, пространственный вывод, пространственный алгоритм (ПА), граф доказательств.
Дизъюнкция (союз “или”) реализуется за счет разделения случаев и отображения каждого своим графом. Так, например, доказательство совпадения S = T двух множеств S и T иногда строится из двух доказательств S ⊆ T и S ⊇ T, помечаемых маркерами $ \subseteq \bigcirc $ и $ \supseteq \bigcirc $ соответственно. То же относится к логической эвивалентности. Доказательство утверждения $\mathcal{A}$ ⇔ $\mathcal{B}$ разбивается на два этапа, открывающихся маркерами $ \Rightarrow \bigcirc $ и $ \Leftarrow \bigcirc $. Подытожим сказанное формулами1515
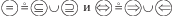 (1.2)
(1.2)
ЛС визуализируют доказательства теорем. В настоящей работе они используются в строчном и планарном виде. Дополнительно с примерами ЛС можно познакомиться в [5, 10, 11]. Там и здесь ЛС являются орграфами. Их вершины образуются предикатами, которые поддаются трактовке как события, следующие друг за другом в соответствии с указателем дискретного времени ↦ (см. ниже обозначение 28), встроенным в ⇒. Однако они могут возникать одновременно, как, например, события ${{\mathcal{A}}_{0}}$, ${{\mathcal{A}}_{1}}$, ${{\mathcal{A}}_{2}}$ или ${{\mathcal{B}}_{1}}$, ${{\mathcal{C}}_{1}}$ в (1.1), и в этом смысле их можно и дóлжно каким-то образом размещать в пространстве, т.е. ЛС являются ПА. Процессоры современных вычислительных машин (ВМ) линейно во времени обслуживают линейную память. В них СИЛЛОГИЗМЫ и даже процедуры следования, что проще, не имеют архитектурно-аппаратной поддержки и пространственные связи реализуются программным моделированием па основе передачи управления, сопровождаемого процессорным преобразованием фиксированной памяти, упорядоченной линейно. Традиционные (современные) алгоритмы ограничиваются управленческими связями1616 и после их прорисовки в виде блок-схем приобретают пространственный вид, однако мы воздержимся называть их пространственными, поскольку создаются они для линейных вычислителей (компьютеров). В анонсированном цикле статей будет показано сочетание работы ЛС с блок-схемами, что позволит сформировать представление о необходимости для автоматизации формирования математических доказательств, в частности, и искусственного интеллекта вообще. Надеемся, что ПА станут предпосылкой формализации так называемых нейронных сетей в рамках математической логики.
ЛС представляют собой часть ЯЗЫКа доказательств, дающего возможность формальной самопроверки (другая часть в виде блок-схем пока скрыта от нас). Его синтаксис задает правила вывода, которые рассчитаны на поток массовых доказательств математических утверждений. Разобранные выше логические основания не имеют отношения к заявленной теме математических исследований, но формируют ее изложение. Необходимо понимать, что используемый ЯЗЫК является неотъемлeмой частью решения поставленных задач. В нем заложены следующие логические и методические принципы:
1. Циклы в графах доказательств используются для установки логической эквивалентности утверждений, что заранее предусматривается и отдельно оговаривается.
2. В остальных случаях доказательство является ациклическим направленным графом. Доказательство в виде логических схем упраздняет использование условных конструкций типа “если…, то …”, загромождающих логику общих утверждений и затрудняющих проверку их корректности.
3. Строгая однозначность анализа и синтеза сущностей доказательств.
То же относится к доказательствам после их материализации в виде ЛС.
4. Визуализация доказательств. “Лучше один раз увидеть, чем сто раз услышать”. Визуализация обеспечивает многовариантную проверку доказательств. ЛС компактны и позволяют держать пути рассуждений от исходных предпосылок до результатов под неусыпным вниманием.
5. Простота обучения правилам доказательств.
Основная цель настоящей работы сформулирована в Аннотации, но во Введении она расширена списком решаемых задач всего цикла работ, которые также являются приглашением, адресованным всем любителям истины, к исследованиям математического вывода и искусственного интеллекта. Возможно, коллекция ЛС, собранная в нем, будет способствовать постановкам новых задач математической логики и их решениям.
2. Отношения и таблицы. 2.1. Сущности. Таблицы двумерны, т.е. они состоят из кортежей, составленных в свою очередь из (значений 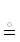 ) элементов доменов, привязанных к атрибутам схемы R
(см. примечание 6). Во всех реализациях систем управления РБД (СУРБД) атрибуты называются полями. Характерной особенностью ТРБД является требование конечности, предъявляемое к схемам
таблиц. Конечность на домены не распространяется. Домены разных атрибутов (
) элементов доменов, привязанных к атрибутам схемы R
(см. примечание 6). Во всех реализациях систем управления РБД (СУРБД) атрибуты называются полями. Характерной особенностью ТРБД является требование конечности, предъявляемое к схемам
таблиц. Конечность на домены не распространяется. Домены разных атрибутов (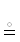 полей) могут совпадать.
полей) могут совпадать.
Определение 4. Домены атрибутов и подсхем [7, гл. 1, § 2, с . 12]. Пусть R – схема, $\mathcal{D}$ – произвольное множество, необязательно конечное, и δ|δ ⊆ R × $\mathcal{D}$ – бинарное отношение1717. Определим домены атрибутов r|r $ \in \to $ R и домены подсхем X|X $\overrightarrow \subset $ R равенствами: dom(r) := rδ: = {d | d ∈ $\mathcal{D}$ и rδd} и dom(X) := $\mathop \times \limits_{x \in X} $dom(x).
Заметим, если Dom(X) := $\mathop \times \limits_{x \in X} $〈x, dom(x)〉 состоит из кортежей, внутренне упорядоченных, если R упорядочено, так как X $\overrightarrow \subset $ R наследует упорядоченность от R. Кроме того, rδ можно назвать правым конусом δ с опорой r, следуя предстоящему обозначению 27 〈3〉.
Далее поэтапно сформулируем основное понятие ТРБД – отношение, и с его помощью определим плоское бинарное отношение (см. определение 16), известное в алгебре как бинарное отношение.
Определение 5. Отношение и таблица.
〈1〉 Отношением,  со схемой R называется μ(R)-арное отношение на совокупности доменов {dom(r) | r ∈ R}. Формально:
со схемой R называется μ(R)-арное отношение на совокупности доменов {dom(r) | r ∈ R}. Формально:  $\overrightarrow \subset $ dom(R).
$\overrightarrow \subset $ dom(R).
〈2〉 Таблицей на схеме (со схемой) R называется пара {R,  } =: {
} =: { , R}.
, R}.
Внимание! Понятия таблица и отношение совпадают, но имеет место синтаксическое различие: в таблицах схемы указываются явно, в отношениях – подразумеваются.
Распространение понятия таблицы на подсхемы дается опосредованно нижеследующей формулой
(2.1). Заметим, что условие μ( ) < ∞ (см. обозначение 9), использующеeся на практике, мы опускаем, т.е. определение
5 допускает использование бесконечных таблиц.
) < ∞ (см. обозначение 9), использующеeся на практике, мы опускаем, т.е. определение
5 допускает использование бесконечных таблиц.
Обозначение 16. Множество $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} } $ всех таблиц на подсхеме X.
Если через {X} обозначить подсхему X|X $\overrightarrow \subset $ R как единое целое, то
(2.1)
$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} } : = \{ X\} \times {{2}^{{dom(X)}}}.$Таблица $ \in \to $ $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} } $ со схемой X состоит из кортежей длины μ(X), составленных из элементов доменов dom($ \in \to $X). Для каждой таблицы множества $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} } $ слово {X} является ее именем по умолчанию и может использоваться в качестве предикатного глагола. Сказанное не ограничивает конструктора в назначении синонимичных имен той же таблицы $ \in \to $ $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} } $.
2.2. Атрибутные преобразования таблиц. Усечение кортежа  |
| ∈
∈  подсхемой X|X ⊆ R будет обозначаться через
подсхемой X|X ⊆ R будет обозначаться через  $ \vdash $ X. Формально
$ \vdash $ X. Формально  $ \vdash $ X := {
$ \vdash $ X := { $ \vdash $ x|x ∈ X}, где
$ \vdash $ x|x ∈ X}, где  $ \vdash $ x – значение кортежа
$ \vdash $ x – значение кортежа  на атрибуте x $ \in \to $ X, т.е.
на атрибуте x $ \in \to $ X, т.е.  $ \vdash $ x ∈ dom(x). Для наглядности элементы в кортежах расположим горизонтально, а кортежи в таблице
$ \vdash $ x ∈ dom(x). Для наглядности элементы в кортежах расположим горизонтально, а кортежи в таблице
 – вертикально, тогда для атрибута x $ \in \to $ R совокупность {
– вертикально, тогда для атрибута x $ \in \to $ R совокупность { $ \vdash $ x|
$ \vdash $ x| ∈
∈  } образует колонку таблицы, реализующую ее поле (
} образует колонку таблицы, реализующую ее поле ( атрибут) x. Внесение элементарной геометрии в таблицу условно, но позволяет прийти к следующим
соглашениям:
атрибут) x. Внесение элементарной геометрии в таблицу условно, но позволяет прийти к следующим
соглашениям:
Синонимы: {{кортеж, строка, ряд}}, {{атрибут, поле, колонка}}, {{проекция, усечение}}, {{атрибутные, вертикальные}} преобразования.
Выделенные курсивом термины являются текущими ключевыми словами ТРБД.
Определение 6. Проекция подсхем на кортежи и отношения. Кортеж  $ \vdash $ X |
$ \vdash $ X |  X $ \dashv $
X $ \dashv $  называется1818 проекцией подсхемы X па
называется1818 проекцией подсхемы X па  . Далее определим
. Далее определим  $ \vdash $ X := X $ \dashv $
$ \vdash $ X := X $ \dashv $  := {
:= { $ \vdash $ X |
$ \vdash $ X |  ∈
∈  } проекцию подсхемы X на отношение
} проекцию подсхемы X на отношение  , дающую неравенство
, дающую неравенство
 могут возникнуть совпадающие кортежи в
могут возникнуть совпадающие кортежи в  $ \vdash $ X, различие между которыми ранее поддерживалось элементами удаленных колонок. Таким
образом автоматически обеспечивается принцип ТРБД “Отсутствие одинаковых кортежей
в таблице” [12, гл.5, § 5.3, с. 166].
$ \vdash $ X, различие между которыми ранее поддерживалось элементами удаленных колонок. Таким
образом автоматически обеспечивается принцип ТРБД “Отсутствие одинаковых кортежей
в таблице” [12, гл.5, § 5.3, с. 166].
Синонимы: проекция подсхемы X на таблицу  (на кортеж
(на кортеж  );
);
усечение ( ограничение) таблицы
ограничение) таблицы  (кортежа
(кортежа  ) подсхемой X.
) подсхемой X.
Тождество R $ \dashv $  ≡
≡  , осуществляя привязку схемы R к отношению
, осуществляя привязку схемы R к отношению  , дает основание для рaсширения синтаксиса определения 5〈2〉:
, дает основание для рaсширения синтаксиса определения 5〈2〉:
В результате таблица R $ \dashv $  получает еще один псевдоним R
получает еще один псевдоним R . В целях экономии места в формулах и выражениях и придания им большей выразительности
уберем из обозначения ограничений таблицы подсхемой знаки проекций, как это сделано
в (2.3).
. В целях экономии места в формулах и выражениях и придания им большей выразительности
уберем из обозначения ограничений таблицы подсхемой знаки проекций, как это сделано
в (2.3).
Примеры: {1 3 2}2 1 3  {2 1 3, {1 2 3}}
{2 1 3, {1 2 3}} 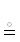 {{1 2 3}, 3 2 1} ← результат формирования одномерной таблицы из множества 1 2 3,
привязанного к атрибуту {1 2 3}.
{{1 2 3}, 3 2 1} ← результат формирования одномерной таблицы из множества 1 2 3,
привязанного к атрибуту {1 2 3}.
Обозначение 17. Х-ограничение отношения  |X ⊆ R:
|X ⊆ R:
X := X $ \dashv $
:= X $ \dashv $  ≡
≡  $ \vdash $ X =:
$ \vdash $ X =:  X ← ограничение отношения
X ← ограничение отношения  подсхемой X.
подсхемой X.
Определение 7. Проекция кортежей и отношений на схему. Результат R $ \vdash $ 
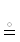
 $ \dashv $ R инвертирования проекций $ \dashv $ и $ \vdash $, играющих роль глаголов, в обозначении (2.3), называемый нами проекцией отношения
$ \dashv $ R инвертирования проекций $ \dashv $ и $ \vdash $, играющих роль глаголов, в обозначении (2.3), называемый нами проекцией отношения
 на подсхему R, нуждается в философской поддержке.
на подсхему R, нуждается в философской поддержке.
Отношение  как совокупность заполненных из соответствующих доменов кортежей является конечным
продуктом. Дальнейшее использование, как правило, не требует обращения к истокам его
создания в лице атрибутной части, которая выше названа схемой. И все же этот возврат
может быть востребован, когда
как совокупность заполненных из соответствующих доменов кортежей является конечным
продуктом. Дальнейшее использование, как правило, не требует обращения к истокам его
создания в лице атрибутной части, которая выше названа схемой. И все же этот возврат
может быть востребован, когда  $ \dashv $ R ⊂ R. Ниже в § 2.3 это будет продемонстрировано на примере операции соединения кортежей.
$ \dashv $ R ⊂ R. Ниже в § 2.3 это будет продемонстрировано на примере операции соединения кортежей.
Лемма 1. Последовательные свойства атрибутного проектирования:
〈1〉 (X $ \dashv $  ) $ \dashv $ R = X ∩ (
) $ \dashv $ R = X ∩ ( $ \dashv $ R) = X $ \vdash $
$ \dashv $ R) = X $ \vdash $  ← равенства 〈1〉 очевидны,
← равенства 〈1〉 очевидны,
〈2〉 (X $ \vdash $  ) $ \dashv $
) $ \dashv $  = X
= X
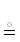
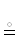 X $ \dashv $
X $ \dashv $  .
.
Доказательство. 〈1〉 ;⇒  $ \dashv $ X = X ∩ (
$ \dashv $ X = X ∩ ( $ \dashv $ R) ;⇒(
$ \dashv $ R) ;⇒( $ \dashv $ X) $ \dashv $
$ \dashv $ X) $ \dashv $  =
=
= (X ∩ ( $ \dashv $ R)) $ \dashv $
$ \dashv $ R)) $ \dashv $  = X $ \dashv $ ((
= X $ \dashv $ (( $ \dashv $ R) $ \dashv $
$ \dashv $ R) $ \dashv $  ) = X
) = X ;⇒ 〈2〉.
;⇒ 〈2〉.
2.3. Объектный синтез. Настоящий раздел статьи посвящается операции соединения ⋈ в виду ее особой важности для теории отношений вообще и ТРБД в частности.
Определение 8. Операция ⋈ соединения кортежей и таблиц.
〈1〉 Соединением кортежей  и $п$ со схемами X :=
и $п$ со схемами X :=  $ \dashv $ R, Y := $п$ $ \dashv $ R и Z := X ∩ Y является кортеж [1, § 2.4, с. 27]
$ \dashv $ R, Y := $п$ $ \dashv $ R и Z := X ∩ Y является кортеж [1, § 2.4, с. 27]
Обозначение $\mathop { \triangleright \triangleleft }\limits_Z $ можно упростить:  ⋈ $п$ :=
⋈ $п$ :=  $\mathop { \triangleright \triangleleft }\limits_Z $$п$ |Z = X ∩ Y, тем более, что
$\mathop { \triangleright \triangleleft }\limits_Z $$п$ |Z = X ∩ Y, тем более, что
Для  ⋈ $п$ = ∅ в силу обозначения 12.5 схема
⋈ $п$ = ∅ в силу обозначения 12.5 схема  ⋈ $п$ может быть любой, например X ∪ Y. Для
⋈ $п$ может быть любой, например X ∪ Y. Для  ⋈ $п$ ≠ ∅ равенство (2.4) очевидно.
⋈ $п$ ≠ ∅ равенство (2.4) очевидно.
〈2〉 Коллективное использование операции ⋈ даст ее обобщение на таблицы  и $П$, с теми же схемами X и Y:
и $П$, с теми же схемами X и Y:  ⋈ $П$ := {
⋈ $П$ := { ⋈ $п$ |
⋈ $п$ |  ∈
∈  , $п$ ∈ $П$}. С помощью ⋈ удобно осуществлять поиск и выбор в таблице R
, $п$ ∈ $П$}. С помощью ⋈ удобно осуществлять поиск и выбор в таблице R кортежей, совпадающих на подсхеме Z $\overrightarrow \subset $ R с каким-либо кортежем $п$|$п$ $ \dashv $ R = Z. Результат дается выражением
кортежей, совпадающих на подсхеме Z $\overrightarrow \subset $ R с каким-либо кортежем $п$|$п$ $ \dashv $ R = Z. Результат дается выражением  ⋈ $п$ | (
⋈ $п$ | ( ⋈ $п$) $ \dashv $ R =
⋈ $п$) $ \dashv $ R =  $ \dashv $ R.
$ \dashv $ R.
Отметим влияние соединителя Z на изменение результата соединения от максимального  × $П$ до минимального ∅: Z = ∅ ⇔
× $П$ до минимального ∅: Z = ∅ ⇔  ⋈ $П$ =
⋈ $П$ =  × $П$;
× $П$;  Z ∩ Z$П$ = ∅ ⇔
Z ∩ Z$П$ = ∅ ⇔  ⋈ $П$ = ∅.
⋈ $П$ = ∅.
Лемма 2. Альтернативное определение соединения:
 ⋈ $П$ = {$ш$ ∈ dom((
⋈ $П$ = {$ш$ ∈ dom(( $ \dashv $ R) ∪ ($П$ $ \dashv $ R)) | (
$ \dashv $ R) ∪ ($П$ $ \dashv $ R)) | ( $ \dashv $ R) $ \dashv $ $ш$ ∈
$ \dashv $ R) $ \dashv $ $ш$ ∈  и ($П$ $ \dashv $ R) $ \dashv $ $ш$ ∈ $П$} =: $Ш$.
и ($П$ $ \dashv $ R) $ \dashv $ $ш$ ∈ $П$} =: $Ш$.
Доказательство. Утверждение  ⋈ $П$ = $Ш$ согласовано с (2.4). Докажем его исходя из X :=
⋈ $П$ = $Ш$ согласовано с (2.4). Докажем его исходя из X :=  $ \dashv $ R, Y := $П$ $ \dashv $ R, Z := Z ∩ Y и используя логическое разделение (1.2):
$ \dashv $ R, Y := $П$ $ \dashv $ R, Z := Z ∩ Y и используя логическое разделение (1.2):
$ \supseteq \bigcirc $ ⇐;  ⋈ $П$ ∋ $ш$ ⇐; $ш$ =
⋈ $П$ ∋ $ш$ ⇐; $ш$ =  ⋈ $п$ ⇐;
⋈ $п$ ⇐;  $ \dashv $ Z = $ш$ $ \dashv $ Z = $п$ $ \dashv $ Z ⇐
$ \dashv $ Z = $ш$ $ \dashv $ Z = $п$ $ \dashv $ Z ⇐
⇐ $ш$ $ \vdash $ X =:  , $ш$ $ \vdash $ Y =: $п$ и $Ш$ ∋ $ш$ ⇐ $ \ltimes $,
, $ш$ $ \vdash $ Y =: $п$ и $Ш$ ∋ $ш$ ⇐ $ \ltimes $,
$ \subseteq \bigcirc $ ⇐;  ∋
∋  = $ш$ $ \vdash $ (R $ \vdash $
= $ш$ $ \vdash $ (R $ \vdash $  ) и $П$ ∋ $п$ = $ш$ $ \vdash $ (R $ \vdash $ $П$) ⇐; $ш$ =
) и $П$ ∋ $п$ = $ш$ $ \vdash $ (R $ \vdash $ $П$) ⇐; $ш$ =  ⋈ $п$ | {{
⋈ $п$ | {{ $ \in \to $
$ \in \to $  и $п$ $ \in \to $ $П$}} ⇐
и $п$ $ \in \to $ $П$}} ⇐
⇐  ⋈ $П$ ∋ $ш$ ⇐ $ \ltimes $.
⋈ $П$ ∋ $ш$ ⇐ $ \ltimes $.
2.4. Сущности семантики таблиц. Каждая ФЗ является упорядоченной парой 〈X, Y〉 =: X→Y =: Y←X (см. обозначение 12.2) подсхем X, Y схемы R. Конструктивно ФЗ проста и может существовать абстрактно вне ТРБД. Именно в таком виде ФЗ на схеме R представлена в обозначениях 18–20, но, начиная с определения 9, будет осуществлен возврат к истокам ФЗ, которыми являются таблицы РБД (см. определение 5).
Обозначение 18. Показательная (степенная) функция множеств:
〈1〉 AW – множество ВСЕХ отображений из множества W в множество А;
〈2〉 2W – множество ВСЕХ подмножеств произвольного множества W|2W := {0, 1}W.
В соглашении 〈2〉 слово 2W сокращает запись {0, 1}W, которая подразумевает взаимнооднозначное соответствие между характеристическими функциями W → {0, 1} и подмножествами в W. Например, 2R × 2R является полным множеством двухкомпонентных кортежей 〈U, V〉|U, V ⊆ R, поскольку в ДП сомножители линейно упорядочены.
Обозначение 19. ФЗ схемы R:
〈1〉 2R→2R| := 2R × 2R ← все ФЗ (см. далее обозначение 21),
〈2〉 X→2R := {X→Z|Z $\overrightarrow \subset $ R}| X $\overrightarrow \subset $ R ← начально определенные ФЗ,
〈3〉 2R→Y := {Z→Y|Z $\overrightarrow \subset $ R}|Y $\overrightarrow \subset $ R ← конечно определенные ФЗ.
Внимание! В обозначениях мы навязываем нижней стрелке роль ДП (см. обозначение 13), хотя в кортежах вида U→V знак '→' является всего лишь направленным соединителем, но не произведением '×'. Это делает выражения 2R→2R и 2R × 2R синонимичными, но первое из них предпочтительнее, поскольку оно визуализирует упорядоченность подмножеств в парах U→V, выбираемых из 2R × 2R, тем более, что само ДП ориентировано.
Обозначение 20. Компоненты ФЗ. Сделаем выбор Φ $ \in \to $ 2R→2R. Слово ΦH обозначает подсхему, фигурирующую в ее Начале, а ΦK – в Конце1919. Из этого следует:
Определение 9. ФЗ таблицы  [1, § 4.1, с. 51; 3, п. 3.6.1, с. 68].
[1, § 4.1, с. 51; 3, п. 3.6.1, с. 68].
Пусть Φ $ \in \to $ 2R→2R – некоторая ФЗ над схемой R. Таблица  – со удовлетворяет Φ, если из
– со удовлетворяет Φ, если из 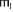 $ \vdash $ ΦH =
$ \vdash $ ΦH = 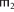 $ \vdash $ ΦHследует
$ \vdash $ ΦHследует 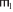 $ \vdash $ ΦK =
$ \vdash $ ΦK = 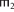 $ \vdash $ ΦKдля ∀ кортежей
$ \vdash $ ΦKдля ∀ кортежей 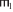 ,
, 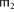 ∈
∈  .
.
Обозначения 3 и 8 позволяют определение 9 представить короче [12, § 10.2, с. 401]:
 удовлетворяет Φ := {{
удовлетворяет Φ := {{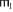 $ \vdash $ ΦH =
$ \vdash $ ΦH = 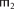 $ \vdash $ ΦH ⇒
$ \vdash $ ΦH ⇒ 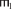 $ \vdash $ ΦK =
$ \vdash $ ΦK = 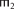 $ \vdash $ ΦK|
$ \vdash $ ΦK|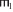 ,
, 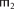 ∈
∈  }}.
}}.
ФЗ, извлекаемые из таблицы с помощью определения 9, отражают ее семантические свойства,
и структуру РБД, получающуюся из таблицы с помощью теоремы Хита (см. [2] и [3, п. 3.6.2, с. 70]). Это означает, что некоторые из них, заданные A PRIORI (см.
примечание 4), могут быть использованы и используются в процессе конструирования РБД.
ФЗ обобщают понятие ключа как совокупности атрибутов, на которых однозначно определяются кортежи отношения.
Ключ в таблице  $ \vdash $ R возникает в виде ΦH, когда ΦK = R. Каждая непустая таблица имеет не менее одной функциональной зависимости, так как
схема R является ее ключом.
$ \vdash $ R возникает в виде ΦH, когда ΦK = R. Каждая непустая таблица имеет не менее одной функциональной зависимости, так как
схема R является ее ключом.
Обозначение 21. Класс 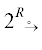 2R разделяющихся ФЗ:
2R разделяющихся ФЗ:
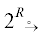 2R := {Θ|ΘH ∩ ΘK = ∅|Θ ∈ 2R→2R} (см. обозначение 2).
2R := {Θ|ΘH ∩ ΘK = ∅|Θ ∈ 2R→2R} (см. обозначение 2).
2.5. Аксиомы вывода.
Определение 10: (влечет) $\mathbb{F}$ $\begin{gathered} \to \hfill \\ \to \hfill \\ \end{gathered} $ A→В (следует) [1, § 4.2, с. 53].
Множество $\mathbb{F}$|$\mathbb{F}$ $\overrightarrow \subset $ 2R→2R влечет за собой A→В | A→В ∈ 2R→2R, если каждое отношение, удовлетворяющее всем зависимостям из $\mathbb{F}$, удовлетворяет также зависимости A→В.
В этом случае будем говорить также, что A→В следует из $\mathbb{F}$, что символически выразим записью $\mathbb{F}$ $\begin{gathered} \to \hfill \\ \to \hfill \\ \end{gathered} $ A→В.
Понятие следования ФЗ из других ФЗ важно для ТРБД, но не кажется конструктивным. Напротив, вывод зависимости A→В из множества $\mathbb{F}$|$\mathbb{F}$ $\overrightarrow \subset $ 2R→2R, обозначаемый далее стрелкой $ \Rrightarrow $, осуществляется шаговым применением к зависимостям из $\mathbb{F}$ правил, именуемых далее F-аксиомами вывода и фигурирующих в табл. 1.
Таблица 1.
F-аксиомы вывода
| Обозначения аксиом вывода | Вход в АВ | $ \Rrightarrow $ | Выход из АВ | |
|---|---|---|---|---|
| литера | имя аксиомы | ФЗ | Результат вывода | |
| F1 | Рефлексивность | $ \Rrightarrow $ | X→Y =: $\bar {X}$ (рефлексия) | |
| F2 | Пополнение | X→Y | $ \Rrightarrow $ | X ∪ Z→Y |
| F3 | Аддитивностъ | X→Y и X→Z | $ \Rrightarrow $ | X→Y ∪ Z |
| F4 | Проективность | X→Y ∪ Z | $ \Rrightarrow $ | X→Y |
| F5 | Транзитивность | X→Y и X→Z | $ \Rrightarrow $ | X→Z |
| F6 | Псевдотранзитивность | X→Y и Y ∪ Z→V | $ \Rrightarrow $ | X ∪ Z→V |
Три аксиомы F1, F2 и F6, называемые аксиомами Армстронга, составляют достаточное и независимое подмножество. Под достаточностью понимается выводимость из них F3, F4 и F5, а независимость означает невозможность вывода каждой аксиомы из оставшихся двух. Такое же самодостаточное множество образуют В-аксиомы [1, § 4.5, с . 60], которые в полном составе размещены в табл. 22020.
Таблица 2.
В-аксиомы вывода
| B1 | Рефлексивность | $ \Rrightarrow $ | X→X =: $\bar {X}$ (рефлексия) | |
| B2 | Накопление | X→(Y ∪ Z) и Y→U | $ \Rrightarrow $ | X→(Y ∪ Z ∪ U) |
| B3 | Проективность | X→(Y ∪ Z) | $ \Rrightarrow $ | X→Y |
Обозначение 22. Подмножества F, В и FB аксиом вывода:
2.6. Неалгоритмический вывод ФЗ.
Определение 11. Замкнутость множества ФЗ. Множество зависимостей $\mathbb{F}$|$\mathbb{F}$ $\overrightarrow \subset $ 2R→2Rзамкнуто или, что то же самое, устойчиво относительно Е|E $\overrightarrow \subset $ FB, если применение аксиом $ \in \to $E к зависимостям из $\mathbb{F}$ дает зависимости из $\mathbb{F}$.
Определение 12. [1, § 4.3, с. 57] Замыканием ${{\mathbb{F}}^{{\mathbf{E}}}}$ множества $\mathbb{F}$ аксиомами из Е назовем множество ФЗ, наименьшее из замкнутых относительно Е надмножеств $\mathbb{F}$.
Определение 12 допускает дуальную формулировку: ${{\mathbb{F}}^{{\mathbf{E}}}}$ является максимальным множеством Ф3, выводимых из $\mathbb{F}$ с помощью аксиом Е|E $\overrightarrow \subset $ FB [12, § 10.4, с. 405].
Следствия def12. Вычисление некоторых замыканий:
Следующее определение выражает понятие Е-вывода зависимости X→Y из множества $\mathbb{F}$ через его замыкание [1, § 4.3, с. 57].
Определение 13. Неалгоритмическая выводимость:
{{X→Y E-выводима из $\mathbb{F}$, если (X→Y) ∈ ${{\mathbb{F}}^{{\mathbf{E}}}}$}} =: $\mathbb{F}$ $\mathop \Rrightarrow \limits^{\mathbf{E}} $ X→Y =: X→Y $\mathop \Lleftarrow \limits^{\mathbf{E}} $ $\mathbb{F}$, $\mathbb{F}$ $ \Rrightarrow $ X→Y := $\mathbb{F}$ $\mathop \Rrightarrow \limits^{{\mathbf{FB}}} $ X→Y ← индифферентная2121 выводимость.
Непосредственно из определений 10 и 13 следует ($\mathbb{F}$ $ \Rrightarrow $ X→Y) ⇒ ($\mathbb{F}$ $\begin{gathered} \to \hfill \\ \to \hfill \\ \end{gathered} $ X→Y) или то же, но словами: если X→Y выводится из $\mathbb{F}$, то $\mathbb{F}$ влечет за собой X→Y.
Большим достижением ТРБД является нижеследующая теорема 1 об эквивалентности вывода $ \Rrightarrow $ и следования $\begin{gathered} \to \hfill \\ \to \hfill \\ \end{gathered} $. Ее изложение в [1] одновременно определяет понятие полноты, включает в себя предыдущее утверждение и обратное к нему.
Теорема 1. [Армстронг] Система F аксиом вывода полна.
X→Y является результатом F-вывода из $\mathbb{F}$ тогда и только тогда, когда $\mathbb{F}$ влечет за собой X→Y. Формально ($\mathbb{F}$ $ \Rrightarrow $ X→Y) ⇔ ($\mathbb{F}$ $\begin{gathered} \to \hfill \\ \to \hfill \\ \end{gathered} $ X→Y).
Ее доказательство можно почерпнуть в [1, § 4.4, теорема 4.1, с. 58].
Лемма 3. Системы аксиом В и F – эквивалентны.
Из леммы 3 следует: система В := В1–ВЗ := {В1, В2, ВЗ} – полна [1, § 4.5, с. 60]. Полнота B-аксиом приводит к возможности заменить F-вывод В-выводом и наоборот и, вообще, использовать на равных индифферентный вывод.
2.7. Алгоритмический вывод ФЗ. Перейдем теперь к “штучной” реализации вывода ФЗ. Пусть $\mathbb{P}$ $\overrightarrow \subset $ 2R→2R – множество ФЗ над схемой R {{⇒ $\mathbb{P}$ – конечно}} . В нижеследующем определении 14 предъявляются требования к алгоритму формирования последовательности вывода [1, § 4.5, с. 59] некоторой ФЗ из множества $\mathbb{P}$.
Определение 14. Последовательность $\mathcal{P}$ вывода Θ|Θ ∈ 2R→2R из $\mathbb{P}$. Внесение линейного порядка в $\mathbb{P}$ делает из него ПВ $\mathcal{P}$ {{⇒ $\mathbb{P}$ ⊆ $\mathcal{P}$}}: если каждая ФЗ в $\mathcal{P}$:
либо выводится из предыдущих ФЗ в $\mathcal{P}$ после применения к ним одной из АВ,
либо не выводима вообще из каких-либо ФЗ множества $\mathbb{P}$, т.е. является членом $\mathbb{P}$.
Внимание! 1. Данное определение допускает повторы ФЗ в $\mathcal{P}$. Это первое препятствие на пути к алгебраизации ПВ. Для его временного преодоления предлагается заменить элементы $ \in \to $$\mathcal{P}$ парами вида №($ \in \to $$\mathcal{P}$)→$ \in \to $$\mathcal{P}$, где №($ \in \to $$\mathcal{P}$) – порядковый номер $ \in \to $$\mathcal{P}$ в $\mathcal{P}$. Этот прием обеспечивает обратимый переход от упорядоченных кортежей $\mathcal{P}$, имеющих тип 〈 〉, к неупорядоченным типа {} с упорядоченными атрибутами №($ \in \to $$\mathcal{P}$). Префикс №($ \in \to $$\mathcal{P}$)→ материализует упорядоченность исходной ПВ в неупорядоченном кортеже. Полностью проблема неоднозначности использования ФЗ в ПВ решается ФЭ-заменой ПВ так называемым плотным выводом в задаче 3) Введения.
2. С проектной точки зрения $\mathbb{P}$ должно состоять из невыводимых в $\mathcal{P}$ зависимостей, но в силу п. 1 элементы $ \in \to $$\mathbb{P}$ имеют право встречаться в $\mathcal{P}$ многажды по причинам повторного использования или вывода, некоторых $ \in \to $$\mathbb{P}$ из других $\overrightarrow \subset $$\mathbb{P}$. В любом случае $\mathbb{P}$ = min{$\mathcal{P}$, =$ \Rrightarrow $} (см. обозначение 23〈2〉) и элементы из $\mathbb{P}$ называются константами. Далее термин “константа” встречается с разными смысловыми оттенками, но идея их принадлежности к min$\mathcal{W}$, где $\mathcal{W}$ – некоторый конус, остается неизменной.
Примечание 1. Местоположение Θ в $\mathbb{P}$ определяется ниже в обозначении 23〈4〉.
Обозначение 23 (от 〈1〉 до 〈4〉). Каскад порядков вывода:
〈1〉 $\mathcal{P}$ является “двухцветным” графом (см. далее обозначения 34):
↠ ребро пошагового формирования, {$\mathbb{P}$, ↠} граф следования,
$ \Rrightarrow $ ребро вывода, {$\mathbb{P}$, $ \Rrightarrow $} граф вывода.
〈2〉 $\mathcal{P}$ является носителем двух структур упорядочения:
=↠ упорядоченность ее формирования,
=$ \Rrightarrow $ порядок вывода в ней ФЗ.
Примечание 2. Общее свойство {{Φ = $ \Rrightarrow $ Ψ ⇒ Φ = ↠Ψ}} делает, в частности, плотную последoвательность вывода каскадно-упорядоченным множеством (см. далее определение 20), что является предметом исследования задач 2),3) Введения.
3. По причине “Внимание! 1” в общем случае =↠ и =$ \Rrightarrow $ не являются частичными порядками, но в пределах одного звена вывода они совпадают с ребром ↠. Поэтому направления вывода можно условно записать в виде min =↠ max и min =$ \Rrightarrow $ max, графически противоположными знаку ≤|(min ≤ max) упорядочения (сравни с “Внимание! 3” в разд. 3.4).
〈3〉 Сборка $\mathcal{P}$: $\mathcal{P}$ ≡ {$\mathbb{P}${↠ =↠}{$ \Rrightarrow $ =$ \Rrightarrow $}} ← трехэлементное множество
〈4〉 ПВ – как процесс и как результат (см. обозначения 9 и 12.3):
$\mathcal{P}$ $ \Rrightarrow $ Θ := {{${{\mathcal{P}}_{{\mu (\mathcal{P}) - 1}}}$ = Θ}} =: Θ $ \Lleftarrow $ $\mathcal{P}$ ← процесс,
$\mathcal{P}$ является выводом для Θ, если ${{\mathcal{P}}_{{\mu (\mathcal{P}) - 1}}}$ = Θ ← тоже словами,
Θ〈〈$\mathbb{P}$〉〉 := ${{\mathcal{P}}_{{\mu (\mathcal{P}) - 1}}}$ =: Θ (см. обозначение 3.37) ← результат.
Представление Θ в виде функции Θ〈〈$\mathbb{P}$〉〉 от констант $\mathbb{P}$ позволит выращивать деревья вывода, используя суперпозиции, как в обозначениях 39 для склеивания так называемых острых множеств (см. далее определение 22) или, как в [4, теорема 3, с. 68], “АР-декомпозиция плотного вывода”.
Обозначение 24. Стилевые классы ФЭПВ: {$\mathbb{F}$ $\mathop \Rrightarrow \limits^{\mathbf{E}} $ A→B} | E $\overrightarrow \subset $ FB.
Ниже приведены примеры классов ФЭПВ стиля Е:
{$\mathbb{F}$ $ \Rrightarrow $ A→B} – все последовательности вывода A→B из $\mathbb{F}$ | E := FB;
{2R→2R $ \Rrightarrow $ Ψ} – все ПВ, выводящие Ψ (все ФЭПВ для вывода Ψ) | E := FB;
{$\mathbb{F}$ $\mathop \Rrightarrow \limits^{{\mathbf{B2}}} $ Ψ $\mathop \Lleftarrow \limits^{{\mathbf{B2}}} $ $\mathbb{G}$} 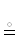 {$\mathbb{F}$ $\mathop \Rrightarrow \limits^{{\mathbf{B2}}} $
{$\mathbb{F}$ $\mathop \Rrightarrow \limits^{{\mathbf{B2}}} $ 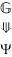 } – все B2-выводы Ψ из $\mathbb{F}$ и $\mathbb{G}$ | E := B2;
} – все B2-выводы Ψ из $\mathbb{F}$ и $\mathbb{G}$ | E := B2;
{$\mathbb{F}$ $\mathop \Rrightarrow \limits^{{\mathbf{B2}}} $ Ψ} – все B2-выводы Ψ из $\mathbb{F}$ | $\mathbb{G}$ = $\mathbb{F}$ | E := B2;
{$\mathbb{F}$ $\mathop \Rrightarrow \limits^{{\mathbf{B23}}} $ A→B} – все выводы A→B из $\mathbb{F}$, использующие B2 и B3 | E := B2 ∪ B3;
{$\mathbb{F}$ $ \Rrightarrow $} := $\bigcup\limits_{\Psi \in {{2}^{R}}_{ \to }{{2}^{R}}}^{} {\{ \mathbb{F} \Rrightarrow \Psi \} } $ – все последовательности выводы из $\mathbb{F}$;
{$\mathbb{F}$ $\mathop \Rrightarrow \limits^{{\mathbf{АЛГ}}} $} – все алгебраические выражения с операндами из $\mathbb{F}$.
Внимание! Наложение в задаче 3) Введения дополнительных условий на вывод $\mathop \Rrightarrow \limits^{\overrightarrow \subset {\mathbf{FB}}} $ приведет к расширению понятия “СТИЛЬ ВЫВОДА”. В результате получим картину
СТИЛИ ВЫВОДА := $\overrightarrow \subset $FB ∪ {RAP АР ALT АЛГ},
в которой к $\overrightarrow \subset $FB добавлены стили RAP, АР, ALT, АЛГ2222.
Обозначение 25. 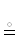 ← символ функциональной эквивалентности ПВ, $\mathcal{P}$
← символ функциональной эквивалентности ПВ, $\mathcal{P}$ 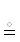 $\mathcal{Q}$ := $\mathcal{P}$, $\mathcal{Q}$ ∈ ∈ {2R→2R $ \Rrightarrow $ Θ}| Θ $ \in \to $ 2R→2R ← формализация использования
$\mathcal{Q}$ := $\mathcal{P}$, $\mathcal{Q}$ ∈ ∈ {2R→2R $ \Rrightarrow $ Θ}| Θ $ \in \to $ 2R→2R ← формализация использования 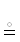 . Ранее символ
. Ранее символ 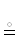 (см. обозначение 1) констатировал эмпирическое совпадение сущностей. Теперь добавим
к нему функцию ФЭПВ за счет переопределения
(см. обозначение 1) констатировал эмпирическое совпадение сущностей. Теперь добавим
к нему функцию ФЭПВ за счет переопределения 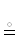 :=
:= 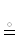 ∪ ФЭПВ, что не противоречит здравому и в том числе прежнему смыслу.
∪ ФЭПВ, что не противоречит здравому и в том числе прежнему смыслу.
Применительно к импликации ⇒, составляющей основу потоков предикатов и ЛС, речь идет об изложении доказательств. Наряду с этим близкий по смыслу к ⇒ символ $ \Rrightarrow $ используется для изображения вывода какой-либо ФЗ из других. К нему применимы те же принципы разветвления:
F3 X→Y $ \Rrightarrow $ X→(Y ∪ Z) $ \Lleftarrow $ X→Z ← аддитивность
F5 X→Y $ \Rrightarrow $ X→Z $ \Lleftarrow $ Y→Z ← транзитивность,
F6 X→Y $ \Rrightarrow $ (X ∪ Z)→V $ \Lleftarrow $ (Y ∪ Z)→V ← псевдотранзитивность,
B2 X→(Y ∪ Z) $ \Rrightarrow $ X→(Y ∪ Z ∪ U) $ \Lleftarrow $ Z→U ← накопление.
${\mathbf{B2}}\bigcirc $ Полагаясь на них, выразим В2 через F-аксиомы:
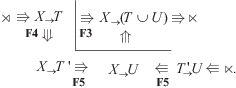
${\mathbf{F3}}\bigcirc $ Аналогично F3 выразим через В-аксиомы (см. $\bar {X}$ “рефлексия” в табл. 1):
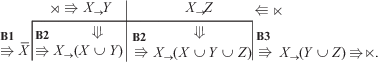
Надо полагать, что близость понятий {{⇒ $ \Rrightarrow $}}, их тесное взаимодействие и конструктивность вывода $ \Rrightarrow $ позволят со временем расширить перечень механизмов силлогизма и представления об его устройстве.
2.8. Бинарные отношения и таблицы (см. определение 5).
Обозначение 26. Θ-ограниченис отношения  (см. обозначение 17):
(см. обозначение 17):
ΘH ΘK := (ΘH ∪ ΘK) $ \dashv $
ΘK := (ΘH ∪ ΘK) $ \dashv $  =:
=:  $ \vdash $ Θ
$ \vdash $ Θ 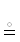 Θ $ \dashv $
Θ $ \dashv $  |Θ ∈ 2R→2R.
|Θ ∈ 2R→2R.
В слове Х Y | X, Y ⊆ R связь X→Y подразумевается. Как ясно из определения 8 и далее из леммы 5, предназначением зависимости
X→Y является возможность строить цепи X1
Y | X, Y ⊆ R связь X→Y подразумевается. Как ясно из определения 8 и далее из леммы 5, предназначением зависимости
X→Y является возможность строить цепи X1 X2
X2 …
… Xk – 1
Xk – 1 Xk | k ∈ ${{\mathbb{Z}}^{ + }}$ для кортежей подсхем X1→ … →Xk := Xk← … ←X1 := 〈X1, …, Xk〉 | Xi$\overrightarrow \subset $ R | I ∈ [1, k] | k ∈ ${{\mathbb{Z}}^{ + }}$. В этих целях ФЗ Xi→Xi + 1 | I ∈ [1, k – 1] должны пониматься в смысле обозначений 19.
Xk | k ∈ ${{\mathbb{Z}}^{ + }}$ для кортежей подсхем X1→ … →Xk := Xk← … ←X1 := 〈X1, …, Xk〉 | Xi$\overrightarrow \subset $ R | I ∈ [1, k] | k ∈ ${{\mathbb{Z}}^{ + }}$. В этих целях ФЗ Xi→Xi + 1 | I ∈ [1, k – 1] должны пониматься в смысле обозначений 19.
Следствие dsg26. Схема отношения, ограниченного зависимостью Θ:
(Θ $ \dashv $  ) $ \dashv $ R = (ΘH ∪ ΘK) ∩ (
) $ \dashv $ R = (ΘH ∪ ΘK) ∩ ( $ \dashv $ R) = (ΘH ∪ ΘK) $ \vdash $
$ \dashv $ R) = (ΘH ∪ ΘK) $ \vdash $  {{⇐лемма 1}}.
{{⇐лемма 1}}.
Определение 15. Параметрические и квадратные отношения.
〈1〉 Параметрическое представление отношения и отношений.
Усечения X и X
и X Y таблицы
Y таблицы  будем называть параметрическими отношениями (ПО) с подсхемами X, Y | X, Y $\overrightarrow \subset $ R в качестве их атрибутных параметров или же проще атрибутов.
будем называть параметрическими отношениями (ПО) с подсхемами X, Y | X, Y $\overrightarrow \subset $ R в качестве их атрибутных параметров или же проще атрибутов.
Термины: X ← унарное ПО (УПО); X
← унарное ПО (УПО); X Y ← бинарное ПО (БПО). Совокупность БПО на подсхеме T | T ⊆ R с $ \ulcorner {\text{атрибутными}} \lrcorner $, (см. примечание 13) параметрами X, Y $\overrightarrow \subset $ R дается выражением X$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{T} } $Y := {Х
Y ← бинарное ПО (БПО). Совокупность БПО на подсхеме T | T ⊆ R с $ \ulcorner {\text{атрибутными}} \lrcorner $, (см. примечание 13) параметрами X, Y $\overrightarrow \subset $ R дается выражением X$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{T} } $Y := {Х Y |
Y |  ∈ $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{T} } $} (см. обозначение 16).
∈ $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{T} } $} (см. обозначение 16).
〈2〉 Алгебраические операции над таблицами – СОЕДИНЕНИЕ и ПРОИЗВЕДЕНИЕ
〈2.1〉 СОЕДИНЕНИЕ ⋈ отношений X Y, Y$П$Z | {{
Y, Y$П$Z | {{ , $П$ $ \in \to $ $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{R} } $ и X, Y, Z $\overrightarrow \subset $ R}}: X
, $П$ $ \in \to $ $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{R} } $ и X, Y, Z $\overrightarrow \subset $ R}}: X Y ⋈ Y$П$Z (см. определение 8(2)).
Y ⋈ Y$П$Z (см. определение 8(2)).
〈2.2〉 ПРОИЗВЕДЕНИЕ $ \boxtimes $ отношений. {{Синонимы: произведение, умножение}}
X Y $ \boxtimes $ Y$П$Z := X(X
Y $ \boxtimes $ Y$П$Z := X(X Y ⋈ Y$П$Z)Z (обобщение для [7, гл. 1, § 2, п. 2, с. 12]).
Y ⋈ Y$П$Z)Z (обобщение для [7, гл. 1, § 2, п. 2, с. 12]).
〈3〉 Квадратное ПО.
В симметричном случае dom(X) = dom(Y) {{;⇒ μ(Х) = μ(Y)}} будем говорить:
1) отношение X Y является квадратным ПО (КПО);
Y является квадратным ПО (КПО);
2) dom(X) является базой квадратного отношения X Y.
Y.
Лемма 4. Инвариантность конечности для операций ⋈ и $ \boxtimes $. Домены подсхем могут быть бесконечными, несмотря на это можно утверждать:
таблицы X Y ⋈ Y$П$Z и X
Y ⋈ Y$П$Z и X Y $ \boxtimes $ Y$П$Z конечны, если X
Y $ \boxtimes $ Y$П$Z конечны, если X Y и Y$П$Z конечны.
Y и Y$П$Z конечны.
Доказательство. Конечность $ \boxtimes $ получается из 〈2.2〉 с очевидностью, поэтому лемму 4 установим только для ⋈ и в виде неравенства μ(X Y ⋈ Y$П$Z) ≤ μ(X
Y ⋈ Y$П$Z) ≤ μ(X Y) ⋅ μ(Y$П$Z) с учетом условий конечности μ(X
Y) ⋅ μ(Y$П$Z) с учетом условий конечности μ(X Y), μ(Y$П$Z) < ∞. Переименуем подсхему Y в Y* для образования еще одного экземпляра Y*$П$Z отношения Y$П$Z и рассмотрим вспомогательное отношение
Y), μ(Y$П$Z) < ∞. Переименуем подсхему Y в Y* для образования еще одного экземпляра Y*$П$Z отношения Y$П$Z и рассмотрим вспомогательное отношение 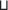 := X
:= X Y × Y*$П$Z ;⇒ ⇒ μ(
Y × Y*$П$Z ;⇒ ⇒ μ(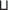 ) = μ(X
) = μ(X Y) ⋅ μ(Y$П$Z). Далее будем действовать формально2323: $Ж$ := X
Y) ⋅ μ(Y$П$Z). Далее будем действовать формально2323: $Ж$ := X Y ⋈ Y$П$Z = {$у$ | $у$ ∈
Y ⋈ Y$П$Z = {$у$ | $у$ ∈ 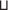 и $у$ $ \vdash $ Y = $у$ $ \vdash $ Y*} $ \vdash $ (X ∪ Y ∪ Z) =: $Э$ ;⇒ μ($Ж$) ≤ μ({$у$ | $у$ ∈
и $у$ $ \vdash $ Y = $у$ $ \vdash $ Y*} $ \vdash $ (X ∪ Y ∪ Z) =: $Э$ ;⇒ μ($Ж$) ≤ μ({$у$ | $у$ ∈ 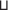 и $у$ $ \vdash $ Y = $у$ $ \vdash $ Y*}) ≤ {{⇐; (2.2)}} ≤ μ(
и $у$ $ \vdash $ Y = $у$ $ \vdash $ Y*}) ≤ {{⇐; (2.2)}} ≤ μ(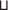 ).
).
Лемма 5. Ассоциативность операций ⋈ и $ \boxtimes $:
(X Y*Y$П$Z)*Z$Ш$V = X
Y*Y$П$Z)*Z$Ш$V = X Y*(Y$П$Z*Z$Ш$V)|*∈{⋈, $ \boxtimes $}.
Y*(Y$П$Z*Z$Ш$V)|*∈{⋈, $ \boxtimes $}.
Докажем всего лишь (X Y*Y$П$Z)*Z$Ш$V ⊆ X
Y*Y$П$Z)*Z$Ш$V ⊆ X Y*(Y$П$Z*Z$Ш$V)|*∈{⋈, $ \boxtimes $}:
Y*(Y$П$Z*Z$Ш$V)|*∈{⋈, $ \boxtimes $}:
 $ \in \to $ (X
$ \in \to $ (X Y*Y$П$Z)*Z$Ш$V ⇒
Y*Y$П$Z)*Z$Ш$V ⇒  = (X
= (X Y*Y$п$Z)*Z$ш$V|{{
Y*Y$п$Z)*Z$ш$V|{{ ∈ X
∈ X Y, $п$ ∈ Y$П$Z, $ш$ ∈ Z$Ш$V и
Y, $п$ ∈ Y$П$Z, $ш$ ∈ Z$Ш$V и  $ \vdash $ Y = $п$ $ \vdash $ Y, $п$ $ \vdash $ Z = $ш$ $ \vdash $ Z ⇐; Z ⊆ (X
$ \vdash $ Y = $п$ $ \vdash $ Y, $п$ $ \vdash $ Z = $ш$ $ \vdash $ Z ⇐; Z ⊆ (X Y*Y$п$Z) $ \vdash $ R (см. определение 7)}}; ⇒
Y*Y$п$Z) $ \vdash $ R (см. определение 7)}}; ⇒
⇒  = X
= X Y*(Y$п$Z*Z$ш$V) ∈ X
Y*(Y$п$Z*Z$ш$V) ∈ X Y*(Y$П$Z*Z$Ш$V) ⇒ $ \rtimes $.
Y*(Y$П$Z*Z$Ш$V) ⇒ $ \rtimes $.
Примечание. Любое из произвольных отображений Y → Y* или Y* → Y можно представить отношением $П$ в форме Y$П$Y*. Полагая dom(Y) = dom(Y*), получим квадратность отношения Y$П$Y*. Для разнообразия в основу $П$ можно положить отношения эквивалентности, упорядоченности и многое другое. Далее
с помощью $П$ определим соединение X Y
Y 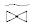 Y$Ш$Z := (X
Y$Ш$Z := (X Y ⋈ ⋈ Y$П$Y* ⋈ Y*$Ш$Z) $ \vdash $ X ∪ Y ∪ Z, которое в технической литературе называется по-разному: эквисоединение, Θ-соединение
и пр. [1, п. 3.5.2, с. 41].
Y ⋈ ⋈ Y$П$Y* ⋈ Y*$Ш$Z) $ \vdash $ X ∪ Y ∪ Z, которое в технической литературе называется по-разному: эквисоединение, Θ-соединение
и пр. [1, п. 3.5.2, с. 41].
Определение 16. Плоские и плоскоквадратные отношения (ПКО).
〈1〉 X Y называется плоским отношением, если X
Y называется плоским отношением, если X Y =
Y =  и Х→Y ∈
и Х→Y ∈ 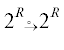 → R = X $ \cup ^\circ $ Y (см. обозначения 4 и 21).
→ R = X $ \cup ^\circ $ Y (см. обозначения 4 и 21).
〈2〉 Плоское и одновременно квадратное отношение будем называть ПКО.
Определение 16 〈1〉 возвращает нас к бинарным отношениям [7, гл. 1, § 2, с. 12]:
(2.5)
$\rho |\rho \,\overrightarrow \subset \,A \times B\quad {\text{или}}\quad \rho |\rho \,\overrightarrow \subset \,A \times A,$ Y | X ∩ Y = ∅ приводится “плоская” интерпретация подсхем X, Y | X ∩ Y = ∅ в качестве операндов таблицы
Y | X ∩ Y = ∅ приводится “плоская” интерпретация подсхем X, Y | X ∩ Y = ∅ в качестве операндов таблицы  :
:
A := {X} и B := {Y} ← атрибуты плоского отношения ρ,
{{X}, {Y}} = {A, B} ← схема отношения ρ,
dom(A) := dom(X) и dom(B) := dom(Y) ← два домена отношения ρ.
Обозначение 27. Плоские таблицы и отношения.
〈1〉 Плоские отношения будут обозначаться строчными греческими буквами. Для них общие обозначения громоздки, хотя вполне применимы. В связи с этим ниже осуществлено упрощение символики плоских (т.е. традиционно бинарных) отношений.
〈2〉 Плоские таблицы (см. (2.3) и там же примеры, а также определения 5):
{A, B, ρ} 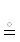 AρB
AρB 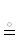 {A × B, ρ} ← двумерная таблица для ρ|ρ $\overrightarrow \subset $ A × B,
{A × B, ρ} ← двумерная таблица для ρ|ρ $\overrightarrow \subset $ A × B,
{A, ρ} 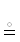 AρA ← то же для ПКО ρ|ρ $\overrightarrow \subset $ A×2 .
AρA ← то же для ПКО ρ|ρ $\overrightarrow \subset $ A×2 .
Заметим, что символы A и B являются именами подсхем схемы R. Поэтому обозначения могут, например, принять вид {3 5 1 0}ρ{11 7 1 20 48} или {3 5 1 0}ρ{0 5 13}. В последнем случае имеет место ПКО.
Примечание. Двуатрибутные таблицы могут служить описателями бинарных отношений, выполняя функции объявления или констатации их свойств, например:
{W, ≤} |  {≤, W} ← отношение ≤ частичной упорядоченности на W,
{≤, W} ← отношение ≤ частичной упорядоченности на W,
{W, ~} | 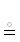 {~, W} ← отношение ~ эквивалентности на множестве W.
{~, W} ← отношение ~ эквивалентности на множестве W.
〈3〉 Конусы плоских отношений (см. определение 6):
($\overrightarrow \subset $A)ρ – правый конус с опорой $\overrightarrow \subset $A; ρ($\overrightarrow \subset $B) – левый конус с опорой $\overrightarrow \subset $B.
〈4〉 Произведение плоских отношений: ρσ := ρ ⋅ σ := (AρB) $ \boxtimes $ (BσC) | σ ⊆ В × С.
〈5〉 Опоры плоского отношения ρ|ρ ⊆ А × В: $\rho \urcorner $ := Аρ – правая; $ \ulcorner \rho $ := ρВ – левая {{;⇒ ρ ⊆ ($ \ulcorner \rho $) × ($\rho \urcorner $)}}; $ \ulcorner \rho \urcorner $ := ($ \ulcorner \rho $) ∪ ($\rho \urcorner $) – общая | 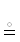 остов.
остов.
〈6〉 Марш аρb | аρb 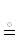 аρb и ребро [аρb] плоского отношения ρ|ρ ⊆ А × В $ \ni $ a→b.
аρb и ребро [аρb] плоского отношения ρ|ρ ⊆ А × В $ \ni $ a→b.
Предикат аρb | ρ ⊆ A × B с глаголом ρ декларирует связь между множествами A и B через a ∈ A и b ∈ B. Его будем называть маршем отношения ρ. На этом фоне ребро [аρb] := !аρb носит безусловный характер (см. обозначение 15 и далее – определение 17(2)).
Синонимы (контекстные): марш 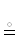 ρ-марш; ребро
ρ-марш; ребро 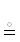 ρ-ребро.
ρ-ребро.
Внимание! ρ-марш и ρ-ребро направлены (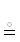 ориентированы) в связи с некоммутативностью ДП (см. обозначение 13).
ориентированы) в связи с некоммутативностью ДП (см. обозначение 13).
Обозначение 28. $ \mapsto $ событие, интервал рабочего времени, шаг алгоритма.
Внимание! Далее смысл и использование символа $ \mapsto $ будет уточняться и развиваться (см. ПРИМИТИВ ПОРЯДКА в разд. 3.2).
Конструкции 1. Первичная алгебра ПКО | ρ ⊆ A×2.
〈1〉 Преобразование множества S в тождественное отношение: $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{S} $ := {s→s | s ∈ S}.
Свойства: $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{S} $ρ ≡ ρ | $ \ulcorner \rho $ ⊆ S и ρ$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{T} $ ≡ ρ | T ⊇ $\rho \urcorner $.
Иными словами, $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{S} $ и $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{T} $ служат левой и правой единицей для соответствующих им отношений, что оправдывает название, данное им выше в заголовке 〈1〉.
Пример. Рефлексии на схеме R: $\underline {{{2}^{R}}} $ = {$\bar {W}$ | W ⊆ R} (см. F1 и В1 в табл. 1 и 2).
〈2〉 Диагональ $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\rho } $ плоскоквадратного отношения ρ: $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\rho } $ := {r|r→r ∈ ρ} = ρ ∩ $\underline { \ulcorner \rho \urcorner } $.
Вариативность использования подчеркивания однозначно устраняется статусом аргумента: множество или бинарное отношение. Вместе с тем последовательное применение операций 〈1〉 и 〈2〉 с точностью до маленького неудобства $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\Lambda } } $∩ приводит к их взаимному уничтожению $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{S} } $ = S и $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\rho } } $ = $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{A} } $ ∩ ρ.
Синонимы: след, диагональ.
Внимание! Не путать с обозначением 16.
〈3〉 Целые степени k ПКО ρ | {{k ∈ 1 + ${{\mathbb{Z}}^{ + }}$ и ρ $\overrightarrow \subset $ A×2}}
ρk := ρ1 ⋅ … ⋅ ρk | ρ1 := … := ρk := ρ ← положительные степени отношения;
ρ–1 := {r→s|s→r ∈ ρ} ← квадратное отношение, обратное к ρ;
ρ–k := (ρ–1)k ← отрицательные степени отношения;
ρ0 := $\underline { \ulcorner \rho \urcorner } $ {{;⇒ρ0 ⊆ $ \ulcorner \rho {{ \urcorner }^{{ \times 2}}}$ ⊆ A×2}} ← полная диагональ квадрата.
Заметим, что в случае рефлексивности ρ, выражаемой свойством ρ0 ⊆ ρ, имеет место цепочка включений ρ0 ⊆ ρ1 ⊆ ρ2 ⊆ … ⊆ ρ+ (см. далее определение 18).
〈4〉 Ядро 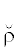 квадратного отношения ρ:
квадратного отношения ρ:
ρI := $\bigcup\limits_{i \in I\,\overrightarrow \subset \,\mathbb{Z}}^{} {{{\rho }^{i}}} $ ← выборочное по I расширение ПКО ρ;
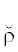 := ρ\${{\rho }^{{{{\mathbb{Z}}^{ + }}{\backslash }\{ 0,1\} }}}$ ← все неразложимо-невырожденные (
:= ρ\${{\rho }^{{{{\mathbb{Z}}^{ + }}{\backslash }\{ 0,1\} }}}$ ← все неразложимо-невырожденные (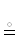 простые) ребра в ρ;
простые) ребра в ρ;
ρ $ \mapsto $ 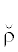 ← минимизация квадратного отношения2424.
← минимизация квадратного отношения2424.
Внимание! Определение 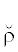 – счетно-конструктивно, т.е. для более чем счетного ρ оно в общих условиях будет
работать непредсказуемо. Нам это не грозит!
– счетно-конструктивно, т.е. для более чем счетного ρ оно в общих условиях будет
работать непредсказуемо. Нам это не грозит!
〈5〉 Целочисленные расширения ПКО ρ $\overrightarrow \subset $ A×2:
ρ+ := ${{\rho }^{{{{\mathbb{Z}}^{ + }}}}}$; ρ– := ${{\rho }^{{{{\mathbb{Z}}^{ - }}}}}$ ← конусно-транзитное расширение ρ,
${{\rho }^{\mathbb{Z}}}$ = ρ+ ∪ ρ– ← полное транзитное расширение ρ.
Примечания: ${{\rho }^{{{{ + }^{k}}}}}$ = ρ+|k ∈ 1 + ${{\mathbb{Z}}^{ + }}$; ρ++ = ρ+; множества ${{\mathbb{Z}}^{ \pm }}$, $\mathbb{Z}$ бесконечны, но мощность (количество) слагаемых в ρ±, ${{\rho }^{\mathbb{Z}}}$, не влагающихся в предшествующее им объединение, конечна в силу конечности $ \ulcorner \rho {{ \urcorner }^{{ \times 2}}}$.
Определение 17. Транзитные расширения ПКО ρ $\overrightarrow \subset $ A×2.
〈1〉 Транзитные ребра [хρiу]|х, у ∈ А|I ∈ 2 + ${{\mathbb{Z}}^{ + }}$ есть результат последовательного сочленения примыкающих друг к другу (конец → начало) ребер отношения ρ, в котором результат [хρiу] может как присутствовать [хρiу] ∈ ρ, так и отсутствовать [хρiу] $ \notin $ ρ.
〈2〉 Маршрут в отношениях ρi$\overrightarrow \subset $ A×2|i ∈ [1, n] :
Мы приподнимаем отношения над строкой ради читабельности – отделения глаголов от сущностей. Для ясности сделаем два замечания.
1. Марши в маршруте упорядочены по номерам 〈1, …, n〉 (см. обозначение 12.2), поэтому ${{a}_{0}}^{{{{\rho }_{1}}}}{{a}_{1}}^{{{{\rho }_{2}}}}{{...}^{{{{\rho }_{n}}}}}{{a}_{n}}$ 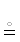 $\langle {{a}_{0}}^{{{{\rho }_{1}}}}{{a}_{1}},...,{{a}_{{i - 1}}}^{{{{\rho }_{i}}}}{{a}_{i}},...,{{a}_{{n - 1}}}^{{{{\rho }_{n}}}}{{a}_{n}}\rangle $ | i ∈ ]0, n].
$\langle {{a}_{0}}^{{{{\rho }_{1}}}}{{a}_{1}},...,{{a}_{{i - 1}}}^{{{{\rho }_{i}}}}{{a}_{i}},...,{{a}_{{n - 1}}}^{{{{\rho }_{n}}}}{{a}_{n}}\rangle $ | i ∈ ]0, n].
2. Маршрут является многоместным предикатом, декларирующим процесс, в котором внутренней параметр i играет роль счетчика дискретного времени. Логическая оценка маршрута зависит от контекста, в котором он фигурирует, о чем сказано в определении 2.
〈3〉 Путь [${{a}_{0}}^{{{{\rho }_{1}}}}{{a}_{1}}^{{{{\rho }_{2}}}}{{...}^{{{{\rho }_{n}}}}}{{a}_{n}}$] из а0 в аn через ai|i ∈ ]0, n[:
Ребро [${{a}_{0}}^{{{{\rho }_{1}}}}{{a}_{1}}$] (см. обозначение 27〈6〉) есть частный случай пути, когда n = 1 .
〈4〉 Скелет [$\overrightarrow \subset $ρ] составляется из ребер отношения ρ: ↓ (см. обозначение 27〈5〉):
[$\overrightarrow \subset $ρ] := {[aρb]|aρb ∈ $\overrightarrow \subset $ρ} =: $\mathcal{S}$ ← скелет; $ \ulcorner \mathcal{S} \urcorner $ := $\bigcup\limits_{[a\rho b] \in \mathcal{S}}^{} {\{ a,b\} } $ – остов скелета $\mathcal{S}$.
〈5〉 Операция ⋅ (точка) соединения маршрутов и путей:
Обозначение 29. Точки пути: {{х $\begin{gathered} \in \hfill \\ \in \to \hfill \\ \end{gathered} $ [${{a}_{0}}^{{{{\rho }_{1}}}}{{...}^{{{{\rho }_{n}}}}}{{a}_{n}}$]}} := {{х $\begin{gathered} \in \hfill \\ \in \to \hfill \\ \end{gathered} $ {a0, …, an}}}.
Обозначение 30. Пучок путей, соединящих точки а, b $ \in \to $ A | aρb: $\left[\kern-0.15em\left[ {a{{\rho }^{ + }}b} \right]\kern-0.15em\right]$ := {[a0ρa1ρ…ρanρb]|ai ∈ ∈ A|i ∈ [1, n] },
↑ все пути отношения ρ|ρ $\overrightarrow \subset $ A×2, составляющие ребро [aρ+b].
Определение 18. Р Т С А ← возможные свойства ПКО.
| Название | Свойство | Пример | [7, Гл. 1, §2, п. 5] | $\left. \begin{gathered} \hfill \\ \hfill \\ \hfill \\ \hfill \\ \hfill \\ \end{gathered} \right\}$ | ρ, σ $\overrightarrow \subset $A×2. | |
| P | Рефлексивность | ρ0 ⊆ ρ | ρ := σ0 ∪ $\overrightarrow \subset $σ | |||
| T | Транзитивность | ρ2 ⊆ ρ | ρ := σ+ | |||
| C | Симетричность | ρ–1 ⊆ ρ | ρ := σ–1 ∪ σ | |||
| A | Антисимметричность | ρ ∩ ρ–1 ⊆ ρ0 | ρ := (σ\σ–1) ∪ $\overrightarrow \subset $ σ0 |
Внимание! Множество {Р Т С А} является вертикальной схемой таблицы определения 18, состоящей из горизонтальных атрибутов, которая таким образом имеет две несинонимичные схемы. Теорией подобных конструкций еще предстоит заняться, тем более, что к ним относятся такие, как таблицы Кэли, латинские и магические квадраты, шахматная доска и пр. В таблице общего вида набор значений ячеек какого-либо ключа также можно трактовать, как вертикальную схему, но это приведет к смешению доменов вертикальных атрибутов. Не исключено, что в этом смешении возможна индивидуализация горизонтальных атрибутов, но это зависит от свойств конкретной таблицы.
Нижеследующее слово типа WXYZ составлется из букв W, X, Y, Z $ \in \to $ {P T С А}.
Обозначение 31. W… Z := класс ПКО, обладающее свойствами W, …, Z.
Примечание. Перестановки букв в W … Z дают синонимичные имена классов.
Обозначение 32. Транзитно-конусное объединение ПКО | ρ, σ $\overrightarrow \subset $ A×2 : ρ ${{ \cup }^{ + }}$ σ := (ρ ∪ σ)+ ≡ ≡ $\bigcup\limits_{k,l \in {{\mathbb{Z}}^{{ + \times \infty }}}}^{} {\prod\limits_{i = 0}^\infty {{{\rho }^{{{{k}_{i}}}}}{{\sigma }^{{{{l}_{i}}}}}} } $ | {{ρ0 : σ0 := (ρ ∪ σ)0 (поправка)}} ;⇒ ρ ${{ \cup }^{ + }}$ σ ∈ T.
3. Частично упорядоченные множества (ЧУМ). 3.1. Сущности.
Определение 19. ЧУМ (см. обозначение 9 и определения 5, 18).
〈1〉 Отношение ρ|ρ ∈ РТА называется частичным порядком (ЧП).
〈2〉 Таблица $\mathcal{R}$ := {R, ρ}|{{μ(R) = 2 и ρ ∈ {РТА}}} называется ЧУМ'ом.
Обозначение 33. Алфавиты порядков. Символы ≤, ≥ и слова (*≥, ≤*) будут служить именами ЧП на множестве, скажем, W. В качестве * возможно использование букв любого алфавита или чисел $ \in \to $${{\mathbb{Z}}^{ + }}$. В соответствии с примечанием определения 27〈2〉 ЧУМ’ы задаются выражениями типа $\mathcal{W}$ := {W, ≤}, $\mathcal{W}$ :={W, ≤*)} или $\mathcal{W}$ := {W, ≤i)}|i ∈ ${{\mathbb{Z}}^{ + }}$.
Внимание! Символы * и индексы i ∈ ${{\mathbb{Z}}^{ + }}$ играют роль меток в именах ≤*), (*≥ и ≤i), ≥i) плоских бинарных отношений, не являясь субъектами ЧУМ, в которых они используются. Верхние скобочки необходимы для отличения меток от степеней отношения.
Следствие defl9. Расслоение ЧУМ на минимальные конусы ≤w | w ∈ $\mathcal{W}$:
$\mathcal{W}$ = $\bigcup\limits_{w \in \mathcal{W}}^{} ( $≤w) ⇐; $\mathcal{W}$ – рефлексивно (см. определение 19 и обозначение 27 〈3〉).
Заметим, что то же относится и к максимальным конусам w≤, но нам они не интересны, поскольку в настоящей работе и ее продолжениях ЧУМ'ы последовательно приводятся к состоянию “дерева”, в котором корень является максимальным элементом. В этом случае максимальные конусы вырождаются в пути от заданной точки w до корня.
Определение 20. Каскад порядков на множестве.
Назовем $\mathcal{W}$ каскадно-упорядоченным множеством (КУМ), а совокупность порядков {≤i)|i ∈ ∈ [0, n[} – каскадом глубины n | n ∈ ${{\mathbb{Z}}^{ + }}$ на $\mathcal{W}$, если
Имея в виду, (2.5), каскадность можно выразить цепочкой включений:
Примечание. КУМ является предметом исследования задачи 2) Введения.
В настоящей работе рассматриваются только ориентированные (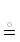 направленные) конечные графы, представляемые плоскоквадратными отношениями. Ниже имена конструктивных
элементов графа являются свободными переменными:
направленные) конечные графы, представляемые плоскоквадратными отношениями. Ниже имена конструктивных
элементов графа являются свободными переменными:
Обозначение 34. Графы
〈1〉 $\mathbb{G}$ – множество вершин графа (местное условие: конечное),
〈2〉 γ|γ $\overrightarrow \subset $ $\mathbb{G}$ × $\mathbb{G}$ – множество ребер графа ;⇒γ суть ПКО на множестве $\mathbb{G}$. Далее отношения типа γ|γ $\overrightarrow \subset $ ${{\mathbb{G}}^{{ \times 2}}}$ таковы, что {$\mathbb{G}$, γ+} являются частично или линейно упорядоченными множествами и γ = 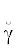 .
.
〈3〉 $\mathcal{G}$ := {$\mathbb{G}$, γ} – граф,
〈4〉 {$\mathcal{G}$} := $ \ulcorner \gamma \urcorner $ – остов графа;
$\mathcal{G}$ $ \mapsto $ {{$\mathcal{G}$}), γ} – минимизация графа (см. обозначение 27 〈5〉),
〈5〉 $\mathbb{G}$\{${{\mathcal{G}}^{2}}$} – множество изолированных вершин графа (конструкция 1〈3〉),
〈6〉 d($g$, $\mathcal{G}$) – полустепень захода в вершину $g$ графа $\mathcal{G}$ [13, § 64, с. 283].
Термины. Сущности графа для a $ \in \to $ A и γ $\overrightarrow \subset $ A×2 (см. определение 17 〈5〉):
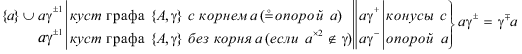
3.2. Элементарные частицы порядка. ПРИМИТИВ ПОРЯДКА: попытка с помощью (2.5) установить линейный порядок на множестве {0, 1} для приведения его к виду 0 × 1 требует использовать тот же порядок на том же множестве, поскольку на нем основан механизм ДП. Это влечет принципиальную неопределяемость порядка на множестве {0, 1}. Остается только поверить в его существование, опираясь на туманные образы нашего сознания. Их основой может быть инстиктивное ощущение времени или, быть может, чувственное восприятие геометрии окружающей среды, т.е. ПРОСТРАНСТВА. С этим надо смириться, так же как человечество смирилось с первичностью понятий ТОЧКА, ПРЯМАЯ, ПЛОСКОСТЬ и пр. В качестве графического образа ПРИМИТИВА ПОРЯДКА в обозначении 28 был предложен символ $ \mapsto $.
Примечание. ПРИМИТИВ ПОРЯДКА неявно присутствует в символах, кодирующих действия: →; ⇒ := $\begin{gathered} \to \hfill \\ \to \hfill \\ \end{gathered} $ → × и пр. (см. также 〈 〉 в обозначении 12.2). Среди прочих действие $ \mapsto $ имеет высший приоритет.
Теорема 2. Алгебраическое восстановление частичного порядка из его ядра.
 ≡ ≤, если частично упорядоченное множество {X, ≤} конечно2525.
≡ ≤, если частично упорядоченное множество {X, ≤} конечно2525.
Доказательство. Начнем с утверждения {{μ(Х) < ∞ и a × b $ \in \to $ X×2}} ⇒ [a ≤ b] = [a =: x0 ≤ ≤ xi ≤ … ≤ xn – 1 ≤ xn := b] | {{n ∈ ${{\mathbb{Z}}^{ + }}$, хi ∈ Х и [xi – 1 ≤ хi] ∈  | i ∈ [1, n]
}}, которое установим, предполагая a ≠ b, ибо прочее очевидно. Конечным перебором элементов в X можно сформировать конечное множество D := {х | а < х < b) ;⇒ {{D = ∅ ∈ a × b ∈
| i ∈ [1, n]
}}, которое установим, предполагая a ≠ b, ибо прочее очевидно. Конечным перебором элементов в X можно сформировать конечное множество D := {х | а < х < b) ;⇒ {{D = ∅ ∈ a × b ∈ 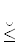 }}. Другая причина D ≠ ∅ позволит или не позволит таким же образом разделить ребра [a < x] и [x < b] каждое на две части. Для каждой ветви деления невозможность его продолжения является
признаком останова. На этом этапе неделящееся ребро становится элементом отношения
}}. Другая причина D ≠ ∅ позволит или не позволит таким же образом разделить ребра [a < x] и [x < b] каждое на две части. Для каждой ветви деления невозможность его продолжения является
признаком останова. На этом этапе неделящееся ребро становится элементом отношения
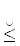 . Мощность μ(Х) ограничивает процесс деления, в силу чего получаем искомый конечный путь [а ≤ x1 ≤ … ≤ хn – 1 ≤ b] = [а ≤ b]|{{хi ∈ Х и [хi – 1 ≤ хi] ∈
. Мощность μ(Х) ограничивает процесс деления, в силу чего получаем искомый конечный путь [а ≤ x1 ≤ … ≤ хn – 1 ≤ b] = [а ≤ b]|{{хi ∈ Х и [хi – 1 ≤ хi] ∈ 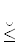 }} | i ∈ [1, n] ;⇒ [a ≤ b] = [a
}} | i ∈ [1, n] ;⇒ [a ≤ b] = [a 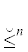 b] ;⇒ a × b ∈
b] ;⇒ a × b ∈ 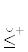 ;⇒ ≤ ⊆
;⇒ ≤ ⊆  . Обратное включение ≤ ⊇
. Обратное включение ≤ ⊇  очевидно ;⇒ теорема 2.
очевидно ;⇒ теорема 2.
3.3. Алгебра ЧУМ.
Определение 21. Операция æ склеивания ЧП:
〈1〉 ≤u) æ${{ \leqslant }^{{{v})}}}$ := ≤u) ∪ (≤u)(U ∩ V)) × ((U ∩ V) ${{ \leqslant }^{{{v})}}}$) ∪ ↓(см. обозначение 27〈5〉),
∪ ${{ \leqslant }^{{{v})}}}$ ∪ (${{ \leqslant }^{{{v})}}}$ (U ∩ V)) × ((U ∩ V)≤u)) =: ε | U = $ \ulcorner {{ \leqslant }^{{u)}}} \urcorner $ и V = $ \ulcorner {{ \leqslant }^{{{v})}}} \urcorner $.
〈2〉 {U, ≤u)}æ{V, ${{ \leqslant }^{{{v})}}}$} := {U ∪ V, ≤u)æ${{ \leqslant }^{{{v})}}}$)} ← склеивание ЧУМ'ов {U, ≤u))} и {V, ${{ \leqslant }^{{{v})}}}$}.
VICE VERSA: то же имеет место после перестановки {u, U} и {${v}$, V}.
★ u $ \in \to $ U и ${v}$ $ \in \to $ V ⇒ {{uε${v}$ ⇒ {$ \in \to $(U ∩ V)|u ≤u) $ \in \to $ (U ∩ V) ${{ \leqslant }^{{{v})}}}{v}$} ≠ ∅}} ← свойство.
Перескажем ★ иначе: если $\exists ${{u ∈ U, ${v}$ ∈ V}} такие, что uε${v}$, то u ≤u)x${{ \leqslant }^{{{v})}}}{v}$ | x∈ U ∩ V.
Для ЧУМ'ов $\mathcal{U}$ := {U, ≤u} и $\mathcal{V}$ := {V, ${{ \leqslant }^{{{v})}}}$)} построим ПКО ε := ≤u)æ${{ \leqslant }^{{{v})}}}$, а также плоскую таблицу $\mathcal{W}$ := {U ∪ V, ε} | ≡ {U, ≤u)}æ{V, ${{ \leqslant }^{{{v})}}}$) и докажем следующие леммы.
Леммa 6. Достаточное условие склеивания порядков2626.
〈1〉 U ∩ V – немощно ⇒ $\mathcal{W}$ – частично упорядоченно (см. обозначение 27〈2〉).
〈2〉 На основе естественных вложений U, V ⊆ W | W := U ∪ V имеют место изоморфные вложения: $\mathcal{U}$ ⊆ $\mathcal{W}$ и $\mathcal{V}$ ⊆ $\mathcal{W}$ (см. далее обозначение 38〈2〉).
Доказательство. Ограничимся проверкой импликации 〈1〉, в рамках которой установим свойство PAT (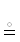 РТА) (см. определения 18 и 19〈1〉) предполагаемого ЧП ε:
РТА) (см. определения 18 и 19〈1〉) предполагаемого ЧП ε:
P $ \ni $ ε ⇐; a×2 ∈ ≤u) ∪ ${{ \leqslant }^{{{v})}}}$ ⊆ ε ⇐; a×2 ∈ ≤u или a×2 ∈ ${{ \leqslant }^{{{v})}}}$ ⇐; a ∈ U или a ∈ V ⇐ a $ \in \to $ $\mathcal{U}$ ⊂ $\mathcal{V}$ ⇐ $ \ltimes $.
А. Расположение a, b ∈ U или а, b ∈ V не вызывает трудностей для вывода [aεbεa] ⇒ а = b. Перейдем к случаю {{a $ \in \to $ U\V и b $ \in \to $ V\U}}, оставив возможность {{а $ \in \to $ V\U и b $ \in \to $ U\V}} без внимания: {{[аεb] ⇒ [а ≤u)x ${{ \leqslant }^{{{v})}}}$ b]|x ∈ U ∩ V и [bεa] ⇒ [b ${{ \leqslant }^{{{v})}}}$ y ≤u)а]|y ∈ U ∩ V}} ;⇒ {{[U ∩ V – немощно ⇒ x = у ;⇒}}; ⇒ [а ≤u)x ≤u)а] и [b ${{ \leqslant }^{{{v})}}}$ x ${{ \leqslant }^{{{v})}}}$ b] ;⇒ {{$ \rtimes $⇒ отношения ≤u) и ${{ \leqslant }^{{{v})}}}$ – рефлексивны ⇒}} а = х = b; ε ∈ A ⇒ $ \rtimes $.
T 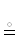 {{[aεbεc]|a, b, c $ \in \to $ $\mathcal{U}$ ∪ $\mathcal{V}$ ⇒ [aεc]}} (см. определение 17〈2〉). Исходя из этого напоминания, для решения вопроса Т выявим возможные, а среди них – необходимые реализации выбора a, b, c $ \in \to $ $\mathcal{U}$ ∪ $\mathcal{V}$. Эта комбинаторная задача сводится к вычислению множества F := {{$\mathcal{U}$}, {$\mathcal{V}$}}{а,b,с} (см. обозначение 18) всех подмножеств множества {а, b, с}, но из него в силу симметрии достаточно оставить подмножества вида $ \in \to $F | ($ \in \to $F)a – {$\mathcal{U}$} . Таким образом останется четыре выбора из восьми, однако из них выбор f | {{f ∈ F и f = {$\mathcal{U}$}}} тривиален, поскольку не выводит решаемую задачу из среды одного ЧУМ'а. Перечислим
оставшиеся варианты:
{{[aεbεc]|a, b, c $ \in \to $ $\mathcal{U}$ ∪ $\mathcal{V}$ ⇒ [aεc]}} (см. определение 17〈2〉). Исходя из этого напоминания, для решения вопроса Т выявим возможные, а среди них – необходимые реализации выбора a, b, c $ \in \to $ $\mathcal{U}$ ∪ $\mathcal{V}$. Эта комбинаторная задача сводится к вычислению множества F := {{$\mathcal{U}$}, {$\mathcal{V}$}}{а,b,с} (см. обозначение 18) всех подмножеств множества {а, b, с}, но из него в силу симметрии достаточно оставить подмножества вида $ \in \to $F | ($ \in \to $F)a – {$\mathcal{U}$} . Таким образом останется четыре выбора из восьми, однако из них выбор f | {{f ∈ F и f = {$\mathcal{U}$}}} тривиален, поскольку не выводит решаемую задачу из среды одного ЧУМ'а. Перечислим
оставшиеся варианты:  a ∈ U, b, c ∈ V,
a ∈ U, b, c ∈ V,  a ∈ U, b ∈ V, c ∈ U,
a ∈ U, b ∈ V, c ∈ U,  a, b ∈ U, c ∈ U.
a, b ∈ U, c ∈ U.
 ⇒ {{[aεb] ⇒}} a × b ∈ (≤u) (U ∩ V)) × ((U ∩ V) ${{ \leqslant }^{{{v})}}}$) ;⇒ a ∈ ≤u)x и b ∈ y ${{ \leqslant }^{{{v})}}}$ | x, y ∈ U ∩ V ;⇒ a ≤u) ($ \in \to $(U ∩ V)) ${{ \leqslant }^{{{v})}}}$ b{{⇐; $ \in \to $(U ∩ V) = x = y ⇐; U ∩ V – немощно}} ;⇒ {{[bεc] и b, c ∈ V ⇒}} a ≤u) ($ \in \to $(U ∩ ∩ V)) ${{ \leqslant }^{{{v})}}}$ b ${{ \leqslant }^{{{v})}}}$ c ;⇒ [aεc] ;⇒ ε ∈ T ⇒ $ \rtimes $.
⇒ {{[aεb] ⇒}} a × b ∈ (≤u) (U ∩ V)) × ((U ∩ V) ${{ \leqslant }^{{{v})}}}$) ;⇒ a ∈ ≤u)x и b ∈ y ${{ \leqslant }^{{{v})}}}$ | x, y ∈ U ∩ V ;⇒ a ≤u) ($ \in \to $(U ∩ V)) ${{ \leqslant }^{{{v})}}}$ b{{⇐; $ \in \to $(U ∩ V) = x = y ⇐; U ∩ V – немощно}} ;⇒ {{[bεc] и b, c ∈ V ⇒}} a ≤u) ($ \in \to $(U ∩ ∩ V)) ${{ \leqslant }^{{{v})}}}$ b ${{ \leqslant }^{{{v})}}}$ c ;⇒ [aεc] ;⇒ ε ∈ T ⇒ $ \rtimes $.
 ⇒ a × b ∈ (≤u) (U ∩ V)) × ((U ∩ V)${{ \leqslant }^{{{v})}}}$) ;⇒ a ≤u)x и y ${{ \leqslant }^{{{v})}}}$ b|x, y ∈ U ∩ V. Текущая ситуация {{[bεc] и b ∈ V, c ∈ U}} с циклической перестановкой U $ \mapsto $ V $ \mapsto $ U и подстановкой b $ \mapsto $ a и c $ \mapsto $ b напоминает пройденный этап, поэтому b ${{ \leqslant }^{{{v})}}}$ x' и y' ≤u)c|x', y' ∈ U ∩ V – немощно ;⇒ a ≤u)x = y' ≤u)c ;⇒ a ≤u)c ;⇒ ⇒ [aεc] ;⇒ ε ∈ T ⇒ $ \rtimes $.
⇒ a × b ∈ (≤u) (U ∩ V)) × ((U ∩ V)${{ \leqslant }^{{{v})}}}$) ;⇒ a ≤u)x и y ${{ \leqslant }^{{{v})}}}$ b|x, y ∈ U ∩ V. Текущая ситуация {{[bεc] и b ∈ V, c ∈ U}} с циклической перестановкой U $ \mapsto $ V $ \mapsto $ U и подстановкой b $ \mapsto $ a и c $ \mapsto $ b напоминает пройденный этап, поэтому b ${{ \leqslant }^{{{v})}}}$ x' и y' ≤u)c|x', y' ∈ U ∩ V – немощно ;⇒ a ≤u)x = y' ≤u)c ;⇒ a ≤u)c ;⇒ ⇒ [aεc] ;⇒ ε ∈ T ⇒ $ \rtimes $.
 В условиях
В условиях  сделаем циклические перестановки U $ \mapsto $ V $ \mapsto $ U и a $ \mapsto $ b $ \mapsto $ c $ \mapsto $ а. Это даст
сделаем циклические перестановки U $ \mapsto $ V $ \mapsto $ U и a $ \mapsto $ b $ \mapsto $ c $ \mapsto $ а. Это даст  , не влияя на справедливость утверждения [аεс] ;⇒ ε ∈ T ⇒ $ \rtimes $.
, не влияя на справедливость утверждения [аεс] ;⇒ ε ∈ T ⇒ $ \rtimes $.
3.4. Синтез острых множеств.
Обозначение 35. Экстремумы ЧУМ $\mathcal{W}$ := {W, ≤}:
max$\mathcal{W}$ := max{W, ≤} := {w|w ≥ $ \in \to $W} ← все максимальные элементы W в $\mathcal{W}$,
min$\mathcal{W}$ := min{W, ≤} := {w|w ≤ $ \in \to $W} ← все минимальные элементы W в $\mathcal{W}$.
Синонимы: {{минимальный {{элемент, параметр, операнд}}, точка входа, константа}}, {{максимальный элемент, тупик, точка выхода, результат}}, {{ВХОД, все минимальные элементы, КОНСТАНТЫ}} {{выход, все максимальные элементы}}.
Обозначение 36. “Черный ящик”  вход $ \mapsto $ выход:
вход $ \mapsto $ выход:
Внимание! 1. Знаки $ \succ \, \prec $ не изображают бинарные отношения между X и $\mathcal{W}$ или Y и $\mathcal{W}$. Они играют роль разделителей и отделяют от $\mathcal{W}$ параметры X и Y, предназначенные для склеивания $\mathcal{W}$ с другими ЧУМ’ами.
2. $\mathcal{W}$ и X в выражениях X $ \prec $ $\mathcal{W}$ и $\mathcal{W}$ $ \prec $ X имеют разные статусы:
$\mathcal{W}$ – ЧУМ; X|X ⊆ W, max$\mathcal{W}$, min$\mathcal{W}$ – абстрактные множества.
3. Знаки {≤ $ \prec $} и $ \mapsto $ разнонаправлены, но одинаково ведут ЧУМ от min$\mathcal{W}$ к max$\mathcal{W}$, т.е., иными словами, от начала к завершению (ср. с примечанием 3 в разд. 2.7).
Конец (ВЫХОД) конусного пути может быть началом (ВХОДом) другого в процессе склеивания острых множеств, к определению которых мы переходим.
Определение 22. Заостренность ЧУМ:
ЧУМ $\mathcal{W}$ := {W, ≤} назовем острым|  заостренным, если μ(max$\mathcal{W}$) = 1.
заостренным, если μ(max$\mathcal{W}$) = 1.
Свойства. Перечислим некоторые свойства острых ЧУМ:
 каждый элемент острого ЧУМ $\mathcal{W}$ связан каким-либо путем с $ \in \to $max$\mathcal{W}$;
каждый элемент острого ЧУМ $\mathcal{W}$ связан каким-либо путем с $ \in \to $max$\mathcal{W}$;
 острое множество является конусам, {{⇐;
острое множество является конусам, {{⇐;  }}, т.е. ≤($ \in \to $max$\mathcal{W}$) = $\mathcal{W}$ | μ(max$\mathcal{W}$) = 1 (см. обозначение 27(3));
}}, т.е. ≤($ \in \to $max$\mathcal{W}$) = $\mathcal{W}$ | μ(max$\mathcal{W}$) = 1 (см. обозначение 27(3));
 совместное применение обозначений 36 и определения 22 не противоречиво:
совместное применение обозначений 36 и определения 22 не противоречиво:
Синонимы: острое ЧУМ, заостренное ЧУМ, острое множество, конус. (3.1)
Обозначение 37. Функциональное представление конуса $\mathcal{W}$:
〈1〉 $\mathcal{W}$ 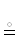 $\mathcal{W}$〈〈$\overrightarrow \subset $min$\mathcal{W}$〉〉
$\mathcal{W}$〈〈$\overrightarrow \subset $min$\mathcal{W}$〉〉 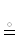 w〈〈〉〉
w〈〈〉〉 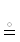 〈〈$\overrightarrow \subset $min$\mathcal{W}$〉〉|{{μ(max$\mathcal{W}$) = 1 и w ∈ max$\mathcal{W}$}},
〈〈$\overrightarrow \subset $min$\mathcal{W}$〉〉|{{μ(max$\mathcal{W}$) = 1 и w ∈ max$\mathcal{W}$}},
〈2〉 $\mathcal{W}$($\overrightarrow \subset $min$\mathcal{W}$) := max$\mathcal{W}$ – максимальный элемент $\mathcal{W}$.
В частности, $\mathcal{W}$() = max$\mathcal{W}$. Общий случай достигается использованием в качестве переменных как элементов из W, так и результатов склеивания острых ЧУМ.
Примеры: $\mathcal{W}$〈〈${{\mathcal{V}}_{0}}$, ${{\mathcal{V}}_{1}}$〈〈${{\mathcal{U}}_{0}}$, ${{\mathcal{U}}_{1}}$〈〈t, ${{\mathcal{T}}_{1}}$〉〉, ${{\mathcal{U}}_{2}}$〉〉, ${{\mathcal{V}}_{2}}$, ${{\mathcal{V}}_{3}}$(w, ${{\mathcal{U}}_{3}}$)〉〉 ← три уровня склеивания,
($\mathcal{W}$〈〈${{\mathcal{V}}_{0}}$, ${{\mathcal{V}}_{1}}$〈〈${{\mathcal{U}}_{0}}$, ${{\mathcal{U}}_{1}}$〈〈${{\mathcal{T}}_{0}}$, ${{\mathcal{T}}_{1}}$〉〉, ${{\mathcal{U}}_{2}}$〉〉, ${v}$, ${{\mathcal{V}}_{3}}$(${{\mathcal{U}}_{3}}$, ${{\mathcal{U}}_{4}}$)〉〉) ← максимальный элемент.
Термины: подмножество $\overrightarrow \subset $min$\mathcal{W}$ состоит из аргументов “функции” w, в то время как остаток min$\mathcal{W}$\($\overrightarrow \subset $min$\mathcal{W}$) содержит константы конуса $\mathcal{W}$. Запись аргументов допустима в виде списка, например w〈〈w1, …, wk〉〉 | wi ∈ min$\mathcal{W}$ | i ∈ [1, k]. Аргументами являются те же $ \in \to $min$\mathcal{W}$. Они предназначены для взаимодействия (склеивания) $\mathcal{W}$ с внешним миром. В конусе $\mathcal{W}$ аргументы могут быть не выбраны. В этом случае $\mathcal{W}$ 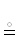 w〈〈〉〉 и min$\mathcal{W}$ состоит из констант. Скобки 〈〈〉〉 являются признаком минимальности элемента w в $\mathcal{W}$ и использования его в качестве функции.
w〈〈〉〉 и min$\mathcal{W}$ состоит из констант. Скобки 〈〈〉〉 являются признаком минимальности элемента w в $\mathcal{W}$ и использования его в качестве функции.
Внимание! 1. Острый ЧУМ W не обязан быть деревом.
2. Контекстность обозначения 37 : В обозначениях типа w〈〈…〉〉 конус $\mathcal{W}$ подразумевается. Он преднамерено скрыт так же, как в традиционном математическом анализе, за обозначением функций типа y(x1, …, xn) не видно сущностей самой функции. Таким образом речь идет об обозначениях типа “Черный ящик”.
Резюме. ЧП создает в своем множестве пространственные структуры.
Синонимы: куст (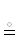 дерево) ЧУМ, функция многих переменных, острый черный ящик.
дерево) ЧУМ, функция многих переменных, острый черный ящик.
Операция æ склеивания ЧУМ'ов $\mathcal{V}$, $\mathcal{W}$ коммутативна в силу опредления 21 и годится для общих случаев, в которых скорее всего
будет громоздкой за счет необходимости привнесения в нее описаний области клея $\mathcal{V}$ ∩ $\mathcal{W}$, которая к тому же может препятствовать образованию ЧП в $\mathcal{V}$æ$\mathcal{W}$. Для острого ЧУМ $\mathcal{V}$, имплантируемого 2727 в ЧУМ $\mathcal{V}$, ситуацию можно упростить, заменив в обозначении 37 слово max$\mathcal{W}$|  {y} на $ \in \to $max$\mathcal{W}$ =: y и связав стороны $\mathcal{W}$ и $\mathcal{V}$ знаком $ \prec $.
{y} на $ \in \to $max$\mathcal{W}$ =: y и связав стороны $\mathcal{W}$ и $\mathcal{V}$ знаком $ \prec $.
Обозначение 38. Склеивание конусов ЧУМ'ов. Для обозначений 38 исходными служат ЧУМ ${{\mathcal{V}}^{i}}$ := {Vi, ≥i)} i ∈ [0, 1] и частичный порядок ≤| := ≤0) æ≤1) {{⇐; лемма 6〈1〉}} в склееном ЧУМ'е ${{\mathcal{V}}^{0}}$æ${{\mathcal{V}}^{1}}$.
〈1〉 Полуострое склеивание ЧУМ – острого ${{\mathcal{V}}^{0}}$ и произвольного ${{\mathcal{V}}^{1}}$ в точке y: ${{\mathcal{V}}^{0}}$ $ \prec $ y ∈ ${{\mathcal{V}}^{1}}$|${{\mathcal{V}}^{1}}$ ∩ ∩ maxV 0 = {y}.
Свойства:
 ${{\mathcal{V}}^{0}}$ $ \prec $ y ∈ ${{\mathcal{V}}^{1}}$
${{\mathcal{V}}^{0}}$ $ \prec $ y ∈ ${{\mathcal{V}}^{1}}$  ${{\mathcal{V}}^{0}}$æ${{\mathcal{V}}^{1}}$;
${{\mathcal{V}}^{0}}$æ${{\mathcal{V}}^{1}}$;  V0 ∩ V1 = {y} | ⇐ {{max${{\mathcal{V}}^{0}}$ ∩ V1 = {y} и μ(V0 ∩ V1) = 1}};
V0 ∩ V1 = {y} | ⇐ {{max${{\mathcal{V}}^{0}}$ ∩ V1 = {y} и μ(V0 ∩ V1) = 1}};
 выражение ${{\mathcal{V}}^{0}}$ $ \prec $ y ∈ ${{\mathcal{V}}^{1}}$ представляет собой неделимое слово, внутри которого символы $ \prec $ и ∈ являются семантическими разделителями, невидимыми снаружи.
выражение ${{\mathcal{V}}^{0}}$ $ \prec $ y ∈ ${{\mathcal{V}}^{1}}$ представляет собой неделимое слово, внутри которого символы $ \prec $ и ∈ являются семантическими разделителями, невидимыми снаружи.
〈2〉 Острое склеивание. Здесь рассматривается частный по сравнению с п. (1), но основной для нас случай последовательного склеивания ${{\mathcal{V}}^{0}}$ с ${{\mathcal{V}}^{1}}$ в точке y ВЫХОДА для ${{\mathcal{V}}^{0}}$|{y} = max${{\mathcal{V}}^{0}}$ и ВХОДА для ${{\mathcal{V}}^{1}}$|y ∈ min${{\mathcal{V}}^{1}}$: ${{\mathcal{V}}^{0}}$ $ \prec $ y $ \prec $ ${{\mathcal{V}}^{1}}$|{y} = max${{\mathcal{V}}^{0}}$ ∩ min${{\mathcal{V}}^{1}}$.
Свойства:
 ${{\mathcal{V}}^{0}}$ $ \prec $ y $ \prec $${{\mathcal{V}}^{1}}$
${{\mathcal{V}}^{0}}$ $ \prec $ y $ \prec $${{\mathcal{V}}^{1}}$  ${{\mathcal{V}}^{0}}$æ${{\mathcal{V}}^{1}}$|{y} = max${{\mathcal{V}}^{0}}$ ∩ min${{\mathcal{V}}^{1}}$;
${{\mathcal{V}}^{0}}$æ${{\mathcal{V}}^{1}}$|{y} = max${{\mathcal{V}}^{0}}$ ∩ min${{\mathcal{V}}^{1}}$;
 знаки $ \prec $ и $ \succ $ соединяют три части в одно целое, хотя внутри общего выражения остаются разделителями,
как и в обозначении 36;
знаки $ \prec $ и $ \succ $ соединяют три части в одно целое, хотя внутри общего выражения остаются разделителями,
как и в обозначении 36;
 ассоциативность: (${{\mathcal{V}}^{0}}$ $ \prec $ ${{{v}}_{0}}$ $ \prec $${{\mathcal{V}}^{1}}$) $ \prec $ ${{{v}}_{1}}$ $ \prec $ ${{\mathcal{V}}^{2}}$ = ${{\mathcal{V}}^{0}}$ $ \prec $ ${{{v}}_{0}}$ $ \prec $ (${{\mathcal{V}}^{1}}$ $ \prec $ ${{{v}}_{1}}$ $ \prec $ ${{\mathcal{V}}^{2}}$)| ${{{v}}_{i}}$ ∈ Vi ∩ Vi + 1|i = 0, 1,
ассоциативность: (${{\mathcal{V}}^{0}}$ $ \prec $ ${{{v}}_{0}}$ $ \prec $${{\mathcal{V}}^{1}}$) $ \prec $ ${{{v}}_{1}}$ $ \prec $ ${{\mathcal{V}}^{2}}$ = ${{\mathcal{V}}^{0}}$ $ \prec $ ${{{v}}_{0}}$ $ \prec $ (${{\mathcal{V}}^{1}}$ $ \prec $ ${{{v}}_{1}}$ $ \prec $ ${{\mathcal{V}}^{2}}$)| ${{{v}}_{i}}$ ∈ Vi ∩ Vi + 1|i = 0, 1,
 последовательное соединение: ${{\mathcal{V}}^{0}}$ ≤ ${{\mathcal{V}}^{1}}$ ≤ ${{\mathcal{V}}^{2}}$;
последовательное соединение: ${{\mathcal{V}}^{0}}$ ≤ ${{\mathcal{V}}^{1}}$ ≤ ${{\mathcal{V}}^{2}}$;
 коммутативность: ${{\mathcal{V}}^{0}}$ $ \prec $ w0$ \prec $ (${{\mathcal{V}}^{1}}$ $ \prec $ w1$ \prec $ $\mathcal{W}$) = ${{\mathcal{V}}^{1}}$ $ \prec $ w1$ \prec $ (${{\mathcal{V}}^{0}}$ $ \prec $ w0$ \prec $ $\mathcal{W}$)|wi ∈ Vi ∩ W|i = 0, 1,
коммутативность: ${{\mathcal{V}}^{0}}$ $ \prec $ w0$ \prec $ (${{\mathcal{V}}^{1}}$ $ \prec $ w1$ \prec $ $\mathcal{W}$) = ${{\mathcal{V}}^{1}}$ $ \prec $ w1$ \prec $ (${{\mathcal{V}}^{0}}$ $ \prec $ w0$ \prec $ $\mathcal{W}$)|wi ∈ Vi ∩ W|i = 0, 1,
 параллельное соединение: ${{\mathcal{V}}^{0}}$ ≤ $\mathcal{W}$ и ${{\mathcal{V}}^{1}}$ ≤ $\mathcal{W}$.
параллельное соединение: ${{\mathcal{V}}^{0}}$ ≤ $\mathcal{W}$ и ${{\mathcal{V}}^{1}}$ ≤ $\mathcal{W}$.
Теоремa 3. Экстремумы полуострого склеивания:
Доказательство. Ниже будут доказываться только $\mathop = \limits^? $.
〈1〉 Переход между знаками = к результату обеспечивается леммой 6 〈2〉: $ \rtimes $⇒ {y} = max${{\mathcal{V}}^{0}}$ ⇒ ⇒ y(0 > $ \in \to $ (V0\{y}) ;⇒ max(${{\mathcal{V}}^{0}}$æ${{\mathcal{V}}^{1}}$) = max((${{\mathcal{V}}^{0}}$æ${{\mathcal{V}}^{1}}$)\(V0\{y})) = max{V1, ≤} = max{V1, ≤1)} = max${{\mathcal{V}}^{1}}$ ;⇒ 
〈2〉 $\mathcal{W}$ ∈ РТА и следствие def19;⇒ min$\mathcal{W}$ = min$\left( {\bigcup\limits_{w \in \mathcal{W}}^{} {( \leqslant w)} } \right)$ = $\bigcup\limits_{w \in \mathcal{W}}^{} {\min } $(≤w) . Это общие рассуждения. Применим их к случаю, когда $\mathcal{W}$ := (${{\mathcal{V}}^{0}}$ $ \prec $ y ∈ ${{\mathcal{V}}^{1}}$)| 
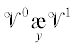 .
.
До сих пор наши умозаключения визуализироваились силлогизмами, в которых использовался союз -И- {{то же, что ∧, -AND-}}. Настала пора внедрения союза -ИЛИ- {{то же, что ∨, -OR-}} в ЛС. Его мы назовем $ \ulcorner {\text{мягким}} \lrcorner $2828 разделителем случаев и будем изображать на схемах иероглифом $ \circledcirc $. Под жестким разделителем ⊙ понимается симметрическая разность типа (a ∨ b) ∧ ¬(a ∧ b). Процессуальные свойства -ИЛИ- мягкого {{то же, что $ \circledcirc $}} и жесткого {{то же, что ⊙}} неизвестны, поэтому действовать будем осторожно:
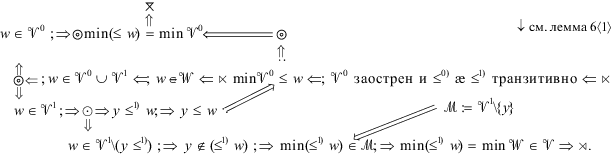
Следствие thr3. Замкнутость острого склеивания острых ЧУМ.
Склеивание острых множеств даст острое множество (см. (3.1)) ⇐ теорема 3〈1〉.
Обозначение 39. Суперпозиция острых множеств.
〈1〉 Независимость острых конусов. ЧУМ $\mathcal{W}$ := {W, ≤} используется ниже для склеивания его острых конусов ${{\mathcal{V}}^{i}}$ := {Vi, ≤} Vi ⊆ W | i ∈ [0, k] | k ∈ ${{\mathbb{Z}}^{ + }}$, обладающих свойством независимости:
(3.2)
$i \ne j \Rightarrow \min {{\mathcal{V}}^{i}} \cap \max {{\mathcal{V}}^{j}} = {{\mathcal{V}}^{i}} \cap {{\mathcal{V}}^{j}}\quad {\text{и}}\quad \mu ({{\mathcal{V}}^{i}} \cap {{\mathcal{V}}^{j}}) \leqslant 1|i,j \in [0,k].$Результат склеивания $\mathcal{V}$ будет представлен в виде суперпозиции функций многих переменных $\mathcal{W}$ ⊇ $\mathcal{V}$ := ${v}_{0}^{0}$|${v}_{j}^{i}$ = max$\mathcal{V}_{j}^{i}$ и $\mathcal{V}_{j}^{i}$ = ${v}_{j}^{i}$〈〈$\overrightarrow \subset $min$\mathcal{V}_{j}^{i}$〉〉 (см. обозначение 37).
〈2〉 Последовательное соединение (склеивание). Для последовательного соединения (3.2) упрощается: μ(${{\mathcal{V}}_{i}}$ ⊇ ${{\mathcal{V}}_{j}}$) =  j = i + 1?|i, j ∈ [0, k] (см. определение 2),
j = i + 1?|i, j ∈ [0, k] (см. определение 2),
$\mathcal{V}$ := ${{{v}}_{0}}$〈〈${{{v}}_{1}}$〈〈${{{v}}_{2}}$〈〈…〉〉, x2, …, y2〉〉, x1, …, y1〉〉 := (${{{v}}_{0}}$ ≻ ${{\mathcal{V}}^{0}}$ ≻ {${{{v}}_{1}}$, x1, …, y1})  (${{{v}}_{1}}$ ≻ ${{\mathcal{V}}^{1}}$ ≻ {${{{v}}_{2}}$, x2, …, y2})
(${{{v}}_{1}}$ ≻ ${{\mathcal{V}}^{1}}$ ≻ {${{{v}}_{2}}$, x2, …, y2}) 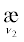 (${{{v}}_{2}}$ ≻ …) … =: {{⇐;
(${{{v}}_{2}}$ ≻ …) … =: {{⇐;  (ассоциативность); ⇒}} =: ${{\mathcal{V}}^{0}}$ ≻ ${{{v}}_{1}}$ ≻ ${{\mathcal{V}}^{1}}$ ≻ ${{{v}}_{2}}$ … ≻ ${{\mathcal{V}}^{{k - 1}}}$ ≻ ${{{v}}_{k}}$ ≻${{\mathcal{V}}^{k}}$ …|${{\mathcal{V}}^{i}}$ = ${{{v}}_{i}}$ ≻ ≻ ${{\mathcal{V}}^{i}}$ ≻ {${{{v}}_{{i + 1}}}$, ${{x}_{{i + 1}}}$, …, ${{y}_{{i + 1}}}$} =: ${{{v}}_{i}}$〈〈${{{v}}_{{i + 1}}}$, ${{x}_{{i + 1}}}$, …, ${{y}_{{i + 1}}}$〉〉|i ∈ [0, k].
(ассоциативность); ⇒}} =: ${{\mathcal{V}}^{0}}$ ≻ ${{{v}}_{1}}$ ≻ ${{\mathcal{V}}^{1}}$ ≻ ${{{v}}_{2}}$ … ≻ ${{\mathcal{V}}^{{k - 1}}}$ ≻ ${{{v}}_{k}}$ ≻${{\mathcal{V}}^{k}}$ …|${{\mathcal{V}}^{i}}$ = ${{{v}}_{i}}$ ≻ ≻ ${{\mathcal{V}}^{i}}$ ≻ {${{{v}}_{{i + 1}}}$, ${{x}_{{i + 1}}}$, …, ${{y}_{{i + 1}}}$} =: ${{{v}}_{i}}$〈〈${{{v}}_{{i + 1}}}$, ${{x}_{{i + 1}}}$, …, ${{y}_{{i + 1}}}$〉〉|i ∈ [0, k].
〈3〉 Параллельное соединение (склеивание). Подстановка острых черных ящиков ${{\mathcal{V}}^{i}}$|i ∈ [1, k] на места аргументов острого множества (см. обозначение 36) ${{\mathcal{V}}^{0}}$ = ${{{v}}_{0}}$〈〈${{{v}}_{1}}$, … ${{{v}}_{k}}$〉〉 := {${{{v}}_{0}}$} ≻ $\mathcal{V}$ ≻ {${{{v}}_{1}}$, …, ${{{v}}_{k}}$} := $\mathcal{V}$|{{{${{{v}}_{0}}$} = max$\mathcal{V}$ и {${{{v}}_{1}}$, … ${{{v}}_{k}}$} ⊆ min$\mathcal{V}$}} дается определением ${{{v}}_{0}}$〈〈${{\mathcal{V}}^{1}}$, … ${{\mathcal{V}}^{k}}$〉〉 := ${{{v}}_{0}}$〈〈${{{v}}_{1}}$ ≻ ${{\mathcal{V}}^{1}}$, …, ${{{v}}_{k}}$ ≻ ${{\mathcal{V}}^{k}}$〉〉.
Согласно теореме 3〈2〉, аргументами параллельного соединения могут быть любые элементы из множества $\bigcup\limits_{i = 1}^k {\min {{\mathcal{V}}^{i}}} $\$\bigcup\limits_{i = 1}^k {\max {{\mathcal{V}}^{i}}} $ по выбору пользователя.
〈4〉 Вывод: (3.2) ⇒ ${v}_{0}^{0}\langle \langle {v}_{0}^{1}\langle \langle ...\rangle \rangle $, …, ${v}_{{{{k}_{1}}}}^{1}$〈〈…〉〉〉〉 ∈ ЗЧУМ ⇐; следствие thr3.
Заключение. Анализ последовательностей вывода. В данной работе Синтез простеньких” ЧУМ, под которыми подразумеваются так называемые однотипные (см. ниже) последовательности вывода ФЗ, лежит в основе АНАЛИЗА произвольных ПВ, которые могут быть сколь угодно сложными ЧУМ. Далее приводится формулировка работы [4, теорема 3, с. 68], являющейся итогом вышеизложенного. Ее расстолкование будет надлежащим образом приведено в статье 3) Введения, но сейчас мы дадим по ее поводу минимальные объяснения.
Определение 23. Однотипность последовательности вывода $\mathcal{P}$. Последовательность $\mathcal{P}$ однотипна, если начальные подсхемы всех ее строго выводимых ФЗ совпадают:
Определение 24. АР-последовательность вывода $\mathcal{P}$.
Примечание. В виду элементарного равенства (X\Y)\Z = X\(Y ∪ Z) условие 〈2〉 можно заменить требованием: множество аксиом ВЗ в $\mathcal{P}$ нéмощно, т.е. μ{ВЗ|∈$\mathcal{P}$} ≤ 1.
Обозначение 40. Немощное разбиение множества А $ \cup \centerdot $ В.
А $ \cup \centerdot $ В := A ∪ B | μ(A ∩ B) ≤ 1 (см. определение 3 и ср. с обозначением 4).
[4, теорема 3, с. 68]. АР-декомпозиция плотного вывода. Плотный вывод $\mathcal{P}$|$\mathcal{P}$ $ \Rrightarrow $ $\Delta _{1}^{1}$ := ${{\mathcal{P}}_{{\mu (\mathcal{P}) - 1}}}$ (см. обозначения 24, 39, 41 и [4, определение 16, с. 68]) можно привести в смысле ФЭПВ к нéмощному разбиению на плотные АР-выводы с результатами вывода $\Delta _{q}^{p}$ | $\Delta _{q}^{p}$ ∈ $\mathcal{P}$, p, q ∈ [1, μ($\mathcal{P}$)[. Все АР-выводы изоморфны лежащим в $\mathcal{P}$ соответствующим фрагментам вывода.
В задаче 3) Введения будет описан процесс уплотнения и доказано, что любую ПВ можно уплотнить. АР-вывод определяется так, чтобы все выводимые в нем ФЗ были бы однотипны в смысле определения 23. Это позволит привести его к функционально эквивалентному алгебраическому выражению, что осуществляется в задаче 4) Введения с легкостью. Разбиение заданного плотного вывода на АР-фрагменты создает предпосылку алгебраизации всей заданной последовательности вывода.
Завершим объяснения с помощью обозначений 24 и 41:
Обозначение 41. Конус вывода. ↓ смысл $\mathbb{C}$ и $\mathbb{P}$ см. в определении 14: $\mathbb{P}$〈〈$\overrightarrow \subset $min$\mathcal{P}$〉〉 := := $\mathbb{P}$ $ \Lleftarrow $= |$\mathbb{P}$ $\overrightarrow \subset $ $\mathbb{C}$ и $\mathcal{P}$ $ \in \to $ {$\mathbb{C}$ $ \Rrightarrow $} (см. термины разд. 3.1 для $ \Rrightarrow $+|$ \Rrightarrow $+ = (=$ \Rrightarrow $)). Переход от круглых скобок (), использующихся в обозначениях 37 и 39, к 〈〈 〉〉 необходим для линейного изображения пространственных структур КУМ’а в ПВ. На фоне самостоятельности $\mathbb{P}$ суффикс 〈〈$\overrightarrow \subset $min$\mathcal{P}$〉〉 делает $\mathbb{P}$〈〈 〉〉 последовательностью вывода. Он также используется для внешнего воздействия на внутренность вывода $\mathcal{P}$, что является основным предназначением скобок в обозначениях функций вообще. Внешние изменения могут затрагивать не все внутренние субъекты $\mathcal{P}$, поэтому здесь используется символ свободного выбора $\overrightarrow \subset $, который может быть пустым.
Для $\mathcal{P}$ $ \in \to $ {$\mathbb{C} \Rrightarrow $ Ψ} в конусе Ψ $ \Lleftarrow $= выберем ФЗ, однотипные с Ψ с примыкающими к ним константами из $\mathbb{C}$. Условием выбора является связность результата Δ0〈〈Δ1, …, Δq〉〉)|Δ0 := Ψ, где Δ1, …, Δq – все ФЗ, выводимые в $\mathcal{P}$, из которых выводится Ψ. Далее с Δ1, …, Δq проделываем ту же операцию до исчерпания $\mathcal{P}$. В результате АНАЛИЗА плотного вывода $\mathcal{P}$ получим его АР-декомпозицию.
Список литературы
Мейер Д. Теория реляционных баз данных. М.: Мир, 1987.
Heath I.J. Unacceptable File Operation in Relational Database // Proc. ACM SIGFIDET Workshop on Data Description, Access and Control. San Diego, CA, USA, 1971.
Ульман Дж. Базы данных на Паскале. М.: Машиностроение, 1990.
Поморцев Л.А., Цурков В.И. Алгебраизация вывода функциональных зависимостей реляционных баз данных // Изв. РАН. ТиСУ. 2019. № 2. С. 66–82.
Поморцев Л.А. Алгебраическая интерпретация полноты аксиом вывода // Фундамент. и прикл. математика 2002. Т. 8. № 1. С. 195–219.
Поморцев Л.А. Алгебры функциональных зависимостей в теории реляционнных баз данных // Тр. Института системного анализа РАН. Динамика неоднородных систем. 2007. Т. 29 (1). № 11. С. 169–183.
Курош А.Г. Лекции по общей алгебре. М.: Физматгиз, 1962.
Яблонский СВ. Введение в дискретную математику. М.: Наука, 1986.
Баранов М.Т., Костяева Т.А., Прудникова А.В. Русский язык. М.: Просвещение, 1987.
Поморцев Л.А. Вычисление моментов порядковых статистик последовательных сумм симметрически зависимых случайных величин // Тр. Московского математического общества. 1983. Т. 46. С. 201–242.
Поморцев Л.А. Комбинаторно-симметрический анализ многомерных случайных блужданий // Дискретная математика. 1991. Т. 3. № 1. С. 21–41.
Дейт К.Дж. Введение в системы Баз Данных. М.–СПб.–Киев: Изд. дом “Вильямс”, 2001.
Емеличев В.А., Мельников О.И., Сарванов В.И. и др. Лекции по теории графов. М.: Наука, 1990.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления