1. На главную
  2. Электронные версии
  3. Известия РАН. Теория и системы управления
  4. № 6, 2020

Известия РАН. Теория и системы управления, 2020, № 6, стр. 32-41

АЛГЕБРАИЧЕСКИЙ МЕТОД НЕПАРАМЕТРИЧЕСКОЙ ИДЕНТИФИКАЦИИ НЕНОРМАЛЬНЫХ РЕЖИМОВ ЭНЕРГОСИСТЕМЫ КАК ДИНАМИЧЕСКОЙ MIMO-СИСТЕМЫ

И. М. Галиаскаров a, Н. Е. Зубов b, *, Е. Ю. Зыбин c, В. Н. Рябченко b, d

a АО “Центр инжиниринга и управления строительством”
Москва, Россия

b МГТУ им. Н.Э. Баумана
Москва, Россия

c ФГУП “ГосНИИАС”
Москва, Россия

d МЭИ (национальный исследовательский ун-т)
Москва, Россия

* E-mail: nik.zubov@gmail.com

Поступила в редакцию 13.11.2019
После доработки 08.05.2020
Принята к публикации 25.05.2020

Полный текст (PDF)

Аннотация

Предлагается подход осуществления идентификации ненормальных режимов энергосистемы в реальном масштабе времени, использующий только данные синхронизированных векторных измерений и не требующий априорной информации о параметрах ее математической модели. Алгоритмическую основу метода составляет алгебраический критерий совместности линейного матричного уравнения идентификации математической модели энергосистемы, он не предполагает решения задач параметрической идентификации или прогнозирования, не использует статистические вычисления и не требует своего предварительного обучения или длительной настройки. Эффективность метода демонстрируется на примере обнаружения момента возникновения аварийной ситуации в Омской энергосистеме.

Введение. Ненормальные режимы энергосистемы, включающие в себя предаварийные, аварийные и послеаварийные режимы, приводят к выходу значений напряжения, тока и частоты из пределов длительно допустимых значений. В зависимости от причины возникновения и характера проявления различают ненормальные режимы короткого замыкания, перегрузки, повышения или понижения напряжения, понижения частоты, качаний, нарушения синхронизма, устойчивости и т.д. При понижении частоты и напряжения создается опасность нарушения нормальной работы потребителей и устойчивости энергосистемы, а повышение напряжения и тока угрожает повреждением оборудования и линий электропередачи. К ненормальным режимам могут быть также отнесены любые переходные режимы работы энергосистемы со значительными изменениями параметров режима.

По мере распространения ненормального режима управляемость энергосистемы резко падает и в результате развития может привести к большему ущербу для народного хозяйства, нарушениям условий безопасности и другим тяжелым последствиям. Здесь под снижением управляемости в зависимости от ситуации понимается как появление неуправляемых мод колебаний, т.е. потеря свойства полной управляемости, например по Калману [1] или Попову–Белевичу–Хотису [2], так и уменьшение индуцированной нормы [2, 3] или иной скалярной функции [4] грамиана управляемости, рассматриваемых в качестве мер управляемости.

Для недопущения аварийной ситуации в энергосистеме необходимо как можно быстрее обнаружить возникновение ненормального режима независимо от его масштаба, места и причины возникновения. Решение данной задачи возможно за счет применения распределенных в пространстве и синхронизированных по времени векторных измерителей (phasor measurement units – PMU), реализованных за рубежом в Европе, США, Китае и других странах в виде системы wide area measurement system (WAMS) и ее российском аналоге – системы мониторинга переходных режимов (СМПР) [5–12].

Известные методы обнаружения повреждений и ненормальных режимов энергосистем можно условно разбить на две группы: параметрические (модельные) и непараметрические (безмодельные, основанные на данных, сигналах, знаниях, правилах и т.д.) [12–30]. В параметрических методах прямо или косвенно применяются параметры математических моделей энергосистем и их элементов. Методы второй группы используют только данные векторных измерений [13].

Параметрические методы являются наиболее распространенными и считаются классическими [14–17]. В этих методах под ненормальным режимом энергосистемы, с формальной точки зрения, понимают непрогнозируемое скачкообразное изменение математической модели ее нормального (рабочего) режима функционирования. Среди них, как правило, выделяют три подхода. Первый основан на определении параметров (инвариантов) моделей контролируемых объектов, второй – на решении задач моделирования (прогнозирования), третий – на аналитической избыточности. Применение параметрических методов требует обеспечения полной наблюдаемости энергосистемы, они характеризуются недостаточной робастностью, например, в смысле “овражистости рельефа” ε-спектра системы [31, 32] или значений ляпуновских показателей [33, 34], высокой вычислительной сложностью, которая нелинейным образом зависит от размерности пространства состояния системы [35, 36].

В отличие от параметрических методов, в методах, основанных только на данных векторных измерений, априорная информация о параметрах модели энергосистемы не требуется. Данные методы базируются на выявлении характерных качественных или количественных признаков контролируемых объектов. Среди них выделяют методы, основанные на сигналах (данных), и методы, основанные на знаниях (правилах) [19, 20].

Методы, основанные на сигналах, включают методы вейвлет и преобразований Фурье, сингулярного разложения и многомерного статистического анализа, методы, построенные с использованием сетей Петри, экспонент Ляпунова и др. Точность работы алгоритмов вейвлет- преобразований определяется высокой частотой дискретизации данных векторных измерений [20], а эффективность преобразования Фурье зависит от ширины окна измерений, получение оптимального значения которого является отдельной трудной задачей [21]. Анализ максимальных сингулярных чисел матрицы векторных измерений эффективно применяются для обнаружения нарушений устойчивости, однако характеризуется невысокой чувствительностью к другим ненормальным режимам энергосистемы [22].

К статистическим методам относятся методы главных компонент/частных наименьших квадратов, методы теории случайных матриц, скрытых марковских моделей и методы, использующие алгоритмы классификации [23, 24]. По определению все статистические алгоритмы требуют достаточно большой выборки данных измерений для проявления статистических свойств анализируемых переменных, что неизбежно приводит к увеличению времени, требуемого для принятия решения. В условиях практической эксплуатации применение статистических методов для обнаружения ненормальных режимов может потребовать время, превышающее критическое время реакции системы защиты, и энергосистема может перейти в невосстанавливаемое состояние.

Сети Петри чувствительны к наличию в энергосистеме распределенных источников электроэнергии и управляемого силового оборудования [21]. Непараметрические реализации метода экспонент Ляпунова не предназначены для обнаружения быстропротекающих изменений в энергосистемы и требуют априорной точной оптимизации ширины окна измерений, которая зависит от типа ненормального режима [25].

Методы, основанные на знаниях, включают методы экспертных систем и машинного обучения [26]. Экспертные системы основаны на субъективных и неполных знаниях, не всегда позволяющих достоверно определить взаимосвязи между возникновением ненормального режима энергосистемы и причиной, его вызвавшей. Методы машинного обучения (нейронные сети, деревья решений, опорных векторов и т.д.) по определению требуют их предварительное обучение/настройку для конкретного объекта с использованием объемных баз данных априорных измерений [27–30].

В статье предлагается новый алгебраический непараметрический метод обнаружения ненормальных режимов энергосистемы в реальном масштабе времени, применяющий только данные синхронизированных векторных измерений и не требующий априорной информации о параметрах ее математической модели. Он не предполагает решения задач идентификации или прогнозирования, не использует статистические вычисления и не требует своего предварительного обучения или длительной настройки.

1. Метод обнаружения ненормальных режимов. Пусть математическая модель нормального режима работы энергосистемы описывается линейной дискретной динамической системой с многими входами и многими выходами (multi input multi output – MIMO) в пространстве состояний в виде

(1.1)
${{x}_{{k + 1}}} = {\mathbf{A}}{{x}_{k}} + {\mathbf{B}}{{v}_{k}},$
где A, B – матрицы собственной динамики и эффективности управления; x – вектор состояний энергосистемы размерности nx, v – вектор входных (управляющих) воздействий размерности ${{n}_{{v}}}$, $k = 0,1$, ... – дискретное время.

Предположим, что в момент времени k + 1 = f в энергосистеме возник ненормальный режим работы, приведший к изменению параметров ее модели в виде пар матриц $\left[ {\begin{array}{*{20}{c}} {{\mathbf{\bar {A}}}}&{{\mathbf{\bar {B}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\mathbf{A}}&{\mathbf{B}} \end{array}} \right]$ + + $\left[ {\begin{array}{*{20}{c}} {\Delta {\mathbf{A}}}&{\Delta {\mathbf{B}}} \end{array}} \right]$. Необходимо только по результатам синхронизированных измерений векторов состояний и входных воздействий обнаружить собственно факт и определить момент возникновения ненормального режима в энергосистеме, т.е. “переключения” (резкой, скачкообразной смены) математической модели режима [37–40]. Это можно выразить следующей импликацией:

(1.2)
$\left[ {\begin{array}{*{20}{c}} {\mathbf{A}}&{\mathbf{B}} \end{array}} \right]\xrightarrow[{k + \;1\; = f}]{}\left[ {\begin{array}{*{20}{c}} {{\mathbf{\bar {A}}}}&{{\mathbf{\bar {B}}}} \end{array}} \right],$
где k + 1 = f – момент “переключения”. Указанные изменения могут носить как локальный, так и глобальный характер, иметь как малые, так и кратные вариации параметров.

Допустим, что наблюдение за энергосистемой на основе синхронизированных векторных измерений ведется на протяжении некоторого времени h + 2. Тогда модель энергосистемы (1.1) можно записать в матричном виде как до возникновения ненормального режима:

(1.3)
${{{\mathbf{X}}}_{{k + 1}}} = {\mathbf{A}}{{{\mathbf{X}}}_{k}} + {\mathbf{B}}{{{\mathbf{V}}}_{k}},\quad k = 0,1,...,f - 2,$
так и после его возникновения:
(1.4)
${{{\mathbf{X}}}_{{k + 1}}} = {\mathbf{\bar {A}}}{{{\mathbf{X}}}_{k}} + {\mathbf{\bar {B}}}{{{\mathbf{V}}}_{k}},\quad k = f + h - 1,f + h,...,$
где
(1.5)
${{{\mathbf{X}}}_{k}} = \left[ {{{x}_{{k - h}}}\;...\;{{x}_{{k - 1}}}\;{{x}_{k}}} \right],\quad {{{\mathbf{V}}}_{k}} = \left[ {{{v}_{{k - h}}}\;...\;{{v}_{{k - 1}}}\;{{v}_{k}}} \right]$
– матрицы измерений, составленные на основе данных PMU.

Решим задачу параметрической идентификации модели энергосистемы в нормальном и аварийном режимах, для чего перепишем выражения (1.3), (1.4) в виде эквивалентных блочно-матричных уравнений, в которых в качестве неизвестных выступают матрицы A, B и ${\mathbf{\bar {A}}}$, ${\mathbf{\bar {B}}}$, соответственно:

(1.6)
$\left[ {\begin{array}{*{20}{c}} {\mathbf{A}}&{\mathbf{B}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{X}}}_{k}}} \\ {{{{\mathbf{V}}}_{k}}} \end{array}} \right] = {{{\mathbf{X}}}_{{k + 1}}},$
(1.7)
$\left[ {\begin{array}{*{20}{c}} {{\mathbf{\bar {A}}}}&{{\mathbf{\bar {B}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{X}}}_{k}}} \\ {{{{\mathbf{V}}}_{k}}} \end{array}} \right] = {{{\mathbf{X}}}_{{k + 1}}}.$

Для решения уравнений (1.6), (1.7) воспользуемся результатами работ [32, 41], где показано, что любое линейное матричное уравнение вида

(1.8)
${\mathbf{YC}} = {\mathbf{D}}$
с известными матрицами C, D разрешимо относительно матрицы Y тогда и только тогда, когда выполняется условие совместности (разрешимости):
(1.9)
${\mathbf{DC}}_{R}^{ \bot } = 0,$
а все множество решений матричного уравнения (1.8) определяется формулой
(1.10)
${\mathbf{Y}} = \left[ {\begin{array}{*{20}{c}} {{\mathbf{DC}}_{R}^{ - }}&\Theta \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathbf{C}}_{L}^{ - }} \\ {{\mathbf{C}}_{L}^{ \bot }} \end{array}} \right] = {\mathbf{DC}}_{{}}^{ - } + \Theta {\mathbf{C}}_{L}^{ \bot },$
где $\Theta $ – произвольная матрица; ${\mathbf{C}}_{L}^{ \bot }$, ${\mathbf{C}}_{R}^{ \bot }$ – левый и правый делители нуля максимального ранга (т.е. матрицы, для которых выполняются условия ${\mathbf{C}}_{L}^{ \bot }{\mathbf{C}} = 0$, ${\mathbf{CC}}_{R}^{ \bot } = 0$), ${\mathbf{C}}_{L}^{ - }$, ${\mathbf{C}}_{R}^{ - }$ – левый и правый делители единицы (т.е. матрицы, удовлетворяющие равенству ${\mathbf{C}}_{L}^{ - }{\mathbf{CC}}_{R}^{ - } = {\mathbf{E}}$, здесь и далее E – единичная матрица); ${\mathbf{C}}_{{}}^{ - } = {\mathbf{C}}_{R}^{ - }{\mathbf{C}}_{L}^{ - }$ – обобщенно-обратная матрица, удовлетворяющая каноническому разложению

(1.11)
${\mathbf{C}} = {{\left[ {\begin{array}{*{20}{c}} {{\mathbf{C}}_{L}^{ - }} \\ {{\mathbf{C}}_{L}^{ \bot }} \end{array}} \right]}^{{ - 1}}}\left[ {\begin{array}{*{20}{c}} {\mathbf{E}}&0 \\ 0&0 \end{array}} \right]{{\left[ {\begin{array}{*{20}{c}} {{\mathbf{C}}_{R}^{ - }}&{{\mathbf{C}}_{R}^{ \bot }} \end{array}} \right]}^{{ - 1}}}.$

Частным  случаем  обобщенно-обратной  матрицы является псевдообратная по Муру–Пенроузу C+ [32].

Каноническое разложение (1.11) имеет в общем случае неединственный вид и фактически формализует прямые и обратные эквивалентные преобразования матрицы [32]. Использование канонического разложения позволяет получать в аналитическом виде множество всех решений матричного уравнения (1.8) с минимальной параметризацией.

Сопоставим уравнению (1.8) уравнения (1.6) и (1.7), используемые для решения задачи параметрической идентификации нормального и ненормального режимов. Тогда в соответствии с (1.9) условием разрешимости (совместности) задачи идентификации, т.е. условием наличия хотя бы одного решения, является выражение

(1.12)
${{{\mathbf{X}}}_{{k + 1}}}\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{X}}}_{k}}} \\ {{{{\mathbf{V}}}_{k}}} \end{array}} \right]_{R}^{ \bot } = 0,$
при выполнении которого все идентифицированные модели, согласно (1.10), могут быть записаны в виде множеств
(1.13)
$\left[ {\begin{array}{*{20}{c}} {\mathbf{A}}&{\mathbf{B}} \end{array}} \right] = {{{\mathbf{X}}}_{{k + 1}}}\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{X}}}_{k}}} \\ {{{{\mathbf{V}}}_{k}}} \end{array}} \right]_{R}^{ - } + \Theta \left[ {\begin{array}{*{20}{c}} {{{{\mathbf{X}}}_{k}}} \\ {{{{\mathbf{V}}}_{k}}} \end{array}} \right]_{L}^{ \bot },$
(1.14)
$\left[ {\begin{array}{*{20}{c}} {{\mathbf{\bar {A}}}}&{{\mathbf{\bar {B}}}} \end{array}} \right] = {{{\mathbf{X}}}_{{k + 1}}}\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{X}}}_{k}}} \\ {{{{\mathbf{V}}}_{k}}} \end{array}} \right]_{R}^{ - } + \bar {\Theta }\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{X}}}_{k}}} \\ {{{{\mathbf{V}}}_{k}}} \end{array}} \right]_{L}^{ \bot },$
где $\Theta $, $\bar {\Theta }$ – произвольные матрицы соответствующих размеров.

При выполнении условия идентифицируемости, т.е. условия получения единственного решения в формулах (1.13), (1.14)

(1.15)
$\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{X}}}_{k}}} \\ {{{{\mathbf{V}}}_{k}}} \end{array}} \right]_{L}^{ \bot } = 0,$
матрицы параметров математических моделей принимают единственный вид, поэтому с помощью анализа изменения их значений можно легко сделать вывод о факте возникновения ненормального режима в энергосистеме.

Этот подход, основанный на идентификации параметров модели, является наиболее эффективным в теоретическом плане, но существенно ограничен в применении на практике проблемами, связанными с неидентифицируемостью в рабочем режиме моделей разомкнутой динамики объектов с замкнутыми системами управления, т.е. принципиальной невозможностью обеспечения условия единственности решения задач идентификации (1.15) [42].

2. Метод обнаружения ненормального режима в MIMO-системе. Покажем далее, как можно решить задачу обнаружения ненормального режима без необходимости определения параметров модели энергосистемы только по результатам наблюдения ее состояний и входных воздействий. Заметим, что условие совместности уравнения задачи идентификации (1.12) выполняется как до, так и после возникновения ненормального режима, однако когда окно измерений содержит момент его возникновения, не существует таких матриц ${\mathbf{\tilde {A}}}$, ${\mathbf{\tilde {B}}}$, с помощью которых поведение энергосистемы может быть описано линейной динамической MIMO-системой:

(2.1)
${{{\mathbf{X}}}_{{k + 1}}} \ne {\mathbf{\tilde {A}}}{{{\mathbf{X}}}_{k}} + {\mathbf{\tilde {B}}}{{{\mathbf{V}}}_{k}},\quad k = f - 1,\quad f,...,f + h - 2$
и, следовательно, не выполняется условие совместности вида (1.12):

(2.2)
${{{\mathbf{X}}}_{{k + 1}}}\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{X}}}_{k}}} \\ {{{{\mathbf{V}}}_{k}}} \end{array}} \right]_{R}^{ \bot } \ne 0.$

Исходя из сказанного, в качестве критерия обнаружения ненормального режима в энергосистеме можно принять норму условия (1.12), вычисляемую для каждого момента времени:

(2.3)
$\varepsilon = \left\| {{{{\mathbf{X}}}_{{k + 1}}}\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{X}}}_{k}}} \\ {{{{\mathbf{V}}}_{k}}} \end{array}} \right]_{R}^{ \bot }} \right\|,$
с использованием ортогонального делителя нуля:

(2.4)
$\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{X}}}_{k}}} \\ {{{{\mathbf{V}}}_{k}}} \end{array}} \right]_{R}^{{ \bot T}}\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{X}}}_{k}}} \\ {{{{\mathbf{V}}}_{k}}} \end{array}} \right]_{R}^{ \bot } = {\mathbf{E}}.$

За счет влияния нелинейностей, действия небольших по интенсивности возмущений, ошибок измерений и других неопределенностей значение этого критерия в нормальном режиме должно быть близким, но не обязательно равным нулю, ε ≈ 0. При возникновении ненормального режима энергосистемы критерий будет превышать некоторое пороговое значение $\varepsilon \geqslant {{\varepsilon }_{{{\text{зад}}}}} \gg 0$ – в эти моменты времени невозможно описать поведение системы с помощью единой линейной матричной модели (1.1), поскольку происходит изменение значений ее параметров. По мере возвращения к послеаварийному режиму (установления новых значений параметров модели) значения критерия снова будут близки к нулю.

Сформулируем далее с использованием представленного метода алгоритм 1 обнаружения ненормального режима в энергосистеме на основе синхронизированных векторных измерений.

Шаг 1. Для каждого момента времени k составляется матрица измерений

(2.5)
$\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{X}}}_{k}}} \\ {{{{\mathbf{V}}}_{k}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{x}_{{k - h}}}\;...\;{{x}_{{k - 1}}}\;{{x}_{k}}} \\ {{{v}_{{k - h}}}\;...\;{{v}_{{k - 1}}}\;{{v}_{k}}} \end{array}} \right],$
ширина которой $h$ + 1 должна быть достаточной для выполнения условий шага 2.

Шаг 2. Определяется нетривиальный правый делитель нуля матрицы измерений

$\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{X}}}_{k}}} \\ {{{{\mathbf{V}}}_{k}}} \end{array}} \right]_{R}^{ \bot } = \left[ {\begin{array}{*{20}{c}} {{{x}_{{k - h}}}\;...\;{{x}_{{k - 1}}}\;{{x}_{k}}} \\ {{{v}_{{k - h}}}\;...\;{{v}_{{k - 1}}}\;{{v}_{k}}} \end{array}} \right]_{R}^{ \bot } \ne 0,$
удовлетворяющий условию ортогональности (2.4).

Шаг 3. Составляется матрица измерений ${{{\mathbf{X}}}_{{k + 1}}} = \left[ {\begin{array}{*{20}{c}} {{{x}_{{k - h + 1}}}\;...\;{{x}_{k}}\;{{x}_{{k + 1}}}} \end{array}} \right]$ и определяется значение критерия (2.3):

(2.6)
$\varepsilon = \left\| {{{{\mathbf{X}}}_{{k + 1}}}\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{X}}}_{k}}} \\ {{{{\mathbf{V}}}_{k}}} \end{array}} \right]_{R}^{ \bot }} \right\| = \left\| {\left[ {\begin{array}{*{20}{c}} {{{x}_{{k - h + 1}}}\;...\;{{x}_{k}}\;{{x}_{{k + 1}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{x}_{{k - h}}}\;...\;{{x}_{{k - 1}}}\;{{x}_{k}}} \\ {{{v}_{{k - h}}}\;...\;{{v}_{{k - 1}}}\;{{v}_{k}}} \end{array}} \right]_{R}^{ \bot }} \right\|.$

Резкий рост значения ε будет соответствовать возникновению ненормального режима энергосистемы, а момент отклонения ε от нуля будет совпадать с временем его возникновения. Таким образом, быстродействие алгоритма обнаружения ненормального режима определяется частотой дискретизации сигналов и совпадает с интервалом времени между двумя последовательными измерениями.

Максимально необходимое количество измерений для настройки алгоритма на режим работы энергосистемы определяется суммой размерностей векторов состояний и управлений $h\; + 1 = {{n}_{x}} + {{n}_{{v}}} + 1$. В случаях вырожденных систем и низкой информативности сигналов количество измерений может быть уменьшено. При этом минимально необходимое количество измерений определяется такой шириной матрицы измерений (2.5), при которой в ней появляются линейно зависимые столбцы.

3. Обнаружение ненормальных режимов в автономной модели энергосистемы. В нормальном режиме модель энергосистемы (1.1) может быть представлена с помощью автономной динамической MIMO-системы вида

(3.1)
${{x}_{{k + 1}}} = {\mathbf{A}}{{x}_{k}}.$

Тогда вместо соотношений (1.3), (1.4) и (1.2) следует записать соответственно

(3.2)
${{{\mathbf{X}}}_{{k + 1}}} = {\mathbf{A}}{{{\mathbf{X}}}_{k}},\quad {{{\mathbf{X}}}_{{k + 1}}} = {\mathbf{\bar {A}}}{{{\mathbf{X}}}_{k}},$
(3.3)
${{{\mathbf{X}}}_{{k + 1}}}\left( {{{{\mathbf{X}}}_{k}}} \right)_{R}^{ \bot } = 0.$

Таким образом, для случая автономных динамических систем, согласно условию (3.3), в качестве критерия обнаружения ненормального режима следует принять выражение

(3.4)
$\varepsilon = \left\| {{{{\mathbf{X}}}_{{k + 1}}}\left( {{{{\mathbf{X}}}_{k}}} \right)_{R}^{ \bot }} \right\| = 0,$
где $\left( {{{{\mathbf{X}}}_{k}}} \right)_{R}^{{ \bot T}}\left( {{{{\mathbf{X}}}_{k}}} \right)_{R}^{ \bot } = {\mathbf{E}}$.

В этом случае алгоритм 2 обнаружения ненормального режима в энергосистеме на основе синхронизированных векторных измерений для случая применения автономной модели принимает вид.

Шаг 1. Для каждого момента времени k составляется матрица измерений

(3.5)
${{{\mathbf{X}}}_{k}} = \left[ {\begin{array}{*{20}{c}} {{{x}_{{k - h}}}\;...\;{{x}_{{k - 1}}}\;{{x}_{k}}} \end{array}} \right],$
ширина которой $h$ + 1 должна быть достаточной для выполнения условий шага 2.

Шаг 2. Определяется нетривиальный правый делитель нуля матрицы измерений

$\left( {{{{\mathbf{X}}}_{k}}} \right)_{R}^{ \bot } = \left[ {\begin{array}{*{20}{c}} {{{x}_{{k - h}}}\;...\;{{x}_{{k - 1}}}\;{{x}_{k}}} \end{array}} \right]_{R}^{ \bot },$
удовлетворяющий условию ортогональности (2.4).

Шаг 3. Составляется матрица измерений ${{{\mathbf{X}}}_{{k + 1}}} = \left[ {\begin{array}{*{20}{c}} {{{x}_{{k - h + 1}}}\;...\;{{x}_{k}}\;{{x}_{{k + 1}}}} \end{array}} \right]$ и находится значение критерия (3.4):

(3.6)
$\varepsilon = \left\| {{{{\mathbf{X}}}_{{k + 1}}}\left( {{{{\mathbf{X}}}_{k}}} \right)_{R}^{ \bot }} \right\| = \left\| {\left[ {\begin{array}{*{20}{c}} {{{x}_{{k - h + 1}}}\;...\,\,{{x}_{k}}\,\,{{x}_{{k + 1}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{x}_{{k - h}}}\,\,...\,\,{{x}_{{k - 1}}}\,\,{{x}_{k}}} \end{array}} \right]_{R}^{ \bot }} \right\|.$

Как и прежде, резкое возрастание ε будет свидетельствовать о возникновении ненормального режима в энергосистеме.

4. Методический пример. Продемонстрируем работоспособность предлагаемого метода на простом символьном примере обнаружения параметрических изменений в модели дискретной динамической системы, представленной в виде автономной системы второго порядка:

(4.1)
$\left[ {\begin{array}{*{20}{c}} {x_{{k + 1}}^{1}} \\ {x_{{k + 1}}^{2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{a}_{1}}}&{ - {{a}_{2}}} \\ {{{a}_{2}}}&{{{a}_{1}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {x_{k}^{1}} \\ {x_{k}^{2}} \end{array}} \right],\quad \left[ {\begin{array}{*{20}{c}} {x_{0}^{1}} \\ {x_{0}^{2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right],\quad a_{1}^{2} + a_{2}^{2} < 1.$

Данная система является всегда асимптотически устойчивой, поскольку корни характеристического полинома матрицы A составляют комплексно-сопряженные числа ${{a}_{1}} \pm i{{a}_{2}},$ i2 = 1, лежащие внутри единичного круга на комплексной плоскости в силу условия $a_{1}^{2} + a_{2}^{2} < 1$ в (4.1).

Рассмотрим по шагам алгоритм 2.

Шаг 1. Поскольку динамическая система (4.1) имеет второй порядок, достаточно использовать матрицу измерений шириной h + 1 = 3:

(4.2)
${{{\mathbf{X}}}_{k}} = \left[ {{{x}_{{k - 2}}}\,\,{{x}_{{k - 1}}}\,\,{{x}_{k}}} \right].$

Тогда в соответствии с (4.1) запишем матрицу измерений для k = 2:

(4.3)
${{{\mathbf{X}}}_{k}} = {{{\mathbf{X}}}_{2}} = \left[ {{{x}_{0}}\,\,{{x}_{1}}\,\,{{x}_{2}}} \right] = \left[ {\begin{array}{*{20}{c}} 0&\vline & { - {{a}_{2}}}&\vline & { - 2{{a}_{1}}{{a}_{2}}} \\ 1&\vline & {{{a}_{1}}}&\vline & {a_{1}^{2} - a_{2}^{2}} \end{array}} \right].$

Шаг 2. Определим ортогональный правый делитель нуля матрицы (4.3):

(4.4)
$\left( {{{{\mathbf{X}}}_{k}}} \right)_{R}^{ \bot } = \left( {{{{\mathbf{X}}}_{2}}} \right)_{R}^{ \bot } = \left[ {\begin{array}{*{20}{c}} 0&\vline & { - {{a}_{2}}}&\vline & { - 2{{a}_{1}}{{a}_{2}}} \\ 1&\vline & {{{a}_{1}}}&\vline & {a_{1}^{2} - a_{2}^{2}} \end{array}} \right]_{R}^{ \bot } = \left[ {\begin{array}{*{20}{c}} {a_{1}^{2} + a_{2}^{2}} \\ { - 2{{a}_{1}}} \\ 1 \end{array}} \right]{{({{(a_{1}^{2} + a_{2}^{2})}^{2}} + 4a_{1}^{2} + 1)}^{{ - \frac{1}{2}}}}.$

Шаг 3. С учетом (4.1) составим матрицу измерений (3.5):

(4.5)
${{{\mathbf{X}}}_{{k + 1}}} = {{{\mathbf{X}}}_{3}} = \left[ {{{x}_{1}}\,\,{{x}_{2}}\,\,{{x}_{3}}} \right] = \left[ {\begin{array}{*{20}{c}} { - {{a}_{2}}}&\vline & { - 2{{a}_{1}}{{a}_{2}}}&\vline & {a_{2}^{3} - 3a_{1}^{2}{{a}_{2}}} \\ {{{a}_{1}}}&\vline & {a_{1}^{2} - a_{2}^{2}}&\vline & {a_{1}^{3} - 3{{a}_{1}}a_{2}^{2}} \end{array}} \right]$
и найдем значение критерия (3.4), подставив в него (4.4) и (4.5):

$\varepsilon = \left\| {{{{\mathbf{X}}}_{{k + 1}}}\left( {{{{\mathbf{X}}}_{k}}} \right)_{R}^{ \bot }} \right\| = \left\| {{{{\mathbf{X}}}_{3}}\left( {{{{\mathbf{X}}}_{2}}} \right)_{R}^{ \bot }} \right\| = \left\| {\left[ {\begin{array}{*{20}{c}} { - {{a}_{2}}}&\vline & { - 2{{a}_{1}}{{a}_{2}}}&\vline & {a_{2}^{3} - 3a_{1}^{2}{{a}_{2}}} \\ {{{a}_{1}}}&\vline & {a_{1}^{2} - a_{2}^{2}}&\vline & {a_{1}^{3} - 3{{a}_{1}}a_{2}^{2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {a_{1}^{2} + a_{2}^{2}} \\ { - 2{{a}_{1}}} \\ 1 \end{array}} \right]{{{({{{(a_{1}^{2} + a_{2}^{2})}}^{2}} + 4a_{1}^{2} + 1)}}^{{ - \frac{1}{2}}}}} \right\| = 0.$

В данном случае его значение равно нулю, таким образом, можно сделать вывод об отсутствии параметрических изменений в системе (4.1).

Предположим теперь, что при k + 1 = 3 в контролируемой системе знак одного из коэффициентов модели изменился:

(4.6)
$\left[ {\begin{array}{*{20}{c}} {x_{{k + 1}}^{1}} \\ {x_{{k + 1}}^{2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{a}_{1}}}&{{{a}_{2}}} \\ {{{a}_{2}}}&{{{a}_{1}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {x_{k}^{1}} \\ {x_{k}^{2}} \end{array}} \right].$

В этом случае корни характеристического полинома равны ${{a}_{1}} \pm {{a}_{2}}$ и энергосистема может выйти за границы устойчивости при ${{a}_{2}} > {{a}_{1}}$.

Тогда на шаге 3 алгоритма в соответствии с (4.6) матрица измерений примет вид

(4.7)
${{{\mathbf{X}}}_{{k + 1}}} = {{{\mathbf{X}}}_{3}} = \left[ {{{x}_{1}}\,\,\,{{x}_{2}}\,\,\,{{x}_{3}}} \right] = \left[ {\begin{array}{*{20}{c}} { - {{a}_{2}}}&\vline & { - 2{{a}_{1}}{{a}_{2}}}&\vline & { - {{a}_{2}}(a_{1}^{2} + a_{2}^{2})} \\ {{{a}_{1}}}&\vline & {a_{1}^{2} - a_{2}^{2}}&\vline & {a_{1}^{3} - 3{{a}_{1}}a_{2}^{2}} \end{array}} \right],$
значение критерия (3.4) с учетом (4.4) и (4.7) уже будет отлично от нуля:

$\varepsilon = \left\| {{{{\mathbf{X}}}_{{k + 1}}}\left( {{{{\mathbf{X}}}_{k}}} \right)_{R}^{ \bot }} \right\| = \left\| {{{{\mathbf{X}}}_{3}}\left( {{{{\mathbf{X}}}_{2}}} \right)_{R}^{ \bot }} \right\| = {{(2a_{1}^{2}{{a}_{2}} - 2a_{2}^{3})}^{2}}{{({{(a_{1}^{2} + a_{2}^{2})}^{2}} + 4a_{1}^{2} + 1)}^{{ - 1}}} \ne 0.$

Если продолжить вычисления, то на следующем шаге алгоритма критерий (3.4) также будет отличен от нуля: $\varepsilon = {\text{||}}{{{\mathbf{X}}}_{4}}\left( {{{{\mathbf{X}}}_{3}}} \right)_{R}^{ \bot }{\text{||}} \approx 0$, однако после прохождения окна измерений момента возникновения параметрических изменений при $k \geqslant 4$ его значения возвращаются к нулевым. Таким образом, на графике поведение критерия во время изменений параметров проявляется в виде импульса шириной h = 2.

5. Обнаружение аварии в энергосистеме. Используемая для исследований эквивалентированная модель энергосистемы соответствовала режиму зимнего максимума нагрузки. Модель содержала 27 узлов и 35 нетрансформаторных ветвей, 32 трансформаторные ветви и 17 ветвей-импедансов (трансформаторных и нетрансформаторных), введенных в схему для замещения ветвей, образовавшихся в результате эквивалентирования модели в программном комплексе RastrWin и содержащих отрицательные активные и/или реактивные сопротивления. Общее количество уравнений, описывающих данную энергосистему, составило 200.

Виртуальные устройства синхронизированных векторных измерений устанавливались в узлах модели энергосистемы, а также на приемных концах воздушных линий. Аварийные ситуации моделировались набросами нагрузки и короткими замыканиями в нетрансформаторных ветвях с успешными и неуспешными автоматическими повторными включениями (АПВ). Во всех случаях набросов нагрузки и коротких замыканий с успешными и неуспешными АПВ метод продемонстрировал удовлетворительные результаты.

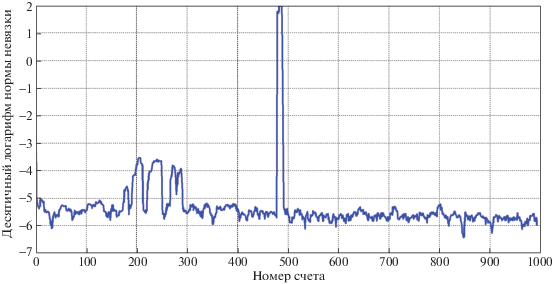
Один из результатов работы предложенного метода обнаружения ненормального режима приведен на рисунке. Явный всплеск критерия (3.4) индицирует короткое замыкание в энергосистеме с успешным АПВ, произошедшее в момент времени k = 493 отсчета. Ось ординат на рисунке дана в логарифмическом масштабе, откуда следует, что в момент возникновения ненормального режима значение критерия увеличилось на 5–6 порядков. Данный результат получен при обработке 29 973 измерений (отсчетов) фазного угла, поступающего с одного устройства синхронизированных измерений, установленного на приемном конце воздушной линии 500 кВ. При этом короткое замыкание произошло на большом удалении от устройства синхронизированных измерений в примыкающей к данной воздушной линии 220 кВ.

В дальнейшем, как видно это из диаграммы на рисунке, в энергосистеме установился послеаварийный режим.

Заключение. В результате проведенных исследований разработан алгебраический метод непараметрической идентификации (обнаружения) ненормальных режимов в энергосистеме в реальном масштабе времени, использующий только данные синхронизированных векторных измерений. Метод не требует априорной информации о параметрах математической модели энергосистемы как динамической MIMO-системы, не предполагает решения задачи прогнозирования, не применяет статистические вычисления, не требует своего предварительного обучения или длительной настройки. В основе численного алгоритма, реализующего метод, лежит алгебраический критерий совместности (разрешимости) линейного матричного уравнения задачи идентификации математической модели энергосистемы.

Работоспособность метода не зависит от параметров модели энергосистемы, а следовательно, и от ошибок в их определении. Предлагаемый метод основан только на информации о наблюдаемых сигналах и не содержит никаких других вспомогательных переменных. Поэтому приведенные результаты вычислений будут подобны полученным при любых ошибках в модели энергосистемы.

Результативность метода демонстрируется на примере обнаружения момента возникновения аварийной ситуации в энергосистеме. Использование данного метода позволяет обнаруживать не только факт возникновения ненормального режима, но и его устранения, например при успешном автоматическом повторном включении.

Рисунок.

График критерия ε, построенный на основе (3.4)

Список литературы

  1. Калман Р., Фалб П., Арбиб М. Очерки по математической теории систем. М.: Мир, 1971.

  2. Kailath T. Linear Systems. N.J.: Prentice Hall, 1990.

  3. Nour-Eldin H.A. Linear Multivariable Systems Controllability and Observability: Numerical Aspects // Systems and Control Encyclopedia/Ed. M.G. Singh. Oxford, UK: Pergamon Press, 1987. P. 2816–2827.

  4. Голован A.A., Парусников Н.А. О связи понятия стохастической оцениваемости с сингулярными разложениями матриц // АиТ. 1998. № 2. С. 45–50.

  5. Гаджиев М.Г., Гулевич Е.А., Рябченко В.Н., Шаров Ю.В. Идентификация математической модели режима энергосистемы с помощью синхронизированных векторных измерений// Электричество. 2018. № 5. С. 4–10.

  6. Eissa M.M., Masoud M.E., Elanwar M.M.M. A Novel Back up Wide Area Protection Technique for Power Transmission Grids Using Phasor Measurement Unit // IEEE Transactions on Power Delivery. 2010. V. 25. № 1. P. 270–278.

  7. Neyestanaki M.K., Ranjbar A.M. An Adaptive PMU-based Wide Area Backup Protection Scheme for Power Transmission Lines // IEEE Transactions on Smart Grid. 2015. V. 6. № 3. P. 1550–1559.

  8. Ge Y., Flueck A.J., Kim D.-K. et al. Power System Real-time Event Detection and Associated Data Archival Reduction Based on Synchrophasors // IEEE Transactions on Smart Grid. 2015. V. 6. № 4. P. 2088–2097.

  9. Biswal M., Brahma S.M., Cao H. Supervisory Protection and Automated Event Diagnosis Using PMU data // IEEE Transactions on Power Delivery. 2016. V. 31. № 4. P. 1855–1863.

  10. Overbye T., Sauer P., DeMarco C. et al. Using PMU Data to Increase Situational Awareness // Power System Engineering Research Center (PSERC) Publication. 2010. V. 21. P. 10–16.

  11. Swain K.B., Mahato C.C. A Brief Review on Fault Detection, Classification and Location on Transmission Lines Using PMUs // International J. Management, Technology And Engineering. 2018. V. 8. Iss. XII. P. 2608–2618.

  12. Aminifar F., Fotuhi-Firuzabad M., Safdarian A., Davoudi A., Shahidehpour M. Synchrophasor Measurement Technology in Power Systems: Panorama and State-of-the-Art // IEEE Access. 2014. V. 2. P. 1607–1628.

  13. Зыбин Е.Ю., Косьянчук В.В. Алгебраический критерий обнаружения факта и времени возникновения отказов в системах управления динамическими объектами // Изв. РАН. ТиСУ. 2016. № 4. С. 50–61.

  14. Мироновский Л.А. Функциональное диагностирование динамических систем М.–СПб.: Изд-во МГУ-ГРИФ, 1998.

  15. Колодежный Л.П., Чернодаров А.В. Надежность и техническая диагностика. М.: Изд-во ВВА им. проф. Н.Е. Жуковского и Ю.А. Гагарина, 2010.

  16. Хуснияров М.Х., Сунагатов М.Ф., Матвеев Д.С. Основы надежности и диагностики технических систем. Уфа: Изд-во УГНТУ, 2011.

  17. Жирабок А.Н. Диагностические наблюдатели и соотношения паритета: сравнительный анализ // АиТ. 2012. № 5. С. 141–160.

  18. Chen K., Huang C., He J. Fault Detection, Classification and Location for Transmission Lines and Distribution Systems: a Review on the Methods // High Voltage. 2016. V. 1. № 1. P. 25–33.

  19. Mohammadi F., Zheng C., Su R. Fault Diagnosis in Smart Grid Based on Data-Driven Computational Methods // Proc. 5th Intern. Conf. on Applied Research in Electrical, Mechanical, and Mechatronics Engineering. Tehran, Iran, 2019. V. 24.

  20. Yang Z., Chen Yu, Zhou N. et al. Data-driven Online Distributed Disturbance Location for large-scale Power Grids // IEEE Transactions on Smart Grid. 2019. V. 2. № 3. P. 381–390.

  21. Mousa M., Abdelwahed S., Kluss J. et al. Review of Fault Types, Impacts, and Management Solutions in Smart Grid Systems // Smart Grid and Renewable Energy. 2019. V. 10. № 04. P. 98.

  22. Glavic M., Van Cutsem T. A Short Survey of Methods for Voltage Instability Detection // IEEE Power and Energy Society General Meeting. Detroit IEEE, 2011. P. 1–8.

  23. Jiang Y., Yin S., Kaynak O. Data-driven Monitoring and Safety Control of Industrial Cyber-physical Systems: Basics and beyond // IEEE Access. 2018. V. 6. P. 47374–47384.

  24. Xiong Y., Yao W., Chen W. et al. A Data-driven Approach for Fault Time Determination and Fault Area Location Using Random Matrix Theory // Intern. J. Electrical Power & Energy Systems. 2020. V. 116. P. 105566.

  25. Huang D., Chen Q., Ma S. et al. Wide-area Measurement-based Model-free Approach for Online Power System Transient Stability Assessment // Energies. 2018. V. 11. № 4. P. 958.

  26. Xu S. A Survey of Knowledge-Based Intelligent Fault Diagnosis Techniques // J. Physics: Conference Series. IOP Publishing, 2019. V. 1187. № 3. P. 032006.

  27. Tokel H.A., Al Halaseh R., Alirezaei G. et al. A New Approach for Machine Learning-based Fault Detection and Classification in Power Systems // IEEE Power & Energy Society Innovative Smart Grid Technologies Conf. (ISGT). IEEE Sarajevo, 2018. P. 1–5.

  28. Kesici M., Saner K.B., Genc V.M.I. et al. Wide Area Measurement Based Online Monitoring and Event Detection Using Convolutional Neural Networks // 2019 7th Intern. Istanbul Smart Grids and Cities Congr. and Fair (ICSG). IEEE Istanbul, 2019. P. 223–227.

  29. Li W., Deka D., Chertkov M. et al. Real-time Faulted Line Localization and PMU Placement in Power Systems through Convolutional Neural Networks // IEEE Transactions on Power Systems. 2019. V. 34. № 6. P. 4640–465.

  30. Karić A., Konjić T., Jahić A. Power System Fault Detection, Classification and Location using Artificial Neural Networks // Intern. Symp. on Innovative and Interdisciplinary Applications of Advanced Technologies. Cham: Springer, 2017. P. 89–101.

  31. Гаджиев М.Г., Мисриханов М.Ш., Рябченко В.Н., Шаров Ю.В. Матричные методы анализа и управления переходными процессами в электроэнергетических системах. М.: Издательский дом МЭИ, 2019.

  32. Зубов Н.Е., Микрин Е.А., Рябченко В.Н. Матричные методы в теории и практике систем автоматического управления летательных аппаратов. М.: Изд-во МГТУ им. Н.Э. Баумана, 2016.

  33. Поляк Б.Т., Щербаков П.С. Робастная устойчивость и управление. М.: Наука, 2002.

  34. Zhou K. Essentials of Robust Control. Upper Saddle River. New Jersey: Prentice Hall, 1998.

  35. Уоткинс Д. Основы матричных вычислений. М.: БИНОМ. Лаборатория знаний, 2006.

  36. Bernstein D.S. Matrix Mathematics. Princeton: Princeton Univ. Press, 2005.

  37. Chang C.-B., Athans M. State Estimation for Discrete Systems with Switching Parameters // IEEE Transactions on Aerospace and Electronic Systems. 1978. № 3. P. 418–425.

  38. Hamilton J.D. Analysis of Time Series Subject to Changes in Regime // J. Econometrics, 1990. № 45 (1). P. 39–70.

  39. Ghahramani Z., Hinton G.E. Switching State-space Models. Technical Report CRG-TR-96-2. Toronto: University of Toronto, 1996.

  40. Fox E., Sudderth E.B., Jordan M.I., Willsky A.S. Nonparametric Bayesian Learning of Switching Linear Dynamical Systems // Advances in Neural Information Processing Systems. 2009. № 1. P. 457–464.

  41. Зыбин Е.Ю., Мисриханов М.Ш., Рябченко В.Н. О минимальной параметризации решений линейных матричных уравнений // Вестн. ИГЭУ. 2004. № 6. С. 127–131.

  42. Зыбин Е.Ю. Об идентифицируемости линейных динамических систем в замкнутом контуре в режиме нормальной эксплуатации // Изв. ЮФУ. Технические науки. 2015. № 4 (166). С. 160–170.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Теория и системы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал