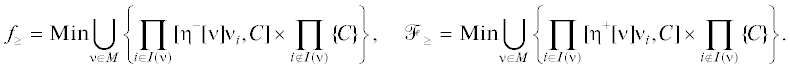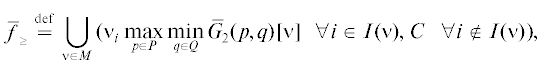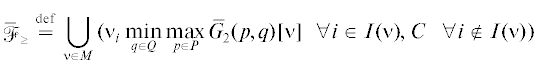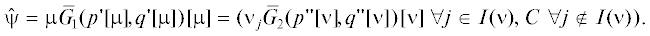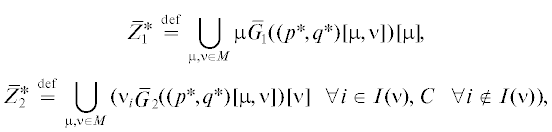Известия РАН. Теория и системы управления, 2020, № 6, стр. 60-82
РАВНОВЕСИЕ И КОМПРОМИСС В МНОГОКРИТЕРИАЛЬНЫХ ИГРАХ ДВУХ ЛИЦ С НУЛЕВОЙ СУММОЙ
Е. М. Крейнес a, Н. М. Новикова b, И. И. Поспелова c, *
a ООО “УК Роснано”
Москва, Россия
b ФИЦ ИУ РАН
Москва, Россия
c МГУ, ф-т ВМК
Москва, Россия
* E-mail: ipospelova05@yandex.ru
Поступила в редакцию 20.05.2020
После доработки 09.06.2020
Принята к публикации 27.07.2020
Аннотация
Поставлена задача формализации решения многокритериальной игры двух лиц с нулевой суммой, обеспечивающего выигрыш обоим игрокам относительно их многокритериально наилучших гарантированных результатов. В качестве базовой концепции решения многокритериальной игры выбрано равновесие по Шепли, для которого применена параметризация с помощью обратной логической свертки, основанной на скаляризации по Гермейеру, т.е. взвешенном максиминном подходе. Исследовано соотношение между равновесным значением игры и ее односторонними значениями, определяемыми для каждого игрока как наилучший гарантированный результат, если этот результат не зависит от порядка ходов. Дано описание возможностей компромисса в многокритериальных играх с нулевой суммой. Для конечной такой игры в смешанных стратегиях введены понятия компромиссного и переговорного значений, установлена их связь с равновесным и с односторонними значениями игры. При этом рассмотрена специальная трактовка многокритериального осреднения результата для игроков, ориентирующихся на использование обратной логической свертки. Проанализирована непустота переговорного множества для такого случая. Полученные выводы продемонстрированы на модельном примере.
0. Введение. Рассматриваемую многокритериальную (МК) игру с нулевой суммой Γ0 = = $\langle X,Y,\Phi \rangle $ можно себе представить как игру (конфликт, конкуренцию) двух лиц, принимающих решения по управлению своими коллективами, далее называемых ЛПР 1 и ЛПР 2, а также игроками. Члены коллектива имеют разные интересы, поэтому у любого ЛПР есть вектор частных критериев [1], учитывающий неполный порядок коллективных предпочтений. Результат коллектива (и ЛПР) определяется не только их собственными действиями, но и действиями конкурирующего коллектива, управляемого своим ЛПР. В условиях жесткой конкуренции выигрыши одного совокупного игрока оборачиваются проигрышами другого, причем по каждому частному критерию. Моделируя крайний случай, приходим к МК-игре с нулевой суммой. Здесь, в отличие от антагонистической игры [2, 3], цель ЛПР заключается не в том, чтобы помешать партнеру в достижении его цели [4], просто так сложилось, что векторы интересов их коллективов противоположны.
В игре Γ0: X – множество стратегий игрока 1, Y – игрока 2, и при выборе игроками пары $(x,y) \in X \times Y$ первый из них получает вектор выигрышей $\Phi (x,y)\;\mathop = \limits^{{\text{def}}} \;({{\varphi }_{1}}(x,y), \ldots ,{{\varphi }_{n}}(x,y))$, а второй получает этот же вектор Φ(x, y) как вектор проигрышей. Тем самым ЛПР 1 стремится к максимуму вектор-функции $\Phi (x,y)$, а ЛПР 2 – к ее минимуму. Значения МК-максимума и минимума будем понимать в слейтеровском смысле [1] и записывать в формулах с большой буквы, подчеркивая этим, что речь идет о множествах. Допустим, что X и Y – конечные или компакты в евклидовом пространстве, в последнем случае функции φi считаем непрерывными по совокупности переменных. И пусть, без ограничения общности, $0 \leqslant \Phi (x,y) \leqslant \bar {c}\;\mathop = \limits^{{\text{def}}} \;(C, \ldots ,C)$. Здесь и далее стандартные знаки неравенств для векторов понимаются как покомпонентные, а в индексах у множеств указывают на применяемые игроком оценки достижимых значений вектора критериев.
Предположим, что оба ЛПР используют при принятии решений гарантированные оценки своего результата с учетом всей имеющейся и ожидаемой информации. Тогда наилучшие гарантированные результаты (НГР) для них (т.е. наибольший гарантированный выигрыш максимизирующего ЛПР и наименьший гарантированный проигрыш минимизирующего) в зависимости от порядка ходов задаются следующим образом. Обозначим через Γ12 игру Γ0, в которой первым делает ход игрок 1, а вторым – игрок 2, уже зная его ход, и через Γ21 – игру Γ0 с обратным порядком ходов. Согласно построениям из [2–6], в игре Γ12: НГР игрока 1 (МК-максимин максимизирующего ЛПР, не информированного о ходе партнера) равен
Большая и малая буквы символов, выбранных для НГР, дополнительно указывают на соотношение между соответствующими значениями: множество с малой буквы не превосходит множество с большой буквы в смысле включения первого в оболочку Эджворта–Парето [1] второго. Формально, введя эту оболочку для любого множества $Z \subset \mathbb{R}_{ + }^{n}$ как $\mathop {{\text{eph}}}\nolimits_ \leqslant (Z)\;\mathop = \limits^{{\text{def}}} \;\{ \psi \in \mathbb{R}_{ + }^{n}\,{\text{|}}\,\exists z \in Z$: ψ ≤ z}, запишем [3, 6]
(0.1)
${{f}_{ \leqslant }} \subseteq \mathop {{\text{eph}}}\nolimits_ \leqslant ({{\mathcal{F}}_{ \leqslant }}),\quad {{f}_{ \geqslant }} \subseteq \mathop {{\text{eph}}}\nolimits_ \leqslant ({{\mathcal{F}}_{ \geqslant }}),$МК-значения максимина и минимакса каждого ЛПР (свои для максимизирующего и для минимизирующего вектор-функцию Φ игрока) дают его оценку гарантированного результата в МК-игре Γ0. В общем случае оценки у ЛПР 1 и ЛПР 2 не совпадают (являются пессимистичными) [2, 8]: существуют векторы Φ(x, y), которые для обоих ЛПР не хуже ни одной точки из их НГР. Описанию множества подобных компромиссных оценок и решений посвящена настоящая статья. В разд. 1 изложим необходимые для дальнейшего сведения по МК-играм двух лиц с нулевой суммой и особенностям параметризации их решений и значений на базе скаляризации с помощью обратной логической свертки (ОЛС) [9]. В разд. 2, 4 рассмотрим разнообразные определения компромиссного и переговорного множеств для ${{\Gamma }^{0}}$ и проанализируем их свойства. В разд. 3, 4 исследуем предложенное в [10] смешанное расширение конечной МК-игры Γ0 в условиях применения ОЛС. Обсудим различие возможностей достичь компромисса между игроками, когда они ориентируются на ОЛС и когда оба используют линейную свертку. В разд. 4 также разберем модельный пример МК-игры для иллюстрации полученных результатов и сравнения с НГР в трактовке [4, 11] (при обычном смешанном расширении).
1. Предварительные сведения. В [3] предложено использовать в качестве решения R0 игры Γ0 классическое понятие МК-равновесия по Шепли [12], но параметризованное не стандартным путем линейной скаляризации согласно [12, 13], а представленное логической скаляризацией [7], у которой коэффициенты свертки находятся в знаменателе [9], и называемой поэтому обратной логической. Последнее представление дает множество, совпадающее с классическим МК-равновесием в регулярном случае и оказывающееся его сужением (за счет ряда непаретовских точек Слейтера) в общем случае [2]. Формально определим равновесное решение МК-игры Γ0 как следующее множество ее исходов:
(1.1)
$\begin{gathered} {{R}^{0}}\;\mathop = \limits^{{\text{def}}} \;\{ ({{x}^{0}},{{y}^{0}}) \in X \times Y\,{\text{|}}\,\exists \mu ,\nu \in M{\kern 1pt} :\;{{x}^{0}} \in {\text{Arg}}\mathop {\max }\limits_{x \in X} \{ \mathop {\min }\limits_{i \in I(\mu )} {{\varphi }_{i}}(x,{{y}^{0}}){\text{/}}{{\mu }_{i}}\} , \\ {{y}^{0}} \in {\text{Arg}}\mathop {\min }\limits_{y \in Y} \{ \mathop {\max }\limits_{j \in I(\nu )} {{\varphi }_{j}}({{x}^{0}},y){\text{/}}{{\nu }_{j}}\} \} . \\ \end{gathered} $Здесь и далее $I(\mu )\;\mathop = \limits^{{\text{def}}} \;\{ i = \overline {1,n} \,{\text{|}}\,{{\mu }_{i}} > 0\} $, $M\;\mathop = \limits^{{\text{def}}} \;\{ \mu \geqslant 0\,{\text{|}}\,{{\mu }_{1}} + \ldots + {{\mu }_{n}} = 1\} $, а $\mu ,\nu \in M$ – параметры (векторы коэффициентов) ОЛС:
(1.2)
${{x}^{0}} \in {\text{Arg}}\mathop {{\text{Max}}}\limits_{x \in X} \Phi (x,{{y}^{0}}),\quad {{y}^{0}} \in {\text{Arg}}\mathop {{\text{Min}}}\limits_{y \in Y} \Phi ({{x}^{0}},y),$Вид ОЛС у каждого игрока свой, так как он зависит от задачи, решаемой ЛПР, в отличие от вида линейной свертки. В задаче МК-максимизации (у ЛПР 1) ОЛС выражена минимумом из частных критериев, приведенных к коэффициентам свертки, а в задаче МК-минимизации (у ЛПР 2) – максимумом. Поэтому даже при одинаковых параметрах свертки у обоих ЛПР, т.е. при ν = μ, игра между ними с функциями выигрыша, равными их ОЛС, если ${\text{|}}I(\mu ){\text{|}} > 1$, формально не относится к играм с противоположными интересами. При использовании линейной свертки ЛПР оптимизируют взвешенную сумму частных критериев, так что возможность компромисса в игре между ними появляется лишь при несовпадении для них векторов весовых коэффициентов – оценок относительной важности частных критериев.
В [3] доказано, что исходы из R0 обеспечивают игрокам 1 и 2 результаты $\Phi ({{x}^{0}},{{y}^{0}})$, не худшие, чем их НГР. А именно пусть множество ${{Z}^{0}}\;\mathop = \limits^{{\text{def}}} \;\{ \Phi ({{x}^{0}},{{y}^{0}})\,{\text{|}}\,({{x}^{0}},{{y}^{0}}) \in {{R}^{0}}\} $ – равновесное значение (в критериальном пространстве) МК-игры ${{\Gamma }^{0}}$, тогда
(1.3)
${{\mathcal{F}}_{ \leqslant }} \subseteq \mathop {{\text{eph}}}\nolimits_ \leqslant ({{Z}^{0}}),\quad {{f}_{ \geqslant }} \subseteq \mathop {{\text{eph}}}\nolimits_ \geqslant ({{Z}^{0}}),$С помощью данных величин удается также представить НГР ${{f}_{ \leqslant }}$ и ${{\mathcal{F}}_{ \leqslant }}$ игрока 1 на основе следующей параметризации множеств гарантированных оценок [2]:
(1.4)
$\bigcup\limits_{x \in X} \,\bigcap\limits_{y \in Y} \,\{ \psi \in \mathbb{R}_{ + }^{n}\,{\text{|}}\,\psi \leqslant \Phi (x,y)\} = \bigcup\limits_{\mu \in M} \,\prod\limits_{i = 1}^n \,[0,{{\theta }^{ - }}[\mu ]{{\mu }_{i}}],$(1.5)
$\bigcap\limits_{y \in Y} \,\bigcup\limits_{x \in X} \,\{ \psi \in \mathbb{R}_{ + }^{n}\,{\text{|}}\,\psi \leqslant \Phi (x,y)\} = \bigcup\limits_{\mu \in M} \,\prod\limits_{i = 1}^n \,[0,{{\theta }^{ + }}[\mu ]{{\mu }_{i}}],$В предположении регулярности [2] задачи векторной максимизации (или минимизации), определяющей НГР, значение ее МК-оптимума дается множеством верхних (или нижних) границ отрезков, фигурирующих в правых частях равенств (1.4), (1.5) (или (1.6)). В отсутствие регулярности к этим границам могут добавиться непаретовские точки слейтеровских отрезков.
Из (1.4)–(1.6) и соотношений между скалярными максиминами и минимаксами наглядны включения (0.1) – МК-аналоги таких соотношений для каждого игрока. Притом включение для игрока 2 можно переписать и в виде ${{\mathcal{F}}_{ \geqslant }} \subseteq \mathop {{\text{eph}}}\nolimits_ \geqslant ({{f}_{ \geqslant }})$. Тогда из (1.3) следует вывод, что равновесное значение не хуже обоих НГР как неинформированного, так и информированного ЛПР (т.е. в обеих МК-играх Γ12 и Γ21).
Для сравнения между собой НГР разных игроков в одной МК-игре, положив в (1.6) $\nu = \mu $, заметим справедливость включений
(1.7)
${{f}_{ \leqslant }} \subseteq \mathop {{\text{eph}}}\nolimits_ \leqslant ({{f}_{ \geqslant }}),\quad {{\mathcal{F}}_{ \leqslant }} \subseteq \mathop {{\text{eph}}}\nolimits_ \leqslant ({{\mathcal{F}}_{ \geqslant }})$(1.8)
$\begin{gathered} \forall \psi \in {{f}_{ \leqslant }},\quad \xi \in {{f}_{ \geqslant }}\quad {\text{выполнено}}\quad \psi \leqslant \xi , \\ {\text{а}}\quad \forall \psi {\kern 1pt} ' \in {{\mathcal{F}}_{ \leqslant }},\quad \xi {\kern 1pt} ' \in {{\mathcal{F}}_{ \geqslant }}\quad {\text{выполнено}}\quad \psi {\kern 1pt} ' \leqslant \xi {\kern 1pt} '. \\ \end{gathered} $Из (1.8) в [2] получено, что для МК-игр, которые не сводятся к однокритериальным, ${{f}_{ \leqslant }} \cap {{f}_{ \geqslant }} = \emptyset $ и ${{\mathcal{F}}_{ \leqslant }} \cap {{\mathcal{F}}_{ \geqslant }} = \emptyset $. Непустота любого из двух пересечений в свою очередь возможна, если в соответствующей МК-игре граница Парето обоих НГР (в критериальном пространстве) состоит из единственной точки $\Phi (\hat {x},\hat {y})$, где $(\hat {x},\hat {y})$ реализует
Значит, решение такой МК-игры оказывается решением и скалярной игры с любым из частных критериев, т.е. МК-игра – вырожденная (распадается на не более n отдельных скалярных игр). В противном случае, а именно в общем МК-случае, предполагающем конфликтующие частные критерии [1, 5], НГР игрока 1 не пересекается с НГР игрока 2 ни в Γ12, ни в Γ21. Указанное свойство отличает МК-игры от скалярных игр с полной информацией [14].
Для игры Γ0 в нормальной форме, где оба игрока делают ход одновременно, т.е. не являются информированными, основное значение приобретает равенство МК-максимина для ЛПР его МК-минимаксу. Это свойство МК-игры (если есть), названное в [3] наличием одностороннего решения, позволяет соответствующему игроку не зависеть от порядка ходов в МК-игре, а самостоятельно выбирать наилучшую гарантирующую стратегию. (Для игрока 1 данное свойство по терминологии [4] определяет чистую игру.) Следующие критерии существования одностороннего решения, полученные в [2], также вытекают из представлений (1.4)–(1.6) НГР с помощью ОЛС:
(1.9)
${{f}_{ \leqslant }} = {{\mathcal{F}}_{ \leqslant }} \Leftrightarrow {{\theta }^{ - }}[\mu ] = {{\theta }^{ + }}[\mu ]\quad \forall \mu \in M,\quad {{f}_{ \geqslant }} = {{\mathcal{F}}_{ \geqslant }} \Leftrightarrow {{\eta }^{ - }}[\nu ] = {{\eta }^{ + }}[\nu ]\quad \forall \nu \in M.$Условия в (1.9) того, что игра ${{\Gamma }^{0}}$ имеет одностороннее решение для игрока 1 (и/или для игрока 2), означают наличие цены каждой скалярной игры с нулевой суммой и функцией выигрыша, равной ОЛС за ЛПР 1 (и/или за ЛПР 2), при всех возможных вариантах коэффициентов свертки. Данные требования гораздо сильнее, чем условия непустоты R0. В [3], в частности, доказано, что решение любой из перечисленных выше скалярных игр, если существует, то находится в R0. Равновесные точки появляются и при переходе кого-либо из игроков к смешанным стратегиям, тогда как существование одностороннего решения в смешанных стратегиях для общего МК-случая получено лишь при модификации понятия смешанного расширения МК-игры (см. ниже в разд. 3). В ситуации отсутствия одностороннего решения возникает (в свете соотношений (0.1)) борьба за право второго хода, описанная для скалярных игр в [15], и вопрос о компромиссе становится еще более важным.
Подчеркнем, что в отличие от равновесного значения, которое для конечных игр допускает не только ОЛС, но и линейную скаляризацию [12], параметризация НГР (в силу невыпуклости НГР в общем случае [16]) основана на ОЛС. Поэтому для поиска потенциально компромиссных решений далее предположим использование ОЛС игроками-ЛПР. Тогда представление НГР и равновесных значений с помощью ОЛС дает игрокам наглядное описание указанных множеств в терминах их предпочтений – с разложением по коэффициентам свертки. На базе ОЛС игроки имеют больше шансов договориться в МК-игре с нулевой суммой, чем если бы они руководствовались линейной сверткой.
2. МК-игры в ОЛС. Считаем, что в МК-игре Γ0 (с нулевой суммой) известно, что игроки-ЛПР ориентируются при скаляризации вектор-функции выигрышей – в целях представления и оценки своих результатов и поиска оптимальных стратегий – на применение ОЛС, т.е. на ${{G}_{1}}(x,y)[\mu ]$ и ${{G}_{2}}(x,y)[\nu ]$, $\mu ,\nu \in M$, для игроков 1 и 2 соответственно.
Допустим для начала, что у обоих ЛПР оказался один и тот же вектор $\mu $ коэффициентов ОЛС. Из (1.4)–(1.6):
любой исход $({{x}^{ - }},{{y}^{ - }})\;\mathop = \limits^{{\text{def}}} \;({{x}^{ - }},{{y}^{ - }})[\mu ] \in X \times Y$, для которого
(2.1)
${{\theta }^{ - }}[\mu ]{{\mu }_{j}} \leqslant {{\varphi }_{j}}({{x}^{ - }},{{y}^{ - }}) \leqslant {{\eta }^{ - }}[\mu ]{{\mu }_{j}}\quad \forall j \in I(\mu )$а исход $({{x}^{ + }},{{y}^{ + }})\;\mathop = \limits^{{\text{def}}} \;({{x}^{ + }},{{y}^{ + }})[\mu ] \in X \times Y$, для которого
(2.2)
${{\theta }^{ + }}[\mu ]{{\mu }_{j}} \leqslant {{\varphi }_{j}}({{x}^{ + }},{{y}^{ + }}) \leqslant {{\eta }^{ + }}[\mu ]{{\mu }_{j}}\quad \forall j \in I(\mu ),$Введенные множества компромиссных исходов не пусты при любых $\mu \in M$.
Исходы, для которых оба неравенства в (2.1) или (2.2) строгие, отнесем к переговорному множеству в МК-игре Γ12 или Γ21 для заданных параметров свертки. Как правило, в одинаковой ситуации значение ОЛС
за максимизирующего игрока должно быть при ${\text{|}}I(\mu ){\text{|}} > 1$ меньше, чем за минимизирующего. Так что есть основания рассчитывать на непустоту
не только (2.1) и (2.2), но и переговорных множеств для игр с фиксированным порядком
ходов. И в этом – главное отличие постановки с нулевой суммой от антагонистической,
в которой ОЛС у игроков 1 и 2 при $\mu = \nu $ совпадают (см. в [3]). Для Γ0, когда  , получаем следующее утверждение.
, получаем следующее утверждение.
Утверждение 1. Если МК-игра Γ0 не распадается на скалярные по частным критериям, то для всех μ > 0 справедливо ${{\theta }^{ - }}[\mu ] < {{\eta }^{ - }}[\mu ]$ и ${{\theta }^{ + }}[\mu ] < {{\eta }^{ + }}[\mu ]$.
Доказательство. В условиях утверждения ${{f}_{ \leqslant }} \cap {{f}_{ \geqslant }} = \emptyset $ [2] и с учетом (1.8) $\forall \psi \in {{f}_{ \leqslant }}$, $\xi \in {{f}_{ \geqslant }}$: $\psi \leqslant \xi $, $\psi \ne \xi $. Значит, ${{\psi }_{i}}{\text{/}}{{\mu }_{i}} \leqslant {{\xi }_{i}}{\text{/}}{{\mu }_{i}}$ $\forall i = \overline {1,n} $ и $\exists i{\kern 1pt} '$: ${{\psi }_{{i{\kern 1pt} '}}}{\text{/}}{{\mu }_{{i{\kern 1pt} '}}} < {{\xi }_{{i{\kern 1pt} '}}}{\text{/}}{{\mu }_{{i{\kern 1pt} '}}}$, откуда выводим θ–[μ] ≤ ψi'/μi' < < ${{\xi }_{{i{\kern 1pt} '}}}{\text{/}}{{\mu }_{{i'}}} \leqslant {{\eta }^{ - }}[\mu ]$. И аналогично для игры Γ21.
Похожие свойства выполнены и для логической свертки. Однако при использовании обоими ЛПР линейных сверток игрокам не о чем договариваться в случае фиксированного порядка ходов, если веса частных критериев для них одинаковы.
Когда отрезки $[{{\theta }^{ - }}[\mu ],{{\eta }^{ - }}[\mu ]]$ и $[{{\theta }^{ + }}[\mu ],{{\eta }^{ + }}[\mu ]]$ пересекаются (например, при наличии одностороннего решения), то об исходах $({{x}^{ \pm }},{{y}^{ \pm }})$, удовлетворяющих (2.1) и (2.2) одновременно, можно говорить как о компромиссных в игре Γ0 в нормальной форме. К сожалению, подобные компромиссы имеются далеко не при всех μ. Для того чтобы дать конкретное достаточное условие, выпишем две скалярные игры с нулевой суммой: ${{\Gamma }^{1}}[\mu ]\;\mathop = \limits^{{\text{def}}} \;\left\langle {X,Y,{{G}_{1}}[\mu ]} \right\rangle $ и ${{\Gamma }^{2}}[\nu ]\;\mathop = \limits^{{\text{def}}} \;\left\langle {X,Y,{{G}_{2}}[\nu ]} \right\rangle $.
Утверждение 2. Пусть для некоторого μ из M существуют решения: $(x{\kern 1pt} *,y{\kern 1pt} *)$ игры ${{\Gamma }^{1}}[\mu ]$ и (x**, y**) игры ${{\Gamma }^{2}}[\mu ]$, тогда компромиссной в МК-игре Γ0 в нормальной форме будет комбинация (x*, y**) из равновесных ситуаций (x*, y*) и (x**, y**).
Доказательство. Для пары $(x{\kern 1pt} *,y{\kern 1pt} *{\kern 1pt} *)$ по определению выполнено:
Отметим, что в предположениях утверждения 2 множества исходов, задаваемые (2.1) и (2.2), совпадают. Таким образом, компромиссными являются и сами решения рассмотренных скалярных игр. Для составленной из них пары стратегий (x*, y**) можно добавить, что когда в приведенных в доказательстве утверждения 2 выкладках неравенства вокруг ${{\varphi }_{j}}(x{\kern 1pt} *,y{\kern 1pt} *{\kern 1pt} *){\text{/}}{{\mu }_{j}}$ будут строгими, найденная пара окажется в переговорном множестве для МК-игры Γ0 с данным $\mu \in M.$ Но для этого достаточных условий не получено (утверждение 1 гарантирует строгое неравенство лишь с одной стороны, причем не обязательно, чтобы с одной и той же для всех частных критериев).
Если одна из указанных игр, например ${{\Gamma }^{1}}[\mu ]$, не имеет решения, то ${{\theta }^{ + }}[\mu ] > {{\theta }^{ - }}[\mu ]$ и для пары $({{x}^{ + }},{{y}^{ + }})$, реализующей ${{\theta }^{ + }}[\mu ]$, будет $\Phi ({{x}^{ + }},{{y}^{ + }}) \geqslant {{\theta }^{ + }}[\mu ]\mu > {{\theta }^{ - }}[\mu ]\mu $, причем $\exists i \in I(\mu )$: ${{\varphi }_{i}}({{x}^{ + }},{{y}^{ + }}) = {{\theta }^{ + }}[\mu ]{{\mu }_{i}}$. Так что в условиях утверждения 1 ${{\theta }^{ + }}[\mu ] < {{\eta }^{ + }}[\mu ]$ и ${{\varphi }_{i}}({{x}^{ + }},{{y}^{ + }}) < {{\eta }^{ + }}[\mu ]{{\mu }_{i}}$. Однако по остальным компонентам вектора $\Phi ({{x}^{ + }},{{y}^{ + }})$ не исключается равенство ${{\eta }^{ + }}[\mu ]\mu $. И тем более нельзя сделать вывод, что значение $\Phi ({{x}^{ + }},{{y}^{ + }})$ меньше (пусть нестрого) оценки ${{\eta }^{ - }}[\mu ]\mu $ даже при ${{\eta }^{ - }}[\mu ] > {{\theta }^{ + }}[\mu ]$. В итоге исход $({{x}^{ + }},{{y}^{ + }})$ вполне может не войти с данным μ в компромиссное множество МК-игры Γ0 в нормальной форме.
Перейдем к общему случаю: ЛПР 1 выбирает ОЛС с вектором коэффициентов μ из M и ЛПР 2 выбирает ОЛС с параметрами $\nu \in M$. Тогда в МК-игре Γ12 введем
(2.3)
${{K}^{ - }}(\mu ,\nu )\;\mathop = \limits^{{\text{def}}} \;\{ (x,y) \in X \times Y\,{\text{|}}\,{{\theta }^{ - }}[\mu ]\mu \leqslant \Phi (x,y),{{\varphi }_{j}}(x,y) \leqslant {{\eta }^{ - }}[\nu ]{{\nu }_{j}}\;\forall j \in I(\nu )\} $Множества компромиссных исходов в МК-играх Γ12 и Γ21 не пусты ни при каких μ, $\nu \in M$ в полном соответствии с существованием решения у скалярных игр с фиксированным порядком ходов [14]. В частности, ${{K}^{ - }}(\mu ,\nu )$ (2.3) включает пару $(x{\kern 1pt} ',y{\kern 1pt} '{\kern 1pt} ')$, где x' – осторожная [15] стратегия ЛПР 1 в скалярной игре ${{\Gamma }^{1}}[\mu ]$ с функцией выигрыша, равной его ОЛС ${{G}_{1}}[\mu ]$, т.е. реализует ${{\theta }^{ - }}[\mu ]$, а y'' реализует
Действительно, по определению справедливы двусторонние неравенства:
Аналогично компромиссным исходом для игры ${{\Gamma }_{{21}}}$ будет $(x{\kern 1pt} '{\kern 1pt} ',y{\kern 1pt} ')$, где x'' реализует
Еще один вариант компромиссного исхода возникает, когда для выбранных векторов коэффициентов μ и $\nu \in M$ существует пара $({{x}^{0}},{{y}^{0}})$, удовлетворяющая (1.1). Тогда для нее будет выполнено и условие в (2.3), так как верны неравенства:
Причем равновесная пара сразу принадлежит пересечению ${{K}^{ - }}(\mu ,\nu )$ и ${{K}^{ + }}(\mu ,\nu )$, т.е. является компромиссной (с данными μ и ν) и для игры Γ0 в нормальной форме – в полном соответствии с включениями (1.3) для равновесия в МК-игре.
Более того, взяв на основе любого $({{x}^{0}},{{y}^{0}}) \in {{R}^{0}}$ с (μ, ν) единый для обоих игроков вектор коэффициентов свертки μ0 с компонентами
(2.4)
$\mu _{i}^{0}\;\mathop = \limits^{{\text{def}}} \;{{\varphi }_{i}}({{x}^{0}},{{y}^{0}}){{\left( {\sum\limits_{k = 1}^n \,{{\varphi }_{k}}({{x}^{0}},{{y}^{0}})} \right)}^{{ - 1}}}\quad \forall i = \overline {1,n} ,$Для параметров (2.4) имеем
Таким образом, представление равновесия Шепли (1.2) с помощью ОЛС, в частности по (2.4), позволяет его структурировать для определения параметров компромиссных исходов в МК-играх с нулевой суммой в нормальной форме и выявления переговорных исходов. А в силу того, что не каждая равновесная пара войдет в переговорное множество, возникает потенциальная содержательная возможность для сужения по сравнению с R0 понятия решения. В этом и есть главный смысл изучения переговорных множеств. Но сначала завершим параметрический ($\forall \mu ,\nu \in M$) анализ свойств компромиссного множества как пересечения ${{K}^{ - }}(\mu ,\nu )$ и ${{K}^{ + }}(\mu ,\nu )$.
Для произвольных μ и ν из M общих критериев выполнения (1.1) авторам не известно. В [3] указаны исходы, удовлетворяющие (1.1), для набора (μ, ν*) с $\nu _{{i{\kern 1pt} *}}^{*} = 1$ или $(\mu {\kern 1pt} *,\nu )$ с $\mu _{{j{\kern 1pt} *}}^{*} = 1$ в случаях существования решения скалярной игры ${{\Gamma }^{1}}[\mu ]$ или ${{\Gamma }^{2}}[\nu ]$, для чего также нет широких достаточных условий. Поэтому воспользоваться уже доказанной непустотой R0 для поиска компромисса под любые наперед заданные наборы (μ, ν) в МК-игре Γ0 в нормальной форме не удается; найти решения (1.1) получается лишь при отдельных $\mu ,\nu \in M$. Компромиссные в такой игре множества с параметрами $\mu ,\nu \in M$ должны содержать пары (x, y), для которых ${{\varphi }_{i}}(x,y)$ не меньше ${{\theta }^{ + }}[\mu ]{{\mu }_{i}}$ $\forall i \in I(\mu )$ и одновременно ${{\varphi }_{j}}(x,y)$ не больше ${{\eta }^{ - }}[\nu ]{{\nu }_{j}}$ $\forall j \in I(\nu )$. Подобные оценки в критериальном пространстве имеются не всегда, так как не со всеми (μ, ν) будет ${{\theta }^{ + }}[\mu ]{{\mu }_{i}} \leqslant {{\eta }^{ - }}[\nu ]{{\nu }_{i}}$ $\forall i \in I(\mu ) \cap I(\nu )$. А если и имеются, то компромиссное множество все равно может оказаться пустым, поскольку не под все оценки ψ обязательно найдутся исходы $(x,y) \in X \times Y$, для которых $\Phi (x,y) = \psi $.
Например, при $I(\mu ) \cap I(\nu ) = \emptyset $ взаимодействие теряет свойства игры с нулевой суммой – оба ЛПР оптимизируют вектор-функции выигрышей с разными компонентами. У них широкое множество переговорных оценок. Но даже для такого случая μ и ν не можем утверждать наперед, что существует компромиссный исход в Γ0 с этими параметрами, если не сделали предположения о наличии равновесия Нэша хотя бы у одной из трех скалярных игр, возникающих после перехода к ОЛС. В частности, для скалярной игры $\Gamma [\mu ,\nu ]\;\mathop = \limits^{{\text{def}}} \;\left\langle {X,Y,{{G}_{1}}[\mu ], - {{G}_{2}}[\nu ]} \right\rangle $ с непротивоположными интересами равновесный по Нэшу исход (когда существует) удовлетворяет (1.1), а значит, будет равновесным и компромиссным в МК-игре Γ0. Другое достаточное условие дается обобщением утверждения 2 на случай $\mu \ne \nu $.
Утверждение 3. Существование решений $(x{\kern 1pt} *,y{\kern 1pt} *)$ и $(x{\kern 1pt} *{\kern 1pt} *,y{\kern 1pt} *{\kern 1pt} *)$ игр ${{\Gamma }^{1}}[\mu ]$ и ${{\Gamma }^{2}}[\nu ]$ обеспечивает непустоту пересечения ${{K}^{ - }}(\mu ,\nu )$ и ${{K}^{ + }}(\mu ,\nu )$ для набора ($\mu $, $\nu $).
Доказательство. По определению решений справедливы соотношения:
Следовательно, исход $(x{\kern 1pt} *,y{\kern 1pt} *{\kern 1pt} *)$ принадлежит ${{K}^{ - }}(\mu ,\nu )$ и ${{K}^{ + }}(\mu ,\nu )$.
Условия утверждения 3 жестче, чем (1.1) – из них вытекает не просто непустота пересечения, но совпадение ${{K}^{ - }}(\mu ,\nu )$ и ${{K}^{ + }}(\mu ,\nu )$ (т.е. компромиссными в Γ0 будут все равновесные исходы игр Γ12 и Γ21 с такими μ, ν) в силу равенств ${{\theta }^{ - }}[\mu ] = {{\theta }^{ + }}[\mu ]$ и ${{\eta }^{ - }}[\nu ] = {{\eta }^{ + }}[\nu ]$. Напомним, что, согласно (1.9), выполнение этих условий для всех $\mu $ и $\nu $ эквивалентно наличию односторонних решений для обоих игроков. Однако в общей постановке МК-игры Γ0 односторонних решений тоже нет. Далее докажем требуемые для их существования равенства и обоснуем непустоту множеств компромиссных исходов при произвольных μ и ν из M для конечных МК-игр Γ0 в смешанных стратегиях, предположив, что при определении МК-средних результатов игроки-ЛПР по своей смешанной стратегии осредняют частные критерии, а по смешанной стратегии противника – свои ОЛС. Модель, в которой игроки применяют осреднение ОЛС и по своим, и по чужим смешанным стратегиям, также дает существование односторонних решений и может изучаться аналогичным образом, но в настоящей работе остановимся на первом варианте МК-смешанного расширения, следуя [3, 10].
3. МК-смешанное расширение конечных МК-игр в ОЛС. Допустим, что игроки-ЛПР 1 и 2 выбирают смешанные стратегии p и q на конечных X и Y соответственно и оценивают свои МК-средние выигрыши и проигрыши с помощью следующих средних ОЛС [3] с параметрами μ и $\nu \in M$:
Обе функции ${{\bar {G}}_{1}}$ и ${{\bar {G}}_{2}}$ являются вогнутыми по p и выпуклыми по q, и потому (в отличие от G1, G2) минимакс для них равен максимину. Обозначим последние величины для ЛПР 1, ЛПР 2 через
(3.1)
${{m}_{1}}[\mu ]\;\mathop = \limits^{{\text{def}}} \;\mathop {max}\limits_{p \in P} \mathop {min}\limits_{q \in Q} {{\bar {G}}_{1}}(p,q)[\mu ] = \mathop {min}\limits_{q \in Q} \mathop {max}\limits_{p \in P} {{\bar {G}}_{1}}(p,q)[\mu ]\quad \forall \mu \in M,$(3.2)
${{m}_{2}}[\nu ]\;\mathop = \limits^{{\text{def}}} \;\mathop {max}\limits_{p \in P} \mathop {min}\limits_{q \in Q} {{\bar {G}}_{2}}(p,q)[\nu ] = \mathop {min}\limits_{q \in Q} \mathop {max}\limits_{p \in P} {{\bar {G}}_{2}}(p,q)[\nu ]\quad \forall \nu \in M,$(3.3)
$\mathop {\bar {f}}\nolimits_ \leqslant \;\mathop = \limits^{{\text{def}}} \;\bigcup\limits_{\mu \in M} \,\mu \mathop {max}\limits_{p \in P} \mathop {min}\limits_{q \in Q} {{\bar {G}}_{1}}(p,q)[\mu ]\quad {\text{и}}\quad \mathop {\bar {\mathcal{F}}}\nolimits_ \leqslant \;\mathop = \limits^{{\text{def}}} \;\bigcup\limits_{\mu \in M} \,\mu \mathop {min}\limits_{q \in Q} \mathop {max}\limits_{p \in P} {{\bar {G}}_{1}}(p,q)[\mu ].$Из (3.1) вытекает, что $\mathop {\bar {f}}\nolimits_ \leqslant = \mathop {\bar {\mathcal{F}}}\nolimits_ \leqslant $, образуя одностороннее значение игры для игрока 1.
Похожим образом можно ввести МК-средние максимин и минимакс ЛПР 2 как
и получить равенство ${{\bar {f}}_{ \geqslant }} = \mathop {\bar {\mathcal{F}}}\nolimits_ \geqslant $. Так что и эти МК-средние НГР (не зависящие от порядка ходов) формируют одностороннее значение игры, но уже для игрока 2. Найденные односторонние значения МК-игры $\bar {\Gamma }_{G}^{0}$, оценивающие ее результат с точки зрения ЛПР 1 или ЛПР 2, обычно не совпадают. Ниже будем обозначать указанные множества оценок (в критериальном пространстве) через N1 и N2. Их свойства проанализируем в разд. 4, а далее вернемся к вопросу о компромиссе.Для рассматриваемой постановки модифицируем множество компромиссных исходов и изучим аналог пересечения ${{K}^{ - }}(\mu ,\nu )$ и ${{K}^{ + }}(\mu ,\nu )$ в смешанных стратегиях
(3.6)
$\bar {K}(\mu ,\nu )\;\mathop = \limits^{{\text{def}}} \;\{ (p,q) \in P \times Q\,{\text{|}}\,{{m}_{1}}[\mu ] \leqslant {{\bar {G}}_{1}}(p,q)[\mu ],{{\bar {G}}_{2}}(p,q)[\nu ] \leqslant {{m}_{2}}[\nu ]\} $Пусть пара $(p{\kern 1pt} '[\mu ],q{\kern 1pt} '[\mu ])$ реализует ${{m}_{1}}[\mu ]$ (3.1), а $(p{\kern 1pt} '{\kern 1pt} '[\nu ],q{\kern 1pt} '{\kern 1pt} '[\nu ])$ реализует ${{m}_{2}}[\nu ]$ (3.2). По определению ${{m}_{1}}[\mu ] = {{\bar {G}}_{1}}(p{\kern 1pt} '[\mu ],q{\kern 1pt} '[\mu ])[\mu ] \leqslant {{\bar {G}}_{1}}(p{\kern 1pt} '[\mu ],q{\kern 1pt} '{\kern 1pt} '[\nu ])[\mu ]$ и ${{\bar {G}}_{2}}(p{\kern 1pt} '[\mu ],q{\kern 1pt} '{\kern 1pt} '[\nu ])[\nu ] \leqslant {{\bar {G}}_{2}}(p{\kern 1pt} '{\kern 1pt} '[\nu ],q{\kern 1pt} '{\kern 1pt} '[\nu ])[\nu ] = {{m}_{2}}[\nu ]$. Отсюда $(p{\kern 1pt} '[\mu ],q{\kern 1pt} '{\kern 1pt} '[\nu ]) \in \bar {K}(\mu ,\nu )$ (в отличие от пары $(p{\kern 1pt} '{\kern 1pt} '[\mu ],q{\kern 1pt} '[\nu ])$, не являющейся компромиссной). Тем самым доказали следующий результат.
Утверждение 4: $\bar {K}(\mu ,\nu ) \ne \emptyset $ при всех $\mu ,\nu \in M.$
При одинаковых параметрах свертки $\mu $ у обоих игроков множество оценок компромиссных значений МК-средних выигрыша ЛПР 1 и проигрыша ЛПР 2 в ОЛС образует на основе отрезка [${{m}_{1}}[\mu ]$, ${{m}_{2}}[\mu ]$] сегмент в критериальном пространстве от ${{m}_{1}}[\mu ]\mu $ до ${{m}_{2}}[\mu ]\mu $. Объединение построенных сегментов по всем μ ∈ M является частью множества компромиссных оценок МК-среднего значения игры $\bar {\Gamma }_{G}^{0}$ и дает параметризацию этой части, позволяющую для каждого варианта μ ∈ M найти свой компромисс даже в такой ситуации, содержательно близкой к однокритериальным задачам с противоположными интересами. Подчеркнем, что без применения смешанных стратегий с осреднением ОЛС (по чужой смешанной стратегии) о непустоте аналогичного (3.6) с ν = μ множества исходов $({{x}^{ \pm }},{{y}^{ \pm }})$, удовлетворяющих и (2.1), и (2.2), не удается сделать вывод в отсутствие дополнительных требований, например, существования решений игр ${{\Gamma }^{1}}[\mu ]$, ${{\Gamma }^{2}}[\mu ]$ или $\Gamma [\mu ,\mu ]$, определенных в разд. 2. Последние в свою очередь не выполняются автоматически, в том числе для билинейных функций φi. Именно поэтому, чтобы получить одностороннее значение для игрока 1 в МК-игре с осредненными частными критериями, в [16] понадобились довольно жесткие предположения (см. также [4]).
Замечание 1. В контексте [4, 16], где рассмотрена антагонистическая трактовка МК-игры, заметим, что для такой трактовки, переходя к введенному МК-смешанному расширению конечной игры, будем иметь не только чистую игру, но и равенство односторонних значений игры для игроков 1 и 2 [3], т.е. полный аналог скалярного равновесия.
Покажем, что появление компромисса после МК-осреднения обусловлено наличием односторонних решений для данной постановки, а не использованием в (3.6) оценок, получаемых с помощью ОЛС, вместо средних значений компонент вектор-функции Φ. Если подставить в определение $\bar {K}(\mu ,\nu )$ средние значения частных критериев, то решение $(p{\kern 1pt} '[\mu ],q{\kern 1pt} ''[\nu ])$ сохранится в качестве компромиссного. Введем
(3.7)
$\bar {K}{\kern 1pt} '(\mu ,\nu )\;\mathop = \limits^{{\text{def}}} \;\{ (p,q) \in P \times Q\,{\text{|}}\,{{m}_{1}}[\mu ]{{\mu }_{i}} \leqslant {{\bar {\varphi }}_{i}}(p,q)\;\forall i \in I(\mu ),{{\bar {\varphi }}_{k}}(p,q) \leqslant {{m}_{2}}[\nu ]{{\nu }_{k}}\;\forall k \in I(\nu )\} .$Утверждение 5: $\bar {K}{\kern 1pt} '(\mu ,\nu ) \ne \emptyset $ при всех $\mu ,\nu \in M$.
Доказательство. Для $(p{\kern 1pt} ',q{\kern 1pt} '{\kern 1pt} ')\;\mathop = \limits^{{\text{def}}} \;(p{\kern 1pt} '[\mu ],q{\kern 1pt} '{\kern 1pt} '[\nu ]) \in \bar {K}(\mu ,\nu )$ имеем $\forall i \in I(\mu )$
Непустота множества $\bar {K}{\kern 1pt} '(\mu ,\nu )$ может быть получена и как следствие результатов разд. 2, если их приложить к МК-игре $\bar {\Gamma }_{S}^{0}\;\mathop = \limits^{{\text{def}}} \;\left\langle {P,Q,\bar {\Phi }(p,q)} \right\rangle $ (при стандартном смешанном расширении). Для дальнейшего введенные в разд. 0–2 обозначения, когда они применяются к игре $\bar {\Gamma }_{S}^{0}$, будем помечать чертой сверху или снабжать индексом S (например, ${{\bar {K}}^{ - }}(\mu ,\nu )$ задается (2.3) для игры $\bar {\Gamma }_{S}^{0}$). В этих обозначениях докажем, что ${{\bar {K}}^{ - }}(\mu ,\nu ) \cup {{\bar {K}}^{ + }}(\mu ,\nu ) \subseteq \bar {K}{\kern 1pt} '(\mu ,\nu )$ $\forall \mu ,\nu \in M$. Тогда совместность условий в (3.7) будет вытекать из непустоты ${{\bar {K}}^{ - }}(\mu ,\nu )$, ${{\bar {K}}^{ + }}(\mu ,\nu )$.
Утверждение 6: $\forall \mu \in M$ ${{m}_{1}}[\mu ] = {{\bar {\theta }}^{ - }}[\mu ]$, ${{m}_{2}}[\mu ] = {{\bar {\eta }}^{ + }}[\mu ]$.
Доказательство. Рассмотрим произвольный вектор коэффициентов μ ∈ M. Поскольку
Правая часть будет не меньше:
С другой стороны,
Тем самым пришли к равенству. Беря максимум по $p \in P$ от обеих его частей, получаем ${{m}_{1}}[\mu ] = {{\bar {\theta }}^{ - }}[\mu ]$. Второе равенство в утверждении доказывается симметрично.
По утверждению 6 множество (3.7) состоит из всех пар смешанных стратегий (p, q), для которых ${{\bar {\theta }}^{ - }}[\mu ]\mu \leqslant \bar {\Phi }(p,q)$ и ${{\bar {\varphi }}_{i}}(x,y) \leqslant {{\bar {\eta }}^{ + }}[\nu ]{{\nu }_{i}}$ $\forall i \in I(\nu )$. Отсюда оно содержит и ${{\bar {K}}^{ - }}(\mu ,\nu )$ $\mathop = \limits^{{\text{def}}} $ $\mathop = \limits^{{\text{def}}} $ {(p, $q) \in P \times Q\,{\text{|}}\,{{\bar {\theta }}^{ - }}[\mu ]\mu \leqslant \bar {\Phi }(p,q),$ ${{\bar {\varphi }}_{i}}(x,y) \leqslant {{\bar {\eta }}^{ - }}[\nu ]{{\nu }_{i}}\;\;\forall i \in I(\nu )\} $, и ${{\bar {K}}^{ + }}(\mu ,\nu )$, так как ${{\bar {\eta }}^{ - }}[\nu ] \leqslant {{\bar {\eta }}^{ + }}[\nu ]$ и ${{\bar {\theta }}^{ - }}[\mu ] \leqslant {{\bar {\theta }}^{ + }}[\mu ]$, исходя из определений разд. 1 в применении к игре $\bar {\Gamma }_{S}^{0}$. В итоге рассматриваемое МК-смешанное расширение заметно увеличивает по сравнению со стандартным потенциальные возможности для компромисса (в силу существования односторонних значений МК-игры $\bar {\Gamma }_{G}^{0}$ в отличие от $\bar {\Gamma }_{S}^{0}$). В МК-игре $\bar {\Gamma }_{S}^{0}$ пересечение ${{\bar {K}}^{ - }}(\mu ,\nu )$ и ${{\bar {K}}^{ + }}(\mu ,\nu )$может быть пустым, тогда как аналогичное пересечение для $\bar {\Gamma }_{G}^{0}$ дается множеством (3.6) или (3.7), т.е. компромиссные стратегии для нормальной формы игры $\bar {\Gamma }_{G}^{0}$ в ОЛС найдутся при любых $\mu ,\nu \in M$.
Компромиссное значение, отвечающее данным параметрам $\mu ,\nu \in M$, для конечной МК-игры Γ0 в смешанных стратегиях можно определять и как объединение средних $\bar {\Phi }(p,q)$ по всем (p, q) из $\bar {K}{\kern 1pt} '(\mu ,\nu )$, и как объединение по всем (p, q) из множества (3.6) векторов ${{\bar {G}}_{1}}(p,q)[\mu ]\mu $ или ${{\bar {G}}_{2}}(p,q)[\nu ]\nu $ соответственно при построении оценок для ЛПР 1 или ЛПР 2. Для $j \in I(\mu ) \cap I(\nu )$ и $(p,q)$ из (3.7) компоненты ${{\bar {\varphi }}_{j}}(p,q)$ не превосходят ${{\bar {G}}_{2}}(p,q)[\nu ]{{\nu }_{j}}$ и не меньше, чем ${{\bar {G}}_{1}}(p,q)[\mu ]{{\mu }_{j}}$. (Важно, чтобы для построения компромиссного значения брались компромиссные исходы игры $\bar {\Gamma }_{G}^{0}$ в ОЛС.)
Объединяя по $\mu ,\nu \in M$ отвечающие им компромиссные значения, увидим, что все их элементы принадлежат множеству
оценок в критериальном пространстве между односторонними значениями МК-игры $\bar {\Gamma }_{G}^{0}$ N1 для ЛПР 1 и N2 для ЛПР 2 (включающему и эти МК-средние НГР), так как при 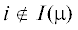 принимаем оценку 0 для i-го частного критерия у игрока 1, а при
принимаем оценку 0 для i-го частного критерия у игрока 1, а при 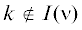 – оценку C для k‑го частного критерия у игрока 2. Указанное множество обозначим через N $\mathop = \limits^{{\text{def}}} $ $\mathop {{\text{eph}}}\nolimits_ \geqslant ({{N}_{1}}) \cap \mathop {{\text{eph}}}\nolimits_ \leqslant ({{N}_{2}})$ и назовем множеством компромиссных средних оценок в МК-игре. Оно является наиболее широким в том смысле, что на оценки вне этого множества
игроки уже никак не могут рассчитывать в игре Γ0. (Построим его для модельного примера в разд. 4.)
– оценку C для k‑го частного критерия у игрока 2. Указанное множество обозначим через N $\mathop = \limits^{{\text{def}}} $ $\mathop {{\text{eph}}}\nolimits_ \geqslant ({{N}_{1}}) \cap \mathop {{\text{eph}}}\nolimits_ \leqslant ({{N}_{2}})$ и назовем множеством компромиссных средних оценок в МК-игре. Оно является наиболее широким в том смысле, что на оценки вне этого множества
игроки уже никак не могут рассчитывать в игре Γ0. (Построим его для модельного примера в разд. 4.)
За счет предложения осреднять ОЛС множества компромиссных пар стратегий оказались не пустыми при любых μ и ν из M: и при $I(\mu ) \cap I(\nu ) = \emptyset $, и при совпадении μ и ν. Поэтому все множество компромиссных решений в смысле (3.6) или (3.7) представимо их объединением по всем парам (μ, ν) из $M \times M$ и параметризуется перебором соответствующих пар. Отметим, что полученные множества вполне могут отличаться от решения конечной МК-игры в смешанных стратегиях, рассмотренного Шепли [12]. Для решения Шепли в [12] используется параметризация равновесия МК-игры $\bar {\Gamma }_{S}^{0}$ (см. (1.2) при замене x, y на p, q и Φ на $\bar {\Phi }$) с помощью линейной скаляризации. А именно указанное решение представлено объединением равновесий по Нэшу скалярных игр двух лиц, функция выигрыша каждого из которых есть линейная свертка математических ожиданий его частных критериев с весами. Объединение берется по всем парам векторов весовых коэффициентов линейных сверток. В силу билинейности линейных сверток средних критериев такие скалярные равновесия всегда существуют.
Аналогично можно применить параметризацию множеств Слейтера, входящих в определение равновесия Шепли МК-игры $\bar {\Gamma }_{S}^{0}$, с помощью ОЛС [9] средних частных критериев. Получим множество ${{\bar {R}}^{0}}$, состоящее из пар (p0, q0), удовлетворяющих условию, что $\exists \mu ,\nu \in M:$
(3.8)
${{p}^{0}} \in {\text{Arg}}\mathop {max}\limits_{p \in P} \mathop {min}\limits_{j \in I(\mu )} {{\bar {\varphi }}_{j}}(p,{{q}^{0}}){\text{/}}{{\mu }_{j}},\quad {{q}^{0}} \in {\text{Arg}}\mathop {min}\limits_{q \in Q} \mathop {max}\limits_{j \in I(\nu )} {{\bar {\varphi }}_{j}}({{p}^{0}},q){\text{/}}{{\nu }_{j}}.$В регулярном случае представление (3.8) равновесия Шепли совпадает с решением Шепли за счет эквивалентности скаляризации множеств Слейтера на базе ОЛС и линейной свертки. Только общих достаточных условий непустоты соотношений в (3.8) с произвольными μ и ν из M не известно.
Для рассматриваемой в настоящей работе постановки с осреднением не частных критериев, а их свертки, при использовании игроками линейной скаляризации ничего не меняется относительно решения Шепли. Но когда игроки ориентируются на ОЛС, приходим к формуле, определяющей равновесие в МК-игре $\bar {\Gamma }_{G}^{0}$ как множество равновесий в скалярных играх $\bar {\Gamma }[\mu ,\nu ] \in \bar {\Gamma }_{G}^{0}$ при всех $\mu ,\nu \in M$, а именно
Равновесия в играх $\bar {\Gamma }[\mu ,\nu ]$ существуют по теореме Нэша [17] в силу выпукло-вогнутости функций ${{\bar {G}}_{1}}$, ${{\bar {G}}_{2}}$. Нетрудно убедиться, что (как и в МК-игре без осреднения) эти равновесия являются компромиссными исходами, отвечающими данному набору (μ, ν), т.е. обеспечивают обоим игрокам результаты не хуже их ${{m}_{1}}[\mu ]$ и ${{m}_{2}}[\nu ]$.
Вместе с тем оказывается, что и равновесные в смысле (3.8) (т.е. (1.1) для средних частных критериев) исходы $({{p}^{0}},{{q}^{0}}) \in {{\bar {R}}^{0}}$ будут компромиссными в смысле (3.7). Действительно, для μ, ν из (3.8) $\forall i \in I(\mu )$
Отсюда путем объединения по всем μ, ν ∈ M получаем включение в построенное с помощью ОЛС компромиссное множество любых равновесных решений конечной МК-игры в смешанных стратегиях – вне зависимости от ее смешанного расширения и применяемых игроками-ЛПР способов скаляризации.
Утверждение 7: $\bar {R}_{G}^{*} \subseteq \bigcup\limits_{\mu \in M,\nu \in M} \,\bar {K}{\kern 1pt} '(\mu ,\nu )$, ${{\bar {R}}^{0}} \subseteq \bigcup\limits_{\mu \in M,\nu \in M} \,\bar {K}{\kern 1pt} '(\mu ,\nu )$.
Замечание 2. Последнее включение не противоречит утверждению из [13] о наиболее широком множестве решений Шепли для конечных МК-игр в смешанных стратегиях, так как не всякий компромиссный исход является равновесным. Но и множество $\bar {R}_{G}^{*}$ не обязано включаться в ${{\bar {R}}^{0}}$, задаваемое (3.8) (хотя для примера, рассмотренного в Приложении, они совпадут). Суть в том, что после замены $\bar {\Phi }$ на ${{\bar {G}}_{1}}$ и ${{\bar {G}}_{2}}$ не выполняется аксиома согласованности CONS из [13] о продолжении принципа оптимальности, принимаемого для себя любым игроком в отдельности, на большее их число. В изученном выше механизме МК-осреднения вектор-функции выигрышей игроки по своим смешанным стратегиям осредняют каждый частный критерий, а по смешанным стратегиям противника – их свертку, причем нелинейную, так что принцип оптимальности меняется. Использование средних ОЛС отличает предложенное МК-смешанное расширение и от смешанных расширений, исследуемых в [18] для игр с произвольно (нелинейно) упорядоченными исходами.
Пусть ${{\bar {Z}}^{0}}$ – равновесное значение МК-игры Γ0 для ее стандартного смешанного расширения $\bar {\Gamma }_{S}^{0}$, т.е. множество векторов $\bar {\Phi }({{p}^{0}},{{q}^{0}})$ для $({{p}^{0}},{{q}^{0}}) \in {{\bar {R}}^{0}}$. Введем объединенное компромиссное среднее значение как множество средних значений вектор-функции выигрышей на компромиссных исходах (3.7), построенных для рассматриваемого в данной работе специального МК-смешанного расширения $\bar {\Gamma }_{G}^{0}$ МК-игры Γ0 в ОЛС,
Из утверждения 7 получаем справедливость следующего включения для значений игры:
Отсюда, как и ранее (см. вывод из утверждения 6), замечаем, что использование множеств (3.7) дает больше возможностей для компромисса, чем стандартный подход, когда решение МК-игры на основании доказанного в [12] (а также аксиомы WEIGHT из [13]) параметризуется с помощью линейной свертки.
Линейная скаляризация удобна тем, что в смешанных стратегиях равновесие для конечных скалярных игр на базе линейной свертки существует при любых весах критериев у игроков. Притом не важно, осредняет игрок каждый критерий или их линейную свертку. Однако линейная свертка не всегда подходит для описания решения, поскольку даже в обычной МК-оптимизации грани эффективного множества задаются единственным набором значений весовых коэффициентов, который не так легко обнаружить при аппроксимации. Кроме того, не исключено, что ОЛС понадобится игроку-ЛПР по содержательным соображениям, в том числе для объективизации процедуры выбора итогового решения. Система аналитической поддержки не должна предопределять форму представления результата за него. В каких-то случаях ЛПР предпочтет метод последовательных уступок [5], в других (в частности, при невзаимозаменяемости критериев [7]) – логическую свертку или ОЛС. Для детерминированных выпуклых задач МК-оптимизации на получаемый ответ это не повлияет, но уже в стохастической МК-оптимизации изменение свертки способно вызвать расхождение оценок [10]. Для МК-игр результирующие множества тоже могут отличаться в зависимости от вида свертки [19, 20] как для решения игры, так и для ее значения – множества неулучшаемых оценок выигрыша или проигрыша.
Различия проявляются, если хотя бы один игрок применяет смешанные стратегии и руководствуется идеей осреднения свертки вместо частных критериев, что существенно для ОЛС. (Поэтому и случай, когда на ОЛС ориентируется лишь один ЛПР, а другой остановился на линейной свертке, для конечной МК-игры в смешанных стратегиях способен продемонстрировать третий вариант значения и решения МК-игры по сравнению с вариантами ОЛС или линейной свертки за обоих игроков-ЛПР [21].) Использование при получении решения конечной МК-игры в смешанных стратегиях рассмотренной нестандартной концепции МК-смешанного расширения позволяет сохранить для ОЛС те же хорошие свойства, что и у традиционной линейной свертки. В итоге увеличивается область применимости логической свертки и ОЛС, имеющих большое распространение в исследовании операций. В разд. 4 для игры $\mathop {\bar {\Gamma }}\nolimits_G^0 $ опишем возможности ОЛС при построении переговорных оценок.
4. Переговорные оценки при МК-смешанном расширении игры Γ0. Для выделения из множества компромиссных исходов (3.7) переговорных можно в принципе воспользоваться тем же приемом, что и для МК-игры в чистых стратегиях (см. в разд. 2), и заменить в (3.7) нестрогие неравенства на строгие. Однако переговоры относительно смешанных стратегий представляются недостаточно конструктивными (для скалярных игр в [15] описаны примеры совместно выбираемых смешанных стратегий, но в другом контексте). К тому же множества переговорных исходов могут для многих $\mu ,\nu $ оказаться пустыми. Поэтому далее формально введем потенциально переговорные оценки МК-средних выигрышей игроков и в первую очередь опишем подмножества переговорных оценок в различных множествах компромиссных средних значений и оценок. Вопрос об исходах, к ним приводящих, затронем лишь отчасти (он пока остается открытым).
Множество компромиссных средних оценок включает в себя НГР N1 и N2 игроков 1 и 2 в МК-игре $\bar {\Gamma }_{G}^{0}$ и все покоординатно промежуточные величины (не выходящие за пределы [0, C]), т.е. пересечение $\mathop {{\text{eph}}}\nolimits_ \geqslant ({{N}_{1}}) \cap \mathop {{\text{eph}}}\nolimits_ \leqslant ({{N}_{2}})$ – в полном соответствии с (3.7). Выше обозначили указанное множество оценок через N. Теоретически оно может быть шире $\bar {Z}_{G}^{0}$, поскольку не для всех оценок $\psi \in N$ (в отличие от векторов из $\bar {Z}_{G}^{0}$) найдутся компромиссные смешанные стратегии (pN, qN): $\bar {\Phi }({{p}^{N}},{{q}^{N}}) = \psi $. Предположив, следуя логике [7, 15, 14], что свои НГР, в данном случае N1 и N2, игроки могут себе обеспечить самостоятельно (тем более с учетом существования односторонних решений в рассматриваемом МК-смешанном расширении игры Γ0), введем в $\bar {\Gamma }_{G}^{0}$ переговорное множество оценок
(4.1)
${{N}^{ + }}\;\mathop = \limits^{{\text{def}}} \;N{\backslash }\left\{ {{{N}_{1}} \cup {{N}_{2}}} \right\}.$Проанализируем его свойства, начав с изучения ${{N}_{1}}$ и ${{N}_{2}}$, заданных (3.3)–(3.5).
Как в (1.7), ${{N}_{1}} \subseteq \mathop {{\text{eph}}}\nolimits_ \leqslant ({{N}_{2}})$ и ${{N}_{2}} \subseteq \mathop {{\text{eph}}}\nolimits_ \geqslant ({{N}_{1}})$. И также справедлив аналог (1.8).
Утверждение 8. Для любых $\psi \in {{N}_{1}},\;\,\xi \in {{N}_{2}}$ выполнено $\psi \leqslant \xi $.
Доказательство. По определению N1 и N2$\forall \psi \in {{N}_{1}},$ $\xi \in {{N}_{2}}$ $\exists \mu ,\nu \in M$:
Следовательно, на базе доказательств утверждений 4, 5
А для 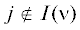 ${{\xi }_{j}} = C \geqslant {{\psi }_{j}}$.
${{\xi }_{j}} = C \geqslant {{\psi }_{j}}$.
Усилим это утверждение, предположив, что задача поиска МК-среднего НГР хотя бы для одного ЛПР не сводится к набору n однокритериальных задач, т.е.
Здесь и далее $\pi ({{N}_{1}})$ и $\pi ({{N}_{2}})$ – множества точек Парето в задачах на MaxN1 и MinN2 соответственно, а ${\text{|}}\pi ( \ldots ){\text{|}}$ обозначает число элементов в множестве $\pi ( \ldots )$.
Утверждение 9. При условии (4.2) ${{N}_{1}} \cap {{N}_{2}} = \emptyset $ и ${{m}_{1}}[\mu ] < {{m}_{2}}[\mu ]$ $\forall \mu > 0$.
Доказательство. Из утверждения 8 вытекает, что при ${{N}_{1}} \cap {{N}_{2}} \ne \emptyset $ это пересечение состоит из единственного вектора (если предположить, что $\psi ,\psi {\kern 1pt} ' \in {{N}_{1}} \cap {{N}_{2}}$, то будет $\psi \leqslant \psi {\kern 1pt} '$ и $\psi {\kern 1pt} ' \leqslant \psi $). Подобный вектор $\hat {\psi }$ равен и ${{m}_{1}}[\mu ]\mu $, и ${{m}_{2}}[\nu ]\nu $ для некоторых $\mu ,\nu \in M$ с учетом компонент с индексами из I(ν) в последнем равенстве, заменяемых на C. Точнее,
По утверждению 8 $\hat {\psi } \geqslant \psi $ $\forall \psi \in {{N}_{1}}$ и $\hat {\psi } \leqslant \xi $ $\forall \xi \in {{N}_{2}}$. Отсюда $\pi ({{N}_{1}}) = \{ \hat {\psi }\} $, $\pi ({{N}_{2}}) = \{ \hat {\psi }\} $ (т.е. других точек Парето в N1 и N2 нет), так что ${\text{|}}\pi ({{N}_{1}}){\text{|}} = 1$ и ${\text{|}}\pi ({{N}_{2}}){\text{|}} = 1$ – пришли к противоречию с (4.2). В итоге ${{N}_{1}} \cap {{N}_{2}} = \emptyset $. Таким образом, $\forall \psi \in {{N}_{1}},$ $\xi \in {{N}_{2}}\;\exists i$: ${{\psi }_{i}} < {{\xi }_{i}}$. В частности, $\forall \mu > 0$ ${{m}_{1}}[\mu ]\mu \leqslant {{m}_{2}}[\mu ]\mu $ и $\exists {{i}^{0}}$: ${{m}_{1}}[\mu ]{{\mu }_{{{{i}^{0}}}}} < {{m}_{2}}[\mu ]{{\mu }_{{{{i}^{0}}}}}$, а значит, и ${{m}_{1}}[\mu ] < {{m}_{2}}[\mu ]$.
Утверждение 10. Если ${\text{|}}\pi ({{N}_{1}}){\text{|}} > 1$ и ${\text{|}}\pi ({{N}_{2}}){\text{|}} > 1$, то ${{N}^{ + }} \ne \emptyset $.
Доказательство. Пусть $\psi ,\psi {\kern 1pt} ' \in \pi ({{N}_{1}})$ и $\psi \ne \psi {\kern 1pt} '$. Введем ${{\psi }^{0}}$ с $\psi _{i}^{0}\;\mathop = \limits^{{\text{def}}} \;max\{ {{\psi }_{i}},\psi _{i}^{'}\} $ $\forall i = \overline {1,n} $, тогда 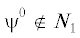 . По утверждению 8 $\forall \xi \in {{N}_{2}}$ имеем $\xi \geqslant \psi $ и $\xi \geqslant \psi {\kern 1pt} '$, т.е. $\xi \geqslant {{\psi }^{0}}$. Поэтому
. По утверждению 8 $\forall \xi \in {{N}_{2}}$ имеем $\xi \geqslant \psi $ и $\xi \geqslant \psi {\kern 1pt} '$, т.е. $\xi \geqslant {{\psi }^{0}}$. Поэтому 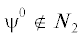 , так как в противном случае $\pi ({{N}_{2}}) = \{ {{\psi }^{0}}\} $, что не соответствует условиям утверждения. Отсюда ${{\psi }^{0}} \in {{N}^{ + }}$.
, так как в противном случае $\pi ({{N}_{2}}) = \{ {{\psi }^{0}}\} $, что не соответствует условиям утверждения. Отсюда ${{\psi }^{0}} \in {{N}^{ + }}$.
Из утверждения 10 следует непустота множества переговорных оценок в широких предположениях, но не ясно, сопоставлены ли этим оценкам какие-либо исходы игры (пары смешанных стратегий). Проанализируем подробнее характерные случаи.
Поскольку у МК-игры $\mathop {\bar {\Gamma }}\nolimits_S^0 $, как правило, нет односторонних значений, то нет оснований ожидать непустоту пересечения компромиссных множеств ${{\bar {K}}^{ - }}$ и ${{\bar {K}}^{ + }}$ для всех μ, ν, кроме отдельных параметров, с которыми найдутся стратегии, удовлетворяющие (3.8), т.е. существует равновесие скалярной игры в ОЛС при осреднении частных критериев. Здесь нет никаких отличий от общих МК-игр, рассмотренных в разд. 2. Так что если ${{\bar {K}}^{ - }}(\mu ,\nu )$ и ${{\bar {K}}^{ + }}(\mu ,\nu )$ не пересекаются, значит, исход $({{p}^{ - }},{{q}^{ - }}) \in {{\bar {K}}^{ - }}(\mu ,\nu )$, реализующий $\mathop {\bar {\eta }}\nolimits^ - [\nu ]\nu $, не принадлежит ${{\bar {K}}^{ + }}(\mu ,\nu )$ и исход $({{p}^{ + }},{{q}^{ + }}) \in {{\bar {K}}^{ + }}(\mu ,\nu )$, реализующий ${{\bar {\theta }}^{ + }}[\mu ]\mu $, не принадлежит ${{\bar {K}}^{ - }}(\mu ,\nu )$, а кроме того, чтобы не войти в противоречие с утверждением 3, одна из скалярных игр ${{\bar {\Gamma }}^{1}}[\mu ]$ или ${{\bar {\Gamma }}^{2}}[\nu ]$ должна не иметь решения. Пусть это будет первая, т.е. ${{\bar {\theta }}^{ - }}[\mu ] < {{\bar {\theta }}^{ + }}[\mu ]$. Тогда для исхода $({{p}^{ + }},{{q}^{ + }})$ имеем
Однако не исключено, что найдутся превышающие ${{\bar {\theta }}^{ + }}[\mu ]{{\mu }_{j}}$ компоненты ${{\bar {\varphi }}_{j}}({{p}^{ + }},{{q}^{ + }})$, которые совпадут с ${{\bar {\eta }}^{ + }}[\nu ]{{\nu }_{j}}$ (окажутся не меньше ${{\bar {\eta }}^{ - }}[\nu ]{{\nu }_{j}}$). И также для (p–, q–) не удается напрямую доказать, что $\bar {\Phi }({{p}^{ - }},{{q}^{ - }}) > {{\bar {\theta }}^{ - }}[\mu ]{\kern 1pt} {\kern 1pt} \mu $, из-за неточного равенства векторов в соотношении $\bar {\Phi }({{p}^{ - }},{{q}^{ - }}) \leqslant {{\bar {\eta }}^{ - }}[\nu ]\nu $. Не получается в явном виде построить $(\bar {p},\bar {q})$ с $\bar {\Phi }(\bar {p},\bar {q}) \in [\mathop {\bar {\eta }}\nolimits^ - [\nu ]\nu ,{{\bar {\theta }}^{ + }}[\mu ]{\kern 1pt} {\kern 1pt} \mu ]$, даже зная, что последний сегмент в ${{\mathbb{R}}^{n}}$ не пустой (например, при $\nu = \mu $).
Для параметров $(\mu ,\nu )$, с которыми ${{\bar {K}}^{ + }}(\mu ,\nu ) \cap {{\bar {K}}^{ - }}(\mu ,\nu ) \ne \emptyset $, если для них ${{\bar {\Gamma }}^{1}}[\mu ]$ или ${{\bar {\Gamma }}^{2}}[\nu ]$ не имеет решения, приходим к тем же неравенствам, что и выше (строгим лишь с одной стороны). Только когда нет решения у обеих игр, векторы $\bar {\Phi }({{p}^{ \pm }},{{q}^{ \pm }})$ для исходов $({{p}^{ \pm }},{{q}^{ \pm }})$ из пересечения компромиссных множеств игры $\bar {\Gamma }_{S}^{0}$ находятся между ${{\bar {\theta }}^{ + }}[\mu ]{\kern 1pt} {\kern 1pt} \mu $ и ${{\bar {\eta }}^{ - }}[\nu ]\nu $, т.е. такие исходы – переговорные. В частности, при ν = μ в данном случае ${{\bar {\eta }}^{ - }}[\mu ] \geqslant {{\bar {\theta }}^{ + }}[\mu ]$ и $\bar {\Phi }({{p}^{ \pm }},{{q}^{ \pm }}) \in [{{\bar {\theta }}^{ + }}[\mu ]{\kern 1pt} {\kern 1pt} \mu ,{{\bar {\eta }}^{ - }}[\mu ]{\kern 1pt} {\kern 1pt} \mu ]$, но достаточно представительных условий, определяющих исход $({{p}^{ \pm }},{{q}^{ \pm }})$, авторы не нашли.
Конкретизируем параметры ОЛС. Пусть $\nu = \mu = {{\bar {\mu }}^{0}}$, где по аналогии с (2.4)
В итоге, если МК-игра Γ0 не сводится к набору отдельных скалярных игр, то ее переговорное множество оценок не пусто. Но при этом проблема существования смешанных стратегий, реализующих оценки из N+, выходит на первый план. Чтобы сразу остаться в терминах значений, а не оценок, можно вместо (4.1) определить:
Последнее множество должно быть наименее широким в силу (3.9). Вопросы о непустоте различных вариантов множеств переговорных оценок и значений МК-игры, а также о соотношении между данными вариантами и об их параметризации в условиях непустоты являются предметом дальнейших исследований. Здесь лишь подробно разберем иллюстративный пример и покажем, что поставленные вопросы допускают нетривиальный ответ.
Рассмотрим модельную МК-игру Студента (С) и Преподавателя (П) из [19, 20] с Φ(x, y) = = $(y\sqrt x {\text{/}}2,\sqrt {1 - x} {\text{/}}y)$ на конечных множествах $X = \{ 0;1\} $, $Y = \{ 1;2\} $ для ее модифицированного МК-смешанного расширения, согласно описанному выше.В матричной форме конечная игра С и П имеет вид
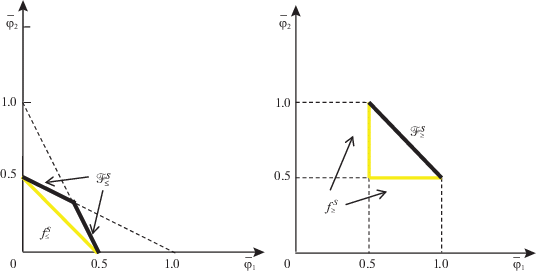
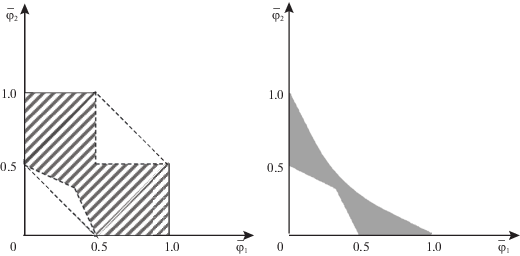
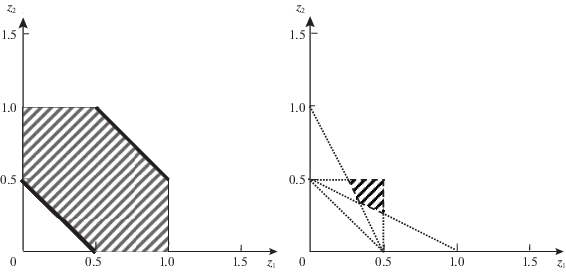
и в [10] для ее МК-смешанного расширения найдены явные решения как для случая стандартного использования игроками линейной скаляризации, так и для игры в ОЛС. Там же для множества равновесных исходов $(p{\kern 1pt} *,q{\kern 1pt} *)[\mu ,\nu ] \in \bar {R}_{G}^{*}$ игры $\bar {\Gamma }_{G}^{0}$ в ОЛС даны МК-средние выигрыш и проигрыш игроков С (максимизирующего – игрок 1) и П (минимизирующего – игрок 2) в критериальном пространстве показанные на рис. 1 слева и справа соответственно (с коррекцией относительно [10] на удаление нулей и срезку с C = 1). Их границы (выделены жирным на рис. 1) – множества N1 и N2, т.е. МК-средние НГР обоих игроков, имеющие смысл односторонних значений игры для каждого игрока, демонстрируют строгое включение в (1.3) для введенного МК-смешанного расширения (расчеты см. в Приложении).На основе отмеченных границ на рис. 2 слева построено множество N компромиссных оценок. Множество переговорных оценок (4.1) получается из него снятием непараллельных осям границ, следовательно, замыкание N+ в ${{\mathbb{R}}^{n}}$ равно N. И аналогично множество ${{\bar {Z}}^{ + }}$ для игры С и П (4.3) совпало с равновесным значением ${{\bar {Z}}^{0}}$ без двух точек на осях, т.е. не дало его сужения. Более интересным оказалось множество, представленное на рис. 2 справа, когда из N убрали оценки, которые не лучше для игроков, чем их МК-средние равновесные в ОЛС значения (4.4) с рис. 1, т.е.
(4.5)
$N{\kern 1pt} *\;\mathop = \limits^{{\text{def}}} \;N{\backslash }\{ \mathop {{\text{eph}}}\nolimits_ \leqslant (\bar {Z}_{1}^{*}) \cup \mathop {{\text{eph}}}\nolimits_ \geqslant (\bar {Z}_{2}^{*})\} .$Поскольку конкретные параметры свертки у ЛПР априори не известны, полученное множество (4.5) можно отнести к сильно переговорным оценкам, доминирующим над НГР и недоминируемым никакими равновесными в ОЛС МК-средними значениями. Однако реализации соответствующих оценок, если и существуют, то не являются равновесными исходами скалярных игр в ОЛС ни при каких коэффициентах свертки.
Для того чтобы приблизиться к сильно переговорным оценкам, оставаясь на позициях равновесных исходов, рассмотрим границу $\partial N{\text{*}}$ множества (4.5). Она соответствует идее переговорного множества как объединения наиболее предпочтительных равновесных векторов выигрышей с позиций каждого игрока. Понятно, что полученная граница представляет равновесия (т.е. решения игр $\bar {\Gamma }[\mu ,\nu ] \in \bar {\Gamma }_{G}^{0}$ для С и П) не при всех μ, ν. Например, вошедшая в $\partial N{\text{*}}$ часть множества $\bar {Z}_{1}^{*}$ для игры (4.3) относится к $(p{\kern 1pt} *,q{\kern 1pt} *)[\mu ,\nu ]$ с ${{\mu }_{1}} \in [1{\text{/}}3,2{\text{/}}3]$. Но так как свои коэффициенты свертки знают лишь ЛПР, то данная граница служит не столько для обоснования, сколько для поддержки принятия решений. В общетеоретическом плане непустота (4.5) в игре Γ0 любопытна сама по себе. Видно, что идея сильно переговорных оценок приводит к вполне содержательным значениям МК-игры с нулевой суммой и заслуживает более подробного изучения. (Вопрос о влиянии априорного уменьшения в МК-игре множества коэффициентов ОЛС у ЛПР при наличии дополнительной информации исследовался в [22].)
Аналогичное множество переговорных оценок в принципе можно построить и на базе классического решения Шепли ${{\bar {R}}^{0}}$ (3.8) и соответствующего значения ${{\bar {Z}}^{0}}$. А именно определим для конечной МК-игры, в частности (4.3), стандартное смешанное расширение $\bar {\Gamma }_{S}^{0}$. Найдем для него НГР по формулам из разд. 1, 2 (при замене частных критериев их средними). Полученные множества пометим верхним индексом S. Для игры (4.3) они приведены на рис. 3. В силу того, что в данной игре $\bar {\Gamma }_{S}^{0}$ нет односторонних решений (в отличие от изучаемой МК-игры $\bar {\Gamma }_{G}^{0}$), значения НГР разные: нижние оценки на рис. 3 светлее. Следовательно, множества компромиссных оценок тоже различаются. В игре $\bar {\Gamma }_{{12}}^{S}$ это промежуток между светлыми линиями на рис. 3, а в игре $\bar {\Gamma }_{{21}}^{S}$ – между темными. Самый широкий вариант ${{N}^{S}}\;\mathop = \limits^{{\text{def}}} \;\mathop {{\text{eph}}}\nolimits_ \geqslant (f_{ \leqslant }^{S}) \cap \mathop {{\text{eph}}}\nolimits_ \leqslant (\mathcal{F}_{ \geqslant }^{S})$ совпадает с N (но в игре $\bar {\Gamma }_{S}^{0}$ такое множество оценок не является компромиссным в отличие от игры $\bar {\Gamma }_{G}^{0}$). Для $\bar {\Gamma }_{S}^{0}$ в нормальной форме множество компромиссных оценок ${{N}^{0}}\;\mathop = \limits^{{\text{def}}} \;\mathop {{\text{eph}}}\nolimits_ \geqslant (\mathcal{F}_{ \leqslant }^{S}) \cap \mathop {{\text{eph}}}\nolimits_ \leqslant (f_{ \geqslant }^{S})$ существенно меньше (левый график на рис. 4). Подобное сужение ожидаемо, поскольку на основании утверждения 6 можем выписать равенства ${{N}_{1}} = f_{ \leqslant }^{S}$ и ${{N}_{2}} = \mathcal{F}_{ \geqslant }^{S}$. Так что, когда в игре нет односторонних решений, компромиссные оценки лежат между более жестких границ, задаваемых НГР информированных обоих игроков. Напомним, что между указанных границ находятся и все равновесные оценки (см. (1.3) для игры $\mathop {\bar {\Gamma }}\nolimits_S^0 $, а также найденные выше соотношения для $\bar {\Phi }({{p}^{0}},{{q}^{0}})$ с помощью параметризации НГР через ${{\bar {\mu }}^{0}}$).
Теперь попробуем воспользоваться равновесным значением ${{\bar {Z}}^{0}}$ (оно в случае линейной скаляризации одинаково для обоих игроков), чтобы ввести множества сильно переговорных оценок в МК-игре $\bar {\Gamma }_{S}^{0}$ по аналогии с $\bar {\Gamma }_{G}^{0}$. Вместо (4.5) придем к $N{\backslash }\left\{ {\mathop {{\text{eph}}}\nolimits_ \leqslant (\mathop {\bar {Z}}\nolimits^0 ) \cup \mathop {{\text{eph}}}\nolimits_ \geqslant (\mathop {\bar {Z}}\nolimits^0 )} \right\} = \emptyset $. Если убрать из формулы оболочку Эджворта–Парето, то останутся оценки, худшие равновесных для кого-либо из ЛПР, т.е. тоже не подходящие в качестве переговорных. Поэтому равновесие ${{\bar {Z}}^{0}}$ для $\bar {\Gamma }_{S}^{0}$ правильно считать переговорным множеством само по себе. Для примера (4.3) множество ${{\bar {Z}}^{0}}$ построено в [10], но для наглядности приведем его на рис. 4 справа. Сопоставляя оба графика с рис. 4, видим, что ${{\bar {Z}}^{0}}$ включается в множество N0 компромиссных оценок и что его верхняя граница предпочтительнее для обоих игроков, чем их НГР. Тем не менее, по мнению авторов, правый график на рис. 2 лучше согласуется с понятием переговорных оценок (еще один довод в пользу скаляризации с помощью ОЛС).
Добавим, что для (4.3) справедливы равенства ${{\bar {R}}^{0}} = \bar {R}_{G}^{*}$ [10] и ${{\bar {Z}}^{0}} = \bar {Z}_{G}^{*} = \bar {Z}_{G}^{0}$, где
В общем случае все точки из $\mathop {\bar {Z}}\nolimits_G^ * $ расположены покоординатно между векторами из $\bar {Z}_{1}^{*}$ и $\bar {Z}_{2}^{*}$, построенными для тех же параметров μ и ν, которым отвечают точки. В разд. 3 доказали включение $\bar {R}_{G}^{*}$ в объединение $\bar {K}(\mu ,\nu )$ по $\mu ,\nu \in M$, а для игры С и П (4.3) получается их равенство и все варианты равновесных и компромиссных исходов дают одно и то же множество $P \times Q$. (Различие значений на рис. 1 и рис. 4 справа обусловлено различием функций ${{\bar {G}}_{1}}$, ${{\bar {G}}_{2}}$ и $\bar {\Phi }$ на этом множестве.)
Замечание 3. В свете сравнения значений МК-игры, получаемых на базе ОЛС, со значением ${{\bar {Z}}^{0}}$, построенным для решения Шепли (при линейной скаляризации), укажем, что для примера (4.3) последнее множество не является многоугольником (несмотря на линейность всех частных критериев при стандартном смешанном расширении конечной МК-игры). Такое свойство для ряда других примеров отмечено в [23]. В случае применения ОЛС и модифицированного МК-смешанного расширения удалось остаться для игры (4.3) в рамках кусочно-линейных ограничений (см. рис. 1, 2).
Заключение. Выяснили, что (из-за наличия субъективной неопределенности) МК-игры с нулевой суммой, в которых многокритериальность существенна, допускают компромисс. Предложены варианты достижения компромисса для ЛПР, руководствующихся ОЛС при скаляризации. Разобран случай применения смешанных стратегий в конечной МК-игре с нулевой суммой, где оба игрока-ЛПР рассчитывают на ОЛС. Для такого случая модифицировано стандартное определение смешанного расширения (напрямую распространявшего на МК-задачи формализацию из скалярных задач). Оказалось, что при этом результаты от использования игроками линейной свертки или ОЛС расходятся. Тем не менее, сохраняется главное свойство МК-игры с нулевой суммой – существование решения.
Обосновано, что игрокам-ЛПР, ориентирующимся на ОЛС или логическую скаляризацию, важно придерживаться и модифицированного подхода к смешанному расширению МК-игры. Показано, что такой (введенный нами в [3] и [10]) способ осреднения МК-выигрыша при наличии смешанных стратегий, являясь содержательно обусловленным, дает еще и удобный математический аппарат для описания множества компромиссных решений в МК-игре с нулевой суммой двух ЛПР, выбирающих ОЛС при скаляризации векторного критерия. Кроме того, выдвинута идея сужения множества компромиссных средних оценок до переговорных (сильно переговорных) путем исключения НГР (равновесных значений). Результаты ее применения продемонстрированы на модельном примере. В дальнейшем для МК-игр планируется развить указанную идею и проанализировать непустоту множеств переговорных и сильно переговорных оценок, а также сравнить их с множествами компромиссных оценок и равновесных значений, в том числе для содержательных примеров. И еще интересно сопоставить классификацию исходов антагонистических игр с произвольным отношением порядка, предложенную в [24], и разбиение множества N, полученное для игры С и П (см. рис. 1–4).
Рис. 1.
МК-средние значения НГР (жирным) и оценки (4.4) выигрыша игрока 1 (слева) и проигрыша игрока 2 (справа) для ЛПР, применяющих ОЛС, в модельной игре С и П [10]
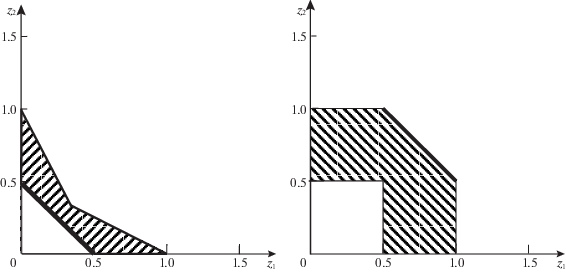
Рис. 2.
Отличие компромиссных средних оценок N (слева) от сильно переговорных N* (справа) для игры С и П в ОЛС
Список литературы
Лотов А.В., Бушенков В.А., Каменев Г.К., Черных О.Л. Компьютер и поиск компромисса. Метод достижимых целей. М.: Наука, 1997.
Крейнес Е.М., Новикова Н.М., Поспелова И.И. Многокритериальные игры двух лиц с противоположными интересами // ЖВМ и МФ. 2002. Т. 42. № 10. С. 1487–1502.
Крейнес Е.М., Новикова Н.М., Поспелова И.И. Многокритериальные игры с противоположными интересами как модели исследования операций // ЖВМ и МФ. 2020. Т. 60. № 9.
Jentzsch G. Some Thoughts on the Theory of Cooperative Games // Advances in Game Theory. Ann. Math. Studies. 1964. V. 52. P. 407–442.
Подиновский В.В., Ногин В.Д. Парето-оптимальные решения многокритериальных задач. М.: Наука, 1982.
Поспелова И.И. Классификация задач векторной оптимизации с неопределенными факторами // ЖВМ и МФ. 2000. Т. 40. № 6. С. 860–876.
Гермейер Ю.Б. Введение в теорию исследования операций. М.: Наука, 1971.
Novikova N.M., Pospelova I.I. Multicriterial Decision Making Under Uncertainty // Math. Prog. 2002. Ser. B 92. P. 537–554.
Смирнов М.М. О логической свертке вектора критериев в задаче аппроксимации множества Парето // ЖВМ и МФ. 1996. Т. 36. № 3. С. 62–74.
Новикова Н.М., Поспелова И.И. Смешанные стратегии в векторной оптимизации и свертка Гермейера // Изв. РАН. ТиСУ. 2019. № 4. С. 106–120.
Blackwell D. An Analog of the Minimax Theorem for Vector Payoffs // Pac. J. Math. 1956. V. 6. P. 1–8.
Shapley L.S. Equilibrium Points in Games with Vector Payoffs // Naval Research Logistics Quaterly. 1959. V. 6. № 1. P. 57–61.
Voorneveld M., Vermeulen D., Borm P. Axiomatizations of Pareto Equilibria in Multicriteria Games // Games and Economic Behavior. 1999. V. 28. P. 146–154.
Гермейер Ю.Б. Игры с непротивоположными интересами. М.: Наука, 1976.
Мулен Э. Теория игр с примерами из математической экономики. М.: Мир, 1985.
Морозов В.В. Смешанные стратегии в игре с векторными выигрышами // Вестн. МГУ. Сер. 15. Вычислительная математика и кибернетика. 1978. № 4. С. 44–49.
Nash J.F. Non Cooperative Games // Annals of Math. T. 2. 1951. V. 54. № 2. P. 286–295.
Розен В.В. Смешанные расширения игр с упорядоченными исходами // ЖВМ и МФ. 2076. Т. 16. № 6. С. 1436–1450.
Зенюков А.И., Новикова Н.М., Поспелова И.И. Метод сверток в многокритериальных задачах с неопределенностью // Изв. РАН. ТиСУ. 2017. № 5. С. 27–45.
Новикова Н.М., Поспелова И.И. Метод сверток в многокритериальных играх // ЖВМ и МФ. 2018. Т. 58. № 2. С. 192–201.
Поспелова И.И., Кононов С.В., Некрасова М.Г. Результаты применения различающихся сверток в многокритериальной игре с нулевой суммой // Тез. докл. научн. конф. “Ломоносовские чтения”, 15–25 апреля 2019 г. М.: МАКС-пресс, 2019. С. 94–95.
Zapata A., Mármol A.M., Monroy L., Caraballo M.A. A Maxmin Approach for the Equillibria of Vector-Valued Games // Group Decision and Negotiation. 2019. V. 82. P. 415–432.
Borm P., Vermeulen D., Voorneveld M. The Structure of the Set of Equilibria for Two Person Multicriteria Games // European J. Operational Research. 2003. V. 148 (3). P. 480–493.
Rozen V.V. Acceptable Points in Antagonistic Games with Ordered Outcomes // Contributions to Game Theory and Management. 2019. V. 12. P. 282–294.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления