Известия РАН. Теория и системы управления, 2021, № 2, стр. 47-61
ПОСТРОЕНИЕ ГРАФОВ ПРОСТЫХ ПУТЕЙ В ТРАНСПОРТНЫХ СЕТЯХ. II. АНАЛИЗ ДВУСВЯЗНОСТИ ГРАФОВ
И. А. Головинский *
Северо-Кавказский федеральный ун-т
Ставрополь, Россия
* E-mail: igolovinskij@gmail.com
Поступила в редакцию 14.08.2019
После доработки 03.07.2020
Принята к публикации 30.11.2020
Аннотация
Задача построения всех простых путей в неориентированном графе, соединяющих попарно вершины из заданного множества, интерпретируется как построение графа, который является объединением этих путей. Данное построение опирается на вычисление компонент двусвязности и мостов исходного графа. Предлагается новый алгоритм, делающий это вычисление более прозрачным и контролируемым. Его идея – отслеживать “открытие” и “закрытие” хорд при обходе графа в глубину. Благодаря наглядности предлагаемого решения его правильность ясна без особого обоснования. В этом его преимущество перед известным алгоритмом Хопкрофта–Тарьяна. Предложенный алгоритм делает наглядным получение компонент двусвязности графа в результате последовательного объединения его фундаментальных циклов, имеющих общие ребра.
Введение. В работе [1] описаны общие решения задач соединения простыми путями вершин, принадлежащих непересекающимся подмножествам множества вершин неориентированного графа. Показано, что эти общие решения строятся на основе вычисления блоков и шарниров графа. Для решения последней задачи известен алгоритм, опубликованный Р.Э. Тарьяном и Дж.Э. Хопкрофтом в 1971–1973 гг. [2–4]. Этот алгоритм излагается практически во всех руководствах, где рассматриваются вопросы анализа двусвязности графов [5–13]. По числу операций он имеет порядок сложности O(n + m), где n – число вершин графа, m – число его ребер. Поскольку при вычислении блоков необходимо обработать каждую вершину и каждое ребро графа хотя бы по одному разу, улучшить данную оценку невозможно в принципе.
Это, однако, не означает, что алгоритм Хопкрофта–Тарьяна нельзя улучшить в другом отношении. Определенный недостаток его состоит в том, что его идея заслонена от пользователя техническими приемами, смысл которых не всегда очевиден. В руководствах, где этот алгоритм излагается, его обычно сопровождают нетривиальным доказательством. Непосредственно из самого́ алгоритма усмотреть его правильность непросто.
В современных разработках сложных систем управления возрастает роль таких свойств алгоритмов, как логическая простота, содержательная ясность. От них зависят трудозатраты на отладку и развитие программ. Путь к сокращению таких затрат лежит через упрощение и прояснение смысла применяемых вычислительных методов. В статье излагается новый метод вычисления блоков и шарниров неориентированных графов, смысл и правильность которого видны просто из его описания. Этим он отличается от алгоритма Хопкрофта–Тарьяна, имея тот же порядок вычислительной сложности O(n + m).
1. Постановка задачи. Рассматриваются неориентированные графы, не содержащие петель и кратных ребер. Собственным шарниром такого графа называется вершина, при удалении которой число компонент связности графа увеличивается. Максимальный связный подграф неориентированного графа, не имеющий собственных шарниров, называется блоком графа [13, с. 58; 14, с. 136]11. Если блок содержит ровно одно ребро, то он называется мостом графа; в противном случае – компонентой двусвязности графа. Вычисление блоков и шарниров графа будем называть анализом его двусвязности.
Пусть в неориентированном графе G выбран какой-то остовный лес и относительно него построена фундаментальная система циклов F(G) [6, с. 98; 13, с. 68]. Циклы, принадлежащие системе F(G), будем для краткости называть ее F-циклами. На множестве F-циклов системы F(G) определим бинарное отношение смежности. Будем говорить, что два F-цикла системы F(G) смежны, если они имеют общее ребро. Очевидно, отношение смежности F-циклов рефлексивно и симметрично. Поэтому его транзитивное замыкание является отношением эквивалентности. Последнее разбивает множество F-циклов системы F(G) на классы эквивалентности. Класс эквивалентных F-циклов совпадает с множеством F-циклов, содержащихся в некоторой компоненте двусвязности графа G. Каждая компонента двусвязности совпадает с объединением всех содержащихся в ней F-циклов (см. [15, с. 126]).
Объединение двух двусвязных графов, имеющих общее ребро, есть двусвязный граф [14, с. 137]. Вычислять компоненту двусвязности графа можно, последовательно объединяя содержащиеся в ней F-циклы через общие ребра. На этом основан метод вычисления блоков графа, предложенный в [15, 16], – метод присоединения фундаментальных циклов. Он устанавливает сводимость анализа двусвязности графа G к анализу простой связности другого графа – биграфа принадлежности ребер графа G фундаментальным циклам22. Этот биграф будет определен в разд. 7.
Остовный лес неориентированного графа строится обходом графа – в ширину, в глубину или как-либо иначе. В общем случае метод присоединения фундаментальных циклов допускает любой порядок обхода графа при построении остовного леса. Известно, что удобным образом строить фундаментальную систему циклов позволяет обход графа в глубину [13, с. 69]. Ниже будет показано, что построение F-циклов обходом графа в глубину можно совместить с процессом их объединения в компоненты двусвязности. Предлагаемый в статье алгоритм основан на этом совмещении.
В алгоритме обхода графа в глубину вершинам присваиваются и проверяются такие признаки их состояния, как “новая”, “открытая” и “закрытая”. В предлагаемом алгоритме контролируются, кроме того, признаки “открытой” и “закрытой” хорды. Поэтому новый алгоритм назван алгоритмом контроля открытых хорд; сокращенно – алгоритмом OCC (open chord control). Алгоритм Хопкрофта–Тарьяна будем для краткости именовать алгоритмом HT.
Алгоритм обхода графа в глубину будем обозначать принятой в литературе аббревиатурой DFS (depth first search). Алгоритмы OCC и HT получаются из алгоритма DFS добавлением к последнему специальных операций обработки вершин и ребер.
2. Свойства разметки графа в глубину. Если исходный анализируемый граф содержит более одной компоненты простой связности, то анализ его двусвязности производится в пределах каждой такой компоненты независимо от остальных компонент простой связности. Поэтому далее исходный анализируемый граф предполагается связным.
Пусть G = (V, E) – связный неориентированный граф, V – множество его вершин, E – множество ребер, T – неориентированное остовное дерево графа G. Ребра дерева T будем называть ветвями. Ребро графа G, не являющееся ветвью остова T, называется хордой в графе G относительно этого остова.
Любую вершину неориентированного дерева можно принять в качестве его корня. Дерево с выделенной вершиной называется корневым. Выделим какую-нибудь вершину в остовном дереве T, обозначив ее ρ. Полученное корневое дерево обозначим T(ρ).
На каждой ветви корневого дерева T(ρ) зададим ориентацию в сторону от корня ρ. Полученное ордерево будет выходящим из вершины ρ. Обозначим его T '(ρ). Построение этого ордерева и его хорд будем называть разметкой графа G, корень ρ остовного ордерева – корнем этой разметки. Если (σ,τ) – ориентированная ветвь ордерева T '(ρ), то вершину σ будем называть ее началом, вершину τ – концом33.
Множество вершин дерева T совпадает с множеством V вершин графа G. Ориентация ветвей ордерева T '(ρ) индуцирует отношение частичного порядка на этом множестве. Пусть вершина σ ∈ V предшествует вершине τ ∈ V в смысле указанного частичного порядка. Будем записывать это как σ < τ. В этом случае вершина σ называется предком вершины τ, вершина τ – потомком вершины σ. Считаем, что вершина не может быть ни предком самой себя, ни потомком. Заметим, что идентификаторами вершин графа могут быть, например, номера, присвоенные в произвольном порядке, однако тогда соотношение σ < τ не будет означать, что номер вершины σ меньше номера вершины τ.
Предок σ вершины τ называется родительской вершиной для τ, если в графе G нет такой вершины π, для которой выполнялись бы одновременно соотношения σ < π и π < τ. Иначе говоря, когда нет вершин между σ и τ. В этом случае вершина τ называется дочерней для σ.
Если остовное ордерево T '(ρ) построено обходом графа в глубину (алгоритмом DFS), то разметку графа G будем называть разметкой в глубину графа G посредством ордерева T '(ρ).
Хорда называется продольной, если ее концы сравнимы в смысле отношения частичного порядка, индуцированного на множестве вершин графа ориентацией остовного ордерева T '(ρ). При разметке графа в глубину все хорды продольны [13, с. 53]. Это позволяет ввести на них ориентацию. Если σ < τ, то считают, что хорда (τ, σ) направлена от τ к σ, т.е. обратно отношению частичного порядка на множестве вершин графа, индуцированного ориентацией остовного ордерева T '(ρ). Вершину τ будем называть началом этой хорды, вершину σ – ее концом. Будем говорить, что в вершине τ эта хорда открывается, в σ – закрывается.
Отметим некоторые свойства блоков и разметки, существенные для понимания анализа двусвязности на основе обхода графа в глубину. В руководствах по графам они освещены неполно [6, с. 102; 7, с. 164; 8, с. 463; 13, с. 56–64].
1. Пусть T – остовное дерево связного графа G, построенное каким-либо обходом графа G (не обязательно в глубину); B – блок графа G. Пересечение T ∩ B будет остовным деревом блока B. На каждой ветви дерева T ∩ B определена ориентация, которую данная ветвь имеет в ордереве T '(ρ). Дерево T ∩ B с этой ориентацией обозначим $T_{B}^{'}$. В этом ордереве имеется ровно одна вершина, относительно которой оно будет выходящим. Эту вершину будем называть начальной вершиной блока B (относительно произведенной разметки графа G).
2. Корень какой-либо разметки связного графа G (не обязательно в глубину) является начальной вершиной каждого блока, которому он принадлежит. Корень разметки принадлежит ровно одному блоку графа G (будучи начальной вершиной этого блока) тогда и только тогда, когда он не является шарниром графа G. Такой блок будем называть начальным блоком графа G (относительно произведенной разметки). Если корень разметки принадлежит двум или более блокам графа G (являясь шарниром графа G), то считаем, что этот граф не имеет начального блока.
3. Если остовное ордерево T '(ρ) строится обходом графа G в глубину, то при этом будет происходить обход в глубину блока B, в результате чего получится остовное ордерево $T_{B}^{'}$. При разметке графа G в глубину блок B будет содержать ровно одну ветвь ордерева $T_{B}^{'}$, выходящую из начальной вершины блока B. Эту ветвь будем называть начальной ветвью блока B.
4. Свойство вершины графа быть шарниром будем называть также свойством ее шарнирности. Распознавание шарнирности корня ρ разметки связного графа G в глубину производится непосредственно алгоритмом DFS, не требуя дополнительных специальных операций, выполняемых алгоритмами HT или OCC. Критерий шарнирности корня при разметке в глубину: корень ρ является шарниром графа G тогда и только тогда, когда из него выходят не менее двух ветвей остовного ордерева T '(ρ). Каждая такая ветвь будет начальной ветвью одного из блоков, содержащих корень ρ. В этом случае граф G не содержит начального блока. Если же из корня разметки в глубину выходит ровно одна ветвь остовного ордерева, то этот корень шарниром не будет. Блок, содержащий эту ветвь, будет начальным блоком графа G.
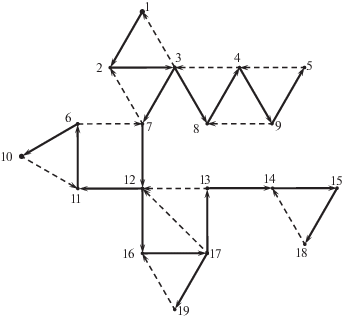
3. Демонстрационный пример и структура исходных данных. Операции алгоритма OCC, включая также операции алгоритма DFS, будем иллюстрировать на примере связного графа H, изображенного на рис. 1. Вершины этого графа перенумерованы целыми числами от 1 до 19. Из чертежа видно, что шарнирами графа H являются вершины 3, 7, 12, 13 и 14.
Сложность алгоритма зависит в том числе от способа представления его исходных данных. Этот способ стремятся выбрать так, чтобы сложность алгоритма минимизировать. Для поиска в глубину граф обычно представляют множеством списков смежности вершин. Это позволяет минимизировать сложность алгоритма по числу операций [6, с. 87; 17, с. 84–85]. Для алгоритмов OCC и HT достаточно задать для каждой вершины графа массив смежных с ней вершин.
Для каждой вершины графа в алгоритме предусматривается переменный указатель на позицию текущего обрабатываемого элемента в ее списке смежности. Эти указатели нужны для того, чтобы при повторных посещениях вершины алгоритму было известно, на каком элементе ее списка смежности он остановился при предыдущем посещении этой вершины.
4. Порядок обхода графа в глубину. Обработку графа алгоритмом DFS опишем несколько подробнее, чем обычно делается в литературе, поясняя особенности, важные для алгоритма OCC.
Обход графа начинается с произвольно выбранной вершины – корня разметки. В демонстрационном примере, представленном на рис. 1 графом H, в качестве начала разметки ρ выберем вершину 1. Остовное ордерево T '(1), получаемое в результате описываемой далее разметки графа в глубину, показано на рис. 2. Ветви этого ордерева изображены сплошными линиями, хорды – штриховыми. Стрелки указывают направления ветвей и хорд. Корень разметки 1 не является шарниром графа H. Поэтому в графе H имеется начальный блок, содержащий корень разметки. Его вершинами являются 1–3 и 7.
В каждую вершину графа, кроме корня разметки, входит ровно одна ветвь остова. Каждую ветвь обозначаем номером вершины, в которую входит эта ветвь. На рис. 2 указаны номера всех вершин и подразумевается, что ветвь, входящая в вершину, имеет номер этой вершины. При необходимости ветвь будем обозначать также упорядоченной парой ее начальной и конечной вершин. Каждая хорда будет обозначаться тоже упорядоченной парой ее начальной и конечной вершин.
Когда алгоритм обработки графа проходит по вершинам графа, говорят, что он посещает вершины. Вершина может посещаться более одного раза. До начала обхода графа алгоритмом (DFS, OCC или HT) каждая вершина графа находится в состоянии “новая” (непосещенная). В момент начала обработки вершины при первом ее посещении алгоритмом данная вершина переходит в состояние “открытая”. Считается, что в этом состоянии она остается до момента, когда заканчивается ее обработка при последнем ее посещении алгоритмом. Открытая вершина считается “активной”, пока алгоритм выполняет при ее посещении относящиеся к ней операции. Когда алгоритм переходит от одной вершины к другой, первая перестает быть активной, но остается открытой, если ее обработка не закончена (не пройден до конца список смежных с ней вершин). Открытую неактивную вершину будем называть “отложенной”. Когда обработка вершины полностью завершается, данная вершина переходит в состояние “закрытая”. К этому моменту будет завершена обработка всех потомков данной вершины. Признаки текущего состояния вершины в течение работы алгоритма запоминаются в переменных, привязанных к идентификатору вершины.
Для управления обходом графа в глубину используется стек. Его можно представить как столбец идентификаторов вершин графа, которые добавляются сверху и сверху же удаляются из стека. Будем говорить также о “вершинах в стеке”, подразумевая идентификаторы вершин. В стеке находятся все открытые вершины и только они. В самой верхней позиции стека находится активная вершина, ниже – отложенные. При переходе вершины из новой в открытую она добавляется в стек сверху. Когда обработка вершины полностью заканчивается, она из стека удаляется, переходя в состояние “закрытая”.
Потомки вершины σ помещаются в стек после вершины σ и удаляются из стека раньше нее. Они находятся в стеке выше вершины σ. Обработка всех потомков вершины σ выполняется в промежутке между помещением вершины σ в стек и ее удалением из стека, т.е. между началом и окончанием обработки вершины σ. Это является характерной особенностью обхода графа в глубину [8, с. 446–452].
Алгоритм начинает обработку графа с первого из списков смежности вершин. В каждом списке смежности алгоритм просматривает поочередно все вершины, проходя по этому списку слева направо. Когда в списке смежности для вершины σ обнаруживается вершина τ, находящаяся в состоянии “новая”, алгоритм DFS определяет ребро (σ, τ) как ветвь остова. Эта ветвь получает направление от σ к τ и добавляется к построенной части ориентированного остова T '(ρ). Атрибуту вершины τ, который называется “номер родительской вершины”, присваивается номер вершины σ. Вершина τ становится открытой и активной и добавляется в стек. Алгоритм приостанавливает проход по списку смежности вершины σ: ее признак “активная” он заменяет на “отложенная” и переходит к обработке вершины τ, делая ее активной. Алгоритм выполняет теперь поиск новой вершины среди вершин, смежных уже с вершиной τ, двигаясь по ее списку смежности.
К обработке отложенной вершины σ алгоритм возвращается после того, как закончит обработку всех вершин, попавших в стек после σ. После первого посещения вершины σ, когда она стала открытой, алгоритм столько раз возвратится в нее, сколько ветвей остова, выходящих из нее, он сможет проложить. Когда весь список смежности для вершины σ будет пройден и ее обработка будет закончена, алгоритм удалит ее из стека и переведет в состояние “закрытая”. Если вершина σ – корень разметки, то ее закрытием алгоритм закончит свою работу. В противном случае в верхней позиции стека окажется вершина π, родительская по отношению к σ. Пока обрабатывалась вершина σ и ее потомки, вершина π была отложенной, но теперь она снова становится активной. Алгоритм возобновляет ее обработку, продолжая проход по списку смежных с ней вершин.
Когда при прохождении по списку смежности алгоритм встречает в нем вершину τ, не являющуюся новой, эта вершина может быть либо открытой, либо закрытой. Первый случай имеет место тогда, когда τ есть предок вершины σ: τ < σ. Если при этом τ не является родительской вершиной для σ, то алгоритм DFS опознает ребро (σ, τ) как хорду и присваивает ей направление от σ к τ. Хорда (σ, τ) в этот момент открывается.
Во втором случае, т.е. если вершина τ оказывается закрытой, она будет потомком вершины σ: τ > σ. Ребро (τ, σ) к этому моменту уже будет опознано как хорда, направленная от τ к σ. В этот момент хорда (τ, σ) закрывается.
При просмотре списка вершин, смежных с σ, все они могут оказаться открытыми. Это будет означать, что они все являются предками вершины σ, а сама эта вершина – концевой44 в остовном дереве T.
Каждую ветвь (α, β) остова алгоритм (DFS, OCC или HT) проходит дважды. Сначала он проходит ее от начала α к концу β. Этот проход будем называть прямым ходом алгоритма, а также перемещением “вперед” или “в глубину”. Обойдя всех потомков вершины β и возвратившись в β, алгоритм затем проходит ветвь (α, β) в обратном направлении – от ее конца β к началу α. Будем говорить, что тогда алгоритм проходит ветвь “назад” или “из глубины”.
5. Принцип контроля открытых хорд. Идея алгоритма OCC состоит в том, чтобы при каждом возврате в отложенную вершину σ контролировать количество хорд, “обходящих” (в обратном направлении) ту выходящую из σ ветвь, со стороны которой алгоритм возвратился в σ. Определим понятия обхода хордой вершины и обхода (шунтирования) хордой ветви.
Будем говорить, что хорда (σ, τ), где σ > τ, обходит вершину α, если σ > α и α > τ. Иначе говоря, когда σ есть потомок вершины α, а τ – предок вершины α. Например, на рис. 2 видно, что вершину 17 обходят хорды (13, 12) и (19, 16).
Будем говорить, что хорда обходит или шунтирует ветвь (в направлении, обратном ориентации ветви), если она обходит хотя бы одну из двух вершин – начало этой ветви или ее конец. Например, хорда (13, 12) шунтирует ветвь 13, обходя начало этой ветви – вершину 17. Эта же хорда шунтирует ветвь 16 (обходя конец ветви – вершину 16) и ветвь 17 (обходя начало 16 и конец 17 ветви).
Для лучшей обозримости случаев обхода хордами вершин и ветвей в демонстрационном графе H его разметка, приведенная на рис. 2, показана на рис. 3 в “развернутом” виде. Ветви представлены сплошными прямыми стрелками, а хорды – штриховыми дугами. Эта же “развернутая” разметка дана также на рис. 4, но с раздельным изображением блоков. Здесь шарниры изображены маленькими незакрашенными окружностями. Разделенные “части” шарниров соединены точечными линями. На обоих рисунках ясно видны F-циклы: каждый F-цикл образован штриховой дугой (хордой) и цепочкой однонаправленных ветвей, начальную и конечную вершины которой эта дуга соединяет.
Рис. 3.
Более наглядное, чем на рис. 2, расположение разметки демонстрационного графа. Показаны значения счетчиков over(σ) и shunt(x)

Рис. 4.
Раздельное изображение блоков графа с разметкой, показанной на рис. 3. Указаны значения счетчиков over(σ), shunt(x) и pass(x)

Предположим, что при возвращении алгоритма в начало ветви (α, β) в графе G оказывается, что все хорды, шунтирующие эту ветвь, в начале α данной ветви закрываются. Если вершина α не является корнем разметки, то можно утверждать, что тогда она является шарниром. В самом деле, если вершину α удалить из графа G (вместе с инцидентными ей ребрами), то в полученном графе ни вершину β, ни какого-либо ее потомка нельзя будет соединить путем в графе G ни с каким предком вершины α. Число компонент связности графа G увеличится при удалении вершины α. Например, в демонстрационном графе ветвь (3, 8) шунтируется одной хордой (4, 3), и эта хорда закрывается в вершине 3. Поэтому вершина 3 есть шарнир.
И обратно, если вершина α – шарнир, то среди ее дочерних вершин имеется такая вершина β, что все хорды, шунтирующие ветвь (α, β), закрываются в вершине α. В самом деле, если такой дочерней вершины β нет, то удаление из графа G вершины α не увеличит число компонент связности графа. Чтобы число компонент связности увеличилось при удалении α, необходимо, чтобы хотя бы для одной ветви, выходящей из α, все хорды, шунтирующие эту ветвь, закрывались в α. Например, вершина 17, из которой выходят две ветви (17, 13) и (17, 19), шарниром не является, потому что первая ветвь шунтируется хордой (19, 16), вторая – хордой (13, 12), и ни та, ни другая хорда в вершине 17 не закрывается. На рис. 4 особенно ясно видно, что в каждом шарнире хотя бы у одной из выходящих из него ветвей закрываются все хорды, шунтирующие эту ветвь.
В предыдущих двух абзацах изложено основание принципа контроля открытых хорд, обеспечивающего распознавание шарниров неориентированных графов. Сформулируем этот принцип в виде теоремы.
Теорема 1. Пусть T '(ρ) – остовное ордерево с корнем ρ связного неориентированного графа G, построенное разметкой этого графа в глубину. Вершина α, отличная от ρ, является шарниром графа G в том и только том случае, когда существует такая ветвь (α, β), что все хорды графа G относительно ордерева T '(ρ), шунтирующие ветвь (α, β), закрываются в вершине α. В этом случае α есть шарнир блока, начальной ветвью которого является (α, β).
Если удалить из этой формулировки последнюю фразу, то оставшаяся часть будет эквивалентна утверждению, которое в иных терминах дано с доказательством в [13, с. 56–57, теорема 2]55.
Для иллюстрации выявления блоков посредством контроля открытых хорд пройдем, например, в графе H от концевой вершины 5 остовного ордерева против направления ветвей. В вершине 5 открывается хорда (5, 4). Она в обратном направлении шунтирует ветви (9, 5) и (4, 9) и закрывается в вершине 4. Но вершина 4 не будет шарниром, потому что ее обходит хорда (9, 8). Эта хорда шунтирует ветви (4, 9) и (8, 4). При дальнейшем движении против направления ветвей первой вершиной, где все хорды, шунтирующие проходимые ветви, окажутся закрытыми, будет вершина 3. Она будет шарниром. Это наиболее наглядно отображено на рис. 4.
Также можно проследить, что при движении против направления ветвей от концевой вершины 18 остова первой вершиной, где все шунтирующие хорды окажутся закрытыми, будет вершина 14. Далее при продолжении обратного хода это свойство обнаруживается у вершины 13. Обе вершины – 13 и 14 – будут шарнирами. Двигаясь дальше обратным ходом, закрытие всех хорд обнаруживаем в вершине 12. При этом учитываем также хорду (19, 16), открывающуюся в концевой вершине 19. Другими словами, при подсчете числа хорд, закрываемых в начале какой-либо ветви (α, β) (в данном случае – ветви (12, 16)), должны быть просмотрены в обратном направлении все пути по ветвям от конца этой ветви β до всех концевых вершин остовного ордерева, являющихся потомками вершины β.
Двигаясь обратным ходом от концевой вершины 10, находим закрытие всех шунтирующих хорд к началу ветви (7, 12) – к вершине 7. Она тоже будет шарниром. Таким образом, посредством контроля открытых хорд мы распознали все шарниры демонстрационного графа H: 3, 7, 12, 13 и 14.
6. Счетчики хорд и их вычисление. Принцип контроля открытых хорд сам по себе достаточно нагляден, но его алгоритмическая реализация требует некоторых несложных технических приспособлений. Ими служат массивы счетчиков числа хорд, находящихся в том или ином отношении к вершинам и ветвям. Этих счетчиков пять типов; их назначение описано в табл. 1.
Таблица 1.
Счетчики хорд
| Аргумент счетчика | Обозначение счетчика | Назначение счетчика |
|---|---|---|
| σ – идентификатор вершины | open(σ) | Число хорд, открывающихся в вершине σ |
| σ – идентификатор вершины | over(σ) | Число хорд, обходящих вершину σ |
| x – идентификатор ветви | shunt(x) | Число хорд, обходящих (шунтирующих) ветвь x |
| x – идентификатор ветви | close(x) | Число хорд, обходящих ветвь x и закрывающихся в ее начале |
| x – идентификатор ветви | pass(x) | Число хорд, обходящих ветвь x и не закрывающихся в ее начале |
Аргументом счетчиков open(σ) и over(σ) является идентификатор обрабатываемой вершины, аргументом счетчиков close(x), shunt(x) и pass(x) – идентификатор обрабатываемой ветви. Множество ветвей остовного дерева взаимно-однозначно соответствует множеству всех вершин графа, за вычетом корня остова. Поэтому последние три счетчика формально тоже могут рассматриваться как функции вершины σ, которая является концом ветви x = (π, σ). При обработке графа в качестве удобного способа обозначения вершин можно использовать порядковые номера, присвоенные им в произвольной очередности. Далее предполагаем, что идентификаторами вершин служат эти порядковые номера.
В начале работы алгоритма значение каждого счетчика для каждой вершины или ветви равно нулю. При каждом посещении вершины алгоритм OCC обновляет значения всех счетчиков, аргументом которых служит данная вершина или входящая в нее ветвь. По номеру вершины алгоритм обращается к соответствующей строке таблицы значений счетчиков хорд (табл. 2). Он считывает значение счетчика из таблицы, прибавляет к нему (если нужно) некоторое приращение и записывает результат в таблицу на место старого значения.
Таблица 2.
Итоговые значения счетчиков хорд для демонстрационного графа
| Номер вершины – σ | open(σ) | close(x) | shunt(x) | pass(x) | over(σ) |
|---|---|---|---|---|---|
| x = (π, σ) | |||||
| 1 | 0 | − | − | − | 0 |
| 2 | 0 | 1 | 1 | 0 | 1 |
| 3 | 1 | 1 | 2 | 1 | 1 |
| 4 | 1 | 1 | 2 | 1 | 1 |
| 5 | 1 | 0 | 1 | 1 | 0 |
| 6 | 1 | 1 | 2 | 1 | 1 |
| 7 | 1 | 0 | 1 | 1 | 0 |
| 8 | 0 | 1 | 1 | 0 | 1 |
| 9 | 1 | 1 | 2 | 1 | 1 |
| 10 | 1 | 0 | 1 | 1 | 0 |
| 11 | 0 | 0 | 1 | 1 | 1 |
| 12 | 0 | 1 | 1 | 0 | 1 |
| 13 | 1 | 0 | 1 | 1 | 0 |
| 14 | 0 | 0 | 0 | 0 | 0 |
| 15 | 0 | 1 | 1 | 0 | 1 |
| 16 | 0 | 2 | 2 | 0 | 2 |
| 17 | 1 | 1 | 3 | 2 | 2 |
| 18 | 1 | 0 | 1 | 1 | 0 |
| 19 | 1 | 0 | 1 | 1 | 0 |
Таблица 2 – это обычная реляционная таблица. Для ясности она показана с некоторыми дополнительными частями, которые в памяти программы хранить не требуется. Это заголовки всех столбцов, а также весь первый столбец, содержащий номера вершин в порядке их возрастания. Эти номера являются порядковыми номерами строк таблицы. В табл. 2 даны итоговые значения счетчиков после окончания работы алгоритма.
Значение open(σ) есть количество хорд, открывающихся в вершине σ. Оно вычисляется алгоритмом OCC при проходе по списку вершин, смежных с σ. Когда в этом списке обнаруживается открытая вершина τ, не являющаяся родительской для σ, ребро (σ, τ) распознается как открывающаяся хорда. В этом случае алгоритм увеличивает счетчик open(σ) на единицу. Вычисление значения open(σ) заканчивается, когда вершина σ закрывается.
Значение close(x) равно числу хорд, закрывающихся в начале ветви x = (τ, π), где π является предком вершины σ. Оно увеличивается на единицу всякий раз, когда алгоритм обнаруживает вершину τ в списке смежности у какого-то из потомков σ вершины π. Спрашивается: как алгоритм узнает номер ветви x (совпадающий с номером вершины π) по номеру σ? Очень просто: по текущему значению указателя вершины в списке смежности для отложенной вершины τ. В момент обработки вершины σ этот указатель дает ту вершину, единственную из смежных с τ, которая является предком текущей активной вершины σ, т.е. вершину π.
Например, при просмотре вершин, смежных с вершиной 4, алгоритм обнаруживает, что смежная вершина 3 открыта. Поскольку она не является родительской для вершины 4, ребро (4, 3) распознается алгоритмом как хорда. Счетчик open (4) увеличивается на 1. В списке смежности для вершины 3 указатель в данный момент показывает на вершину π = 8, поскольку именно через нее алгоритм углубился от вершины 3 до вершины 4. Алгоритм увеличивает на 1 значение close (8): обнаружена хорда, закрывающаяся в начале ветви (3, 8). Обратим внимание, что в close (8) подсчитывается число хорд, которые закрываются не в вершине 8, а в ее родительской вершине 3, т.е. в начале единственной ветви (3, 8), входящей в вершину 8.
Значения счетчиков shunt(x), pass(x) и over(σ) алгоритм OCC вычисляет рекурсивно при возвращении алгоритма “из глубины”, начиная с концевых вершин остова графа. Счетчик shunt(x) выражает число хорд, шунтирующих ветвь x = (π, σ). Если σ есть концевая вершина остова T графа G, то ветвь x могут шунтировать только хорды, открывающиеся в σ. В этом случае
Например, вершина 5 является концевой. В этой концевой вершине открывается одна хорда – (5, 4), так что open(5) = 1. В вершину 5 входит ветвь под номером 5. Поэтому shunt(5) = 1.
Если же вершина σ не является концевой в остове T, но не является и его корнем, то
где x = (π, σ). К моменту вычисления по этой формуле величина over(σ) будет уже известна, а open(σ) определяется непосредственно в вершине σ. Если, например, в графе H σ = 17, то x = = (16, 17). Тогда over(17) = 2 и open(17) = 1, откуда shunt(17) = 3.В концевых вершинах остова хорды могут только открываться, но не могут в них закрываться или обходить их. Так что если вершина σ концевая, то over(σ) = 0. Поэтому формула (6.1) является частным случаем формулы (6.2).
Счетчик pass(x) выражает число всех хорд, шунтирующих (обходящих) ветвь x и не закрывающихся в ее начале. Он вычисляется по очевидной формуле
Например, ветвь 16 шунтируется хордами (13, 12) и (17, 12). Обе они закрываются в вершине 12, являющейся началом ветви 16. Поэтому shunt(16) = 2 и close(16) = 2, откуда pass(16) = 0. А ветвь 17 шунтируют три хорды: (13, 12), (17, 12) и (19, 16), но в начальной вершине 16 этой ветви закрывается только одна из них – хорда (19,1 6). Поэтому shunt(17) = 3 и close(17) = 1, откуда pass(17) = 2.
Подставляя в (6.3) выражение для shunt(x) из (6.2), получим
для любой ветви x = (π, σ).С помощью счетчика pass(x) сформулированный выше критерий шарнирности в алгоритме OCC (теорема 1) можно выразить следующим образом.
Теорема 1'. Пусть вершина α неориентированного графа G не является корнем его разметки в глубину; pass(x) – число всех хорд относительно этой разметки, шунтирующих ветвь x и не закрывающихся в ее начале. Вершина α будет шарниром графа G тогда и только тогда, когда pass(x) = 0 хотя бы для одной ветви x, выходящей из α. В этом случае ветвь x будет начальной ветвью блока, которому она принадлежит.
Например, в демонстрационном графе pass(16) = 0, и поэтому ветвь 16 будет начальной ветвью блока, а ее начальная вершина 12 – шарниром. А, например, вершина 16 шарниром не будет, так как для единственной выходящей из нее ветви 17 имеем pass(17) = 2.
Величина over(σ) есть число хорд, обходящих вершину σ. Если σ – корень разметки или концевая вершина остова, то over(σ) = 0; в противном случае over(σ) формируется в результате обработки всех вершин, дочерних к σ. Тогда из вершины σ может выходить более одной ветви остовного ордерева. Хорда, обходящая вершину, может открываться в любом из ее потомков. Для вычисления over(σ) требуется знать pass(xj) для каждой ветви x1, x2, …, выходящей из вершины σ:
Например, из вершины 17 выходят две ветви – 13 и 19. Со стороны ветви 13 вершину 17 обходит хорда (13, 12), а со стороны ветви 19 эту вершину обходит хорда (19, 16). Имеем соответственно pass(13) = 1 и pass(19) = 1. Отсюда
При первом посещении алгоритмом OCC вершины σ, из которой выходят ветви x1, x2, …, значение over(σ) равно 0. При каждом следующем посещении этой вершины к текущему значению over(σ) прибавляется очередное слагаемое из правой части формулы (6.5). Если при возврате алгоритма в вершину σ по ветви xj окажется pass(xj) = 0, то вершина σ будет шарниром, а ветвь xj – начальной ветвью блока. Счетчик over(σ) получает окончательное значение, когда список смежности для вершины σ пройден и ее обработка заканчивается.
Все арифметические операции алгоритма OCC выражаются формулами (6.4) и (6.5). Счетчик shunt(x) в них не входит: он является промежуточным и использован здесь для подробного объяснения алгоритма. Остальные операции в программе, реализующей алгоритм OCC, обеспечивают обход графа в глубину и определение состояния вершин.
Итоговые значения счетчиков shunt(x), pass(x) и over(σ) показаны, кроме табл. 2, также на рис. 3 и 4. На них при каждой вершине указан ее номер, и тот же номер имеет ветвь, входящая в данную вершину. При номере каждой вершины в квадратных скобках указано значение over(σ). При каждой ветви x в круглых скобках указано значение shunt(x). На рис. 4, кроме того, к значению shunt(x), указанному для каждой ветви x в круглых скобках, еще приписано в фигурных скобках значение pass(x).
Если ветвь выходит из шарнира, который не является корнем остовного ордерева T '(ρ), то она может не быть начальной ветвью блока. Примеры дают ветви (3, 7) и (12, 11). Пусть из шарнира σ выходит более одной ветви. Тогда на рис. 4 в блоке, которому шарнир σ принадлежит, но не является его начальной вершиной, значение функции over(σ) показано в виде σ[pass(x)+…], где x – ветвь этого блока, выходящая из σ. Многоточие здесь означает сумму значений функции pass(xj) для всех ветвей xj, выходящих из шарнира σ, но принадлежащих другим блокам. Там каждая из этих ветвей будет начальной. Например, надпись 3[1+…] при вершине 3 в блоке, начальная ветвь которого есть (1, 2), указывает на то, что вершина 3 является шарниром и начальной вершиной другого блока. Это будет блок с начальной ветвью (3, 8).
7. Сводимость анализа двусвязности к анализу простой связности и к объединению F-циклов. В [15] показано, что метод присоединения фундаментальных циклов выявляет сводимость анализа двусвязности графа к анализу простой связности другого графа – графа инцидентности ветвей F-циклам. Пусть G – связный неориентированный граф, T – его остовное дерево. Принадлежность ребер графа G фундаментальным циклам можно наглядно показать посредством биграфа (двудольного графа). Для этого каждый F-цикл представим графом-звездой66. Хорду, определяющую F-цикл, будем представлять центральной вершиной звезды, ветви остова в этом F-цикле – концевыми вершинами данной звезды. Центральной вершине звезды присвоим идентификатор хорды F-цикла, концевым вершинам – идентификаторы его ветвей. Каждый мост графа G будем изображать отдельной вершиной, присвоив ей идентификатор этого моста как ветви.
Звезды всех F-циклов графа G объединим как графы, совмещая те концевые вершины разных звезд, которые представляют одну и ту же ветвь. Добавим изолированные вершины, соответствующие всем мостам графа G. Полученный биграф обозначим DG(P1, P2, L) или просто DG. Он будет состоять из долей P1, P2 и множества ребер L. Доля P1 будет множеством вершин, взаимно-однозначно представляющих все ветви остовного дерева T. Доля P2 будет множеством вершин, взаимно-однозначно представляющих все хорды графа G относительно остовного дерева T, и тем самым – фундаментальные циклы графа G. Таким образом, множество вершин графа DG будет взаимно-однозначно соответствовать множеству ребер графа G.
Полученный биграф DG назовем биграфом принадлежности ветвей F-циклам относительно остовного леса T графа G. В [15] доказана следующая теорема.
Теорема 2. Множество компонент связности биграфа принадлежности ветвей F-циклам неориентированного связного графа G взаимно-однозначно соответствует множеству блоков графа G.
Таким образом, анализ двусвязности графа G сводится к анализу простой связности биграфа DG.
На рис. 5 показан биграф DH, изображающий принадлежность ветвей F-циклам в демонстрационном графе H. Исходный граф H связен, но его биграф DH не связен: он состоит из шести компонент простой связности. Они представляют блоки графа H. Обозначения компонент связности биграфа DH образованы буквой “B” и приписанным к ней номером начальной ветви блока графа H, отображаемого данной компонентой. Начальная ветвь блока однозначно определяет этот блок. Так, начальной ветвью блока, которому в биграфе на рис. 5 соответствует компонента связности B12, является ветвь (7, 12). Изолированная вершина 14 биграфа DH выражает единственный мост графа H – ветвь (13, 14). Остальные компоненты связности биграфа DH представляют компоненты вершинной двусвязности графа H.
Рис. 5.
Биграф принадлежности ветвей демонстрационного графа его F-циклам: объединение звезд F-циклов и изолированных вершин мостов

Алгоритм OCC можно интерпретировать как процесс последовательного объединения F-циклов графа G через их общие ветви при обратном ходе алгоритма по остовному ордереву. Если вершина графа не является ни концевой, ни шарниром, ни корнем остовного ордерева, то ее обходит хотя бы одна хорда. Если хорда a обходит вершину σ, в которой открывается хорда b, то эти две хорды как бы “зацепляются” друг за друга. В этом случае F-циклы, определяемые хордами a и b, будут иметь общую ветвь (π, σ), входящую в σ. Объединение этих двух F-циклов через их общее ребро (π, σ) будет двусвязным графом. Такие объединения будут выявляться при обратном ходе алгоритма, пока он не возвратится к такой ветви z, у которой все шунтирующие ее хорды будут закрываться в ее начале. Это начало будет шарниром графа G (если оно не корень разметки), а объединившиеся перед этим F-циклы дадут компоненту двусвязности графа G. Если же ветвь z не шунтируется ни одной хордой, то она – мост.
В общем случае “зацепление” двух хорд означает просто наличие общих ветвей у двух F-циклов, определяемых этими хордами. В биграфе DG это выражается в наличии общих концевых вершин у звезд, представляющих данные F-циклы. Последовательному объединению F-циклов графа G через их общие ветви остова соответствует последовательное соединение звезд F-циклов через их общие концевые вершины, в результате чего будут получаться компоненты простой связности биграфа DG.
Последовательность попарных “зацеплений” хорд, приводящую к объединению F-циклов в двусвязную компоненту графа, проиллюстрируем примером вычисления блока B8 в графе H. Через Φ(α, β) будем обозначать F-цикл, определяемый хордой (α, β). Операцию объединения графов будем выражать символом “+”.
При движении от вершины 5 к шарниру 3 алгоритм OCC последовательно выявляет F-циклы Φ(5, 4), Φ(9, 8) и Φ(4, 3). Сначала он обнаруживает, что ветвь (4, 9) шунтируется двумя хордами (5, 4) и (9, 8), “зацепляющимися” одна за другую. Ветвь (4, 9) принадлежит одновременно двум соответствующим F-циклам – Φ(5, 4) и Φ(9, 8). Их объединение Φ(5, 4) + Φ(9, 8) есть двусвязный подграф выявляемого блока.
Далее алгоритм OCC аналогичным образом распознает “зацепление” хорды (9, 8) за хорду (4, 3) посредством шунтирования ими обеими ветви (8, 4). Эта ветвь является общим ребром двух F-циклов – Φ(9, 8) и Φ(4, 3). Поэтому объединение F-цикла Φ(4, 3) с двусвязным графом Φ(5, 4) + Φ(9, 8) дает двусвязный граф, выражаемый формулой Φ(5, 4) + Φ(9, 8) + Φ(4, 3). К последнему добавить новые F-циклы уже нельзя: перейдя с ветви (8, 4) на ветвь (3, 8), алгоритм OCC установит равенство pass(8) = 0. Оно означает прекращение последовательного “зацепления” хорд. Таким образом, оказывается выявленным блок
Попарное объединение F-циклов Φ(5, 4) с Φ(9, 8) и Φ(9, 8) с Φ(4, 3) через общие ветви (4, 9) и (8, 4) представлено в биграфе DH соединением звезд этих F-циклов через их концевые вершины 9 и 4 (рис. 5).
8. Сравнение с методом Хопкрофта–Тарьяна. Алгоритм OCC производит однократный обход графа в глубину – точно так же, как алгоритм HT. Оба алгоритма в одинаковом порядке просматривают списки смежности открытых вершин. В силу этого оба имеют одинаковый порядок сложности по числу операций. Для связных графов эта оценка есть O(m), для несвязных – O(n + m), где n – число вершин графа, m – число его ребер. Затраты памяти компьютера у обоих алгоритмов тоже одинаковы. Они определяются размерами таблицы списков смежности вершин – O(n + m), а также размерами стека и массивов вычисляемых целочисленных функций вершин – O(n).
Выявление алгоритмом OCC последовательности “зацепления” хорд в пределах одной компоненты двусвязности графа делает наглядной суть этого алгоритма. Алгоритм HT такой наглядности не дает.
Метод OCC позволяет легко обосновать алгоритм Хопкрофта–Тарьяна. Обозначим через $\bar {G}$ орграф, полученный из графа G заданием ориентации на ветвях и хордах, как описано в разд. 2. Эта ориентация показана для демонстрационного графа H на рис. 2 и 3. Алгоритм HT при обходе графа в глубину присваивает каждой вершине σ графа порядковый “глубинный” номер Dnum(σ) и вычисляет для нее номер Lnum(σ) – наименьший из “глубинных” номеров вершин, достижимых из вершины σ в орграфе $\bar {G}$ по путям, каждый из которых содержит не более одной хорды.
Согласно критерию OCC, вершина σ, не являющаяся корнем остова, будет шарниром тогда и только тогда, когда хотя бы для одной ее дочерней вершины τ ни одна хорда, шунтирующая ветвь (σ, τ), не будет обходить вершину σ. Тогда всякая хорда, шунтирующая ветвь (σ, τ), должна закрываться в вершине σ. Если такая хорда существует, то Lnum(τ) = Dnum(σ), если нет, то Lnum(τ) > Dnum(σ). В любом случае получается Lnum(τ) ≥ Dnum(σ), а это и есть критерий Хопкрофта–Тарьяна, характеризующий шарнирность вершины σ.
С другой стороны, из критерия HT вытекает критерий OCC. Неравенство Lnum(τ) ≥ Dnum(σ), где (σ,τ) есть ветвь ордерева T '(ρ), означает, что каждая хорда, начало которой достижимо из вершины τ по ориентированным ветвям, закрывается либо в вершине σ, либо в ее потомке. Это условие совпадает с критерием OCC.
Алгоритм HT вычисляет две целочисленные функции вершин – Dnum(σ) и Lnum(σ). В формулах (6.4) и (6.5), к которым сводятся вычисления в алгоритме OCC, фигурируют четыре целочисленные функции вершин: open(σ), close(x), over(σ) и pass(x). Это больше, чем две функции, вычисляемые алгоритмом HT. Является ли это недостатком алгоритма OCC? Нет, ибо это просто эффект большей понятийной детализации алгоритма OCC по сравнению с HT. Она реализуется в OCC посредством таких понятий, как “открытие хорды в вершине”, “закрытие хорды в вершине”, “обход вершины хордой”, “обход ветви хордой”. Благодаря этому алгоритм OCC получается наглядным и не требует дополнительных обоснований после его описания.
Заключение. При достигнутых на сегодня вычислительных мощностях компьютеров практическая ценность алгоритма характеризуется не только его вычислительной сложностью. Возрастает роль таких факторов, как легкость понимания алгоритма человеком, удобство алгоритма для программирования и для контроля работы реализующей его программы. Алгоритм должен быть “удобным” не только для компьютера, но и для программиста.
В статье описан новый метод вычисления шарниров и блоков неориентированных графов. Известный алгоритм Хопкрофта–Тарьяна, решающий эту задачу, не обладает такой наглядностью и простотой обоснования, как алгоритм, предложенный в настоящей работе. В основе нового алгоритма, названного здесь OCC, лежит идея отслеживания числа хорд, обходящих (шунтирующих) вершины и ветви остова анализируемого графа. Благодаря этому контролю становится очевидным, как последовательное объединение фундаментальных циклов графа, имеющих общие ребра, приводит к построению его компонент двусвязности.
На базе метода OCC легко устанавливается эквивалентность двух критериев шарнирности вершин – критерия Хопкрофта–Тарьяна и критерия OCC.
Поскольку предложенный алгоритм OCC, как и алгоритм Хопкрофта–Тарьяна, основан на обходе графа в глубину, оценки вычислительной сложности обоих одинаковы. Они сводятся к оценке сложности обхода неориентированного графа в глубину, выражаемой как O(n + m), где n – число вершин графа, m – число ребер.
Список литературы
Головинский И.А. Построение графов простых путей в транспортных сетях. I. Общие решения и примеры // Изв. РАН. ТиСУ. 2021. № 1. С. 124–159.
Hopcroft J., Tarjan R. Efficient Algorithms for Graph Manipulation. Tech. Rep. 207, Computer Science Department, Stanford University, Stanford, Calif., 1971. URL: http://i.stanford.edu/pub/cstr/reports/cs/tr/71/207/CS-TR-71-207.pdf (дата обращения: 20.05.2020).
Tarjan R.E. Depth First Search and Linear Graph Algorithms // BIAM J. Computing. 1972. V. 1 (2). P. 146–160.
Hopcroft J.E., Tarjan R.E. Efficient Algorithms for Graph Manipulation // Comm. ACM. 1973. V. 16 (6). P. 372–378.
Рейнгольд Э., Нивергельт Ю., Део Н. Комбинаторные алгоритмы. Теория и практика. М.: Мир, 1980.
Липский В. Комбинаторика для программистов. М.: Мир, 1988. 213 с.
Асанов М.О., Баранский В.А., Расин В.В. Дискретная математика: графы, матроиды, алгоритмы. Ижевск: НИЦ “Регулярная и хаотическая динамика”, 2001. 288 с.
Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. М.: МЦНМО, 2001. 960 с.
Седжвик Р. Фундаментальные алгоритмы на C++. Ч. 5. Алгоритмы на графах. СПб.: ООО “ДиаСофтЮП”, 2002. 496 с.
Ахо А.В., Хопкрофт Дж.Э., Ульман Дж.Д. Структуры данных и алгоритмы. М., СПб., Киев: Вильямс, 2003. 384 с.
Макконнелл Дж. Основы современных алгоритмов. Изд. 2-е. М.: Техносфера, 2004. 368 с.
Окулов С.М. Программирование в алгоритмах. М.: БИНОМ. Лаборатория знаний, 2004. 341 с.
Алексеев В.Е., Таланов В.А. Графы и алгоритмы. Структуры данных. Модели вычислений. М.: БИНОМ. Лаборатория знаний, 2011. 320 с.
Емеличев В.А., Мельников О.И., Сарванов В.И., Тышкевич Р.И. Лекции по теории графов. М.: Наука, 1990. 384 с.
Тумаков А.В., Головинский И.А. Анализ двусвязности графов: обоснование и варианты метода фундаментальных циклов // Информационные технологии моделирования и управления. 2013. № 2 (80). С. 123–137.
Головинский И.А., Тумаков А.В. Анализ двусвязности графов методом присоединения фундаментальных циклов // Информационные технологии моделирования и управления. 2013. № 2 (80). С. 92–105.
Дасгупта С., Пападимитриу Ч., Вазирани У. Алгоритмы. М.: Изд-во МЦНМО, 2014. 320 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления