Известия РАН. Теория и системы управления, 2021, № 3, стр. 168-176
МОДЕЛИРОВАНИЕ И УПРАВЛЕНИЕ ДВИЖЕНИЕМ МАНИПУЛЯТОРА С ЗАМКНУТОЙ КИНЕМАТИЧЕСКОЙ ЦЕПЬЮ И ЛИНЕЙНЫМ ПРИВОДОМ
М. Алхаддад *
* E-mail: alkhaddad.m@phystech.edu
Поступила в редакцию 11.09.2020
После доработки 11.10.2020
Принята к публикации 30.11.2020
Аннотация
Предлагается и исследуется способ робастного управления специализированным манипулятором, предназначенным для работы в составе робототехнического комплекса для обслуживания вертикальных поверхностей. Комплекс состоит из колесной платформы, колесного робота вертикального перемещения с вакуумным контактным устройством и манипулятора. В транспортном положении робот прикреплен к рабочему органу (схвату) манипулятора и расположен на платформе так, что его контактная плоскость почти параллельна плоскости платформы. После подъезда платформы к стене манипулятор приводит робот в рабочее положение, подводя его контактной плоскостью к поверхности стены. Затем включается вакуумный насос робота, робот присасывается к стене, отсоединяется от схвата манипулятора и в дальнейшем передвигается по стене в автономном режиме. В статье описывается работа манипулятора на этапе приведения робота в рабочее положение.
Введение. Данное исследование мотивировано разработкой в лаборатории робототехники и мехатроники Института проблем механики им. А.Ю. Ишлинского Российской академии наук мобильного робототехнического комплекса для обслуживания сильно наклонных и вертикальных поверхностей. Комплекс состоит из колесной платформы и малогабаритного колесного робота, который удерживается на вертикальной поверхности за счет разрежения воздуха в полости, отделяющей днище робота от поверхности перемещения. На рис. 1 изображен лабораторный образец робота и показаны его основные компоненты. Робот состоит из жесткого основания 1 круглой формы, на котором крепятся два колеса 2, управляемые независимыми электроприводами 3, и центробежный вакуумный насос 4. Оси вращения колес расположены на одной прямой, проходящей через центр основания. Колеса снабжены шинами, материал которых подбирается так, чтобы обеспечить максимально высокий коэффициент трения колес о поверхность перемещения. Под днищем основания имеется полость 5, в которой создается разрежение воздуха. Благодаря этому робот избыточным внешним атмосферным давлением прижимается к поверхности перемещения с силой, которая позволяет создать трение между колесами и поверхностью, достаточное для удержания робота на поверхности при заблокированных колесах и его движения в любом направлении при включенных приводах. Предусмотрено регулирование степени разреженности воздуха в зависимости от наклона поверхности перемещения и физических условий контакта. Это позволяет экономно расходовать электроэнергию на работу вакуумного насоса. Исследованиям динамических свойств робота, определению состава сенсоров и разработке алгоритмов управления посвящены работы [1–3].
Для описанного робота планируется создать транспортно-манипуляционное устройство, которое будет доставлять робот к месту его использования и приводить в рабочее положение на обслуживаемой поверхности. Устройство состоит из четырехколесной мобильной платформы (тележки) и манипулятора. В транспортном положении робот крепится к выходному звену манипулятора днищем вверх. После подъезда платформы к стене, обслуживаемой роботом, поворотом выходного звена он приводится в положение, в котором днище и колеса обращены к стене, и в контакт со стеной. Затем включается вакуумный насос, робот присасывается к стене, освобождается от закрепления на манипуляторе и начинает функционировать в автономном режиме.
Ниже описывается конструктивная схема манипулятора, формируется его математическая модель и предлагается алгоритм управления на этапе приведения робота в рабочее положение. Манипулятор представляет собой плоский механизм с замкнутой кинематической цепью, звенья которого соединены тремя цилиндрическими (вращательными) и одним призматическим (поступательным) шарнирами. Цилиндрические шарниры пассивны, а призматический шарнир связан с линейным приводом. Механизм имеет одну степень свободы и управляется силой, действующей между компонентами призматического шарнира. Алгоритм управления основан на линеаризации уравнения движения в окрестности положений, через которые последовательно должен пройти манипулятор, и использовании пропорционально-интегрально-дифференциального регулятора (ПИД-регулятора) со ступенчатым изменением коэффициентов обратной связи при изменении целевой точки. Настраиваемые коэффициенты не чувствительны к изменениям инерционных параметров выходного звена с расположенным на нем объектом манипулирования. Это позволяет обеспечивать достаточную точность позиционирования манипулятора независимо от нагрузки. Приводятся результаты математического моделирования, свидетельствующие о приемлемом качестве перереходных процессов при управлении позиционированием манипулятора в соответствии с предложенным алгоритмом.
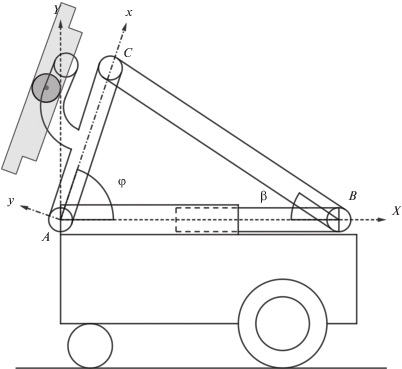
1. Математическая модель манипуляционного механизма. Схема манипулятора изображена на рис. 2. Манипулятор состоит из активного (приводного, входного) звена $AB$ с изменяемой длиной и двух пассивных звеньев $AC$ и $BC$, длины которых неизменны; звено $AC$ является выходным для манипулятора, к нему прикрепляется объект манипулирования (в рассматриваемом случае – робот вертикального перемещения). Звенья соединены цилиндрическими шарнирами, оси которых параллельны друг другу и плоскости мобильной платформы, на которой укреплен манипулятор. Шарнир A жестко связан с платформой, шарнир $B$ также располагается на платформе, но не связан с ней жестко, его ось может перемещаться относительно платформы при изменении длины приводного звена. В данной статье манипулятор моделируется плоским механизмом треугольной формы, плоскость $\Pi $ которого вертикальна; вершины треугольника суть следы осей шарниров манипулятора в плоскости $\Pi $. В дальнейшем шарниры отождествляются с вершинами треугольника $ABC$, моделирующего механизм. Будем предполагать, что во время работы манипулятора платформа не движется.
Приводное звено будем трактовать как телескопический механизм состоящий из неподвижной прямолинейной трубки цилиндрической формы (статора) и соосного с ним подвижного цилиндра (ползуна), без зазора вставленного в статор. Звено $BC$, соединяющее приводное и выходное звенья, считается однородным стержнем, центр масс которого лежит на прямой $BC$, а выходное звено (с объектом манипулирования или без него) – абсолютно твердым телом, центр масс которого лежит в плоскости $\Pi $. Манипулятор управляется силой F, приложенной статором к ползуну. Эта сила создается приводом.
Введем в плоскости $\Pi $ систему координат $AXY$, жестко связанную с платформой, и систему координат $Axy$, жестко связанную с выходным звеном $AC$. Ось $AX$ направим вдоль прямой $AB$, соединяющей соответствующие шарниры (эта прямая предполагается горизонтальной), от $A$ к $B$, ось $AY$ – вертикально вверх, ось $Ax$ – вдоль прямой $AC$ от $A$ к $C$, ось $Ay$ – перпендикулярно оси $Ax$ так, что при совмещении осей $Ax$ и $AX$ совмещаются оси $Ay$ и $AY$.
Составим уравнения Лагранжа для описанной системы, приняв в качестве обобщенной координаты угол φ между осями $AX$ и $Ax$ (угол поворота выходного звена относительно платформы). Для удобства присвоим приводному звену AB номер 1, промежуточному звену $BC$ – номер 2, выходному звену $AC$ – номер 3. Введем следующие обозначения: $r = {\text{|}}AC{\text{|}}$ – длина выходного звена; $L = {\text{|}}BC{\text{|}}$ – длина промежуточного звена; ${{m}_{1}}$ – масса ползуна, ${{m}_{2}}$ – масса звена $BC$; ${{m}_{3}}$ – масса звена $AC$; ${{J}_{2}}$ – момент инерции звена 2 относительно оси шарнира B; ${{a}_{2}}$ – расстояние от шарнира B до центра масс звена 2; ${{a}_{3}}$ и ${{b}_{3}}$ – x- и y-координаты центра масс выходного звена в системе координат $Axy$; ${{J}_{3}}$ – момент инерции выходного звена относительно оси шарнира $A$; $s$ – координата шарнира B на координатной оси $AX$; $\beta $ – угол между звеньями 1 и 2, отсчитываемый, как показано на рис. 2; $g$ – ускорение силы тяжести. Предположим, что конструкция манипулятора такова, что r < L и угол $\varphi $ изменяется в интервале $[0,\pi {\text{/}}2]$. Тогда координата s лежит в интервале $[\sqrt {{{L}^{2}} - {{r}^{2}}} ,L + r]$, а угол $\beta $ – в интервале $[0,{\text{arcsin}}(r{\text{/}}L)]$. Это предположение оправдано назначением манипулятора. Манипулятор должен иметь возможность принимать горизонтальную конфигурацию, когда объект манипулирования (робот вертикального перемещения) находится в транспортном положении, и его выходное звено должно быть расположенным вертикально при приведении робота в рабочее состояние.
Кинетические энергии звеньев 1–3 представляются следующими выражениями:
(1.1)
${{T}_{1}} = \frac{1}{2}{{m}_{1}}{{\dot {s}}^{2}},\quad {{T}_{2}} = \frac{1}{2}({{m}_{2}}{{\dot {s}}^{2}} + {{J}_{2}}{{\dot {\beta }}^{2}} + 2{{m}_{2}}{{a}_{2}}\dot {s}\dot {\beta }sin\beta ),\quad {{T}_{3}} = \frac{1}{2}{{J}_{3}}{{\dot {\varphi }}^{2}},$Геометрия механизма налагает две связи на переменные φ, β и s:
Уравнения (1.3) и (1.4) позволяют выразить переменные $\beta $ и s через угол $\varphi $ и принять этот угол за обобщенную координату манипулятора:
(1.5)
$\beta = {\text{arcsin}}\left( {\frac{r}{L}sin\varphi } \right),\quad s = rcos\varphi + \sqrt {{{L}^{2}} - {{r}^{2}}si{{n}^{2}}\varphi } .$Дифференцирование равенств (1.5) дает
(1.6)
$\dot {\beta } = \frac{{rcos\varphi }}{{\sqrt {{{L}^{2}} - {{r}^{2}}si{{n}^{2}}\varphi } }}\dot {\varphi },\quad \dot {s} = - rsin\varphi \left( {1 + \frac{{rcos\varphi }}{{\sqrt {{{L}^{2}} - {{r}^{2}}si{{n}^{2}}\varphi } }}} \right)\dot {\varphi }.$Подставляя выражения (1.3) и (1.6) в (1.1) и затем вычисляя сумму (1.2), получим кинетическую энергию системы как функцию переменных φ и $\dot {\varphi }$, квадратичную по обобщенной скорости $\dot {\varphi }$:
где(1.8)
$\begin{gathered} M(\varphi ) = ({{m}_{1}} + {{m}_{2}}){{r}^{2}}si{{n}^{2}}\varphi \mathop {\left( {1 + \frac{{rcos\varphi }}{{\sqrt {{{L}^{2}} - {{r}^{2}}si{{n}^{2}}\varphi } }}} \right)}\nolimits^2 - 2{{m}_{2}}{{a}_{2}}\frac{{{{r}^{3}}si{{n}^{2}}\varphi cos\varphi }}{{L\sqrt {{{L}^{2}} - {{r}^{2}}si{{n}^{2}}\varphi } }}\left( {1 + \frac{{rcos\varphi }}{{\sqrt {{{L}^{2}} - {{r}^{2}}si{{n}^{2}}\varphi } }}} \right) + \\ \, + {{J}_{2}}\frac{{{{r}^{2}}co{{s}^{2}}\varphi }}{{{{L}^{2}} - {{r}^{2}}si{{n}^{2}}\varphi }} + {{J}_{3}},\quad M(\varphi ) > 0. \\ \end{gathered} $Потенциальная энергия системы в поле силы тяжести есть сумма потенциальных энергий звеньев 2 и 3 и определяется выражением
(1.9)
$U = {{m}_{2}}g{{a}_{2}}sin\beta + {{m}_{3}}g({{a}_{3}}sin\varphi + {{b}_{3}}cos\varphi ) = g\left[ {\left( {\frac{r}{L}{{m}_{2}}{{a}_{2}} + {{m}_{3}}{{a}_{3}}} \right)sin\varphi + {{m}_{3}}{{b}_{3}}cos\varphi } \right].$Вычислим теперь обобщенную силу ${{Q}_{\varphi }}$, отвечающую управляющей силе $F$ и обобщенной координате $\varphi $. Поскольку сила F действует вдоль оси $AX$ и приложена к ползуну, ее элементарная работа определяется выражением $\delta A = F\delta s$, где $\delta s$ – вариация координаты точки приложения силы F. Подставляя вместо $\delta s$ вариацию выражения (1.5) для переменной $s$, получим
(1.10)
$\delta A = - Frsin\varphi \left( {1 + \frac{{rcos\varphi }}{{\sqrt {{{L}^{2}} - {{r}^{2}}si{{n}^{2}}\varphi } }}} \right)\delta \varphi .$Следовательно,
(1.11)
${{Q}_{\varphi }} = - Frsin\varphi \left( {1 + \frac{{rcos\varphi }}{{\sqrt {{{L}^{2}} - {{r}^{2}}si{{n}^{2}}\varphi } }}} \right).$Уравнение Лагранжа второго рода для механической системы с кинетической энергией (1.7), потенциальной энергией (1.9) и обобщенной силой (в общем случае непотенциальной) (1.11) имеет вид
(1.12)
$M\ddot {\varphi } + \frac{1}{2}\frac{{\partial M}}{{\partial \phi }}{{\dot {\varphi }}^{2}} - (acos\varphi + bsin\varphi ) = {{Q}_{\varphi }},\quad a = g\left( {\frac{r}{L}{{m}_{2}}{{a}_{2}} + {{m}_{3}}{{a}_{3}}} \right),\quad b = g{{m}_{3}}{{b}_{3}}.$Будем допускать, что параметры выходного звена (масса и момент инерции) известны неточно, например из-за неточного знания параметров объекта манипулирования, который может меняться. Таким образом, коэффициенты $a$ и $b$, а также функция $M = M(\varphi )$ известны неточно. Если области возможных значений геометрических и инерционных параметров системы ограничены, то и области возможных значений величин M, $a$ и $b$ ограничены. Оценим функцию $M(\varphi )$ сверху величиной ${{M}_{{max}}}$:
а параметры a и b представим выражениями где ${{a}_{0}}$ и ${{b}_{0}}$ – известные номинальные значения параметров, а ${{\Delta }_{a}}$ и ${{\Delta }_{b}}$ – неизвестные отклонения от номинальных значений, лежащие в заданных пределах:(1.15)
${\text{|}}{{\Delta }_{a}}{\text{|}} \leqslant A,\quad {\text{|}}{{\Delta }_{b}}{\text{|}} \leqslant B.$2. Цель и алгоритм управления. Предлагается способ управления манипулятором в процессе перемещения объекта манипулирования в рабочее положение. Цель управления – приведение выходного звена манипулятора в вертикальное положение с достаточной степенью точности с учетом неполной информации о параметрах системы, в частности, массы и момента инерции выходного звена (эти параметры зависят от объекта манипулирования, которым нагружен манипулятор, и от способа его крепления к манипулятору). Данная операция не требует высокого быстродействия, но требует надежности. Поэтому предлагается простой способ управления, обеспечивающий прохождение системы через фиксированную последовательность промежуточных положений со стабилизацией системы в этих положениях. Промежуточные положения располагаются достаточно близко друг к другу, чтобы можно было рассчитывать управление переходом между двумя последовательными положениями исходя из уравнения движения, линеаризованного в окрестности положения (равновесия), в которое система приводится на очередном этапе.
Пусть φi, $i = 0,1, \ldots ,n$, – промежуточные положения выходного звена манипулятора. Опишем управление системой на этапе перехода из положения равновесия ${{\varphi }_{{i - 1}}}$ в положение равновесия φi.
Будем строить управление на этом этапе в виде ${{Q}_{\varphi }} = Q_{i}^{0} + {{u}_{i}}$ так, чтобы при ${{u}_{i}} = 0$ положение φi было положением равновесия системы (1.12) при номинальных значениях параметров a и b. Отсюда следует, что
Подставляя выражение ${{Q}_{\varphi }} = Q_{i}^{0} + {{u}_{i}}$ в (1.12) и линеаризуя получившееся уравнение в окрестности точки ${{\varphi }_{i}}$, получим
(2.2)
$\begin{gathered} {{M}_{i}}{{{\ddot {e}}}_{i}} + {{k}_{i}}{{e}_{i}} = {{u}_{i}} + {{f}_{i}},\quad {{e}_{i}} = \varphi - {{\varphi }_{i}},\quad {{M}_{i}} = M({{\varphi }_{i}}), \\ {{k}_{i}} = asin{{\varphi }_{i}} - bcos{{\varphi }_{i}},\quad {{f}_{i}} = {{\Delta }_{a}}cos{{\varphi }_{i}} + {{\Delta }_{b}}sin{{\varphi }_{i}}. \\ \end{gathered} $Уравнение (2.2) описывает динамику линейной управляемой системы второго порядка с постоянными (хотя и неизвестными) коэффициентами Mi и ${{k}_{i}}$, подверженной постоянному (хотя и неизвестному) возмущению fi. Коэффициент Mi положителен из-за положительности кинетической энергии системы при $\dot {\varphi } \ne 0$; коэффициент ${{k}_{i}}$ может иметь любой знак.
Используем в этой системе ПИД-регулятор, соответствующий управлению
(2.3)
${{u}_{i}} = - {{K}_{i}}{{e}_{i}} - {{D}_{i}}\mathop {\dot {e}}\nolimits_i - {{I}_{i}}\int\limits_0^t \,{{e}_{i}}(\xi )d\xi ,\quad {{K}_{i}} > 0,\quad {{D}_{i}} > 0,\quad {{I}_{i}} > 0.$Постоянные коэффициенты ${{K}_{i}}$, ${{D}_{i}}$ и ${{I}_{i}}$ должны быть выбраны так, чтобы любое решение ${{e}_{i}}(t)$ системы (2.2), (2.3) стремилось к нулю при неограниченном росте времени t. Для того, чтобы выяснить, какие ограничения надо наложить на коэффициенты обратной связи управления (2.3), подставим это управление в уравнение (2.2) и продифференцируем получившееся равенство по времени; получим линейное дифференциальное уравнение третьего порядка с постоянными коэффициентами:
(2.4)
${{M}_{i}}{{\dddot e}_{i}} + {{D}_{i}}{{\ddot {e}}_{i}} + ({{k}_{i}} + {{K}_{i}}){{\dot {e}}_{i}} + {{I}_{i}}{{e}_{i}} = 0.$Коэффициенты обратной связи следует выбрать так, чтобы нулевое решение этого уравнения было асимптотически устойчивым. Характеристический полином уравнения (2.4) имеет вид
(2.5)
$P(\lambda ) = {{M}_{i}}{{\lambda }^{3}} + {{D}_{i}}{{\lambda }^{2}} + ({{k}_{i}} + {{K}_{i}})\lambda + {{I}_{i}}.$С учетом положительности коэффициентов ${{M}_{i}}$, ${{D}_{i}}$, ${{K}_{i}}$ и ${{I}_{i}}$ для устойчивости этого полинома необходимо и достаточно выполнение неравенства
Это неравенство следует, например, из критерия Рауса–Гурвица [4–6].
Оценим снизу множество возможных значений коэффициента ki, определенного в (2.2). Этот коэффициент можно представить выражением
(2.7)
$\begin{gathered} {{k}_{i}} = \sqrt {{{a}^{2}} + {{b}^{2}}} sin({{\varphi }_{i}} + \psi ), \\ cos\psi = \frac{a}{{\sqrt {{{a}^{2}} + {{b}^{2}}} }},\quad sin\psi = - \frac{b}{{\sqrt {{{a}^{2}} + {{b}^{2}}} }}, \\ \end{gathered} $С учетом выражений (1.14) и (1.15) получаем
(2.9)
$\sqrt {{{a}^{2}} + {{b}^{2}}} \leqslant \sqrt {{{{({\text{|}}{{a}_{0}}{\text{|}} + A)}}^{2}} + {{{({\text{|}}{{b}_{0}}{\text{|}} + B)}}^{2}}} .$Из (2.8) и (2.9) имеем оценку
(2.10)
${{k}_{i}} \geqslant - \sqrt {{{{({\text{|}}{{a}_{0}}{\text{|}} + A)}}^{2}} + {{{({\text{|}}{{b}_{0}}{\text{|}} + B)}}^{2}}} .$Из (1.13), (2.6) и (2.10) следует, что устойчивость будет заведомо обеспечена, если положительные коэффициенты ${{K}_{i}}$, ${{D}_{i}}$ и ${{I}_{i}}$ ПИД-регулятора будут выбраны исходя из неравенства
(2.11)
${{D}_{i}}({{K}_{i}} - \sqrt {{{{({\text{|}}{{a}_{0}}{\text{|}} + A)}}^{2}} + {{{({\text{|}}{{b}_{0}}{\text{|}} + B)}}^{2}}} ) > {{M}_{{max}}}{{I}_{i}}.$Отметим, что коэффициенты ПИД-регулятора, воообще говоря, различны для различных этапов управления. Выбор этих коэффициентов диктуется желаемым качеством переходного процесса на соответствующем этапе. Например, их можно выбирать, максимизируя степень устойчивости соответствующей линейной системы. Степень устойчивости асимптотически устойчивой линейной системы определяется как модуль максимальной вещественной части корней ее характеристического полинома [7]. Степень устойчивости характеризует быстроту переходного процесса. Поскольку коэффициенты обратной связи меняются от этапа к этапу, предложенный алгоритм можно рассматривать как адаптивный алгоритм, который, в отличие от традиционных адаптивных алгоритмов [8], не требует идентификации параметров системы в процессе управления.
3. Численное моделирование. Для численного моделирования процесса управления манипулятором в соответствии с алгоритмом, описанным в предыдущем разделе, были выбраны следующие значения параметров.
Геометрические параметры ненагруженного манипулятора:
(3.1)
$r = 0.16\;{\text{м}},\quad L = 0.52\;{\text{м}},\quad {{a}_{2}} = 0.26\;{\text{м}},\quad {{a}_{3}} = 0.08\;{\text{м}},\quad {{b}_{3}} = 0.01\;{\text{м}}.$Геометрические параметры нагруженного выходного звена:
Инерционные параметры ненагруженного манипулятора:
(3.3)
$\begin{array}{*{20}{c}} {{{m}_{1}} = 0.3\;{\text{кг}},\quad {{m}_{2}} = 1\;{\text{кг}},\quad {{m}_{3}} = 1\;{\text{кг}},} \\ {{{J}_{2}} = 0.0901\;{\text{кг}} \cdot {{{\text{м}}}^{2}},\quad {{J}_{3}} = 0.0091\;{\text{кг}} \cdot {{{\text{м}}}^{2}}.} \end{array}$Инерционные параметры нагруженного выходного звена:
Набор промежуточных значений угла $\varphi $:
Коэффициенты ПИД-регулятора подбирались методом проб и ошибок в процессе численного моделирования так, чтобы переходные процессы при движении между промежуточными положениями манипулятора имели приемлемые характеристики. Коэффициенты, выбранные для этапов с различными ${{\varphi }_{i}}$, приведены в таблице 1. Отметим, что коэффициенты ${{K}_{i}}$, ${{D}_{i}}$ и ${{I}_{i}}$ – размерные величины, размерности которых в системе единиц СИ суть
(3.6)
$[{{K}_{i}}] = {\text{кг}} \cdot {{{\text{м}}}^{2}}{\text{/}}{{{\text{с}}}^{2}},\quad [{{D}_{i}}] = {\text{кг}} \cdot {{{\text{м}}}^{2}}{\text{/с}}\quad [{{I}_{i}}] = {\text{кг}} \cdot {{{\text{м}}}^{2}}{\text{/}}{{{\text{с}}}^{3}}.$Таблица 1.
Коэффициенты ПИД-регулятора при каждом положении равновесия
| Коэффициенты ПИД-регулятора | ||||||
|---|---|---|---|---|---|---|
| φi [rad] | без нагрузки | с нагрузкой | ||||
| Ki | Ii | Di | Ki | Ii | Di | |
| 0.87 | 32.06 | 58.06 | 3.96 | 55.03 | 99.66 | 6.79 |
| 0.92 | 31.81 | 57.61 | 3.93 | 53.95 | 97.71 | 6.66 |
| 0.97 | 31.69 | 57.41 | 3.91 | 53.11 | 96.27 | 6.56 |
| 1.02 | 31.71 | 57.43 | 3.91 | 52.65 | 95.29 | 6.49 |
| 1.07 | 31.82 | 57.63 | 3.93 | 52.28 | 94.70 | 6.45 |
| 1.12 | 32.02 | 57.99 | 3.95 | 52.14 | 94.44 | 6.44 |
| 1.17 | 32.29 | 58.49 | 3.98 | 52.17 | 94.49 | 6.44 |
| 1.22 | 32.64 | 59.11 | 4.03 | 52.35 | 94.81 | 6.46 |
| 1.27 | 33.04 | 59.85 | 4.08 | 52.67 | 95.39 | 6.50 |
| 1.32 | 33.51 | 60.69 | 4.13 | 53.11 | 96.20 | 6.56 |
| 1.37 | 34.03 | 61.63 | 4.20 | 53.69 | 97.24 | 6.63 |
| 1.42 | 34.60 | 62.66 | 4.27 | 54.38 | 98.49 | 6.71 |
| 1.47 | 35.21 | 63.78 | 4.35 | 55.18 | 99.95 | 6.81 |
| 1.52 | 35.87 | 64.98 | 4.43 | 56.11 | 101.6 | 6.93 |
| 1.57 | 36.58 | 66.26 | 4.52 | 57.14 | 103.5 | 7.05 |
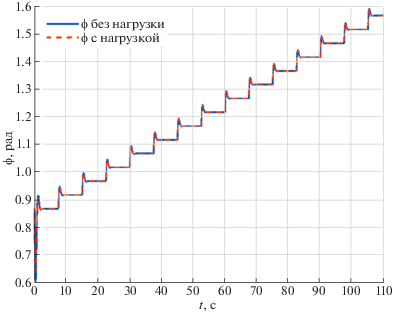
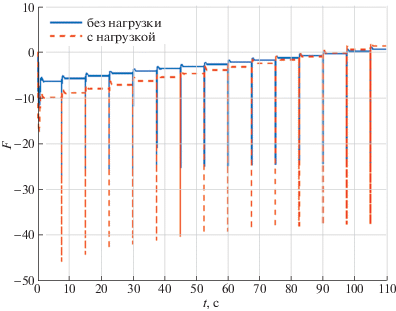
В таблице значения этих коэффициентов даны в единицах СИ без указания размерностей. Поведение системы при коэффициентах ПИД-регулятора, приведенных в таблице, иллюстрируется на рис. 3 и 4. Сплошные кривые относятся к ненагруженному манипулятору, штриховые – к нагруженному. На рис. 3 показан угол $\varphi $ отклонения выходного звена манипулятора от горизонтального положения как функция времени, а на рис. 4 изображена зависимость от времени управляющей силы F. Сила F рассчитывалась по известной обобщенной силе ${{Q}_{\varphi }}$ при помощи формулы (1.11). Из этих рисунков видно, что сплошные и штриховые кривые близки одна к другой, что свидетельствует о невысокой чувствительности переходных процессов к изменениям геометрических и инерционных параметров выходного звена, связанным с его нагружением. Из рис. 3 видно, что движение системы с ПИД-регулятором происходит с небольшим перерегулированием, которое может быть нежелательно, если выходное звено приводится в вертикальное положение и тележка находится близко к стене. Нежелательных последствий перерегулировния, в частности удара робота о стену, можно избежать, приводя робот в вертикальное положение, когда тележка находится на безопасном расстоянии от стены. После затухания переходного процесса тележку следует придвинуть к стене вплотную. Точность позиционирования манипулятора в терминальном положении при предложенном алгоритме управления практически не зависит от его нагрузки, т.е. этот алгоритм обладает свойством робастности по отношению к геометрическим и инерционным параметрам выходного звена, которые зависят от соответствующих параметров объекта манипулирования.
Заключение. Для манипулятора, приводящего робот вертикального перемещения из транспортного положения на мобильной платформе в рабочее положение, предложен алгоритм управления, в соответствии с которым система приходит в конечное положение через ряд промежуточных положений. В качестве управляющего устройства предлагается использовать классический ПИД-регулятор, коэффициенты которого рассчитываются исходя из уравнения движения манипулятора, линеаризованного в окрестности очередной целевой точки. При переходе от одной целевой точки к другой коэффициенты обратной связи ПИД-регулятора пересчитываются, так что получившийся в итоге алгоритм управления можно трактовать как ПИД-регулятор со ступенчато изменяющимися коэффициентами. Такой алгоритм обладает свойством робастности по отношению к инерционным параметрам, зависящим от объекта манипулирования. Численное моделирование процесса управления в соответствии с предложенным алгоритмом свидетельствует о качестве и времени переходных процессов, приемлемых для разрабатываемого манипуляционного устройства.
Список литературы
Нунупаров А.М., Чащухин В.Г. Система управления робота вертикального перемещения с аэродинамическим прижатием // Изв. РАН. ТиСУ. 2020. № 2. С. 168–176.
Chashchukhin V.G. Orientation System of the Aerodynamically Adhesive Wall Climbing Robot // Extreme Robotics. 2019. T. 1. № 1. C. 145–148.
Чащухин В.Г. Исследование параметров движения робота со скользящи уплотнением // Вестн. Нижегородского ун-та им. Н.И. Лобачевского. 2011. № 4–2. С. 347–349.
Гантмахер Ф.Р. Теория матриц. М.: Физматлит, 2004. 560 с.
Гантмахер Ф.Р. Лекции по аналитической механике. М.: Физматлит, 2004. 262 с.
Ким Д.П. Теория автоматического управления. Т. 1. Линейные системы. М.: Физматлит, 2003.
Цыпкин Я.З., Бромберг П.В. О степени устойчивости линейных систем // Изв. АН СССР. Сер. ОТН. 1945. № 12. С. 1163–1168.
Slotine J.-J. E., Li W. Applied Nonlinear Control. New Jersey: Prentice-Hall, Inc., 1991.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления