Известия РАН. Теория и системы управления, 2021, № 3, стр. 98-110
ЧИСЛЕННЫЙ АНАЛИЗ СИСТЕМЫ С ГЕТЕРОГЕННЫМИ СЕРВЕРАМИ И МГНОВЕННОЙ ОБРАТНОЙ СВЯЗЬЮ
С. Г. Алиева a, А. З. Меликов a, *, М. О. Шахмалыев a
a Институт систем управления, Национальная академия наук Азербайджана
Баку, Азербайджан
* E-mail: agassi.melikov@gmail.com
Поступила в редакцию 10.09.2019
После доработки 17.11.2020
Принята к публикации 25.01.2021
Аннотация
Изучается система с гетерогенными серверами, пуассоновским потоком с Марковской модуляцией и мгновенной обратной связью. Обслуживание первичных заявок выполняется в высокоскоростном сервере, и после завершения обслуживания каждая заявка, согласно схеме Бернулли, либо покидает систему, либо требует повторного обслуживания. Повторные заявки обслуживаются в медленном сервере, при этом эти заявки после завершения обслуживания также, согласно схеме Бернулли, либо покидают систему, либо требуют повторного обслуживания в медленном сервере. Если в момент поступления первичной заявки длина очереди таких заявок превышает некоторое пороговое значение и медленный сервер свободен, то поступившая заявка, согласно схеме Бернулли, либо направляется в медленный сервер, либо присоединяется в свою очередь. Считается, что длины очередей перед каждым сервером являются бесконечными величинами. Построена адекватная математическая модель изучаемой системы в виде трехмерной цепи Маркова с бесконечным пространством состояний. Получено условие эргодичности данной цепи, предложен приближенный алгоритм расчета стационарных вероятностей состояний и показана его высокая точность. Приводятся результаты численных экспериментов.
Введение. При построении математических моделей коммуникационных процессов, а также процессов, связанных с обработкой деталей в производственных системах, процессов управления запасами и т.д., возникает необходимость учета повторной обработки некоторых заявок. Так, во многих системах передачи информации ошибочно переданные данные (пакеты, кадры и т.д.) передаются повторно, так как эффективность работы таких систем зачастую оценивается достоверностью передачи данных. Если выпускаемые детали имеют определенные дефекты, то и в производственных системах в некоторых ситуациях требуется их повторная обработка.
Учет эффекта повторения обслуживания заявок приводит к необходимости использования моделей систем с обратной связью (feed back queue, (FBQ)). Такие модели впервые были введены в [1, 2]. Следует различать системы с мгновенной обратной связью (instantaneous feed back queue (IFBQ)), где повторение происходит сразу после завершения обслуживания заявки, и системы с отсроченной обратной связью (delayed feed back queue (DFBQ)), в которых повторение запроса для обслуживания происходит после определенного положительного времени.
Современное состояние проблемы исследования моделей FBQ подробно изложено в [3], поэтому здесь не будем останавливаться на изложении известных в этом направление результатов. В указанной работе отмечается, что в подавляющем большинстве публикаций изучаются модели FBQ без буфера для ожидания заявок. Вместе с тем во многих системах организуются буфера для хранения ожидающих в очереди заявок. Поэтому для адекватного описания работы таких систем возникает необходимость изучения моделей FBQ с очередями.
Исходя из вышеизложенных фактов, в настоящей статье исследуется модель IFBQ с очередями. Отметим, что в доступной литературе мало работ, которые посвящены изучению таких моделей, например [4–13]. Простые одномерные модели IFBQ с одним сервером и нетерпеливыми заявками при использовании различных механизмов удержания их в очереди в моменты завершения допустимого времени ожидания, рассмотрены в [4–10]. Модель с двумя гетерогенными серверами и ограниченной очередью, в которых поступающие заявки с известными вероятностями назначаются в сервера, приведена в [11]. Отметим, что в [4–11] не различаются исходные заявки и заявки, которые требуют повторного обслуживания. Поэтому с помощью предложенного в них подхода невозможно найти распределение числа заявок, которые требуют повторного обслуживания. Более сложная модель IFBQ с одним сервером и ограниченной очередью изучена в [12], где входящий поток является MAP-потоком (Markov arrival process (MAP)) и время обслуживания заявок имеет функцию распределения фазового типа. Показано, что математической моделью системы будет некоторая четырехмерная цепь Маркова (ЦМ) и вычислены характеристики системы. В недавней публикации [13] рассмотрена модель IFBQ с одним сервером и двумя пуассоновскими потоками заявок. Считается, что для заявок каждого типа имеются раздельные буфера бесконечного размера, при этом лишь заявки высокого приоритета могут, согласно схеме Бернулли, повторять запросы для обслуживания. Предполагается, что заявки, которые требуют повторного обслуживания, направляются в очередь заявок низкого приоритета, при этом изучаются модели с относительными и абсолютными приоритетами. В [12, 13] для исследования предложенных моделей используется матрично-геометрический метод [14].
Анализ доступных работ показал, что они базируются на ряде допущений. Основными из них являются следующие: (1) первичные и повторные заявки идентичны по всем показателям; (2) заявки могут лишь один раз повторять запрос для обслуживания; (3) заявки обоих типов передаются единым сервером.
Однако во многих реальных системах эти допущения не выполняются, поэтому в целях повышения адекватности моделей в настоящей статье изучается IFBQ, в которой указанные выше допущения не выполняются. При этом считается, что сервера специализированы по типу заявок и они являются гетерогенными, т.е. имеют различные скорости обслуживания (ранее системы с гетерогенными серверами при отсутствии обратной связи были изучены во многих работах, см., например, [15] и список ее литературы). Кроме того, в отличие от стандартного допущения о том, что входящий поток является пуассоновским, здесь изучается модель с пуассоновским потоком с Марковской модуляцией (Markov modulated Poisson process, MMPP-поток) [16]. Отметим, что для изучения предложенной модели используется метод иерархического укрупнения состояний многомерных ЦМ [17]. Применение данного метода позволяет разработать эффективные численные процедуры расчета характеристик представленной системы.
Статья имеет следующую структуру. В разд. 1 описана изучаемая система и дана постановка задачи. В разд. 2 приведена математическая модель системы в виде 3DMC и определена ее производящая матрица. Получено условие эргодичности модели и разработан приближенный метод расчета стационарных вероятностей состояний и характеристик системы. В разд. 3 приводятся результаты численных экспериментов.
1. Описание системы с мгновенной обратной связью и постановка задачи. Структурная схема изучаемой системы показана на рис. 1. На вход одноканальной системы с неограниченным буфером поступает MMPP-поток с параметрами $\left( {\Sigma ,\,\Lambda } \right)$, где $\Sigma = \left\| {{{\sigma }_{{ij}}}} \right\|$ – производящая матрица (ПМ) ЦМ с $N > 1$ возможными состояниями, которая управляет интенсивностью входящего потока, а вектор $\Lambda = \left( {{{\lambda }_{1}},\,{{\lambda }_{2}},\,...,\,{{\lambda }_{N}}} \right)$ задает значения интенсивностей входящего потока. Это означает, что ${{\sigma }_{{ij}}}$ определяет интенсивность перехода из состояния i в состояние j, где
Считается, что когда ЦМ находится в состояние $n$, интенсивность входящего извне потока равна ${{\lambda }_{n}},\,n = \overline {1,\,N} $, и с изменением состояния управляющей ЦМ мгновенно изменяется и интенсивность входящего потока.
Система содержит два сервера: высокоскоростной (F-сервер) и низкоскоростной (S-сервер), при этом p-заявки, как правило, обслуживаются в F-сервере. После завершения обслуживания p-заявка, согласно схеме Бернулли, либо с вероятностью α покидает систему, либо с вероятностью $1 - \alpha $ направляется обслуживаться в S-сервере. Заявки, которые требуют повторного обслуживания (вторичные заявки, s-заявки), могут образовывать очередь перед S-сервером. Считается, что s-заявки многократно могут потребовать повторного обслуживания, т.е. после завершения обслуживания каждая s-заявка независимо от других заявок, согласно схеме Бернулли, либо с вероятностью β окончательно покидает систему, либо с дополнительной вероятностью $1 - \beta $ мгновенно требует повторного обслуживания в S-сервере. Времена обслуживания заявок в F-сервере и в S-сервере являются случайными величинами, которые имеют экспоненциальное распределение с параметрами ${{\mu }_{f}}$ и ${{\mu }_{s}}$ соответственно, при этом ${{\mu }_{s}} < {{\mu }_{f}}$.
Если в момент поступления p-заявки число заявок в очереди перед F-сервером выше определенного порогового значение $M > 0$ и при этом S-сервер не занят, то поступившая p-заявка либо с вероятностью $\sigma $ направляется для обслуживания в S-сервер, либо с дополнительной вероятностью $1 - \sigma $ она присоединяется в “свою” очередь. Обслуживание разнотипных заявок и изменения состояний ЦМ, которая управляет интенсивностью входящего потока, являются независимыми друг от друга случайными процессами.
Задача состоит в нахождении совместного распределения состояний MMPP-потока и числа заявок каждого типа в системе. Решение этой задачи позволит найти характеристики системы – среднее число p-заявок $\left( {{{L}_{p}}} \right)$ и s-заявок $\left( {{{L}_{s}}} \right)$ в системе; интенсивность p-заявок, которые обслуживаются в S-сервере $\left( {{{R}_{{ps}}}} \right)$.
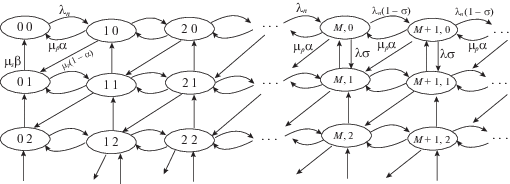
2. Расчет стационарного распределения системы и ее характеристики. Состояние системы определяется трехмерным вектором $(n,\,k,\,r)$, где $n$ – состояние управляющей интенсивностью входящего потока ЦМ, k – суммарное число заявок перед F-сервером и заявки в нем, r – суммарное число заявок перед S-сервером и заявки в нем. Тогда пространство состояний этой трехмерной ЦМ определяется как декартово произведение трех множеств:
(2.1)
$E = \{ \overline {1,\,N} \} \times \left\{ {0,\,1,\,...,\,} \right\} \times \left\{ {0,\,1,\,...,\,} \right\}.$Интенсивность перехода из состояния $(n,k,r)$ в состояние $(n{\kern 1pt} ',k{\kern 1pt} ',r{\kern 1pt} ')$ обозначим через q((n, k, r), $(n{\kern 1pt} ',k{\kern 1pt} ',r{\kern 1pt} '))$. Эти величины вычисляются следующим образом:
– переходы $(n,k,r) \to \left( {n{\kern 1pt} ',k,r} \right)$, $n{\kern 1pt} ' \ne n$ осуществляются с интенсивностью ${{\sigma }_{{n,n{\kern 1pt} '}}}$ при изменении состояния MMPP-потока;
– переходы $(n,k,r) \to \left( {n,k + 1,r} \right)$, r > 0, и $(n,k,0) \to \left( {n,k + 1,0} \right)$, $k < M$, осуществляются с интенсивностью ${{\lambda }_{n}}$ при поступлении p-заявки;
– переходы $\left( {n,k,0} \right) \to \left( {n,k + 1,0} \right)$, $k \geqslant M$, осуществляются с интенсивностью ${{\lambda }_{n}}\left( {1 - \sigma } \right)$ при поступлении p-заявки;
– переходы $\left( {n,k,0} \right) \to \left( {n,k + 1,1} \right)$, $k \geqslant M$, осуществляются с интенсивностью ${{\lambda }_{n}}\sigma $ при поступлении p-заявки;
– переходы $(n,k,r) \to \left( {n,k - 1,r} \right)$, k > 0, осуществляются с интенсивностью ${{\mu }_{f}}\alpha $ при завершении обслуживания p-заявки в F-сервере и ухода ее из системы;
– переходы $(n,k,r) \to \left( {n,k - 1,r + 1} \right)$, k > 0, осуществляются с интенсивностью ${{\mu }_{f}}\left( {1 - \alpha } \right)$ при завершении обслуживания p-заявки в F-сервере и возвращении в S-сервер для повторного обслуживания;
– переходы $(n,0,r) \to \left( {n,0,r - 1} \right)$, r > 0, осуществляются с интенсивностью ${{\mu }_{s}}\beta $ при завершении обслуживания заявки в S-сервере.
Следовательно, положительные элементы ПМ данной трехмерной ЦМ определяются из следующих соотношений:
(2.2)
$q\left( {\left( {n,k,r} \right),\left( {n{\kern 1pt} ',k{\kern 1pt} ',r{\kern 1pt} '} \right)} \right) = \left\{ \begin{gathered} {{\sigma }_{{nn'}}},\quad {\text{если}}\quad n{\kern 1pt} ' \ne n,\quad k{\kern 1pt} ' = k,\quad r{\kern 1pt} ' = r, \hfill \\ {{\lambda }_{n}},\quad {\text{если}}\quad r > 0,\quad n{\kern 1pt} ' = n,\quad k{\kern 1pt} ' = k + 1,\quad r{\kern 1pt} ' = r \hfill \\ {\text{или}}\quad k < M,\quad r = 0,\quad n{\kern 1pt} ' = n,\quad k{\kern 1pt} ' = k + 1,\quad r{\kern 1pt} ' = r, \hfill \\ {{\lambda }_{n}}\sigma ,\quad {\text{если}}\quad r = 0,\quad n{\kern 1pt} ' = n,\quad k{\kern 1pt} ' = k,\quad r{\kern 1pt} ' = 1, \hfill \\ {{\lambda }_{n}}(1 - \sigma ),\quad {\text{если}}\quad k \geqslant M,\quad r = 0,\quad n{\kern 1pt} ' = n,\quad k{\kern 1pt} ' = k + 1,\quad r{\kern 1pt} ' = r, \hfill \\ {{\mu }_{f}}\alpha ,\quad {\text{если}}\quad k > 0,\quad n{\kern 1pt} ' = n,\quad k{\kern 1pt} ' = k - 1,\quad r{\kern 1pt} ' = r, \hfill \\ {{\mu }_{f}}(1 - \alpha ),\quad {\text{если}}\quad k > 0,\quad n{\kern 1pt} ' = n,\quad k{\kern 1pt} ' = k - 1,\quad r{\kern 1pt} ' = r + 1,{\text{ }} \hfill \\ {{\mu }_{s}}\beta ,\quad {\text{если}}\quad k = 0,\quad r > 0,\quad n{\kern 1pt} ' = n,\quad k{\kern 1pt} ' = 0,\quad r{\kern 1pt} ' = r - 1. \hfill \\ \end{gathered} \right.$Стационарную вероятность состояния $(n,k,r) \in E$ обозначим через $p(n,k,r)$. Условие существования стационарного режима получено ниже.
Нахождения вероятностей состояний являются достаточным для вычисления характеристики изучаемой системы. Так, среднее число p-заявок (Lp) и s-заявок (Ls) в системе определяются как математическое ожидание соответствующих случайных величин:
(2.3)
${{L}_{p}} = \sum\limits_{n = 1}^N {\sum\limits_{k = 1}^\infty {k\sum\limits_{r = 0}^\infty {p\left( {n,k,r} \right)} } } ;$(2.4)
${{L}_{s}} = \sum\limits_{n = 1}^N {\sum\limits_{r = 1}^\infty {r\sum\limits_{k = 0}^\infty {p\left( {n,k,r} \right)} } } .$Интенсивность p-заявок, которые обслуживаются в S-сервере $\left( {{{R}_{{ps}}}} \right)$, определяется как
(2.5)
${{R}_{{ps}}} = \sigma \sum\limits_{n = 1}^N {{{\lambda }_{n}}} \sum\limits_{k = M}^\infty {p\left( {n,k,0} \right)} .$Использование метода многомерных производящих функций для нахождения вероятностей состояний сталкивается с рядом методологических и вычислительных трудностей. Исходя из этого, ниже приводится альтернативный метод решения данной задачи, основанный на иерархическом методе фазового укрупнения состояний многомерных ЦМ [17].
Предложенный метод можно корректно применить для систем, в которых MMPP-поток является инерционным, т.е. в достаточно больших интервалах времени интенсивность входящего потока является постоянной величиной.
При выполнении указанного выше допущения рассмотрим следующее расщепление пространства состояний (2.1):
(2.6)
$E = \bigcup\limits_{n = 1}^N {{{E}_{n}}} ,\quad {{E}_{n}} \cap {{E}_{{n{\kern 1pt} '}}} = \emptyset ,\quad {\text{если}}\quad n \ne n{\kern 1pt} ',$Все состояния из класса ${{E}_{n}}$ объединяются в одно укрупненное состояние 〈n〉, и на основе расщепления (2.6) в пространстве состояний (2.1) определяется функция укрупнения ${{U}_{1}}(n,k,r)$ = $\langle n\rangle $, $(n,k,r) \in {{E}_{n}}$. Множество укрупненных состояний 〈n〉 обозначим через ${{\Omega }_{1}} = \{ \langle n\rangle {\kern 1pt} :\;n = \overline {1,N} \} $. Тогда приближенные значения вероятностей состояний исходной модели, обозначаемые через $\tilde {p}(n,k,r),$ определяются как (см. [17])
где ${{\rho }_{n}}\left( {k,r} \right)$ – вероятность состояния (k, r) внутри расщепленной модели с пространством состояний ${{E}_{n}}$, ${{\pi }_{1}}\left( {\left\langle n \right\rangle } \right)$ – вероятность укрупненного состояния $\left\langle n \right\rangle \in {{\Omega }_{1}}.$Как было отмечено выше, переходы между состояниями управляющей интенсивностью входящего потока ЦМ не зависят от статусов F-сервера и S-сервера, поэтому вероятности состояний ${{\pi }_{1}}\left( {\left\langle n \right\rangle } \right)$, $\left\langle n \right\rangle \in {{\Omega }_{1}}$, определяются с помощью ее ПМ Σ.
Следовательно, для нахождения вероятности состояний исходной модели потребуется лишь определение стационарных распределений двумерных ЦМ с пространствами состояний En, $n = \overline {1,\,N} $ (см. формулу (2.7)). Для решения задачи к этим двумерным ЦМ применяется процедура укрупнения (второй уровень иерархии). Поскольку все расщепленные модели с пространствами состояний En идентичны, то зафиксируем значение параметра $n,\,\,n = \overline {1,\,N} $. Граф переходов между состояниями En показан на рис. 2.
В классе ${{E}_{n}}$ рассмотрим следующее разбиение:
(2.8)
${{E}_{n}} = \bigcup\limits_{r = 0}^\infty {E_{n}^{r}} ,\quad E_{n}^{r} \cap E_{n}^{{r{\kern 1pt} '}} = \emptyset ,\quad {\text{если }}r \ne r{\kern 1pt} ',$Все состояния из класса $E_{n}^{r}$ объединяются в одно укрупненное состояние $\left\langle r \right\rangle $, и на основе расщепления (2.8) в пространстве состояний En определяется функция укрупнения ${{U}_{2}}\left( {k,r} \right) = \left\langle r \right\rangle $, $\left( {k,r} \right) \in E_{n}^{r}$. Множество укрупненных состояний $\left\langle r \right\rangle $ обозначим через ${{\Omega }_{2}} = \left\{ {\left\langle r \right\rangle {\kern 1pt} :\;n = 0,1,2,...} \right\}.$
Согласно [17], имеем
(2.9)
${{\rho }_{n}}\left( {k,r} \right) = \rho _{n}^{r}\left( k \right)\pi _{2}^{n}\left( {\left\langle r \right\rangle } \right),$В классе $E_{n}^{r}$, $r = 0,1,...$, в векторе состояний вторая компонента является постоянной и равна r. Поэтому при изучении расщепленных моделей с пространством $E_{n}^{r}$ каждое состояние $(k,r)$ может быть задано лишь первой компонентой, т.е. далее состояние $(k,r) \in E_{n}^{r}$ обозначается как k, $k = 0,1,...$
Тогда из соотношений (2.2) заключаем, что интенсивности переходов между состояниями расщепленной модели с пространством состояний $E_{n}^{r}$, $r = 0,1,...$, зависят от параметра r, $r = 0,1$, ..., и определяются следующим образом (см. рис. 2).
Для случая r = 0:
(2.10)
$q_{n}^{0}\left( {k,k{\kern 1pt} '} \right) = \left\{ \begin{gathered} {{\lambda }_{n}},\quad {\text{если}}\quad k < M,\quad k{\kern 1pt} ' = k + 1, \hfill \\ {{\lambda }_{n}}\left( {1 - \sigma } \right),\quad {\text{если}}\quad k \geqslant M,\quad k{\kern 1pt} ' = k + 1, \hfill \\ {{\mu }_{f}}\alpha ,\quad {\text{если}}\quad k{\kern 1pt} ' = k - 1. \hfill \\ \end{gathered} \right.$Для случаев r > 0:
(2.11)
$q_{n}^{r}\left( {k,k{\kern 1pt} '} \right) = \left\{ \begin{gathered} {{\lambda }_{n}},\quad {\text{если}}\quad k{\kern 1pt} ' = k + 1, \hfill \\ {{\mu }_{f}}\alpha ,\quad {\text{если}}\quad k{\kern 1pt} ' = k - 1. \hfill \\ \end{gathered} \right.$Из (2.10) получаем, что при выполнении условия ${{\nu }_{n}} < {{\left( {1 - \sigma } \right)}^{{ - 1}}}$, ${{\nu }_{n}} = {{{{\lambda }_{n}}} \mathord{\left/ {\vphantom {{{{\lambda }_{n}}} {{{\mu }_{f}}\alpha }}} \right. \kern-0em} {{{\mu }_{f}}\alpha }}$, вероятности состояний расщепленной модели с пространством состояний $E_{n}^{0}$ определяются так:
(2.12)
$\rho _{n}^{0}\left( k \right) = \left\{ \begin{gathered} \nu _{n}^{k}\rho _{n}^{0}\left( 0 \right),\quad {\text{если}}\quad 0 \leqslant k \leqslant M, \hfill \\ \frac{1}{{{{{\left( {1 - \sigma } \right)}}^{M}}}}{{\left( {{{\nu }_{n}}\left( {1 - \sigma } \right)} \right)}^{k}}\rho _{n}^{0}\left( 0 \right),\quad {\text{если}}\quad k > M, \hfill \\ \end{gathered} \right.$После стандартных преобразований получим
(2.13)
$\rho _{n}^{0}\left( 0 \right) = {{\left( {\frac{{1 - \nu _{n}^{{M + 1}}}}{{1 - {{\nu }_{n}}}} + \nu _{n}^{{M + 1}}\frac{{1 - \sigma }}{{1 - {{\nu }_{n}}\left( {1 - \sigma } \right)}}} \right)}^{{ - 1}}}.$Замечание 1. Поскольку условие ${{\nu }_{n}} < {{\left( {1 - \sigma } \right)}^{{ - 1}}}$ верно для каждого $n,\,n = \overline {1,\,N} $, то получаем, что должно выполняться условие
(2.14)
$\mathop {\max }\limits_{n = \overline {1,N} } \left\{ {{{\nu }_{n}}} \right\} < {{\left( {1 - \sigma } \right)}^{{ - 1}}}\;.$Из (2.11) получаем, что если ${{\nu }_{n}} < 1$, то вероятности состояний расщепленных моделей с пространствами состояний $E_{n}^{r}$ не зависят от индекса $r,\,r = 0,\,1,\,...,$ и определяются как
(2.15)
$\rho _{n}^{r}\left( k \right) = \left( {1 - {{\nu }_{n}}} \right)\nu _{n}^{k},\quad k = 0,1,...$Замечание 2. Поскольку условие ${{\nu }_{n}} < 1$ должно быть верно для каждого $n,\,n = \overline {1,\,N} $, то должно выполняться условие
Тогда, объединяя (2.14) и (2.16), получаем первое условие эргодичности модели, т.е. должно выполняться (2.16).
Учитывая (2.2), (2.12), (2.13) и (2.15), интенсивности переходов между состояниями ${{\Omega }_{2}}$ определяются следующим образом (см. рис. 2):
(2.17)
${{q}_{n}}\left( {\left\langle r \right\rangle ,\left\langle {r{\kern 1pt} '} \right\rangle } \right) = \left\{ \begin{gathered} {{\eta }_{n}}\left( {0,1} \right),\quad {\text{если}}\quad r = 0,\quad r{\kern 1pt} ' = 1, \hfill \\ {{\mu }_{f}}\left( {1 - \alpha } \right){{\nu }_{n}},\quad {\text{если}}\quad r > 0{\kern 1pt} ',\quad r{\kern 1pt} ' = r + 1, \hfill \\ {{\mu }_{s}}\beta ,\quad {\text{если}}\quad r > 0,\quad r{\kern 1pt} ' = r - 1. \hfill \\ \end{gathered} \right.$Согласно (2.12) и (2.13), величина ${{\eta }_{n}}\left( {0,\,1} \right)$ в формуле (2.17) определяется как
Из (2.17) получаем, что при выполнении условия ${{\psi }_{n}} < 1$, ${{\psi }_{n}} = {{{{\mu }_{f}}\left( {1 - \alpha } \right){{\nu }_{n}}} \mathord{\left/ {\vphantom {{{{\mu }_{f}}\left( {1 - \alpha } \right){{\nu }_{n}}} {{{\mu }_{s}}\beta }}} \right. \kern-0em} {{{\mu }_{s}}\beta }}$, вероятности состояний укрупненной модели с пространством состояний Ω2 находятся так (см. рис. 2):
(2.18)
$\pi _{2}^{n}\left( {\left\langle r \right\rangle } \right) = \left\{ \begin{gathered} {{\theta }_{n}}\pi _{2}^{n}\left( {\left\langle 0 \right\rangle } \right),\quad {\text{если}}\quad r = 1, \hfill \\ {{\theta }_{n}}\psi _{n}^{{r - 1}}\pi _{2}^{n}\left( {\left\langle 0 \right\rangle } \right),\quad {\text{если}}\quad r > 1, \hfill \\ \end{gathered} \right.$После стандартных преобразований получим
(2.19)
$\pi _{2}^{n}\left( {\left\langle 0 \right\rangle } \right) = \frac{{1 - {{\psi }_{n}}}}{{1 - {{\psi }_{n}} + {{\theta }_{n}}}}.$Замечание 3. Поскольку условие ${{\psi }_{n}} < 1$ верно для каждого $n,\,n = \overline {1,\,N} $, то находим второе условие эргодичности модели:
(2.20)
$\mathop {\max }\limits_{n = \overline {1,N} } \left\{ {{{\nu }_{n}}} \right\} < \frac{{{{\mu }_{s}}\beta }}{{{{\mu }_{f}}\left( {1 - \alpha } \right)}}\;.$Объединяя соотношения (2.16) и (2.20), получаем следующее условие эргодичности модели:
(2.21)
$\mathop {\max }\limits_{n = \overline {1,N} } \left\{ {{{\nu }_{n}}} \right\} < \min \left\{ {\frac{{{{\mu }_{s}}\beta }}{{{{\mu }_{f}}\left( {1 - \alpha } \right)}}\;,\,\;1} \right\}.$Таким образом, при выполнении условия эргодичности модели (2.21) с учетом соотношений (2.7), (2.9), (2.12), (2.13), (2.18) и (2.19) находятся приближенные значения стационарных вероятностей состояний исходной трехмерной ЦМ.
Далее с использованием стационарных вероятностей состояний могут быть рассчитаны приближенные значения характеристик (2.3)–(2.5). Действительно, из (2.7) и (2.9) заключаем, что указанные характеристики вычисляются следующим образом:
(2.22)
${{L}_{p}} \approx \sum\limits_{n = 1}^N {{{\pi }_{1}}\left( {\left\langle n \right\rangle } \right)} \sum\limits_{k = 1}^\infty {k\sum\limits_{r = 0}^\infty {\rho _{n}^{r}\left( k \right)\pi _{2}^{n}\left( {\left\langle r \right\rangle } \right)} } ;$(2.23)
${{L}_{s}} \approx \sum\limits_{n = 1}^N {{{\pi }_{1}}\left( {\left\langle n \right\rangle } \right)\sum\limits_{r = 1}^\infty {r\pi _{2}^{n}\left( {\left\langle r \right\rangle } \right)} } ;$(2.24)
${{R}_{{ps}}} \approx \sigma \sum\limits_{n = 1}^N {{{\pi }_{1}}\left( {\left\langle n \right\rangle } \right)\sum\limits_{k = M}^\infty {\rho _{n}^{0}\left( k \right)\pi _{2}^{n}\left( {\left\langle 0 \right\rangle } \right)} } .$Тогда после определенных математических выкладок из (2.22)–(2.24) получим
(2.25)
${{L}_{p}} \approx \sum\limits_{n = 1}^N {{{\pi }_{1}}\left( {\left\langle n \right\rangle } \right)} (\Psi _{n}^{1} + \Psi _{n}^{2} + \Psi _{n}^{3}),$(2.26)
${{L}_{s}} \approx \sum\limits_{n = 1}^N {{{\pi }_{1}}\left( {\left\langle n \right\rangle } \right)\pi _{2}^{n}\left( {\left\langle 0 \right\rangle } \right)\frac{{{{\theta }_{n}}}}{{{{{\left( {1 - {{\psi }_{n}}} \right)}}^{2}}}}} ,$(2.27)
${{R}_{{ps}}} \approx \sigma \sum\limits_{n = 1}^N {\frac{{\nu _{n}^{M}}}{{1 - {{\nu }_{n}}\left( {1 - \sigma } \right)}}{{\pi }_{1}}\left( {\left\langle n \right\rangle } \right)\pi _{2}^{n}\left( {\left\langle 0 \right\rangle } \right)\rho _{n}^{0}\left( 0 \right)} .$3. Численные результаты. Проводимые здесь численные эксперименты имеют две цели: 1) показать высокую точность разработанного алгоритма приближенного вычисления стационарных вероятностей состояний изучаемой системы; 2) изучить поведение характеристик системы относительно изменения порогового параметра $M$ и решить задачу выбора его оптимального (в заданном смысле) значения.
Точность приближенного алгоритма оценивается с помощью имитационного моделирования. При этом близость результатов, полученных с применением различных подходов, оценивается с помощью нормы подобия косинуса, т.е.
(3.1)
$\left\| {\rm N} \right\| = \frac{{\left( {{\mathbf{p}},{\mathbf{\tilde {p}}}} \right)}}{{\left| {\mathbf{p}} \right|\left| {{\mathbf{\tilde {p}}}} \right|}},$Отметим, что, как правило, норма подобия косинуса используется для определения ориентации двух векторов, а не для сравнения их величин. Однако в нашем случае эта мера адекватно оценивает близость конечных точек векторов p и ${\mathbf{\tilde {p}}}$, так как, согласно нормирующему условию, имеем
Иными словами, конечные точки векторов p и ${\mathbf{\tilde {p}}}$ находятся в одной гиперплоскости.
Сначала рассмотрим случай, когда значения интенсивностей входящего потока фиксированы, а интенсивности обслуживания разнотипных серверов меняются. В этом случае в проводимых экспериментах исходные данные гипотетической модели определяются следующим образом. ПМ ЦМ, которая управляет интенсивностью входящего MMPP-потока с N = 3 состояниями, задается как
Значения интенсивностей входящего потока $\Lambda = \left( {15,\,10,\,5} \right)$. Параметры схем Бернулли выбирались так: $\alpha = 0.8$; $\beta = 0.4$; σ = 0.1.
Сравнительный анализ результатов приближенного алгоритма и метода имитационного моделирования для этой серии вычислительных экспериментов показаны в табл. 1.
Таблица 1.
Оценка точности алгоритма вычисления стационарных вероятностей состояний системы. Случай фиксированных значений интенсивностей входящего MMPP-потока
| $\left( {{{\mu }_{f}},\,\;{{\mu }_{s}}} \right)$ | M | Значения нормы (3.1) |
|---|---|---|
| (60, 45) | 1 | 0.9945 |
| 2 | 0.9940 | |
| 3 | 0.9914 | |
| (60, 50) | 1 | 0.9931 |
| 2 | 0.9948 | |
| 3 | 0.9927 | |
| (60, 55) | 1 | 0.9943 |
| 2 | 0.9951 | |
| 3 | 0.9954 | |
| (65, 45) | 1 | 0.9936 |
| 2 | 0.9944 | |
| 3 | 0.9936 | |
| (65, 50) | 1 | 0.9941 |
| 2 | 0.9958 | |
| 3 | 0.9953 | |
| (65, 55) | 1 | 0.9952 |
| 2 | 0.9949 | |
| 3 | 0.9958 | |
| (70, 45) | 1 | 0.9946 |
| 2 | 0.9955 | |
| 3 | 0.9950 | |
| (70, 50) | 1 | 0.9944 |
| 2 | 0.9968 | |
| 3 | 0.9960 | |
| (70, 55) | 1 | 0.9964 |
| 2 | 0.9970 | |
| 3 | 0.9960 |
Нами также выполнены вычислительные эксперименты для случаев, когда и значения интенсивностей входящего потока, и интенсивности обслуживания разнотипных серверов меняются. В проводимых трех сериях экспериментов параметры схем Бернулли оставались неизменными. В первой серии экспериментов ПМ ЦМ, которая управляет интенсивностью входящего MMPP-потока с N = 3 состояниями, выбиралась так же, как и ранее (т.е. она равна ${{\Sigma }_{1}}$), при этом значения интенсивностей входящего потока выбирались как ${{\Lambda }_{1}} = (10,5,3)$. Во второй и третьей сериях экспериментов ПМ ЦМ, которые управляют интенсивностями входящего MMPP-потока с N = 3 состояниями, и соответствующие им значения интенсивностей входящего потока выбирались следующим образом:
Результаты указанных экспериментов показаны в табл. 2. Из табл. 1 и 2 видно, что разработанный алгоритм имеет высокую точность, так как значение нормы (3.1) практически равно единице.
Таблица 2.
Оценка точности алгоритма вычисления стационарных вероятностей состояний системы. Случай нефиксированных значений интенсивностей входящего MMPP-потока
| Λ | $\left( {{{\mu }_{f}},\,\;{{\mu }_{s}}} \right)$ | M | Значения нормы (3.1) |
|---|---|---|---|
| (10, 5, 3) | (60, 45) | 1 | 0.9979 |
| 2 | 0.9979 | ||
| 3 | 0.9973 | ||
| (65, 50) | 1 | 0.9983 | |
| 2 | 0.9984 | ||
| 3 | 0.9971 | ||
| (70, 55) | 1 | 0.9986 | |
| 2 | 0.9986 | ||
| 3 | 0.9986 | ||
| (15, 12, 17) | (60, 45) | 1 | 0.9924 |
| 2 | 0.9934 | ||
| 3 | 0.9914 | ||
| (65, 50) | 1 | 0.9953 | |
| 2 | 0.9949 | ||
| 3 | 0.9945 | ||
| (70, 55) | 1 | 0.9955 | |
| 2 | 0.9962 | ||
| 3 | 0.9964 | ||
| (20, 10, 5) | (60, 45) | 1 | 0.9892 |
| 2 | 0.9868 | ||
| 3 | 0.9867 | ||
| (65, 50) | 1 | 0.9903 | |
| 2 | 0.9904 | ||
| 3 | 0.9917 | ||
| (70, 55) | 1 | 0.9933 | |
| 2 | 0.9938 | ||
| 3 | 0.9936 |
Замечание 4. Поскольку система является бесконечномерной (по второй и третьей компоненте вектора состояний), то при вычислении нормы (3.1) максимальное число заявок каждого типа в системе сверху огранивается достаточно большими конечными величинами. Такая замена является оправданной, так как при превышении этими величинами определенных (достаточно больших) значений соответствующие вероятности состояний становятся бесконечно малыми величинами, т.е. практически равными нулю.
Разработанные приближенные формулы позволяют также изучить поведения нормы подобия (3.1) относительно изменения любых (структурных и нагрузочных) параметров системы. Из-за ограниченности объема работы и для конкретности изложения здесь приводятся лишь результаты, которые показывают поведение указанной величины относительно изменения параметра $\sigma $ (рис. 3). Из графика видно, что с ростом значения этого параметра ухудшается точность формул вычисления приближенных значений вероятностей состояний исходной трехмерной ЦМ. Иными словами, чем меньше значения указанного параметра, тем выше точность предложенных формул. Однако даже в наихудших случаях, когда значения этого параметра близки к единице, значения нормы (3.1) оказываются больше 0.9, т.е. разработанные приближенные формулы имеют достаточно высокую точность.
Такое поведение нормы (3.1) относительно параметра $\sigma $ имеет вполне логическое объяснение. Действительно, из теории фазового укрупнения состояний ЦМ [3] известно, что чем меньше интенсивности переходов между расщепленными классами состояний, тем выше точность алгоритмов метода фазового укрупнения. Для изучаемой здесь модели при малых значениях параметра $\sigma $ интенсивности переходов между расщепленными классами $E_{n}^{r}\,,\,r = 0,\,1,\,...$ (см. формулы (2.8) и рис. 2), оказываются малыми величинами и с его ростом увеличивается интенсивность переходов между расщепленными классами.
Отметим, что аналогичные поведения нормы (3.1) наблюдаются относительно изменения параметров $\alpha $ и $\beta $, т.е. с ростом параметра $\alpha $ значениe нормы систематически растет, а с ростом параметра $\beta $, наоборот, она систематически уменьшается (отметим, что в отличие от параметра $\sigma $, области изменения параметров $\alpha $ и $\beta $ определяются из условия эргодичности системы (2.21)).
Поведения характеристик системы относительно изменения порогового параметра M при указанных выше параметрах MMPP-потока и при $({{\mu }_{f}},{{\mu }_{s}}) = (70,55)$, $\sigma = 0.4$, показаны на рис. 4. Функция Lp является неубывающая (рис. 4, а), что и следовало ожидать, так как с увеличением параметра M растут шансы первичных заявок присоединиться к своей очереди. По той же причине функции ${{L}_{s}}$ (рис. 4, б) и ${{R}_{{ps}}}$ (рис. 4, в) являются невозрастающими.
Отметим, что с увеличением параметра $\beta $ увеличивается нагрузка S-сервера и тем самым уменьшаются шансы первичных заявок обслуживаться в этом сервере, поэтому увеличивается число таких заявок перед F-сервером (см. рис. 4, а). С увеличением параметра $\alpha $ уменьшается нагрузка S-сервера, тем самым уменьшается число таких заявок в системе (см. рис. 4, б). Значения функции ${{R}_{{ps}}}$ при различных соотношениях параметров $\alpha $ и $\beta $ почти не отличаются друг от друга (см. рис. 4, в).
Заметим, что для выбранных исходных данных при $M \geqslant 3$ изучаемые функции становятся почти постоянными. Это обстоятельство позволяет ставить задачу нахождения таких значений этого параметра, чтобы минимизировать суммарные штрафы (total cost, (TC)), связанные с пребыванием разнотипных заявок в очереди и обслуживанием первичных заявок в низкоскоростном сервере. Так, пусть штрафы за пребывания одной первичной и повторной заявки в системе равны cp и cs, а штраф за обслуживания p-заявки в S-сервере равен ${{c}_{{ps}}}$. Тогда задача оптимизации ставится так:
где $TC = {{c}_{p}}{{L}_{p}} + {{c}_{s}}{{L}_{s}} + {{c}_{{ps}}}{{R}_{{ps}}}\;.$Результаты решения задачи (3.2) для следующих исходных данных показаны в табл. 3:
Таблица 3.
Результаты решения задачи (3.2)
| $\left( {{{\mu }_{f}},\,\;{{\mu }_{s}}} \right)$ | α | M* | $T{{C}_{{\min }}}$ |
|---|---|---|---|
| (60, 45) | 0.7 | 6 | 2.927 |
| 0.8 | 8 | 1.959 | |
| 0.9 | 11 | 1.482 | |
| (65, 45) | 0.7 | 8 | 2.509 |
| 0.8 | 10 | 1.708 | |
| 0.9 | 13 | 1.303 | |
| (65, 50) | 0.7 | 7 | 2.389 |
| 0.8 | 10 | 1.681 | |
| 0.9 | 13 | 1.295 | |
| (70, 55) | 0.7 | 9 | 2.033 |
| 0.8 | 12 | 1.475 | |
| 0.9 | 15 | 1.152 |
К сожалению, не удается решить задачу (3.2) аналитически из-за сложного вида функционала. Потому и не удается делать какие-то общие выводы относительно решения задачи (3.2). Вместе с тем в проводимых численных экспериментах существует оптимальное решение задачи (3.2), при этом указанное в табл. 3 оптимальное значение ${{M}^{*}}$является минимальным значением этого параметра, при котором достигается минимум функционала TC, т.е. при $M \geqslant M{\text{*}}$ он становится постоянным.
Заключение. В работе изучается модель системы с гетерогенными серверами, MMPP-потоком и мгновенной обратной связью. После завершения обслуживания в высокоскоростном сервере первичные заявки, согласно схеме Бернулли, либо покидают систему, либо мгновенно требуют повторного обслуживания. Повторные заявки обслуживаются в S-сервере, при этом после завершения обслуживания повторные заявки могут многократно повторяться. Если в момент поступления первичной заявки S-сервер свободен и число заявок в очереди перед F-сервером превышает определенное пороговое значение, то поступившая заявка, согласно схеме Бернулли, либо направляется для обслуживания в S-сервер, либо присоединяется в свою очередь. Считается, что первичные и повторные заявки могут образовать очереди бесконечной длины.
Показано, что математической моделью изучаемой системы является некоторая трехмерная ЦМ с бесконечномерным пространством состояний. Найдено условие эргодичности модели и разработан приближенный алгоритм расчета вероятностей состояний соответствующей ЦМ. С помощью численных экспериментов показана высокая точность рассмотренного алгоритма и решена задача нахождения оптимального значения введенного порогового параметра, чтобы минимизировать суммарные штрафы, связанные с пребыванием разнотипных заявок в очереди и обслуживанием первичных заявок в S-сервере.
Список литературы
Takacs L. A Single Server Queue with Feedback // Bell System Technical J. 1963. V. 42. P. 505–519.
Takacs L. A Queuing Model with Feedback // Operations Research. 1977. V. 11. P. 345–354.
Melikov A.Z., Ponomarenko L.A., Rustamov A.M. Methods for Analysis of Queuing Models with Instantaneous and Delayed Feedbacks // Communications in Computer and Information sciences. 2015. V. 564. P. 185–199.
Sharma S.K., Kumar R. A Markovian Feedback Queue with Retention of Reneged Customers // Advanced Modeling and Optimization. 2012. V. 14. Iss. 3. P. 673–680.
Sharma S.K., Kumar R. A Markovian Feedback Queue with Retention of Reneged Customers and Balking // Advanced Modeling and Optimization. 2012. V. 14. Iss. 3. P. 681–688.
Sharma S.K., Kumar R. M/M/1 Feedback Queueing Model with Retention of Reneged Customers and Balking // American J. Operational Research. 2013. V. 3. Iss. 3 (2A). P. 1–6.
Sharma S.K., Kumar R. A Single Server Markovian Feedback Queuing System with Discouraged Arrivals and Retention of Reneged Customers // American J. Operational Research. 2013. V. 4. Iss. 3. P. 35–39.
Kumar R., Jain N.K., Som B.K. Optimization of an M/M/1/N Feedback Queue with Retention of Reneged Customers // Operations Research and Decisions. 2014. V. 24. Iss. 3. P. 45–58.
Santkumaran A., Thangaraj V. A Single Server Queue with Impatient and Feedback Customers // Information and Management Science. 2000. V. 11. Iss. 3. P. 71–79.
Som B.K., Seth S. M/M/c/N Queuing System with Encouraged Arrivals, Reneging, Retention and Feedback Customers // Yugoslav J. of Operations Research. 2018. V. 28. Iss. 3. P. 333–344.
Bouchentouf A.A., Kadi M., Rabhi A. Analysis of Two Heterogeneous Server Queuing Model with Balking, Reneging and Feedback // Mathematical Sciences and Applications E-notes. 2013. V. 2. Iss. 2. P. 10–21.
Dudin A.N., Kazimirsky A.V., Klimenok V.I., Breuer L., Krieger U. The Queuing Model MAP/PH/1/N with Feedback Operating in a Markovian Random Environment // Austrian J. Statistics. 2005. V. 34. Iss. 2. P. 101–110.
Krishnamoorthy A., Manjunath A.S. On Queues with Priority Determined by Feedback // Calcutta Statistical Association Bulletin. 2018. V. 70. Iss. 1. P. 33–56.
NeutsM.F. Matrix-geometric solutions in stochastic models. An algorithmic approach. Baltimore: John Hopkins University Press, 1981. 332 p.
Меликов А.З., Мехбалыева Э.В. Анализ и оптимизация систем с гетерогенными серверами и скачкообразными приоритетами // Изв. РАН. ТиСУ. 2018. № 5. С. 56–74.
Fisher W., Meier-Hellstern K. The Markov Modulated Poisson Process (MMPP) cookbook // Performance Evaluation. 1992. V. 18. P. 149–171.
Melikov A. Z., PonomarenkoL.A., RustamovA.M. Hierarchical Space Merging Algorithm to Analysis of Open Tandem Queuing Networks // Cybernetics and System Analysis. 2016. V. 52. Iss. 6. P. 867–877.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления