Известия РАН. Теория и системы управления, 2021, № 6, стр. 136-146

Введение. Непрерывное повышение требований к точности пространственной ориентации космических аппаратов (КА) в процессе предстартовой подготовки выдвигает в качестве одной из главных задач повышение точности систем их начальной ориентации в условиях помех различной физической природы, возмущающих основание данных систем – сейсмоколебаний, ветровых возмущений, вибраций от работы агрегатов объекта и др. [1–10]. На сегодняшний день уже предложен ряд методов начальной ориентации бесплатформенных инерциальных навигационных систем (БИНС) в условиях действия различных возмущающих факторов [11–19]. Так в работах [11–13] получил развитие способ векторного согласования, который дает возможность осуществлять начальную выставку БИНС относительно предварительно выставленной базовой системы навигации (БСН). При этом предполагается, что БИНС абсолютно точно согласована с базовой системой отсчета. Очевидными недостатками такого подхода являются, во-первых, необходимость расширения приборного состава навигационной системы, во-вторых, обязательное решение задачи начальной ориентации БСН (причем также в условиях возмущающих воздействий) и, в-третьих, неизбежное повторение ошибок выставки БСН в определении начальной ориентации БИНС. Другими словами, здесь общая ошибка начальной ориентации БИНС есть сумма ошибок “памяти” БСН и ошибки выставки БИНС относительно БСН [11].

Другой способ, получивший в последнее время широкое применение, заключается в использовании глобальных навигационных спутниковых систем (ГНСС) [14–19]. Данный способ, в зависимости от решаемой задачи, предполагает установку на подвижном объекте двух или трех пространственно разнесенных антенн и определение угловой ориентации БИНС по показаниям разнесенных спутниковых приемников. Преимуществом такого подхода является отсутствие процедуры интегрирования показаний чувствительных элементов, приводящей к накоплению ошибок измерений с течением времени. В то же время низкая частота выдачи выходной информации ГНСС (от 1 до 20 Гц) и слабая помехоустойчивость алгоритмов обработки информации с разнесенных спутниковых приемников существенно затрудняют применение данного подхода для начальной выставки БИНС на подвижном основании [20–22].

В современных БИНС, использующих низкоточные микромеханические гироскопы, для решения задачи начальной выставки [23] широкое распространение получили комплементарные фильтры [23–27]. Принцип их действия состоит в суммировании с заданным весом углов ориентации, определенных по показаниям датчиков угловой скорости (ДУС) и акселерометров. Существенным недостатком данного подхода является отсутствие возможности учета динамических свойств параметров ориентации, измеряемых к тому же в условиях помех высокой интенсивности, свойства которых также не учитываются. Все это не позволяет достичь в комплементарных фильтрах требуемой на сегодняшний день точности и устойчивости процесса начальной ориентации БИНС на высокодинамичном подвижном основании [1–5].

В связи с этим возникает необходимость разработки динамического алгоритма оценки стохастических параметров начальной ориентации БИНС, инвариантного к характеру движения основания и обеспечивающего устойчивость и требуемую точность оценивания при самых общих предположениях о характере помех чувствительных элементов (ЧЭ) БИНС.

1. Постановка задачи. Для последующего решения задачи начальной ориентации БИНС на подвижном основании в общей постановке полагаем далее, что центр масс (ЦМ) КА соединен жестким стержнем длиной R (моделирующим корпус ракеты-носителя) с точкой на поверхности Земли с известной широтой φ и может вращаться вокруг нее с произвольной угловой скоростью во всех направлениях под действием внешних возмущений (рис. 1).

Также введем следующие системы координат (СК):

приборную СК (ПСК) J $0xyz$ с началом в ЦМ объекта, оси которой направлены по взаимно ортогональным осям чувствительности ЧЭ, входящих в состав БИНС;

географическую СК (ГСК) G OX_гY_гZ_г с началом в точке крепления стержня длиной R, ось X_г которой лежит в плоскости местного меридиана ($\Omega $ – угловая скорость вращения Земли), ось Y_г направлена от центра Земли, а ось Z_г дополняет систему координат до правой;

сопровождающую СК (ССК) S OXYZ с началом в ЦМ КА, ось Y которой проходит вдоль стержня длиной R, направления осей X, Y, Z в начальный момент времени совпадают с направлениями соответствующих осей ГСК X_г, Y_г, Z_г.

В соответствии с введенными СК под задачей начальной ориентации БИНС на подвижном основании далее понимается текущая оценка параметров разворота (в качестве которых рассматриваются углы Эйлера–Крылова) ПСК J относительно ГСК G.

Полагаем также, что в состав БИНС в качестве ЧЭ входят три акселерометра и три датчика угловой скорости, расположенные ортогонально в ЦМ объекта. С целью сохранения общности решения в качестве моделей помех чувствительных элементов БИНС выберем аддитивные белые гауссовские шумы (БГШ) с нулевыми математическими ожиданиями и известными интенсивностями как наиболее адекватные практике использования БИНС. Учет корреляции помех или наличия в них регулярных составляющих (в том числе с неизвестными параметрами) легко обеспечивается соответствующим расширением вектора оцениваемых параметров и не влияет на существо предлагаемого далее подхода [23]. В этом случае модели выходных сигналов чувствительных элементов БИНС имеют следующий вид:

для акселерометров

где ${{{\mathbf{Z}}}_{{\mathbf{a}}}} = \left[ {\begin{array}{*{20}{c}} {{{Z}_{{ax}}}}&{{{Z}_{{ay}}}}&{{{Z}_{{az}}}} \end{array}} \right]{{\,}^{{\text{T}}}}$ – вектор выходных сигналов трех ортогональных акселерометров, ${{{\mathbf{а}}}_{{\mathbf{J}}}} = \left[ {\begin{array}{*{20}{c}} {{{а}_{x}}}&{{{а}_{y}}}&{{{а}_{z}}} \end{array}} \right]{{\,}^{{\text{T}}}}$ – вектор ускорений ЦМ объекта в ПСК, ${{{\mathbf{W}}}_{{\mathbf{a}}}} = {{[\begin{array}{*{20}{c}} {{{W}_{{{{a}_{x}}}}}}&{{{W}_{{{{a}_{y}}}}}}&{{{W}_{{{{a}_{z}}}}}} \end{array}]}^{{\text{T}}}}$ – вектор помех измерения акселерометров (центрированный БГШ с матрицей интенсивностей ${{{\mathbf{D}}}_{{\mathbf{a}}}}$);

для ДУСов

где ${{{\mathbf{Z}}}_{{\mathbf{d}}}}\, = \,{{[\begin{array}{*{20}{c}} {{{Z}_{x}}}&{{{Z}_{y}}}&{{{Z}_{z}}} \end{array}]}^{{\text{T}}}}$ – вектор выходных сигналов трёх ортогональных ДУСов, Ω_J = ${{\left[ {\begin{array}{*{20}{c}} {{{\Omega }_{x}}}&{{{\Omega }_{y}}}&{{{\Omega }_{z}}} \end{array}} \right]}^{{\text{T}}}}$ – вектор абсолютной угловой скорости вращения ПСК, ${{{\mathbf{W}}}_{{\mathbf{d}}}} = {{\left[ {\begin{array}{*{20}{c}} {{{W}_{x}}}&{{{W}_{y}}}&{{{W}_{z}}} \end{array}} \right]}^{{\text{T}}}}$ – вектор помех измерения ДУСов (центрированный БГШ с матрицей интенсивностей D_d).

Таким образом, окончательно поставленную задачу можно сформулировать как задачу стохастического оценивания текущей ориентации ПСК J (триэдра БИНС) относительно ГСК G по зашумленным измерениям ЧЭ БИНС при apriori неопределенном характере изменения, во-первых, вектора угловой скорости ЦМ объекта относительно начала ГСК G (точки крепления стержня длиной R), а во-вторых, вектора угловой скорости триэдра БИНС относительно ЦМ объекта при неизвестных углах начального рассогласования ПСК J и ГСК G.

2. Решение задачи. На первом шаге для построения алгоритма оценки случайных текущих углов α, β, γ  разворота ПСК J относительно ССК S рассмотрим уравнения их истинного изменения во времени – уравнения Эйлера–Крылова [28]:

где ${{\alpha }_{0}},{{\beta }_{0}},{{\gamma }_{0}}$ – неизвестные углы начального рассогласования ПСК J и ССК S (т.е. и ГСК G), ${{\alpha }_{0}}$ – угол рыскания, ${{\beta }_{0}}$ – угол тангажа, ${{\gamma }_{0}}$ – угол крена, ${{{\mathbf{\omega }}}_{{\mathbf{J}}}} = \left[ {\begin{array}{*{20}{c}} {{{\omega }_{x}}}&{{{\omega }_{y}}}&{{{\omega }_{z}}} \end{array}} \right]{{\,}^{{\text{T}}}}$ – вектор случайной угловой скорости ПСК J (триэдра БИНС) относительно ССК S,

Вектор ω_J случайной угловой скорости триэдра БИНС относительно ССК S может быть описан в общем случае векторным нелинейным стохастическим дифференциальным уравнением

где ${\mathbf{f}}({{{\mathbf{\omega }}}_{{\mathbf{J}}}},t)$ – известная нелинейная вектор-функция, ${{{\mathbf{W}}}_{{\mathbf{\omega }}}}$ – центрированный БГШ с матрицей интенсивностей ${{{\mathbf{D}}}_{{\mathbf{\omega }}}}$.

На втором шаге рассмотрим динамику изменения текущих углов α₁, β₁, γ₁ разворота ССК S относительно ГСК G, которая задает также уравнениями Эйлера–Крылова аналогично (2.1):

где ${{\alpha }_{1}}$, ${{\beta }_{1}}$, ${{\gamma }_{1}}$ – углы разворота ССК S относительно ГСК G, ${{{\mathbf{\omega }}}_{{\mathbf{S}}}} = \left[ {\begin{array}{*{20}{c}} {{{\omega }_{X}}}&{{{\omega }_{Y}}}&{{{\omega }_{Z}}} \end{array}} \right]{{\,}^{{\text{T}}}}$ – вектор угловой скорости вращения ССК S относительно ГСК G.

Для описания вектора ${{{\mathbf{\omega }}}_{{\mathbf{S}}}}$ угловой скорости движения ССК S относительно ГСК G воспользуемся выражением для вектора ускорения, возникающего при движении материальной точки (МТ) по сфере радиуса R, записанным в ССК S:

где ${{{\mathbf{A}}}_{{\mathbf{S}}}} = \left[ {\begin{array}{*{20}{c}} {{{A}_{X}}}&{{{A}_{Y}}}&{{{A}_{Z}}} \end{array}} \right]{{\,}^{{\text{T}}}}$ – вектор ускорений МТ в ССК, ${{{\mathbf{V}}}_{{\mathbf{S}}}} = \left[ {\begin{array}{*{20}{c}} {{{V}_{X}}}&{{{V}_{Y}}}&{{{V}_{Z}}} \end{array}} \right]{{\,}^{{\text{T}}}}$ – вектор скорости МТ в ССК, ${{{\mathbf{\Omega }}}_{{\mathbf{S}}}} = {{[\begin{array}{*{20}{c}} {{{\Omega }_{X}}}&{{{\Omega }_{Y}}}&{{{\Omega }_{Z}}} \end{array}]}^{{\text{T}}}}$ − вектор угловой скорости вращения Земли в ССК, ${{{\mathbf{\omega }}}_{{\mathbf{S}}}} = {{[\begin{array}{*{20}{c}} {{{\omega }_{X}}}&0&{{{\omega }_{Z}}} \end{array}]}^{{\text{T}}}}$ – вектор угловой скорости ССК относительно ГСК, ${{{\mathbf{g}}}_{{\mathbf{S}}}} = \left[ {\begin{array}{*{20}{c}} {{{{\text{g}}}_{{\text{X}}}}}&{{{g}_{Y}}}&{{{g}_{Z}}} \end{array}} \right]{{\,}^{{\text{T}}}}$ – вектор ускорения силы тяжести в ССК.

Так как проекции вектора угловой скорости вращения Земли на оси ГСК G имеют вид

а вектора ускорения силы тяжести ${{{\mathbf{g}}}_{{\text{г}}}} = \left[ {\begin{array}{*{20}{c}} {{{g}_{{{{X}_{{\text{г}}}}}}}}&{{{g}_{{{{Y}_{{\text{г}}}}}}}}&{{{g}_{{{{Z}_{{\text{г}}}}}}}} \end{array}} \right]{{\,}^{{\text{T}}}}$ соответственно g – гравитационное ускорение, r – радиус Земли, то для рассматриваемой ориентации осей ССК проекции векторов ${{{\mathbf{g}}}_{{\mathbf{S}}}}$ и ${{{\mathbf{\Omega }}}_{{\mathbf{S}}}}$ на оси ССК определяются как где вид матрицы поворота $A\left( {{{\alpha }_{1}},{{\beta }_{1}},{{\gamma }_{1}}} \right)$ (направляющих косинусов) CСК S относительно ГСК G имеет вид

Система уравнений (2.4) в проекциях на оси выбранной ССК с учетом очевидных равенств ${{\omega }_{X}} = {{V}_{Z}}{{R}^{{ - 1}}},$ ${{\omega }_{Z}} = - {{V}_{X}}{{R}^{{ - 1}}}$, а также приведенных выше проекций векторов ${{{\mathbf{g}}}_{{\mathbf{S}}}}$ и ${{{\mathbf{\Omega }}}_{{\mathbf{S}}}}$ трансформируется как

В свою очередь вектор ускорений ${{{\mathbf{A}}}_{{\mathbf{S}}}}$ может быть представлен через вектор ускорений ${{{\mathbf{а}}}_{{\mathbf{J}}}}$, измеряемых акселерометрами, следующим образом:

где ${{{\mathbf{Z}}}_{{\mathbf{a}}}} = \left[ {\begin{array}{*{20}{c}} {{{Z}_{{ax}}}}&{{{Z}_{{ay}}}}&{{{Z}_{{az}}}} \end{array}} \right]{{\,}^{{\text{T}}}}$ – вектор выходных сигналов акселерометров БИНС, ${{А}_{*}} = A\left( {\alpha ,\beta ,\gamma } \right)$ – матрица поворота (направляющих косинусов) ПСК J относительно CСК S.

Данное соотношение совместно с уравнениями (2.5) позволяет сформировать стохастические уравнения, описывающие вектор ${{{\mathbf{\omega }}}_{{\mathbf{S}}}}$ угловой скорости движения ССК S относительно ГСК G:

Здесь важно отметить, что полученная система уравнений, описывающая текущую ориентацию ССК в ГСК, в соответствии с поставленной задачей оказывается полностью инвариантна к характеру динамики движения основания, качающегося относительно начала ГСК.

Объединяя системы уравнений (2.1)–(2.3), (2.6), полный вектор параметров текущей ориентации БИНС на подвижном основании запишем следующим образом:

где ${\mathbf{Y}} = {{[\begin{array}{*{20}{c}} \alpha &\beta &{\gamma \,{\mathbf{\omega }}_{{\mathbf{J}}}^{{\mathbf{T}}}\,{{\alpha }_{1}}\,{{\beta }_{1}}\,{{\gamma }_{1}}\,{{\omega }_{X}}\,{{\omega }_{Z}}} \end{array}]}^{{\text{T}}}},$ ${\mathbf{W}} = \left[ \begin{gathered} {{{\mathbf{W}}}_{{\mathbf{\omega }}}} \hfill \\ {{{\mathbf{W}}}_{{\mathbf{а}}}} \hfill \\ \end{gathered} \right]$,

Здесь Е₃ – единичная матрица размерности 3, О – нулевая матрица соответствующей размерности.

Для стохастической оценки состояния нелинейных динамических систем вида (2.7) наиболее эффективным подходом в настоящее время является использование методов теории стохастической фильтрации [29, 30], из которых самым широко известным и общеупотребительным будет обобщенный (нелинейный) фильтр Калмана–Бьюси. Но для его применения необходим предварительный синтез уравнения наблюдателя компонентов вектора Y (т.е. информационной модели сигнала измерения, явно зависящей от составляющих вектора Y).

В рассматриваемом случае в качестве сигналов наблюдения вектора Y можно выбрать выходные сигналы трех ортогональных ДУСов. Действительно, вектор ${{{\mathbf{\Omega }}}_{{\mathbf{J}}}}$ абсолютной угловой скорости вращения ПСК J, измеряемый ДУСами, определяется суммой вектора ${{{\mathbf{\omega }}}_{{\mathbf{J}}}}$ и векторов ${{{\mathbf{\omega }}}_{{{{{\mathbf{S}}}_{{\mathbf{J}}}}}}}$, ${{{\mathbf{\Omega }}}_{{{{{\mathbf{S}}}_{{\mathbf{J}}}}}}}$, заданных в ПСК J:

где ${{{\mathbf{\omega }}}_{{{{{\mathbf{S}}}_{{\mathbf{J}}}}}}} = {{A}_{*}}{{{\mathbf{\omega }}}_{{\mathbf{S}}}}\,,$ ${{{\mathbf{\Omega }}}_{{{{{\mathbf{S}}}_{{\mathbf{J}}}}}}}\left( {\alpha ,\beta ,\gamma ,{{\alpha }_{1}},{{\beta }_{1}},{{\gamma }_{1}}} \right) = {{A}_{*}}A\left[ {\begin{array}{*{20}{c}} {\Omega {\text{cos}}\varphi } \\ {\Omega {\text{sin}}\varphi } \\ 0 \end{array}} \right].$

Это позволяет, исходя из приведенного выражения для ${{{\mathbf{\Omega }}}_{{\mathbf{J}}}}$ и уравнения вектора выходных сигналов трех ортогональных ДУСов (1.2), представить стохастическую модель вектора наблюдения следующим образом:

Характерной особенностью данного наблюдателя является возможность наблюдения всех параметров ориентации БИНС в явном виде, что существенно влияет на сходимость и устойчивость процесса их оценивания.

В качестве дополнительного наблюдателя, расширяющего информационные возможности системы наблюдения, можно использовать выходной сигнал любого из акселерометров, формируя уравнение наблюдения из второго уравнения системы (2.5), неиспользованного при выводе уравнений полного вектора состояния. Так, выбирая в качестве наблюдателя выходной сигнал акселерометра Z_ax и учитывая, что

имеем где ${{а}_{{ij}}} = {{а}_{{ij}}}\left( {\alpha ,\beta ,\gamma } \right) - ij$-й элемент матрицы ${{А}_{*}}\left( {\alpha ,\beta ,\gamma } \right)$.

Но при использовании данного наблюдателя следует учитывать очевидную сложность функциональных зависимостей, входящих в функцию наблюдения, что, несмотря на расширение информационных возможностей системы наблюдения, может существенно затруднить практическую реализацию фильтра.

Обобщенный фильтр Калмана–Бьюси, построенный по уравнениям “объект-наблюдатель” (2.7), (2.8) и обеспечивающий принципиальное решение поставленной задачи, имеет следующий вид [29]:

где ${\mathbf{\hat {Y}}}$ – вектор текущей оценки вектора состояния ${\mathbf{Y}}\left( t \right)$, $R({\mathbf{\hat {Y}}},t)$ – апостериорная ковариационная матрица,

Для иллюстрации возможности эффективной практической реализации предложенного подхода рассмотрим следующий пример.

3. Результаты имитационного моделирования. Для анализа устойчивости и сходимости процесса оценивания вектора ${\mathbf{Y}} = {{[\begin{array}{*{20}{c}} \alpha &\beta &{\gamma \,{\mathbf{\omega }}_{{\mathbf{J}}}^{{\mathbf{T}}}\,{{\alpha }_{1}}\,{{\beta }_{1}}\,{{\gamma }_{1}}\,{{\omega }_{X}}\,{{\omega }_{Z}}} \end{array}]}^{{\text{T}}}}$ с помощью фильтра (2.9) было выполнено численное моделирование процесса начальной выставки БИНС на высокодинамичном подвижном основании.

Моделирование осуществлялось на временном интервале [0; 1000] с с использованием при интегрировании уравнений оценки метода Рунге–Кутты 4-го порядка с шагом 0.01 с.

Угловые скорости, определяющие истинную динамику движения БИНС относительно ССК, были заданы следующим образом:

а динамика движения ССК относительно ГСК равна (в соответствии с экспериментальными данными о колебаниях корпуса ракеты-носителя, приведенными в [31]).

Определение истинного углового положения БИНС осуществлялось путем интегрирования уравнений Эйлера–Крылова (2.1), (2.3) с учетом выбранных моделей движения (3.1), (3.2) и заданных начальных условий, $\alpha \left( 0 \right) = {\pi \mathord{\left/ {\vphantom {\pi 5}} \right. \kern-0em} 5}$, $\beta \left( 0 \right) = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$, $\gamma \left( 0 \right) = {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3}$.

Компоненты векторов помех измерения акселерометров ${{{\mathbf{W}}}_{{\mathbf{a}}}}$ и ДУС ${{{\mathbf{W}}}_{{\mathbf{d}}}}$ моделировались центрированными случайными гауссовскими последовательностями с соответствующими средним квадратическим отклонением (с.к.о.), приведенными ниже. Формирование реальных показаний ДУС осуществлялось путем наложения случайных гауссовских последовательностей на сумму вектора ${{{\mathbf{\omega }}}_{{\mathbf{J}}}}$ и векторов ${{{\mathbf{\omega }}}_{{{{{\mathbf{S}}}_{{\mathbf{J}}}}}}}$, ${{{\mathbf{\Omega }}}_{{{{{\mathbf{S}}}_{{\mathbf{J}}}}}}}$, заданных в ПСК J, при расчете которых формирование матриц направляющих косинусов происходило с помощью углов α, β, γ, α₁, β₁, γ₁, полученных путем интегрирования уравнений (2.1), (2.3).

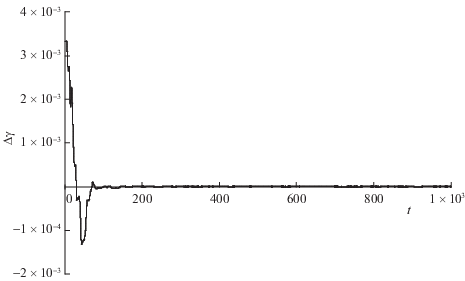
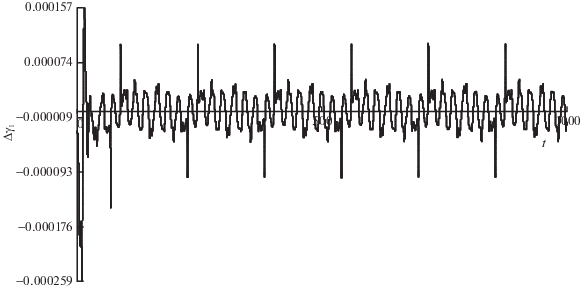
На рис. 2–7 представлены графики изменения ошибок оценивания всех углов, определяющих текущую ориентацию БИНС относительно ГСК.

Анализ результатов моделирования позволяет сделать следующие выводы.

1. Предложенный алгоритм начальной ориентации обеспечивает быструю сходимость и высокую устойчивость процесса оценивания. Требуемая для современных систем ориентации ошибка оценивания углового положения БИНС (не более 4 × 10^–5 рад) по всем углам ориентации достигалась за время, не превышающее 200 с.

2. Увеличение ошибок начальной оценки углов $\alpha ,\beta ,\gamma $ приводит к увеличению времени начальной ориентации. Так, при начальных ошибках, равных 0.3 рад по всем трем углам, время достижения точности начальной выставки, приведенной в п. 1, увеличивается в 3 раза.

3. Вариации частоты и амплитуды колебаний основания в пределах 50–80% приводят к незначительному росту ошибок оценивания (не более 4%), т.е. их влияние на точность ориентации оказывается существенно меньше, нежели ошибок начальной оценки и с.к.о. шумов измерений.

На рис. 2–4 приведены ошибки оценивания углов $\alpha ,\beta ,\gamma $. Ошибки начальной оценки для углов $\alpha ,\beta ,\gamma $ были заданы в пределах 0.004 рад (весьма критичных для современных систем начальной ориентации [18, 22]), с.к.о. помех ДУС – 10^–4 рад/с, с.к.о. помех акселерометров – 10^–5 м/с².

При данном уровне помех ошибка оценки угла α со 150-й с не превышала $5 \times {{10}^{{ - 6}}}$ рад на всем последующем интервале моделирования; для угла β – $3 \times {{10}^{{ - 6}}}$ рад, для угла γ – $3.5 \times {{10}^{{ - 6}}}$  рад, оставаясь стационарной на всем интервале моделирования.

На рис. 5–7 приведены ошибки оценивания углов ${{\alpha }_{1}}{\text{,}}{{\beta }_{{\text{1}}}},{{\gamma }_{1}}$ при ошибках их начальной оценки, заданных в пределах 0.003 рад. Как следует из полученных результатов, ошибки оценки углов ${{\alpha }_{1}}{\text{,}}{{\beta }_{{\text{1}}}},{{\gamma }_{1}}$ с 80-й с не превышают величины $1.5 \times {{10}^{{ - 4}}}$ рад, также оставаясь стационарными на всем последующем интервале оценивания.

Очевидно, что полученные точности оценки начальной ориентации БИНС удовлетворяют как современным, так и перспективным требованиям по точности и оперативности для подавляющего большинства систем начальной ориентации КА.

Заключение. В целом, результаты имитационного моделирования позволяют сделать вывод о том, что устойчивость и высокая точность предложенного алгоритма обеспечивают возможность его использования для решения задачи оперативной начальной ориентации средне- и высокоточных БИНС, расположенных на качающемся основании, без коррекции в течение достаточно длительного времени.