Известия РАН. Теория и системы управления, 2022, № 1, стр. 165-176
ТРАЕКТОРНОЕ УПРАВЛЕНИЕ ПРОЦЕССОМ НАБЛЮДЕНИЯ ПОДВИЖНОГО ЦИФРОВОГО ПЕЛЕНГАТОРА В ТОПОЛОГИИ ДОРОЖНОЙ СЕТИ
В. В. Хуторцев *
* E-mail: hvv.56@mail.ru
Поступила в редакцию 19.04.2020
После доработки 23.08.2021
Принята к публикации 27.09.2021
- EDN: NHPPTH
- DOI: 10.31857/S0002338822010073
Аннотация
Рассмотрено решение задачи определения траекторного управления процессом наблюдения подвижного цифрового пеленгатора в топологии дорожной сети при оценивании пространственной конфигурации системы дискретных источников радиоизлучения. Предложен критерий качества, позволяющий использовать при синтезе закона управления принципы дискретного динамического программирования. Определена его взаимосвязь с критериями качества, основанными на корреляционных матрицах ошибок оценивания. Приведен пример.
Введение. Определение пространственной конфигурации источников радиоизлучения (ИРИ) является одной из разновидностей задач радиотехнического мониторинга [1–3]. Ее решение часто проводится применительно к ИРИ, находящимся на поверхности Земли [2]. При этом базирование средств приема и обработки сигналов может осуществляться на борту космических аппаратов, воздушных летательных аппаратов или на наземных транспортных средствах.
Системы третьего типа эффективно используются при определении пространственной конфигурации ИРИ на земной поверхности, например, после первичной работы спутниковых систем геолокации, определяющих с достаточно большими погрешностями координаты местоположения нерегламентированных для спутниковых систем связи источников электромагнитного излучения. Задача наземных систем радиомониторинга при этом сводится к поиску источников сигнала в полученной области неопределенности.
Оценивание пространственной конфигурации ИРИ с использованием наземных подвижных систем радиомониторинга, перемещающихся в топологии дорожной сети, может быть также связано с определением местоположения людей и автотранспорта в различного рода аварийных ситуациях.
Одним из резервов повышения эффективности систем определения пространственной конфигурации ИРИ, в том числе и наземных, является рациональный выбор управления наблюдениями входящих в их состав измерителей [4–6].
Частным, но достаточно важным случаем такого управления является управление траекторией наблюдателя или траекторное управление наблюдениями [6–9]. Его принципы часто используются при определении пространственной конфигурации ИРИ и особенно актуальны при однопозиционной локации с применением подвижных унипараметрических измерителей [10]. При решении такой задачи наиболее эффективным с технической точки зрения будет использование угломерной информации [11, 12], формируемой, как правило, с помощью подвижного цифрового пеленгатора (ЦП) [13].
Необходимым условием определения координат местоположения ИРИ при этом будет перемещение ЦП, осуществляемое, как правило, в топологии дорожной сети. Одним из основных факторов, влияющих на точность однопозиционной локации, служит рациональный выбор траектории такого перемещения [10–13].
Определение траекторного управления процессом наблюдения подвижного ЦП в рассмотренных условиях приобретает ряд особенностей, связанных, во-первых, с дискретным характером такого управления и, во-вторых, с ограничением, обусловленным принадлежностью подвижного ЦП топологии дорожной сети. В указанной ситуации применение традиционных подходов к выбору оптимальной траектории перемещения измерителя [4–6] оказывается затруднительным.
С другой стороны, структура топологии дорожной сети является удобной для использования принципов дискретного динамического программирования [14]. Однако обычно применяемые в задачах планирования эксперимента целевые функции, основанные на корреляционных матрицах ошибок оценивания [4–6], в силу своей неаддитивной структуры для дискретного динамического программирования оказываются неприемлемыми.
Таким образом, разработка процедуры синтеза оптимального траекторного управления процессом наблюдения подвижного ЦП в топологии дорожной сети при определении пространственной конфигурации ИРИ является актуальной.
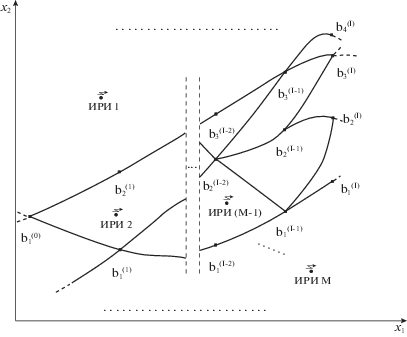
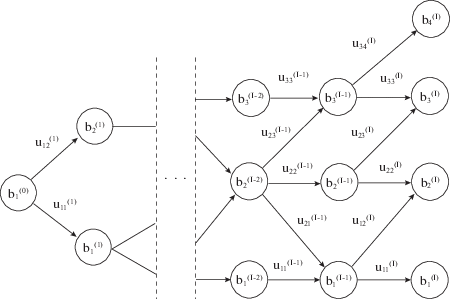
1. Модель топологии дорожной сети. Рассмотрим фрагмент топологии дорожной сети, представленный на рис. 1. Он состоит из множества взаимосвязанных одномерных многообразий. Такому фрагменту может быть поставлен в соответствие граф состояний $b_{{{{j}_{i}}}}^{{(i)}},$ $i = \overline {1,I} ,$ ${{j}_{i}} = {{\overline {1,J} }_{i}},$ ${{J}_{0}} = 1$ (рис. 2), общее количество шагов которого равно I, а количество состояний на каждом шаге определяется как ${{J}_{i}}$. Граф состояний задает возможные траектории перемещения подвижного ЦП.
Множество взаимосвязанных одномерных многообразий можно представить в виде
(1.1)
$\mu = \{ X = \tilde {F}_{{{{j}_{{i - 1}}}}}^{{(i)}}(l,u_{{{{j}_{{i - 1}}}{{j}_{i}}}}^{{(i)}}),\;i = \overline {1,I} ,\;{{J}_{0}} = 1,\;{{j}_{i}} = {{\overline {1,J} }_{i}}\} ,$(1.2)
$\tilde {F}_{{{{j}_{{i - 1}}}}}^{{(i)}}(l,u_{{{{j}_{{i - 1}}}{{j}_{i}}}}^{{(i)}}) = \left\{ {\begin{array}{*{20}{l}} {F_{{{{j}_{{i - 1}}}{{j}_{i}}}}^{{(i)}}(l),\quad если\quad u_{{{{j}_{{i - 1}}}{{j}_{i}}}}^{{(i)}} = 1,} \\ {0,\quad {\text{если}}\quad u_{{{{j}_{{i - 1}}}{{j}_{i}}}}^{{(i)}} = 0.} \end{array}} \right.$Параметры $u_{{{{j}_{{i - 1}}}{{j}_{i}}}}^{{(i)}},$ $u_{{{{j}_{{i - 1}}}{{j}_{i}}}}^{{(i)}}$ образуют множества
(1.3)
${{\tilde {U}}^{{(i)}}} = \left\{ {u_{{{{j}_{{i - 1}}}{{j}_{i}}}}^{{(i)}} = \{ 0,1\} ,\;{{J}_{0}} = 1,\;{{j}_{i}} = {{{\overline {1,J} }}_{i}}} \right\},\quad i = \overline {1,I} .$Уравнение элемента дорожной сети при условии, что узлы $b_{{{{j}_{{i - 1}}}}}^{{(i - 1)}},\;b_{{{{j}_{i}}}}^{{(i)}}$ соединены между собой ($u_{{{{j}_{{i - 1}}}{{j}_{i}}}}^{{(i)}}$ = 1), определяется соотношением
где $F_{{{{j}_{{i - 1}}}{{j}_{i}}}}^{{(i)}}(l) = {{[F_{{1{{j}_{{i - 1}}}{{j}_{i}}}}^{{(i)}}(l)\;\;F_{{2{{j}_{{i - 1}}}{{j}_{i}}}}^{{(i)}}(l)]}^{{\text{T}}}}$ – непрерывно дифференцируемая по l векторная функция.Дискретные множества
(1.5)
$\begin{gathered} {{U}^{{(i)}}} = \left\{ {u_{{{{j}_{{i - 1}}}{{k}_{i}}}}^{{(i)}} = 1,\;{{j}_{{i - 1}}} = {{{\overline {1,J} }}_{{i - 1}}},\;{{J}_{0}} = 1,\;{{k}_{i}} \in Q_{{{{j}_{{i - 1}}}}}^{{(i)}} \in \{ {{{\overline {1,J} }}_{i}}\} } \right\} \in {{{\tilde {U}}}^{{(i)}}},\quad i = \overline {1,I} , \\ U = \{ {{U}^{{(i)}}},i = \overline {1,I} \} , \\ \end{gathered} $(1.6)
$X = F_{{{{j}_{{i - 1}}}{{k}_{i}}}}^{{(i)}}(l),\quad {{j}_{{i - 1}}} = {{\overline {1,J} }_{{i - 1}}},\quad {{J}_{0}} = 1,\quad {{k}_{i}} \in Q_{{{{j}_{{i - 1}}}}}^{{(i)}} \in \{ {{\overline {1,J} }_{i}}\} ,\quad i = \overline {1,I} .$Определим через $L_{{{{j}_{{i - 1}}}{{k}_{i}}}}^{{(i)}}$ общую длину элемента дорожной сети, описываемого соотношением (1.6).
Множество одномерных многообразий (1.1) может быть сформировано, например, с использованием массивов данных, лежащих в основе электронных карт.
Отметим, что к модели (1.4) можно свести любую форму описания одномерных многообразий. Соотношение (1.4), в частности, можно рассматривать как решение пространственно-дифференциальных уравнений, полученных на основании формул Френе [15].
Будем полагать скорость перемещения ЦП вдоль траектории неизменной ${{dl} \mathord{\left/ {\vphantom {{dl} {dt}}} \right. \kern-0em} {dt}} = {{{v}}_{l}} = {\text{const}}$.
2. Критерий качества траекторного управления процессом наблюдения подвижного ЦП в топологии дорожной сети. Постановка задачи. Предположим, что траектория перемещения ЦП, задаваемая соотношением
(2.1)
${{X}_{{{\text{ЦП}}}}}(l) = \sum\limits_{i = 1}^I {F_{{{{j}_{{i - 1}}}{{k}_{i}}}}^{{(i)}}(l)} ,\quad {{j}_{{i - 1}}} = {{\overline {1,J} }_{{i - 1}}},\quad {{J}_{0}} = 1,\quad {{k}_{i}} \in Q_{{{{j}_{{i - 1}}}}}^{{(i)}} \in \{ {{\overline {1,J} }_{i}}\} ,$Перемещение ЦП осуществляется из начального $b_{1}^{{(0)}}$ в одно из конечных состояний $b_{{{{j}_{I}}}}^{{(I)}},$ ${{j}_{I}} = \overline {1,{{J}_{I}}} $. Время движения пеленгатора вдоль траектории и соответственно время наблюдения равно ${{T}_{{\text{н}}}} = L{\text{/}}{{v}_{l}}$.
Рассмотрим оценку параметров пространственной конфигурации M дискретных ИРИ, функционирование каждого из которых осуществляются в дискретном режиме, чередующем периоды излучения радиосигнала и периоды радиомолчания. Будем полагать указанные режимы независимыми и случайными. Для их описания воспользуемся совокупностью M независимых дискретных марковских процессов с двумя состояниями [13, 16]:
(2.2)
${{\Omega }_{m}}(t) \in \{ {{\omega }_{{m0}}} = 0,{{\omega }_{{m1}}} = 1\} ,\quad m = \overline {1,M} ,$Установившиеся вероятностные характеристики (2.2) представим соотношениями
(2.3)
${{p}_{{m1}}} = \frac{{{{\alpha }_{m}}}}{{{{\alpha }_{m}} + {{\beta }_{m}}}},\quad {{p}_{{m0}}} = 1 - {{p}_{{m1}}},\quad m = \overline {1,M} ,\quad t \in [0,{{T}_{{\text{н}}}}],$Зададим структуру уравнения наблюдения ЦП (уравнения в отклонениях). Она определяется возможностью ЦП, построенного на базе цифровой антенной решетки, осуществлять параллельное определение угловых координат всех ИРИ, находящихся в зоне его контроля [13].
С учетом (2.2), (2.3) получим
где $y \in {{R}^{M}};$ $\Omega = {\text{diag}}\{ {{\Omega }_{m}},\;m = \overline {1,M} \} \in {{R}^{{M \times M}}}$ – диагональная матрица; H = diag{hm, m = = $\overline {1,M} \} \in {{R}^{{M \times 2M}}}$ – блочно-диагональная матрица; ${{h}_{m}} = \left[ {{{h}_{{m1}}}\;{{h}_{{m2}}}} \right];$ $z = {{[z_{1}^{{\text{T}}}\;z_{2}^{{\text{T}}}\;...\;z_{M}^{{\text{T}}}]}^{{\text{T}}}} \in {{R}^{{2M}}};$ ${{z}_{m}} \in {{R}^{2}}$, $m = \overline {1,M} $ – векторы случайных отклонений значений координат ИРИ от их математических ожиданий $\bar {z} = {{\left[ {\bar {z}_{1}^{{\text{T}}}\;\;\bar {z}_{2}^{{\text{T}}}\;...\;\;\bar {z}_{M}^{{\text{T}}}} \right]}^{{\text{T}}}} \in {{R}^{{2M}}};$ ${{\bar {z}}_{m}} \in {{R}^{2}};$ ρ = diag{ρm, $m = \overline {1,M} \} \in {{R}^{{M \times M}}};$ ${{\rho }_{m}} = {{\rho }_{m}}({{\bar {z}}_{m}},{{X}_{{{\text{цп}}}}})$ – функция, характеризующая условия прогнозируемой наблюдаемости ЦП m-го ИРИ в ходе перемещения ЦП вдоль траектории, $0 \leqslant {{\rho }_{m}} \leqslant 1$; $N = {{\left[ {{{n}_{1}}\;...\;{{n}_{M}}} \right]}^{{\text{T}}}}$ – векторный белый гауссовский шум наблюдения с характеристиками ${\text{M}}\left[ N \right] = 0;$ ${\text{M}}[N(t){{N}^{{\text{T}}}}\left( {t - \tau } \right)] = {\text{Q}}\delta \left( \tau \right);$ ${\text{Q}} = {\text{diag}}\{ {{{\text{Q}}}_{m}},\;m = \overline {1,M} \} $ – диагональная матрица с элементами(2.6)
$\begin{gathered} {{D}_{m}} = \sum\limits_{i = 1}^I {D_{{{{j}_{{i - 1}}}{{k}_{i}}}}^{{(i)}}({{{\bar {z}}}_{m}},} {{{v}}_{l}}t) = \sum\limits_{i = 1}^I {{{{[{{{({{{\bar {z}}}_{m}} - F_{{{{j}_{{i - 1}}}{{k}_{i}}}}^{{(i)}}({{{v}}_{l}}t))}}^{{\text{T}}}}({{{\bar {z}}}_{m}} - F_{{{{j}_{{i - 1}}}{{k}_{i}}}}^{{(i)}}({{{v}}_{l}}t))]}}^{{0.5}}}} , \\ {{j}_{{i - 1}}} = {{\overline {1,J} }_{{i - 1}}},\quad {{J}_{0}} = 1,\quad {{k}_{i}} \in Q_{{{{j}_{{i - 1}}}}}^{{(i)}} \in \{ {{\overline {1,J} }_{i}}\} \\ \end{gathered} $(2.7)
$\begin{gathered} {{h}_{m}} = \sum\limits_{i = 1}^I {h_{{{{j}_{{i - 1}}}{{k}_{i}}}}^{{(i)}}({{{\bar {z}}}_{m}},} {{{v}}_{l}}t) = \sum\limits_{i = 1}^I {{{{\left[ {\frac{{\partial s({{{\bar {z}}}_{m}},F_{{{{j}_{{i - 1}}}{{k}_{i}}}}^{{(i)}}({{{v}}_{l}}t))}}{{\partial {{{\bar {z}}}_{m}}}}} \right]}}^{{\text{T}}}}} \in {{R}^{{1 \times 2}}}, \\ {{j}_{{i - 1}}} = {{\overline {1,J} }_{{i - 1}}},\quad {{J}_{0}} = 1,\quad {{k}_{i}} \in Q_{{{{j}_{{i - 1}}}}}^{{(i)}} \in \{ {{\overline {1,J} }_{i}}\} , \\ \end{gathered} $Значения $\mu $ и $\kappa $ в (2.5) определяются характеристиками излучающих систем ИРИ и приемной системы пеленгатора. Координаты ЦП ${{X}_{{{\text{ЦП}}}}}$ для каждого $t \in [0,{{T}_{{\text{н}}}}]$ полагаются известными.
Определим для модели траектории (1.2) и модели наблюдения (2.4) информационную матрицу Фишера [17, 18]. С учетом дискретного характера режимов функционирования ИРИ [13, 16] она может быть представлена в виде
(2.8)
$\Phi = \int\limits_0^{{{T}_{{\text{н}}}}} {P{{H}^{{\text{T}}}}\rho {{{\text{Q}}}^{{ - 1}}}\rho Hdt = } \int\limits_0^{{{T}_{{\text{н}}}}} {\phi ({{{v}}_{l}}t)} dt,$Отметим, что $\Phi \in {{R}^{{2M \times 2M}}}.$ Из (2.4), (2.8) следует, что Φ имеет блочно-диагональную структуру
гдеИсходя из структуры модели (2.1), подынтегральное выражение в (2.8) можно записать как
(2.10)
$\begin{gathered} \phi ({{\nu }_{l}}t) = \sum\limits_{i = 1}^I {\phi _{{{{j}_{{i - 1}}}{{k}_{i}}}}^{{(i)}}({{{v}}_{l}}t)} , \\ {{j}_{{i - 1}}} = {{\overline {1,J} }_{{i - 1}}},\quad {{J}_{0}} = 1,\quad {{k}_{i}} \in Q_{{{{j}_{{i - 1}}}}}^{{(i)}} \in \{ {{\overline {1,J} }_{i}}\} , \\ \end{gathered} $Таким образом, информационная матрица Фишера допускает следующее представление:
(2.11)
$\Phi = \sum\limits_{i = 1}^I {\Phi _{{{{j}_{{i - 1}}}{{k}_{i}}}}^{{(i)}}} ,\quad {{j}_{{i - 1}}} = {{\overline {1,J} }_{{i - 1}}},\quad {{J}_{0}} = 1,\quad {{k}_{i}} \in Q_{{{{j}_{{i - 1}}}}}^{{(i)}} \in \{ {{\overline {1,J} }_{i}}\} ,$Расчет значений $\Phi _{{{{j}_{{i - 1}}}{{k}_{i}}}}^{{(i)}}$ может быть проведен заранее на основании априорных данных о топологии дорожной сети, условиях наблюдаемости дискретных ИРИ, вероятностных характеристиках их режимов функционирования и параметрах каналов наблюдения:
(2.12)
$\begin{gathered} \Phi _{{{{j}_{{i - 1}}}{{k}_{i}}}}^{{(i)}} = \int\limits_{l_{{{{j}_{{i - 1}}}}}^{{(i - 1)}}}^{l_{{{{k}_{i}}}}^{{(i)}}} {\phi _{{{{j}_{{i - 1}}}{{k}_{i}}}}^{{(i)}}(l){v}_{l}^{{ - 1}}dl} \simeq \sum\limits_{\gamma = 1}^{\Gamma _{{{{j}_{{i - 1}}}{{k}_{i}}}}^{{(i)}}} {\phi _{{{{j}_{{i - 1}}}{{k}_{i}}}}^{{(i)}}(l_{{{{j}_{{i - 1}}}}}^{{(i - 1)}} + \gamma \Delta l){v}_{l}^{{ - 1}}} \Delta l, \\ {{j}_{{i - 1}}} = {{\overline {1,J} }_{{i - 1}}},\quad {{J}_{0}} = 1,\quad {{k}_{i}} \in Q_{{{{j}_{{i - 1}}}}}^{{(i)}} \in \{ {{\overline {1,J} }_{i}}\} , \\ \end{gathered} $Определим терминальный критерий качества для траекторного управления процессом наблюдения подвижного ЦП в топологии дорожной сети как максимум следа информационной матрицы Фишера в конце интервала наблюдения:
(2.13)
$\begin{gathered} \Psi = \sum\limits_{i = 1}^I {{{\Psi }^{{(i)}}}(b_{{{{j}_{{i - 1}}}}}^{{(i - 1)}},u_{{{{j}_{{i - 1}}}{{k}_{i}}}}^{{(i)}}) = } \sum\limits_{i = 1}^I {{\text{tr}}{{\Phi }^{{(i)}}}(b_{{{{j}_{{i - 1}}}}}^{{(i - 1)}},u_{{{{j}_{{i - 1}}}{{k}_{i}}}}^{{(i)}})} \to \mathop {\max }\limits_{u_{{{{j}_{{i - 1}}}{{k}_{i}}}}^{{(i)}} \in {{U}^{{(i)}}},\;i = \overline {1,I} } , \\ {{j}_{{i - 1}}} = {{\overline {1,J} }_{{i - 1}}},\quad {{J}_{0}} = 1,\quad {{k}_{i}} \in Q_{{{{j}_{{i - 1}}}}}^{{(i)}} \in \{ {{\overline {1,J} }_{i}}\} , \\ \end{gathered} $(2.14)
${{\Psi }^{{(i)}}}(b_{{{{j}_{{i - 1}}}}}^{{(i - 1)}},u_{{{{j}_{{i - 1}}}{{k}_{i}}}}^{{(i)}}) = {\text{tr}}{{\Phi }^{{(i)}}}(b_{{{{j}_{{i - 1}}}}}^{{(i - 1)}},u_{{{{j}_{{i - 1}}}{{k}_{i}}}}^{{(i)}})$Из (2.13) следует, что целевая функция выбранного критерия качества обладает свойством аддитивности.
Предположим, что информационная матрица Фишера не вырождена. Тогда справедливым является следующее утверждение.
Утверждение. Целевая функция критерия (2.13) максимума следа информационной матрицы Фишера для несмещенной оценки координат местоположения ИРИ эквивалентна целевой функции критерия минимума нижней границы следа корреляционной матрицы ошибок оценивания $K \in {{R}^{{2M \times 2M}}}$ вектора $z \in {{R}^{{2M}}}$:
Здесь
– блочно-диагональная матрица; ${{K}_{m}} \in {{R}^{{2 \times 2}}}$, $m = \overline {1,M} $.Доказательство приведено в Приложении.
Поставим задачу разработать процедуру синтеза оптимального в смысле критерия качества (2.13) траекторного управления процессом наблюдения подвижного ЦП в топологии дорожной сети:
(2.17)
$\{ u_{{{{j}_{{i - 1}}}}}^{{*(i)}} = u_{{{{j}_{{i - 1}}}k_{i}^{ * }}}^{{(i)}} \in {{U}^{{(i)}}},\,i = \overline {1,I} \;,{{j}_{{i - 1}}} = {{\overline {1,J} }_{{i - 1}}},\;{{J}_{0}} = 1\} ,$3. Траекторное управления процессом наблюдения подвижного ЦП в топологии дорожной сети. Проведем формальное описание динамической системы, соответствующей графу состояний, представленному на рис. 2. Если ЦП находится в узле $b_{{{{j}_{{i - 1}}}}}^{{(i - 1)}}$, т.е. в точке ${{j}_{{i - 1}}}$ сечения i – 1, тогда необходимо выбрать такое управление $u_{{{{j}_{{i - 1}}}{{k}_{i}}}}^{{(i)}},$ ${{j}_{{i - 1}}} = {{\overline {1,J} }_{{i - 1}}},$ ${{k}_{i}} \in Q_{{{{j}_{{i - 1}}}}}^{{(i)}} \in \{ {{\overline {1,J} }_{i}}\} $, которое в совокупности с другими управлениями приводило бы к максимуму целевой функции критерия (2.13).
Рассмотрим процедуру выбора траекторного управления процессом наблюдения подвижного ЦП в топологии дорожной сети, обладающего наилучшими информационными характеристиками в смысле критерия (2.13) при оценивании пространственной конфигурации дискретных ИРИ.
В соответствии с принципом дискретного динамического программирования решение задачи проводится в два этапа – обратном и прямом. Реализация обратного этапа начинается с конечных состояний.
Для каждого из узлов $b_{{{{j}_{{I - 1}}}}}^{{(I - 1)}}$, ${{j}_{{I - 1}}} = {{\overline {1,J} }_{{I - 1}}}$, запишем значения частных целевых функции ${{\Psi }^{{(I)}}}(b_{{{{j}_{{I - 1}}}}}^{{(I - 1)}}$, $u_{{{{j}_{{I - 1}}}{{k}_{I}}}}^{{(I)}})$. Здесь ${{k}_{I}} \in Q_{{{{j}_{{I - 1}}}}}^{{(I)}},$ $Q_{{{{j}_{{I - 1}}}}}^{{(I)}} \in \{ {{\overline {1,J} }_{I}}\} $ определяется в соответствии с (1.5). Выберем максимальное из них:
(3.1)
${{\overline \Psi }^{{(I)}}}(b_{{{{j}_{{I - 1}}}}}^{{(I - 1)}}) = \mathop {\max }\limits_{u_{{{{j}_{{I - 1}}}{{k}_{I}}}}^{{(I)}} \in {{U}^{{(I)}}},{{k}_{I}} \in Q_{{{{j}_{{I - 1}}}}}^{{(I)}}} {{\Psi }^{{(I)}}}(b_{{{{j}_{{I - 1}}}}}^{{(I - 1)}},u_{{{{j}_{{I - 1}}}{{k}_{I}}}}^{{(I)}}),\quad {{j}_{{I - 1}}} = {{\overline {1,J} }_{{I - 1}}}.$Условно оптимальные управления, обеспечивающие выполнение (3.1), или оптимальные управления при условии, что ЦП находится в одном из узлов $b_{{{{j}_{{I - 1}}}}}^{{(I - 1)}}$, ${{j}_{{I - 1}}} = {{\overline {1,J} }_{{I - 1}}}$, графа состояний (рис. 2), обозначим как
(3.2)
$u_{{{{j}_{{I - 1}}}}}^{{ * (I)}} = \arg \mathop {\max }\limits_{u_{{{{j}_{{I - 1}}}{{k}_{I}}}}^{{(I)}} \in {{U}^{{(I)}}},{{k}_{I}} \in Q_{{{{j}_{{I - 1}}}}}^{{(I)}}} {{\Psi }^{{(I)}}}(b_{{{{j}_{{I - 1}}}}}^{{(I - 1)}},u_{{{{j}_{{I - 1}}}{{k}_{I}}}}^{{(I)}}).$Рассмотрим состояния $b_{{{{j}_{{I - 2}}}}}^{{(I - 2)}}$, ${{j}_{{I - 2}}} = {{\overline {1,J} }_{{I - 2}}}$. Соответствующие им условно оптимальные значения частных целевых функций формируются с учетом (3.1) и определяются соотношением
(3.3)
${{\overline \Psi }^{{(I - 1)}}}(b_{{{{j}_{{I - 2}}}}}^{{(I - 2)}}) = \mathop {\max }\limits_{u_{{{{j}_{{I - 2}}}{{k}_{{I - 1}}}}}^{{(I - 1)}} \in {{U}^{{(I - 1)}}},\;{{k}_{{I - 1}}} \in Q_{{{{j}_{{I - 2}}}}}^{{(I - 1)}}} \{ {{\Psi }^{{(I - 1)}}}(b_{{{{j}_{{I - 2}}}}}^{{(I - 2)}},u_{{{{j}_{{I - 2}}}{{k}_{{I - 1}}}}}^{{(I - 1)}}) + {{\overline \Psi }^{{(I)}}}(b_{{{{k}_{{I - 1}}}}}^{{(I - 1)}})\} ,$(3.4)
$\quad u_{{{{j}_{{I - 2}}}}}^{{*(I - 1)}} = \arg \mathop {\max }\limits_{u_{{{{j}_{{I - 2}}}{{k}_{{I - 1}}}}}^{{(I - 1)}} \in {{U}^{{(I - 1)}}},{{k}_{{I - 1}}} \in Q_{{{{j}_{{I - 2}}}}}^{{(I - 1)}}} \{ {{\Psi }^{{(I - 1)}}}(b_{{{{j}_{{I - 2}}}}}^{{(I - 2)}},u_{{{{j}_{{I - 2}}}{{k}_{{I - 1}}}}}^{{(I - 1)}}) + {{\overline \Psi }^{{(I)}}}(b_{{{{k}_{{I - 1}}}}}^{{(I - 1)}})\} .$Рассмотренная процедура повторяется вплоть до начального состояния графа дорожной сети $b_{1}^{{(0)}}$:
(3.5)
${{\overline \Psi }^{{(1)}}}(b_{1}^{{(0)}}) = \mathop {\max }\limits_{u_{{1{{k}_{1}}}}^{{(1)}} \in {{U}^{{(1)}}},{{k}_{1}} \in Q_{0}^{{(1)}}} \{ {{\Psi }^{{(1)}}}(b_{1}^{{(0)}},u_{{1{{k}_{1}}}}^{{(1)}}) + {{\overline \Psi }^{{(2)}}}(b_{{{{k}_{1}}}}^{{(1)}})\} .$В силу единственности начального состояния ${{k}_{1}} \in Q_{0}^{{(1)}},$ $Q_{0}^{{(1)}} = \{ {{\overline {1,J} }_{1}}\} $ и условно оптимальное управление для него также будет единственным и оптимальным:
(3.6)
$u_{1}^{{*(1)}} = \arg \mathop {\max }\limits_{u_{{1{{k}_{1}}}}^{{(1)}} \in {{U}^{{(1)}}},{{k}_{1}} \in Q_{0}^{{(1)}}} \{ {{\Psi }^{{(1)}}}(b_{1}^{{(0)}},u_{{1{{k}_{1}}}}^{{(1)}}) + {{\overline \Psi }^{{(2)}}}(b_{{{{k}_{1}}}}^{{(1)}})\} .$Формированием управления (3.6) реализация обратного этапа процедуры поиска оптимального траекторного управления наблюдениями подвижного ЦП завершается. Далее начинается прямой этап или этап определения оптимальной траектории перемещения ЦП в топологии дорожной сети. Он реализуется в прямом направлении от начального до конечного состояний.
Введем для (3.6) обозначение
(3.7)
${{\left. {u_{{{{j}_{0}}}}^{{*(1)}}} \right|}_{{{{j}_{0}} = 1}}} = u_{{1k_{1}^{ * }}}^{{(1)}} \in {{U}^{{(1)}}},$Для второго шага с учетом обозначений, введенных в (3.7), получим ${{\left. {u_{{{{j}_{1}}}}^{{*(2)}}} \right|}_{{{{j}_{1}} = k_{1}^{ * }}}}$ = $u_{{k_{1}^{ * }}}^{{*(2)}}$ = = $u_{{k_{1}^{ * }k_{2}^{ * }}}^{{(2)}} \in {{U}^{{(2)}}},$ где $k_{2}^{*}$ – номер узла из множества $Q_{1}^{{(2)}}$, соответствующего оптимальной траектории перемещения ЦП на втором шаге. И так далее до управления ${{\left. {u_{{{{j}_{{I - 1}}}}}^{{*(I)}}} \right|}_{{{{j}_{{I - 1}}} = k_{{I - 1}}^{ * }}}} = u_{{k_{{I - 1}}^{ * }}}^{{*(I)}} = u_{{k_{{I - 1}}^{ * }k_{I}^{ * }}}^{{(I)}} \in {{U}^{{(I)}}}$ на заключительном шаге.
В результате оптимальный закон управления можно представить в форме
(3.8)
$u{\kern 1pt} * = \left\{ {{{{\left. {u_{{{{j}_{0}}k_{1}^{ * }}}^{{(1)}}} \right|}}_{{{{j}_{0}} = 1}}};\;u_{{k_{1}^{ * }k_{2}^{ * }}}^{{(2)}};\;u_{{k_{2}^{ * }k_{3}^{ * }}}^{{(3)}};\;...;\;u_{{k_{{I - 2}}^{ * }k_{{I - 1}}^{ * }}}^{{(I - 1)}};\;u_{{k_{{I - 1}}^{ * }k_{I}^{ * }}}^{{(I)}}} \right\} \in U.$Траекторное управление (3.8) процессом наблюдения подвижного ЦП соответствует информационно оптимальной в смысле критерия (2.13) траектории его перемещения в топологии дорожной сети (1.1)
(3.9)
$X_{{{\text{цп}}}}^{*}(l) = \sum\limits_{i = 1}^I {F_{{k_{{i - 1}}^{ * }k_{i}^{ * }}}^{{(i)}}(l)} ,\quad k_{0}^{*} = {{j}_{0}} = 1,$Выигрыш от оптимизации в терминах следа информационной матрицы составляет
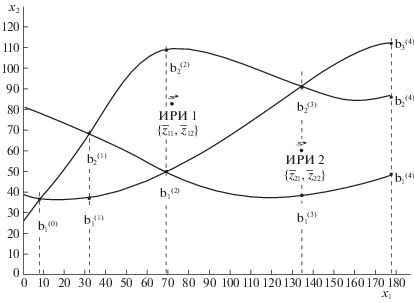
4. Пример определения траекторного управления процессом наблюдения подвижного ЦП в топологии дорожной сети. Рассмотрим задачу определения пространственной конфигурации двух дискретных ИРИ $(M = 2)$ для фрагмента топологии дорожной сети, представленной на рис. 3.
Положим, что ${{\bar {z}}_{{11}}} = 75,$ ${{\bar {z}}_{{12}}} = 80,$ ${{\bar {z}}_{{21}}} = 135,$ ${{\bar {z}}_{{22}}} = 58,$ ${{\rho }_{{1,2}}} = 1,$ $\kappa = 2,$ $\mu = {{10}^{{ - 7}}},$ ${{v}_{l}} = 60$. Здесь и далее переменные приведены в безразмерных единицах. В соответствии с (2.7) для угловых измерений полагалось, что
(4.1)
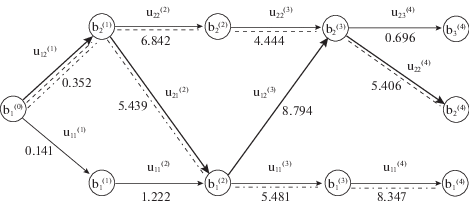
${{h}_{1}} = \left[ { - \frac{{{{{\bar {z}}}_{{12}}} - {{x}_{{2{\text{ЦП}}}}}}}{{D_{1}^{2}}}\quad \frac{{{{{\bar {z}}}_{{11}}} - {{x}_{{{\text{1ЦП}}}}}}}{{D_{1}^{2}}}} \right],\quad {{h}_{2}} = \left[ { - \frac{{{{{\bar {z}}}_{{22}}} - {{x}_{{2{\text{ЦП}}}}}}}{{D_{2}^{2}}}\quad \frac{{{{{\bar {z}}}_{{21}}} - {{x}_{{{\text{1ЦП}}}}}}}{{D_{2}^{2}}}} \right],$Граф состояния для фрагмента топологии дорожной сети представлен на рис. 4.
Ниже каждого ребра графа приведены значения частных целевых функций (2.14), рассчитанные на основании априорных данных о структуре дорожной сети, каналах наблюдения и режимах функционирования дискретных ИРИ в соответствии с (2.3), (2.6), (2.7), (2.9), (2.12).
Оптимальное траекторное управление получено в соответствии с алгоритмом, описанным в разд. 3. Его структура соответствует (3.8) и для ${{\alpha }_{1}} = {{\beta }_{1}},$ ${{\alpha }_{2}} = {{\beta }_{2}}$ имеет вид
(4.2)
$u{\kern 1pt} * = \{ u_{1}^{{*(1)}} = u_{{12}}^{{(1)}};\;u_{2}^{{*(2)}} = u_{{21}}^{{(2)}};\;u_{1}^{{*(3)}} = u_{{12}}^{{(3)}};\;u_{2}^{{*(4)}} = u_{{22}}^{{(4)}}\} ,$Соответствующие ребра графа на рис. 4 выделены жирными линиями. Оптимальным конечным состоянием является состояние $b_{2}^{{(4)}}$. Относительный выигрыш, получаемый в терминах минимума нижней границы следа корреляционной матрицы ошибок оценивания $\underline {{\text{tr}}} \{ {{K}_{{{\text{опт}}}}}\} $ (2.15), для оптимальной траектории $\{ b_{1}^{{(0)}},b_{2}^{{(1)}},b_{1}^{{(2)}},b_{2}^{{(3)}},b_{2}^{{(4)}}\} $ по отношению к аналогичной характеристике $\underline {{\text{tr}}} \{ \tilde {K}\} $, полученной, например, для траектории $\{ b_{1}^{{(0)}},b_{1}^{{(1)}},b_{1}^{{(2)}},b_{2}^{{(3)}},b_{2}^{{(4)}}\} $, составил
На рис. 4 также приведены оптимальные траектории для случаев, когда α2 = 0, ${{\beta }_{1}} = 0$ (p11 = 1, ${{p}_{{10}}} = 0,{{p}_{{21}}} = 0,{{p}_{{20}}} = 1)$ и ${{\alpha }_{1}} = 0,$ ${{\beta }_{2}} = 0$ $({{p}_{{11}}} = 0,\;{{p}_{{10}}} = 1,$ ${{p}_{{21}}} = 1,{{p}_{{20}}} = 0)$, соответственно $\{ b_{1}^{{(0)}},b_{2}^{{(1)}},b_{2}^{{(2)}},b_{2}^{{(3)}},b_{2}^{{(4)}}\} $ – пунктирная линия и $\{ b_{1}^{{(0)}},b_{2}^{{(1)}},b_{1}^{{(2)}},b_{1}^{{(3)}},b_{1}^{{(4)}}\} $ – штрихпунктирная линия. Они являются наилучшими в случае, когда сигнал излучает либо только первый, либо только второй ИРИ.
Заключение. Рассмотрена задача определения траекторного управления наблюдениями подвижного ЦП, осуществляющего в процессе перемещения в топологии дорожной сети оценку пространственной конфигурации системы дискретных ИРИ.
Первая особенность ее решения связана с дискретным характером управления, затрудняющим использование традиционных подходов к оптимизации активного эксперимента. Вторая особенность определяется неаддитивной структурой целевых функций, базирующихся на корреляционных матрицах ошибок оценивания и обычно применяемых при оптимизации наблюдений, не позволяющей использовать метод дискретного динамического программирования.
Переход к критерию качества, основанному на использовании информационной матрицы Фишера, дал возможность разработать процедуру синтеза оптимального траекторного управления на основе применения эффективного для рассмотренного класса задач метода дискретного динамического программирования.
Установленная взаимосвязь между целевой функцией критерия максимума следа информационной матрицы Фишера для несмещенной оценки координат местоположения ИРИ и целевой функцией критерия минимума нижней границы следа корреляционной матрицы ошибок оценивания позволяет осуществлять проекцию получаемых результатов на точностные характеристики определения пространственной конфигурации ИРИ.
Рассмотренный пример показал эффективность использования предложенного подхода.
Список литературы
Вознюк В.В., Зайцев С.А. Космическая система радиотехнического мониторинга на основе группировки низкоорбитальных малогабаритных космических аппаратов // Изв. вузов. Приборостроение. 2005. Т. 48. № 6. С. 26–31.
Кураков В.А. Космическая система мониторинга наземных источников излучения // Матер. XIII Междунар. научной конф. “Решетневские чтения”. Красноярск, 2009. Ч. 1. С. 150–151.
Козирацкий Ю.Л., Козирацкий А.Ю., Паринов М.Л. и др. Способ пространственного мониторинга источников электромагнитного излучения: пат. 2540126 РФ, заявл. 25.09.2013; опубл. 10.02.2015. Бюл. № 4.
Черноусько Ф.Л., Колмановский В.Б. Оптимальное управление при случайных возмущениях. М.: Наука, 1978.
Григорьев Ф.Н., Кузнецов Н.А., Серебровский А.П. Управление наблюдениями в автоматических системах. М.: Наука, 1986.
Малышев В.В., Красильщиков М.Н., Карлов В.И. Оптимизация наблюдения и управления летательных аппаратов. М.: Машиностроение, 1989.
Рубинович Е.Я. Траекторные управления наблюдениями в дискретных стохастических задачах оптимизации // АиТ. 1980. № 3. С. 93–102.
Рубинович Е.Я. О программности траекторного управления наблюдениями за подвижной целью // АиТ. 2020. Вып. 3. С. 157–173.
Sulema Aranda, Martinez S., Bullob F. On Optimal Sensor Placement and Motion Coordination for Target Tracking // IEEE Intern. Conf. on Robotics and Automation. Barcelona. Spain, 2005. P. 4544–4549.
Хуторцев В.В. Терминальная оптимизация пространственной траектории однопозиционного унипараметрического наблюдателя // Изв. РАН. ТиСУ. 2015. № 2. С. 147–154.
Андреев К.В., Рубинович Е.Я. Траекторное управление наблюдателем за мобильной целью по угломерной информации // АиТ. 2016. № 1. С. 134–162.
Oshman Y., Davidson P. Optimization of Observer Trajectories for Bearings-Only Target Localization // IEEE Transactions on Aerospace and Electronic Systems. 1999. V. 35 (3). P. 892–902.
Khutortsev V.V. Local Optimization of Trajectory Control of Observations for Mobile Digital Direction-Finder in the Location of Discrete Sources of Radiation System // Automatic Control and Computer Sciences. 2016. V. 50. № 4. P. 211–219.
Беллман Р. Динамическое программирование. М.: Наука, 1964.
Дубровин Б.А., Новиков С.П., Фоменко А.Т. Современная геометрия. Методы и приложения. М.: Наука, 1986.
Хуторцев В.В. Совместная оптимизация управления траекторией и наблюдениями в задаче оценки координат источников с дискретно изменяющимися интенсивностями излучения // Изв. РАН. ТиСУ. 2016. № 5. С. 131–141.
Математическая теория планирования эксперимента / Под ред. С.М. Ермакова. М.: Наука, 1983.
Левин Б.Р. Теоретические основы статистической радиотехники. М.: Радио и связь, 1989.
Хорн Р., Джонсон Ч. Матричный анализ. М.: Мир, 1989.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления