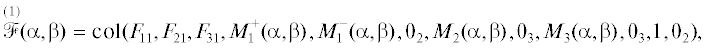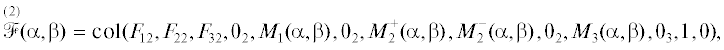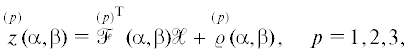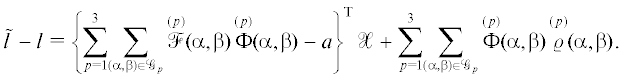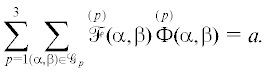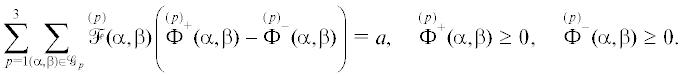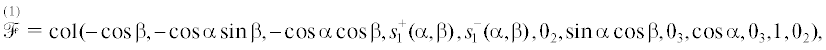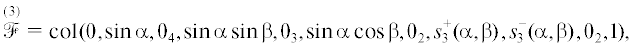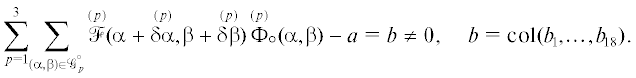Известия РАН. Теория и системы управления, 2022, № 2, стр. 107-119

Введение. Инерциальные навигационные системы [1, 2] широко применяются в технике. Блок из трех ньютонометров является одним из основных сенсоров инерциальной навигационной системы. Этот блок нуждается в калибровке перед началом функционирования навигационной системы. Калибровке блока ньютонометров (в технике они называются акселерометрами) посвящена обширная литература (см., например, [3–24]). На протяжении долгого времени предполагалось, что угловые и геометрические погрешности прецизионных стендов малы настолько, что ими можно пренебречь. Однако анализ экспериментов показывает, что, кроме ошибок самого блока, разумно включать в состав оцениваемых параметров возможные геометрические погрешности номинально высокоточного стенда (перекосы осей вращения, негоризонтальность основания из-за просадки фундамента) и его инструментальные погрешности (систематические ошибки измерения углов поворота). При этом задача оценивания становится многопараметрической, и тогда выбор плана экспериментов не очевиден [8]. Использование гарантирующего подхода к калибровке позволяет достаточно просто найти оптимальные угловые положения стенда и построить оптимальные алгоритмы калибровки блока ньютонометров (см., например, [3, 4, 8, 9]).

Однако традиционные линейные модели показаний блока ньютонометров не всегда вполне удовлетворительны. В ряде случаев допускают, что ошибки масштабных коэффициентов блока зависят от знака сигнала, поступающего на вход ньютонометра. В работе рассматривается асимметричная (кусочно-линейная) модель блока ньютонометров. В рамках гарантирующего подхода к оцениванию параметров определяется оптимальный план экспериментов и строятся соответствующие алгоритмы оценивания.

1. Постановка задачи оценивания. Опишем кратко двухстепенной стенд [8]. Пусть основание стенда неподвижно относительно Земли. Предполагается, что из-за неточности установки основания внешняя ось стенда отклонена от горизонтальной плоскости на малый угол $\kappa $. Внешняя рама стенда может вращаться относительно основания вокруг внешней оси; обозначим угол соответствующего поворота через ${{\alpha }_{{{\text{tr}}}}}$; внутренняя рама может вращаться относительно внешней рамы вокруг внутренней оси; обозначим угол соответствующего поворота через ${{\beta }_{{{\text{tr}}}}}$. Указанные углы поворота рам измеряются на фоне шумов:

где $(\alpha $, $\beta )$ – результаты измерений, $\Delta \alpha $, $\Delta \beta $ – неизвестные одинаковые для всех измерений константы, $\Delta {{\alpha }_{{{\text{fl}}}}}$, $\Delta {{\beta }_{{{\text{fl}}}}}$ – неизвестные непараметрические (флуктуационные) составляющие, разные для разных измерений углов. Для высокоточных стендов в дальнейшем будем пренебрегать флуктуационными составляющими $\Delta {{\alpha }_{{{\text{fl}}}}}$, $\Delta {{\beta }_{{{\text{fl}}}}}$, считая их достаточно малыми (порядка 1 угл. с).

При ${{\alpha }_{{{\text{tr}}}}} = 0$ внутренняя ось направлена (почти) по географической вертикали; отклонение внутренней оси от вертикальной плоскости, образованной внешней осью и географической вертикалью, вследствие негоризонтальности основания обозначим малым углом α*. Будем считать, что внешняя и внутренняя оси пересекаются в точке ${{M}^{b}}$, но могут не быть в точности ортогональны; малый угол их неортогональности обозначим через $\varepsilon $. С внутренней рамой жестко свяжем систему координат ${{M}^{b}}j$ следующим образом. Третья ось ${{M}^{b}}{{j}_{3}}$ направлена по внутренней оси. Ось ${{M}^{b}}{{j}_{1}}$ при ${{\beta }_{{{\text{tr}}}}} = 0$ лежит в плоскости, образованной внешней и внутренней осями, ортогональна ${{M}^{b}}{{j}_{3}}$ и близка к внешней оси. Ось ${{M}^{b}}{{j}_{2}}$ образует с ${{M}^{b}}{{j}_{1}}$ и ${{M}^{b}}{{j}_{3}}$ правый ортогональный трехгранник.

С блоком ньютонометров свяжем правый ортогональный трехгранник Mz, по осям которого должны (при отсутствии погрешностей блока) располагаться оси чувствительности ньютонометров (точка M является центром блока). Трехгранник Mz называется приборным. Блок ньютонометров устанавливается на внутренней раме так, чтобы оси приборного трехгранника Mz как можно точнее были направлены по осям трехгранника Mf, который связан с внутренней рамой и развернут относительно ${{M}^{b}}j$ заданным образом. Пусть этот разворот определяется известной ортогональной матрицей ориентации $Q$: $\chi {\kern 1pt} '{\kern 1pt} ' = Q\chi {\kern 1pt} '$, где $\chi {\kern 1pt} '$ и $\chi {\kern 1pt} '{\kern 1pt} '$ – проекции произвольного вектора на оси ${{M}^{b}}j$ и $Mf$ соответственно. Погрешность установки Mz по осям Mf опишем неизвестным вектором малого поворота $\vartheta = ({{\vartheta }_{1}},{{\vartheta }_{2}},{{\vartheta }_{3}}{{)}^{{\text{T}}}}$. Ошибку в знании ускорения силы тяжести в точке проведения испытаний обозначим через $\Delta g$.

Структурная модель показаний блока ньютонометров имеет вид

где $f{\kern 1pt} ' \in {{\mathbb{R}}^{3}}$ – показания блока ньютонометров, ${{I}_{3}} \in {{\mathbb{R}}^{{3 \times 3}}}$ – единичная матрица, $\Gamma \in {{\mathbb{R}}^{{3 \times 3}}}$ – матрица погрешностей блока (в которой диагональные элементы характеризуют ошибки масштабных коэффициентов, а внедиагональные – угловые несоосности ньютонометров), ${{f}_{z}} \in {{\mathbb{R}}^{3}}$ – вектор удельной силы, действующей на чувствительную массу ньютонометра, в проекциях на оси приборного трехгранника (при рассматриваемых нами статических экспериментах эта удельная сила равна ускорению силы тяжести с обратным знаком), $\Delta {{f}^{0}} \in {{\mathbb{R}}^{3}}$ – систематические смещения показаний блока, $\Delta {{f}^{s}} \in {{\mathbb{R}}^{3}}$ – флуктуационные погрешности (влияние которых существенно снижается осреднением до уровня остаточного немоделируемого сигнала электромеханического контура блока ньютонометров).

Пусть $\langle f{\kern 1pt} '\rangle $ – известные осредненные показания блока ньютонометров в некотором неподвижном относительно Земли угловом положении, $(\alpha ,\beta )$ – результат измерения углов поворота внешней и внутренней рам стенда, $\tilde {f}(\alpha ,\beta )$ – предсказанные по непосредственному измерению углов поворота рам стенда показания блока (они точно известны). Тогда измерения для соответствующей задачи оценивания формируются как нормированная разность осредненных показаний блока ньютонометров и их предсказанных значений по измерениям углов стенда. В линейном приближении вектор этих измерений имеет вид

где $g$ – модельное значение ускорения силы тяжести, ${{g}^{G}}(\alpha ,\beta ,{{q}_{{}}})$ – истинное значение вектора ускорения силы тяжести в проекциях на оси трехгранника ${{M}^{b}}j$ (связанного с внутренней рамой), $q = (\kappa ,\epsilon ,\Delta \alpha ,\Delta \beta ,\alpha {\kern 1pt} *,\Delta g{\text{/}}g{{)}^{{\text{T}}}}$ – вектор параметров погрешностей стенда, ${{\tilde {g}}^{G}}(\alpha ,\beta ) = {{g}^{G}}(\alpha ,\beta ,0)$ – точно вычисляемый по измерениям углов прогнозируемый вектор ускорения силы тяжести в проекциях на оси трехгранника ${{M}^{b}}j$, $\varrho (\alpha ,\beta )$ – вектор флуктуационных составляющих ошибок измерений [3, 8].

После простых, но громоздких выкладок нетрудно подсчитать, что в линейном приближении

Тогда из (1.2) получим, что

Представим (1.3) в более стандартной форме:

где (здесь индексы над F означают номера столбцов) имеет вид (здесь $ \otimes $ – символ кронекеровского произведения матриц), $x = {\text{col}}{\kern 1pt} \left( {u,{v},w} \right) \in {{\mathbb{R}}^{{15}}}$,

В отличие от стандартных подходов в данной работе считается, что ошибка масштабного коэффициента p-го ньютонометра ${{\Gamma }_{{pp}}}$ зависит от знака входного сигнала ньютонометра $f_{p}^{{{\text{inp}}}}$, т.е. является асимметричной (кусочно-постоянной) по входу:

(при нулевом входном сигнале значение масштабного коэффициента не существенно).

Однако входные сигналы ньютонометров ${{f}^{{{\text{inp}}}}} = {\text{col}}(f_{1}^{{{\text{inp}}}},f_{2}^{{{\text{inp}}}},f_{3}^{{{\text{inp}}}})$ непосредственно не доступны, поэтому построим их оценки. Имеет место соотношение

Ясно, что входной сигнал описывается формулой (1.1), в которой надо положить равными нулю масштабные коэффициенты, систематические смещения и флуктуационную составляющую помехи:

Тогда, очевидно,

Здесь

где 0_n – нулевой вектор-столбец размерности n.

Обозначим через $u_{k}^{{\max }}$, $k = 1,2,3$, и ${v}_{s}^{{0\max }}$, $s = \overline {1,9} $, максимальные абсолютные значения компонент ${{u}_{k}}$ и ${v}_{s}^{0}$; введем верхние границы для компонент вектора ${{F}^{{\text{T}}}}(\alpha ,\beta ){{x}^{0}}$:

Введем также обозначение:

Поэтому, если

то знак входного сигнала p-го ньютонометра определен. В противном случае надежная информация о знаке входного сигнала отсутствует, и такие измерения следует исключить из рассмотрения. Угловые положения, при которых для p-й группы измерений выполнено условие (1.9), назовем допустимыми.

Итак, следует модифицировать модель измерений таким образом, чтобы она, оставаясь линейной по оцениваемым параметрам, отражала бы неоднозначность масштабных коэффициентов:

Это можно осуществить, вводя расширенные векторы из ${{\mathbb{R}}^{{18}}}$:

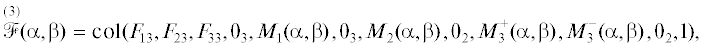в которых

Тогда измерения для случая зависимых от знака входного сигнала ошибок масштабных коэффициентов можно представить в следующем расширенном виде:

где $\mathcal{X} = {\text{col}}(u,{{{v}}^{ \pm }},w) \in {{\mathbb{R}}^{{18}}}$,

Требуется по измерениям (1.11) при всевозможных допустимых угловых положениях из $[0,2\pi ] \times [0,2\pi ]$ оценить: (a) погрешности стенда; (b) масштабные коэффициенты (с точностью до ошибки знания ускорения силы тяжести); (c) несоосности осей чувствительности ньютонометров; (d) погрешности углов установки блока ньютонометров на планшайбу (с точностью до систематического смещения в измерении угла поворота внутренней рамы); (e) систематические смещения показаний ньютонометров.

При калибровке принимается одно из двух соглашений (можно принять любое): (A1) матрица $\Gamma $ является нижнетреугольной; (A2) матрица $\Gamma $ – симметричной. В случае (A1) это соответствует оцениванию следующих параметров: (a) ${{\mathcal{X}}_{1}}$, ${{\mathcal{X}}_{2}}$, ${{\mathcal{X}}_{3}}$; (b) ${{\mathcal{X}}_{4}},{{\mathcal{X}}_{5}}$, ${{\mathcal{X}}_{9}},{{\mathcal{X}}_{{10}}}$, ${{\mathcal{X}}_{{14}}},{{\mathcal{X}}_{{15}}}$; (c) ${{\mathcal{X}}_{6}} + {{\mathcal{X}}_{8}}$, ${{\mathcal{X}}_{7}} + {{\mathcal{X}}_{{12}}}$, ${{\mathcal{X}}_{{11}}} + {{\mathcal{X}}_{{13}}}$; (d) ${{\mathcal{X}}_{8}}$, $ - {{\mathcal{X}}_{{12}}}$, ${{\mathcal{X}}_{{13}}}$; (e) ${{\mathcal{X}}_{{16}}}$, ${{\mathcal{X}}_{{17}}}$, ${{\mathcal{X}}_{{18}}}$. В случае (A2) наборы оцениваемых параметров (a), (b), (e) совпадают с наборами для случая (A1), а наборы (c) и (d) заменяются на: (c) $1{\text{/}}2\left( {{{\mathcal{X}}_{6}} + {{\mathcal{X}}_{8}}} \right)$, $1{\text{/}}2\left( {{{\mathcal{X}}_{7}} + {{\mathcal{X}}_{{12}}}} \right)$, $1{\text{/}}2\left( {{{\mathcal{X}}_{{11}}} + {{\mathcal{X}}_{{13}}}} \right)$; (d) $1{\text{/}}2\left( {{{\mathcal{X}}_{8}} - {{\mathcal{X}}_{6}}} \right)$, ${\text{1/}}2\left( {{{\mathcal{X}}_{7}} - {{\mathcal{X}}_{{12}}}} \right)$, $1{\text{/}}2\left( {{{\mathcal{X}}_{{13}}} - {{\mathcal{X}}_{{11}}}} \right)$.

Для численных расчетов на квадрате $[0,2\pi ] \times [0,2\pi ]$ зададим сетку. Множество элементов сетки, для которых выполнено условие (1.9), обозначим через ${{\mathcal{G}}_{p}}$.

2. Метод гарантирующего оценивания. Опишем кратко метод гарантирующего оценивания [3, 25–32]. Рассмотрим три группы измерений (1.11). Будем полагать, что погрешности измерений могут быть произвольными числами, ограниченными известной величиной $\sigma $:

Подчеркнем, что модель (2.1) вполне соответствует задаче калибровки блока ньютонометров, поскольку после обязательного осреднения показаний ньютонометров погрешности измерений состоят из суммы остаточного сигнала электромеханического контура блока ньютонометров и отброшенных малых квадратичных членов. Эти погрешности измерений не имеют ни четкой параметрической модели, ни устойчивого спектра.

Пусть требуется оценить скалярную величину $l = {{a}^{{\text{T}}}}\mathcal{X}$, где $a \in {{\mathbb{R}}^{{18}}}$ – заданный вектор. Обозначим единичный координатный орт из ${{\mathbb{R}}^{{18}}}$ с единицей на $\nu $-м месте через ${{e}^{{(\nu )}}}$. Тогда для решения задачи калибровки нужно решить 18 задач. Причем в случае нижнетреугольной матрицы $\Gamma $: $a = {{e}^{{(\nu )}}}$, $\nu = \overline {1,5} ,\overline {8,10} ,\overline {13,18} $ и $a = {{e}^{{(6)}}} + {{e}^{{(8)}}}$, $a = {{e}^{{(7)}}} + {{e}^{{(12)}}}$, $a = {{e}^{{(11)}}} + {{e}^{{(13)}}}$, $a = - {{e}^{{(12)}}}$; а в случае симметричной матрицы $\Gamma $: $a = {{e}^{{(\nu )}}}$, $\nu = \overline {1,5} ,9,10,\overline {14,18} $ и $a = 1{\text{/}}2({{e}^{{(6)}}} + {{e}^{{(8)}}})$, $a = 1{\text{/}}2({{e}^{{(7)}}} + {{e}^{{(12)}}})$, $a = 1{\text{/}}2({{e}^{{(11)}}} + {{e}^{{(13)}}})$, $a = 1{\text{/}}2({{e}^{{(8)}}} - {{e}^{{(6)}}})$, $a = 1{\text{/}}2({{e}^{{(7)}}} - {{e}^{{(12)}}})$, $a = 1{\text{/}}2({{e}^{{(13)}}} - {{e}^{{(11)}}})$.

Рассмотрим линейные оцениватели для $l = {{a}^{{\text{T}}}}\mathcal{X}$ вида

где $\mathop \Phi \limits^{(p)} (\alpha ,\beta )$ – некоторые весовые коэффициенты.

Величина

называется гарантированной ошибкой оценки; укороченная запись ${\text{|}}\varrho (\alpha ,\beta ){\text{|}} \leqslant \sigma $ означает выполнение условия (2.1). При выбранном оценивателе – это максимальное значение ошибки оценки при всевозможных значениях неопределенных факторов $\mathcal{X}$ и $\varrho $.

Будем искать весовые коэффициенты $\mathop \Phi \limits^{(p)} (\alpha ,\beta )$, минимизирующие гарантированную ошибку оценки:

(здесь под $\Phi (\alpha ,\beta )$ понимается набор из $\mathop \Phi \limits^{(p)} (\alpha ,\beta )$, $p = 1,2,3$). Такая задача называется задачей оптимального гарантирующего оценивания.

Итак, для решения задачи калибровки и диагностики стенда нужно решить 18 отдельных задач. Можно показать, что привлечение произвольных нелинейных оценивателей в дополнение к линейным оценивателям вида (2.2) не приводит к уменьшению гарантированной ошибки оценки [32], т.е. можно ограничиться линейными оценивателями.

Легко убедиться, что

Явно вычисляя гарантированную ошибку оценки с учетом предыдущей формулы, можно показать, что эта задача сводится к вариационной задаче вида

при ограничениях

Величина функционала (2.4) определяет гарантированную ошибку оценки. Условия (2.5) называются условиями несмещенности, так как при их выполнении в отсутствие ошибок измерений оценка $\tilde {l}$ совпадает с l.

Имеет место утверждение [26, 31, 33].

Утверждение. Решение задачи (2.4), (2.5) существует и, по крайней мере, одно решение в совокупности содержит не более чем 18 отличных от нуля компонент.

Это означает, что решение задачи оптимального гарантирующего оценивания (для каждого оцениваемого параметра) из всех элементов сетки $\mathcal{G} = \cup _{{p = 1}}^{3}{{\mathcal{G}}_{p}}$ выделяет не более чем 18 необходимых угловых положений стенда, т.е. одновременно доставляет оптимальный план измерений. Это обстоятельство делает применение гарантирующего подхода весьма эффективным для решения задачи калибровки блока ньютонометров и диагностики стенда.

Негладкая вариационная задача сводится к следующей канонической задаче линейного программирования [26, 31]:

при ограничениях

Если $\{ {{\mathop \Phi \limits^{(p)} }_{^\circ }}^{ + }(\alpha ,\beta ),{{\mathop \Phi \limits^{(p)} }_{^\circ }}^{ - }(\alpha ,\beta )\} _{{(\alpha ,\beta ) \in {{\mathcal{G}}_{p}}}}^{{p = 1,2,3}}$ является ее решением, то $\{ {{\mathop \Phi \limits^{(p)} }_{^\circ }}(\alpha ,\beta )\} _{{(\alpha ,\beta ) \in {{\mathcal{G}}_{p}}}}^{{p = 1,2,3}}$ = $\{ {{\mathop \Phi \limits^{(p)} }_{^\circ }}^{ + }(\alpha ,\beta )\; - $ ‒ ${{\mathop \Phi \limits^{(p)} }_{^\circ }}^{ - }(\alpha ,\beta )\} _{{(\alpha ,\beta ) \in {{\mathcal{G}}_{p}}}}^{{p = 1,2,3}}$ – решение исходной вариационной задачи (2.4), (2.5). Задача (2.6), (2.7) может быть численно решена симплекс-методом или методом внутренней точки [33–36].

3. Численное решение. Для численного решения задачи (2.4), (2.5) (или (2.6), (2.7)) рассмотрим случай, когда приборный трехгранник устанавливается по осям внутренней рамы, т.е. при $Q = {{I}_{3}}$. Тогда приведенные выше выражения для регрессионных векторов упрощаются и принимают вид

где

Здесь $s_{p}^{{\max }}(\alpha ,\beta )$, $p = 1,2,3$, определяются формулой (1.7), в которой $v_{s}^{{0\max }}$ есть максимальное значение s-го элемента вектора

и

При вычислениях на исходном квадрате всех значений $(\alpha ,\beta )$ была взята сетка с шагом в 1° по обоим углам. С некоторым загрублением было положено, что $u_{k}^{{\max }} = 3 \times {{10}^{{ - 3}}}$, $k = 1,2,3$, а $v_{s}^{{0\max }}$ = = 10^–2, $s = \overline {4,12} $. Расчеты выполнялись при помощи пакета IBM ILOG CPLEX Optimization Studio. Применялись два численных метода: метод внутренней точки и симплекс-метод; они дали одинаковые результаты.

На рисунке изображена область допустимых значений сетки ${{\mathcal{G}}_{1}}$, соответствующая принятым величинам $u_{k}^{{\max }}$ и $v_{s}^{{0\max }}$, и указаны оптимальные положения углов для оценивания компоненты ${{\mathcal{X}}_{4}}$. Области ${{\mathcal{G}}_{2}}$ и ${{\mathcal{G}}_{3}}$ весьма близки к ${{\mathcal{G}}_{1}}$. Результаты расчетов представлены в табл. 1 и 2. В них в первом столбце указаны оцениваемые параметры, во втором – через запятую приведены значения (в градусах) пар углов поворота стенда $(\alpha ,\beta )$ и номера используемых для построения соответствующей оценки ньютонометров, в третьем – значения весовых коэффициентов оценивателя, а в четвертом – оптимальные точности гарантирующего оценивания (значения функционалов).

4. Субоптимальные угловые положения. Обозначим оптимальные угловые положения для p-й группы измерений $\mathop z\limits^{(p)} (\alpha ,\beta )$ (соответствующие отличным от нуля компонентам ${{\{ {{\mathop \Phi \limits^{(p)} }_{^\circ }}(\alpha ,\beta )\} }_{{(\alpha ,\beta ) \in {{\mathcal{G}}_{p}}}}}$) через $\mathcal{G}_{p}^{^\circ }$. В некоторых случаях технически не легко в точности реализовать требуемые оптимальные угловые положения $\mathcal{G}_{p}^{^\circ }$, а можно поставить стенд в близкие угловые положения (α + $\mathop {\delta \alpha }\limits^{(p)} ,\beta + \mathop {\delta \beta )}\limits^{(p)} $ для $(\alpha ,\beta ) \in \mathcal{G}_{p}^{^\circ }$.

При наличии ошибок установки углов условия несмещенности (2.5), вообще говоря, уже не будут выполнены:

Если множество $\mathcal{G}_{{}}^{^\circ } = \cup _{{p = 1}}^{3}\mathcal{G}_{p}^{^\circ }$ состоит из 18 элементов и соответствующий набор 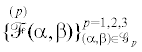линейно независим, то в силу малости $(\mathop {\delta \alpha }\limits^{(p)} ,\mathop {\delta \beta }\limits^{(p)} )$ набор также будет линейно независимым. Несмещенный субоптимальный оцениватель находится из условий несмещенности. Ясно, что гарантированная ошибка оценки субоптимального оценивателя будет близка к оптимальной.

Рассмотрим теперь случай, когда множество $\mathcal{G}_{{}}^{^\circ }$ содержит менее 18 элементов. Пусть дополнительно известно, что ${\text{|}}{{\mathcal{X}}_{\nu }}{\text{|}} \leqslant \mathcal{X}_{\nu }^{{\max }}$, $\nu = \overline {1,18} $ (для краткости будем обозначать эти условия как ${\text{|}}\mathcal{X}{\text{|}} \leqslant {{\mathcal{X}}^{{\max }}}$). Тогда с учетом (2.3) гарантированная величина ошибки оценки параметра l имеет вид

Если

то неточность в выставке углов стенда приемлема. В противном случае надо воспользоваться схемой компенсации, описанной и обоснованной в [9]. Пусть подлежат оценке величины ${{l}^{{(\nu )}}} = {{a}^{{(\nu )T}}}\mathcal{X}$, $\nu = \overline {1,18} $, причем векторы ${{a}^{{(1)}}}, \ldots ,{{a}^{{(18)}}}$ линейно независимы (в нашем случае это, очевидно, так). Тогда субоптимальные оценки ${{\tilde {l}}^{{(\nu )}}}$ параметров ${{l}^{{(\nu )}}}$, $\nu = \overline {1,18} $, следует строить по формуле, аналогичной соответствующей формуле в [9]: где

Множество $\{ \mathop z\limits^{(p)} (\alpha + \mathop {\delta \alpha }\limits^{(p)} ,\beta + \mathop {\delta \beta }\limits^{(p)} )\} _{{(\alpha ,\beta ) \in \mathcal{G}_{p}^{^\circ }}}^{{p = 1,2,3}}$ образовано измерениями в близких к оптимальным угловых положениях, а наборы 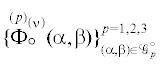состоят из отличных от нуля компонент оптимальных решений вариационной задачи (2.4), (2.5) для $a = {{a}^{{(\nu )}}}$, $\nu = \overline {1,18} $. Аналогично тому, как это сделано в [9], можно показать, что при достаточно малых $(\mathop {\delta \alpha }\limits^{(p)} ,\mathop {\delta \beta }\limits^{(p)} )$ обратная матрица к $\mathcal{W}$ существует, а полученные субоптимальные оценки являются несмещенными и их гарантированные ошибки оценок близки к оптимальным.

5. Краткое описание обработки экспериментов. Разработанная теория была применена для калибровки реального блока ньютонометров на высокоточном испытательном стенде. Сначала была проверена корректность полученных в экспериментах “сырых” данных. Во-первых, была подтверждена стабильность угловых положений блока ньютонометров. Для этого были вычислены средние (по времени) значения и разброс показаний датчиков углов в каждом угловом положении. Кроме того, угловые данные тестировались на наличие линейного тренда. Вычисления показали практическое отсутствие линейного тренда и высокий уровень стабильности угловых положений. Поэтому положения блока для каждой пары углов можно считать жестко фиксированными относительно Земли.

Во-вторых, для каждого ньютонометра во всех положениях вычислялись средние (по времени) значения и разбросы их показаний; кроме того, оценивался соответствующий линейный тренд. Экспериментальные данные показали наличие большого начального временного интервала температурной нестабильности показаний ньютонометров и позволили определить моменты времени, начиная с которых средние показания ньютонометров можно было считать надежными. Результаты экспериментов также подтвердили необходимость осреднения показаний ньютонометров в каждом положении и указали на наличие незначительного остаточного линейного (по-видимому, температурного) тренда. При этом вариации средних значений показаний ньютонометров, трактующиеся как ошибки измерений, заведомо принадлежали нужному диапазону точности.

Описанная выше методика калибровки использовала линеаризацию соответствующих соотношений и тем самым предполагала малость значений оцениваемых параметров. В то же время на исходные показания блока заметно влияли слишком большие ошибки масштабных коэффициентов, что ставило под сомнение точность линеаризации и тем самым препятствовало непосредственному применению разработанной в данной статье теории. Поэтому предварительно была проведена “грубая” калибровка блока ньютонометров, при которой игнорировались как асимметрия ошибок масштабных коэффициентов, так и наличие несоосностей ньютонометров. После этого исходная модель показаний блока была нужным образом скорректирована для ее соответствия предлагаемой методике. Таким образом, решению задачи оценивания предшествовал трудоемкий этап обработки исходных данных для их подготовки к “точной” калибровке. В итоге с помощью процедуры “точной” калибровки были получены оценки погрешностей блока ньютонометров, которые, в частности, выявили значимую асимметрию ошибок масштабных коэффициентов в одном из ньютонометров блока.

Заключение. Для калибровки блока ньютонометров в случае асимметрии ошибок масштабных коэффициентов применен гарантирующий подход. Этот подход позволил достаточно просто получить оптимальный план угловых калибровочных положений. Эффективность гарантирующего подхода к оцениванию подтверждена реальными экспериментами на испытательном стенде.