Известия РАН. Теория и системы управления, 2022, № 5, стр. 3-13
МЕТОД ПОСТРОЕНИЯ ИНТЕРВАЛЬНЫХ НАБЛЮДАТЕЛЕЙ ДЛЯ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ
А. Н. Жирабок a, b, *, В. В. Зуев a, b, Ким Чхун Ир a
a Дальневосточный федеральный ун-т
Владивосток, Россия
b Институт проблем морских технологий ДВО РАН
Владивосток, Россия
* E-mail: zhirabok@mail.ru
Поступила в редакцию 25.01.2022
После доработки 21.03.2022
Принята к публикации 28.03.2022
- EDN: EKPYZK
- DOI: 10.31857/S0002338822040151
Аннотация
Рассматривается задача построения интервальных наблюдателей для динамических систем с неопределенностями, описываемых линейными моделями. Приводятся соотношения, позволяющие построить интервальный наблюдатель минимальной сложности, который оценивает множество допустимых значений заданной линейной функции вектора состояния системы. Теоретические результаты иллюстрируются примером.
Введение. Задача построения интервальных наблюдателей, в каждый момент времени вырабатывающих оценку множества допустимых значений вектора состояния для различных классов динамических систем с неопределенностями, активно исследуется последние годы. Обстоятельный обзор полученных результатов содержится в [1], отдельные проблемы, в частности, применительно к различным практическим приложениям, можно найти в [2–7]. В этих работах, как правило, определяется оценка множества допустимых значений всего вектора состояния, в то время как для практических приложений может потребоваться аналогичная оценка только для заданной линейной функции вектора состояния. Соответствующий интервальный наблюдатель может оказаться существенно проще наблюдателя полной размерности, а класс систем, для которых такой наблюдатель может быть построен, расширится.
В работе ставится и решается задача построения интервальных наблюдателей для стационарных динамических систем с неопределенностями, описываемых линейными моделями, которые позволяют оценить множество допустимых значений заданной линейной функции вектора состояния. Эту задачу можно рассматривать как обобщение задачи построения виртуальных датчиков, решенной в [8] на основе модели исходной системы минимальной размерности. Аналогичный подход предлагается применить и к решению поставленной задачи.
1. Основные модели и постановка задачи. Рассмотрим систему, описанную линейной моделью
(1.1)
$\begin{gathered} \dot {x}(t) = Fx(t) + Gu(t) + L\rho (t), \\ y(t) = Hx(t) + v(t), \\ \end{gathered} $Требуется построить интервальный наблюдатель минимальной размерности, формирующий нижнюю $\underline z (t)$ и верхнюю $\bar {z}(t)$ границы известной линейной вектор-функции вектора состояния $x(t)$, заданной матрицей M в виде $z(t) = Mx(t)$, $z(t) \in {{R}^{s}}$, для которых справедливо неравенство $\underline z (t) \leqslant z(t) \leqslant \bar {z}(t)$ при всех $t \geqslant 0$, понимаемое покомпонентно.
Искомый интервальный наблюдатель может быть построен на основе обычного наблюдателя минимальной размерности двумя методами. В первом из них по аналогии с виртуальным датчиком [8] такой наблюдатель должен обладать двумя свойствами. Во-первых, он должен оценивать некоторую компоненту вектора выхода ${{y}_{*}}(t) = {{H}_{*}}{{x}_{*}}(t)$, которая определяется матрицей-строкой ${{R}_{*}}$ для формирования невязки $r(t) = {{R}_{*}}y(t) - {{y}_{*}}(t)$, обеспечивающей устойчивость наблюдателя. Здесь ${{x}_{*}}(t)$ – вектор состояния наблюдателя. Компонента ${{y}_{*}}(t)$ и матрица-строка ${{R}_{*}}$ неизвестны, они определяются в процессе решения основной задачи. Во-вторых, наблюдатель должен оценивать заданную переменную $z(t) = Mx(t)$. Во втором методе наблюдатель оценивает только переменную $z(t)$, его устойчивость обеспечивается другим способом.
Рассмотрим вначале первый метод. Здесь решение задачи основывается на модели минимальной размерности, оценивающей переменные $z(t)$ и ${{y}_{*}}(t)$, в общем случае имеющей вид
(1.2)
$\begin{gathered} {{y}_{*}}(t) = {{H}_{*}}{{x}_{*}}(t),{\text{ }} \\ z(t) = {{H}_{z}}{{x}_{*}}(t) + Qy(t), \\ \end{gathered} $Замечание 1. Если переменная z(t) совпадает с одной из компонент вектора выхода, можно принять ${{y}_{*}}(t) = z(t)$, что упрощает процедуру построения модели.
Предлагаемое решение задачи осуществляется в три этапа. На первом строится линейная модель минимальной размерности, оценивающая переменную ${{y}_{*}}(t)$, на втором проверяется возможность выполнения равенства
на третьем этапе ищется матрица $K$, обеспечивающая устойчивость наблюдателя.2. Решение задач первого и второго этапов. Для получения решения на первом этапе матрицы ${{F}_{*}}$ и ${{H}_{*}}$ ищутся в каноническом виде:
(2.1)
${{F}_{*}} = \left( {\begin{array}{*{20}{c}} 0&1&0& \cdots &0 \\ 0&0&1& \cdots &0 \\ 0&0&0& \cdots &0 \\ \cdots & \cdots & \cdots & \ddots & \cdots \\ 0&0&0& \cdots &0 \end{array}} \right),\quad {{H}_{*}} = (\begin{array}{*{20}{c}} 1&0&0& \cdots &0 \end{array}).$Замечание 2. Переменную $z(t)$ в модели (1.2) можно оценивать и с помощью матрицы ${{H}_{*}}$, т.е. принять $z(t) = {{H}_{*}}{{x}_{*}}(t)$. Это позволит автоматически выполнить условие построения интервального наблюдателя (приведенное в разд. 4), но такой вариант не гарантирует наблюдаемости модели, что необходимо для обеспечения устойчивости.
Предполагается, что векторы x(t) и ${{x}_{*}}(t)$ связаны матрицей $\Phi $:
Известно, что матрицы, описывающие модель, удовлетворяют следующим уравнениям [9, 10]:
(2.2)
${{R}_{*}}H = {{H}_{*}}\Phi ,\quad \Phi F = {{F}_{*}}\Phi + {{J}_{*}}H,\quad {{G}_{*}} = \Phi G.$Из (1.1), (1.2) и (2.2) можно получить уравнения для отдельных строк этих матриц [9, 10]:
(2.3)
${{R}_{*}}H = {{\Phi }_{1}},\quad {{\Phi }_{i}}F = {{\Phi }_{{i + 1}}} + {{J}_{{*i}}}H,\quad i = \overline {1,k - 1} ,\quad {{\Phi }_{k}}F = {{J}_{k}}H,$Как показано в [9, 10], уравнения (2.3) могут быть сведены в одно уравнение
Запишем его в виде
(2.4)
$(\begin{array}{*{20}{c}} {{{R}_{*}}}&{ - {{J}_{{*1}}}}& \ldots &{ - {{J}_{{*k}}}} \end{array}){{V}^{{(k)}}} = 0,$Известно, что условие нечувствительности к возмущениям имеет вид $\Phi L = 0$, которое, согласно [9, 10], может быть объединено с (2.4):
(2.5)
$(\begin{array}{*{20}{c}} {{{R}_{*}}}&{ - {{J}_{{*1}}}}& \ldots &{ - {{J}_{{*k}}}} \end{array})({{V}^{{(k)}}}{\text{ }}{{L}^{{(k)}}}) = 0,\quad k = \overline {1,n - 1} ,$Уравнение (2.5) имеет нетривиальное решение, если
Для построения модели из (2.6) определяется минимальное k и из (2.5) – строка $(\begin{array}{*{20}{c}} {{{R}_{*}}}&{ - {{J}_{{*1}}}}& \ldots &{ - {{J}_{{*k}}}} \end{array})$, затем на основе соотношений (2.3) строится матрица $\Phi $, на чем заканчивается первый этап. Невыполнение условия (2.6) при всех $k < n$ означает, что модель, не чувствительная к возмущениям, не существует, необходимо обращаться к робастным методам, описанным в разд. 6.
Для реализации второго этапа представим уравнение (1.3) вместе с $z(t) = Mx(t)$ в виде
откуда следует(2.7)
$M = {{H}_{z}}\Phi + QH = (\begin{array}{*{20}{c}} {{{H}_{z}}}&Q \end{array})\left( {\begin{array}{*{20}{c}} \Phi \\ H \end{array}} \right),$(2.8)
${\text{rank}}\left( {\begin{array}{*{20}{c}} \Phi \\ H \end{array}} \right) = {\text{rank}}\left( {\begin{array}{*{20}{c}} \Phi \\ H \\ M \end{array}} \right).$Выполнение условия (2.8) означает, что матрица M может быть выражена через ${{({{\Phi }^{{\text{T}}}}{{H}^{{\text{T}}}})}^{{\text{T}}}}$ и построенная линейная модель будет оценивать заданную переменную z = Mx; матрицы ${{H}_{z}}$ и Q определяются из алгебраического уравнения (2.7). Если условие (2.8) не верно, следует найти другое решение уравнения (2.5) при прежней или увеличенной размерности k.
3. Обеспечение устойчивости. Искомый наблюдатель отличается от модели наличием обратной связи по сигналу невязки $r(t) = {{R}_{*}}y(t) - {{y}_{*}}(t)$:
(3.1)
$\begin{gathered} {{{\dot {x}}}_{*}}(t) = {{F}_{*}}{{x}_{*}}(t) + {{J}_{*}}Hx(t) + {{G}_{*}}u(t) + Kr(t) = \\ \, = ({{F}_{*}} - K{{H}_{*}}){{x}_{*}} + {{J}_{*}}Hx(t) + {{G}_{*}}u(t) + K{{R}_{*}}y(t). \\ \end{gathered} $Для определения матрицы K, обеспечивающей устойчивость наблюдателя на третьем этапе, введем ошибку по состоянию $e(t) = \Phi x(t) - {{x}_{*}}(t)$ и с учетом (1.1), (1.2) и (2.2) запишем и преобразуем уравнение для $\dot {e}(t)$:
Будем искать матрицу$K$ в виде $K = {{(\begin{array}{*{20}{c}} {{{a}_{1}}}&{{{a}_{2}}}& \ldots &{{{a}_{k}}} \end{array})}^{{\text{T}}}}$. Тогда
(3.2)
${{F}_{*}} - K{{H}_{*}} = \left( {\begin{array}{*{20}{c}} 0&1&0& \cdots &0 \\ 0&0&1& \cdots &0 \\ 0&0&0&1&0 \\ \cdots & \cdots & \cdots & \ddots & \cdots \\ 0&0&0& \cdots &0 \end{array}} \right) - K(\begin{array}{*{20}{c}} 1&0&0& \cdots &0 \end{array}) = \left( {\begin{array}{*{20}{c}} { - {{a}_{1}}}&1&0& \cdots &0 \\ { - {{a}_{2}}}&0&1& \cdots &0 \\ { - {{a}_{3}}}&0&0&1&0 \\ \cdots & \cdots & \cdots & \ddots & \cdots \\ { - {{a}_{k}}}&0&0& \cdots &0 \end{array}} \right).$Коэффициенты ${{a}_{1}},{{a}_{2}},...,{{a}_{k}}$ связаны с собственными числами ${{\lambda }_{1}},{{\lambda }_{2}},...,{{\lambda }_{k}}$ матрицы ${{F}_{*}} - K{{H}_{*}}$ известными соотношениями:
(3.3)
${{a}_{1}} = - ({{\lambda }_{1}} + {{\lambda }_{2}} + ... + {{\lambda }_{k}}),\;{{a}_{2}} = {{\lambda }_{1}}{{\lambda }_{2}} + {{\lambda }_{1}}{{\lambda }_{3}}... + {{\lambda }_{{k - 1}}}{{\lambda }_{k}},\;...,\;{{a}_{k}} = {{( - 1)}^{k}}{{\lambda }_{1}}{{\lambda }_{2}}...{{\lambda }_{k}}.$Исходя из заданных требований к качеству переходного процесса, можно выбрать собственные числа ${{\lambda }_{1}},{{\lambda }_{2}},...,{{\lambda }_{k}}$ и определить коэффициенты ${{a}_{1}},{{a}_{2}},...,{{a}_{k}}$. Будем полагать для простоты, что собственные числа ${{\lambda }_{1}},{{\lambda }_{2}},...,{{\lambda }_{k}}$ выбираются разными и отрицательными.
4. Построение интервального наблюдателя. По аналогии с [1] такой наблюдатель определяется следующими соотношениями:
(4.1)
$\underline z (t) = {{H}_{z}}{{\underline x }_{*}}(t) + Qy(t),\quad \bar {z}(t) = {{H}_{z}}{{\bar {x}}_{*}}(t) + Qy(t),$(4.2)
$\begin{gathered} {{\underline {\dot {x}} }_{*}}(t) = ({{F}_{*}} - K{{H}_{*}}){{\underline x }_{*}}(t) + ({{J}_{*}} + K{{R}_{*}})y(t) + {{G}_{*}}u(t)\; - \;{\text{|}}{{J}_{*}}{\text{|}}{{I}_{k}}{{v}_{*}}, \\ {{{\dot {\bar {x}}}}_{*}}(t) = ({{F}_{*}} - K{{H}_{*}}){{{\bar {x}}}_{*}}(t) + ({{J}_{*}} + K{{R}_{*}})y(t) + {{G}_{*}}u(t)\; + \;{\text{|}}{{J}_{*}}{\text{|}}{{I}_{k}}{{v}_{*}}. \\ \end{gathered} $Замечание 3. Доказательство формулируемой ниже теоремы связано с особенностями матрицы ${{F}_{*}} - K{{H}_{*}}$ в (4.2). Требуется, чтобы она была метцлеровой, т.е. ее внедиагональные элементы должны быть неотрицательными; устойчивой она будет по построению. Поскольку матрица (3.2) не является метцлеровой, ее необходимо привести к требуемому виду. Как показано в [2], это всегда можно сделать, используя преобразование подобия, трансформирующее матрицу ${{F}_{*}} - K{{H}_{*}}$ к форме Жордана [11], которая есть диагональная в силу того, что собственные числа ${{\lambda }_{1}},{{\lambda }_{2}},...,{{\lambda }_{k}}$ по построению различны. Матрица S такого преобразования может быть составлена на основе собственных векторов матрицы ${{F}_{*}} - K{{H}_{*}}$. Известно [11], что преобразование подобия сохраняет собственные числа, поэтому полученная в итоге матрица будет устойчивой. Получим описание преобразованного наблюдателя, умножив обе части уравнений (3.1) слева на матрицу $S$ и выполняя соответствующие операции построения интервального наблюдателя:
(4.3)
$\begin{gathered} \dot {\bar {x}}_{*}^{'}(t) = F_{*}^{'}\bar {x}_{*}^{'}(t) + S({{J}_{*}} + K{{R}_{*}})y(t) + S{{G}_{*}}u(t)\; + \;{\text{|}}S{{J}_{*}}{\text{|}}{{I}_{k}}{{v}_{*}}, \\ \underline z (t) = {{H}_{z}}{{S}^{{ - 1}}}\underline x _{*}^{'}(t) + Qy(t),\quad \bar {z}(t) = {{H}_{z}}{{S}^{{ - 1}}}\bar {x}_{*}^{'}(t) + Qy(t), \\ \end{gathered} $Другой способ получения метцлеровой матрицы описан в разд. 5.
По аналогии с [1] для векторов ${{x}^{{(1)}}},{{x}^{{(2)}}} \in {{R}^{n}}$ и k × k-матриц ${{A}^{{(1)}}},\;{{A}^{{(2)}}}$ отношения ${{x}^{{(1)}}} \leqslant {{x}^{{(2)}}}$ и ${{A}^{{(1)}}} \leqslant {{A}^{{(2)}}}$ понимаются поэлементно.
Теорема 1. Пусть выполняется условие ${{H}_{z}}{{S}^{{ - 1}}} \geqslant 0$ и $\underline x _{*}^{'}(0) \leqslant S{{x}_{{*0}}} \leqslant {\text{ }}\bar {x}_{*}^{'}(0)$, тогда для интервального наблюдателя (4.3) верны соотношения
(4.4)
$\underline x _{*}^{'}(t) \leqslant x_{*}^{'}(t) \leqslant \bar {x}_{*}^{'}(t),\quad \underline z (t) \leqslant z(t) \leqslant \bar {z}(t).$Доказательство. По аналогии с [1] введем ошибки оценивания
(4.5)
$\begin{gathered} {{\underline e }_{*}}(t) = S{{x}_{*}}(t) - \underline x _{*}^{'}(t),\quad {{{\bar {e}}}_{*}}(t) = \bar {x}_{*}^{'}(t) - S{{x}_{*}}(t), \\ {{\underline e }_{z}}(t) = z(t) - \underline z (t),\quad {{{\bar {e}}}_{z}}(t) = \bar {z}(t) - z(t). \\ \end{gathered} $С учетом (3.1) и (4.3) можно получить дифференциальные уравнения
(4.6)
$\begin{gathered} {{\underline {\dot {e}} }_{*}}(t) = F_{*}^{'}{{\underline e }_{*}}(t) + S{{J}_{*}}(Hx(t) - y(t))\; + \;{\text{|}}S{{J}_{*}}{\text{|}}{{I}_{k}}{{v}_{*}} = F_{*}^{'}{{\underline e }_{*}}(t) - S{{J}_{*}}v(t)\; + \;{\text{|}}S{{J}_{*}}{\text{|}}{{I}_{k}}{{v}_{*}}, \\ {{{\dot {\bar {e}}}}_{*}}(t) = F_{*}^{'}{{{\bar {e}}}_{*}}(t) + S{{J}_{*}}(y(t) - Hx(t))\; + \;{\text{|}}S{{J}_{*}}{\text{|}}{{I}_{k}}{{v}_{*}} = F_{*}^{'}{{{\bar {e}}}_{*}}(t) + S{{J}_{*}}v(t)\; + \;{\text{|}}S{{J}_{*}}{\text{|}}{{I}_{k}}{{v}_{*}}. \\ \end{gathered} $Так как ${\text{|}}S{{J}_{*}}{\text{|}}{{I}_{k}}{{v}_{*}} \pm S{{J}_{*}}v(t) \geqslant 0$ при всех $t \geqslant 0$ и матрица $F_{*}^{'}$ метцлерова, система (4.6) называется монотонной или неотрицательной [1]. Ее решения при ${{\underline e }_{*}}(0) \geqslant 0$, ${{\bar {e}}_{*}}(0) \geqslant 0$ будет поэлементно неотрицательным, т.е. ${{\underline e }_{*}}(t) \geqslant 0$, ${{\bar {e}}_{*}}(t) \geqslant 0$ для всех $t \geqslant 0$ [1], откуда, согласно (4.5), следует $\underline x _{*}^{'}(t) \leqslant S{{x}_{*}}(t) \leqslant \bar {x}_{*}^{'}(t)$. Так как $z(t) = {{H}_{z}}{{S}^{{ - 1}}}S{{x}_{*}}(t) + Qy(t)$, то из (4.1) и (4.3) имеем
Тогда с учетом (4.5), ${{H}_{z}}{{S}^{{ - 1}}} \geqslant 0$ и ${{\underline e }_{*}}(t) \geqslant 0$, ${{\bar {e}}_{*}}(t) \geqslant 0$ получаем ${{\underline e }_{z}}(t) \geqslant 0,$ ${{\bar {e}}_{z}}(t) \geqslant 0$, что эквивалентно второму соотношению в (4.4). Теорема доказана.
Укрупненный алгоритм синтеза интервального наблюдателя можно представить следующим образом.
1. Построить модель минимальной размерности k, оценивающую заданную переменную $z(t) = Mx(t)$.
2. Задать собственные числа ${{\lambda }_{1}},{{\lambda }_{2}},...,{{\lambda }_{k}}$ и определить матрицу обратной связи K.
3. Преобразовать матрицу ${{F}_{*}} - K{{H}_{*}}$ к форме Жордана.
4. Построить интервальный наблюдатель.
5. Решение вторым методом. По аналогии с первым методом второе решение также основывается на модели минимальной размерности, оценивающей переменную $z(t)$:
В отличие от первого метода, где матрицы ${{F}_{*}}$ и ${{H}_{*}}$ имели канонический вид (2.1) и требовались дальнейшие преобразования, во втором методе матрица ${{F}_{*}}$ сразу ищется в жордановой форме:
(5.1)
${{F}_{*}} = \left( {\begin{array}{*{20}{c}} {{{\lambda }_{1}}}&0& \cdots &0 \\ 0&{{{\lambda }_{2}}}& \cdots &0 \\ \vdots & \vdots & \ddots & \vdots \\ 0&0& \cdots &{{{\lambda }_{k}}} \end{array}} \right),$Дополнительное требование $\Phi L = 0$ – нечувствительность к возмущениям – учитывается следующим образом. Введем матрицу L0 максимального ранга, такую, что ${{L}_{0}}L = 0$, тогда $\Phi = N{{L}_{0}}$ для некоторой матрицы $N$. В результате уравнение (5.2) может быть записано в виде
(5.3)
$({{N}_{i}}{\text{ }} - {{J}_{{*i}}})\left( {\begin{array}{*{20}{c}} {{{L}_{0}}(F - {{\lambda }_{i}}{{E}_{n}})} \\ H \end{array}} \right) = 0,\quad i = \overline {1,k} .$Здесь En – n × n единичная матрица. Условием его разрешимости является ранговое неравенство
Если при всех $\lambda < 0$ это условие не выполняется, то модель с требуемыми свойствами не существует и поставленная задача решается робастными методами.
Задавая конкретные значения ${{\lambda }_{i}}$, из уравнения (5.3) можно найти строки ${{\Phi }_{i}} = {{N}_{i}}{{L}_{0}}$ и ${{J}_{{*i}}}$ матриц $\Phi $ и ${{J}_{*}}$ соответственно. Далее, проверив условие (2.8), определим матрицы ${{H}_{z}}$ и $Q$ из алгебраического уравнения (2.7) и ${{G}_{*}}$ – из (2.2). Матрицы ${{R}_{*}}$ и ${{H}_{*}}$ в синтезе наблюдателя предлагаемым методом не участвуют, поскольку в первом методе они использовались для введения обратной связи с целью обеспечения устойчивости наблюдателя, которая теперь прямо следует из жордановой формы матрицы ${{F}_{*}}$. Отметим, что отсутствие необходимости оценивать переменную ${{y}_{*}}(t)$ позволяет в ряде случаев уменьшить размерность наблюдателя.
Замечание 4. Из (5.3) следует, что, варьируя собственными числами ${{\lambda }_{1}},{{\lambda }_{2}},...,{{\lambda }_{k}}$, можно добиться такого решения для строк матрицы $\Phi $, которое позволит удовлетворить условию (2.8). Из (5.2) получаем, что если принять ${{J}_{{*i}}} = 0$ для некоторого i, то строка ${{\Phi }_{i}}$ является транспонированным собственным вектором матрицы $F$, соответствующим собственному числу ${{\lambda }_{i}}$. Из сказанного можно сделать вывод, что если существует собственный вектор ${{v}_{0}}$ этой матрицы, такой, что
Наблюдатель (4.1) в рассматриваемом подходе принимает вид
Теорема 2. Пусть ${{H}_{z}} \geqslant 0$, ${{\underline x }_{*}}(0) \leqslant {{x}_{{*0}}} \leqslant {\text{ }}{{\bar {x}}_{*}}(0)$ и матрица ${{F}_{*}}$ имеет вид (5.1), тогда для интервального наблюдателя (5.4) выполняются соотношения
Доказательство. Повторяет доказательство теоремы 1 с заменой в нем матрицы ${{F}_{*}} - K{{H}_{*}}$ на ${{F}_{*}}$.
6. Робастное решение. Если условиe (2.6) не выполняются при всех $k < n$, необходимо искать робастное решение. Детально оно описано в [9], приведем соответствующую процедуру, опуская подробности.
Вклад возмущения в модель (2.1) оценим нормой Фробениуса ${{\left\| {\Phi L} \right\|}_{F}}$ матрицы $\Phi L$, которая может быть представлена в виде $\Phi L = (\begin{array}{*{20}{c}} {{{R}_{*}}}&{ - {{J}_{{*1}}}}&{...}&{ - {{J}_{{*k}}}} \end{array}){{L}^{{(k)}}}$. В этом случае задача минимизации вклада возмущения в невязку сводится к минимизации нормы ${{\left\| {(\begin{array}{*{20}{c}} {{{R}_{*}}}&{ - {{J}_{{*1}}}}&{...}&{ - {{J}_{{*k}}}} \end{array}){{L}^{{(k)}}}} \right\|}_{F}}$ при выполнении условия (2.5).
Найдем минимальную размерность k, для которой уравнение (2.4) имеет несколько линейно независимых решений вида $(\begin{array}{*{20}{c}} {R_{*}^{{(j)}}}&{ - J_{{*1}}^{{(j)}}}& \ldots &{ - J_{{*k}}^{{(j)}}} \end{array})$, $j = \overline {1,{{n}_{*}}} $. Все эти решения сводятся в матрицу W:
В [8] показано, что его решением является и произвольная линейная комбинация строк этой матрицы с вектором весовых коэффициентов $w = ({{w}_{1}}, \ldots ,{{w}_{{{{n}_{*}}}}})$. Задача состоит в определении такого вектора w, который дает минимум нормы ${{\left\| {wW{{L}^{{(k)}}}} \right\|}_{F}}$ при условии $\left\| w \right\| = 1$.
Для решения этой задачи найдем сингулярное разложение произведения $W{{L}^{{(k)}}}$:
где UL и VL – ортогональные матрицы, ΣL в зависимости от соотношения чисел строк и столбцов матрицы $W{{L}^{{(k)}}}$ имеет видТеорема 3. Указанный выбор вектора $w$ обеспечивает оптимальное решение в смысле минимума нормы ${{\left\| {(\begin{array}{*{20}{c}} {{{R}_{*}}}&{ - {{J}_{{*1}}}}&{...}&{ - {{J}_{{*k}}}} \end{array})L_{{}}^{{(k)}}} \right\|}_{F}}$, равной минимальному сингулярному числу.
Доказательство. Прямо вытекает из свойств сингулярного разложения.
Из сказанного следует, что линейная комбинация решений, представленных строками матрицы W с весами ${{w}_{1}}, \ldots ,{{w}_{{{{n}_{*}}}}}$, дает оптимальное решение с матрицами ${{R}_{*}}$, ${{J}_{*}}$ и $\Phi $, строки последней определяются из (2.3). Далее находятся матрицы ${{G}_{*}} = \Phi G$ и ${{L}_{*}} = \Phi L$, чем завершается синтез модели (1.2), минимально чувствительной к возмущениям. Отметим, что это решение будет оптимальным для найденной размерности модели. Увеличение размерности сверх минимальной может дать лучший вариант решения задачи по критерию минимума нормы ${{\left\| {(\begin{array}{*{20}{c}} {{{R}_{*}}}&{ - {{J}_{{*1}}}}&{...}&{ - {{J}_{{*k}}}} \end{array}){{L}^{{(k)}}}} \right\|}_{F}}$.
Из-за появления слагаемого ${{L}_{*}}\rho (t)$ в модели (1.2) динамику интервального наблюдателя необходимо скорректировать. Рассмотрим это на примере второго метода:
Выражения (4.5) для ошибок оценивания также корректируются:
Нетрудно видеть, что искомый результат следует из доказательства теоремы 1 и очевидного дополнительного неравенства ${\text{|}}{{L}_{*}}{\text{|}}{{I}_{k}}{{\rho }_{*}} \pm {{L}_{*}}\rho (t) \geqslant 0$.
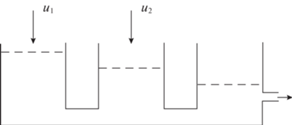
7. Пример. Рассмотрим систему управления
(7.1)
$\begin{gathered} {{{\dot {x}}}_{2}}(t) = {{u}_{2}}(t){\text{/}}{{\vartheta }_{2}} + {{b}_{1}}({{x}_{1}}(t) - {{x}_{2}}(t)) - {{b}_{2}}({{x}_{2}}(t) - {{x}_{3}}(t)), \\ {{{\dot {x}}}_{3}}(t) = {{b}_{2}}({{x}_{2}}(t) - {{x}_{3}}(t)) - {{b}_{3}}({{x}_{3}}(t) - {{\vartheta }_{3}}) + \rho (t), \\ \end{gathered} $Уравнения (7.1) описывают так называемую трехтанковую систему (рис. 1), состоящую из трех резервуаров, соединенных между собой трубами. Жидкость поступает в первый и второй танки и выливается из третьего танка. Уровни жидкости в танках обозначены как ${{x}_{1}}(t)$, ${{x}_{2}}(t)$ и ${{x}_{3}}(t)$; ${{\vartheta }_{1}}$, ${{\vartheta }_{2}}$, ${{\vartheta }_{3}}$, ${{b}_{1}}$, ${{b}_{2}}$ и ${{b}_{3}}$ – коэффициенты, значения которых определяются геометрическими размерами системы. Для простоты зададим ${{\vartheta }_{1}} = {{\vartheta }_{2}} = 1$, ${{\vartheta }_{3}} = 0$, ${{b}_{1}} = {{b}_{2}} = {{b}_{3}} = 1$.
Система (7.1) была рассмотрена в [13], где для нее был построен виртуальный датчик, оценивающий переменную ${{x}_{1}}(t)$. Постоим интервальный наблюдатель, решающий ту же задачу, приняв $M = (\begin{array}{*{20}{c}} 1&0&0 \end{array})$. Приведем матрицы, описывающие систему:
Проверим возможность применения первого метода построения интервального наблюдателя. По аналогии с [13] нетрудно показать, что минимальная размерность $k = 2$, при этом решение уравнения (2.5) дает следующие результаты:
Выберем ${{\lambda }_{1}} = - 1$, ${{\lambda }_{2}} = - 2$; тогда $K = {{(\begin{array}{*{20}{c}} 3&2 \end{array})}^{{\text{T}}}}$ и
Вычисления дают два собственных вектора матрицы ${{F}_{*}} - K{{H}_{*}}$: ${{w}_{1}} = {{(\begin{array}{*{20}{c}} 1&2 \end{array})}^{{\text{T}}}}$ и ${{w}_{2}} = {{(\begin{array}{*{20}{c}} 1&1 \end{array})}^{{\text{T}}}}$, на основе которых определяются матрицы
Нетрудно проверить, что
Очевидно, что матрица ${{H}_{z}}{{S}^{{ - 1}}} = (\begin{array}{*{20}{c}} 2&1 \end{array})$ удовлетворяет условию ${{H}_{z}}{{S}^{{ - 1}}} \geqslant 0$, и наблюдатель размерности 2, оценивающий переменную $z(t) = (\begin{array}{*{20}{c}} 1&0&0 \end{array})x(t) = {{x}_{1}}(t)$, может быть построен.
Поскольку все собственные числа матрицы $F$ отрицательны, второй метод позволяет уменьшить размерность. Так как
уравнение (5.3) запишем какПримем $\lambda = - 1$, тогда $N = (\begin{array}{*{20}{c}} 1&0 \end{array})$, ${{J}_{*}} = (\begin{array}{*{20}{c}} 1&0 \end{array})$, откуда $\Phi = (\begin{array}{*{20}{c}} 1&0&0 \end{array})$, ${{G}_{*}} = (\begin{array}{*{20}{c}} 1&0 \end{array})$. Нетрудно проверить, что условие (2.8) выполняется и ${{H}_{z}} = 1$, Q = 0. Интервальный наблюдатель принимает вид
(7.2)
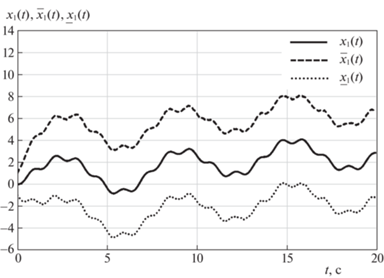
$\begin{gathered} {{{\dot {\bar {x}}}}_{*}}(t) = - {{\underline x }_{*}}(t) + {{y}_{1}}(t) + {{u}_{1}}(t) + {{{v}}_{{1*}}}, \\ \underline z (t) = {{\underline x }_{*}}(t),\quad \bar {z}(t) = {{{\bar {x}}}_{*}}(t), \\ \end{gathered} $Для моделирования рассмотрим систему (7.1) и наблюдатель (7.2) с ${{u}_{1}}(t) = 2{\text{sin}}(t)$, u2(t) = = $8\sin (5t)$; шумы ${{v}_{1}}$ и ${{v}_{2}}$ представляют собой случайные процессы с дисперсией, равной 2; $x(0) = 0$, $\underline x (0) = - 1$, $\bar {x}(0) = 1$. Результаты моделирования приведены на рис. 2 и 3, где показано поведение переменной ${{x}_{1}}(t)$ и ее верхней и нижней оценок ${{\underline x }_{1}}(t)$ и ${{\bar {x}}_{1}}(t)$ для двух значений константы ${{v}_{{1*}}}$: ${{v}_{{1*}}} = 2$ и ${{v}_{{1*}}} = 4$.
Рис. 2.
Поведение переменной ${{x}_{1}}(t)$ и ее верхней и нижней оценок ${{\underline x }_{1}}(t)$ и ${{\bar {x}}_{1}}(t)$ для ${{v}_{{1*}}} = 2$
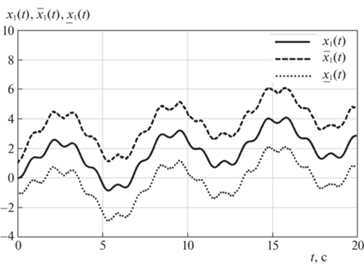
Рис. 3.
Поведение переменной ${{x}_{1}}(t)$ и ее верхней и нижней оценок ${{\underline x }_{1}}(t)$ и ${{\bar {x}}_{1}}(t)$ для ${{v}_{{1*}}} = 4$
Заключение. Рассмотрена задача построения интервальных наблюдателей в системах с неопределенностями, описываемых линейными моделями, которые позволяют оценивать множество допустимых значений заданной линейной функции вектора состояния системы. Предложены два метода построения интервальных наблюдателей, в первом из которых вначале строится обычный наблюдатель с матрицами, заданными в идентификационной канонической форме, который далее преобразуется к виду с жордановой матрицей динамики, а затем к интервальной форме. Во втором методе наблюдатель сразу ищется в форме с жордановой матрицей динамики, на основе которой затем строится интервальный наблюдатель. Второй метод в ряде случаев позволяет уменьшить размерность наблюдателя.
Список литературы
Ефимов Д.В. Построение интервальных наблюдателей для динамических систем с неопределенностями // АиТ. 2016. № 2. С. 5–49.
Kolesov N., Gruzlikov A., Lukoyanov E. Using Fuzzy Interacting Observers for Fault Diagnosis in Systems with Parametric Uncertainty // Proc. XII-th Inter. Sympos. “Intelligent Systems”, INTELS’16.Moscow, Russia, 2016. P. 499–504.
Кремлев А.С., Чеботарев С.Г. Синтез интервального наблюдателя для линейной системы с переменными параметрами // Изв. вузов. Приборостроение. 2013. Т. 56. № 4. С. 42–46.
Mazenc F., Bernard O. Asymptotically Stable Interval Observers for Planar Systems with Complex Poles // IEEE Trans. Automatic Control. 2010. V. 55. № 2. P. 523–527.
Blesa J., Puig V., Bolea Y. Fault Detection Usingin Terval LPV Models in an Open-flow Canal // Control Engineering Practice. 2010. V. 18. P. 460–470.
Zheng G., Efimov D., Perruquetti W. Interval State Estimation for Uncertain Nonlinear Systems // IFAC Nolcos 2013. Toulouse, France, 2013.
Zhang K., Jiang B., Yan X., Edwards C. Interval Sliding mode Based Fault Accommodation for Non-minimal Phase LPV Systems with Online Control Application // Intern. J. Control. 2019. https://doi.org/10.1080/00207179.2019.1687932
Жирабок А.Н., Ким Чхун Ир. Виртуальные датчики в задаче функционального диагностирования нелинейных систем // Изв. РАН. ТиСУ. 2022. № 1. С. 40–48.
Жирабок А.Н., Зуев А.В., Шумский А.Е. Методы идентификации и локализации дефектов в линейных системах на основе скользящих наблюдателей // Изв. РАН. ТиСУ. 2019. № 6. С. 73–89.
Жирабок А.Н., Зуев А.В., Шумский А.Е. Диагностирование линейных динамических систем: подход на основе скользящих наблюдателей // АиТ. 2020. № 2. С. 18–35.
Ланкастер П. Теория матриц. М.: Наука, 1978.
Low X., Willsky A., Verghese G. Optimally Robust Redundancy Relations for Failure Detection in Uncertain Systems // Automatica. 1996. V. 22. P. 333–344.
Жирабок А.Н., Ким Чхун Ир. Виртуальные датчики в задаче функционального диагностирования // Мехатроника, автоматизация, управление. 2021. Т. 22. № 6. С. 298–303.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления