Известия РАН. Теория и системы управления, 2023, № 2, стр. 164-176
СРАВНИТЕЛЬНЫЙ АНАЛИЗ СТРАТЕГИЙ УПРАВЛЕНИЯ ПОТОКАМИ В МНОГОПОЛЬЗОВАТЕЛЬСКОЙ ТЕЛЕКОММУНИКАЦИОННОЙ СЕТИ
Ю. Е. Малашенко a, И. А. Назарова a, *
a ФИЦ ИУ РАН
Москва, Россия
* E-mail: irina-nazar@yandex.ru
Поступила в редакцию 28.10.2022
После доработки 30.10.2022
Принята к публикации 05.12.2022
- EDN: JEVYNL
- DOI: 10.31857/S0002338823020130
Аннотация
В рамках многопродуктовой сетевой модели рассматриваются стратегии управления распределением потоков по различным маршрутам передачи. Оценки допустимых загрузок сети формируются на основе вектора совместно допустимых межузловых потоков. Изучаются две стратегии управления. При реализации первой передаваемые межузловые потоки равны друг другу. Вторая стратегия предполагает поиск недискриминирующего распределения потоков, при передаче которых достигаются равные нагрузки. Под нагрузкой, создаваемой некоторой парой узлов, понимается суммарная величина пропускных способностей, необходимая для обеспечения свзи данного вида. Для оценки минимальных удельных затрат на передачу потока определенного вида строятся все кратчайшие пути между соответствующей парой узлов. Для получения верхней оценки затрат ресурсов при соединении корреспондентов для каждой пары узлов вычисляется максимальный однопродуктовый поток по всем ребрам сети. Вычислительные эксперименты проводились для сетей с различной структурой и позволили провести сранительный анализ уравнительных стратегий управления при расщеплении межузловых потоков для передачи по различным маршрутам.
Введение. Данная работа продолжает исследование проблемы управления потоками в телекоммуникационных территориально-распределенных системах связи [1, 2]. В рамках вычислительных экспериментов на многопродуктовой сетевой модели анализируются результирующие загрузки ребер для двух стратегий управления потоками. Под межузловой нагрузкой понимается суммарная величина пропускных способностей, выделяемых в сети для обеспечения передачи информационного потока определенного вида. Сумма всех дуговых потоков разных видов, проходящих по некоторому ребру, трактуется как реберная загрузка. Общая допустимая загрузка ребер сети, возникающая при одновременной передаче межузловых информационных потоков для всех пар-корреспондентов, считается заданной.
Анализируются две стратегии управления и диспетчерские правила маршрутизации. При реализации первой стратегии осуществляется распределение межузловых потоков, равных друг другу. Вторая стратегия управления предполагает распределение потоков, при котором межузловые нагрузки оказываются одинаковыми по величине для всех корреспондентов. Для поиска допустимых интервалов управления для каждой пары узлов в монопольном режиме [3] вычисляется максимальный однопродуктовый поток. Маршруты передачи потока каждого вида прокладываются по ребрам соответствующих минимальных разрезов. Для всех пар-корреспондентов подсчитываются межузловые нагрузки. На основе найденных значений и с учетом ограничений определяются результирующие реберные загрузки, допустимые при одновременной передаче межузловых потоков.
При использовании каждой стратегии управления сравниваются правила маршрутизации. При передаче каждого вида потока по всем кратчайшим маршрутам производится оценка удельных затрат. Решение стандартной задачи о максимальном потоке и минимальном разрезе применяется для построения дополнительных путей передачи при формировании маршрутно-адресных таблиц в случае возможных повреждений и/или перегрузки сети. Анализ результатов экспериментов позволяет оценить распределение реберных загрузок для описанных стратегий управления в многопользовательских сетях с различными структурными особенностями.
При создании, развитии и эксплуатации телекоммуникационных систем в настоящее время используются потоковые модели [4]. В частности, указанные модели применяются для поиска стратегий управления и построения диспетчерских правил распределения потоков, нагрузок и ресурсов в многопользовательских сетях [5–7]. Методы анализа сетевых систем с учетом вектора требований всех равноправных и невзаимозаменяемых пользователей создаются на основе формализма многокритериальной оптимизации [8, 9]. В русле исследований по разработке SPLIT-методов [10–12] лежат представленные в разд. 2–4 алгоритмические схемы выравнивания нагрузок и получения уравнительных распределений межузловых потоков по различным маршрутам. Для решения оптимизационных многопродуктовых сетевых задач разработаны специальные алгоритмы [13, 14]. В данной работе используются процедуры поиска всех кратчайших путей и максимального однопродуктового пототока с полиномиальными оценками вычислительных затрат [15, 16].
1. Математическая модель. Для описания многопользовательской сетевой системы связи воспользуемся следующей математической записью модели передачи многопродуктового потока. Сеть G задается множествами $\langle V,\;R,\;U,P\rangle $: узлов (вершин) сети $V = \{ {{{v}}_{1}},{{{v}}_{2}},...,{{{v}}_{n}},...,{{{v}}_{N}}\} $; неориентированных ребер $R = \{ {{r}_{1}},{{r}_{2}},...,{{r}_{k}},...,{{r}_{E}}\} $; ориентированных дуг $U = \{ {{u}_{1}},{{u}_{2}},...,{{u}_{k}},...,{{u}_{{2E}}}\} $; пар узлов-корреспондентов $P = \{ {{p}_{1}},{{p}_{2}},...,{{p}_{M}}\} $. Предполагается, что в сети отсутствуют петли и сдвоенные ребра.
Ребро ${{r}_{k}} \in R$ соединяет смежные вершины ${{{v}}_{{{{n}_{k}}}}}$, ${{{v}}_{{{{j}_{k}}}}}$. Каждому ребру ${{r}_{k}}$ ставятся в соответствие две ориентированные дуги ${{u}_{k}}$, ${{u}_{{k + E}}}$ из множества $U$. Дуги $\{ {{u}_{k}},{{u}_{{k + E}}}\} $ определяют прямое и обратное направления передачи потока по ребру ${{r}_{k}}$ между концевыми вершинами ${{{v}}_{{{{n}_{k}}}}}$, ${{{v}}_{{{{j}_{k}}}}}$.
В многопользовательской сети G рассматривается $M = N(N - 1)$ независимых, невзаимозаменяемых и равноправных межузловых потоков различных видов. Каждой паре узлов-корреспондентов ${{p}_{m}}$ из множества $P$ соответствуют: вершина-источник с номером ${{s}_{m}}$, из ${{s}_{m}}$ входной поток m-го вида поступает в сеть; вершина-приемник с номером ${{t}_{m}}$, из ${{t}_{m}}$ поток m-го вида покидает сеть. Обозначим через ${{z}_{m}}$ величину межузлового потока m-го вида, поступающего в сеть через узел с номером ${{s}_{m}}$ и покидающего сеть из узла с номером ${{t}_{m}}$; ${{x}_{{mk}}}$, ${{x}_{{m(k + E)}}}$ – поток m-го вида, который передается по дугам ${{u}_{k}}$ и ${{u}_{{k + E}}}$, согласно направлению передачи, ${{x}_{{mk}}} \geqslant 0$, ${{x}_{{m(k + E)}}} \geqslant 0$, $m = \overline {1,M} $, $k = \overline {1,E} $; $S({{{v}}_{n}})$ – множество номеров исходящих дуг, по ним поток покидает узел ${{{v}}_{n}}$; $T({{{v}}_{n}})$ – множество номеров входящих дуг, по ним поток поступает в узел ${{{v}}_{n}}$. Состав множеств $S({{{v}}_{n}})$, $T({{{v}}_{n}})$ однозначно формируется в ходе выполнения следующей процедуры. Пусть некоторое ребро ${{r}_{k}} \in R$ соединяет вершины с номерами $n$ и $j$, такими, что $n < j$. Тогда ориентированная дуга ${{u}_{k}} = ({{{v}}_{n}},{{{v}}_{j}})$, направленная из вершины ${{{v}}_{n}}$ в ${{{v}}_{j}}$, считается исходящей из вершины ${{{v}}_{n}}$, и ее номер k заносится в множество $S({{{v}}_{n}})$, а дуга ${{u}_{{k + E}}}$, направленная из ${{{v}}_{j}}$ в ${{{v}}_{n}}$, – входящей для ${{{v}}_{n}}$, и ее номер $k + E$ помещается в список $T({{{v}}_{n}})$. Дуга ${{u}_{k}}$ является входящей для ${{{v}}_{j}}$, и ее номер k попадает в $T({{{v}}_{j}})$, а дуга ${{u}_{{k + E}}}$ – исходящей, и номер $k + E$ вносится в список исходящих дуг $S({{{v}}_{j}})$.
Во всех узлах сети ${{{v}}_{n}} \in V$, $n = \overline {1,N} $, для каждого вида потока должны выполняться условия сохранения потоков:
(1.1)
$\begin{gathered} \sum\limits_{i \in S({{{v}}_{n}})} {{x}_{{mi}}} - \sum\limits_{i \in T({{{v}}_{n}})} {{x}_{{mi}}} = \left\{ \begin{gathered} {{z}_{m}},\quad {\text{если}}\quad {{{v}}_{n}} = {{{v}}_{{{{s}_{m}}}}}{\text{,}} \hfill \\ - {{z}_{m}},\quad {\text{если}}\quad {{{v}}_{n}} = {{{v}}_{{{{t}_{m}}}}}{\text{,}} \hfill \\ 0\quad {\text{в}}\;{\text{остальных}}\;{\text{случаях,}} \hfill \\ \end{gathered} \right. \\ n = \overline {1,N} ,\quad m = \overline {1,M} ,\quad {{x}_{{mi}}} \geqslant 0,\quad {{z}_{m}} \geqslant 0. \\ \end{gathered} $Величина zm равна входному межузловому потоку m-го вида, проходящему от источника к приемнику пары ${{p}_{m}}$ при распределении потоков ${{x}_{{mi}}}$ по дугам сети.
Каждому ребру ${{r}_{k}} \in R$ приписывается неотрицательное число ${{d}_{k}}$, определяющее суммарный предельно допустимый поток, который можно передать по ребру ${{r}_{k}}$ в обоих направлениях. В исходной сети компоненты вектора пропускных способностей ${\mathbf{d}} = ({{d}_{1}},{{d}_{2}},...,{{d}_{k}},...,{{d}_{E}})$ – наперед заданные положительные числа ${{d}_{k}} > 0$. Вектор d задает следующие ограничения на сумму потоков всех видов, передаваемых по ребру ${{r}_{k}}$ одновременно:
(1.2)
$\sum\limits_{m = 1}^M ({{x}_{{mk}}} + {{x}_{{m(k + E)}}}) \leqslant {{d}_{k}},\quad {{x}_{{mk}}} \geqslant 0,\quad {{x}_{{m(k + E)}}} \geqslant 0,\quad k = \overline {1,E} .$Ограничения (1.1), (1.2) задают множество допустимых значений компонент вектора межузловых потоков ${\mathbf{z}} = ({{z}_{1}},{{z}_{2}},...,{{z}_{m}},..,{{z}_{M}})$:
В рамках данной модели пропускная способность ребер сети измеряется в условных единицах потока и трактуется как ресурсное ограничение. Обозначим через $D(0)$ суммарную величину пропускной способности сети. Значение $D(0)$ считается заданным:
Для каждой пары узлов-корреспондентов ${{p}_{m}} \in P$, для некоторого допустимого межузлового потока ${{\tilde {z}}_{m}}$ и соответствующих дуговых потоков ${{\tilde {x}}_{{mk}}}$, $k = \overline {1,2E} $, величина
характеризует результирующую межузловую нагрузку (МР-нагрузку) на сеть при передаче межузлового потока величины ${{\tilde {z}}_{m}}$ из узла-источника ${{s}_{m}}$ в узел-приемник ${{t}_{m}}$. Величина ${{\tilde {y}}_{m}}$ показывает, какая суммарная пропускная способность сети потребуется для передачи дуговых потоков ${{\tilde {x}}_{{mk}}}$. В рамках модели отношение МР-нагрузки и межузлового потокаВводится величина
2. Уравнительное распределение МР-нагрузки. В рамках модели проводились вычислительные эксперименты для оценки распределения РС-загрузки сети при равных МР-нагрузках для всех пар-корреспондентов. При подготовке данных формировался вектор исходных пропускных способностей ${\mathbf{d}}(0)$ для сети G(0). В сети G(0) при заданных ${{d}_{k}}(0)$ для каждой пары узлов ${{p}_{m}}$, $m = \overline {1,M} $, последовательно решалась задача поиска максимального независимого однопродуктового потока [15], передаваемого в монопольном режиме управления [3].
Задача 1. Для некоторой пары узлов ${{p}_{a}}$ найти
При последовательном решении задачи 1 для каждой пары ${{p}_{a}} \in P$ вычисляются максимальный межузловой поток $z_{a}^{0}(0)$ и дуговые потоки $(x_{{ak}}^{0}(0),x_{{a(k + E)}}^{0}(0))$, $k = \overline {1,E} $. Далее подсчитываются: МР-нагрузка
для найденных $y_{a}^{0}(0)$ нормирующий коэффициент и дуговые потоки:При передаче дуговых потоков $x_{{ak}}^{0}$ соответствующая МР-нагрузка $y_{a}^{0}$ равна единице для межузлового потока $z_{a}^{0} = \theta _{a}^{0}(0)z_{a}^{0}(0)$.
Задача 1 решается последовательно для всех ${{p}_{m}} \in P$, и для дуговых потоков $x_{{mk}}^{0}$ определяется РС-загрузка ребер сети при передаче межузловых потоков $z_{m}^{0}$:
Для заданного значения D(0) подсчитывается допустимое перераспределение РС-загрузок:
(2.1)
$\beta (0)\left[ {\sum\limits_{m = 1}^M \theta _{m}^{0}(0)(x_{{mk}}^{0}(0) + x_{{m(k + E)}}^{0}(0))} \right] = \Delta _{k}^{0}(0),\quad k = \overline {1,E} .$В рамках модели суммарная величина РС-загрузки численно равна суммарной пропускной способности D(0):
Из соотношений (2.1), (2.2) находится значение $\beta (0)$:
На основе найденных значений формируется сеть $G(1)$, в которой
В сети $G(1)$ для всех пар узлов ${{p}_{a}} \in P$, $a = \overline {1,M} $, определяется максимальный однопродуктовый поток.
Задача 2. Найти $z_{a}^{0}(1) = \max \{ {{z}_{a}}\,{\text{|}}\,({\mathbf{z}},x) \in \mathcal{Z}({\mathbf{d}}{\kern 1pt} *({\mathbf{1}}))\} $
На основе последовательного решения задачи 2 задаются коэффициенты нормировки
Вычисляются β*(1), $\Delta _{k}^{0}(1)$, $k = \overline {1,E} $, и формируется “новая” сеть $G(2)$, в ней пропускные способности $d_{k}^{*}(2)$ полагаются равными РС-загрузкам $\Delta _{k}^{0}(1)$, т. е.
Для полученных решений находим $z_{m}^{*}(1)$ – распределение межузловых потоков при равных значениях МР-нагрузок $y_{m}^{0}(1)$:
3. Уравнительное распределение межузловых потоков. В рамках модели проводились вычислительные эксперименты для оценки РС-загрузки сети при равных межузловых потоках. В сети $G(0)$ при заданных ${{d}_{k}}(0)$ последовательно для каждой пары узлов ${{p}_{m}} \in P$, $m = \overline {1,M} $, решалась задача 1 поиска максимального независимого однопродуктового потока, передаваемого в монопольном режиме управления [3].
При последовательном решении задачи 1 для каждой пары ${{p}_{a}} \in P$ вычисляются максимальный межузловой поток $z_{a}^{0}(0)$ и соответствующие дуговые потоки $(x_{{ak}}^{0}(0),x_{{a(k + E)}}^{0}(0))$, $k = \overline {1,E} $. Определяются нормирующий коэффициент
и дуговые потоки:При передаче дуговых потоков $x_{{ak}}^{0}$ межузловой поток $z_{a}^{0}$ равен единице:
Задача 1 решается последовательно для всех ${{p}_{m}} \in P$, и для дуговых потоков $x_{{mk}}^{0}(0)$ определяется РС-загрузка ребер сети при передаче единичных потоков для всех корреспондентов:
(3.1)
$\alpha (0)\left[ {\sum\limits_{m = 1}^M \xi _{m}^{0}(0)(x_{{mk}}^{0}(0) + x_{{m(k + E)}}^{0}(0))} \right] = \Delta _{k}^{0}(0).$Величина РС-загрузки численно равна требуемой суммарной пропускной способности $D(0)$, которая считается заданной:
Из соотношений (3.1), (3.2) находится значение $\alpha (0)$:
На основе найденных значений формируется сеть $G(1)$, в ней
В сети G(1) для всех пар узлов ${{p}_{a}} \in P$, $a = \overline {1,M} $, определяется максимальный однопродуктовый поток.
Задача 3. Найти $z_{a}^{0}(1) = \max \{ {{z}_{a}}\,{\text{|}}\,({\mathbf{z}},x) \in \mathcal{Z}({\mathbf{d}}{\kern 1pt} {\text{*}}{\mathbf{(1)}})\} $
На основе решения задачи 3 последовательно задаются коэффициенты нормировки
Вычисляются $\alpha {\kern 1pt} *(1)$, ${{y}^{1}}(k)$, $k = \overline {1,E} $, и формируется “новая” сеть $G(2)$, в которой пропускные способности $d_{k}^{*}(2)$ полагаются равными $\Delta _{k}^{0}(1)$, т. е.
Для полученных решений подсчитываются межузловые потоки $z_{m}^{*}(1) = \alpha {\kern 1pt} {\text{*}}(1)$ для всех пар ${{p}_{m}} \in P$. Таким образом, все межузловые потоки равны α*(1), а суммарный поток
Алгоритмическая схема, изложенная в разд. 2, 3, далее называется SFMC-процедурой (от английского split flow minimum cut – расщепление потока по ребрам минимального разреза). При проведении вычислительных экспериментов SFMC-процедура позволяет получать оценки РС-загрузок при расщеплении межузловых потоков по ребрам минимального разреза.
4. Распределение межузловых потоков по кратчайшим маршрутам. Для оценки минимальных удельных затрат различных уравнительных стратегий управления использовалась SFSR-процедура (от английского split flow shortest route – расщепление потока по всем кратчайшим маршрутам). SFSP-процедура позволяет распределять межузловые потоки по маршрутам, состоящим из минимального числа ребер.
При проведении эксперимента на первом этапе для каждой пары узлов ${{p}_{m}} = ({{s}_{m}},{{t}_{m}})$ в сети G(0) определяется множество всех кратчайших путей [17], которые далее используются как маршруты передачи $m$-го вида потока
где ${{h}^{j}}(m) = \{ k_{1}^{j}(m),k_{2}^{j}(m),...,k_{{\mu (m)}}^{j}(m)\} $ – список номеров ребер в j-м кратчайшем пути между узлами ${{s}_{m}}$ и ${{t}_{m}}$, $\mu (m)$ – число ребер в кратчайшем маршруте ${{h}^{j}}(m)$, а $J(m)$ – число кратчайших маршрутов для m-й пары.Для оценки возможности “расщепления” потока по различным маршрутам на втором этапе для каждой пары ${{p}_{m}} \in P$ по каждому маршруту из ${{H}^{0}}(m)$ передается единичный межузловой поток zm и подсчитываются значения индикаторной функции:
Вычисляются дуговые потоки для пары pm:
(4.1)
$x_{{mk}}^{0}(0) = \sum\limits_{j = 1}^{J(m)} \eta _{k}^{j}(m),\;\;m = \overline {1,M} ,\;\;k = \overline {1,E} .$Величина межузлового потока $z_{m}^{0}(0)$ между узлами ${{s}_{m}}$ и ${{t}_{m}}$ определятся по формулам (1.1) и (4.1). Рассчитывается нормирующий коэффициент
Находятся дуговые потоки:
при передаче которых по ребрам сети межузловой поток из узла ${{s}_{m}}$ в узел ${{t}_{m}}$ равен единице.Для заданного значения D(0) подсчитываются допустимые РС-загрузки ребер сети:
Подсчитываются суммарный межузловой поток
и норма РС-загрузки:Для оценки РС-загрузок при уравнительном распределении МР-нагрузок для всех пар узлов ${{p}_{m}} \in P$ также использовалась SPSR-процедура. На первых двух этапах, согласно (4.1), определяются реберные потоки $x_{{mk}}^{0}(0)$ для $m = \overline {1,M} $ и $k = \overline {1,E} $ при передаче единичных потоков по всем кратчайшим маршрутам из ${{H}^{0}}(m)$, $m = \overline {1,M} $. Для каждой пары ${{p}_{m}} \in P$ вычисляются МР-нагрузки:
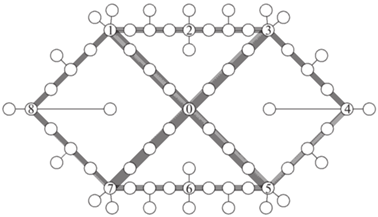
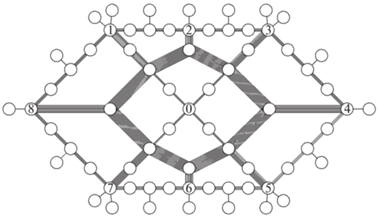
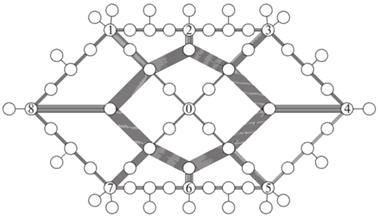
нормирующие коэффициенты:5. Вычислительный эксперимент. Вычислительные эксперименты проводились на моделях сетевых систем, представленных на рис. 1, 2 (базовая и кольцевая сети соответственно). В каждой сети имеется 69 узлов. Пропускные способности ребер ${{d}_{k}}$ выбираются случайным образом из отрезка [900, 999] и совпадают для ребер, присутствующих в обеих сетях. В кольцевой сети пропускная способность каждого из добавленных ребер равна 900. В ходе эксперимента проводилась нормировка, и суммарная пропускная способность в обеих сетях была одинакова:
Результаты вычислительных экспериментов с использованием SFMC-процедуры для оценки реберных загрузок при равных межузловых нагрузках для всех пар корреспондентов представлены на рис. 3–6. Толщина ребер на рисунках пропорциональна результирующей РС-загрузке. В состав внутреннего кольца на рис. 2, 4 вошли четыре висячих узла из базовой сети, и соответствующие ребра образовали мостики для транзитных потоков.
В базовой сети основная РС-загрузка – 1400 единиц – приходится на радиальные ребра, исходящие из центрального узла, а на ребрах внешнего кольца не превышает 1250 единиц. При формировании кольцевой сети в состав внутреннего кольца включаются четыре узла, которые в базовой являются висячими. Соответствующие ребра образуют мостики для передачи транзитных потоков между внутренним и внешним кольцом. РС-загрузка ребер внутреннего кольца составляет 2050 единиц, на внешнем не превышает 800, а на ребрах- мостиках – 1500. В обеих сетях минимальная загрузка достигается на висячих ребрах: 300 единиц для базовой и 400 для кольцевой. Указанные значения определяются собственными информационными потоками, передающимися из каждого узла. При этом транзитные нагрузки, например, на ребрах внутреннего кольца на порядок превышают собственные потоки инцидентных узлов.
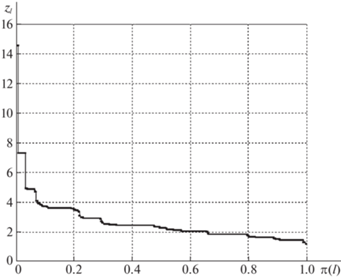
Для полученных значений МР-нагрузок вычисляются межузловые потоки $z_{m}^{*}(1)$. Результирующие диаграммы представлены на рис. 5, 6 . На них приведены значения ${{z}_{l}}$, $l = \overline {1,m} $, упорядоченные по величине от большего к меньшему. На вертикальной оси по невозрастанию откладываются ${{z}_{l}}$, а по горизонтальной указываются порядковые номера в данной упорядоченной последовательности:
где M – общее число элементов в множестве пар-корреспондентов P. Полученные результаты, представленные на рис. 5, 6 в виде диаграмм, свидетельствуют, что как суммарный, так и медианное значения межузлового потока на 50% больше в кольцевой сети при равных пропускных способностях в обеих сетях. Дело в том, что при вычислении максимального потока, а в дальнейшем при поиске равных нагрузок используются все пути, проходящие через минимальные сечения. В кольцевой сети маршруты соединения оказываются короче, чем в базовой для большого числа пар узлов, что уменьшает межузловые нагрузки и удельные затраты ресурсов. В базовой сети только 46 ребер пригодны для транзитной передачи, а в кольцевой – 58, что только на 25% больше, однако позволяет на 30% увеличить суммарный межузловой поток и более чем на 50% медианное значение. Величина суммы межузловых потоков в базовой и кольцевой сетях соответственно равны:Значение медианы в базовой сети ${{z}^{ = }} = 1.5$, в кольцевой ${{z}^{ = }} = 2.3$.
Результаты расчетов на рис. 5, 6 показывают, что для 80% пар межузловые потоки близки к медианному значению, а для 20% – в несколько раз превышают его. Для пар узлов, кратчайший путь между которыми состоит из одного или двух ребер, межузловые потоки превышают медианное значение. Следует отметить, что при использовании последовательного максиминного правила распределения потоков и нагрузок близко расположенные корреспонденты также оказываются в привилегированном положении и получают преимущество при уравнительных способах дележа [1, 3].
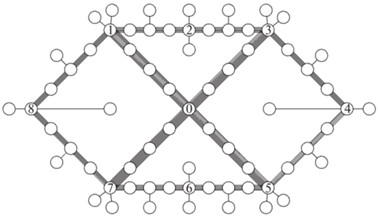
Результаты вычислительных экспериментов с использованием SFMC-процедуры для оценки РС-загрузок при равных межузловых потоках для всех пар корреспондентов представлены на рис. 7, 8 и в табл. 1. РС-загрузка ребер-“мостиков” составляет 1630 единиц, наибольшие значения достигаются на ребрах внутреннего кольца – 2230 единиц, а на внешнем не превышает 830. Напротив, в базовой сети основная РС-нагрузка – 1600 единиц – приходится на радиальные ребра, исходящие из центра, а на ребрах внешнего кольца не превышает 1270 единиц. В обеих сетях минимальная реберная загрузка достигается на висячих ребрах: 210 единиц для базовой и 310 единиц для кольцевой. Указанные значения отвечают собственным информационным потокам, передаваемым из каждого узла без учета транзитных. Загрузки на ребрах внутреннего кольца на порядок превышают собственные потоки инцидентных узлов.
Таблица 1
| Сеть | Базовая | Кольцевая | ||||||
|---|---|---|---|---|---|---|---|---|
| Значения | SFMC-стратегия | SFSR-стратегия | SFMC-стратегия | SFSR-стратегия | ||||
| Медиана потоков | z* | z(y*) | z** | z(y**) | z* | z(y*) | z** | z(y**) |
| 1.54 | 1.5 | 1.85 | 1.82 | 2.26 | 2.3 | 2.5 | 2.4 | |
| Сумма межузловых потоков | 7220 | 9390 | 8670 | 12 810 | 10 600 | 12 400 | 11 750 | 15 650 |
| Удельные затраты | 9.5 | 7.3 | 7.9 | 5.3 | 6.4 | 5.5 | 5.8 | 4.4 |
| Норма вектора РС-загрузок | 9270 | 8940 | 9210 | 9000 | 9430 | 9380 | 9520 | 9160 |
Результаты, представленные в таблице, свидетельствуют, что как суммарный, так и каждый отдельно взятый межузловой поток на 50% больше в кольцевой сети при равной суммарной пропускной способности обеих. Дело в том, что при поиске и передаче максимального потока используются все пути, проходящие через минимальные сечения. В кольцевой сети маршруты соединения короче (не длиннее) для многих пар узлов, что уменьшает транзитную загрузку и удельные затраты ресурсов. В базовой сети 46 ребер пригодны для транзитной передачи, а в кольцевой – 58, что только на 25% больше, однако при той же пропускной способности это позволяет увеличивать потоки на 50%.
Полученные значения медиан распределений потоков можно интерпретировать как представительные оценки функциональных возможностей сети в условиях неопределенности и равноправности корреспондентов. Все межузловые потоки, не превышающие медианных значений, можно передать в сети одновременно. Для последних наблюдается разброс для различных стратегий управления и правилах маршрутизации. Финальные потоки при предельных распределениях для 80% пар практически равны медианным, хотя средние показатели отличаются при равных нагрузках. Для 20% пар финальные значения при равных нагрузках значительно превышают медианные и средние показатели, что позволяет оценивать эффективность использования ресурсов при передаче однородных межузловых потоков в стационарном режиме. В рамках модели медианы можно трактовать как нормативные характеристики управления при работе сети в стационарном режиме при однородных нагрузках в заданном диапазоне.
Заключение. В работе изучались распределения межузловых потоков разных видов. Предполагалось, что для всех пар корреспондентов соответствующие потоки невзаимозаменяемы. Проводилась оценка допустимых межузловых потоков в сети при различных стратегиях управления. Анализировались достижимые значения потоков и нагрузок при уравнительном предельном распределении ресурсов.
Предложенный метод позволяет оценивать допустимые распределения межузловых потоков при изменении структуры сети. Построение нескольких путей соединения дает возможность анализировать нагрузку на сеть с учетом обходов для транзитных потоков. Полученные агрегированные показатели для потоков, проходящих через узлы сети, могут быть использованы при построении маршрутно-адресных таблиц, подготовке графиков обходов и замен (ГОЗ) для работы в аварийных режимах и в критически опасных повреждениях. Кроме того, описанная вычислительная схема позволяет производить оценку и сравнивать различные способы формирования сети, построенной на основе арендованных каналов связи при сохранении их общего числа. Изменение структуры при переходе от базовой к кольцевой значительно увеличивает межузловые потоки, хотя общее число арендуемых каналов совпадает в обеих сетях.
Список литературы
Малашенко Ю.Е., Назарова И.А. Оценки распределения ресурсов в многопользовательской сети при равных межузловых нагрузках // Информатика и ее применения. 2023. Т. 33. № 1. С. 21–26.
Малашенко Ю.Е., Назарова И.А. Оценки распределения потоков при предельной загрузке многопользовательской сети // Системы и средства информатики. 2022. Т. 32. № 3. С. 71–80.
Малашенко Ю.Е. Максимальные межузловые потоки при предельной загрузке многопользовательской сети // Информатика и ее применения, 2021. Т. 15. № 3. С. 24–28.
Salimifard K., Bigharaz S. The Multicommodity Network Flow Problem: State of the Art Classification, Applications, and Solution Methods // J. Oper. Res. Int. 2020. V. 22. Iss. 2. P. 1–47.
Ogryczak W., Luss H., Pioro M. et al. Fair Optimization and Networks: A Survey // J. Appl. Math. 2014. V. 3. P. 1–25.
Luss H. Equitable Resource Allocation: Models, Algorithms, and Applications. Hoboken: John Wiley & Sons, 2012.
Balakrishnan A., Li G., Mirchandani P. Optimal Network Design with End-to-End Service Requirements // Oper. Res. 2017. V. 65. Iss. 3. P. 729–750.
Radunovic B., Le Boudec J.-Y. A Unified Framework for Max-Min and Min-Max Fairness With Applications // IEEE/ACM Transactions on Networking. 2007. V. 15. Iss. 5. P. 1073–1083.
Nace D., Doan L.N., Klopfenstein O. et al. Max-min Fairness in Multicommodity Flows // Comput. Oper. Res. 2008. V. 35. Iss. 2. P. 557–573.
Baier G., Kohler E., Skutella M. The k-Splittable Flow Problem // Algorithmica. 2005. V. 42. Iss. 3–4. P. 231–248.
Kabadurmus O., Smith A.E. Multicommodity k-Splittable Survivable Network Design Problems with Relays // Telecommun. Syst. 2016. V. 62. Iss. 1. P. 123–133.
Bialon P. A Randomized Rounding Approach to a k-Splittable Multicommodity Flow Problem with Lower Path Flow Bounds Affording Solution Quality Guarantees // Telecommun. Syst. 2017. V. 64. Iss. 3. P. 525–542.
Ramaswamy R., Orlin J.B., Chakravarti N. Sensitivity Analysis for Shortest Path Problems and Maximum Capacity Path Problems in Undirected Graphs // Math. Prog. 2005. V. 102. Iss. 2. P. 355–369.
Hajjem M., Bouziri H., Talbi E.-G. A Metaheuristic Framework for Dynamic Network Flow Problems // Recent Developments in Metaheuristics. Operations Research/Computer Science Interfaces Series. V. 62. Cham: Springer, 2018. P. 285–304.
Йенсен П., Барнес Д. Потоковое программирование. М.: Радио и связь, 1984.
Кормен Т.Х., Лейзерсон Ч.И., Ривест Р.Л. и др. Алгоритмы: построение и анализ. М.: Вильямс, 2005.
Берж К. Теория графов и ее применения. М.: Изд-во иностр. лит., 1962.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления