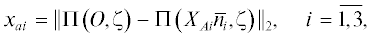Известия РАН. Теория и системы управления, 2023, № 3, стр. 90-105
ВОССТАНОВЛЕНИЕ СТРУКТУРНОЙ ИНФОРМАЦИИ ОБ АНТРОПОГЕННЫХ ОБЪЕКТАХ ИЗ ОДИНОЧНЫХ АЭРОКОСМИЧЕСКИХ ИЗОБРАЖЕНИЙ
Н. В. Антипова a, b, *, О. Г. Гвоздев a, c, **, В. А. Козуб a, ***, А. Б. Мурынин a, b, ****, А. А. Рихтер a, *****
a НИИ “АЭРОКОСМОС”
Москва, Россия
b ФИЦ ИУ РАН
Москва, Россия
c ФГБОУ ВО “Московский государственный университет геодезии и картографии” (МИИГАиК)
Москва, Россия
* E-mail: antipova@phystech.edu
** E-mail: gvozdev@miigaik.ru
*** E-mail: postbox-kozub@ya.ru
**** E-mail: amurynin@bk.ru
***** E-mail: urfin17@yandex.ru
Поступила в редакцию 06.01.2023
После доработки 20.01.2023
Принята к публикации 06.02.2023
- EDN: EUCSLC
- DOI: 10.31857/S0002338823030010
Аннотация
Описан метод трехмерной реконструкции зданий по одиночному аэрокосмическому изображению, состоящий из двух этапов – извлечение семантической информации и восстановление геометрии. Рассмотрена топология искусственных нейронных сетей по семантической сегментации компонентов зданий и эталонных объектов. По второму этапу представлены некоторые математические преобразования: по расчету фотометрических параметров изображения на базе метаданных или эталонных объектов, по преобразованию пространственных координат в осевые и плоские координаты изображения и др. Показаны два примера по вычислению фотометрических параметров и трехмерной модели здания по одиночным спутниковому изображению и аэрофотоснимку.
Введение. Задача трехмерной реконструкции исследуется в научном сообществе уже более 20 лет. Трехмерные модели могут использовать, например, для симуляции распространения шума, света и электромагнитных волн, что может быть очень полезно при создании планов застройки и планирования расположения объектов телекоммуникационной инфраструктуры [1]. Рост интереса к данной проблеме в последние годы вызван бурным развитием вычислительной техники и алгоритмов глубокого обучения, позволившим создавать намного более робастные алгоритмы, что в свою очередь привело к значительному улучшению качества таких алгоритмов и повышению уровня автоматизации решения данной проблемы. Тем не менее, задача построения устойчиво работающего алгоритма трехмерной реконструкции по одному оптическому изображению с приемлемым уровнем детализации все еще остается нерешенной.
3D-реконструкция объектов по данным дистанционного зондирования Земли (ДЗЗ) заключается в обнаружении объектов и определении их трехмерных свойств, таких как высота и форма. Как правило, результат работы конечного алгоритма представляет собой набор векторных моделей. Для описания точности получаемых моделей обычно используют уровни детализации LoD (level of details) [2], из которых стоит отметить LoD1 и LoD2. В зависимости от конкретного метода уровень детализации может немного различаться, но обычно под уровнем LoD1 понимают призматическую модель здания (восстанавливается форма основания и высота), в то время как модель LoD2 дополнительно содержит информацию о форме крыши (без формообразующих элементов, таких, как вентиляционные трубы, слуховые окна и т.д.). Проблема является плохо поставленной, поэтому стандартным подходом будет ее декомпозиция на более простые и четко сформулированные подзадачи. В свою очередь определение подзадач опирается, главным образом, на тот набор данных (их природу и качество), которые будут поданы на вход алгоритма реконструкции. В работе в качестве входных данных используется одно оптическое спутниковое изображение сверхвысокого разрешение (<1 м/пк). Существует также большое количество методов, опирающихся на применение многопозиционной съемки [3–5] или результаты лидарного сканирования местности [6–8]. Однако они в некоторой степени отличаются от методов восстановления по одному аэрокосмическому изображению и поэтому рассматриваться здесь не будут.
1. Анализ существующих методов решения задачи. Представленные в литературе способы трехмерной реконструкции можно условно разделить на два типа: основанные на моделях и на данных.
Первый тип предполагает наличие некоторой библиотеки моделей. Задача реконструкции в этом случае заключается в определении для каждого объекта подходящей модели с уточнением параметров этой модели. Среди ранних работ в данном направлении можно отметить [9], где использовалась библиотека из восьми форм оснований, а сегментация проводилась на базе специально подобранной функции энергии. С помощью методов, адаптированных к работе только с оптическими изображениями, фактическим стандартом стало применение искусственных нейронных сетей (ИНС) для семантического анализа изображений. Только эта технология способна на данный момент обеспечить достаточно высокое качество извлечения семантики сцены. В некоторых методах задача трехмерной реконструкции решается полностью с помощью нейросетевых алгоритмов. Например, в [10] реализован алгоритм реконструкции, аппроксимирующий здания кубоидами, параметры которых определяются непосредственно с помощью сверточной сети детекции. Преимуществом модельного подхода является меньшая подверженность ошибкам из-за шума в данных, за что в свою очередь приходится платить ограниченностью форм восстанавливаемых объектов теми вариантами, которые заранее определены разработчиками в библиотеке моделей.
Методы, основанные на данных, предлагают определение всех геометрических форм объектов через набор простых элементов (прямых, углов, плоскостей и т.д.) и не ограничивают возможности их взаимного расположения. Так, в [11] рассмотрен подход реконструкции по одному аэрофотоснимку. Для реконструкции разработан алгоритм, основанный на правилах и геометрических построениях, который в качестве входных данных использует сегментацию линий (изгибов) крыш и нормализованную цифровую модель поверхности (NDSM). Для построения NDSM и масок сегментации применяется Y-образная сверточная сеть с двумя декодерами. Другой интересный способ реконструкции предложен в [12], где авторы описывают image-to-mesh ИНС архитектуру, результатом работы которой является непосредственно 3D-модель здания. Метод не рассчитан на работу со спутниковой съемкой в качестве входного изображения, зато имеется возможность работы с наземной или аэрофотосъемкой.
Подходы, основанные на данных, теоретически позволяют восстанавливать объекты более разнообразной формы, нежели подходы, основанные на моделях. Однако они сильно зависят от качества нахождения используемых базовых элементов. В случае плохой сегментации элементов результат может выходить крайне нереалистичным, чего не может случиться для методов, основанных на моделях. Тем не менее, бурное развитие технологий глубокого обучения дало возможность производить быструю и качественную сегментацию даже очень сложных объектов. Можно полагать, что качество работы сверточных нейронных сетей (СНС) в ближайшее время будет только расти. Поэтому для разработки собственного решения был выбран подход, основанный на данных, как наиболее перспективный.
2. Предлагаемый подход. 2.1. Основная идея. Предлагаемый метод реконструкции состоит из двух этапов (или блоков).
Извлечение семантической информации. Подразумевает семантическую сегментацию изображения по определенному набору классов, производящуюся с использованием СНС. Наиболее важными классами являются стены, крыши и тени зданий, а также производные от них. Для определения эталонов возможно выделение других классов: автомобильной полосы или железнодорожной колеи, автомобильных или железнодорожных столбов (при подходящем пространственном разрешении). Выбор и формализация классов являются важной задачей, от решения которой зависит качество последующей реконструкции [13–15].
Восстановление геометрии. Основан на детерминированных необучаемых алгоритмах проективной геометрии, статистических методах, а также наборе правил (предположений) об объектах. В общем случае восстановление геометрии можно разделить на следующие стадии:
введение системы координат в пространстве и на плоскости;
выделение опорных точек по результатам сегментации и определение их координат на плоскости изображения;
определение связей между опорными точками;
нахождение пространственных координат опорных точек;
построение модели объекта.
Данное разделение имеет ряд преимуществ. Во-первых, блочная структура позволяет независимо менять (обновлять) отдельные части алгоритма, важно лишь сохранение интерфейса. Во-вторых, для каждого этапа в отдельности легче построить систему оценки качества.
2.2. Извлечение семантической информации с помощью ИНС. Наибольший интерес в задаче реконструкции имеют объекты хозяйственной инфраструктуры, которые ввиду большого разнообразия геометрических и текстурных признаков невозможно сегментировать с надлежащим качеством при помощи классических методов машинного обучения. Поэтому для решения этой задачи использовались искусственные сверточные нейронные сети (ИСНС).
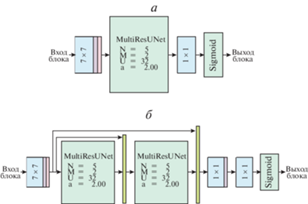
Первые опыты проводились с топологиями на основе U-net [16], состоящими из одного кодировщика и нескольких декодеровщиков [13]. Однако, как показали дальнейшие исследования, более предпочтительной для данной задачи является топология MultiResUNet [17]. Во множестве проведенных экспериментов она стабильно показывала высокие результаты как с точки зрения качества получаемого результата, так и с точки зрения скорости обучения. Топология представляет собой улучшенный вариант U-net с возможностью параметрического масштабирования. Схематичное изображение архитектуры MultiResUnet представлено на рис. 1. Используемые параметры масштабирования вместе с их описанием представлены в табл. 1, 2.
Рис. 1.
Схемы параметрической топологии, разработанной на базе MultiResUNet: а – принципиальная схема; б – условные обозначения, используемые в схемах нейросетевых моделей; в – плотносвязанный остаточный путь (MultiResPath); г – простой остаточный путь (ResPath)
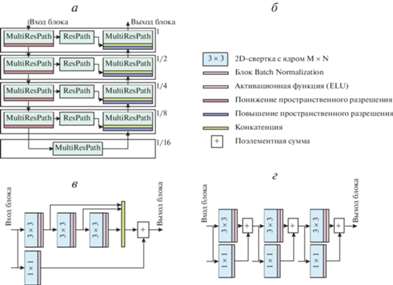
Таблица 1.
Используемые параметры топологии MultiResUNet
| Обозначение/формула | Значение по умолчанию | Описание |
|---|---|---|
| N | 5 | Количество слоев |
| M | 2 | Множитель слоя |
| U | 32 | Базовое количество ядер |
| α | 1.67 | Коэффициент количества ядер |
| n | Текущий слой $n \in \overline {1,N} $ | |
| 1/n | Текущий масштабный уровень | |
| b = $\left\lfloor {\alpha U{{M}^{n}}} \right\rfloor $ | Базовый коэффициент количества ядер в группах плотносвязанных остаточных путей | |
| $\frac{b}{6}$ | Количество ядер в первой группе плотносвязанного остаточного пути | |
| $\frac{b}{3}$ | Количество ядер во второй группе плотносвязанного остаточного пути | |
| $\frac{b}{2}$ | Количество ядер в третьей группе плотносвязанного остаточного пути | |
| $N - n - 1$ | Количество операций свертки в простом остаточного пути слоя n | |
| N | Количество ядер в операциях свертки простого остаточного пути слоя n |
Таблица 2.
Параметры и соотношения параметризации топологии MultiResUNet, предложенные в проекте
| Масштабный уровень | Количество ядер свертки | ||
|---|---|---|---|
| Кодировщик | Skip-connection | Декодировщик | |
| 1 | 8, 17, 26 | 32, 32, 32, 32 | 8, 17, 26 |
| 1/2 | 17, 35, 53 | 64, 64, 64 | 17, 35, 53 |
| 1/4 | 31, 72, 106 | 128, 128 | 31, 72, 106 |
| 1/8 | 71, 142, 213 | 256 | 71, 142, 213 |
| 1/16 | 142, 284, 427 | ||
Приведенная параметрическая структура стала основой для разработанных базовой и усиленной топологий сегментации. Базовая топология (рис. 2,а) представляет собой MultiResUnet-сеть, дополненную в начале сверткой с размером фильтра 7 × 7, а также сверткой 1 × 1 с сигмоидальной функцией активации в конце. Усиленная топология (рис. 2,б) представляет комбинацию из двух MultiResUnet-сетей, дополненных остаточными соединениями с конкатенацией, сверткой с размером фильтра 7 × 7 в начале, а также двумя свертками с размером фильтра 1 × 1, батч-нормализацией и сигмоидальной функцией активации в конце.
Целевым источником данных для разрабатываемого метода являются изображения дистанционного зондирования. Космические аппараты дистанционного зондирования имеют свои особенности аппаратуры, что приводит к значительным различиям в поступающей от них информации даже при совпадающем пространственном разрешении. Поэтому для получения качественной сегментации необходимо иметь набор размеченных данных с целевого аппарата, в частности Ресурс-П. Однако собранное количество данных все еще достаточно мало. Для решения проблемы была разработана техника аугментации, позволяющая, с одной стороны, расширить количество данных для обучения (с помощью линейных искажений и шума), а с другой – сбалансировать классы, симулируя больше участков из мест, где представлены редкие классы [18, 19]. Оценка качества сегментации для основных классов: “здания целиком” – $F1 = ~$ 0.8962, IoU = 0.8119; “крыши зданий” – F1 = 0.8963, IoU = 0.8121; “тени зданий” – F1 = 0.8717, IoU = 07726, где $F1$ и IoU – количественные меры при оценке качества сегментации. Вычисляются по формулам:
2.3. Восстановление геометрии. Рассматривались в основном объекты из набора классов, стандартного для такой задачи: здания, автомобильные и железные дороги, вагоны, столбы [13, 20–23 ].
В данном случае изображение представляется как двумерная проекция трехмерного пространства. В работах приводятся два типа проекций: ортогональные и перспективные. Очевидно, что при проектировании часть информации теряется. Объекты интереса, такие, как здания, раскладываются на геометрические примитивы: линии, плоские и пространственные (такие, как цилиндры, пирамиды) фигуры. Примитивы можно описать набором геометрических точек (углов) и связей (отрезков) между ними.
Для восстановления пространственной формы объекта привлекаются различные предположения, в частности:
плоскости стен здания являются ортогональными между собой и по отношению к поверхности земли;
для зданий с плоской крышей ее поверхность параллельна плоскости земли;
направления линий окон перпендикулярны между собой и параллельны соответствующим линиям контуров стен.
3. Разработанные алгоритмы. В рамках описанной концепции были исследованы два метода реконструкции.
3.1. Трехмерная реконструкция по спутниковому изображению [13, 20–22]. Позволяет в общем случае получать призматические (LoD1) модели зданий, а в некоторых случаях – модели уровня детализации LoD2. Содержит следующие принципиальные этапы обработки:
применение к сегментационным маскам морфологических операций для уменьшения влияния ошибок на этапе сегментации;
приближение контуров крыш и стен кусочно-линейными кривыми (линеаризация);
определение на изображении вертикального направления и направления падения тени;
определение высоты здания из метаданных съемки и средней высоты стены;
построение призматической модели в предположении, что контур фундамента совпадает с контуром крыши;
форма крыши оценивается на основе профилей стен, а также с привлечением дополнительной информации o гранях крыши.
Пример 1. Построим трехмерную модель здания ${{С}_{1}}$ по его спутниковому изображению (рис. 3,а). Местоположение объекта: адрес – Красноярский край, г. Норильск, Вокзальная ул., 2Б; географические координаты – 69°21′23.50″С, 88°08′59.31″В. Предполагаем, что входными данными алгоритма являются сегментационные маски стен, крыши и тени здания, которые создаются в автоматическом режиме с использованием ИСНС.
Рис. 3.
Изображение здания C1 (а), а также сегментационные маски крыш (б), стен (в) и теней (г), наложенные на изображение этого здания

Для удобства дальнейших построений, на изображениях для элементов объектов будем различать фотометрические и теневые проекции. Обозначим фотометрические проекции строчными буквами, а сами трехмерные объекты – прописными; I и S – изображение и тенеобразование объекта, которые идентифицируются набором фотометрических параметров. Преобразование некоторого физического или геометрического объекта $A$ в его фотометрическую проекцию a запишем как $a = I\left( A \right)$, а в теневую проекцию $A'$ – в виде $A' = S(A)$. Таким образом, полагаем a двухмерным, A и A' – трехмерными, опорными точками являются ${{A}_{0}}, \cdots ,{{A}_{9}}$. При этом также определяется соответствие точек и их теневых проекций по формулам:
После ряда морфологических преобразований и линеаризации контуров сегментационных масок (рис. 3, б–г) выделяются опорные точки, на основании которых производится реконструкция здания. Изображения опорных точек ${{A}_{0}}, \cdots ,{{A}_{9}}$, ${{a}_{0}} = I({{A}_{0}}), \cdots ,{{a}_{9}} = I({{A}_{9}})$ представлены на рис. 4. В свою очередь координаты ${{a}_{0}}, \cdots ,{{a}_{9}}$ в системе координат (СК) изображения (p, q) – в табл. 3. Точки ${{A}_{0}}, \ldots ,{{A}_{4}}$ соответствуют стыкам стен с крышей или поверхностью земли (либо являются тенями таких точек) и необходимы для восстановления формы здания уровня LoD1. Кроме того, на крыше есть надстройка (будка выхода или машинное отделение лифта). Поэтому для более детального восстановления формы к опорным добавляются: ${{A}_{5}},~{{A}_{6}},~{{A}_{7}}$ – точки вдоль карниза надстройки, ${{A}_{8}}$ – точка в углу основания надстройки.
Таблица 3.
Координаты опорных точек на изображении
| i | pi | qi |
|---|---|---|
| 0 | 136 | 59 |
| 1 | 217 | 40 |
| 2 | 158 | 152 |
| 3 | 127 | 56 |
| 4 | 137 | 38 |
| 5 | 159 | 91 |
| 6 | 166 | 90 |
| 7 | 161 | 101 |
| 8 | 154 | 90 |
| 9 | 159 | 84 |
Будем использовать пространственную СК $O{{X}_{1}}{{X}_{2}}{{X}_{3}},$ привязанную к объекту C1. Считаем, что C1 имеет прямоугольную крышу и ортогонально ориентированные несущие стены; $O = {{A}_{0}}$ – на углу крыши, $O{{X}_{1}}~$ и $O{{X}_{2}}~$ – вдоль карниза крыши, $O{{X}_{3}}$ – по стыку несущих стен; $O{{X}_{1}},~O{{X}_{2}},~O{{X}_{3}}$ задаются по точкам O и ${{A}_{1}},~{{A}_{2}},~{{A}_{3}}$, т.е.
В начале определяются основные фотометрические параметры для ортотрансформированного изображения [13, 14, 21]:
Параметры ζ могут быть оценены как без использования метаданных, так и с помощью них.
I. По эталонным размерам. По сегментациям эталонных объектов на базе определенных алгоритмов находятся опорные точки этих объектов. Если для эталонных объектов предполагаются эталонные размеры (линейные размеры в данных точках), то можно оценить ζ:
(3.1)
$\overline {{{n}_{j}}} = \frac{{\overline {{{b}_{j}}} }}{{{{b}_{j}}}},\quad \overline {{{b}_{j}}} = I\left( {\overline {{{B}_{j}}} } \right),\quad j = 1,3;\quad \overline {{{n}_{s}}} = \frac{{\overline {{{b}_{s}}} }}{{{{b}_{s}}}},\quad \overline {{{b}_{s}}} = {{I}_{S}}( - \overline {{{B}_{3}}} ),$Здесь $\overline {{{B}_{j}}} $ – некоторые векторы в опорных точках, сонаправленные осям $O{{X}_{j}}$; $B$ и $B'$ – некоторые отрезки в опорных точках, параллельные соответственно плоскости $O{{X}_{1}}{{X}_{2}}$ и оси OX3.
В нашем случае $\overline {{{B}_{j}}} = \overline {O{{A}_{j}}} $. Тогда $\overline {{{b}_{j}}} = \overline {o{{a}_{j}}} = \overline {{{a}_{0}}{{a}_{j}}} ,~\,\,j = \overline {1,3} $, а $\overline {{{b}_{s}}} = I(S( - \overline {O{{A}_{3}}} )) = I(\overline {{{A}_{3}}{{A}_{4}}} ) = \overline {{{a}_{3}}{{a}_{4}}} $. Отсюда находим $\left\{ {\overline {{{n}_{1}}} ,\overline {{{n}_{2}}} ,~\overline {{{n}_{3}}} ,~\overline {{{n}_{s}}} } \right\}$.
В табл. 4 и на рис. 4 представлены примеры эталонных объектов в составе железнодорожной инфраструктуры и расчетов параметров $\left\{ {m,{{m}_{3}},{{m}_{s}}} \right\}$ по опорным точкам {di}.
Таблица 4.
Примеры эталонных объектов и расчетов фотометрических параметров
| Эталонный объект | Опорные точки | Эталонные размеры | Расчет $\left\{ {m,{{m}_{3}},{{m}_{s}}} \right\}$ | |
|---|---|---|---|---|
| E1 | Железнодорожный вагон: вагон-цистерна | D1, D2, D10 – на “крыше” вагона, D3 – в основании, D4 – тень точки D1 | Длина B = D1D2 (B = 10.77 м) | b = I(B) = d1d2, m = B/b |
| Ширина B = D2D10 (B = 3.23 м) | b = I(B) = d2d10, m = B/b | |||
| Высота B' = D1D3 (B' = 4.625 м) | b' = I(B) = d1d3 = 0, m3 = = B'/b' – не определено b" = IS(B) = IS(D1D3) = = I(D1D4) = d1d4, ms = B'/b" |
|||
| E2 | Железнодорожная колея | D5, D6 – на рельсах колеи напротив друг друга | Ширина колеи B = D5D6 (B = 1.52 м) | b = I(B) = d5d6, m = B/b |
| E3 | Железнодорожный столб: ригельная опора контактной сети для гибких поперечин | D7 – в основании столба, D9 – на пике столба, D8 – тень точки D9 | Высота B' = D7D9 (B' = 12 м) | b' = I(B) = d7d9, m3 = B'/b' b" = IS(B) = IS(D7D9) = = I(D7D8) = d7d8, ms = B'/b" |
II. По метаданным. Для разных спутниковых систем структуры данных в файлах метаданных разные. В табл. 5 отражены метаданные {τi} и их токены для Ресурс-П, экстрагируемые из файлов метаданных, для вычисления $\zeta '$:
Таблица 5.
Метаданные для вычисления параметров изображения, Ресурс-П
| Параметр | Название | Атрибут | Формат | Токен (на примере снимка) |
|---|---|---|---|---|
| τ1 | Азимут сканирования | aAzimutScan | GGG:MM:SS.SSSSSS | <aAzimutScan>191:47:52.640213</aAzimutScan> |
| τ2 | Азимут Солнца | aSunAzim | GGG:MM:SS.SSSSSS | <aSunAzim>157:42:39.382120</aSunAzim> |
| τ3 | Угол наклона съемки | aAngleSum | GGG:MM:SS.SSSSSS | <aAngleSum>28:47:46.016694</aAngleSum> |
| τ4 | Высота Солнца | aSunElevC | GGG:MM:SS.SSSSSS | <aSunElevC>36:10:22.919741</aSunElevC> |
| τ5 | Пространственное разрешение | nPixelImg | Double | <nPixelImg>0.688857049648087</nPixelImg> |
Ясно, что ${{\varphi }_{3}} = {{\tau }_{1}},~{{\varphi }_{s}} = {{\tau }_{2}}$. Векторы $\overline {{{n}_{1}}} ,\overline {~{{n}_{2}}} $ находятся по формуле (3.1)$.$ Расчеты по способу I дают:
После определения фотометрических параметров восстанавливается пространственная информация об объекте. Запишем горизонтальные L и вертикальные $L'~$ размеры:
где $l = I\left( L \right),~l' = I\left( {L'} \right),~l'' = {{I}_{S}}\left( {L'} \right)$. Тогда получим:габариты основной части:
габариты надстройки:
положение надстройки:
наклон здания и надстройки (наклон оси $O{{X}_{1}}$ от направления на Север):
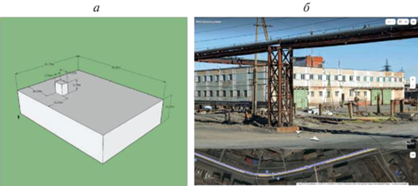
На рис. 5 рассмотрена простейшая геометрическая модель объекта C1(a), выполненная для демонстрации в программе Sketch Up, и ее соотнесение с наземным изображением (Яндекс Карты, панорамный режим съемки). Визуальная оценка высоты здания, включая чердачный пролет и цоколь, с учетом стандартной высоты окна 1.53 м – примерно $8~\, \cdot \,~1.53 = 12.24$ м, что дает точность оценки высоты 92%.
Рис. 5.
Трехмерная модель объекта C1 [Sketch Up] (а) и ее сопоставление с наземной фотографией (б) [Яндекс Карты]
3.2. Трехмерная реконструкция по перспективному изображению. Вводятся декартовые координаты $O{{X}_{1}}{{X}_{2}}{{X}_{3}}$ в пространстве и плоские координаты $wpq$ на изображении. По информации об условиях и типе съемки определяется форма проецирования и отображение пространственных координат в плоские (уравнение проектирования) ${{\Pi }}:\left( {{{X}_{1}},~{{X}_{2}},{{X}_{3}},\zeta } \right) \to \left( {p,~q} \right)$, где ζ – набор фотометрических параметров.
В качестве входных данных алгоритм принимает следующие наборы.
Набор опорных точек ${{\Xi }} = {\text{\{ }}{{a}_{i}} = \left( {{{p}_{i}},{{q}_{i}}} \right)~{\text{|}}i = \overline {1,~n} \} ~$ объекта и системы координат на изображении объекта. Предполагается, что точки определяются автоматически с использованием методов компьютерного зрения. Очевидно, что набольший интерес в данном случае представляют угловые точки (т.е. точки стыка стен с крышей и ландшафтом, точки стыка граней крыши, углы окон и т.д.).
Набор функциональных связей о расположении точек, дающий информацию о форме объекта, который можно определить в виде множества $\Phi = {\text{\{ }}{{\phi }_{j}}\left( {{{A}_{1}}, \ldots ,~{{A}_{n}},~{{K}_{j}}} \right) = 0{\text{|}}~j = \overline {1,m} \} $, где ${{\Pi }}\left( {{{A}_{i}},\zeta } \right) = {{a}_{i}}~\forall ~i \in \overline {1,r} ,$ а Kj – набор параметров связи ϕj. Примеры некоторых связей:
три или более точек лежат на одной прямой;
четыре или более точек лежат в одной плоскости;
два отрезка параллельны;
непосредственно значение одной или нескольких пространственных координат точки.
На основе описанной выше информации составляется система уравнений:
Далее производится попытка численно разрешить систему относительно неизвестных ζ и {Kj}. Решение системы можно вычислить при условии, что она содержит достаточное количество независимых уравнений.
Удобным является введение так называемых осевых координат. Для некоторой точки $A = \left( {{{X}_{{A1}}},~{{X}_{{A2}}},~{{X}_{{A3}}}} \right)$, изображение которой есть $a = {{\Pi }}\left( {{\text{A}},\zeta } \right),$ осевые координаты определяются по формуле
где ${{\bar {n}}_{i}}$ – направляющие векторов ${{\overline {ox} }_{i}}$, а ${\text{||}} \cdots {\text{|}}{{{\text{|}}}_{2}}$ – Евклидова норма (корень суммы квадратов разности компонент векторов).На рис. 6 представлены иллюстрации, поясняющие суть осевых координат для случая ортогонального (а) и перспективного (б) изображений. В каждом из случаев $wpq$ – система плоских декартовых координат на изображении (как правило, оси p и q направлены вдоль его граней, а w – его левый верхний угол). В этой системе спроецированы оси некоторой пространственной СК $O{{X}_{1}}{{X}_{2}}{{X}_{3}}$ (оси обозначаются соответственно $o{{x}_{1}}{{x}_{2}}{{x}_{3}}$). Точки ${{g}_{1}},{{g}_{2}},{{g}_{3}}$ являются изображениями проекций некоторой точки A (ее изображение есть a) на соответствующие пространственные оси (т.е. ${{g}_{i}} = \,\,~\Pi \left( {{{X}_{{Ai}}}~{{{\bar {n}}}_{i}},\zeta } \right),~i = \overline {1,3} $), также $o = {{\Pi }}\left( {O,\zeta } \right)$ – изображение центра пространственных координат O. При введенных обозначениях осевые координаты точки A есть нормы плоских векторов ${{x}_{{ai}}} = {\text{||}}\overline {o{{g}_{i}}} {\text{|}}{{{\text{|}}}_{2}},~~i = \overline {1,3} ~$.
Рис. 6.
Пояснение к введенным системам координат для случая ортогонального (а) и перспективного (б) изображений
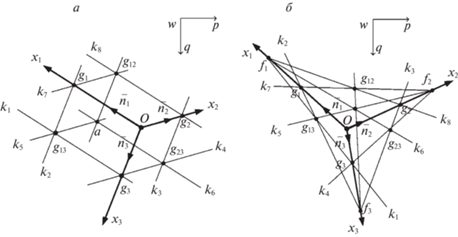
При центральном проецировании преобразование из осевых координат в пространственные имеет вид
(3.2)
${{X}_{{Ai}}} = {\text{lo}}{{{\text{g}}}_{{\left( {1 - \frac{{{{x}_{{mi}}}}}{{{{x}_{{fi}}}}}} \right)}}}\left( {1 - \frac{{{{x}_{{ai}}}}}{{{{x}_{{fi}}}}}} \right){{X}_{{mi}}}.$Здесь $\left\{ {{{x}_{{fi}}},{{x}_{{mi}}},{{X}_{{mi}}}} \right\},i = \overline {1,3} ,$ – некоторые фотометрические параметры; ${{x}_{{fi}}} = o{{f}_{i}}$, fi – некоторые точки (так называемые фокусы), постоянные для выбранной СК, условий и типа съемки; ${{x}_{{mi}}}$ – эталоны осевых координат, которым соответствуют эталоны пространственных координат ${{X}_{{mi}}}$. Для перспективных изображений ${{x}_{{fi}}}$ конечно (рис. 6,б), для ортотрансформированных ${{x}_{{fi}}} \to \infty $ (рис. 6,а). В последнем случае перепишем (3.2):
(3.3)
${{X}_{{Ai}}} = \frac{{\ln \left( {1 + {{y}_{i}}} \right)}}{{\ln \left( {1 + {{y}_{{mi}}}} \right)}}{{X}_{{mi}}},\quad {{y}_{i}} = - \frac{{{{x}_{{ai}}}}}{{{{x}_{{fi}}}}},\quad {{y}_{{mi}}} = - \frac{{{{x}_{{mi}}}}}{{{{x}_{{fi}}}}}$.Так как $\left| {{{y}_{i}}} \right| < 1,\left| {{{y}_{{mi}}}} \right| < 1$, разложим числитель и знаменатель в (3.3) в ряды Маклорена и найдем предел дроби при ${{x}_{{fi}}}\,~ \to \infty $:
Пример 2. Проведем реконструкцию здания C2 по его аэрофотоснимку (рис. 7). Местоположение объекта: адрес – Московская область, г. Балашиха, мкр. Железнодорожный, Лесопарковая ул., 5; географические координаты – 55°45′12.87″С, 38°00′25.25″В (полное изображение доступно по ссылке https://clck.ru/338Nog).
Аналогично конструктивному подходу имеем опорные точки ${{A}_{i}}$, $i = \overline {1,9} $, изображения которых ${{a}_{i}} = I\left( {{{A}_{i}}} \right)~$ представлены на рис. 7. В свою очередь координаты $\left( {{{p}_{i}},{{q}_{i}}} \right)$ (в пикселях) точек ${{a}_{i}}$ отражены в табл. 6.
Таблица 6.
Координаты опорных точек на изображении
| i | pi | qi |
|---|---|---|
| 0 | 454 | 273 |
| 1 | 632 | 228 |
| 2 | 374 | 218 |
| 3 | 448 | 181 |
| 4 | 576 | 123 |
| 5 | 576 | 106 |
| 6 | 601 | 101 |
| 7 | 563 | 82 |
| 8 | 542 | 88 |
| 9 | 761 | 750 |
Система координат $O{{X}_{1}}{{X}_{2}}{{X}_{3}}$ привязана к объекту C2. Считаем, что C2 имеет прямоугольную крышу и ортогонально ориентированные несущие стены; $O = {{A}_{0}}$ – на углу основания, OX1 и OX2 – вдоль основания, $O{{X}_{3}}$ – по стыку несущих стен, ${{A}_{3}}$ – в углу крыши, видимой на изображении. Координаты $O{{X}_{1}},~O{{X}_{2}},~O{{X}_{3}}$ задаются по точкам O и ${{A}_{1}},~{{A}_{2}},~{{A}_{3}}$; $o = I\left( O \right),~\,\,o{{x}_{i}} = I\left( {O{{X}_{i}}} \right)$. У стены есть пристройка (для размещения лестничной коробки и/или лифтовой шахты), подобная зданию по форме. Опорные точки ${{A}_{4}} - {{A}_{9}}$ соответствуют точкам в видимых углах этой пристройки.
Основные фотометрические параметры для перспективного изображения [13, 22]:
По сегментациям эталонных объектов на базе определенных алгоритмов находятся опорные точки этих объектов. Если для эталонных объектов предполагаются эталонные размеры (линейные и угловые размеры в данных точках), то можно оценить ζ:
Здесь $\overline {{{B}_{j}}} $ – некоторые векторы в опорных точках, сонаправленные осям $O{{X}_{j}};$ ${{V}_{j}} = B_{j}^{'}B_{j}^{{''}}$ – отрезок, параллельный $O{{X}_{j}}$, длина которого известна. В нашем случае $\overline {{{B}_{j}}} = \overline {O{{A}_{j}}} $. Тогда $\overline {{{b}_{j}}} = \overline {o{{a}_{j}}} = \overline {{{a}_{0}}{{a}_{j}}} ,~\,\,j = \overline {1,3} $. Отсюда находим $\left\{ {\overline {{{n}_{1}}} ,\overline {{{n}_{2}}} ,~\overline {{{n}_{3}}} } \right\}$.
Параметры $\left\{ {{{x}_{{mj}}},{{X}_{{mj}}}} \right\}$ оцениваются по отрезкам Vj по-разному в зависимости от их пространственного положения. Приведем два случая.
I. ${{V}_{j}} \subset O{{X}_{j}}{{X}_{{j'}}},~{{V}_{j}}||O{{X}_{j}}$:
(3.4)
${{x}_{{mj}}} = o\hat {b}_{j}^{'},\quad {{X}_{{m1}}} = B_{j}^{'}B_{j}^{{''}}{{\left| {{\text{lo}}{{{\text{g}}}_{{\left( {1 - \frac{{{{x}_{{mj}}}}}{{{{x}_{{fj}}}}}} \right)}}}\left( {1 - \frac{{{{x}_{{\hat {b}_{j}^{{''}}j}}}}}{{{{x}_{{fj}}}}}} \right) - 1} \right|}^{{ - 1}}},$II. ${{V}_{j}}||O{{X}_{j}},B_{j}^{'} \subset O{{X}_{{j'}}}{{X}_{{j''}}}$:
В табл. 7 и на рис. 7 рассмотрены примеры эталонных объектов в составе железнодорожной инфраструктуры и расчетов параметров $\left\{ {{{x}_{{mj}}},{{X}_{{mj}}}} \right\}$ по опорным точкам {di}. Расчеты дают:
Таблица 7.
Примеры эталонных объектов и расчетов фотометрических параметров
| Эталонный объект | Опорные точки | Эталонные размеры | Расчет $\{ {{x}_{{mj}}},{{X}_{{mj}}}\} $ по формуле | |
|---|---|---|---|---|
| E4 | Железнодорожная колея | D1, D2 – на одной рельсе на соседних шпалах | Расстояние между шпалами ${\text{B}}_{1}^{'}$ = D1, ${\text{B}}_{1}^{{''}}$ = D2 (V1 = 0.6 м), j = 1, j' = 2 | (3.4) |
| D3, D4 – на рельсах колеи напротив друг друга | Ширина колеи ${\text{B}}_{1}^{'}$ = D3, ${\text{B}}_{1}^{{''}}$ = = D4 (V2 = 1.52 м), j = 2, j' = 1 | (3.4) | ||
| E5 | Железнодорожный столб: ригельная опора контактной сети для жестких поперечин | D5 – в основании столба, D6 – на пике столба | Высота ${\text{B}}_{3}^{'}$ = D5, ${\text{B}}_{3}^{{''}}$ = D6 (V3 = 12 м), j = 3, j' = 1, j" = 2 | (3.5) |
| E6 | D7 – в основании столба, D8 – на пике столба | Высота ${\text{B}}_{3}^{'}$=D7, ${\text{B}}_{3}^{{''}}$=D8 (V3 = 12 м), j = 3, j' = 1, j'' = 2 | (3.5) | |
| E7 | D9 – в основании столба, D10 – на пике столба | Высота ${\text{B}}_{3}^{'}$ = D9, ${\text{B}}_{3}^{{''}}$ = D10 (V3 = 12 м), j=3, j'=1, j''=2 | (3.5) | |
После определения фотометрических параметров восстанавливается пространственная информация об объекте. Пространственные координаты ${{X}_{{{{A}_{i}}j}}}$ точек Ai здания рассчитываются по (3.2), где
Таблица 8.
Результаты расчетов осевых и пространственных координат точек здания
| $i$ | xi1, пк | xi2, пк | xi3, пк | Xi1, м | Xi2, м | Xi3, м |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 55 0 | 0 | 0 | 0 |
| 1 | 183.6001 | 0 | 0 | 31.5915 | 0 | 0 |
| 2 | 0 | 97.0824 | 0 | 0 | 16.0903 | 0 |
| 3 | 0 | 0 | – | 0 | 0 | 12.5504 |
| 4 | 183.6001 | 50.0861 | – | 31.5915 | 8.1407 | 12.5504 |
| 5 | 183.6001 | 97.0824 | – | 31.5915 | 16.0903 | 12.5504 |
| 6 | 183.6001 | 50.0861 | – | 31.5915 | 8.1407 | 14.0076 |
| 7 | 204.6138 | 50.0861 | – | 35.2989 | 8.1407 | 14.0076 |
| 8 | 204.6138 | 97.0824 | – | 35.2989 | 16.0903 | 14.0076 |
| 9 | 183.6001 | 97.0824 | – | 31.5915 | 16.0903 | 14.0076 |
На рис. 8 показана простейшая геометрическая модель объекта C2(a), выполненная для демонстрации в программе Sketch Up, и ее соотнесение с наземным изображением (Яндекс Карты, панорамный режим съемки, вид справа со двора жилого массива). Также продемонстрировано соотнесение с аэрофотоснимком (рис. 1, вид сверху), визуальная оценка высоты основного здания, включая парапет, чердачный пролет и цоколь (2 м), с учетом стандартной высоты одного этажа для здания детского сада (3.3 м) – $2 + 3\, \cdot \,3.3 \approx 12$ м, что дает точность оценки высоты 95%. Высота пристройки равна высоте основной части плюс выступающая ее часть над крышей: с учетом высоты дверного проема (2 м) она равна примерно 15 м, что дает точность 93%. Точность определения горизонтальных размеров сравнивалась с оценками, полученными в геоинформационных системах (ГИС) Google Maps и Yandex Maps с помощью линейки, результаты сравнения представлены в табл. 9.
Рис. 8.
Трехмерная модель объекта C1 [Sketch Up] (а) и ее сопоставление с наземной фотографией (б) [Яндекс Карты]
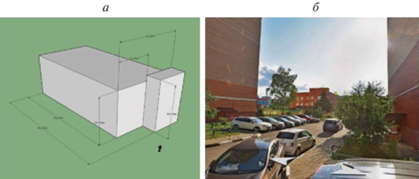
Таблица 9.
Результаты оценки точности восстановления горизонтальных элементов
| Размер | Реконструкция (м) | Оценка, м | Точность (%) |
|---|---|---|---|
| Основание по оси OX1 | 27 | 31.59 | 83 |
| Основание по оси OX2 | 22 | 16.09 | 73 |
| Основание пристройки по оси OX1 | 3.25 | 3.7 | 78 |
| Основание пристройки по оси OX2 | 9 | 7.95 | 88 |
| Отступ пристройки от основной части вдоль оси OX2 | 13 | 8.14 | 63 |
Высотные размеры (ориентированные по $O{{X}_{3}}~$оценены более точно, чем размеры, ориентированные по OX1 и OX2. Данное обстоятельство обусловлено точностью определения фокуса fj, которое зависит от количества взятых отрезков по каждой оси, причем определяемые впоследствии размеры весьма чувствительны к рассчитанным положениям фокусов. В нашем случае по каждой оси взято только по одному отрезку.
4. Полученные результаты. Описаны два подхода к трехмерной реконструкции зданий: по спутниковому и перспективному изображениям. В обоих случаях при расчете фотометрических параметров практически для каждого оцениваемого параметра следует получить выборку его значений, в частности: выборку ${{m}_{s}}$ по ${{E}_{1}}$ и ${{E}_{3}}$ по нескольким эталонным объектам (см. пример 1) или облако точек fj по нескольким прямым, параллельным j-й оси (см. пример 2). Результирующие оценки можно найти, прибегнув к различным статистическим характеристикам (выборочное среднее, выборочная медиана и т.д.). Комплементарным подходом является расчет фотометрических параметров по метаданным с учетом их оценки по эталонным объектам. Линейные и угловые связи между опорными точками могут определяться как методами компьютерного зрения, так и исходя из набора предположений (например, если группа точек принадлежит одной стене здания, то они лежат в одной плоскости).
Разработаны базовые алгоритмы расчета трехмерных параметров изображенного объекта в условиях дефицита входных данных. Фотометрические параметры могут быть оценены как по метаданным изображения, так и без них (по сегментациям эталонных объектов). Приведены примеры расчета геометрических параметров по одному изображению, в основе которых лежит сегментация главных компонентов зданий (крыша, стена, тень). По ним вычисляется призматическая модель здания, в том числе с учетом его надстроек и пристроек.
Заключение. В рамках представленной концепции трехмерной реконструкции описано два подхода: по спутниковому и перспективному изображениям.
Особенности предлагаемой концепции:
оценка трехмерной модели ригидного объекта проводится по одному изображению;
машинное обучение в условиях дефицита обучающих данных;
допустимо невысокое качество сегментации информативных классов, в частности растры компонентов объектов могут иметь произвольную форму границ и с наличием пустот;
качество оценки трехмерной модели объекта зависит от полноты известной растровой информации об этом объекте;
используются предположения о видах, размерах и пространственной ориентации видимых элементов на изображении.
Также допускается вариативность входных данных, которая состоит в том, что:
возможности использования изображений с различными наборами спектральных каналов, в том числе полутоновых изображений;
метаданные изображения на входе опциональны, и при их отсутствии на входе альтернативой является наличие эталонных стандартизированных объектов;
полная или частичная видимость объектов на изображении;
вариативность входных данных на этапе векторизации объектов по растрам.
В настоящее время проводится дальнейшая разработка алгоритмов, производится разметка новых данных и дообучение на них подобранных нейросетевых архитектур сегментации, работы над программой и ее тестированием по извлечению фотометрической информации из изображений, расчета трехмерных параметров и моделирования представленных объектов.
Список литературы
Biljecki F., Stoter J., Ledoux H., Zlatanova S., Çöltekin A. Applications of 3D City Models: State of the Art Review // ISPRS Intern. J. Geo-Information. 2015. V. 4. № 4. P. 2842–2889.
Tang L., Li L., Ying S., Lei Y. A Full Level-of-Detail Specification for 3D Building Models Combining Indoor and Outdoor Scenes // ISPRS Intern. J. Geo-Information. 2018. V. 7. № 11. P. 419.
Yu D., Ji S., Liu J., Wei S. Automatic 3D Building Reconstruction from Multi-view Aerial Images with Deep Learning // ISPRS J. Photogrammetry and Remote Sensing. 2021. V. 171. P. 155–170.
Leotta M.J., Long C., Jacquet B., Zins M., Lipsa D., Shan J., Xu B., Li Z., Zhang X., Chang S.F. et al. Urban Semantic 3D Reconstruction From Multiview Satellite Imagery // IEEE/CVF Conf. on Computer Vision and Pattern Recognition Workshops (CVPRW). California, 2019. P. 1451–1460.
Anzhu Y., Wenyue G., Bing L., Xin C., Xin W., Xuefeng C., Bingchuan J. Attention Aware Cost Volume Pyramid Based Multi-view Stereo Network for 3D Reconstruction // ISPRS J. Photogrammetry and Remote Sensing. 2021. V. 175. P. 448–460.
Yi C., Zhang Y., Wu Q., Xu Y., Remil O., Wei M., Wang J. Urban Building Reconstruction from Raw LiDAR Point Data // Computer-Aided Design. 2017. V. 93. P. 1–14.
Reconstructing 3D Buildings from Aerial LiDAR with Deep Learning. 2020. URL: https://developers.arcgis.com/python/samples/building-reconstruction-using-mask-rcnn/
Wang R., Peethambaran J., Chen D. LiDAR Point Clouds to 3-D Urban Models: A Review // IEEE J. Selected Topics in Applied Earth Observations and Remote Sensing. 2018. V. 11. № 2. P. 606–627.
Karantzalos K., Paragios N. Automatic Model-based Building Detection from Single Panchromatic High Resolution Images // The Intern. Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. 2008. V. 37. № 3Ba.
Wang K., Frahm J.M. Single View Parametric Building Reconstruction from Satellite Imagery // International Conf. on 3D Vision (3DV). Qingdao, 2017. P. 603–611.
Alidoost F., Arefi H., Hahn M. Y-shaped Convolutional Neural Network for 3D roof Elements Extraction to Reconstruct Building Models from a Single Aerial Image // ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences. 2020. V. 2. P. 321–328.
Biljecki F., Pang H.E. 3D Building Reconstruction from Single Street View Images Using Deep Learning // Intern. J. of Applied Earth Observation and Geoinformation. 2022. V. 112.
Гвоздев О.Г., Козуб В.А., Рихтер А.А., Мурынин А.Б., Кошелева Н.В. Построение трехмерных моделей ригидных объектов по спутниковым изображениям высокого пространственного разрешения с использованием сверточных нейронных сетей // Исслед. Земли из космоса. 2020. № 5. С. 78–96.
Kazaryan M., Richter A., Gvozdev O., Murynin A., Kozub V., Pukhovsky D., Shakhramanyan M., Semeni-shchev E. Reconstruction of 3-D Models of Infrastructure Objects from Satellite Images Based on Typed Elements // Proc. SPIE 12269, Conf. Remote Sensing Technologies and Applications in Urban Environments VII, 122690J. Edinburgh, 2022.
Мурынин А.Б., Рихтер А.А. Особенности применения методов и алгоритмов реконструкции трехмерной формы ригидных объектов по данным панорамной съемки // Машинное обучение и анализ данных. 2018. V. 4. № 4. P. 235–247.
Ronneberger O., Fischer P., Brox T. U-Net: Convolutional Networks for Biomedical Image Segmentation // Medical Image Computing and Computer-Assisted Intervention (MICCAI 2015) Springer International Publishing. 2015. P. 234–241.
Nabil I., M. Sohel R. MultiResUNet: Rethinking the U-Net Architecture for Multimodal Biomedical Image Segmentation // Neural Networks. 2020. V. 121. P. 74–87.
Гвоздев О.Г., Касинская К.А., Мурынин А.Б., Рихтер А.А. Получение информации об антропогенном замусоривании земной поверхности по данным спутниковой съемки // Тез. докл. второй Междунар. конф. “Ситуация, язык, речь. Модели и приложения”. Москва, Россия–Рим, Италия, 2019. P. 50–51.
Гвоздев О.Г., Мурынин А.Б., Рихтер А.А. Комплекс прикладных решений по построению и обучению искусственных нейронных сетей для семантической сегментации аэрокосмических изображений произвольной канально-спектральной структуры в условиях дефицита обучающих данных // Матер. 19-й Всеросс. конф. с междунар. участием: Математические методы распознавания образов (ММРО-2019). М.: Российская академия наук, 2019. С. 344–348.
Gvozdev O., Kosheleva N., Murynin A., Richter A. 3D-modeling Infrastructure Facilities Using Deep Learning Based on High Resolution Satellite Images // 20th Intern. Multidisciplinary Scientific GeoConf. SGEM. Albena, 2020. P. 149–156.
Гвоздев О.Г., Козуб В.А., Кошелева Н.В., Мурынин А.Б., Рихтер А.А. Нейросетевой метод построения трехмерных моделей ригидных объектов по спутниковым изображениям // Мехатроника, автоматизация, управление. 2021. V. 22 (1). P. 48–55.
Рихтер А.А., Гвоздев О.Г., Мурынин А.Б., Козуб В.А., Кошелева Н.В. Восстановление геометрических моделй объектов железнодорожной инфраструктуры по спутниковым изображениям на основе искусственных нейронных сетей // Матер. 18-й Вероссийской открытой конф. “Современные проблемы дистанционного зондирования Земли из космоса”. М., 2020. P. 41.
Gvozdev O.G., Kozub V.A., Kosheleva N.V., Murynin A.B., Richter A.A. Constructing 3D Models of Rigid Objects from Satellite Images with Spatial Resolution Using Convolutional Neural Networks // Izvestiya, Atmospheric and Oceanic Physics. 2020. V. 56. № 12. P. 1664–1677.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления