1. На главную
  2. Электронные версии
  3. Известия РАН. Теория и системы управления
  4. № 3, 2023

Известия РАН. Теория и системы управления, 2023, № 3, стр. 3-13

БЕЗРЕВЕРСНОЕ ДВИЖЕНИЕ СИСТЕМЫ ВЗАИМОДЕЙСТВУЮЩИХ ТЕЛ ВДОЛЬ ШЕРОХОВАТОЙ ГОРИЗОНТАЛЬНОЙ ПРЯМОЙ

Н. Н. Болотник a, *, Т. Ю. Фигурина a, **

a ИПМех РАН
Москва, Россия

* E-mail: bolotnik@ipmnet.ru
** E-mail: t_figurina@mail.ru

Поступила в редакцию 15.11.2022
После доработки 21.01.2023
Принята к публикации 06.02.2023

Полный текст (PDF)

Аннотация

Рассматривается локомоционная система в виде цепочки конечного числа тел (материальных точек), движущихся по прямой на горизонтальной шероховатой плоскости за счет сил взаимодействия между телами. Эти силы служат управляющими переменными. Между телами и плоскостью действует сухое кулоново трение. Получены необходимые и достаточные условия, при которых возможно безреверсное перемещение всех тел системы на одно и то же расстояние в предположении, что в начальном и конечном положениях скорости всех тел равны нулю. Под безреверсным движением понимается движение, при котором ни одно из тел не изменяет направления своей скорости в процессе перемещения.

Введение. Объект исследования данной работы – локомоционные системы, выполненные в виде цепочек тел, последовательно соединенных друг с другом призматическими (поступательными) шарнирами. Тела системы взаимодействуют между собой и с внешней средой. Силы взаимодействия тел, внутренние по отношению к рассматриваемой механической системе, играют роль управляющих переменных. Силы взаимодействия тел с внешней средой (силы трения) являются внешними силами. Управляющие силы изменяют скорости тел системы относительно среды, благодаря чему изменяются силы трения, действующие на эти тела. Таким образом, управляя внутренними силами, можно управлять внешними силами, что позволяет контролировать движение цепочки тел как целого, перемещая ее на произвольное расстояние в различных режимах, в частности так, что расстояния между телами и скорости этих тел относительно среды изменяются периодически.

Рассматриваемые системы относятся к широкому классу локомоционных (мобильных) систем с изменяемой конфигурацией, которые могут перемещаться в сопротивляющихся средах без специальных движителей (ног, колес, гусениц, гребных винтов и т.п.) за счет изменения относительного положения тел, составляющих систему, при неизменных областях контакта этих тел со средой. Управление такими системами осуществляется внутренними силами, посредством которых тела взаимодействуют друг с другом. Многие системы с изменяемой конфигурацией имитируют движение различных животных, которые не имеют конечностей и перемещаются за счет изменения формы своего тела (змеи, черви, некоторые виды рыб и земноводных). К системам этого класса в настоящее время наблюдается растущий интерес ученых в области механики (в частности, биомеханики) и управления, а также инженеров, занимающихся созданием мобильных роботов. Систематические исследования проблем управления мобильными системами с изменяемой конфигурацией, ориентированные на технические приложения, инициированы работами [1–4] и в настоящее время активно ведутся в России [5–14], Китае [15–17], Германии [18, 19], Великобритании [20–24] и ряде других стран. Упомянутые работы не отражают всего разнообразия исследований по этой тематике. Проблемам динамики и управления движением мобильных систем с изменяемой конфигурацией посвящена монография [5], в которой, в частности, дан обзор российских и зарубежных публикаций и приведен их библиографический список.

В статье рассматривается цепочка из произвольного конечного числа тел, перемещающаяся поступательно вдоль прямой по шероховатой горизонтальной плоскости. Между телами и плоскостью перемещения действует сухое кулоново трение. Массы тел и коэффициенты их трения о плоскость перемещения в общем случае различны. Динамике, управлению движением и оптимизации режимов перемещения цепочек тел вдоль прямой посвящены работы [25–36]. Для цепочек тел, перемещающихся вдоль прямой с сухим трением, важна возможность движения в безреверсном режиме, при котором ни одно из тел системы не изменяет направление скорости своего движения. Основное преимущество безреверсного движения состоит в том, что оно обеспечивает абсолютный минимум затрат энергии на компенсацию работы сил сухого трения при перемещении цепочки между любыми двумя заданными положениями на прямой. Проблема существования безреверсного движения была поставлена и решена в [36] для системы двух тел при дополнительном условии, что расстояние между телами и их скорости изменяются периодически. Доказано, что безреверсное периодическое движение системы двух тел возможно, если и только если силы трения скольжения тел различны и масса тела с большей силой трения скольжения не больше массы тела с меньшей силой трения скольжения. Это условие, в частности, не допускает безреверсного периодического движения системы двух тел с одинаковыми коэффициентами сухого трения о плоскость перемещения. В настоящей работе для цепочки, состоящей из произвольного конечного числа тел, решается задача о безреверсном перемещении всех тел на одно и то же расстояние при условии, что в начальном и конечном положениях скорости всех тел равны нулю. Доказываются необходимые и достаточные условия реализуемости требуемого режима перемещения.

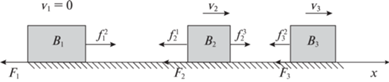
1. Постановка задачи. Рассматривается система $n$ взаимодействующих тел ${{B}_{1}},\; \ldots ,\;{{B}_{n}}$, $n \geqslant 3$, движущихся поступательно вдоль прямой по горизонтальной плоскости при наличии сухого кулонова трения между телами и плоскостью. Тела моделируются материальными точками. Обозначим: ${{m}_{i}}$ – масса тела ${{B}_{i}}$; ${{x}_{i}}$ – координата тела ${{B}_{i}}$ на прямой движения системы; ${{{v}}_{i}}$ – скорость тела ${{B}_{i}}$; $f_{i}^{j}$ – сила, приложенная к телу ${{B}_{i}}$ телом ${{B}_{j}}$; ${{F}_{i}}$ – сила сухого кулонова трения, действующая на тело ${{B}_{i}}$; ${{k}_{i}}$ – коэффициент сухого трения между плоскостью и телом ${{B}_{i}}$; g – ускорение силы тяжести. Описанная механическая система изображена на рис. 1 для случая трех тел, n = 3.

На относительные положения тел никаких ограничений не налагается.

Согласно третьему закону Ньютона, для сил $f_{j}^{i}$ взаимодействия между телами имеет место равенство

(1.1)
$f_{j}^{i} = - f_{i}^{j},\quad i,j = \overline {1,n} ,\quad i \ne j.$

Для удобства будем использовать это соотношение и при i = j, что не приведет к ошибке, поскольку из (1.1) при i = j получаем $f_{i}^{i} = 0$, $i = \overline {1,n} $, т.е. тела не взаимодействует сами с собой.

В дальнейшем будем считать, что хотя бы один из коэффициентов трения ${{k}_{i}}$ не равен нулю. Если все ${{k}_{i}} = 0$, то внутренними силами невозможно вывести центр масс системы из состояния покоя. Занумеруем тела в порядке невозрастания произведений их масс на коэффициенты трения о плоскость движения:

(1.2)
${{k}_{1}}{{m}_{1}} \geqslant {{k}_{2}}{{m}_{2}} \geqslant \; \ldots \; \geqslant {{k}_{n}}{{m}_{n}}.$

Динамика описанной механической системы подчиняется совокупности дифференциальных уравнений:

(1.3)
${{\dot {x}}_{i}} = {{{v}}_{i}},\quad {{m}_{i}}{{{\dot {v}}}_{i}} = \sum\limits_{j = 1}^n {f_{i}^{j}} + {{F}_{i}},\quad i = \overline {1,n} .$

Без ограничения общности можно считать, что каждое из тел ${{B}_{i}}$, $i = \overline {2,n - 1} $, взаимодействует с двумя телами ${{B}_{{i - 1}}}$ и ${{B}_{{i + 1}}}$, тело ${{B}_{1}}$ взаимодействует только с телом ${{B}_{2}}$, а тело ${{B}_{n}}$ – только с телом ${{B}_{{n - 1}}}$. При этом систему тел можно представлять в виде цепочки тел, каждое из “внутренних” тел которой взаимодействует только с двумя соседними телами, а крайние тела – только с одним соседним телом. Это утверждение следует из того, что для любой совокупности сил взаимодействия между каждой парой тел $f_{i}^{j}$, $i,j = \overline {1,n} $, существует совокупность сил взаимодействия между соседними телами $\tilde {f}_{i}^{{i + 1}}$, $i = \overline {1,n - 1} $, такая, что суммарная сила, действующая на любое из тел, одинакова, а именно

(1.4)
$\begin{gathered} \sum\limits_{j = 1}^n {f_{1}^{j}} = \tilde {f}_{1}^{2}, \\ \sum\limits_{j = 1}^n {f_{i}^{j}} = \tilde {f}_{i}^{{i - 1}} + \tilde {f}_{i}^{{i + 1}},\quad i = \overline {2,n - 1} , \\ \sum\limits_{j = 1}^n {f_{n}^{j}} = \tilde {f}_{n}^{{n - 1}}. \\ \end{gathered} $

С учетом равенств $\tilde {f}_{i}^{{i + 1}} = - \tilde {f}_{{i + 1}}^{i}$, вытекающих из третьего закона Ньютона, из системы уравнений (1.4) однозначно находим

(1.5)
$\begin{gathered} \tilde {f}_{1}^{2} = \sum\limits_{j = 1}^n {} f_{1}^{j}, \\ \tilde {f}_{i}^{{i + 1}} = \sum\limits_{k = 1}^i {\sum\limits_{j = 1}^n {f_{k}^{j}} } ,\quad i = \overline {2,n - 1} . \\ \end{gathered} $

Сделав подстановку (1.4) в (1.3) и опустив тильды в обозначении сил взаимодействия соседних тел, получим уравнения движения следующего вида:

(1.6)
${{\dot {x}}_{i}} = {{{v}}_{i}},\quad {{m}_{i}}{{{\dot {v}}}_{i}} = f_{i}^{{i - 1}} + f_{i}^{{i + 1}} + {{F}_{i}},\quad i = \overline {1,n} .$

Здесь формально доопределены величины $f_{1}^{0}$, $f_{n}^{{n + 1}}$:

(1.7)
$f_{1}^{0} = f_{n}^{{n + 1}} = 0.$

Сила сухого кулонова трения подчиняется соотношениям

(1.8)
${{F}_{i}} = \left\{ \begin{gathered} - {{k}_{i}}{{m}_{i}}g{\text{sign}}{\kern 1pt} {{{v}}_{i}},\quad {{{v}}_{i}} \ne 0, \hfill \\ - (f_{i}^{{i - 1}} + f_{i}^{{i + 1}}),\quad {{{v}}_{i}} = 0,\quad \left| {f_{i}^{{i - 1}} + f_{i}^{{i + 1}}} \right| \leqslant {{k}_{i}}{{m}_{i}}g, \hfill \\ - {{k}_{i}}{{m}_{i}}g{\text{sign}}(f_{i}^{{i - 1}} + f_{i}^{{i + 1}}),\quad {{{v}}_{i}} = 0,\quad \left| {f_{i}^{{i - 1}} + f_{i}^{{i + 1}}} \right| > {{k}_{i}}{{m}_{i}}g. \hfill \\ \end{gathered} \right.$

Для описанной механической системы поставим задачу управления.

Задача. Управляя силами взаимодействия тел $f_{i}^{{i + 1}}(t)$, $i = \overline {1,n - 1} $, привести систему (1.6)–(1.8) из начального состояния

(1.9)
${{x}_{i}}(0) = 0,\quad {{{v}}_{i}}(0) = 0,\quad i = \overline {1,n} ,$
за конечное (заранее не фиксированное) время T в терминальное состояние
(1.10)
${{x}_{i}}(T) = L,\quad {{{v}}_{i}}(T) = 0,\quad i = \overline {1,n} ,\quad L > 0,$
при условии, что тела не изменяют направления своего движения:

(1.11)
${{{v}}_{i}}(t) \geqslant 0,\quad i = \overline {1,n} ,\quad t \in [0,T].$

Ограничений на управляющие силы $f_{i}^{{i + 1}}(t)$ не налагается, допускается мгновенное (ударное) взаимодействие тел, при котором скорости тел меняются скачком.

Таким образом, в задаче требуется перевести систему тел в безреверсном режиме (ни одно из тел не изменяет направления своего движения) из начального состояния покоя в конечное состояние покоя при условии тождественности ее конфигурации в начальном и конечном состояниях (все тела перемещаются на одно и то же расстояние L). Предположение о равенстве нулю координат всех тел в начальном состоянии не ограничивает общности. Если ${{x}_{i}}(0) = x_{i}^{0} \ne 0$, то заменой переменной $x_{i}^{'} = {{x}_{i}} - x_{i}^{0}$, относительно которой уравнения движения (1.6)–(1.8) инвариантны, достигается равенство $x_{i}^{'}(0) = 0$. Предположение о равенстве нулю скоростей всех тел системы в начальном и конечном состояниях ограничивает общность и вводится для простоты.

Эту задачу можно рассматривать как частный (с условием обращения в нуль скоростей всех тел в некоторый момент времени) случай задачи о периодическом безреверсном перемещении системы тел. Так как уравнения движения системы инвариантны к сдвигу времени, движение, являющееся решением поставленной задачи, можно продолжить на бесконечное время, при этом скорости всех тел будут T-периодическими функциями времени и за каждый период все тела будут перемещаться на одно и то же расстояние L.

Безреверсный периодический режим движения возможен не всегда. Так, в [36] показано, что при n = 2 периодический безреверсный режим возможен, если и только если ${{m}_{1}}{{k}_{1}} > {{m}_{2}}{{k}_{2}}$ и ${{m}_{1}} \leqslant {{m}_{2}}$ или ${{m}_{1}}{{k}_{1}} < {{m}_{2}}{{k}_{2}}$ и ${{m}_{1}} \geqslant {{m}_{2}}$. Решение задачи включает определение условий, при которых безреверсный режим движения возможен при $n \geqslant 3$.

2. Частный случай. Предположим, что выполнено неравенство

(2.1)
${{k}_{1}}{{m}_{1}} < \sum\limits_{j = 2}^n {{{k}_{j}}} {{m}_{j}},$
из которого с учетом (1.2) вытекают неравенства

(2.2)
${{m}_{i}}{{k}_{i}} < \sum\limits_{j \ne i} {{{m}_{j}}} {{k}_{j}},\quad i = \overline {1,n} .$

Тогда безреверсное перемещение системы из состояния (1.9) в состояние (1.10) возможно, причем это перемещение можно осуществить многими способами. Приведем один их них.

При выполнении соотношения (2.1) любое тело Bi, $i = \overline {1,n} $, может при покоящихся остальных телах двигаться в положительном направлении, разгоняясь с ускорением $w_{i}^{ + }$ или замедляясь с ускорением $ - w_{i}^{ - }$, где

(2.3)
$\begin{gathered} w_{i}^{ + } = \frac{1}{{{{m}_{i}}}}\left( {\sum\limits_{j \ne i} {{{m}_{j}}} {{k}_{j}}g - {{m}_{i}}{{k}_{i}}g} \right), \\ w_{i}^{ - } = \frac{1}{{{{m}_{i}}}}\sum\limits_{j = 1}^n {{{m}_{j}}} {{k}_{j}}g. \\ \end{gathered} $

При этом на движущееся тело со стороны покоящихся тел действует суммарная сила, равная по абсолютной величине сумме максимально возможных для этих тел сил трения покоя; поэтому $w_{i}^{ + }$ и $w_{i}^{ - }$ есть максимально возможные абсолютные величины ускорения тела ${{B}_{i}}$ при его разгоне и торможении соответственно.

Силы взаимодействия тел, $f_{j}^{{j + 1}}$, $j = \overline {1,n - 1} $, реализующие разгон тела ${{B}_{i}}$ с ускорением $w_{i}^{ + }$, определяются следующими выражениями:

(2.4)
$\begin{gathered} f_{j}^{{j - 1}} = \sum\limits_{s = 1}^{j - 1} {{{m}_{s}}} {{k}_{s}}g,\quad j \leqslant i, \\ f_{j}^{{j + 1}} = \sum\limits_{s = j + 1}^n {{{m}_{s}}} {{k}_{s}}g,\quad j \geqslant i. \\ \end{gathered} $

Силы, обеспечивающие торможение тела Bi с ускорением $ - w_{i}^{ - }$, отличаются от сил (2.4) знаком.

Будем перемещать тела Bi по очереди. Вначале будем перемещать тело Bn, используя следующий закон движения:

(2.5)
${{\ddot {x}}_{n}} = w_{n}^{ + },\quad 0 \leqslant t < {{\tau }_{n}};\quad {{\ddot {x}}_{n}} = - w_{n}^{ - },\quad {{\tau }_{n}} \leqslant t \leqslant {{T}_{n}}.$

Для определения параметров ${{\tau }_{n}}$ и Tn нужно решить дифференциальное уравнение (2.5) с начальными условиями ${{x}_{n}}(0) = 0$, ${{\dot {x}}_{n}}(0) = 0$ и полученное решение ${{x}_{n}}(t)$ подчинить терминальным условиям ${{x}_{n}}({{T}_{n}}) = L$, ${{\dot {x}}_{n}}({{T}_{n}}) = 0$.

Затем будем перемещать тело ${{B}_{{n - 1}}}$ так, что:

(2.6)
${{\ddot {x}}_{{n - 1}}} = w_{{n - 1}}^{ + },\quad {{T}_{n}} \leqslant t < {{T}_{n}} + {{\tau }_{{n - 1}}},$
(2.7)
${{\ddot {x}}_{{n - 1}}} = - w_{{n - 1}}^{ - },\quad {{T}_{n}} + {{\tau }_{{n - 1}}} \leqslant t \leqslant {{T}_{n}} + {{T}_{{n - 1}}}.$

Аналогично по очереди переместим все тела. Длительность этапа разгона ${{\tau }_{i}}$ и общее время движения ${{T}_{i}}$ тела ${{B}_{i}}$ определяются формулами

(2.8)
${{\tau }_{i}} = \sqrt {\frac{{2Lw_{i}^{ - }}}{{w_{i}^{ + }(w_{i}^{ - } + w_{i}^{ + })}}} ,\quad {{T}_{i}} = \sqrt {\frac{{2L(w_{i}^{ - } + w_{i}^{ + })}}{{w_{i}^{ + }w_{i}^{ - }}}} ,\quad i = \overline {1,n} .$

Таким образом, безреверсное движение системы в случае (2.1) построено.

3. Решение задачи в общем случае. Рассмотрим теперь общий случай, при котором неравенство (2.1) может быть не выполнено. Обозначим через x и ${v} = \dot {x}$ координату и скорость центра масс системы, через p – суммарный импульс системы, а через M – суммарную массу тел:

(3.1)
$x = \frac{1}{M}\sum\limits_{i = 1}^n {{{m}_{i}}} {{x}_{i}},\quad {v} = \frac{1}{M}\sum\limits_{i = 1}^n {{{m}_{i}}} {{{v}}_{i}},\quad M = \sum\limits_{i = 1}^n {{{m}_{i}}} ,\quad p = Mv.$

Лемма. Решение задачи существует тогда и только тогда, когда оно существует в классе попеременных движений тел, таких, что в каждый момент времени одно из тел движется, а все остальные покоятся.

Доказательство. Пусть задано безреверсное движение ${{x}_{i}}(t)$, $t \in [0,T]$, $i = \overline {1,n} $, решающее задачу. Рассмотрим интервал времени $[{{t}_{1}},{{t}_{2}}] \in [0,T]$, такой, что каждое из тел либо покоится, либо движется на всем этом интервале. Построим на этом интервале другое безреверсное движение системы, такое, что тела движутся по очереди, скорости всех тел в моменты времени ${{t}_{1}}$ и ${{t}_{2}}$ совпадают в исходном и построенном движениях и каждое из тел проходит одинаковое расстояние в исходном и построенном движениях. Перенумеруем тела так, что тела Bi, $i = \overline {1,\tilde {n}} $, покоятся, а тела Bj, $j = \overline {\tilde {n} + 1,{\kern 1pt} n} $, движутся с положительной скоростью. По-прежнему будем считать, что взаимодействуют только пары тел с соседними номерами. Обозначим через $\Delta {{x}_{j}}$ расстояния, пройденные телами Bj на интервале времени $\left[ {{{t}_{1}},{{t}_{2}}} \right]$. Для системы подвижных тел Bj, $j = \overline {\tilde {n} + 1,{\kern 1pt} n} $, внешними являются только силы трения и сила, действующая на тело ${{B}_{{\tilde {n} + 1}}}$ со стороны тела ${{B}_{{\tilde {n}}}}$. Поскольку тела ${{B}_{i}}$, $i = \overline {1,\tilde {n}} $, неподвижны, то импульс всей системы подчиняется уравнению

(3.2)
$\dot {p} = f_{{\tilde {n} + 1}}^{{\tilde {n}}} - \sum\limits_{j = \tilde {n} + 1}^n {{{k}_{j}}} {{m}_{j}}g.$

Построим безреверсное движение, при котором тела движутся попеременно, т.е. в каждый момент времени движется только одно тело, а все остальные покоятся. Передадим в момент времени ${{t}_{1}}$ весь импульс системы телу Bn; в этот момент времени скорости всех тел, кроме Bn, становятся равными нулю. На интервале $\left[ {{{t}_{1}},{{t}_{1}} + {{\tau }_{n}}} \right]$ зададим силы взаимодействия тел следующим образом. Силы $f_{i}^{{i + 1}}(t)$, $i = 1,\; \ldots ,\;\tilde {n}$, действующие между телами, неподвижными в исходном движении, а также между телом ${{B}_{{\tilde {n}}}}$ и телом ${{B}_{{\tilde {n} + 1}}}$, оставим неизменными. Остальные силы определим так:

(3.3)
$f_{{i + 1}}^{i} = f_{{\tilde {n} + 1}}^{{\tilde {n}}} - \sum\limits_{j = \tilde {n} + 1}^i {{k}_{j}}{{m}_{j}}g,\quad i = \overline {\tilde {n} + 1,n - 1} .$

При этом сила, действующая на тело Bi со стороны соседних тел, вычисляется как

$f_{i}^{{i + 1}} + f_{i}^{{i - 1}} = {{k}_{i}}{{m}_{i}}g,\quad i = \overline {\tilde {n} + 1,\;n - 1} ,$
а соответствующая сила трения равна ${{F}_{i}} = - {{k}_{i}}{{m}_{i}}g$, поэтому все тела Bi, $i = \overline {\tilde {n} + 1,\;n - 1} $, остаются в состоянии покоя на интервале $\left[ {{{t}_{1}},{{t}_{1}} + {{\tau }_{n}}} \right]$.

Сила, действующая на тело Bn со стороны тела ${{B}_{{n - 1}}}$, имеет вид

(3.4)
$f_{n}^{{n - 1}} = f_{{\tilde {n} + 1}}^{{\tilde {n}}} - \sum\limits_{j = \tilde {n} + 1}^{n - 1} {{{k}_{j}}} {{m}_{j}}g.$

Поскольку сила трения, действующая на Bn, равна $ - {{k}_{n}}{{m}_{n}}g$, а все остальные тела, кроме Bn, покоятся, получаем, что уравнение для импульса системы в построенном движении совпадает с уравнением (3.2). Определим длительность ${{\tau }_{n}}$ движения тела Bn. В качестве момента времени ${{t}_{1}} + {{\tau }_{n}}$ выберем момент, в который путь, пройденный телом Bn, будет равен $\Delta {{x}_{n}}$. Такой момент времени существует. Действительно, импульс системы $p(t)$ построенного движения совпадает с импульсом исходного движения. Поскольку в исходном движении центр масс на интервале времени $\left[ {{{t}_{1}},{{t}_{2}}} \right]$ перемещается на расстояние

(3.5)
$\Delta x = \frac{1}{M}\sum\limits_{i = \tilde {n} + 1}^n {{{m}_{i}}} \Delta {{x}_{i}},$
а в новом движении центр масс перемещается на расстояние $\Delta x{\text{*}}$, меньшее, чем $\Delta x$:
(3.6)
$\Delta x* = \frac{1}{M}{{m}_{n}}\Delta {{x}_{n}} < \Delta x,$
то момент времени, в который тело Bn проходит путь $\Delta {{x}_{n}}$, существует и принадлежит интервалу $\left[ {{{t}_{1}},{{t}_{2}}} \right]$.

В момент времени ${{t}_{1}} + {{\tau }_{n}}$ передадим мгновенно импульс телу ${{B}_{{n - 1}}}$ и на интервале времени $\left[ {{{t}_{1}} + {{\tau }_{n}},{{t}_{1}} + {{\tau }_{n}} + {{\tau }_{{n - 1}}}} \right]$ все тела, кроме ${{B}_{{n - 1}}}$, будут покоиться, а тело ${{B}_{{n - 1}}}$ будет двигаться вперед. Повторяя почти дословно рассуждения, с помощью которых была доказана возможность перемещения тела ${{B}_{n}}$ на расстояние $\Delta {{x}_{n}}$ за время ${{\tau }_{n}}$, меньшее, чем ${{t}_{2}} - {{t}_{1}}$, можно показать, что тело ${{B}_{{n - 1}}}$ может быть перемещено на расстояние $\Delta {{x}_{{n - 1}}}$ за время ${{\tau }_{{n - 1}}}$, меньшее, чем ${{t}_{2}} - {{t}_{1}} - {{\tau }_{n}}$. Будем передавать импульс последовательно телам ${{B}_{{n - 2}}}$, ${{B}_{{n - 3}}}$ и т.д. до тела ${{B}_{{\tilde {n} + 1}}}$. Получим, что к моменту времени ${{t}_{2}}$ каждое из тел Bj, $j = \overline {\tilde {n} + 1,n} $, проходит расстояние $\Delta {{x}_{j}}$, такое же, как и в исходном движении. Импульс системы $p$ на интервалах движения каждого из тел подчиняется уравнению (3.2) и на всем отрезке $\left[ {{{t}_{1}},{{t}_{2}}} \right]$ совпадает с импульсом в исходном движении, поэтому можно перераспределить его между телами в момент времени t2, так чтобы и скорости тел в момент времени t2 совпадали со скоростями в исходном движении. Таким образом, на интервале $\left[ {{{t}_{1}},{{t}_{2}}} \right]$ построено безреверсное движение системы тел, такое, что тела движутся по очереди, при этом каждое из них проходит то же расстояние, что и в исходном движении, и скорости каждого из тел в построенном и исходном движениях совпадают в момент времени ${{t}_{1}}$, а также в t2.

Разобьем интервал движения системы [0, T] на сумму конечного числа непересекающихся отрезков $[t_{1}^{j},t_{2}^{j}]$, таких, что на каждом из этих отрезков каждое тело либо движется, либо покоится на всем отрезке. Получим, что на каждом из этих отрезков, а значит, и на всем отрезке [0, T] исходное движение может быть заменено на безреверсное движение, в котором тела движутся поочередно.

Безреверсность попеременного движения тел следует из того, что по построению импульс системы в таком движении совпадает с импульсом системы в исходном движении. Этот импульс неотрицателен, поскольку исходное движение безреверсное и скорости движущихся тел положительны. Поэтому и при попеременном движении импульс движущегося тела положителен и тела перемещаются в одном и том же (положительном) направлении, что и означает безреверсность.

Итак, для каждого движения, решающего задачу, существует движение, решающее задачу, в котором тела движутся попеременно. Лемма доказана.

Будем искать решение задачи о безреверсном движении в классе попеременных движений тел системы, таких, что в каждый момент времени движется одно тело, а все остальные тела покоятся. Рассмотрим вспомогательную задачу о максимизации импульса системы для попеременных движений.

Утверждение 1. Пусть существует движение, приводящее систему (1.6)–(1.8) из начального состояния

(3.7)
${{x}_{i}}(0) = 0,\quad {{{v}}_{i}}(0) = 0,\quad i = \overline {1,n} ,$
за конечное (заранее не фиксированное) время ${{T}_{1}}$ в терминальное состояние
(3.8)
${{x}_{i}}({{T}_{1}}) = {{a}_{i}},\quad \quad {{a}_{i}} \geqslant 0,\quad i = \overline {1,n} ,$
при условии, что тела движутся поочередно и не изменяют направления своего движения:

(3.9)
${{{v}}_{i}}(t) \geqslant 0,\quad i = \overline {1,n} ,\quad t \in \left[ {0,{{T}_{1}}} \right].$

Тогда максимальный импульс системы pmax в конечный момент движения системы, берущийся по всем таким возможным движениям, удовлетворяет соотношению

(3.10)
$p_{{\max }}^{2} = 2g\sum\limits_{i = 1}^n {{{m}_{i}}} {{a}_{i}}\left( {\sum\limits_{s \ne i} {{{k}_{s}}} {{m}_{s}} - {{k}_{i}}{{m}_{i}}} \right).$

Доказательство. Рассмотрим движение системы, удовлетворяющее условиям (3.7)–(3.9). Пусть каждое из тел ${{B}_{i}}$ в этом движении движется ${{\alpha }_{i}}$ раз, смещаясь на расстояния $a_{i}^{j}$, $j = \overline {1,{{\alpha }_{i}}} $, причем

(3.11)
$\sum\limits_{j = 1}^{{{\alpha }_{i}}} {a_{i}^{j}} = {{a}_{i}}.$

Пусть ${{p}_{ - }}$ – импульс системы в начале одного из таких движений, а ${{p}_{ + }}$ – импульс в конце этого движения. Найдем максимум ${{p}_{ + }}$ при заданном ${{p}_{ - }}$ и заданном смещении $a_{i}^{j}$. Максимальная суммарная сила, приложенная к телу ${{B}_{i}}$ со стороны всех остальных покоящихся тел, равна сумме максимальных сил трения покоя этих тел, при этом движение тела ${{B}_{i}}$ подчиняется уравнению

(3.12)
${{m}_{i}}{{{\dot {v}}}_{i}} = \sum\limits_{s \ne i} {{{k}_{s}}} {{m}_{s}}g - {{k}_{i}}{{m}_{i}}g.$

При таком движении импульсы системы в конце и начале движения связаны соотношением

(3.13)
$p_{ + }^{2} = 2g{{m}_{i}}a_{i}^{j}\left( {\sum\limits_{s \ne i} {{{k}_{s}}} {{m}_{s}} - {{k}_{i}}{{m}_{i}}} \right) + p_{ - }^{2}.$

Это соотношение следует из теоремы об изменении кинетической энергии. Формула (3.13) дает выражение для максимально возможного значения ${{p}_{ + }}$, при заданном значении ${{p}_{ - }}$ и заданном расстоянии $a_{i}^{j}$, пройденном телом ${{B}_{i}}$. Заметим, что значение ${{p}_{ + }}$ монотонно возрастает при возрастании ${{p}_{ - }}$. Максимизируем аналогично описанному выше импульс на правом конце каждого из интервалов времени движения каждого из тел при заданном значении его импульса на левом конце. При этом каждое из тел на каждом отрезке своего движения будет двигаться вправо с максимально возможным ускорением. Состыкуем полученные движения, полагая импульс системы в начале каждого следующего отрезка равным импульсу в конце предыдущего отрезка. Получим при условии $p(0) = 0$, что импульс в конце движения будет равен

(3.14)
${{p}^{2}} = 2g\sum\limits_{i = 1}^n {{{m}_{i}}} \sum\limits_{j = 1}^{{{\alpha }_{j}}} {a_{i}^{j}} \left( {\sum\limits_{s \ne i} {{{k}_{s}}} {{m}_{s}} - {{k}_{i}}{{m}_{i}}} \right).$

С учетом равенства (3.11) имеем

(3.15)
${{p}^{2}} = p_{{\max }}^{2} = 2g\sum\limits_{i = 1}^n {{{m}_{i}}} {{a}_{i}}\left( {\sum\limits_{s \ne i} {{{k}_{s}}} {{m}_{s}} - {{k}_{i}}{{m}_{i}}} \right).$

Заметим, что из данного равенства следует, что порядок чередования движения тел не важен. Не важно также, сколько раз движется каждое из тел. Максимизация импульса в конце движения при заданном порядке чередования движущихся тел и заданных расстояниях, пройденных телами, приводит к одному и тому же результату, зависящему только от суммарных расстояний ai, пройденных телами. Поэтому можно менять порядок движения тел; в чаАстности, можно считать, что каждое из тел движется один раз. Единственное ограничение на порядок движения тел состоит в том, что импульс системы не должен, в силу требования безреверсности движения тел, быть меньше нуля. Это может произойти, только когда движется тело ${{B}_{1}}$, у которого значение произведения массы на коэффициент трения максимально (1.2); при этом импульс системы $p(t)$ может убывать со временем. Чтобы избежать такой ситуации, достаточно считать, что тело ${{B}_{1}}$ движется последним. В этом случае из неотрицательности импульса системы при $t = {{T}_{1}}$ в построенном движении (что следует из неотрицательности импульса в исходном движении) следует неотрицательность импульса на всем отрезке движения тела ${{B}_{1}}$. Итак, можно считать, что каждое из тел движется за все время движения один раз, причем тело ${{B}_{1}}$ движется последним.

Таким образом, показано, что максимальное значение импульса системы в конце движения при безреверсном перемещении каждого из тел на заданное расстояние ai  удовлетворяет формуле (3.15), что и доказывает утверждение.

Следствие 1. Систему (1.6), (1.8) можно привести из начального состояния (3.7) в терминальное состояние (3.8) при условиях безреверсного и поочередного движения тел тогда и только тогда, когда

(3.16)
$\sum\limits_{i = 1}^n {} {{m}_{i}}{{a}_{i}}\left( {\sum\limits_{s \ne i} {{{k}_{s}}} {{m}_{s}} - {{k}_{i}}{{m}_{i}}} \right) \geqslant 0.$

Доказательство. Действительно, если такое движение существует, то, согласно утверждению 1, существует и движение, при котором импульс в конце движения выражается формулой (3.15), что доказывает необходимость неравенства (3.16). Достаточность его доказывает построенное в утверждении 1 движение, в котором все тела движутся по одному разу и последним движется тело ${{B}_{1}}$.

Утверждение 2. Решение задачи существует тогда и только тогда, когда выполнено неравенство

(3.17)
$\sum\limits_{i = 1}^n {{{m}_{i}}} \left( {\sum\limits_{s \ne i} {{{k}_{s}}} {{m}_{s}} - {{k}_{i}}{{m}_{i}}} \right) \geqslant 0.$

Доказательство. Полагая в (3.16) все значения ai одинаковыми и равными L, получаем необходимость выполнения этого неравенства. Достаточность докажем, построив явно движение, решающее задачу.

Положим все величины ai из утверждения 1 одинаковыми и равными a. Тогда систему можно за конечное время ${{T}_{1}}$ переместить на любое расстояние a так, что максимальный импульс в конце движения будет определяться формулой (3.15), где следует положить ${{a}_{i}} = a$, $i = \overline {1,n} $, т.е.

(3.18)
${{p}^{2}}({{T}_{1}}) = 2g\sum\limits_{i = 1}^n {{{m}_{i}}} a\left( {\sum\limits_{s \ne i} {{{k}_{s}}} {{m}_{s}} - {{k}_{i}}{{m}_{i}}} \right).$

Перераспределим в момент времени ${{T}_{1}}$ импульс системы между телами так, чтобы скорости всех тел стали равными:

(3.19)
${{{v}}_{i}}({{T}_{1}}) = p({{T}_{1}}){\text{/}}M,\quad i = \overline {1,n} .$

После этого будем тормозить всю систему как единое твердое тело с силой трения, равной

$ - \sum\limits_{i = 1}^n {{{k}_{i}}} {{m}_{i}}g.$

Tормозной путь $S$ при этом определяется выражением

(3.20)
$S = \frac{{{{p}^{2}}({{T}_{1}})}}{{2Mg\sum\limits_{i = 1}^n {{{k}_{i}}} {{m}_{i}}}} = \frac{{a\sum\limits_{i = 1}^n {{{m}_{i}}} \left( {\sum\limits_{s \ne i} {{{k}_{s}}} {{m}_{s}} - {{k}_{i}}{{m}_{i}}} \right)}}{{2M\sum\limits_{i = 1}^n {{{k}_{i}}} {{m}_{i}}}}.$

Решив уравнение $a + S = L$ c учетом последнего равенства, найдем значение a, которое обеспечивает решение исходной задачи. Утверждение доказано.

Следствие 2. Если

(3.21)
$\sum\limits_{s \ne i} {{{k}_{s}}} {{m}_{s}} > {{k}_{i}}{{m}_{i}},\quad i = \overline {1,n} ,$
то решение задачи существует.

Действительно, при условии (3.21) неравенство (3.17) выполняется, поскольку каждая из скобок в его левой части положительна. Данный случай подробно рассмотрен в разд. 2.

Следствие 3. Если

(3.22)
$\sum\limits_{s \ne i} {{{m}_{s}}} > {{m}_{i}},\quad i = \overline {1,n} ,$
то решение задачи существует.

Действительно, перегруппировав слагаемые в левой части неравенства (3.17), представим его в виде

(3.23)
$\sum\limits_{i = 1}^n {{{k}_{i}}} {{m}_{i}}\left( {\sum\limits_{s \ne i} {{{m}_{s}}} - {{m}_{i}}} \right) \geqslant 0.$

Поскольку каждая из скобок в левой части этого неравенства положительна в силу (3.22), то неравенство (3.23) выполнено.

Неравенства (3.21) и (3.22) дают достаточные условия существования решения задачи.

Для иллюстрации использования неравенства (3.17) рассмотрим случай, в котором массы всех тел, кроме ${{B}_{1}}$, одинаковы и равны $m$, тело ${{B}_{1}}$ имеет массу $M$ и коэффициенты трения всех тел о плоскость перемещения одинаковы и равны k. Положив в (3.17)

${{m}_{1}} = M,\quad {{m}_{i}} = m,\quad i = \overline {2,n} ,$
${{k}_{i}} = k,\quad i = \overline {1,n} ,$
получим неравенство
(3.24)
${{(M + (n - 1)m)}^{2}} - 2{{M}^{2}} - 2(n - 1){{m}^{2}} \geqslant 0,$
выражающее необходимое и достаточное условие разрешимости задачи при сделанных допущениях. Обозначим $\mu = M{\text{/}}m$ и представим неравенство (3.24) в виде

(3.25)
${{\mu }^{2}} - 2(n - 1)\mu - (n - 1)(n - 3) \leqslant 0.$

Решение этого неравенства относительно $\mu $ для $\mu > 0$ дает

(3.26)
$\mu \leqslant n - 1 + \sqrt {2(n - 1)(n - 2)} .$

Достаточное условие разрешимости задачи, выражаемое неравенством (3.22), в данном случае имеет вид

(3.27)
$\mu \leqslant n - 1.$

Это условие не дает полного множества значений $\mu $, при которых задача разрешима. Полное множество значений $\mu $, определяемое неравенством (3.26), шире множества, задаваемого неравенством (3.27).

Система двух тел (n = 2) также может быть исследована методами, изложенными выше для $n \geqslant 3$. Однако в этом случае потребуется дополнительно предположить, что ${{k}_{1}}{{m}_{1}} \ne {{k}_{2}}{{m}_{2}}$, поскольку при ${{k}_{1}}{{m}_{1}} = {{k}_{2}}{{m}_{2}}$ нельзя начать движение из состояния покоя так, чтобы двигалось только одно из тел; начнут двигаться оба тела, причем в противоположных направлениях. Неравенства ${{k}_{1}}{{m}_{1}} \ne {{k}_{2}}{{m}_{2}}$ и (3.17) при n = 2 дают необходимые и достаточные условия для возможности безреверсного перемещения системы двух тел на произвольное заданное расстояние из состояния покоя так, чтобы перемещения обоих тел были одинаковыми и по окончании движения скорости тел были нулевыми. Эти условия имеют вид

${{k}_{1}}{{m}_{1}} \ne {{k}_{2}}{{m}_{2}},\quad ({{k}_{1}}{{m}_{1}} - {{k}_{2}}{{m}_{2}})({{m}_{2}} - {{m}_{1}}) \geqslant 0$
и совпадают с условиями, полученными в [36].

Заключение. Решена задача о перемещении системы взаимодействующих тел из начального состояния покоя в конечное состояние покоя вдоль прямой на горизонтальной шероховатой плоскости при условии, что каждое тело перемещается на одно и то же расстояние и не изменяет направления движения (безреверсный режим). Трение между плоскостью перемещения и телами системы считается кулоновым. Управление осуществляется силами взаимодействия тел, которые являются внутренними силами по отношению к системе. Ограничения на управляющие силы не налагаются. Найдено необходимое и достаточное условие, при котором такое перемещение возможно. Данное условие выражено неравенством, в которое входят массы тел и коэффициенты трения между этими телами и плоскостью перемещения.

Рис. 1.

Механическая система.

Список литературы

  1. Черноусько Ф.Л. Движение многозвенника по горизонтальной плоскости // ПММ. 2000. Т. 64. Вып. 1. С. 8–18.

  2. Черноусько Ф.Л. Волнообразные движения многозвенника по горизонтальной плоскости // ПММ. 2000. Т. 64. Вып. 4. С. 518–531.

  3. Черноусько Ф.Л. О движении трехзвенника по плоскости // ПММ. 2001. Т. 65. Вып. 1. С. 15–20.

  4. Черноусько Ф.Л. Управляемые движения двузвенника по горизонтальной плоскости // ПММ. 2001. Т. 65. Вып. 4. С. 578–591.

  5. Черноусько Ф.Л., Болотник Н.Н. Динамика мобильных систем с управляемой конфигурацией. М.: Физматлит, 2022.

  6. Ворочаева Л.Ю., Наумов Г.С., Яцун С.Ф. Моделирование движения трехзвенного робота с управляемыми силами трения по горизонтальной шероховатой поверхности // Изв. РАН. ТиСУ. 2015. № 1. С. 156–170.

  7. Ворочаева Л.Ю., Пановко Г.Я., Савин С.И., Яцун А.С. Моделирование движения пятизвенного ползающего робота с управляемым трением // Пробл. машиностроения и надежности машин. 2017. № 6. С. 12–19.

  8. Голицына М.В. Периодический режим вибрационного робота при ограничении по управлению // ПММ. 2018. Т. 82. Вып. 1. С. 3–15.

  9. Голицына М.В., Самсонов В.А. Оценка области допустимых параметров системы управления вибрационным роботом // Изв. РАН. ТиСУ. 2018. № 2. С. 85–101.

  10. Егоров А.Г., Захарова О.С. Оптимальное по энергетическим затратам движение виброробота в среде с сопротивлением // ПММ. 2010. Т. 74. Вып. 4. С. 620–632.

  11. Егоров А.Г., Захарова О.С. Энергетически оптимальное движение виброробота в среде с наследственным законом сопротивления // Изв. РАН. ТиСУ. 2015. № 3. С. 168–176.

  12. Иванов А.П., Сахаров А.В. Динамика твердого тела с подвижными внутренними массами и ротором на шероховатой плоскости // Нелинейная динамика. 2012. Т. 8. № 4. С. 763–772.

  13. Сахаров А.В. Поворот тела с двумя подвижными внутренними массами на шероховатой плоскости // ПММ. 2015. Т. 79. Вып. 2. С. 196–209.

  14. Досаев М.З., Климина Л.А., Самсонов В.А., Селютский Ю.Д. Плоскопараллельное движение робота-змеи при наличии анизотропого сухого трения и единственного управляющего сигнала // Изв. РАН. ТиСУ. 2022. № 5. С. 152–161.

  15. Xu J., Fang H. Improving Performance: Recent Progress on Vibration-driven Locomotion systems // Nonlinear Dynamics. 2019. V. 98. № 4. P. 2651–2669.

  16. Zhan X., Xu J., Fang H. Planar Locomotion of a Vibration-driven System with Two Internal Masses // Applied Mathematical Modelling. 2016. V. 40. № 2. P. 871–885.

  17. Zhan X., Xu J., Fang H. A Vibration-driven Planar Locomotion Robot – Shell // Robotica. 2018. V. 36. № 9. P. 1402–1420.

  18. Zimmermann K., Zeidis I., Behn C. Mechanics of Terrestrial Locomotion with a Focus on Nonpedal Motion Systems. Heidelberg: Springer, 2010.

  19. Steigenberger J., Behn C. Worm-like Locomotion Systems: an Intermediate Theoretical Approach. Munich: Oldenbourg Wissenschaftsverlag, 2012.

  20. Liu Y., Islam S., Pavlovskaya E., Wiercigroch M. Optimization of the Vibro-impact Capsule System // J. Mech. Eng. 2016. V. 62. P. 430–439.

  21. Liu Y., Pavlovskaia E., Hendry D., Wiercigroch M. Vibro-impact Responses of Capsule System with Various Friction Models // Intern. J. Mechanical Sciences. 2013. V. 72. P. 39–54.

  22. Liu Y., Pavlovskaya E., Wiercigroch M. Experimental Verification of the Vibro-impact Capsule Model // Nonlinear Dynamics. 2016. V. 83. P. 1029–1041.

  23. Liu Y., Pavlovskaia E., Wiercigroch M., Peng Z.K. Forward and Backward Motion Control of a Vibro-impact Capsule System // Intern. J. Nonlinear Mechanics. 2015. V. 70. P. 30–46.

  24. Liu Y., Wiercigroch M., Pavlovskaia E., Yu Y. Modelling of a Vibro-impact Capsule System // Intern. J. Mechanical Sciences. 2013. V. 66. P. 2–11.

  25. Черноусько Ф.Л. Оптимальное прямолинейное движение двухмассовой системы // ПММ. 2002. Т. 66. Вып. 1. С. 3–9.

  26. Черноусько Ф.Л. Анализ и оптимизация прямолинейного движения двухмассовой системы // ПММ. 2011. Т. 75. Вып. 5. С. 707–717.

  27. Фигурина Т.Ю. Оптимальное управление системой материальных точек на прямой с сухим трением // Изв. РАН. ТиСУ. 2015. № 5. С. 3–9.

  28. Черноусько Ф.Л. Поступательное движение цепочки тел в сопротивляющейся среде // ПММ. 2017. Т. 81. Вып. 4. С. 380–388.

  29. Zimmermann K., Zeidis I., Bolotnik N., Pivovarov M. Dynamics of a Two-module Vibration-driven System Moving along a Rough Horizontal Plane // Multibody System Dynamics. 2009. V. 22. P. 199–219.

  30. Zimmermann K., Zeidis I., Pivovarov M., Behn C. Motion of Two Interconnected Mass Points under Action of Non-symmetric Viscous Friction // Arch. Appl. Mech. 2010. V. 80. № 11. P. 1317–1328.

  31. Bolotnik N., Pivovarov M., Zeidis I., Zimmermann K. The Undulatory Motion of a Chain of Particles in a Resistive Medium // ZAMM. 2011. V. 91. № 4. P. 259–275.

  32. Bolotnik N., Pivovarov M., Zeidis I., Zimmermann K. The Undulatory Motion of a Chain of Particles in a Resistive Medium in the Case of a Smooth Excitation Mode // ZAMM. 2013. V. 93. № 12. P. 895–913.

  33. Bolotnik N., Pivovarov M., Zeidis I., Zimmermann K. The Motion of a Two-body Limbless Locomotor along a Straight Line in a Resistive Medium in the Case of a Smooth Excitation Mode // ZAMM. 2016. V. 96. № 4. P. 429–452.

  34. Bolotnik N., Schorr P., Zeidis I., Zimmermann K. Periodic Locomotion of a Two-body Crawling System along a Straight Line on a Rough Inclined Plane // ZAMM. 2018. V. 98. № 11. P. 1930–1946.

  35. Wagner G., Lauga E. Crawling scallop: Friction-based Locomotion with One Degree of Freedom // J. Theor. Biol. 2013. V. 324. P. 42–51.

  36. Болотник Н.Н., Губко П.А., Фигурина Т.Ю. О возможности безреверсного периодического прямолинейного движения системы двух тел на шероховатой плоскости // ПММ. 2018. Т. 82. № 2. С. 138–148.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Известия РАН. Теория и системы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал