Известия РАН. Теория и системы управления, 2023, № 5, стр. 103-126
МОДЕЛИ И АЛГОРИТМЫ МНОГОАГЕНТНОЙ ИЕРАРХИЧЕСКОЙ МАРШРУТИЗАЦИИ С ВРЕМЕННЫМИ ОКНАМИ
М. Г. Козлова a, *, Д. В. Лемтюжникова b, c, **, В. А. Лукьяненко a, ***, О. О. Макаров a, ****
a ФГАОУ ВО “Крымский федеральный университет им. В.И. Вернадского”,
Симферополь, Россия
b ИПУ им. В.А. Трапезникова РАН
Москва, Россия
c Московский авиационный институт (национальный исследовательский ун-т)
Москва, Россия
* E-mail: art-inf@mail.ru
** E-mail: darabbt@gmail.com
*** E-mail: art-inf@yandex.ru
**** E-mail: fantom2.00@mail.ru
Поступила в редакцию 28.03.2023
После доработки 18.04.2023
Принята к публикации 05.06.2023
- EDN: ODFMEZ
- DOI: 10.31857/S0002338823050098
Аннотация
Рассматривается задача моделирования реальных логистических систем, устроенных иерархическим образом. Формируются кластеры потребителей нижнего уровня, отвечающие ограничениям временных окон для каждого потребителя и кластера в целом. На каждом таком кластере строится маршрут агента-коммивояжера и выделяется вершина, наиболее близкая к центральному узлу, которая является вершиной перегрузки товара с большегрузных транспортных средств на малогрузные транспортные средства, обслуживающие кластеры потребителей. Вершины перевалки, в свою очередь, объединяются в маршруты коммивояжера более высокого уровня с учетом временных окон для маршрутов этого уровня. Программная реализация тестируется на известных сетях. Методика применима для синтеза центрального распределительного центра и системных распределительных центров нижнего уровня, а также для расчета необходимого числа транспортных средств (агентов).
Введение. Обсуждаются проблемы моделирования реальных задач прикладной алгоритмической логистики с помощью многоагентных иерархических задач маршрутизации. Модели реальных задач существенно сложнее, бесспорно красивых, академических моделей задач такого класса. Логистика перевозок (маршрутизация) на сложных сетях включает в себя задачи планирования транспортных маршрутов с учетом: необходимых транспортных средств (ТС); распределения грузов по потребителям (клиентам); количества перевозок; расписания (график) работы водителей (если это автомобильные перевозки); времени в пути, временных окон для погрузочных и разгрузочных работ; отдыха водителей; сборов на платных дорогах и мн. др. Глобальная модель содержит огромное число переменных, множество локальных и технологических критериев оптимальности, большое число ограничений и т.п. В этом случае проверка разрешимости, устойчивости, разработка и реализация алгоритмов является практически нереализуемой задачей. Необходим набор достаточно простых, реализуемых моделей, направленных на снижение размерности (например, с помощью декомпозиции), таких, чтобы на подсистемах (кластерах) было возможно использовать полиномиальные алгоритмы или экспоненциальные (точные) на кластере сети малой размерности. Поставленной цели можно добиваться с помощью иерархической кластеризации HC (hierarchical clustering) и межкластерной многоагентной маршрутизации. Существенным является применение любой доступной информации о структуре сети, прецедентных моделях, использование мобильных и спутниковых коммуникационных технологий, а также возможность снятия некоторых ограничений для упрощения модели по управлению логистическими процессами с целью оптимизации всех ресурсов в режиме реального времени.
Укажем на обзорные работы [1, 2], в которых проводится классификация задач и метаэвристик VRP (vehicle routing problem), применимых для многоагентных задач коммивояжера с временными окнами MTSPTW (multiple traveling salesman problem with time window). Иерархия вершин, наличие многих депо (складов), кластеризация потребителей отражены в работах [3, 4], где приводятся задачи MECVRP (multi-echelon capacitated VRP) для случая 2E-CVRP (two-echelon capacitated vehicle routing problem). Также рассматриваемые задачи можно отнести к задачам теории расписаний.
Задачи маршрутизации (TSPTW – traveling salesman problem with time windows, VRPTW – vehicle routing problem with time windows) с временными окнами с несколькими уровнями иерархии маршрутов отвечают сложившимся моделям логистики поставок. Такие задачи еще не исследованы на достаточном уровне.
Целью работы является разработка подходов по синтезу многоагентных маршрутов с временными окнами, устроенных иерархическим образом. Для этого приводится обзор существующих моделей, задач и алгоритмов решения близких задач. Предлагаются модели и алгоритмы иерархической маршрутизации, согласованной с маршрутами коммивояжеров на кластерах.
1. Задачи и алгоритмы маршрутизации. 1.1. Обзор моделей, задач и алгоритмов. В ряде статей рассматриваются близкие к исследуемым в работе задачи. В [5] исследован случай VRPTW (vehicle routing problem with time windows – задача маршрутизации транспортных средств с временными окнами) с неопределенным количеством транспортных средств и одновременным обслуживанием доставки и самовывоза VRPTW-SDP (vehicle routing problem with time windows and simultaneous delivery and pick-up service – задача маршрутизации ТС с временными окнами с неопределенным количеством ТС и одновременным обслуживанием доставки и самовывоза). Задача VRPTW-SDP является расширением VRPTW с целью минимизации транспортных расходов. Утверждается, что классические подходы для решения VRP и VRPTW, такие, как, например, k-деревья [6] или метод ветвей и границ, мало эффективны при решении сложных задач. Предложен эволюционный алгоритм EA (evolutionary algorithm) роя частиц. Алгоритм оптимизации роя частиц PSO (particle swarm optimization) является эффективным алгоритмом для решения многих сложных задач оптимизации. Но PSO иногда находит только локальное оптимальное значение, поэтому его точность ограничена. В качестве улучшенного PSO предложен многороевой кооперативный алгоритм MCPSO (multi-swarm cooperative particle swarm optimization). Он использует многороевую кооперативную эволюционную стратегию, в которой ведущий рой меняет свои частицы на основе собственных знаний и знаний частиц в ведомых роях, а ведомые рои выполняют PSO самостоятельно. Сравнения с алгоритмом PSO и алгоритмом GA (genetic algorithm, генетический алгоритм) показывают, что простой и надежный алгоритм MCPSO более эффективен для решения предложенной VRPTW-SDP.
В [7] представлена разработка новых методов решения задачи маршрутизации ТС с временными окнами (VRPTW). Обсуждаются два основных направления развития точных методов для VRPTW. Одно из них связано с общим подходом к декомпозиции и решением определенных двойственных к VRPTW задач. Другое, более современное направление, связано с анализом полиэдральной структуры VRPTW. Рассмотрена релаксация Лагранжа набора ограничений, требующих, чтобы каждый клиент был обслужен ровно одним ТС, что приводит к ограничениям в подпроблеме кратчайшего пути. Представлен регуляризированный алгоритм секущих плоскостей в рамках линейного программирования для решения соответствующей двойственной задачи Лагранжа. Этот алгоритм приводит к более простым подпроблемам кратчайшего пути с ограничениями, поскольку вводится меньше отрицательных циклов и более быстро сходятся множители, благодаря стабилизации двойственных переменных. Авторами встроен устойчивый алгоритм секущей плоскости в метод ветвей и границ и введены сильные допустимые неравенства на уровне главной задачи с помощью релаксации Лагранжа. В результате получен алгоритм Лагранжа с ветвлением, отсечением и ценой LBCP (lagrangian branch-and-cut-and-price) для VRPTW. Использование этой стратегии на уровне главной задачи дает значительное ускорение по сравнению с другими алгоритмами. Решены две тестовые задачи, представленные в 2001 г. Герингом и Хомбергером, с 400 и 1000 клиентами соответственно, которые на сегодняшний день являются самыми большими задачами, когда-либо решенными оптимально. Реализован алгоритм LBCP, используя фреймворк ABACUS с открытым исходным кодом для решения смешанных целочисленных линейных программ методом ветвления, отсечения и цены. В [7] представлена новая формулировка VRPTW, включающая только двоичные переменные, связанные с дугами в базовом диграфе. Новая формулировка основана на модели асимметричной задачи коммивояжера с временными окнами и имеет преимущество в том, что позволяет избежать дополнительных переменных и связывающих ограничений. В новой формулировке VRPTW временные окна моделируются с помощью неравенств путей. Неравенства путей устраняют невыполнимые по времени и пропускной способности пути. Представлен новый класс усиленных неравенств путей, основанный на полиэдральных результатах, которые получены в контексте асимметричной задачи коммивояжера с дугами пополнения запасов. Изучен политоп VRPTW и определена его размерность. Показано, что при определенных предположениях неравенства путей являются гранеопределяющими.
В [8] рассматривается вариант задачи маршрутизации ТС с временными окнами и несколькими маршрутами MVRPTW (vehicle routing problem with time windows and multiple routes). В этой задаче учитывается, что данное ТС может быть назначено на более чем один маршрут за период планирования, учитываются дополнительные ограничения на продолжительность маршрута и генерируются все возможные маршруты ТС априори. В статье предложен новый точный алгоритм для этой задачи. Он является итерационным и опирается на псевдополиномиальную модель сетевого потока, узлы которой представляют (дискретные) моменты времени, дуги – осуществимые маршруты ТС, а решение состоит из набора путей, каждый из которых представляет рабочий день. Проблема псевдополиномиальной модели заключается в том, что ее размер зависит от продолжительности рабочих дней. Моменты времени, которые рассматриваются в модели, являются целыми, и поэтому для нецелых моментов используются процедуры округления, которые позволяют получить (сильную) нижнюю границу. Затем модель встраивается в точный алгоритм, который итеративно добавляет новые временные моменты в модель сетевого потока и реоптимизирует ее, пока не будет доказано, что найденное решение выполнимо. Согласно сравнению, данный алгоритм превосходит алгоритм, основанный на генерации столбцов. В тех случаях, когда оба метода находят решение, метод, представленный в [8], значительно сокращает время вычислений. Алгоритм, обсуждаемый в этой работе, был протестирован на наборе эталонных примеров. Согласно полученным результатам, сделан вывод, что данный метод способен решить большее количество примеров, чем другой точный метод, описанный до сих пор в литературе, и он явно превосходит его по времени вычислений.
Для VRPTW с целевыми функциями минимизации количества ТС и минимизации временных потерь, вызванных ранним прибытием в процессе доставки в [9] предлагается гибридный многокритериальный эволюционный алгоритм HMOEA-GL (hybrid multiobjective evolutionary algorithm with fast sampling strategy-based global search). Используются схемы с глобальным поиском на основе стратегии быстрой выборки FSS-GS (fast sampling strategy-based global search) и локальным поиском на базе различий в последовательности маршрутов RSD-LS (route sequence difference-based local search). В алгоритме FSS-GS исследуется все пространство решений с быстрым выбором поиска к центру и краевым областям, и таким образом, получая новую популяцию. Алгоритм RSD-LS выполняется для объектов с низкой производительностью в популяции с целью повышения поисковой способности базового алгоритма HMOEA-GL. Разработаны подходящие методы кодирования и генетические операторы. Для уменьшения количества ТС в VRPTW используется простой поиск по вставке. Сравнение HMOEA-GL с NSGA-II (non-dominated sorting genetic algorithm II), SPEA2 (strength pareto evolutionary algorithm) и MOEA/D (multi-objective evolutionary algorithm by decomposition) по 12 тестовым задачам из выборки Solomon [11] показывает, что предложенный алгоритм хорошо сходится, сохраняя удовлетворительную производительность распределения ТС и заявок.
В задаче маршрутизации ТС с временным окном (VRPTW) целью является минимизация количества ТС, а затем минимизация общего времени в пути TD (total distance) при том же количестве маршрутов. Каждый маршрут начинается на автобазе и заканчивается у клиента, посещая по пути несколько клиентов, каждый по одному разу, без возвращения на автобазу. Спрос каждого клиента должен быть полностью удовлетворен одним ТС. Суммарный спрос, обслуживаемый каждым автомобилем, не должен превышать вместимость автомобиля. Для решения этой задачи в [10] предлагается эффективная эвристика табу-поиска для маршрутизации ТС с временным окном TS-VRPTW (tabu search for vehicle routing problem with time window). В TS-VRPTW пространство поиска представляет собой универсальное множество дуг в полном графе VRPTW. Позиция, которая является набором маршрутов доставки для парка ТС, определяется как подмножество дуг и строится конструктивно. В этом представлении полностью воплощены характеристики VRPTW. Также предложен новый метод принятия решений для обработки первичных и вторичных целей VRPTW. Этот метод подходит не только для TS-VRPTW, но и потенциально полезен в других подходах к решению VRPTW. Предложенный TS-VRPTW – один из немногих алгоритмов TS, который был протестирован на всех эталонах Solomon [11]. На основании результатов вычислений на эталонных тестах Solomon, состоящих из шести различных наборов данных, показано, что предложенная TS-VRPTW сопоставима по качеству решения с наиболее эффективными опубликованными эвристиками.
В [12] исследуется многофакторный эволюционный алгоритм MFEA (multifactorial evolutionary algorithm), модифицированный за счет интеграции остовного маршрута и локального поиска на больших окрестностях. Он используется для решения многокритериальной VRPTW, которая моделируется как две связанные задачи. Основная задача представляет собой многокритериальную версию VRPTW, а вспомогательная задача – версию VRPTW с одной целевой функцией. Полученный в результате многокритериальный многофакторный меметический алгоритм MOMFMA (multi-objective multi-factorial memetic algorithm) решает две задачи одновременно, причем обмен информацией между задачами происходит в процессе эволюции. В дополнение к неявной передаче информации MFEA вводится остовный маршрут для обеспечения явной передачи информации между задачами. В частности, остовные маршруты создаются как промежуточные решения и используются при локальном поиске на больших окрестностях. Для ускорения сходимости алгоритма остовный маршрут и локальный поиск на больших окрестностях работают вместе. Показана эффективность алгоритма MOMFMA на 56 примерах из выборки Solomon [11].
В [13] для решения VRPTW представлен двухэтапный многокритериальный эволюционный алгоритм, основанный на классифицированной совокупности TSCEA (two-stage multi-objective evolutionary algorithm based on classified population). Решается задача дискретной оптимизации с тремя целевыми функциями: минимизация общей стоимости расстояния, минимизация количества ТС и оптимизация баланса маршрутов в течение ограниченного времени. Алгоритм TSCEA состоит из двух этапов. На первом этапе происходит процесс классификации популяции. Популяция исследуется с использованием предложенного алгоритма, а затем классифицируется в соответствии с количеством ТС. На втором этапе путем повторной оптимизации классифицированной совокупности получается набор решений Парето для VRPTW с тремя целевыми функциями. В качестве тестовых наборов выбраны эталонные экземпляры Solomon [11]. Результаты моделирования показывают, что TSCEA превосходит сравниваемые алгоритмы с точки зрения качества или расширения.
В [14] показан подход оптимизации эволюционного переноса ETO (evolutionary transfer optimization) для VRPTW. В работе исследуется общий механизм отбора высокопотенциальных решений для эволюционных алгоритмов. Изучаются характеристики строительных блоков для генетических и меметических алгоритмов.
В [15] рассматриваются затраты на отправку, штрафы за нарушение границ временного окна, затраты на топливо и влияние скорости движения ТС, уклона дороги и загрузки ТС на расход топлива. Сформулирована модель смешанного целочисленного программирования, основанная на предварительной оптимизации и стратегии повторной оптимизации. Рассматривается влияние зависящих от времени сетей на оптимизацию маршрута. Моделирование базируется на асимметричном графе, что увеличивает сложность задачи. На этапе предварительной оптимизации генерируется схема, основанная на некоторой мере достоверности. На этапе повторной оптимизации используется новая стратегия для устранения узлов сбоя обслуживания. Разработан хаотический генетический алгоритм с переменным поиском окрестностей. Введена псевдослучайность хаоса для обеспечения разнообразия начальных решений и адаптивного времени поиска окрестностей. Для повышения производительности алгоритма предложены стратегия и механизм принятия некачественного решения. Численные результаты показывают, что предложенные модель и алгоритм эффективны.
В [16] рассматривается VRPTW в условиях двух неопределенностей: времени обслуживания и времени в пути. Вводятся новые подходы к решению этой робастной задачи и эффективная параллельная процедура для генерации всех возможных сценариев. Наилучшее надежное решение для каждого сценария может быть достигнуто с помощью параллельной адаптивной метаэвристики поиска по большой окрестности. Для нахождения наилучшего баланса между сокращенным временем выполнения и наилучшим решением исследуются четыре различные комбинации параллельных / последовательных подходов. Вычислительные эксперименты выполняются и тестируются на выборке Solomon [11] и больших случайно сгенерированных экземплярах. Полученные результаты представляют решения, которые защищены от задержек во время обслуживания в разумные сроки и в первую очередь для больших примеров.
В [17] применяется генетический алгоритм смещенного случайного ключа BRKGA (biased random key genetic algorithm) для решения VRPTW с ограничениями синхронизации. Каждая заявка имеет одно из двух свойств или же оба сразу. Поэтому для обслуживания каждой заявки требуется ТС, удовлетворяющее свойству заявки. Заявки с двумя свойствами должны обслуживаться разными ТС либо одновременно, либо с соблюдением очередности. Эти требования вносят нелинейность в проблему, поскольку небольшое изменение на одном маршруте потенциально влияет на все остальные маршруты, затрудняя определение эффективной процедуры локального поиска. Для обхода нелинейности задачи используется генетический алгоритм, который улучшает последовательность, где все варианты обслуживания встроены в маршруты. Генетический алгоритм превзошел подход коррекции и оптимизации на 25% и выполнился в 2 раза быстрее на примерах задачи домашнего здравоохранения.
В [18] представлен новый вариант VRP с временными окнами и гибкими местами доставки VRPTW-FL (the VRP with time windows and flexible delivery locations). Как правило, в VRP каждый клиент обслуживается в одном фиксированном месте обслуживания. Однако в VRPTW-FL каждый клиент обслуживается в одном из множества потенциальных мест обслуживания, каждое из которых имеет определенную пропускную способность. Теоретически VRPTW-FL сложно решить из-за ограниченных возможностей местоположения. При обслуживании клиента доступность места должна быть обеспечена в любое время. Так как задача VRPTW-FL не может быть описана с помощью некоторого числа линейных ограничений, то для решения этой проблемы в [18] предложена гибридная метаэвристика, основанная на адаптивном поиске по большим окрестностям ALNS (adaptive large neighborhood search) и управляемом локальном поиске GLS (guided local search). Эвристика построения основана на вставке, добавляется механизм отката для изменения неудовлетворительных решений на ранней стадии. Решение, полученное в результате применения эвристики, улучшается с помощью гибридной ALNS. Расширяется самоадаптивность ALNS, допуская нарушения выполнимости, которые штрафуются в целевой функции. Веса штрафов динамически корректируются в соответствии с подходом GLS, что добавляет устойчивости ALNS и может сделать ее более подходящей для будущих приложений. Основываясь на полученных результатах, сделан вывод, что алгоритмические особенности значительно улучшают качество решения, эвристика работает хорошо; сочетание ALNS с GLS приводит эвристику к значительно лучшим областям горизонта планирования, а откат назад обеспечивает гораздо лучшие начальные решения, чем традиционные эвристики построения.
В ряде работ для решения VRPTW применяются технологии машинного обучения ML (machine learning). В статье [19] реализуется: 1) построение классификационной модели ML, предсказывающей количество автомобилей реализуются, необходимых для обслуживания клиентов; 2) попытка предложить алгоритм кластеризации, который использует знания о классификации, разработанные ранее, в рамках оптимизации для минимизации общего количества необходимых ТС; 3) разработка RL-модели (reinforcement learning, обучение с подкреплением), решающая задачу VRPTW; исследование важности обучающих данных, а также встраивания входных данных. Представлен ML-подход для решения крупномасштабных VRPTW, основанный на схеме “разделяй и властвуй”. Сначала спрос делится на более мелкие кластеры с помощью алгоритма кластеризации, который использует прогнозы на уровне кластеров о количестве ТС, необходимых для их обслуживания. Эти прогнозы получены с помощью древовидного метода OCT (optimal classification trees), использующего совокупность характеристик на уровне кластера. Опираясь на эти прогнозы и древовидную архитектуру модели прогнозирования, алгоритм кластеризации разделяет узлы спроса таким образом, чтобы минимизировать общее количество ТС, получаемых в результате этих кластеров. Затем в пределах каждого кластера явная маршрутизация обрабатывается алгоритмом RL (reinforcement learning), основанным на методе actorcritic. Для оценки эффективности этой идеи определены примеры VRPTW и проанализирована производительность анализа кластеризации и предложенного RL-подхода. Результаты показывают, что кластерный подход является конкурентоспособным по отношению к кластеризации на основе k-means (k-средних), обеспечивая улучшение до 5% по количеству ТС. Этот подход в настоящее время не может конкурировать с промышленными решателями, так как он приводит к решению с большим количеством ТС. Однако он предоставляет метод, с помощью которого алгоритмы маршрутизации могут быть распараллелены на каждом из кластеров, что потенциально приводит к сокращению времени вычислений. Полученная авторами в [19] система является гибкой, требуется незначительная настройка параметров. Результаты подтверждают целесообразность использования RL для решения сильно ограниченных комбинаторных задач, таких, как VRPTW. Они также указывают на существующее ограничение в обобщении подхода RL, когда обучающие и тестовые наборы данных происходят из схожих, но различных распределений.
Приведенный обзор показывает перспективность применения методов кластеризации для снижения размерности задачи и использования метаэвристик для TSP (traveling salesman problem) с временными окнами.
1.2. Постановка задачи. В работе исследуется иерархическая модель маршрутизации с окнами.
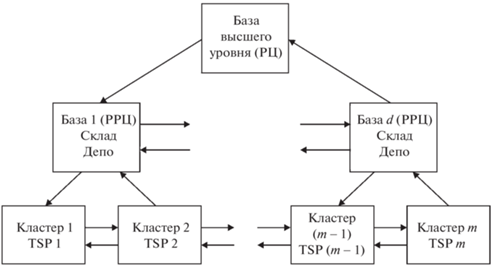
Рассмотрим двухуровневую логистическую сеть по доставке грузов. Предполагается наличие центрального склада или распределительного центра (РЦ), с которого груз доставляется на региональные распределительные центры (РРЦ) – склады, перевалочные пункты, с которых в свою очередь грузы распределяются по потребителям. Вариант такой структуры сети приведен на рис. 1. Региональный центр (база высшего уровня) перераспределяет грузы по базам нижнего уровня (РРЦ), которые обслуживают один или несколько кластеров потребителей. Такую задачу будем называть иерархической многоагентной задачей коммивояжера HMTSP (hierarchical multiple traveling salesman problem). Более сложной является задача синтеза иерархической сети такого типа.
Задачу HMTSP с временными окнами – временными ограничениями на доставку грузов, будем обозначать HMTSPTW (hierarchical multiple traveling salesman problem with time window). Временные окна TW (time window) могут быть связаны с режимом погрузочно-разгрузочных работ, перевозкой скоропортящихся грузов и др. Во многих случаях включение временных окон в математическую модель является обязательным. В [20] предложен метод расчета маршрутов с TW, включающий иерархические решения. Конечно, построение маршрутов TSP на кластерах потребителей зависит от потребности в грузах (товарах) или от их производства. Например, в сети аптек потребность в товарах определяется заявками аптек. В аналогичной сети почтовых отделений доставляемый груз и собранный определяются только в среднем (формируется случайным образом). Естественно, с данной моделью связаны задачи MTSP, китайского почтальона, медианы, рюкзака и др. С экономикой цепочек поставок в такой сети возникает задача расчета парка ТС различной грузоподъемности.
В [21] рассматривается система сбора и вывоза твердых бытовых отходов. Для Симферополя подобная проблема рассматривалась в [22]. В [23] авторами приведена модель транспортного планирования работы паромной переправы, а также разработана математическая модель погрузки порожних вагонов на железнодорожном транспортном узле, в которой учитываются требования владельца по применению вагонов, возможность добавления групп порожних вагонов в поезда пересадки, поезда очистители и промышленные поезда, работающие по плотному графику с учетом уровня эксплуатационной работы железнодорожных станций транспортного узла. В [24] авторы представляют модель инвентаризации, которая объединяет непрерывный мониторинг с производством и распределением для цепочек поставок, включающих фармацевтическую компанию, и цепочку поставок в больницу. В [25] изучается итальянская сеть здравоохранения. Заметим, что в настоящий момент широко представлена литература по математическому моделированию цепочек поставок и расчету необходимых ТС, начиная с работ по управлению цепочками поставок [26]. Далее приведем уточнение моделей и алгоритмов, лежащих в основе разработанных программ маршрутизации.
2. Модели и алгоритмы иерархической маршрутизации. Предположим, что груз (товар) концентрируется на распределительном центре (РЦ). Это может быть центральная база снабжения (склад), на которой грузы распределяются по региональным РЦ (базам). На РРЦ грузы перегружаются, например, с большегрузных ТС на ТС меньшей грузоподъемности, с помощью которых доставляются потребителям, объединенным в кластеры вокруг баз нижнего уровня (см. рис. 1).
Если не учитывать время, затраченное в пути ТС с учетом TW и грузоподъемность ТС, то задачу можно свести к задаче коммивояжера по обходу РЦ и РРЦ; кластеризации потребителей, согласованной с маршрутами коммивояжера на каждом кластере, привязанном к своей базе РРЦ. Такую многоагентную задачу назовем иерархической кластерной задачей коммивояжера HCMTSP (hierarchical cluster multiple traveling salesman problem).
Пусть задана транспортная сеть $S = (D,V,R)$, где $D = ({{d}_{0}},{{d}_{1}},...,{{d}_{k}})$ – вершины баз, d0 – центральная база РЦ, ${{d}_{i}},\;i = \overline {1,k} $ – базы нижнего уровня РРЦ; $V = ({{{v}}_{1}},{{{v}}_{2}},...,{{{v}}_{n}})$ – множество остальных вершин сети; ${{I}_{D}},\;{{I}_{V}}$ – множества индексов вершин D и V; R = {rij}, $i,j \in {{I}_{D}} \cup {{I}_{V}}$, ${{r}_{{ij}}}$ – веса (расстояния, время прохождения дуги $(i,j)$), m – число кластеров потребителей. Для решения HCMTSP предложен алгоритм 1.
Алгоритм 1. HCMTSP.
Вход: сеть $S = (D,\,\,V,R)$.
Выход: маршруты доставки грузов.
Шаг 1. Построить m кластеров потребителей Cj (вершин из V) с учетом их структуры и требований близости вершин (далее по умолчанию, если не оговорено иного, $j = \overline {1,m} $).
Шаг 2. На каждом кластере Cj найти решение $TS{{P}_{j}}$.
Шаг 3. Сравнить маршруты $TS{{P}_{j}}$, согласно заданным критериям (сбалансированность по количеству вершин или длине маршрутов; минимум общей длины). Если маршруты на кластерах удовлетворяют заданным требованиям, перейти на шаг 5, иначе – на шаг 4.
Шаг 4. Уточнить кластеры Cj, перебрасывая вершины, и построить маршруты $TS{{P}_{j}}$, перейти на шаг 3.
Шаг 5. Для каждого кластера Cj найти ближайшую базу ${{d}_{i}}$, $i = \overline {1,k} $.
Шаг 6. Найти решение TSP на вершинах ${{d}_{i}}$, $i \in {{I}_{D}} = \{ 0,1,2,...,k\} $.
Количество кластеров m может быть равно числу РРЦ с вершинами из D. Вершины D могут быть фиксированными или определяться. Например, ${{d}_{j}}$ – вершины кластеров Cj, а ${{d}_{0}}$ – ближайшая ко всем ${{d}_{j}}$.
В алгоритме HCMTSP критерием оптимальности считается минимальность расстояния по всем маршрутам (РЦ, РЦ и маршруты $TS{{P}_{j}}$). Модификация алгоритма HCMTSP в случае учета TW содержит временные критерии, так как предполагается, что есть только ограниченное время, в течение которого могут быть доставлены грузы. В качестве критериев выбирается:
а) минимальное общее время в пути (зависит от TW);
б) минимальный общий путь во всей системе (верхнего и нижнего уровней иерархии) или, кроме того, минимум в тонно-километрах (если учитывается вид транспорта и затраты на перевозку, пробег транспорта).
2.1. Кластеризация и маршрутизация в сети с учетом TW. Пусть заданы расстояния и время пути между всеми вершинами транспортной сети S. Группировка вершин V в кластеры Cj, $j = \overline {1,m} $, должна быть согласована с соответствующим маршрутом $TS{{P}_{j}}$, причем время, затраченное на прохождение пути от базы ${{d}_{j}}$ (ближайшей к кластеру Cj) к кластеру Cj и времени прохождения $TS{{P}_{j}}$, должно быть меньше или равно TW кластера Cj, например, может быть задано окно с указанием начала поставки ${{A}_{j}}$ и конца ${{B}_{j}}$: $[{{A}_{j}},{{B}_{j}}]$ – $TW{{C}_{j}}$. Другими словами, число вершин в кластере определяется маршрутом коммивояжера и временными рамками. Считаем, что центры (базы) нижнего уровня ${{d}_{j}}$ необходимо определить как вершины кластеров потребителей, ближайшие к центру высшего уровня ${{d}_{0}}$. Внутри кластера Cj время из вершины ${{{v}}_{{k - 1}}}$ в ${{{v}}_{k}}$ будем обозначать ${{t}_{{jk}}}$.
Выбор вершин для кластера Cj с учетом TW находим с помощью алгоритма 2.
Алгоритм 2. Включение вершин в кластер с учетом временных окон.
Вход: время между вершинами для кластера.
Выход: группа вершин, входящих в кластер.
Шаг 1. Построим кластер Cj, выбирая вершины кластера, например, случайно.
Шаг 2. Для каждой вершины ${v} \in {{C}_{j}}$ найдем минимальное время пути из ${{d}_{0}}$ в ${v}$. Выберем ${{d}_{1}}$ такое, что время ${{t}_{0}} = t({{d}_{0}},{{d}_{j}}) = \mathop {\min }\limits_{v} \{ t({{d}_{0}},{v}),\;\forall {v} \in {{C}_{j}}\} $, где $t(a,b)$ – время, затрачиваемое на путь из вершины $a$ в $b$.
Шаг 3. Следующую вершину ${{{v}}_{{j1}}} \in {{C}_{j}}$ выбираем из условия, что
Шаг 4. Если найдена вершина ${{{v}}_{{j(k - 1)}}} \in {{C}_{j}}$, то ${{{v}}_{{jk}}} \in {{C}_{j}}$ определяем из условия
Шаг 5. Процесс заканчивается, если после добавления вершин поочередно в каждой ветви дерева выполняется критерий
Шаг 6. Выбрать группу вершин из Cj с наименьшим ${{T}_{j}}$.
Таким образом, в кластер Cj включается конечное число узлов ${{n}_{j}}$.
2.2. Задача агента-коммивояжера TSP на k-м кластере ${{C}_{k}}$. Пусть на вновь созданном кластере сосредоточено ${{n}_{k}}$ вершин ${{{v}}_{{k1}}},{{{v}}_{{k2}}},...,{{{v}}_{{k{{n}_{k}}}}}$, которые обходит агент-коммивояжер, начиная с вершины-склада ${{d}_{k}}$, за минимальное время, не превосходящее $TW{{C}_{k}}$. Для реализации TSP-маршрута может понадобиться несколько ТС, количество которых определяется отдельно (декомпозиция по маршрутам и ТС). На кластере Cj через ${{t}_{{ij}}}$ обозначим время прохождения от вершины $i$ до вершины $j$ (вместо трехиндексного обозначения $t_{{ij}}^{k}$).
Соответствующая модель имеет вид:
(2.1)
$\sum\limits_{i = 1}^{{{n}_{k}}} {\sum\limits_{j = i + 1}^{{{n}_{k}}} {{{t}_{{ij}}}{{x}_{{ij}}}} } \to \min ,$(2.2)
$\sum\limits_{i = 1}^{{{n}_{k}}} {{{x}_{{ij}}}} = 1,\quad \sum\limits_{j = 1}^{{{n}_{k}}} {{{x}_{{ij}}}} = 1,\quad i,j = \overline {1,{{n}_{k}}} ,$(2.3)
${{t}_{k}} + \sum\limits_{i = 1}^{{{n}_{k}}} {\sum\limits_{j = i + 1}^{{{n}_{k}}} {{{t}_{{ij}}}} } \leqslant TW{{C}_{k}},$(2.4)
${{u}_{i}} - {{u}_{j}} + {{n}_{k}}{{x}_{{ij}}} \leqslant {{n}_{k}} - 1,\quad i,j = \overline {2,{{n}_{k}}} ,\quad i \ne j.$Здесь
Условие (2.4) обеспечивает условия TW для кластера ${{C}_{k}}$, ${{t}_{k}}$ – время $t({{d}_{0}},{{d}_{k}})$ прохождения от центральной вершины (распределительного центра) ${{d}_{0}}$ до вершины ${{d}_{k}}$ – склада нижнего уровня, с которого товар распределяется по потребителям кластера ${{C}_{k}}$, $k = \overline {1,m} $.
2.3. Интегрирование кластеров нижнего уровня. На нижнем уровне была проведена кластеризация потребителей в зависимости от TW, времени пути по маршруту коммивояжера-агента на кластере и определена вершина ${{d}_{j}}$ как начало маршрута на кластере Cj. Теперь необходимо интегрировать узлы ${{d}_{j}}$ кластеров в маршрут, который связывает наибольшее количество вершин ${{d}_{j}}$ (или все) в маршрут перевозки следующего уровня, по которому осуществляется доставка грузов в ${{d}_{j}}$ транспортом большей вместимости для перевалки в ТС малой вместимости для доставки потребителям кластера Cj. Таким образом, снова осуществляется процесс кластеризации на более высоком уровне в большем масштабе. Группируются узлы (вершины начала маршрутов – узлы перевалки для кластеров нижнего уровня Cj). На первом этапе группировка осуществляется, исходя из TW, а затем находится оптимальный маршрут с помощью решения $TW{{C}_{j}}$ на выделенном кластере Cj.
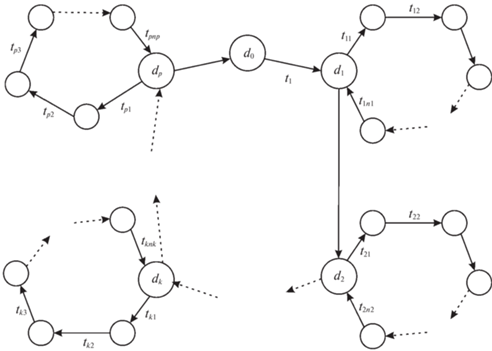
На рис. 2 показан маршрут обхода $p \leqslant m$ кластеров Cj, $j = \overline {1,m} $. При этом необходимо соблюдение TW каждого кластера Cj.
Рассмотрим ограничения, соответствующие рис. 2. Для первого кластера на маршруте
Аналогично для ${{C}_{k}}$:
Для ${{C}_{p}}$ (последний кластер, включенный в маршрут обхода кластеров)
Последнее неравенство обеспечивает ограничение по TW для кластера ${{C}_{p}}$, всех промежуточных $TW{{C}_{k}}$, $k = \overline {1,p - 1} $, и для всех в целом $TWC$ для большегрузного ТС. Аналогично поступаем с остальными кластерами ${{C}_{k}}$, $k = \overline {p + 1,m} $.
3. Реализация алгоритмов маршрутизации ТС. 3.1. Алгоритм кооперации муравьиных колоний. Рассматривается вариант обхода кластера с учетом требуемого количества агентов (ТС) и потребностей клиентов (потребителей).
Для численной реализации решения задачи маршрутизации ТС с TW и несколькими маршрутами VRPTW выберем алгоритм, основанный на системе кооперации муравьиных колоний MACS-VRPTW (multiple ant colony system for vehicle routing problem with time windows). Близкий алгоритм основан на многороевой кооперативной оптимизации роя частиц MCPSO (multi-swarm cooperative particle swarm optimizer), т.е. MCPSO-VRPTW (multi-swarm cooperative particle swarm optimizer for vehicle routing problem with time windows).
MACS-VRPTW базируется на системе муравьиных колоний ACS (ant colony system) [27, 28], и, в более общем смысле, на оптимизации муравьиной колонии ACO (ant colony optimization), метаэвристическом подходе, основанном на поведении реальных колоний муравьев. В последнее время было предложено множество алгоритмов ACO для решения различных типов задач комбинаторной оптимизации. В частности, было показано, что алгоритмы ACO очень эффективны в сочетании со специализированными процедурами локального поиска для решения симметричных и асимметричных задач коммивояжера [27–29].
Одной из наиболее эффективных реализаций ACO является ACS с особой процедурой обновления феромонной тропы, полезной для интенсификации поиска в окрестностях наилучшего вычисленного решения. Рассмотрим расширение ACS, способное решать проблему маршрутизации TC с TW (VRPTW). VRPTW определяется как проблема минимизации времени и затрат в случае, когда ТС должны распределить товары со склада по множеству клиентов. VRPTW минимизирует двухкритериальную, иерархическую целевую функцию: первая цель – минимизировать количество маршрутов (туров, агентов или ТС), а вторая – минимизировать общее время в пути. Решение с меньшим числом туров всегда предпочтительнее, даже если время в пути больше. Идея адаптации ACS к этим целям заключается в определении двух колоний ACS, каждая из которых предназначена для оптимизации различных целевых функций. В MACS-VRPTW реализуется агентное управление, при котором колонии сотрудничают, обмениваясь информацией через обновление феромонов. Заметим, что MACS-VRPTW конкурирует с лучшими из существующих методов как по качеству решения, так и по времени вычислений. Более того, MACS-VRPTW улучшает решения, известные в литературе для некоторых экземпляров задач.
Во Введении для VRPTW приведен ряд точных и эвристических методов. Среди точных методов одним из наиболее эффективных является метод [30], с помощью которого удалось решить несколько задач для 100 клиентов. Заметим, что точные методы более эффективны, если пространство решений ограничено узкими TW, поскольку для определения выполнимых туров можно использовать меньшее количество комбинаций клиентов. Наиболее успешными эвристическими методами для VRPTW являются адаптивные программы с памятью (введение в адаптивное программирование с памятью см. в [31]), поиск с встраиванием табу [32, 33], управляемый локальный поиск [34] и поиск по большой окрестности [35]. Отметим, что метод [33] также можно рассматривать как разновидность поиска по большой окрестности.
Обсудим ACS [28, 29], примененную к задаче TSP. MACS-VRPTW предназначена для решения VRPTW, в которой необходимо минимизировать как количество ТС, так и время в пути. Эта многоцелевая минимизация достигается путем использования двух искусственных муравейников на основе ACS. ACS применяется к TSP, связывая две меры с каждой дугой графа TSP: близость ${{\eta }_{{ij}}}$ и феромонный след ${{\tau }_{{ij}}}$. Близость, определяемая как обратная величина длины дуги, является статическим эвристическим значением, которое никогда не меняется для данной задачи, в то время как феромонный след динамически изменяется муравьями во время выполнения. Поэтому наиболее важным компонентом ACS будет управление феромонными тропами, которые используются вместе с целевой функцией для построения новых решений.
Неформально уровни феромонов дают меру того, насколько желательно вставить данную дугу в решение. Феромонные тропы применяются для разведки и эксплуатации. Исследование касается вероятностного выбора компонентов, используемых для построения решения: более высокая вероятность дается элементам с сильным феромоновым следом. Выбирается компонент, который максимизирует сочетание значений феромонного следа и эвристических оценок.
Цель ACS – найти кратчайший тур. В ACS m муравьев строят туры параллельно, где m – параметр. Каждый муравей случайным образом назначается на начальный узел и должен построить решение, т.е. полный тур. Тур строится узел за узлом: каждый муравей итеративно добавляет новые узлы, пока не будут посещены все узлы. Когда муравей k находится в узле i, он вероятностно выбирает следующий узел j из множества выполнимых узлов $N_{i}^{k}$ (т.е. множества узлов, которые еще нужно посетить).
Каждый муравей выбирает узел для посещения независимо. Пусть вероятность перехода муравья k из города i в город j равна $P_{{ij}}^{k}(t)$, которая описывается следующей формулой:
(3.1)
$P_{{ij}}^{k}(t) = \left\{ \begin{gathered} \frac{{\tau _{{ij}}^{\alpha }(t)\eta _{{ij}}^{\beta }(t)}}{{\sum\limits_{j \in N_{i}^{k}} {\tau _{{ij}}^{\alpha }(t)\eta _{{ij}}^{\beta }(t)} }},\quad j \in N_{i}^{k}, \hfill \\ 0,\quad j \notin N_{i}^{k}, \hfill \\ \end{gathered} \right.$После того, как муравьи построили полное решение, оно предварительно улучшается с помощью процедуры локального поиска. Затем лучшее решение, найденное в начале процесса, используется для обновления феромонных троп. Процесс итерируется путем повторного запуска m муравьев до тех пор, пока не будет выполнено условие завершения. ACS завершается, когда становится верным хотя бы одно из следующих условий: сгенерировано фиксированное количество решений, истекло фиксированное время процессора или не было достигнуто никакого улучшения в течение заданного количества итераций.
Рассмотрим процедуру обновления следа. В ACS тропа феромонов обновляется как локально, так и глобально. Локальное обновление выполняется во время построения решений, в то время как глобальное обновление – в конце конструктивной фазы. Эффект локального обновления заключается в динамическом изменении желательности ребер: каждый раз, когда муравей использует ребро, количество феромона, связанного с этим ребром, увеличивается и ребро становится более привлекательным. С другой стороны, глобальное обновление используется для интенсификации поиска в окрестностях наилучшего вычисленного решения. В ACS только лучшее решение применяется для глобального изменения феромонного следа. Эта стратегия обновления [28, 29] оказалась более эффективной, чем та, которая используется в муравьиной системе AS (ant system) [36, 37], где все построенные решения служат для обновления феромонных троп. Это объясняется тем, что таким образом в матрице феромонных троп запоминается “предпочтительный маршрут” и будущие муравьи воспользуются этой информацией для генерации новых решений в окрестностях предпочтительного маршрута.
Величина ${{\tau }_{{ij}}}$ обновляется следующим образом:
(3.2)
${{\tau }_{{ij}}}: = (1 - \rho ){{\tau }_{{ij}}} + \frac{\rho }{{J_{\psi }^{{gb}}}}\quad {\text{для любого}}\quad (i,j) \in {{\psi }^{{gb}}},$Локальное обновление выполняется следующим образом: когда муравей перемещается от узла i к узлу j, количество феромонного следа на дуге $(i,j)$ увеличивается в соответствии со следующим правилом:
где ${{\tau }_{0}}$ – начальное значение. Было установлено, что ${{\tau }_{0}} = 1{\text{/}}(nJ_{\psi }^{h})$ является хорошим значением для этого параметра, где $J_{\psi }^{h}$ – длина начального решения, полученного с помощью эвристики ближайшего соседа [38], а n – количество узлов.MACS-VRPTW использует модель решения, в которой каждый муравей строит один тур на локальной копии графа. Муравей стартует из склада и на каждом шаге перемещается к еще не посещенному узлу, который не нарушает ограничений TW и возможностей TC. Муравей, находящийся в узле i, вероятностно выбирает следующий узел j для посещения, применяя механизмы разведки и эксплуатации. Привлекательность j вычисляется с учетом времени в пути и ${{\tau }_{{ij}}}$ между узлами i и j, TW, связанного с узлом j.
Каждый раз, когда муравей переходит от одного узла к другому, осуществляется локальное обновление феромонного следа в соответствии с (3.3). Наконец, в конце конструктивной фазы решение может быть неполным (некоторые клиенты могли быть пропущены), и решение предварительно завершается с помощью дальнейших вставок. Вставка совершается при рассмотрении всех непосещенных клиентов, отсортированных по убыванию количества поставок. Для каждого клиента производится поиск наилучшей выполнимой вставки (наименьшее время в пути) до тех пор, пока не будет найдена ни одна другая вставка. Кроме того, в алгоритме реализована процедура локального поиска для улучшения качества выполнимых решений. Локальный поиск использует ходы, аналогичные обмену CROSS (CROSSover) [32]. Эта процедура основана на обмене двумя подцепочками клиентов. Одна из этих подцепочек в конечном итоге может оказаться пустой, реализуя более традиционное введение клиентов.
3.2. Описание реализуемых алгоритмов. Описанная методика решения HMTSPTW (VRPTW) опирается на построение нескольких муравьиных колоний. В [39], кроме муравьиных колоний, приводится ряд метаэвристик и их сравнительный анализ. Обобщенный алгоритм, согласно которому исходной сети ставится в соответствие сеть облета (проекция на плоскость), применяется с рядом эвристик и кластеризацией для решения задачи определения маршрутов многих коммивояжеров MTSP по реальным данным Ялты в случае чрезвычайных ситуаций. Методика [39] применима для VRPTW и HMTSPTW.
В рамках реализации описанного выше подхода были сформированы два алгоритма решения VRPTW. Первая версия – однокритериальная, здесь используется одна целевая функция по оптимизации TW. Создается единственная колония, в которой каждый муравей строит субоптимальный маршрут, основываясь на заданных временных ограничениях. Вторая версия – двухкритериальная, здесь применяются две целевые функции: на оптимизацию TW и на минимизацию количества TC. В описанных алгоритмах используется структура файлов, принятая в наборах Solomon [11]. Допускаются .txt и .csv форматы файла со строгой структурой (табл. 1). Считается, что первая запись является базой.
Таблица 1.
Пример структуры файла данных
| CUST NO | XCOORD | YCOORD | DEMAND | READY TIME | DUE DATE | SERVICE TIME |
|---|---|---|---|---|---|---|
| 0 | 40 | 50 | 0 | 0 | 1236 | 0 |
| 1 | 45 | 68 | 10 | 912 | 967 | 90 |
Здесь
CUST NO – индекс клиента;
XCOORD, YCOORD – координаты клиента;
DEMAND – количество продукта, которое необходимо клиенту;
READY TIME – момент времени, начиная с которого клиент готов принять ТС;
DUE DATE – момент времени, до которого клиент готов принять ТС;
SERVICE TIME – время, необходимое ТС на обслуживание клиента.
Таким образом, READY TIME и DUE DATE формирует TW для каждого клиента. Время считается в условных единицах, начиная со старта TC с базы.
Под внутренним графом будем понимать сформированную на основе данных программную абстракцию, которая необходима для решения задачи.
Алгоритм 3. Формирование внутреннего графа.
Вход: путь к файлу с данными для построения графа.
Выход: внутренний граф.
Шаг 1. Считать файл.
Шаг2. Найти строку с ключевыми словами (CUST NO, XCOORD, YCOORD и т.д.).
Шаг 3. Присвоить каждому ключевому слову индекс, соответствующий его позиции в списке.
Шаг 4. Считать следующую строку, разбить ее по отступам и, в соответствии с индексом шага 3, записать данные в матрицу.
Шаг 5. Если не конец файла, перейти к шагу 4.
Алгоритм 4. Однокритериальный VRPTW.
Вход: Внутренний граф, пользовательские параметры (k – количество муравьев, beta – коэффициент влияния феромона, M – максимальное количество итераций, ${{q}_{0}}$ – коэффициент вероятности случайного выбора вершины, rho – коэффициент улетучивания феромонов).
Выход: маршрут обхода графа.
Шаг 1. Произвести инициализацию с пользовательскими параметрами.
Шаг 2. Инициализируем счетчик итераций iteration:=0 и лучший маршрут best_path:= infinity.
Шаг 3. Если iteration $ \geqslant M$, то переходим к шагу 10.
Шаг 4. Инициализируем список ant_list из k муравьев.
Шаг 5. Берем следующего муравья из ant_list.
Шаг 5.1. Пока список доступных вершин для посещения не пустой.
Шаг 5.1.1. Выбрать следующую вершину с наибольшей вероятностью перехода на основе уравнения (3.1).
Шаг 5.1.2. С вероятностью ${{q}_{0}}$ перейти в случайную вершину, если вероятность не сработала, то перейти в вершину, найденную на шаге 5.1.1.
Шаг 5.1.3. Проверить, подходит ли выбранная вершина под ограничения (проверка на загрузку, проверка на время возврата в депо, проверка на время окончания приема узла после пути до этого узла).
Шаг 5.1.4. Если вершина подходит, то обновляем данные о маршруте муравья (добавляем расстояние, увеличиваем загрузку и время на количество времени, потраченное на путь и на количество времени, затраченное на обслуживание клиента). Также обновляем феромон на пройденной дуге согласно формуле (3.2).
Шаг 5.1.5. Если вершина не подходит, то возвращаемся к шагу 5.1.1. Если таких попыток было больше трех, то возвращаем муравья в депо, обновляем данные о маршруте и феромона на пройденной дуге и переходим к шагу 5.1.
Шаг 6. Посчитать общую длину маршрута каждого из k муравьев.
Шаг 7. Если полученный маршрут короче, чем best_path, то записываем его в best_path.
Шаг 8. Увеличиваем iteration на 1.
Шаг 9. Переходим к шагу 3.
Шаг 10. Вернуть best_path.
Алгоритм 5. Двухкритериальный VRPTW.
Вход: Внутренний граф, пользовательские параметры (k – количество муравьев, beta – коэффициент влияния феромона, M – максимальное количество итераций, ${{q}_{0}}$ – коэффициент вероятности случайного выбора вершины, rho – коэффициент улетучивания феромонов).
Выход: маршрут обхода графа.
Шаг 1. Произвести инициализацию с пользовательскими параметрами.
Шаг 2. Инициализируем счетчик итераций iteration:=0 и лучший маршрут best_path:= infinity.
Шаг 3. Инициализируем best_path и best_path_vehicle_num при помощи метода ближайшего соседа.
Шаг 4. Инициализируем поток acs_time_thread для колонии, производящей поиск оптимального маршрута, и поток acs_vehicle_thread для колонии, производящей поиск решения с меньшим количеством ТС.
Шаг 5. Если iteration $ \geqslant M$, то переходим к шагу 14.
Шаг 6. Передать best_path потокам acs_time_thread и acs_vehicle_thread.
Шаг 7. Запустить поток acs_time_thread.
Шаг 8. Запустить поток acs_vehicle_thread с best_path_vehicle_num$ - 1$.
Шаг 9. Дождаться, пока потоки сообщат о новом решении new_path.
Шаг 10. Сравнить найденное решение с best_path. Если new_path лучше, то обновить best_path.
Шаг 11. Сравнить количество ТС в найденном решении с best_path_vehicle_num. Если new_path_vehicle_num лучше, то обновить best_path.
Шаг 12. Дождаться момента, когда потоки закончат работу.
Шаг 13. Увеличиваем iteration на 1.
Шаг 14. Вернуть best_path.
Алгоритм 6. Двухкритериальный алгоритм ACS минимизации ТС (acs_vehicle_thread).
Вход: внутренний граф (G), пользовательские параметры (vehicle_num – количество ТС, k – количество муравьев).
Выход: маршрут обхода графа.
Шаг 1. Инициализация.
Шаг 1.1. Инициализируем current_path при помощи метода ближайшего соседа c максимальным количеством ТС = vehicle_num.
Шаг 1.2. Инициализируем unused_vehicle_count:=vehicle_num – количество свободных ТС в депо.
Шаг 2. Отыщем непосещенные вершины NTV (need to visit) из G в current_path; NTV = G \ current_path.
Шаг 3. Создаем k муравьев.
Шаг 4. Инициализируем список ant_list из k муравьев.
Шаг 4.1. Пока список доступных вершин для посещения не пустой и есть свободные ТС (unused_vehicle_count>0).
Шаг 4.1.1. Найти список таких вершин, переход в которые допустим (выполняются ограничения по времени и загрузке).
Шаг 4.1.2. Если список вершин шага 4.1.1 пуст, то unused_vehicle_count:=unused_vehicle_count$ - 1$ и возвращаем муравья в депо, обновляем данные о маршруте и феромоне на пройденной дуге и переходим к шагу 4.1.
Шаг 4.1.3. Выбрать из этого списка следующую вершину с наибольшей вероятностью перехода на основе уравнения (3.1).
Шаг 4.1.4. С вероятностью ${{q}_{0}}$ перейти в случайную вершину. Если вероятность не сработала, то перейти в вершину, найденную на шаге 4.1.3.
Шаг 4.1.5. Обновить данные о маршруте муравья (добавляем расстояние, увеличиваем загрузку и время на количество времени, потраченное на путь и на количество времени, затраченное на обслуживание клиента). Также обновляем феромон на пройденной дуге согласно (3.2).
Шаг 4.2. Пробуем вставить непосещенные вершины в полученный маршрут (не должны нарушаться ограничения по нагрузке и времени).
Шаг 4.3. Если количество непосещенных вершин с шага 4.2 меньше, чем было NTV, то запишем это решение в current_path.
Шаг 4.4. Если current_path содержит все вершины G, то уведомить главный поток о найденном решении с меньшим количеством ТС.
Шаг 5. Если не удалось отыскать current_path, содержащий все вершины G, то прервать поток.
Алгоритм 7. Двухкритериальный алгоритм ACS минимизации времени (acs_time_thread).
Вход: внутренний граф (G), пользовательские параметры (vehicle_num – количество ТС, k – количество муравьев, global_best_path – глобальное лучшее решение, M – максимальное количество итераций).
Выход: маршрут обхода графа.
Шаг 1. Инициализируем счетчик итераций iteration=0.
Шаг 2. Если iteration $ \geqslant M$, то переходим к шагу 8.
Шаг 3. Инициализируем список ant_list из k муравьев.
Шаг 3.1. Пока список доступных вершин для посещения не пустой.
Шаг 3.1.1. Найти список таких вершин, переход в которые допустим (выполняются ограничения по времени и загрузке).
Шаг 3.1.2. Если список вершин шага 3.1.1 пуст, то возвращаем муравья в депо, обновляем данные о маршруте и феромоне на пройденной дуге и переходим к шагу 3.1.
Шаг 3.1.3. Выбрать из этого списка следующую вершину с наибольшей вероятностью перехода на основе (3.1).
Шаг 3.1.4. С вероятностью ${{q}_{0}}$ перейти в случайную вершину. Если вероятность не сработала, то перейти в вершину, найденную на шаге 3.1.3.
Шаг 3.1.5. Обновить данные о маршруте муравья (добавляем расстояние, увеличиваем загрузку и время на количество времени, потраченное на путь и на количество времени, затраченное на обслуживание клиента). Также обновляем феромон на пройденной дуге, согласно (3.2).
Шаг 4. Посчитать общую длину маршрута каждого из k муравьев.
Шаг 5. Если полученный маршрут короче, чем global_best_path, то уведомить главный поток о найденном решении с меньшим временем.
Шаг 6. Увеличиваем iteration на 1.
Шаг 7. Перейти в шаг 2.
Шаг 8. Прервать поток.
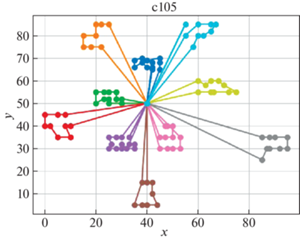
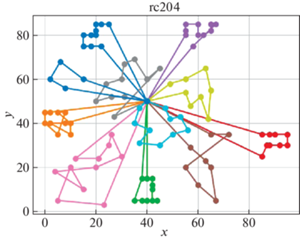
3.3. Численный эксперимент. Рассмотренные алгоритмы были программно реализованы с помощью языка программирования Python. В качестве тестовых данных использовались наборы Solomon [11] для 100, 200, 400 вершин. Двухкритериальная версия реализует две колонии муравьев, задача одной колонии отыскать кратчайший путь, а второй – минимизировать количество ТС, используемых в текущем решении. Предварительно граф кластеризуется методом иерархической кластеризации из библиотеки scipy [40] на основе максимального среднего расстояния ребер в графе. Затем вызывается для каждого из полученных кластеров. Также в табл. 1 приводится сравнительный анализ с классическим решением TSP на тех же кластерах, которые были получены в VRPTW. Решение TSP не учитывает TW, а только расстояния между узлами, что позволяет увидеть более оптимальный способ обхода, чем с TW, и сравнить с ситуацией, когда на тот же граф накладываются ограничения в виде TW.
Стоит отметить, что в данном эксперименте производится сравнение с классической TSP, так как считается, что решение TSP наиболее близкое к оптимальному, а TW лишь накладывают дополнительные ограничения и ухудшают исходный результат. Таким образом, можно проследить, насколько хорошо работает алгоритм на кластерах с TW относительно решений TSP на тех же кластерах.
Таблица 2.
Результаты тестирования алгоритмов
| TSP Concorde | Двухкритериальная версия | Лучшее решение | ||||
|---|---|---|---|---|---|---|
| Набор данных | Количество ТС | Длина маршрута | Количество ТС | Длина маршрута | Количество ТС | Длина маршрута |
| R112 | 14 | 996 | 14 | 1205 | 9 | 982 |
| C105 | 14 | 829 | 14 | 1004 | 10 | 828 |
| RC204 | 11 | 1110 | 11 | 1250 | 3 | 798 |
| R111 | 15 | 996 | 15 | 1297 | 10 | 1097 |
| C205 | 12 | 1008 | 12 | 1170 | 3 | 588 |
| RC208 | 11 | 1110 | 11 | 1180 | 3 | 828 |
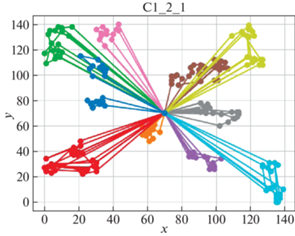
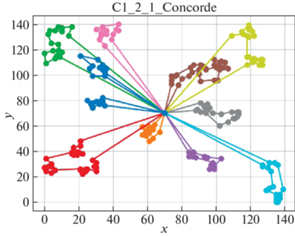
| C1_2_1 | 34 | 1728 | 34 | 4786 | 20 | 2704 |
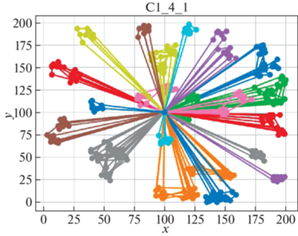
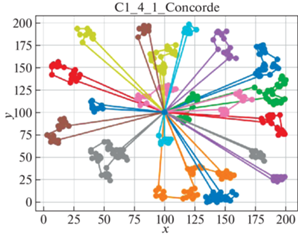
| C1_4_1 | 77 | 4389 | 77 | 13 980 | 40 | 7152 |
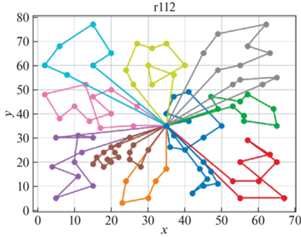
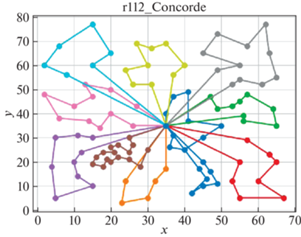
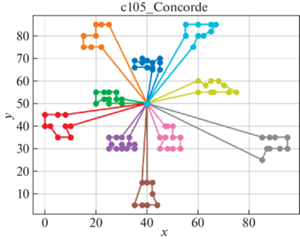
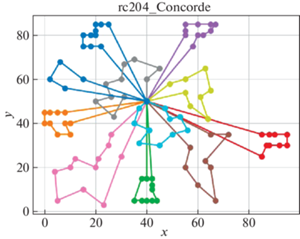
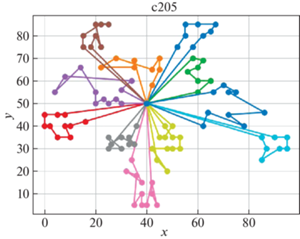
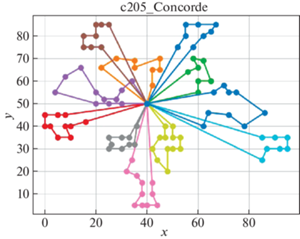
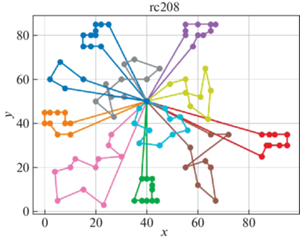
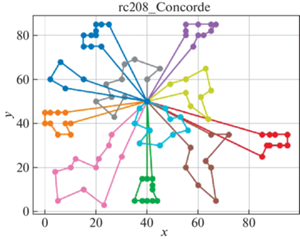
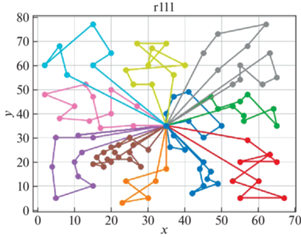
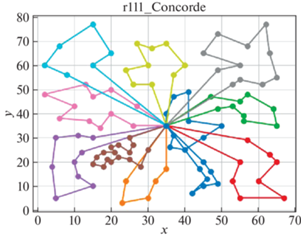
В качестве решателя TSP используется Concorde [41]. Это связанно с тем, что он показал себя действенным и эффективным комплексом для решения TSP на большом количестве тестовых примеров. Для внедрения в разработанный программный продукт использовалась обертка PyConcorde [42]. Этот адаптер позволяет вызывать методы Concordу Solver, написанного на C, из среды Python. Полученные результаты приведены в табл. 2. Лучшее известное решение взято из [11]. На рис. 3–18 представлены результаты эксперимента.
Видно, что для некоторых из тестовых примеров получены результаты, которые далеки от лучших известных на данный момент. Это отчасти ожидаемо, так как здесь делается акцент на скорости получения решения, т. е. запуск производится на относительно малых значениях пользовательских переменных, отвечающих за количество итераций. С другой стороны, при помощи TSP Concorde находятся маршруты без учета TW и двухкритериальности.
Заключение. Для модели построения многоагентных маршрутов в сети потребителей, региональных баз и центральной базы приводятся алгоритмы, обеспечивающие временные ограничения и оптимальность поставок в такой иерархической сети. На уровне региональных центров приводится более общий алгоритм, направленный как на минимизацию количества агентов (TC), так и на оптимальность маршрутов на кластерах с учетом TW.
Для решения многоагентной иерархической задачи HMTSPTW реализуется предложенный алгоритм MACS-VRPTW на основе оптимизации муравьиной колонии для решения задач маршрутизации TC с TW. В частности, алгоритм разработан для решения задач маршрутизации TC с двумя целевыми функциями: минимизация количества агентов (или TC) и минимизация общего времени в пути, где минимизация количества агентов имеет приоритет над минимизацией времени в пути.
На основе проведенных вычислительных экспериментов можно отметить ряд преимуществ и недостатков реализованного подхода. Данный метод хорошо показывает себя на графах, которые поддаются примененной кластеризации. В случае, когда в кластер попадают узлы с “неудобными” TW, метод показывает не такие хорошие результаты. Таким образом, подход нуждается в доработке методов кластеризации, которые смогут одновременно учитывать расстояния и TW узлов.
Благодаря сравнительному анализу можно увидеть, насколько TW влияют на решение. Так, Concorde Solver позволил увидеть близкие к оптимальным маршруты с точки зрения расстояний между вершинами графа. А решение с учетом TW в некоторых случаях сильно отдаляется от решения TSP. В идеальном случае решение с TW должно приближаться к решению TSP. Таким образом можно моделировать синтез составления оптимальных TW для вершин графа с целью минимизации затрат на перемещение и количество агентов.
Алгоритм на основе кооперации муравьиных колоний MACS-VRPTW представляет методологию для оптимизации нескольких целевых функций. Главная идея заключается в координации деятельности различных муравьиных колоний, каждая из которых оптимизирует свою цель. Эти колонии работают, используя независимые феромонные тропы, но сотрудничают, обмениваясь информацией. Решение многоцелевой задачи с помощью алгоритма оптимизации с несколькими муравьиными колониями является перспективным. Численный расчет показывает, что применение системы муравьиных колоний конкурирует с лучшими из существующих алгоритмов как по качеству решения, так и по времени вычислений. Тестирование проводилось на наборах Solomon. Выбранные параметры (число итераций и др.) могут быть оптимизированы. Данные результаты подтверждают работоспособность предложенных алгоритмов. Более полные результаты численных экспериментов размещены авторами по ссылке https://github.com/ssstelsss/TSP_test_solutions.
Список литературы
Liu F., Lu Ch., Gui L., Zhang Q., Tong X., Yuan M. Heuristics for Vechicle Ruoting Problem: a Survey and Recent Advance. 2023. arXiv:2303.04147v1 [cs.AI]. https://doi.org/10.48550/arXiv.2303.04147.
Tan S.-Y., Yen W.-C. The Vehicle Routing Problem: State-of-the-Art Classification and Review // Applied Sciences. 2021. V. 11 (21). P. 10295. https://doi.org/10.3390/app112110295
Li H., Wang H., Chen J., Bai M. Two-Echelon Vehicle Routing Problem with Satellite Bi-Synchronization // European J. Operational Research. 2020. V. 288 (3). https://doi.org/10.1016/j.ejor.2020.06.019
Baldacci R., Mingozzi A., Roberti R., Clavo R. An Exact Algorithm for the Two-Echelon Capacitated Vehicle Routing Problem // Operation Research. 2013. V. 61 (2). P. 298–314. https://doi.org/10.1287/opre.1120.1153
Xiaobing G., Wang Y., Li Sh., Niu B. Vehicle Routing Problem with Time Windows and Simultaneous Delivery and Pick-Up Service Based on MCPSO // Mathematical Problems in Engineering. 2012. V. 2. https://doi.org/10.1155/2012/104279
Fisher M.L. Optimal Solution of Vehicle Routing Problems Using Minimum K-trees // Operations Research. 1994. V. 42 (2). P. 626–642.
Kallehauge B., Larsen J., Madsen O., Solomon M. Vehicle Routing Problem with Time Windows // Column Generation. Springer US, 2006. https://doi.org/10.1007/0-387-25486-2_3
Macedo R., Alves C., Carvalho J., Clautiaux F., Hanafi S. Solving the Vehicle Routing Problem with Time Windows and Multiple Routes Exactly Using a Pseudo-polynomial Model // European J. Operational Research. 2011. V. 214 (3). P. 536–545. https://doi.org/10.1016/j.ejor.2011.04.037
Zhang W., Yang D., Zhang G., Gen M. Hybrid Multiobjective Evolutionary Algorithm with Fast Sampling Strategy-Based Global Search and Route Sequence Difference-Based Local Search for VRPTW // Expert Systems with Applications. 2020. V. 145. https://doi.org/10.1016/j.eswa.2019.113151
Mahmoud M., Hedar A.-R. Three Strategies Tabu Search for Vehicle Routing Problem with Time Windows // Computer Science and Information Technology. 2014. V. 2 (2). P. 108–119. https://doi.org/10.13189/csit.2014.020208
Solomon benchmark. URL: https://www.sintef.no/projectweb/top/vrptw/solomon-benchmark/.
Zhou Z., Ma X., Liang Z., Zhu Z. Multi-objective Multi-factorial Memetic Algorithm Based on Bone Route and Large Neighborhood Local Search for VRPTW // IEEE Congress on Evolutionary Computation (CEC). Glasgow, United Kingdom, 2020. https://doi.org/10.1109/CEC48606.2020.9185528.
Shu H., Zhou H., He Z., Hu X. Two-Stage Multi-objective Evolutionary Algorithm Based on Classified Population for Tri-objective VRPTW // International J. Unconventional Computing. 2021. V. 16 (2–3). P. 141–171.
Xu W., Wang X., Guo Q. Gathering Strength, Gathering Storms: Knowledge Transfer via Selection for VRPTW // Mathematics. 2022. V. 10 (16). https://doi.org/10.3390/math10162888
Fan H., Ren X., Zhang Y. A Chaotic Genetic Algorithm with Variable Neighborhood Search for Solving Time-Dependent Green VRPTW with Fuzzy Demand // Symmetry. 2022. V. 14 (10). https://doi.org/10.3390/sym14102115
Nasri M., Hafidi I., Metrane A. Multithreading Parallel Robust Approach for the VRPTW with Uncertain Service and Travel Times // Symmetry. 2020. V. 13 (1). https://doi.org/10.3390/sym13010036
Kummer A.F., Buriol L.S., de Araújo O.C.B. A Biased Random Key Genetic Algorithm Applied to the VRPTW with Skill Requirements and Synchronization Constraints // GECCO’20: Genetic and Evolutionary Computation Conf. Cancun, Mexico, 2020. https://doi.org/10.1145/3377930.3390209
Jungwirth A., Frey M., Kolisch R. The Vehicle Routing Problem with Time Windows, Flexible Service Locations and Time-Dependent Location Capacity, 2020. URL: https://www.semanticscholar.org/paper/The-vehicle-routing-problem-with-time-windows%2C-and-Jungwirth-Frey/22db87ca3cba4ea33561667c190f0443a93925bf.
Poullet J. Leveraging Machine Learning to Solve the Vehicle Routing Problem with Time Windows, 2020. URL: https://hdl.handle.net/1721.1/127285.
Figliozzi M.A. An Iterative Construction and Improvement Algorithm for the Vehicle Routing Problem with Soft Time Windows // Transp. Res. P. C. Emerg. Technol. 2010. V. 18 (5). https://doi.org/10.1016/j.trc.2009.08.005
Melnikov A.N., Lyubimov I.I., Manayev K.I. Improvement of the Vehicles Fleet Structure of a Specialized Motor Transport Enterprise // Proc. Eng. 2016. V. 150. P. 1200–1208. https://doi.org/10.1016/j.proeng.2016.07.236
Германчук М.С., Козлова М.Г., Лукьяненко В.А. Модели обобщенных задач коммивояжера в интеллектуализации поддержки принятия решений для геоинформационных систем // Географические и геоэкологические исследования на Украине и сопредельных территориях: сб. научных статей / Под общ. ред. Б.А. Вахрушева. Симферополь: ДИАЙПИ, 2013. Т. 1. С. 413–415.
Rakhmangulov A., Kolga A., Osintsev N. Mathematical Model of Optimal Empty Rail Car Distribution at Railway Transport Nodes // Transp. Probl. 2014. V. 9 (3). P. 19–32.
Uthayakumar R., Prlyan S. Pharmaceutical Supply Chain and Inventory Management Strategies: Optimization for a Pharmaceutical Company and a Hospital // Oper. Res. Heal Care. 2013. V. 2 (3). P. 52–64. https://doi.org/10.1016/j.orhc.2013.08.001
Azzi A., Sgarbossa F., Bonin M. Drug Inventory Management And Distribution: Outsourcing Logistics to Third-Party Providers // Strateg Outsourcing Int. J. 2013. V. 6 (1). P. 48–64. https://doi.org/10.1108/17538291311316063
French Ch., Smykay E.W., Bowersox D.J., Mossman F.H. Physical Distribution Management // Amer. J. Agric. Econ. 1961. V. 43 (3). P. 728–30.
Dorigo M., Gambardella L.M. Ant Colony System: A Cooperative Learning Approach to the Traveling Salesman Problem // IEEE Transactions on Neural Networks. 1997. V. 1 (1). P. 53–66. https://doi.org/10.1109/4235.585892
Dorigo M., Gambardella L.M. Ant Colonies for the Traveling Salesman Problem // BioSystems. 1997. V. 43. P. 73–81. https://doi.org/10.1016/S0303-2647(97)01708-5
Stützle T. Local Search Algorithms for Combinatorial Problems – Analysis, Improvements, and New Applications // Dissertation. Germany, 1998. URL: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.71.1869&rep=rep1&type=pdf
Kohl N., Desrosiers J., Madsen O.B.G., Solomon M.M., Soumis F. 2-Path Cuts for the Vehicle Routing Problem with Time Windows // Transportation Science. 1999. V. 33. P. 101–116. https://doi.org/10.1287/trsc.33.1.101
Taillard É.D. FANT: Fast Ant System // Technical Report. Istituto Dalle Molle Di Studi Sull Intelligenza Artificiale. Lugano.1998.
Badeau P., Gendreau M., Guertin F., Potvin J.-Y., Taillard É.D. A Parallel Tabu Search Heuristic for the Vehicle Routing Problem with Time Windows // Transp. Res. P. C. Emerg. Technol. 1997. V. 5 (2). P. 109–122. https://doi.org/10.1016/S0968-090X(97)00005-3
Taillard É.D., Badeau P., Gendreau M., Guertin F., Potvin J.-Y. A Tabu Search Heuristic for the Vehicle Routing Problem with Soft Time Windows // Transportation Science. 1997. V. 31. P. 170–186.
Kilby P., Prosser P., Shaw P. Guided Local Search for the Vehicle Routing Problem with Time Windows // Meta-Heuristics. Springer, Boston, MA, 1999. https://doi.org/10.1007/978-1-4615-5775-3_32
Shaw P. Using Constraint Programming and Local Search Methods to Solve Vehicle Routing Problems // Fourth Intern. Conf. on Principles and Practice of Constraint Programming, Springer-Verlag, 1998. P. 417–431.
Dorigo M., Maniezzo V., Colorni A. Positive Feedback as a Search Strategy // Technical Report 91-016, Dipartimento di Elettronica, Politecnico di Milano, Italy, 1991. URL: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.52.6342&rep=rep1&type=pdf.
Dorigo M., Maniezzo V., Colorni A. The Ant System: Optimization by a Colony of Cooperating Agents // IEEE Transactions on Systems, Man, and Cybernetics. 1996. V. 26 (1). P. 29–41. https://doi.org/10.1109/3477.484436
Flood M.M. The Traveling Salesman Problem // Operations Research. 1956. V. 4. P. 61–75.
Germanchuk M.S., Lukianenko V.A., Lemtyuzhnikova D.V. Metaheuristic Algorithms for Multiagent Routing Problems // Automation and Remote Control. 2021. V. 82 (10). P. 1787–1801. .https://doi.org/10.1134/S0005117921100155
Scipy. URL: https://scipy.org/.
Concorde TSP Solver. URL: https://www.math.uwaterloo.ca/tsp/concorde.html.
PyConcorde. URL: https://github.com/jvkersch/pyconcorde.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления