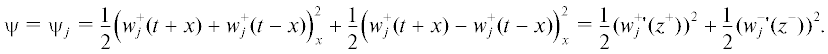Известия РАН. Теория и системы управления, 2023, № 6, стр. 93-109
ОПТИМИЗАЦИЯ ПРОДОЛЬНЫХ ДВИЖЕНИЙ УПРУГОГО СТЕРЖНЯ С ПОМОЩЬЮ ПЕРИОДИЧЕСКИ РАСПРЕДЕЛЕННЫХ ПЬЕЗОЭЛЕКТРИЧЕСКИХ СИЛ
А. А. Гавриков a, Г. В. Костин a, *
a ИПМех РАН
Москва, Россия
* E-mail: kostin@ipmnet.ru
Поступила в редакцию 30.03.2023
После доработки 25.04.2023
Принята к публикации 05.06.2023
- EDN: OHEOEA
- DOI: 10.31857/S0002338823050062
Аннотация
Изучаются продольные колебания упругого стержня, управляемого посредством распределенной силы, которая приложена к отдельным участкам стержня. Полагается, что сила изменяется в пространстве кусочно-постоянным образом. Подобная механическая система может быть реализована с помощью пьезоактюаторов, прикрепленных вдоль стержня. Динамика системы определяется из решения вариационной задачи в соответствии с методом интегродифференциальных соотношений. Вариационная задача разрешается аналитически. Для этого на пространственно-временной сетке вводятся бегущие волны Даламберовского типа, задающие непрерывные перемещения и динамический потенциал. Последний связывает плотность импульса и напряжения. Ставится задача управления при условии взвешенной минимизации механической энергии колебаний, запасаемой стержнем в конечный момент времени, и средней потенциальной энергии, порождаемой управляющими воздействиями. Экстремальное движение и соответствующий закон управления находятся явным образом посредством решения уравнений Эйлера–Лагранжа. В качестве примера исследуются возможности управления для определенных конфигураций пьезоэлектрических элементов.
Введение. Задачи управления системами с распределенными параметрами возникают, как правило, в приложениях, где описания механической системы с помощью одной независимой переменной (например, времени) недостаточно. Зачастую это приводит к необходимости управлять уравнениями в частных производных (УЧП). В этом случае функции управления могут входить как в краевые условия, так и в сами уравнения [1, 2]. Для колебательных систем появление управления в краевых условиях означает управление силой, моментом или иной величиной, заданной на части границы (например, на краю мембраны или конце стержня). Такой тип воздействия представляется удобным для инженерных приложений, но поиск оптимального управления в этом случае затруднен, в частности, вследствие естественных ограничений на скорость прохождения управляющего сигнала [3]. Если управление входит непосредственно в УЧП, то в идеале возможно управлять каждой модой колебаний в отдельности [2, 4], что облегчает построение оптимального решения [5]. Однако такое распределенное управление зачастую затруднительно реализовать непосредственно на практике (например, из-за необходимости прилагать заданную силу в каждой точке мембраны/стержня). Как следствие, может потребоваться пространственная дискретизация управляющего воздействия, так что сила действует только на часть системы или сила постоянна на части пространственной области.
В работе рассматривается механическая система, в которой управляющие воздействия дискретны и прилагаются только к определенным частям объекта. В качестве модельной задачи изучаются продольные колебания стержня, по длине которого периодически расположены пьезоэлектрические актюаторы. В промежутках между ними управление не прилагается, а создаваемая сила считается постоянной вдоль каждого актюатора, меняясь лишь во времени и от актюатора к актюатору.
Как правило, такие системы описываются УЧП, в которых возникают обобщенные функции в правых частях уравнений вследствие скачков сил в пространстве при переходе от актюатора к участку, свободному от нагрузки [6]. Таким образом, решение может быть построено только лишь в терминах обобщенных функций. В данной работе авторы применяют метод интегродифференциальных соотношений (МИДС) [7], который позволяет поставить вариационную задачу динамики и найти аналитически решение оптимизационной задачи в виде непрерывных функций для непрерывных начальных условий. Под решением понимается пара функций: перемещения точек стержня и так называемый динамический потенциал, связанный дифференциальными соотношениями с импульсом и напряжениями. Задача динамики разрешается при помощи бегущих волн Даламберовского типа, определенных на пространственно-временной сетке, образованной характеристиками, а задача оптимизации (взвешенная минимизация терминальной механической энергии и энергетических затрат на управление) – используя уравнения Эйлера–Лагранжа. И в том и в другом случае неизвестные переменные находятся явным образом путем разрешения линейных соотношений, возникающих между бегущими волнами и компонентами вектора управления в силу условий непрерывности на сетке.
Ранее авторы использовали этот подход для построения оптимального управления продольными колебаниями при наличии терминальных условий для стрежня, управляемого только с границы при условии минимизации как средней механической энергии [8], так и управления [9], а также когда между распределенными управляющими элементами отсутствуют промежутки. Были рассмотрены конфигурации, при которых граничное управление отсутствует [10], общий случай использования как граничного, так и распределенного управления [11], а также при условии дополнительно минимизации управления [12]. Частный случай горизонта управления, кратного безразмерной длине управляющего элемента, изучен в [13].
В работах [10, 14] затронут вопрос управляемости отдельных мод колебаний и разбиения мод на группы, каждая из которых управляется определенной комбинацией входов. Принципиальное отличие данной статьи – в наличии промежутков между управляющими элементами. Для определенных конфигураций это всегда приводит к потере управляемости отдельными группами мод, что является частным случаем проблемы неуправлямости волнового уравнения при воздействии только на часть длины [15]. Кроме того, авторы показывают на примере, что от геометрических соотношений между длинами элементов и промежутков зависит и эффективность управления как в смысле возможностей минимизации механической энергии, так и в смысле требуемых затрат энергии на управление. Выбор оптимального расположения актюаторов – крайне актуальная задача для инженерных приложений [16–18], когда относительные размеры актюаторов и управляемой системы фиксированы в силу технических ограничений. Используемый здесь подход может в дальнейшем помочь в постановке и решении подобных оптимизационных задач. Приводится пример исследования возможностей управления для различных конфигураций при фиксированном относительно длины стержня минимальном размере актюатора.
1. Постановка начально-краевой задачи. Рассматриваются продольные движения тонкого упругого стержня, схематически изображенного на рис. 1. Его длина вдоль оси x равна $2L$, начало координат расположено в геометрическом центре стержня, продольная жесткость которого $\kappa > 0$ и линейная плотность $\rho > 0$ не меняются вдоль оси x.
Помимо упругой силы в поперечном сечении стержня действует изменяющаяся во времени $t \geqslant 0$ управляющая сила $f(t,x)$, которая кусочно-постоянно распределена по длине. В рамках упрощенной модели такая сила может создаваться, например, группами пьезоэлектрических актюаторов (управляющими элементами), которые создают сжимающие или растягивающие напряжения на отдельных участках стержня, выделенных на рис. 1 серым тоном для случая трех элементов.
В этой работе мы ограничимся только периодическим расположением управляющих элементов с периодом ${{\lambda }_{p}}$, $L = K{{\lambda }_{p}}{\text{/}}2$, $K \in \mathbb{N}$. Длина единственного на периоде активного элемента равна ${{\lambda }_{c}} \leqslant {{\lambda }_{p}}$. Крайний левый элемент стержня отстоит на расстоянии ${{\lambda }_{s}}$ от граничной точки с координатой $x = - L$. Внутри каждого интервала управления ${{\mathfrak{U}}_{k}} = (x_{k}^{ - },x_{k}^{ + })$ с номером $k \in \mathfrak{K}$ сила f распределена равномерно. Здесь для удобства записи введено множество индексов $\mathfrak{K} = \{ 1 - K,3 - K, \ldots ,K - 1\} $ с шагом 2. Вне управляющих элементов сила f равна нулю. Координаты концов интервала ${{\mathfrak{U}}_{k}}$ определены как
Вне этих управляющих элементов сила f равна нулю. Таким образом распределенная сила f задается в форме
(1.1)
$\begin{array}{*{20}{c}} {f(t,x) = \left\{ \begin{gathered} {{f}_{k}}(t),\quad x \in {{\mathfrak{U}}_{k}},\quad k \in \mathfrak{K}, \hfill \\ 0,\quad x \in \mathfrak{X}{{\backslash }}\bigcup\limits_{k \in \mathfrak{K}} {{\mathfrak{U}}_{k}}. \hfill \\ \end{gathered} \right.} \end{array}$В качестве области определения $\mathfrak{D}$ для переменных, задающих механическое состояние стержня, введем декартово произведение временного ($\mathfrak{T}$) и пространственного ($\mathfrak{X}$) интервалов:
Закон изменения импульса (второй закон Ньютона) связывает две искомые функции p и s:
Здесь нижние индексы $t$ и $x$ обозначают соответственно частные производные по времени и пространству. В свою очередь импульс и сила связаны с первыми производными функции перемещения, согласно локальным законам состояния:
(1.3)
$p(t,x) = \rho {{v}_{t}}(t,x),\quad s(t,x) = \kappa {{v}_{x}}(t,x) + f(t,x),\quad (t,x) \in \mathfrak{D}.$Если функция f дифференцируема, классическое уравнение движения [19] получается после подстановки (1.3) в (1.2):
(1.4)
$\rho (x){{v}_{{tt}}}(t,x) - {{(\kappa (x){{v}_{x}}(t,x))}_{x}} = {{f}_{x}},\quad (t,x) \in \mathfrak{D}.$В терминах введенных переменных на положение и импульс точек стержня накладываются начальные условия в момент времени t = 0:
где ${{v}^{0}}$ и p0 – известные достаточно гладкие распределения [20]. Концы стержня $x = \pm L$ свободны от нагрузок:При этом необходимо учитывать, что, хотя функция f кусочно-непрерывна, стержень должен оставаться сплошным телом, а сила в сечении, согласно третьему закону Ньютона, не может иметь скачков. Это накладывает дополнительные условия непрерывности на функции $v$ и s в точках $x_{k}^{ \pm }$.
Согласно МИДС [7], для перехода к обобщенной формулировке начально-краевой задачи (1.2)–(1.6) введем на области $\mathfrak{D}$ новую функцию (“динамический” потенциал) $r:\mathfrak{D} \to \mathbb{R}$ таким образом, что
Непосредственной подстановкой (1.7) в (1.2) проверяется, что второй закон Ньютона при такой замене выполняется автоматически.
Чтобы устранить из рассмотрения переменные p и s, необходимо переписать уравнения состояния (1.3) как
(1.8)
$\left\{ {\begin{array}{*{20}{l}} {{{r}_{t}}(t,x) - \kappa (x){{v}_{x}}(t,x) = 0,\quad } \\ {{{r}_{x}}(t,x) - \rho (x){{v}_{t}}(t,x) = f(t,x),} \end{array}} \right.\quad (t,x) \in \mathfrak{D}.$Через кинематическую и динамическую переменные $v$, $r$ выражаются как начальное состояние (1.5), так и краевые условия (1.6), а именно:
(1.9)
$\begin{array}{*{20}{c}} {v(0,x) = {{v}^{0}}(x),\quad r(0,x) = {{r}^{0}}(x) = \int\limits_{ - L}^x {{p}^{0}}(\chi )d\chi + {{c}^{0}},\quad x \in \bar {\mathfrak{X}};} \\ {r(t,L) = {{r}^{0}}(L),\quad r(t, - L) = {{r}^{0}}( - L),\quad t \in \bar {\mathfrak{T}}.} \end{array}$Отметим особенность такого представления механического состояния системы: динамическая переменная $r$ задана с точностью до произвольной константы c0, значение которой не влияет на движение упругого тела. Ненулевые правые части ${{r}^{0}}( \pm L)$ появляются в краевых условиях, заданных в (1.9), чтобы обеспечить необходимую, как будет показано ниже, непрерывность решения. Этим достигается совместность начальных и краевых условий при t = 0 и $x = \pm L$.
2. Обобщенная формулировка задачи. Локальное представление законов состояния (1.8) требует определенной гладкости начального распределения (1.9) и прикладываемой нагрузки f [20]. Для рассмотрения более широкого класса решений с учетом разрывного характера функции f два дифференциальных уравнения (1.8) можно объединить, согласно МИДС [7], в одно интегральное соотношение. Нахождение решения в этом случае сводится к условной минимизации функционала, квадратичного по кинематической и динамической переменным $v$, $r$.
Сформулируем соответствующую обобщенную начально-краевую задачу.
Даны квадратично-интегрируемые со своими первыми производными начальные распределения ${{v}_{0}},{{r}_{0}} \in {{H}^{1}}(\mathfrak{X})$ и квадратично-интегрируемая сила $f \in {{L}^{2}}(\mathfrak{D})$. Найти кинематическую и динамическую функции состояния $v{\kern 1pt} *(t,x)$ и $r{\kern 1pt} *(t,x)$ в пространстве ${{H}^{1}}(\mathfrak{D})$, которые минимизируют функционал:
(2.1)
$\begin{array}{*{20}{c}} {\Phi [v{\kern 1pt} *,r{\kern 1pt} *] = \mathop {\min }\limits_{vr \in {{H}^{1}}(\mathfrak{D})} \Phi [v,r] = 0,\quad \Phi = \int\limits_\mathfrak{D} \varphi {\kern 1pt} d\mathfrak{D} \geqslant 0,\quad d\mathfrak{D} = dtdx,} \\ {\varphi \triangleq \frac{1}{4}({{g}^{2}} + {{h}^{2}}),\quad g \triangleq \sqrt \rho {{v}_{t}} - \frac{{{{r}_{x}}}}{{\sqrt \rho }},\quad h \triangleq \sqrt \kappa {{v}_{x}} - \frac{{{{r}_{t}} - f}}{{\sqrt \kappa }},} \end{array}$В (2.1) интегральное соотношение $\Phi = 0$, реализуемое на точном решении, заменяет локальные уравнения состояния (1.8), при этом условная минимизация $\Phi $ проходит при строгом выполнении равенств (1.9). Вводятся специальным образом масштабированные функции состояния $g$, $h$, квадратичная форма которых $\varphi $ имеет размерность линейной плотности энергии. В свою очередь функционал состояния $\Phi $ имеет размерность действия. Положительное значение $\Phi [v,r] > 0$ оценивает отклонение приближения $(v,r)$ от точного решения $({{v}_{*}},{{r}_{*}})$, на котором достигается абсолютный минимум функционала $\Phi = 0$. Требование интегрируемости в квадрате как функций состояния, так и их первых производных в вариационной задаче (1.9), (2.1) вытекает из того, что в $\Phi $ входят квадраты производных по $t$ и $x$ от неизвестных $v$ и $r$.
3. Задача оптимального управления. Введем в рассмотрение вектор-функцию ${\mathbf{f}}:\mathfrak{T} \to {{\mathbb{R}}^{K}}$, ${\mathbf{f}} = {{\left( {{{f}_{k}}} \right)}_{{k \in \mathfrak{K}}}}$, компоненты которой – это определенные в (1.1) силы ${{f}_{k}}(t)$, создаваемые $k$-м управляющим элементом. Относительно f решается следующая задача управления.
Пусть, согласно (2.1), с учетом начальных и краевых условий (1.9) функции $v,r \in {{H}^{1}}(\mathfrak{D})$ минимизируют функционал состояния $\Phi $ для произвольного управления ${\mathbf{f}} \in {{L}^{2}}(\mathfrak{T};{{\mathbb{R}}^{K}})$, определяющего силы f в соответствии с (1.1). Найти такую допустимую вектор-функцию ${\mathbf{f}}{\kern 1pt} *(t)$, которая на фиксированном интервале времени $\mathfrak{T}$ минимизирует целевой функционал:
(3.1)
$\begin{array}{*{20}{c}} {\Theta [{\mathbf{f}}{\kern 1pt} *] = \mathop {\min }\limits_{{\mathbf{f}} \in {{L}^{2}}(\mathfrak{T};{{\mathbb{R}}^{K}})} \Theta [{\mathbf{f}}],\quad \Theta = \Upsilon + {{{10}}^{\gamma }}\Psi ,} \\ {\Upsilon = \frac{{{{\lambda }_{c}}}}{{2\kappa T}}\int\limits_\mathfrak{T} {{{\mathbf{f}}}^{2}}{\kern 1pt} dt,\quad \Psi = \int\limits_\mathfrak{X} \psi {{{\text{|}}}_{{t = T}}}{\kern 1pt} dx,\quad \psi \triangleq \frac{{\kappa {v}_{x}^{2}}}{2} + \frac{{r_{x}^{2}}}{{2\rho }}.} \end{array}$Задача (3.1) – это задача поиска экстремума при условии, что для произвольной вектор-функции $f(t)$ переменные $v$ и $r$ доставляют функционалу $\Phi $ из (2.1) минимальные нулевые значения, строго выполняя ограничения-равенства, а именно условия (1.9). Здесь $\Upsilon $ – средняя потенциальная энергия, порождаемая силой $f(t,x)$, $\Psi $ – механическая энергия стержня в конце процесса, $\psi (t,x)$ – линейная плотность энергии, $\gamma $ – безразмерный весовой коэффициент. Решение прямой задачи динамики (1.9), (2.1) – пара функций $(v,r)$. В представлении плотности энергии $\psi $ входят обе переменные. Первое слагаемое в $\psi $ определяет потенциальную энергию упругих деформаций стержня в перемещениях, второе – кинетическую энергию через динамический потенциал.
Для упрощения описания системы перейдем без потери общности к безразмерным переменным (далее индекс $*$ опускается):
(3.2)
$\begin{array}{*{20}{c}} {v = Lv{\kern 1pt} *,\quad r = \kappa {{\tau }_{*}}r{\kern 1pt} *,\quad x = Lx{\kern 1pt} *,\quad t = {{\tau }_{0}}t{\kern 1pt} *,\quad \tau _{*}^{2} = \frac{{{{L}^{2}}\rho }}{\kappa }.} \end{array}$Такая замена эквивалентна выбору динамической системы с параметрами $L = \rho = \kappa = 1$.
4. Решение начально-краевой задачи. Далее решение $(v,r)$ задачи (1.9), (2.1) ищется в виде бегущих волн в представлении Даламбера. В общем случае произвольного набора параметров актюаторов поиск аналитического решения затруднен. В [10] рассмотрен частный случай расположения актюаторов без зазоров, т.е. когда ${{\lambda }_{c}} = {{\lambda }_{p}}$ и, следовательно, ${{\lambda }_{s}} = 0$. Для такой конфигурации можно привести систему за безразмерное время $T \geqslant 4{\text{/}}K$ в периодическое терминальное состояние с периодом $\lambda = 2{\text{/}}K$. В терминах собственных функций неуправляемыми являются все моды с волновыми числами, кратными K/2.
Ниже описывается алгоритм решения задачи для случая, в котором параметры длин и время управления кратны безразмерной длине $\lambda $:
(4.1)
$\begin{array}{*{20}{c}} {\lambda = 2{\text{/}}N,\quad {{\lambda }_{p}} = {{N}_{p}}\lambda ,\quad {{\lambda }_{c}} = {{N}_{c}}\lambda ,\quad {{\lambda }_{s}} = {{N}_{s}}\lambda ,\quad T = M\lambda ,} \\ {N = K{{N}_{p}},\quad \{ K,M,{{N}_{c}},{{N}_{p}}\} \subset \mathbb{N},\quad {{N}_{s}} \in {{\mathbb{Z}}_{ + }},\quad {{N}_{c}} + {{N}_{s}} \leqslant {{N}_{p}}.} \end{array}$Расположение элементов управления считается периодическим при выполнении соотношения (4.1). Иначе говоря, отсчитывая от левого края стержня при $x = - 1$, первыми расположены ${{N}_{s}} \geqslant 0$ элементарных интервалов без управления каждый длины $\lambda $, затем ${{N}_{c}}$ интервалов этой же длины с управлением. Замыкать период могут ${{N}_{p}} - {{N}_{c}} - {{N}_{s}} \geqslant 0$ интервалов опять без управляющего воздействия. Отсчитывая с правого конца текущего периода, структура повторяется.
В этом соразмерном случае удается сформировать конечную сетку из характеристик на пространственно-временной области $\mathfrak{D}$, на которой можно, как будет показано ниже, точно разрешить начально-краевую задачу (1.9), (2.1). Кратность числу $\lambda $ времени управления T не обязательна для построения конечной сетки и получения аналитического решения [11], но это приводит к увеличению более чем вдвое числа элементов сетки и усложнению алгоритма решения. В этой работе для упрощения изложения ограничимся дискретным набором интервалов времени, определенных в (4.1).
Для построения сетки на области $\mathfrak{D}$ разобьем временной интервал $\mathfrak{T}$ на M подынтервалов ${{\mathfrak{T}}_{m}}$, а пространственный интервал $\mathfrak{X}$ – на N подынтервалов ${{\mathfrak{X}}_{j}}$ так, что
(4.2)
$\begin{array}{*{20}{c}} {{{\mathfrak{T}}_{m}} = ({{t}_{m}},{{t}_{{m + 1}}}),\quad {{t}_{i}} = i\lambda ,\quad m \in \mathfrak{M} = \{ 0, \ldots ,M - 1\} ,} \\ {{{\mathfrak{X}}_{j}} = ({{x}_{{j - 1}}},{{x}_{{j + 1}}}),\quad j \in \mathfrak{J} = \{ 1 - N,3 - N \ldots ,N - 1\} ,} \\ {{{x}_{n}} = n\lambda {\text{/}}2,\quad n \in \mathfrak{N}{\kern 1pt} *,\quad \mathfrak{N}{\kern 1pt} * = \{ - N,2 - N, \ldots ,N\} .} \end{array}$Каждому интервалу ${{\mathfrak{X}}_{j}}$ соответствует открытая подобласть ${{\mathfrak{D}}_{j}} = \mathfrak{T} \times {{\mathfrak{X}}_{j}}$ области $\mathfrak{D}$ и три одномерные функции:
(4.3)
$\begin{array}{*{20}{c}} {w_{j}^{ + }:({{x}_{{j - 1}}},T + {{x}_{{j + 1}}}) \to \mathbb{R},\quad w_{j}^{ - }:( - {{x}_{{j + 1}}},T - {{x}_{{j - 1}}}) \to \mathbb{R},} \\ {{{y}_{j}}:(0,T) \to \mathbb{R},\quad {{y}_{j}}(t) = {{\lambda }^{{ - 1}}}\int\limits_{{{\mathfrak{X}}_{j}}} \int\limits_0^t f(\tau ,x){\kern 1pt} d\tau {\kern 1pt} dx.} \end{array}$На области ${{\mathfrak{D}}_{j}}$ искомые функции $v$ и $r$ представляются в виде
(4.4)
$\left\{ {\begin{array}{*{20}{l}} {v(t,x) = w_{j}^{ + }(t + x) + w_{j}^{ - }(t - x),} \\ {r(t,x) = w_{j}^{ + }(t + x) - w_{j}^{ - }(t - x) + {{y}_{j}}(t),} \end{array}} \right.\quad (t,x) \in {{\mathfrak{D}}_{j}},\quad j \in \mathfrak{J}.$Непосредственной подстановкой показывается, что функционал состояния $\Phi $ равен нулю при выполнении соотношений (4.4), так как ${{r}_{x}} = {{v}_{t}},$ ${{r}_{t}} = {{v}_{x}} + f.$
Чтобы увидеть, как одномерные функции определяют решение (4.4) на двумерной области $\mathfrak{D}$, обратимся к рис. 2. Для компактности записи вводятся новые координаты $({{z}^{ + }},{{z}^{ - }})$, оси которых связанны с двумя характеристиками решения (сплошные наклонные линии). Два семейства характеристик – это отрезки в области $\mathfrak{D}$, на которых не меняются значения функций $w_{j}^{ \pm }(t \pm x)$. Новые координаты связаны с $(t,x)$ биективными линейными преобразованиями:
(4.5)
${{z}^{ \pm }} = t \pm x,\quad t = \frac{{{{z}^{ + }} + {{z}^{ - }}}}{2},\quad x = \frac{{{{z}^{ + }} - {{z}^{ - }}}}{2}.$Рис. 2.
Сетка на пространственно-временной области $\mathfrak{D}$ для $N = 6$, $K = 2$, ${{N}_{c}} = {{N}_{s}} = 1$, M = 6
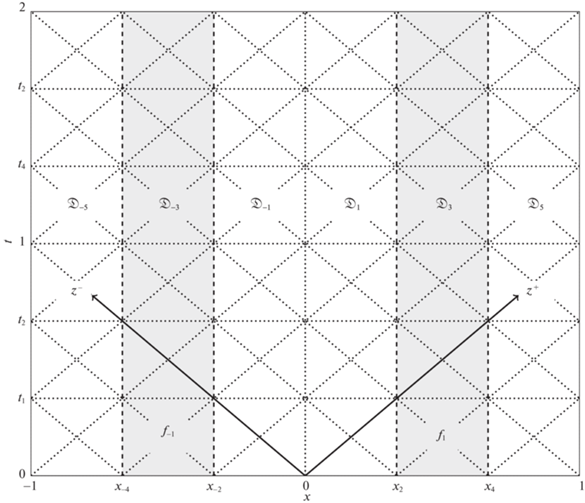
Показанные пунктиром на рис. 2 наклонные ребра сетки – это характеристики, определяемые в новых координатах как
Пространственные и временные ребра сетки проще задать в старых координатах в виде
Для выполнения условий непрерывности на этих ребрах понадобится ввести на каждой подобласти ${{\mathfrak{D}}_{j}}$ следующие функции:
(4.6)
$\begin{gathered} w_{{j,m}}^{ \pm }:\mathfrak{Z} \to \mathbb{R}:\quad w_{{j,m}}^{ \pm }(z) = w_{j}^{ \pm }(z + z_{{j,m}}^{ \pm }),\quad z_{{j,m}}^{ \pm } = z_{j}^{ \pm } + m\lambda , \\ z_{j}^{ \pm } = \frac{{ \pm j \mp 1}}{2}\lambda ,\quad j \in \mathfrak{J},\quad m \in \mathfrak{M}{\kern 1pt} *,\quad \mathfrak{Z} = (0,\lambda ); \\ {{y}_{{j,m}}}:\mathfrak{Z} \to \mathbb{R}:\quad {{y}_{{j,m}}}(z) = {{y}_{j}}(z + {{t}_{m}}),\quad j \in \mathfrak{J},\quad m \in \mathfrak{M}. \\ \end{gathered} $Согласно (4.4), линейная комбинация функций $w_{{i,m}}^{ + }$, $w_{{j,m}}^{ - }$ и ${{y}_{{j,m}}}$ с допустимой комбинацией индексов $i$, $j$, $m$, $n$ однозначно определяет переменные состояния ${v}$, $r$ на соответственном треугольном элементе сетки.
Поскольку $v,r \in {{H}^{1}}(\mathfrak{D})$, из линейной зависимости следуют аналогичные свойства и для одномерных функций $w_{{j,m}}^{ \pm } \in {{H}^{1}}(\mathfrak{Z})$, ${{y}_{{j,m}}} \in {{H}^{1}}(\mathfrak{Z})$. В силу леммы Соболева [21] эти функции должны быть непрерывны и непрерывно продолжаемы на замыкание своей области определения: $w_{{j,m}}^{ \pm } \in {{C}^{0}}(\bar {\mathfrak{Z}})$, ${{y}_{{j,m}}} \in {{C}^{0}}(\bar {\mathfrak{Z}})$.
Для построения непрерывного решения начально-краевой задачи на замыкании области $\bar {\mathfrak{D}}$ необходимо выполнить начальные, краевые и межэлементные условия на сегментах $\mathfrak{S}_{0}^{t}$, $\mathfrak{S}_{n}^{x}$, $n \in \mathfrak{N}{\text{*}}$. Учитывая (1.9), (4.4), (4.6) и вытекающие из (4.3) условия по построению ${{y}_{{j,0}}}(0) = 0$, начальные ограничения на $\mathfrak{S}_{0}^{t}$ для каждой подобласти ${{\mathfrak{D}}_{j}}$ представляются в виде
(4.7)
$\left\{ {\begin{array}{*{20}{l}} {w_{{j,0}}^{ + }(z) + w_{{j,0}}^{ - }(\lambda - z) = {{v}^{0}}(z + z_{j}^{ + }),} \\ {w_{{j,0}}^{ + }(z) - w_{{j,0}}^{ - }(\lambda - z) = {{r}^{0}}(z + z_{j}^{ + }),} \end{array}} \right.\quad j \in \mathfrak{J}.$Краевые условия из (1.9) для каждого ребра сетки, лежащего на граничных сегментах $\mathfrak{S}_{{ \pm N}}^{x}$, переписываются в форме:
(4.8)
$\left\{ {\begin{array}{*{20}{l}} {w_{{N - 1,m + 1}}^{ + }(z) - w_{{N - 1,m}}^{ - }(z) + {{y}_{{N - 1,m}}}(z) = {{r}^{0}}(1),} \\ {w_{{1 - N,m}}^{ + }(z) - w_{{1 - N,m + 1}}^{ - }(z) + {{y}_{{1 - N,m}}}(z) = {{r}^{0}}( - 1),} \end{array}} \right.\quad m \in \mathfrak{M}.$К этим ограничениям необходимо добавить еще и межэлементные условия непрерывности функций $v$ и $r$ на внутренних сегментах $\mathfrak{S}_{n}^{x}$. Эти условия задаются следующим образом:
(4.9)
$\begin{array}{*{20}{c}} {\left\{ \begin{gathered} w_{{n + 1,m + 1}}^{ + }(z) + w_{{n + 1,m}}^{ - }(z) = w_{{n - 1,m}}^{ + }(z) + w_{{n - 1,m + 1}}^{ - }(z), \hfill \\ w_{{n + 1,m + 1}}^{ + }(z) - w_{{n + 1,m}}^{ - }(z) + {{y}_{{n + 1,m}}}(z) = w_{{n - 1,m}}^{ + }(z) - w_{{n - 1,m + 1}}^{ - }(z) + {{y}_{{n - 1,m}}}(z), \hfill \\ \end{gathered} \right.} \\ {m \in \mathfrak{M},\quad n \in \mathfrak{N} = \{ 2 - N,4 - N \ldots ,N - 2\} .} \end{array}$Число уравнений ${{N}_{e}} = 2N(M + 1)$ в линейной алгебраической системе (4.7)–(4.9) равно числу неизвестных функций $w_{{j,m}}^{ \pm }$, $j \in \mathfrak{J}$, $m \in \mathfrak{M}{\kern 1pt} *$. Аргумент z пробегает значения от 0 до $\lambda $. Чтобы подтвердить разрешимость этой системы относительно функций бегущих волн, можно предложить следующий алгоритм.
Вначале попарно разрешаются начальные условия (4.7): каждая пара относительно двух переменных $w_{{j,0}}^{ + }$ и $w_{{j,0}}^{ - }$ для $j \in \mathfrak{J}$. После соответствующей замены аргумента $z{\kern 1pt} ' = \lambda - z$ и констант $z_{j}^{ - } = z_{j}^{ + } + \lambda $ полученные значения этих переменных выражаются явно через начальные распределения:
(4.10)
$\left\{ {\begin{array}{*{20}{l}} {w_{{j,0}}^{ + }(z) = \frac{1}{2}{{v}^{0}}(z_{j}^{ + } + z) + \frac{1}{2}{{r}^{0}}(z_{j}^{ + } + z),} \\ {w_{{j,0}}^{ - }(z{\kern 1pt} ') = \frac{1}{2}{{v}^{0}}(z_{j}^{ - } - z{\kern 1pt} ') - \frac{1}{2}{{r}^{0}}(z_{j}^{ - } - z{\kern 1pt} '),} \end{array}} \right.\quad j \in \mathfrak{J}.$На втором этапе, увеличивая индекс m от 0 до $M - 1$, последовательно удовлетворяются краевые и межэлементные условия (4.8), (4.9). При этом два краевых уравнения из (4.8) для текущего значения m разрешаются относительно переменных $w_{{N - 1,m + 1}}^{ + }$ и $w_{{1 - N,m + 1}}^{ - }$. Для этого же m попарно разрешаются $2(N - 1)$ уравнений из (4.9) относительно функций бегущих волн $w_{{n + 1,m + 1}}^{ + }$ и $w_{{n - 1,m + 1}}^{ - }$. Входящие в эту подсистему функции со вторым индексом $m$ ($w_{{j,m}}^{ \pm }$, $j \in \mathfrak{J}$) уже выражены на предыдущих шагах алгоритма относительно начальных функций ${{v}^{0}}$, ${{r}^{0}}$ и неизвестных ${{y}_{{j,i}}}$, $i = 0, \ldots ,m - 1$, $j \in \mathfrak{J}$.
5. Сведение задачи оптимального управления к классической вариационной. Решение линейной системы уравнений (4.7)–(4.9) относительно переменных $w_{{j,m}}^{ \pm }$, где $j \in \mathfrak{J}$ и $m \in \mathfrak{M}{\kern 1pt} *$, зависит от начальных распределений ${{v}^{0}}(x)$, ${{r}^{0}}(x)$, $x \in \bar {\mathfrak{X}}$ и функций ${{y}_{{j,m}}}(z)$, $z \in \bar {\mathfrak{Z}}$ с индексами $j \in \mathfrak{J}$ и $m \in \mathfrak{M}$. В свою очередь, согласно (1.1), (4.3), (4.6), в зависимости от расположения интервала ${{\mathfrak{X}}_{j}}$ на оси $x$ функция ${{y}_{{j,m}}}$ либо равна нулю, если ${{\mathfrak{X}}_{j}} \subset \mathfrak{X}{{\backslash }}\bigcup\nolimits_{k \in \mathfrak{K}} {{\mathfrak{U}}_{k}}$, либо зависит от одной из управляющих сил ${{f}_{k}}$, если ${{\mathfrak{X}}_{j}} \subset {{\mathfrak{U}}_{k}}$. Чтобы явно выразить эту зависимость, введем новые независимые функции управления:
(5.1)
$\begin{array}{*{20}{c}} {{{u}_{{k,m}}}:\bar {\mathfrak{Z}} \to \mathbb{R}:\quad {{u}_{{k,m}}}(z) = \int\limits_{{{t}_{m}}}^{{{t}_{m}} + z} {{f}_{k}}(\tau ){\kern 1pt} d\tau ,\quad k \in \mathfrak{K},\quad m \in \mathfrak{M}.} \end{array}$В этом представлении ${{y}_{{j,m}}}(z) = {{u}_{{k,m}}}(z)$ при условии, что ${{\mathfrak{X}}_{j}} \subset {{\mathfrak{U}}_{k}}$. Введем в рассмотрения вектор-функцию управления ${\mathbf{u}}:\bar {\mathfrak{Z}} \to {{\mathbb{R}}^{{KM}}}$ с компонентами:
(5.2)
$\begin{array}{*{20}{c}} {{\mathbf{u}} = ({{u}_{i}})_{{i = 1}}^{{KM}},\quad {{u}_{j}} = {{u}_{{k,m}}},} \\ {j = M(K - 1 - k){\text{/}}2 + m + 1,\quad k \in \mathfrak{K},\quad m \in \mathfrak{M}.} \end{array}$Для того чтобы кинематическая и динамическая функции $v$, $r$ были непрерывны, на сегментах $\mathfrak{S}_{m}^{t}$, $m \in \mathfrak{M}$, должны быть согласованы узловые значения функций управления:
(5.3)
$\begin{array}{*{20}{c}} {{{u}_{{k,m}}}(\lambda ) = {{u}_{{k,m + 1}}}(0),\quad m \in \mathfrak{M},\quad {{u}_{{k,0}}}(0) = 0,\quad k \in \mathfrak{K}.} \end{array}$Удобнее представить эти соотношения в векторной форме:
(5.4)
$\begin{array}{*{20}{c}} {{\mathbf{u}}(0) + {\mathbf{Bu}}(\lambda ) = 0,\quad {\mathbf{B}} \in {{\mathbb{R}}^{{(KM) \times (KM)}}}.} \end{array}$Рассмотрим структуру целевого функционала $\Theta $ из (3.1) с учетом представления Даламбера и введенных функций управления. В силу своей аддитивности функционал $\Upsilon $ переписывается в терминах вектор-функции управления u как
Обращая внимание на выражения для $v$ и $r$ в (4.4) и учитывая (4.3), функцию плотности энергии $\psi $, определенную в (3.1), можно представить на подобласти ${{\mathfrak{D}}_{j}}$:
Учитывая значения координат ${{z}^{ \pm }}$ в конечный момент времени $t = T$, получим выражение для терминальной энергии стержня:
Здесь последняя строка вытекает из того, что 2N функции $w_{{j,M}}^{ + }(x)$ как решение системы (4.7)–(4.9) зависят от начального состояния и линейной комбинации функций управления ${{u}_{{k,m}}}$. Эта зависимость выражается соответственно через заданную вектор-функцию a и матрицу A.
Таким образом, путем представления искомых $v$ и $r$ в виде линейной комбинации бегущих волн, являющихся функциями одной переменной z, задача оптимального управления (1.9), (2.1), (3.1) после перенормировки сводится к классической краевой задаче вариационного исчисления относительно первой производной вектор-функции ${\mathbf{u}}(z)$. Нужно найти такое управление ${\mathbf{u}}{\kern 1pt} {\text{*}}(z)$ на интервале $z \in \bar {\mathfrak{Z}}$, которое минимизирует квадратичный функционал:
(5.5)
$\begin{array}{*{20}{c}} {\tilde {\Theta }[{\mathbf{u}}{\kern 1pt} *] = \mathop {\min }\limits_{{\mathbf{u}} \in {{H}^{1}}(\mathfrak{Z};{{\mathbb{R}}^{{KM}}})} \tilde {\Theta }[{\mathbf{u}}],\quad \tilde {\Theta } = \int\limits_0^\lambda \theta (z,{\mathbf{u}}{\kern 1pt} '(z)){\kern 1pt} dz,} \\ {\theta = {{{({\mathbf{u}}{\kern 1pt} ')}}^{2}} + \tilde {\gamma }{{{(A{\mathbf{u}}{\kern 1pt} '\; + {\mathbf{a}})}}^{2}},\quad \tilde {\gamma } = 2KT\lambda _{c}^{{ - 1}}{{{10}}^{\gamma }} > 0,} \end{array}$Для нахождения необходимых условий экстремальности решения вариационной задачи (5.4), (5.5) введем вектор-функцию, сопряженную к ${\mathbf{u}}$, согласно
(5.6)
$\begin{array}{*{20}{c}} {{\mathbf{p}} = \frac{{\partial \theta }}{{\partial {\mathbf{u}}{\kern 1pt} '}} = 2({\mathbf{E}} + \tilde {\gamma }{{A}^{{\text{T}}}}A){\mathbf{u}}{\kern 1pt} '\; + 2\tilde {\gamma }{{A}^{{\text{T}}}}{\mathbf{a}},} \end{array}$(5.7)
$\begin{array}{*{20}{c}} {({\mathbf{E}} + \tilde {\gamma }{{A}^{{\text{T}}}}A){\mathbf{u}}{\kern 1pt} '{\kern 1pt} '(z) + \tilde {\gamma }{{A}^{{\text{T}}}}{\mathbf{a}}{\kern 1pt} '(z) = 0,\quad z \in \mathfrak{Z}.} \end{array}$Выпишем условие трансверсальности задачи:
(5.8)
$\begin{array}{*{20}{c}} {{{{\mathbf{p}}}^{{\text{T}}}}(0)\delta {\mathbf{u}}(0) - {{{\mathbf{p}}}^{{\text{T}}}}(\lambda )\delta {\mathbf{u}}(\lambda ) = 0,} \end{array}$(5.9)
$\begin{array}{*{20}{c}} {{\mathbf{p}}(\lambda ) = - {{{\mathbf{B}}}^{{\text{T}}}}{\mathbf{p}}(0).} \end{array}$Важно отметить, что вектор управления ${\mathbf{u}}(t)$, удовлетворяющий необходимые условия стационарности (5.4), (5.7) и (5.9), доставляет абсолютный минимум целевому функционалу $\tilde {\Theta }$. Это напрямую следует из квадратичности и неотрицательности $\tilde {\Theta }$.
6. Вопросы управляемости динамической системы. Хотя в задаче управления (1.9), (3.1) не требуется строгого приведения стержня в наперед заданное состояние в конце процесса, значение минимизируемой в момент $t = T$ механической энергии $\Psi $ будет напрямую зависеть от ресурсов выбранной структуры управления. Некоторые выводы об управляемости можно сделать, применяя метод Фурье.
Применим метод разделения переменных для уравнения (1.4) и спроецируем его в пространстве ${{L}^{2}}(\mathfrak{X})$ на базисные функции ${{\{ {{e}_{i}}(x)\} }_{{i \in {{\mathbb{Z}}_{ + }}}}}$, которые являются решением соответствующей краевой задачи на собственные значения:
(6.1)
$\begin{array}{*{20}{c}} {e_{i}^{{''}}(x) = - \omega _{i}^{2}{{e}_{i}}(x),\quad e_{i}^{'}( \pm 1) = 0,\quad i \in {{\mathbb{Z}}_{ + }}.} \end{array}$При таком подходе решение исходной начально-краевой задачи представимо как разложение по этому ортогональному базису в виде
С использованием интегрирования по частям и с учетом разрывного характера функции силы f из (1.1), приходим к линейной системе обыкновенных дифференциальных уравнений:
(6.3)
${{\ddot {v}}_{i}} + \omega _{i}^{2}{{v}_{i}} = \sum\limits_{n \in \mathfrak{N}{\kern 1pt} *} {{e}_{i}}({{x}_{n}})y_{n}^{'},\quad {{v}_{i}}(0) = v_{i}^{0},\quad {{\dot {v}}_{i}}(0) = p_{i}^{0},\quad i \in {{\mathbb{Z}}_{ + }}.$Здесь ${{v}_{i}}$, $v_{i}^{0}$ и $p_{i}^{0}$ – соответственно проекции решения $v(t,x)$ и начальных распределений ${{v}^{0}}(x)$ и ${{p}^{0}}(x)$ на ${{e}_{i}}(x)$. Дополнительно в (6.3) введены функции скачков интеграла силы f:
(6.4)
${{y}_{n}}(t) \triangleq {{y}_{{n + 1}}}(t) - {{y}_{{n - 1}}}(t),\quad n \in \mathfrak{N}{\kern 1pt} *,\quad {{y}_{{ - N - 1}}} = {{y}_{{N + 1}}} = 0.$Использование одного и того же символа как для значений интегралов ${{y}_{j}}$, так и для скачков ${{y}_{n}}$ не вызывает противоречий, потому что индексы этих функций принадлежат соответственно непересекающимся множествам $j \in \mathfrak{J}$ и $n \in \mathfrak{N}{\kern 1pt} *$ (ср. (4.3)).
Таким образом, из (6.3) следует, что на движение стержня влияют только скачки интегралов. Более того, i-я мода неуправляема, если для произвольного управления ${\mathbf{u}}$ правая часть соответствующего уравнения из (6.3) тождественно равна нулю:
(6.5)
${{\bar {f}}_{i}}(t) \triangleq \sum\limits_{n \in \mathfrak{N}{\kern 1pt} *} {{e}_{i}}({{x}_{n}})y_{n}^{'}(t) \equiv 0.$Если значения нескольких собственных функций такие, что ${{e}_{i}}({{x}_{n}}) = с{{e}_{j}}({{x}_{n}})$ при $i \ne j$ для всех $n \in \mathfrak{N}{\kern 1pt} *$, будем считать, что все эти моды принадлежат одной группе. В случае однородного стержня при $\rho = \kappa = 1$ в безразмерном виде нормированные собственные функции имеют вид
(6.6)
$\begin{array}{*{20}{c}} {{{e}_{i}}(x) = \cos \frac{{i\pi (x + 1)}}{2},\quad {{\omega }_{i}} = \frac{{i\pi }}{2},\quad i = 1,2, \ldots ,} \\ {{{e}_{0}} = \frac{{\sqrt 2 }}{2},\quad {{\omega }_{0}} = 0.} \end{array}$Значение функции
пробегает лишь конечное число величин для каждого $n \in \mathfrak{N}{\kern 1pt} *$ при фиксированном $N$. Следовательно, и число линейных комбинаций ${{\bar {f}}_{i}}$, введенных в (6.5), ограничено. В результате все моды колебаний разбиваются на $N + 1$ счетномерных подсистем (групп мод) с одним управляющим входом. Группа с номером $k = 0, \ldots ,N$ объединяет моды с номерами $i = 2Nj \pm k \geqslant 0$, где $j \in {{\mathbb{Z}}_{ + }}$.Исходя из помодового разложения (6.3) приходим к некоторым априорным представлениям о возможностях гашения колебаний для различных конфигураций управляющих элементов. Как было показано в [10], даже при наличии $K = N$ управляющих элементов, расположенных без промежутков (см. на рис. 3 верхнюю левую схему стержня для $N = 6$), мы не можем повлиять на нулевую группу мод, т.е. остановить движение стержня как целого и изменить амплитуды мод с номерами $2iN$, $i \in \mathbb{N}$. Действительно, подставляя значения ${{e}_{{2jN}}}({{x}_{n}})$, где $j \in {{\mathbb{Z}}_{ + }}$, из (6.6) в (6.5) с учетом (6.4), получаем, что
Рис. 3.
Возможные периодические структуры управления стержнем при N = 6 и соответствующие множества индексов неуправляемых мод (серым обозначены участки с приложенными силами)

Эти силы не зависят от значения остальных функций ${{y}_{j}}$, $j \in \mathfrak{J}$, поэтому для фиксированного числа элементарных интервалов $N$ при любых других конфигурациях системы управления ($K < N$) нулевая группа мод остается неуправляемой.
Уменьшение управляющих входов K может лишь ухудшить ситуацию и вызвать потерю управляемости и в других группах. Например, если управляющий элемент на каждом периоде занимает два элементарных интервала (${{N}_{c}} = 2$, см. третью и шестую сверху схему слева на рис. 3), для N-й группы значения соответствующих собственных форм ${{e}_{{(2i - 1)N}}}({{x}_{n}}) = \cos (\pi (N + n){\text{/}}2)$ при $n \in \mathfrak{N}{\kern 1pt} *$ и $i \in \mathbb{N}$ на концах $x = x_{k}^{ \pm }$ интервала ${{\mathfrak{U}}_{k}}$ равны ${{e}_{{(2i - 1)N}}}(x_{k}^{ + }) = {{e}_{{(2i - 1)N}}}(x_{k}^{ - })$. Из этого напрямую следует, что действующая, согласно (1.1), на этом интервале постоянная сила $f(t,x) = {{f}_{k}}(t)$ входит в линейную комбинацию управления ${{\bar {f}}_{{(2i - 1)N}}}$ моды с номером $(2i - 1)N$ дважды с коэффициентом +1 и дважды же с коэффициентом –1. Пробегая по всем индексам $k \in \mathfrak{K}$, получаем ${{\bar {f}}_{{(2i - 1)N}}}(t) \equiv 0$. Это значит, что неуправляемыми для таких конфигураций являются моды с номерами $iN$, где $i \in {{\mathbb{Z}}_{ + }}$.
Еще один интересный пример структуры с дополнительной потерей управляемости – это случай с длиной периода $3\lambda $ (${{N}_{p}} = 3$, $N = 3K$) и ${{N}_{s}} = {{N}_{c}} = 1$ (см., например, пятую сверху схему слева на рис. 3). Для этой конфигурации неуправляемыми являются моды с длиной волны, кратной $3\lambda $ (группа с номером $2K$). В рассматриваемой группе мод собственные функции ${{e}_{i}}$ принимают на границе интервалов ${{\mathfrak{X}}_{j}}$, $j \in \mathfrak{J}$, следующие значения:
В узловых точках $x_{k}^{ \pm }$ $k$-го периода на границе интервала управления ${{\mathfrak{U}}_{k}}$ для $k \in \mathfrak{K}$ значения собственных функций совпадают: ${{e}_{i}}(x_{k}^{ + }) = {{e}_{i}}(x_{k}^{ - })$. Следовательно, для этих мод правые части уравнений (6.3) обнулятся (${{\bar {f}}_{i}}(t) \equiv 0$).
Можно обобщить рассуждения предыдущего абзаца на случай, когда управляющий интервал ${{\mathfrak{U}}_{k}}$ расположен симметрично на k-м периоде структуры, т.е. когда ${{N}_{p}} = 2{{N}_{s}} + {{N}_{c}}$. Учитывая симметричность относительно центра периода собственных функций ${{e}_{i}}$ с длиной волны, кратной ${{N}_{p}}\lambda $, можно утверждать, что в линейную комбинацию ${{\bar {f}}_{i}}$ функция управляющей силы fk войдет ${{N}_{i}}$ раз как с коэффициентом $ + c$, так и с коэффициентом $ - c$. Из этого вытекает неуправляемость $i$-й моды.
7. Пример оптимизации движения. Для наглядности рассмотрим пример оптимального управления продольными перемещениями упругого стержня при заданном времени $T = 3$. Выбраны следующие параметры структуры управляющих элементов: $K = 3$, $N = 6$, ${{N}_{c}} = 1$, ${{N}_{s}} = 0$ (${{N}_{p}} = 2$, M = 9). Это означает, что по длине стержня укладываются три периода, каждый из которых разделен на два одинаковых участка: слева с управлением, справа – без управления (см. вторую сверху схему слева на рис. 3). В качестве начальных значений заданы функции
(7.1)
${{v}^{0}}(x) = - {{r}^{0}}(x) = a\cos \frac{{4\pi x}}{3},\quad {{a}^{2}} = \frac{9}{{\pi (16\pi - 3\sqrt 3 )}}.$Коэффициент $a$ выбирается так, чтобы начальная механическая энергия системы равнялась единице. Несмотря на четность тригонометрической функции в начальных условиях, функция плотности импульса ${{p}^{0}}(x)$ антисимметрична относительно начала координат, так как она равна, согласно (1.9), производной $r_{x}^{0}$, которая нечетна по координате $x$. Из (7.1) следует, что центр масс стержня находится в покое в момент времени $t = 0$. Для рассматриваемой системы центр масс в отсутствие внешних сил будет оставаться неподвижным на всем интервале времени $t \in [0,T]$.
Для весового коэффициента $\gamma = - 1$ оптимальные перемещения точек стрежня $v(t,x)$ показаны на рис. 4. При выборе такого параметра большее внимание уделяется уменьшению интенсивности управления (квадрат нормы $\Upsilon = 0.01794$), что приводит к достаточно большим остаточным деформациям (терминальная энергия $\Psi = 0.08846$). Как видно из графика, функция перемещения непрерывна, но видны изломы, расположенные на характеристиках, которые изображены на рис. 2 пунктирными линиями для других параметров системы.
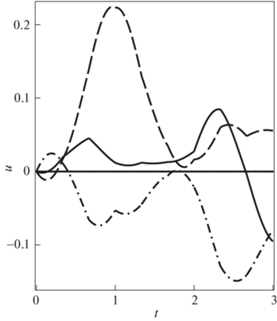
Оптимальные интегралы управления ${{u}_{k}}(t)$, которые воздействуют на стержень в пределах интервалов ${{\mathfrak{U}}_{k}} = {{\mathfrak{X}}_{j}}$, где $k = - 2,0,2$ и $j = - 5, - 1,3$, изображены на рис. 5 сплошной, штриховой и штрихпунктирной линиями соответственно. Это непрерывные функции с нулевыми по построению начальными значениями. Для выбранных начальных условий (7.1) интегралы управления представляют собой линейные комбинации тригонометрических и полиномиальных функций.
Рис. 5.
Оптимальные управления ${{u}_{k}}(t)$ при $\gamma = - 1$ для $k = - 2$ (сплошная линия), k = 0 (штриховая) и k = 2 (штрихпунктирная)
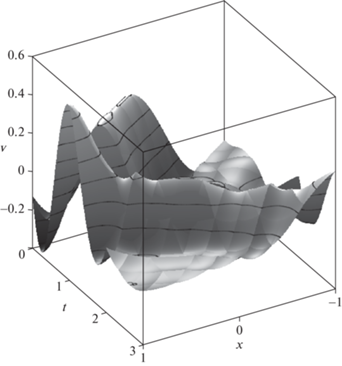
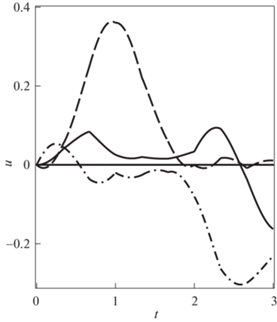
Выберем весовой коэффициент равным $\gamma = 1$. В этом случае для минимизации входных сигналов требуется больший ресурс управления ($\Upsilon = 0.03957$), при этом остаточная энергия снижается более чем на 2 порядка ($\Psi = 0.00831$) по сравнению с начальной. На рис. 6 показаны соответствующие оптимальные перемещения. Как видно, хотя терминальные деформации уменьшились, все же присутствуют неуправляемые моды колебаний с периодом, кратным $\lambda = 1{\text{/}}3$. На рис. 7 заметно почти удвоение амплитуды интегралов силы ${{u}_{k}}(t)$ (ср. рис. 5).
Рис. 7.
Оптимальные управления ${{u}_{k}}(t)$ при γ = 1 для $k = - 2$ (сплошная линия), k = 0 (штриховая) и k = 2 (штрихпунктирная)
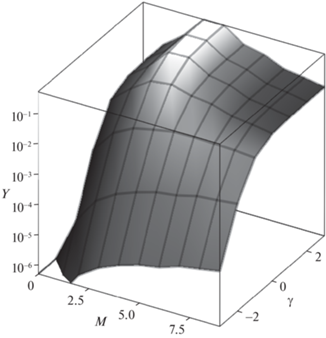
На рис. 8 в логарифмическом масштабе показана зависимость оптимальных значений среднего квадрата вектора управлений $\Upsilon $ от параметра времени M и весового коэффициента $\gamma $. Наивысших значений $\Upsilon $ достигает при M = 3 и больши́х положительных значениях $\gamma $. При дальнейшем увеличении времени T в той же области значений $\gamma $ функционал управления $\Upsilon $ монотонно убывает.
Рис. 8.
Зависимость оптимального значения функционала $\Upsilon $ от параметра времени M и весового коэффициента $\gamma $
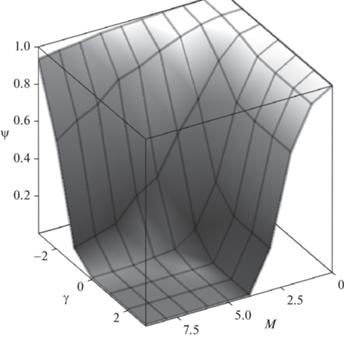
Терминальная энергия стержня $\Psi $, показанная на рис. 9 также в зависимости от $\gamma $ и M, монотонно уменьшается с увеличением времени. При $M \geqslant 4$ и положительных значениях $\gamma $ этот функционал быстро приближается к предельному значению $\Psi {\kern 1pt} * = 0.00829$, равному суммарной энергии мод с номерами $i \in 12\mathbb{N}$ (см. разд. 6). При малом времени $T$ или отрицательных значениях $\gamma $ энергия почти не изменяется в процессе управления и остается близкой к единице.
Рис. 9.
Зависимость оптимального значения функционала $\Psi $ от параметра времени M и весового коэффициента $\gamma $
8. Анализ оптимальных значений целевых функционалов. Изучим поведение оптимальных значений квадрата нормы управления $\Upsilon $ и терминальной механической энергии $\Psi $, определенных в (3.1), при изменении конфигурации пьезоэлектрических элементов (табл. 1). Для примера возьмем начальные условия (7.1), зафиксируем число элементарных интервалов $N = 6$, временной параметр $M = 12$ ($T = 4$) и весовой коэффициент $\gamma = 3$. Выбор достаточно больших значений M и $\gamma $ нацелен на достижение в момент времени T предельно низких энергий $\Psi $. Как показывают расчеты, дальнейшее увеличение как M, так и $\gamma $ не приводит к заметному снижению терминальной энергии.
Таблица 1.
Оптимальные значения функционалов $\Upsilon $ и $\Psi $ для различных конфигураций управляющих элементов при $M = 2N = 12$ и $\gamma = {{10}^{3}}$
| ${{N}_{p}}$ | ${{N}_{c}}$ | ${{N}_{s}}$ | $\Upsilon $ | $\Psi $ | ${{N}_{p}}$ | ${{N}_{c}}$ | ${{N}_{s}}$ | $\Upsilon $ | $\Psi $ |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | $0.01033$ | $0.00829$ | 0 | 0 | 0 | 0 | 1 |
| 2 | 1 | 0 | $0.02066$ | $0.00829$ | 6 | 2 | 0 | $0.04274$ | $0.04205$ |
| 2 | 2 | 0 | $0.01434$ | $0.04205$ | 6 | 2 | 1 | $0.02243$ | $0.49284$ |
| 3 | 1 | 0 | $0.04266$ | $0.00829$ | 6 | 2 | 2 | $0.01349$ | $0.5$ |
| 3 | 1 | 1 | $0.02256$ | $0.16823$ | 6 | 3 | 0 | $0.07285$ | $0.16823$ |
| 3 | 2 | 0 | $0.02197$ | $0.04205$ | 6 | 3 | 1 | $0.10309$ | $0.16823$ |
| 3 | 3 | 0 | $0.03643$ | $0.16823$ | 6 | 4 | 0 | $0.03756$ | $0.49284$ |
| 6 | 1 | 0 | $0.17171$ | $0.00829$ | 6 | 4 | 1 | $0.00273$ | $0.95079$ |
| 6 | 1 | 1 | $0.04512$ | $0.16823$ | 6 | 5 | 0 | $0.42874$ | $0.00829$ |
| 6 | 1 | 2 | $0.07994$ | $0.00829$ | 6 | 6 | 0 | $0.03125$ | $0.5$ |
С точностью до симметрии относительно начала координат x = 0 на рис. 3 для выбранного параметра $N$ показаны все возможные периодические расположения и размеры управляющих элементов, обозначенные на каждой схеме серым фоном. Справа от схемы символически указано соответствующее множество номеров мод, на которые для заданной конфигурации не подается никаких управляющих воздействий.
Первая базовая схема слева на рис. 3 отвечает случаю с максимальным числом управляющих входов, $K = N = {{N}_{p}} = {{N}_{c}} = 6$. К ней относятся первые шесть чисел во второй строке сверху в таблице. Благодаря большему управляющему ресурсу в конце процесса удается прийти в состояние с довольно низкой энергией $\Psi = \Psi {\kern 1pt} * \approx 0.008$ при наименьшей норме управления $\sqrt \Upsilon $. При этом каждая двенадцатая мода колебаний, отсчитывая от нулевой, неуправляема.
Такой же эффективности в подавлении колебаний можно достичь и при использовании трех управляющих входов малой длины ($K = 3$, ${{N}_{c}} = 1$, см. вторую схему сверху на рис. 3 слева). За это приходится платить более интенсивным управлением – функционал $\Upsilon $ увеличивается вдвое (третья строка таблицы, левая половина). Следует отметить, что для этой схемы вдвое увеличивается критическое время достижимости минимального значения энергии с $T{\kern 1pt} * = 2{\text{/}}3$ для $K = 6$ до $T{\kern 1pt} * = 4{\text{/}}3$, см. [10]. При той же размерности $K = 3$ вектора управления ${\mathbf{u}}(t)$ увеличение длины управляющего элемента до ${\text{|}}{{\mathfrak{U}}_{k}}{\text{|}} = 2{\text{/}}3$ (${{N}_{c}} = 2$, третья сверху схема на рис. 3 слева и четвертая строка в левой половине таблицы) приводит к потере управляемости каждой шестой моды и к заметному увеличению остаточных колебаний.
Следующие четыре схемы на рис. 3 слева (с четвертой по седьмую сверху) показывают возможные расположения и длины элементов управления для случая $K = 2$, ${{N}_{p}} = 3$. При ${{N}_{c}} = 1$ и ${{N}_{s}} = 0$ вновь можно достичь минимального значения энергии $\Psi = \Psi {\kern 1pt} *$, хотя функционал управления $\Upsilon $ увеличивается более чем вчетверо по сравнению с базисным случаем при ${{N}_{p}} = {{N}_{c}} = 1$. Наикратчайшее время достижимости этой энергии тоже увеличивается до $T{\kern 1pt} * = 2$. Интересно отметить схему с двумя управляющими элементами при ${{N}_{c}} = {{N}_{s}} = 1$ (пятая строка на рис. 3). Более чем в 20 раз увеличивается терминальная энергия $\Psi $ при таком симметричном расположении управляющего элемента на периоде. Можно показать, что для такой схемы неуправляемыми становятся моды с номерами, кратными 4. Для конфигураций с двумя входами при ${{N}_{c}} = 2$ или ${{N}_{c}} = 3$ не могут быть изменены амплитуды колебаний либо каждой четвертой, либо каждой шестой моды соответственно.
Остальные схемы на рис. 3 (кроме первой сверху справа, без актюаторов) отвечают случаю одного управляющего сигнала $K = 1$, иначе ${{N}_{p}} = 6$. Среди них хотелось бы выделить три конфигурации с параметрами ${{N}_{c}} = 1$ и ${{N}_{s}} = 0$, ${{N}_{c}} = 1$ и ${{N}_{s}} = 2$, ${{N}_{c}} = 5$ и ${{N}_{s}} = 0$. Для них за время $T \geqslant T{\kern 1pt} * = 3$ достижим наименьший для всех рассмотренных схем уровень остаточной энергии $\Psi = \Psi {\kern 1pt} *$. Из двух первых конфигураций с коротким управляющим элементом ${{N}_{c}} = 1$ более выгодным с точки зрения затрат управления оказывается второй вариант с бóльшим сдвигом элемента к центру стержня. Самой затратной из трех оказывается конфигурация с длинным элементом, ${{N}_{c}} = 5$.
Для случая с одним управляющим сигналом стоит отметить две схемы с симметричным относительно геометрического центра расположением элемента – это конфигурации с параметрами ${{N}_{c}} = {{N}_{s}} = 2$ и ${{N}_{c}} = 6$ (${{N}_{s}} = 0$). Из-за упомянутой симметрии неуправляемыми оказываются все четные моды, причем для начальных условий (7.1) в них содержится ровно половина запасаемой стержнем энергии (см. левую половину таблицы, пятая строка сверху и последняя строка). Для этих же начальных условий наибольшие колебания остаются для симметричного случая ${{N}_{c}} = 4$ и ${{N}_{s}} = 1$, когда нет возможности управлять не только четными модами, но и модами с индексами, кратными 3.
Выбранные примеры расположения управляющих элементов из-за своей ограниченности не позволяют сделать однозначные выводы о возможностях структурной оптимизации исследуемой динамической системы с распределенными параметрами. Следует указать при этом, что разумное уменьшение размеров пьезоэлементов при нарушении как геометрической симметрии их расположения, так и соразмерности различных частей конфигурации могут положительно сказаться на повышении эффективности управления в смысле уменьшения нормы входных сигналов и энергии остаточных колебаний.
Заключение. Рассмотрены продольные перемещения тонкого однородного упругого стержня с периодической структурой пьезоэлектрических элементов. Дана обобщенная формулировка начально-краевой задачи, решение которой ищется относительно кинематической и динамической переменных в энергетическом пространстве. Для случая стержня, управляемого с помощью дискретно распределенных в пространстве продольных сил, при заданном законе воздействия предложен алгоритм построения оптимального движения в виде комбинации бегущих волн. При фиксированном интервале времени управления найдено решение задачи минимизации целевого функционала, который представляет собой взвешенную сумму квадрата нормы вектора управления и терминальной механической энергии стержня. Для этого двумерная по пространству и времени задача управления сведена к одномерной вариационной задаче с фиксированными концами. Исследована зависимость оптимальных значений нормы интеграла пьезоэлектрической силы и терминальной энергии от времени управления и весового коэффициента. Продемонстрировано изменение этих значений для ряда конфигураций управляющих элементов. Предложенный подход позволяет сравнить эффективность различных структур управления и таким образом поставить задачу о поиске в некотором смысле оптимальной конфигурации.
Список литературы
Lions J.L. Optimal Control of Systems Governed by Partial Differential Equations. N.Y.: Springer-Verlag, 1971. 400 p.
Бутковский А.Г. Теория оптимального управления системами с распределенными параметрами. М.: Наука, 1965. 474 с.
Романов И.В., Шамаев А.С. О задаче граничного управления для системы, описываемой двумерным волновым уравнением // Изв. РАН. ТиСУ. 2019. № 1. С. 109–116.
Черноусько Ф.Л., Ананьевский И.М., Решмин С.А. Методы управления нелинейными механическими системами. М.: Физматлит, 2006. 328 с.
Chen G. Control and Stabilization for the Wave Equation in a Bounded Domain. II // SIAM J. Control Optim. 1981. V. 19. № 1. P. 114–122.
Kucuk I., Sadek I., Yilmaz Y. Optimal Control of a Distributed Parameter System with Applications to Beam Vibrations Using Piezoelectric Actuators // J. Franklin Inst. 2014. V. 351. № 2. P. 656–666.
Kostin G.V., Saurin V.V. Dynamics of Solid Structures. Methods Using Integrodifferential Relations. Berlin: De Gruyter, 2018.
Гавриков А.А., Костин Г.В. Оптимальное управление продольным движением упругого стержня с помощью граничных сил // Изв. РАН. ТиСУ. 2021. № 5. С. 74–90.
Kostin G., Gavrikov A. Energy-Optimal Control by Boundary Forces for Longitudinal Vibrations of an Elastic Rod // Lecture Notes in Mechanical Engineering Advanced Problems in Mechanics III. Springer, 2023.
Kostin G., Gavrikov A. Controllability and Optimal Control Design for an Elastic Rod Actuated by Piezoelements // IFAC-PapersOnLine. 2022. V. 55. № 16. P. 350–355. https://doi.org/10.1016/j.ifacol.2022.09.049
Kostin G., Gavrikov A. Optimal Motions of an Elastic Structure Under Finite-dimensional Distributed Control // ArXiv. 2023. arXiv:2304.05765. P. 1–17. https://doi.org/10.48550/arXiv.2304.05765.
Kostin G., Gavrikov A. Optimal Motion of an Elastic Rod Controlled by Piezoelectric Actuators and Boundary Forces // 16th Intern. Conf. “Stability and Oscillations of Nonlinear Control Systems” (Pyatnitskiy’s Conference) (STAB). M.: IEEE, 2022. P. 1–4. https://doi.org/10.1109/STAB54858.2022.9807484.
Kostin G., Gavrikov A. Modeling and Optimal Control of Longitudinal Motions for an Elastic Rod with Distributed Forces // ArXiv. 2022. arXiv:2206.06139 5. P. 1–11. https://doi.org/10.48550/arXiv.2206.06139.
Gavrikov A., Kostin G. Optimal LQR Control for Longitudinal Vibrations of an Elastic Rod Actuated by Distributed and Boundary Forces // Mechanisms and Machine Science. V. 125. Berlin: Springer, 2023. P. 285–295. https://doi.org/10.1007/978-3-031-15758-5_28
Ho L.F. Exact Controllability of the One-dimensional Wave Equation with Locally Distributed Control // SIAM J Control Optim. 1990. V. 28. № 3. P. 733–748.
Bruant I., Coffignal G., Lene F., Verge M. A Methodology for Determination of Piezoelectric Actuator and Sensor Location on Beam Structures // J. Sound and Vibration. 2001. V. 243. № 5. P. 861–882. https://doi.org/10.1006/jsvi.2000.3448
Gupta V., Sharma M., Thakur N. Optimization Criteria for Optimal Placement of Piezoelectric Sensors and Actuators on a Smart Structure: A Technical Review // J. Intelligent Material Systems and Structures. 2010. V. 21. № 12. P. 1227–1243. https://doi.org/10.1177/1045389X10381659
Botta F., Rossi A., Belfiore N.P. A Novel Method to Fully Suppress Single and Bi-modal Excitations Due to the Support Vibration by Means of Piezoelectric Actuators // J. Sound and Vibration. 2021. V. 510. № 13. P. 116260.https://doi.org/10.1016/j.jsv.2021.116260
Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Наука, 1977. 735 с.
Михлин С.Г. Курс математической физики. М.: Наука, 1968. 576 с.
Иосида К. Функциональный анализ. М.: Мир, 1968. 624 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления