Известия РАН. Теория и системы управления, 2023, № 6, стр. 137-149

Введение. Работа продолжает исследование основных функциональных характеристик при предельных загрузках в телекоммуникационных системах [1–3]. В качестве многопараметрической оценки функциональных возможностей многопользовательской сети используются векторы исходящих узловых мультипотоков. Компонентами указанного вектора являются все межузловые потоки с источником в выбранной вершине и стоками во всех остальных узлах сети.

В ходе вычислительных экспериментов определяются допустимые распределения всех межузловых потоков, которые передаются одновременно всеми корреспондентами по кратчайшим маршрутам. На основе найденных межузловых потоков формируются взаимно допустимые векторы исходящих мультипотоков из всех узлов сети. В рамках модели предполагается, что система управления позволяет выравнивать величины исходящих узловых потоков в ситуациях, когда внешняя нагрузка на узлы сети превышает нормативные ограничения. В работе изучаются пиковые распределения при полной загрузке сети. Пропускная способность ребер сети рассматривается как вектор ресурсов. Ресурсы распределяются между пользователями (узлами-корреспондентами) для обеспечения передачи потоков. Для каждого узла оцениваются требуемые затраты ресурсов при передаче всех исходящих межузловых потоков, для которых данный узел является источником.

Для построения последовательных оценок допустимого исходящего мультипотока из узла с помощью модели анализируется динамический процесс “заполнения” ребер сети при монотонном увеличении межузловых нагрузок. Предполагается что система управления обеспечивает передачу межузловых потоков по всем доступным кратчайшим маршрутам при текущих значениях пропускной способности ребер. На каждом шаге часть остаточной пропускной способности распределяется равными долями между корреспондентами для увеличения соответствующих межузловых потоков. На каждом этапе подсчитываются суммарные затраты ресурсов и последовательно анализируются результаты выравнивания исходящих мультипотоков. За конечное число итераций достигается полная загрузка сети и вычисляются гарантированные оценки [4] допустимых исходящих узловых мультипотоков, передаваемых из всех узлов сети одновременно всеми корреспондентами. Предложенный способ моделирования дает возможность сравнивать и выявлять различия в распределении ресурсов при использовании уравнивающих стратегий. Полученные оценки можно трактовать как ограничения на величину каждого межузлового потока определенного вида, который можно будет гарантированно передать в сети одновременно с потоками других корреспондентов, если условия совместной передачи на остальные виды потоков не будут нарушены. Результаты, полученные в ходе экспериментов, можно рассматривать как алгоритмически заданное описание функциональных возможностей сети при предельной загрузке. Предложенный метод позволяет проследить в динамике взаимосвязь изменения узловых мультипотоков и пропускной способности ребер сети от минимальных значений до достижения предельной загрузки.

Данная статья находится в русле исследований стратегий управления и построения диспетчерских правил распределения потоков, нагрузок и ресурсов в многопользовательских сетях [5–9]. Далее для построения всех кратчайших путей и максимального однопродуктового потока используются процедуры поиска с полиномиальными оценками вычислительных затрат [10, 11].

1. Математическая модель. Для описания многопользовательской сетевой системы связи воспользуемся следующей математической записью модели передачи многопродуктового потока. Сеть $G$ задается множествами $\langle V,\;R,\;U,P\rangle $: узлов (вершин) сети $V = \{ {{{v}}_{1}},{{{v}}_{2}},...,{{{v}}_{n}},...,{{{v}}_{N}}\} $; неориентированных ребер $R = \{ {{r}_{1}},{{r}_{2}},...,{{r}_{k}},...,{{r}_{E}}\} $; ориентированных дуг $U = \{ {{u}_{1}},{{u}_{2}},...,{{u}_{k}},...,{{u}_{{2E}}}\} $; пар узлов-корреспондентов $P = \{ {{p}_{1}},{{p}_{2}},...,{{p}_{M}}\} $. Предполагается, что в сети отсутствуют петли и сдвоенные ребра.

Ребро ${{r}_{k}} \in R$ соединяет смежные вершины ${{{v}}_{{{{n}_{k}}}}}$, ${{{v}}_{{{{j}_{k}}}}}$. Каждому ребру r_k ставятся в соответствие две ориентированные дуги ${{u}_{k}}$, ${{u}_{{k + E}}}$ из множества U. Дуги $\{ {{u}_{k}},{{u}_{{k + E}}}\} $ определяют прямое и обратное направления передачи потока по ребру r_k между концевыми вершинами ${{{v}}_{{{{n}_{k}}}}}$, ${{{v}}_{{{{j}_{k}}}}}$.

В многопользовательской сети G рассматривается $M = N(N - 1)$ независимых, невзаимозаменяемых и равноправных межузловых потоков различных видов. Каждой паре узлов-корреспондентов p_m из множества $P$ соответствуют: вершина-источник с номером ${{s}_{m}}$, из ${{s}_{m}}$ входной поток m-го вида поступает в сеть; вершина-приемник с номером ${{t}_{m}}$, из ${{t}_{m}}$ поток m-го вида покидает сеть. Для каждой вершины ${{{v}}_{n}} \in V$, $n = \overline {1,N} $, формируется подмножество $P({{{v}}_{n}})$ всех пар-корреспондентов, для которых вершина ${{{v}}_{n}}$ является узлом-источником:

а для каждого $P({{{v}}_{n}})$ – список номеров $M(n)$ пар ${{p}_{m}}$, входящих в подмножество $P({{{v}}_{n}})$:

Обозначим через z_m величину межузлового потока m-го вида, поступающего в сеть через узел с номером ${{s}_{m}}$ и покидающего сеть из узла с номером t_m; ${{x}_{{mk}}}$, ${{x}_{{m(k + E)}}}$ – поток m-го вида, который передается по дугам ${{u}_{k}}$ и ${{u}_{{k + E}}}$, согласно направлению передачи, ${{x}_{{mk}}} \geqslant 0$, ${{x}_{{m(k + E)}}} \geqslant 0$, $m = \overline {1,M} $, $k = \overline {1,E} $; $S({{{v}}_{n}})$ – множество номеров исходящих дуг, по ним поток покидает узел ${{{v}}_{n}}$; $T({{{v}}_{n}})$ – множество номеров входящих дуг, по ним поток поступает в узел ${{{v}}_{n}}$. Состав множеств $S({{{v}}_{n}})$, $T({{{v}}_{n}})$ однозначно формируется в ходе выполнения следующей процедуры. Пусть некоторое ребро ${{r}_{k}} \in R$ соединяет вершины с номерами n и $j$, такими, что $n < j$. Тогда ориентированная дуга ${{u}_{k}} = ({{{v}}_{n}},{{{v}}_{j}})$, направленная из вершины ${{{v}}_{n}}$ в ${{{v}}_{j}}$, считается исходящей из вершины ${{{v}}_{n}}$, и ее номер k заносится в множество $S({{{v}}_{n}})$, а дуга ${{u}_{{k + E}}}$, направленная из ${{{v}}_{j}}$ в ${{{v}}_{n}}$, – входящей для ${{{v}}_{n}}$, и ее номер $k + E$ помещается в список $T({{{v}}_{n}})$. Дуга ${{u}_{k}}$ является входящей для ${{{v}}_{j}}$, и ее номер k попадает в $T({{{v}}_{j}})$, а дуга ${{u}_{{k + E}}}$ – исходящей, и номер $k + E$ вносится в список исходящих дуг $S({{{v}}_{j}})$.

Во всех узлах сети ${{{v}}_{n}} \in V$, $n = \overline {1,N} $, для каждого вида потока должны выполняться условия сохранения потоков:

Величина ${{z}_{m}}$ равна входному межузловому потоку $m$-го вида, проходящему от источника ${{s}_{m}}$ к приемнику ${{t}_{m}}$ пары p_m при распределении потоков ${{x}_{{mi}}}$ по дугам сети.

Каждому ребру ${{r}_{k}} \in R$ приписывается неотрицательное число ${{d}_{k}}$, определяющее суммарный предельно допустимый поток, который можно передать по ребру ${{r}_{k}}$ в обоих направлениях. В исходной сети компоненты вектора пропускных способностей ${\mathbf{d}} = ({{d}_{1}},{{d}_{2}},...,{{d}_{k}},...,{{d}_{E}})$ – положительные числа ${{d}_{k}} > 0$. Вектор d определяет следующие ограничения на сумму потоков всех видов, передаваемых по ребру ${{r}_{k}}$ одновременно:

Ограничения (1.1), (1.2) задают множество допустимых значений компонент вектора межузловых потоков ${\mathbf{z}} = ({{z}_{1}},{{z}_{2}},...,{{z}_{m}},..,{{z}_{M}})$:

В рамках формализма модели для каждого узла ${{{v}}_{n}} \in V$, $n = \overline {1,N} $, формируется вектор исходящего мультипотока $\overleftarrow {\mathbf{z}} (n)$, компонентами которого являются межузловые потоки ${{z}_{m}}$ для всех пар ${{p}_{m}} \in P({{v}_{n}})$ с узлами-источниками ${{s}_{m}}$, расположенными в вершине ${{{v}}_{n}}$:

2. Допустимые узловые мультипотоки. При проведении вычислительных экспериментов векторы $\overleftarrow {\mathbf{z}} (n)$ допустимых исходящих мультипотоков формируются на основе найденных распределений совместно допустимых межузловых потоков ${{z}_{m}}$, ${{p}_{m}} \in P({{{v}}_{n}})$, передаваемых одновременно из всех узлов сети. Для каждой пары узлов-корреспондентов ${{p}_{m}} \in P$, для некоторого заданного допустимого межузлового потока ${{\tilde {z}}_{m}}$ и соответствующих значений дуговых потоков ${{\tilde {x}}_{{mk}}}$, $k = \overline {1,2E} $, величина

характеризует результирующую межузловую нагрузку (далее RI-нагрузку от английского resulting internodal load) на ребра сети при передаче межузлового потока ${{\tilde {z}}_{m}}$ из узла-источника ${{s}_{m}}$ в узел-приемник ${{t}_{m}}$. Величина ${{\tilde {y}}_{m}}$ показывает, какая суммарная пропускная способность сети потребуется для передачи дуговых потоков ${{\tilde {x}}_{{mk}}}$. В рамках модели отношение RI-нагрузки и межузлового потока можно трактовать как удельные затраты ресурсов сети при передаче единичного потока m-го вида между узлами ${{s}_{m}}$ и ${{t}_{m}}$ при дуговых потоках ${{\tilde {x}}_{{mi}}}$.

Для получения гарантированных оценок узловых мультипотоков предполагается, что межузловые потоки передаются по маршрутам, содержащим минимальное число ребер (далее MER-маршруты от английского minimum edge route). При проведении вычислительных экспериментов для оценки величин “расщепленного” потока на первом этапе для каждой пары узлов ${{p}_{m}} = ({{s}_{m}},{{t}_{m}})$ в сети G(1) формируется набор ${{H}_{m}}(1)$ всех путей, которые далее используются как MER-маршруты передачи m-го вида потока:

где $h_{m}^{j}(1)$ – список номеров дуг в  j-м пути в сети G(1) между узлами ${{s}_{m}}$ и ${{t}_{m}}$; ${{\mu }_{m}}(1)$ – минимальное число ребер в MER-маршруте $h_{m}^{j}(1)$, а ${{J}_{m}}(1)$ – число MER-маршрутов для $m$-й пары.

Для каждой пары ${{p}_{m}} \in P$ по всем MER-маршрутам из ${{H}_{m}}(1)$ передается единичный межузловой поток ${{z}_{m}}$ и подсчитываются значения индикаторной функции:

Определяются дуговые потоки для пары p_m:

Межузловой поток по MER-маршрутам (далее MER-поток) $z_{m}^{0}(1)$ между узлами ${{s}_{m}}$ и ${{t}_{m}}$ вычисляется по формулам (1.1) и (2.1). Рассчитываются нормирующий коэффициент

и дуговые потоки:

При передаче всех потоков $x_{{mk}}^{0}$ по ребрам сети межузловой поток из узла s_m в узел ${{t}_{m}}$ равен единице.

Распределение совместно допустимых межузловых потоков последовательно определяется на основе MER-маршрутов и дуговых потоков $x_{{mk}}^{0}$. Подсчитываются остаточные пропускные способности и формируется сеть для проведения следующей итерации. На последующих итерациях с учетом текущих пропускных способностей строятся новые MER-маршруты и формируется множество равных по величине межузловых потоков, которые можно передавать одновременно. Финальные межузловые потоки, при одновременной передаче которых полностью используется пропускная способность всех ребер сети, вычисляются за конечное число итераций, не превосходящее общего количества ребер сети. Описанная выше процедура далее называется MEREF-процедура (от английского minimum edge route equal flow) или для краткости MF-процедура.

При проведении вычислительных экспериментов на первом шаге ($t = 1$) MF-процедуры пропускная способность ${{d}_{k}}(1)$ каждого ребра ${{r}_{k}} \in R$ для сети $G(1)$ полагается равной пропускной способности исходной сети, а его длина – единице:

По формуле (2.2) и с учетом MER-потока $z_{a}^{0}(1)$ определяются нормирующие коэффициенты $\omega _{m}^{0}(1)$, $m = \overline {1,M} $. На втором этапе указанные коэффициенты используются для поиска текущих квот на передачу совместно допустимых потоков одновременно между всеми парами ${{p}_{m}},m = \overline {1,M} $.

Задача 1. Найти $\alpha {\kern 1pt} {\text{*}}(1) = \mathop {\max }\limits_\alpha \alpha $

Для всех пар ${{p}_{m}} \in P$, $m = \overline {1,M} $, и всех дуг ${{u}_{k}}$, $k \in {{H}_{m}}(1)$ с помощью α*(1) вычисляются дуговые и межузловые потоки:

Таким образом каждой паре корреспондентов на этом этапе MF-процедуры выделяется одна и та же квота α*(1) на передачу допустимого потока при заданных кратчайших маршрутах соединения. Решение задачи 1 позволяет получить уравнительное распределение квот на одновременную передачу межузловых потоков различных видов и соответствующие нагрузки, численно равные $y_{m}^{*}(1)$, $m = \overline {1,M} $.

Для найденных дуговых потоков вычисляется остаточная пропускная способность всех ребер, формируется сеть G(2), для которой

Текущая длина каждого ребра ${{r}_{k}}$ для сети $G(t)$ на следующей итерации $\left( {t \geqslant 2} \right)$ определяется по следующему правилу:

На первом этапе шага $t$ ($t \geqslant 2$) в сети $G(t)$ для каждой пары узлов ${{p}_{a}} \in P$ при текущих ${{l}_{k}}(t)$ определяется длина ${{L}_{a}}(t)$ MER-маршрута:

Если длина ${{L}_{a}}(t) \geqslant {{N}^{2}}$, то для пары ${{p}_{a}}$ в сети $G(t)$ нет пути соединения и значение MER-потока здесь и далее полагается равным нулю:

Если же длина ${{L}_{a}}(t) < {{N}^{2}}$, то для пары ${{p}_{a}}$ строится множество ${{H}_{a}}(t)$ всех MER-маршрутов и, согласно MF-процедуре, вычисляются текущий MER-поток $z_{a}^{0}(t)$, дуговые потоки $x_{{ak}}^{0}(t),x_{{a(k + E)}}^{0}(t)$ для дуг ${{u}_{k}}$, $k \in {{H}_{a}}(t)$, а также коэффициенты:

Для определения величины текущей квоты α*(t) решается задача 2.

Задача 2. Найти $\alpha {\kern 1pt} {\text{*}}(t) = \mathop {\max }\limits_\alpha \alpha $

На шаге $t$ ($t \geqslant 2$) с помощью решения задачи 2 находятся: текущие допустимые значения межузловых потоков, которые могут передаваться в сети $G(t)$ одновременно для всех пар ${{p}_{m}} \in P$:

На заключительном этапе шага $t$ ($t \geqslant 2$) для каждого ребра сети вычисляется остаточная пропускная способность сети $G(t + 1)$:

и осуществляется проверка следующих условий.

Если после завершения шага t окажется, что хотя бы для одного ребра ${{r}_{k}} \in R$ остаточная пропускная способность ${{d}_{k}}(t + 1) > 0$, то формируется новая сеть $G(t + 1)$ и производится переход к следующей итерации.

Если ${{d}_{k}}(t + 1) = 0$ для всех $k = \overline {1,E} $, то происходит останов, все пропускные способности ребер исчерпаны и сеть полностью загружена. Финальная итерация обозначается $t: = T$.

На каждом шаге t результирующие межузловые потоки и реберные нагрузки для каждой пары ${{p}_{m}}$, $m = \overline {1,M} $, обозначаются через $z_{m}^{*}(t)$, $y_{m}^{*}(t)$ и соответственно равны:

Удельные затраты $w_{m}^{*}(t)$ при передаче межузловых потоков одновременно по всем MER-маршрутам ${{H}_{m}}(1),{{H}_{m}}(2),...,{{H}_{m}}(t)$:

Для анализа результатов вычислительных экспериментов на каждой итерации $t = \overline {1,T} $ полученные данные $z_{m}^{*}(t)$, $y_{m}^{*}(t)$, $w_{m}^{*}(t)$ помещаются в массивы Z*(t), Y*(t), W*(t), а также формируются векторы допустимых исходящих узловых мультипотоков, которые обозначаются

3. Уравнительное распределение нагрузок. Для анализа допустимых исходящих мультипотоков при уравнительном распределении межузловых нагрузок для всех пар узлов ${{p}_{m}} \in P$ использовалась MERER-процедура (от английского minimum edge route equal resourse) или для краткости MR-процедура, которая состоит в следующем. На первом этапе при передаче единичных потоков по каждому MER-маршруту из ${{H}_{m}}(t)$, $m = \overline {1,M} $, определяются реберные загрузки для $m = \overline {1,M} $ и $k = \overline {1,E} $. Для каждой пары ${{p}_{m}} \in P$ вычисляются нагрузки:

нормирующие коэффициенты: при которых результирующие межузловые нагрузки $y_{m}^{0} = \theta _{m}^{0}(t)y_{m}^{0}(t)$ будут равны единице, если соответствующий межузловой поток будет передан по всем маршрутам ${{H}_{m}}(t)$, $m = \overline {1,M} $.

На текущем шаге t MR-процедуры в сети $G(t)$ для значений ${{d}_{k}}(t)$ и ${{l}_{k}}(t)$ для каждой пары ${{p}_{a}} \in P$ находится набор MER-маршрутов ${{H}_{a}}(t)$.

С учетом $y_{a}^{0}(t)$ при передаче межузлового MER-потока $z_{a}^{0}(t)$ по всем MER-маршрутам из ${{H}_{a}}(t)$ нормирующие коэффициенты $\theta _{a}^{0}(t)$ вычисляются по формуле (3.1). Указанные коэффициенты в задаче 3 используются для поиска равных нагрузок при передаче соответствующих межузловых потоков одновременно между всеми парами ${{p}_{a}} \in P$.

Задача 3. Найти $\begin{gathered} \beta {\kern 1pt} {\text{*}}(t) = {{\max }_{{\beta > 0}}}\beta \hfill \\ \hfill \\ \end{gathered} $

при условиях: $\beta \sum\nolimits_{m = 1}^M \theta _{m}^{0}(t)(x_{{mk}}^{0}(t) + x_{{m(k + E)}}^{0}(t)) \leqslant {{d}_{k}}(t)$, $k = \overline {1,E} $.

Решение задачи 3 $\beta {\kern 1pt} *(t)$ определяет текущие совместно допустимые значения дуговых потоков и реберных нагрузок:

На шаге $t$ решение задачи 3 позволяет получить уравнительное распределение нагрузки. Межузловые потоки, соответствующие дуговым потокам $x_{{mk}}^{{**}}(t)$ и нагрузкам $y_{m}^{{**}}(t) = \beta {\kern 1pt} {\text{*}}(t)$, согласно (1.1), обозначим через $z_{m}^{\Delta }(y_{m}^{{**}}(t))$ и вычислим остаточную пропускную способность ребер в сети $G(t + 1)$:

После завершения шага $t$ производится проверка условий:

если хотя бы для одного ребра ${{r}_{k}} \in R$ остаточная пропускная способность ${{d}_{k}}(t + 1) > 0$, то формируется новая сеть $G(t + 1)$, для нее определяется текущая длина ребер:

и происходит переход к итерации t + 1;

если же ${{d}_{k}}(t + 1) = 0$ для всех $k = \overline {1,E} $, то все пропускные способности ребер исчерпаны и сеть полностью загружена.

Финальная итерация обозначается $t: = T$. При этом для каждого $t$ вычисляются: результирующие значения межузловых потоков для каждой пары ${{p}_{m}}$:

суммарные реберные нагрузки, соответствующие предельному распределению пропускной способности ребер сети: удельные затраты $w_{m}^{{**}}(t)$ при передаче межузловых потоков по всем маршрутам ${{H}_{m}}( \cdot )$:

В ходе эксперимента на каждом шаге $t = \overline {1,T} $ все полученные $z_{m}^{{**}}(t)$, $y_{m}^{{**}}(t)$, $w_{m}^{{**}}(t)$ заносятся в массивы Z**(t), Y**(t), W**(t) и формируются векторы совместно допустимых исходящих узловых мультипотоков, которые обозначаются

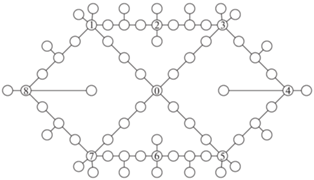
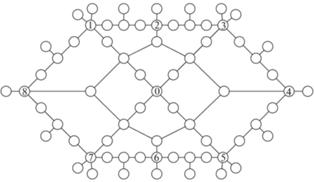
4. Построение оценок показателей функционирования. Вычислительные эксперименты проводились на моделях сетевых систем, представленных на рис. 1, 2 (базовая и кольцевая сети соответственно). В каждой сети имеется 69 узлов. Пропускные способности ребер d_k выбираются случайным образом из отрезка [900, 999] и совпадают для ребер, присутствующих в обеих сетях. В кольцевой сети пропускная способность каждого из добавленных ребер равна 900. В ходе эксперимента проводилась нормировка и суммарная пропускная способность в обеих сетях была одинакова:

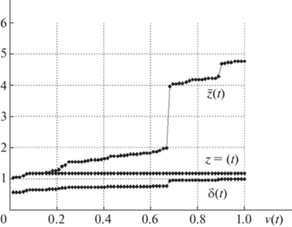
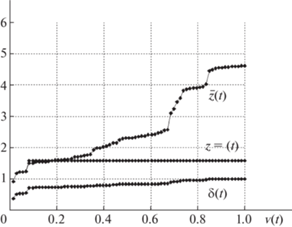
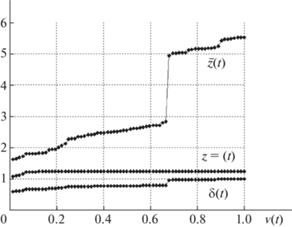
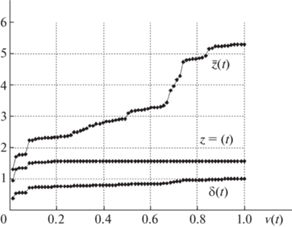
Диаграммы, представленные на рисунках с нечетными номерами, относятся к базовой сети, а с четными – к кольцевой. На каждом из рис. 3–6 представлены три кривые, характеризующие изменения основных параметров: использованную пропускную способность, медианы и средние значения межузловых потоков. В частности, указанные кривые позволяют проследить по шагам, сравнить общие тенденции и оценить закономерности в ходе вычислительного эксперимента.

По горизонтальной оси указаны (относительные) номера итераций

Нижняя кривая $\delta (t)$ отображает изменения при использовании ресурсов сети на каждом шаге

где $D(t)$ – сумма загруженной пропускной способности сети за $t$ шагов при одновременной передаче всех исходящих допустимых узловых мультипотоков $\overleftarrow {\mathbf{z}} {\kern 1pt} {\text{*}}(n,t)$ в базовой и $\overleftarrow {\mathbf{z}} {\kern 1pt} {\text{*}}{\kern 1pt} {\text{*(}}n,t)$ в кольцевой сети, $n = \overline {1,N} $.

На рис. 3–6 все кривые расхода ресурсов $\delta (t)$ демонстрируют одинаковую тенденцию – после 10-й итерации расходуется более 80% ресурсов, а на оставшихся итерациях равными порциями распределяются оставшиеся 20% пропускной способности.

На диаграммах вторая кривая ${{z}^{ = }}(t)$ отражает значения медиан межузловых потоков. Здесь так же, как и в случае расходования ресурсов, после 10-й итерации устанавливается некий стационарный режим, и медианы не меняются до момента останова. Для базовой сети на рис. 3, 5 значения ${{z}^{ = }}(t)$ соответственно равны 1.18 и 1.21, для кольцевой на рис. 4, 6 – 1.57 и 1.58. Таким образом после 10-й итерации исчерпывается 80% пропускной способности сети и более 70% пар-корреспондентов сохраняют достигнутые значения потоков. Остаточный ресурс распределяется поровну между узлами, инцидентными висячим дугам.

На рис. 3–6 верхняя кривая $\overline z (t)$ отвечает средним значениям межузловых потоков по итерациям. Цифры на рисунках отличаются, но общий вид диаграмм подтверждает общую тенденцию. В начале ресурсы сети распределяются равными долями почти между всеми парами. Однако когда использовано 80% ресурсов, многие узлы оказываются изолированными, а сеть распадается на отдельные фрагменты. Остаточная пропускная способность висячих ребер распределяется между узлами, расположенными “близко” друг к другу, и для некоторых пар-корреспондентов потоки оказываются столь значительными, что резко меняют средние значения.

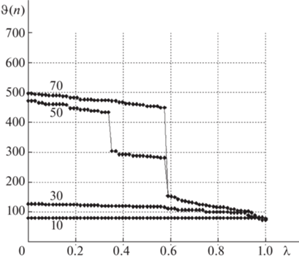
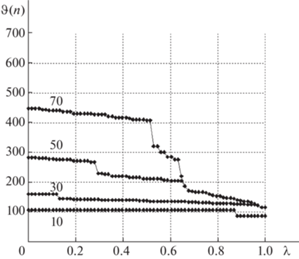
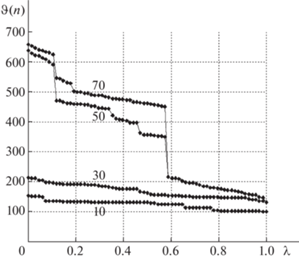
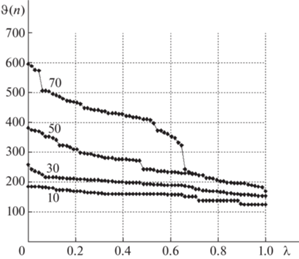
На рис. 7–10 представлены диаграммы, которые позволяют проанализировать, как меняются допустимые исходящие узловые мультипотоки в ходе выполнения MF- и MR-процедур. По горизонтальной оси откладываются относительные номера узлов ${{{v}}_{n}} \in V$:

По вертикальной оси откладываются значения суммарных узловых мультипотоков на итерации $t$:

Цифры, указанные непосредственно над кривыми, отвечают номеру итерации t, в данном случае на всех рисунках это 10, 30, 50, 70.

Диаграммы на рис. 7–10 подтверждают выводы, сделанные ранее. На начальных этапах значения исходящих потоков почти равны 100 единицам и соответствующие кривые почти параллельны горизонтальной оси и лежат в коридоре значений $100 \leqslant \vartheta ( \cdot ) \leqslant 200$, что отвечает почти равным медианам (см. рис. 3–6 ). На рис. 7–10 при $t = 50$ и 70, когда сеть распадается на отдельные фрагменты, распределение остаточной пропускной способности происходит между небольшим числом смежных узлов. В результате смежные пары-корреспонденты получают дополнительно от 200 до 400 единиц потока. Дуги, ведущие к висячим вершинам, не являются транзитными, и остаточная пропускная способность на последних итерациях может составлять до 700 единиц в кольцевой сети.

Формально полная загрузка сети достигается на последней итерации (t = T). С содержательной точки зрения в реальных системах остаточные ресурсы и мало загруженные ребра указывают на структуру сети, в которой неэффективно используются ресурсы.

Схема проведения вычислительных экспериментов позволяет применять полученные результаты при построении гарантированных оценок функциональных характеристик. Параметризованные векторы

при любых $\gamma $ и предельных загрузках сети определяют допустимый вектор исходящих мультипотоков, передаваемых из всех узлов.

Заключение. Предложенная математическая модель и проведенные эксперименты позволили провести оценку функциональных возможностей и структурных особенностей многопользовательских сетевых систем. В рамках модели предполагалось, что система управления и диспетчерские правила поддерживают уравнительное распределение ресурсов и/или выравнивание невзаимозаменяемых потоков разных видов для всех пар равноправных корреспондентов. Анализ потоков между смежными узлами и загрузки соответствующих ребер показал неэффективное использование ресурсов этими корреспондентами. Совместно допустимые векторы узловых мультипотоков можно рассматривать как многокритериальные оценки пропускной способности сети. Линейную однопараметрическую комбинацию векторов узловых потоков при полной загрузке можно применять для агрегированных оценок уязвимости и живучести сети при изменении пропускной способности ее ребер. Значения узловых мультипотоков при загрузке сети на 70–80% позволяют проводить оценку пропускной способности сети в стационарном “рабочем” режиме.