Теплоэнергетика, 2021, № 4, стр. 27-34

Развитие подходов к анализу движения расплава по поверхности тепловыделяющего элемента

Э. В. Усов^a, *, П. Д. Лобанов^a, b, Н. А. Прибатурин^a, b

^a Институт проблем безопасного развития атомной энергетики РАН
115191 Москва, Большая Тульская ул., д. 52, Россия

^b Институт теплофизики им. С.С. Кутателадзе СО РАН
630090 г. Новосибирск, просп. Академика Лаврентьева, д. 1, Россия

^* E-mail: usovev@gmail.com

Поступила в редакцию 23.05.2020
После доработки 02.07.2020
Принята к публикации 26.08.2020

DOI: 10.1134/S0040363621030085

Полный текст (PDF)

Аннотация

На основе анализа экспериментов, которые были выполнены на имитаторах твэлов с оболочкой из легкоплавких металлов, предложены модели плавления и движения расплава по поверхности твэлов. Представленная работа является продолжением экспериментальных и теоретических работ, проводимых совместно в ИБРАЭ РАН и ИТ СО РАН по изучению особенностей движения расплава по цилиндрической поверхности, имитирующей поверхность твэла. В ней проанализированы факторы, которые определяют термическое разрушение твэлов. Одним из важных выводов, сделанных при проведении анализа экспериментальных данных, был вывод о преобладающем пленочном ламинарном режиме стекания в обогреваемой части имитатора твэла. С использованием данного предположения была построена аналитическая модель, позволяющая предсказывать массу твэла, вынесенную за его пределы во время плавления. В результате расчетов с помощью предложенной модели было показано, что для аварии с введением положительной реактивности, когда рост мощности может достигать 10 номиналов, необходима модификация модели, чтобы учесть турбулентный режим стекания. Для этого была построена упрощенная модель движения расплава. Проведено сравнение с известными методиками и показано, что предложенный подход дает возможность с удовлетворительной точностью описывать турбулентный режим течения. Модифицированная модель позволила рассчитать особенности движения расплава нержавеющей стали по поверхности твэла реактора на быстрых нейтронах (БН). Была получена информация о толщине расплава, скорости его движения и числе Рейнольдса в зависимости от условий стекания, а также о массе, вынесенной за пределы активной зоны.

Ключевые слова: твэл, расплав, математическая модель, оболочка, движение, тяжелая авария, пленка, трение, гидродинамика, теплообмен, плавление, АЭС, реактор, тепловыделяющая сборка

Первый этап тяжелой аварии в реакторной установке сопровождается разрушением в ней твэлов. Причина разрушения твэлов – нарушение теплового баланса в активной зоне, вызванное снижением интенсивности охлаждения твэлов из-за уменьшения расхода теплоносителя при неизменном энерговыделении или резким ростом энерговыделения вследствие введения избыточной положительной реактивности. Необходимо провести численный расчет подобных процессов, чтобы проанализировать последствия тяжелых аварий. Для этого должны быть развиты алгоритмы, базирующиеся на современном представлении об особенностях разрушения твэлов. В твэлах реакторов БН имеются активная часть, в которой происходит основное энерговыделение, и бланкет, в котором энерговыделение фактически отсутствует (рис. 1). Наличие холодной бланкетной части может существенно влиять на движение расплава при его затвердевании. Одним из препятствий для развития алгоритмов является отсутствие надежных экспериментальных данных. По этой причине в ИБРАЭ РАН и ИТ СО РАН были проведены экспериментальные исследования по плавлению имитаторов оболочки твэлов, в процессе которых изучались особенности плавления и движения расплава, а также измерялись температура оболочки и потеря ее массы [1, 2].

Рис. 1.

Схема твэла

МОДЕЛЬ ПОТЕРИ МАССЫ ОБОЛОЧКИ ПРИ ЕЕ ПЛАВЛЕНИИ

Один из важных выводов, сделанных при анализе экспериментальных данных, – стекание расплава в обогреваемой части имитатора твэла происходит в пленочном ламинарном режиме [1, 2]. С учетом этого предположения и результатов работы [3] выражение для вычисления среднемассовой скорости течения расплава U при ламинарном режиме стекания его по цилиндрической поверхности и одновременном действии силы тяжести и напряжения трения с потоком газа можно записать в следующем виде:

(1)

$\begin{gathered} U = \frac{{\rho g}}{{8{\mu }}}\left[ {{{{\left( {R + \delta } \right)}}^{2}} - {{R}^{2}}} \right] + \frac{{{{R}^{2}}}}{{{{{\left( {R + \delta } \right)}}^{2}} - {{R}^{2}}}} \times \\ \times \,\,\left[ {\left( {R + \delta } \right)\frac{{{{{\tau }}_{c}}}}{{\mu }} - \frac{{\rho g{{{\left( {R + \delta } \right)}}^{2}}}}{{2{\mu }}}} \right] \times \\ \times \,\,\left[ {{{{\left( {1 + \frac{\delta }{R}} \right)}}^{2}}\ln \left( {1 + \frac{\delta }{R}} \right) - \frac{1}{2}{{{\left( {1 + \frac{\delta }{R}} \right)}}^{2}} + \frac{1}{2}} \right], \\ \end{gathered} $

где $\rho {\text{,}}$ ${\mu ,}$ $\delta $ – плотность, динамический коэффициент вязкости и толщина пленки расплава соответственно; $R$ – радиус поверхности, по которой стекает расплав; g – ускорение свободного падения; ${{{\tau }}_{с}} = \frac{\xi }{8}{{{\rho }}_{с}}U_{с}^{2}$ – напряжение трения между расплавом и потоком газа (здесь $\xi = 0.02$ – коэффициент трения, индекс с от англ. coolant).

Масса пленки расплава m_f вычисляется по уравнению

${{m}_{f}} = \rho L\pi \left[ {{{{\left( {R + \delta } \right)}}^{2}} - {{R}^{2}}} \right],$

где L – длина оболочки; $R = {{R}_{{{\kern 1pt} 1}}} - \Delta $ (здесь ${{R}_{{\,1}}}$ – начальный внешний радиус оболочки; $\Delta $ – толщина расплавленной части оболочки твэла, индекс f от англ. film).

Полная масса расплава ${{m}_{l}}$ (индекс l от англ. liquid), образующегося в результате плавления оболочки твэла, рассчитывается по выражению

${{m}_{l}} = \rho L\pi \left( {R_{{{\kern 1pt} 1}}^{2} - {{R}^{2}}} \right).$

В приведенных выше выражениях учтено плавление оболочки изнутри благодаря теплообмену между ней и топливным сердечником. При этом стекание расплава, как было обнаружено в [1, 2], происходит по внешней поверхности оболочки.

Уравнения баланса массы расплава оболочки и толщины его пленки с учетом того, что его образование определяется плавлением, а исчезновение – стеканием, выглядят следующим образом:

$\begin{gathered} \left\{ \begin{gathered} {{{\text{d}}{{m}_{f}}} \mathord{\left/ {\vphantom {{{\text{d}}{{m}_{f}}} {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}} = {N \mathord{\left/ {\vphantom {N {\Delta h - }}} \right. \kern-0em} {\Delta h - }} \hfill \\ - \,\,U\rho \pi \left[ {{{{\left( {{{R}_{{{\kern 1pt} 1}}} - \Delta + \delta } \right)}}^{2}} - {{{\left( {{{R}_{{{\kern 1pt} 1}}} - \Delta } \right)}}^{2}}} \right]; \hfill \\ {{{\text{d}}{{m}_{l}}} \mathord{\left/ {\vphantom {{{\text{d}}{{m}_{l}}} {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}} = {N \mathord{\left/ {\vphantom {N {\Delta h;}}} \right. \kern-0em} {\Delta h;}} \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} {{{\text{d}}\delta } \mathord{\left/ {\vphantom {{{\text{d}}\delta } {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}} = {N \mathord{\left/ {\vphantom {N {\left( {2\Delta h\rho L\pi R} \right) - }}} \right. \kern-0em} {\left( {2\Delta h\rho L\pi R} \right) - }} \hfill \\ - \,\,U{{\left[ {{{{\left( {R + \delta } \right)}}^{2}} - {{R}^{2}}} \right]} \mathord{\left/ {\vphantom {{\left[ {{{{\left( {R + \delta } \right)}}^{2}} - {{R}^{2}}} \right]} {\left[ {2L\left( {R + \delta } \right)} \right];}}} \right. \kern-0em} {\left[ {2L\left( {R + \delta } \right)} \right];}} \hfill \\ {{{\text{d}}\Delta } \mathord{\left/ {\vphantom {{{\text{d}}\Delta } {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}} = {N \mathord{\left/ {\vphantom {N {(2\Delta h\rho L\pi R),}}} \right. \kern-0em} {(2\Delta h\rho L\pi R),}} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $

где t – время; N – мощность нагревателя; $\Delta h$ – удельная теплота плавления.

Используя приведенные уравнения, можно определить потерю массы в любой момент времени. Необходимо отметить, что эти уравнения получены при допущении, что профиль скорости в пленке расплава по толщине расплава устанавливается фактически мгновенно независимо от скорости образования расплава. Справедливость подобного подхода будет обоснована далее путем сравнения результатов расчетов и представленных в литературе экспериментальных данных.

ВАЛИДАЦИЯ МОДЕЛИ

Для валидации модели были использованы данные экспериментальных исследований авторами скорости потери массы Δm оболочек имитаторов твэлов при их плавлении [1, 2]. Эксперименты были выполнены с использованием модельных оболочек из свинцово-висмутового сплава или олова. Результаты расчета и экспериментальные данные из [1, 2] показаны на рис. 2, 3 .

Рис. 2.

Зависимость экспериментальной (1) и расчетной (2) скорости потери массы эвтектического сплава Pb (44.5%)–Bi (55.5%) от времени t. N, Вт: 3 – 93.0; 4 – 170.5; 5 – 259.7

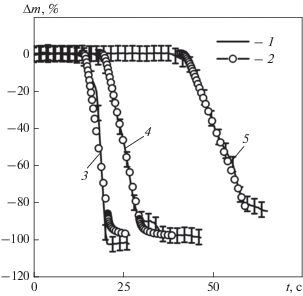
Рис. 3.

Зависимость экспериментальной (1) и расчетной (2) скорости потери массы Sn от времени. N, Вт: 3 – 91.0; 4 – 174.4; 5 – 262.2

Имитатор твэла имел длину 0.18 м. На него была нанесена модельная оболочка толщиной 0.001 м. Внутри имитатора находился трубчатый цилиндрический нагреватель, на который была нанесена модельная оболочка. Нижняя часть оболочки длиной 0.02 м была необогреваемой и имитировала холодную часть твэла. Длина верхней обогреваемой части модельной оболочки была равна 0.16 м.

Как следует из рисунков, представленная модель с удовлетворительной точностью позволяет моделировать потерю массы модельной оболочки при ее плавлении. Различия наблюдаются только при самом малом энерговыделении для оболочки из олова. Меньшая скорость потери массы расплава может быть объяснена его частичным замерзанием на холодной нижней части имитатора (бланкете) и уменьшением скорости его стекания. В представленной выше математической модели замерзание на поверхности не учитывается.

С использованием разработанной модели были проведены расчеты для оболочки из нержавеющей стали типа 316 (зарубежная классификация, аналог Х18Н12М3) при номинальном энерговыделении в активной зоне 450 МВт/м³ реакторной установки типа БН [4]. Была рассмотрена авария, при которой происходят резкое уменьшение расхода теплоносителя вследствие остановки насосов при неизменной мощности реактора [авария с потерей теплоносителя типа ULOF (unprotected loss of flow)], вскипание теплоносителя, кризис теплообмена и, как следствие, плавление оболочки твэла. Длина модельного твэла составляла 1.0 м, радиус – 0.005 м, толщина оболочки – 0.001 м.

Перенос данных с модельного расплава на расплав, относящийся к реальной оболочке твэла, может быть выполнен в соответствии с теорией подобия по числу Рейнольдса

$\operatorname{Re} = \frac{{4\rho U\delta }}{{\mu }} = - \frac{{{\text{d}}m}}{{{\text{d}}t}}\frac{2}{{{\mu }\pi R}} = \frac{{q\delta L}}{{{\mu }\Delta h}},$

где q – тепловой поток с поверхности стержня твэла.

Движущимся газом в этом случае (см. рис. 1) являются пары натрия, которые образуются вследствие его кипения. Стоит отметить, что скорость движения пара может достигать нескольких сот метров в секунду из-за высокой энергонагруженности активной зоны и затесненности пучка стержней. Действительно, в соответствии с законом сохранения массы может быть сделана следующая оценка:

${{U}_{g}} = \frac{{4q{{L}_{r}}{{n}_{r}}}}{{{{D}_{h}}\Delta {{h}_{e}}{{\rho }_{{{\text{Na}}}}}}},$

где U_g – скорость движения паров натрия; ${{L}_{r}}$ – длина твэла; n_r – количество стержней в тепловыделяющей сборке (индекс r от англ. rod); D_h – гидравлический диаметр тепловыделяющей сборки (индекс h от англ. heat); $\Delta {{h}_{e}}$ – удельная теплота парообразования (индекс e от англ. evaporation); ${{\rho }_{{{\text{Na}}}}}$ – плотность паров натрия.

При $q = {{10}^{6}}$ Вт/м², ${{n}_{r}} = 300,$ ${{D}_{h}} = 3 \times {{10}^{{ - 3}}}$ м, $\Delta {{h}_{e}} = 4 \times {{10}^{6}}$ Дж/кг, $\rho = {{10}^{3}}$ кг/м³, $L = 1$ м скорость движения паров натрия составляет 100 м/с.

Результаты расчета потери массы при разных скоростях обдува твэла газовым потоком U_g (индекс g от англ. gas), толщины пленки расплава и числа Рейнольдса показаны на рис. 4. На рис. 4, а “баланс тепла” обозначает решение системы уравнений, при котором предполагается, что весь расплав, который образовался вследствие плавления, вытекает мгновенно, т.е. без учета конечной скорости стекания. На рис. 4, б при скорости газа 150 м/с наблюдаются два пика в расчете числа Рейнольдса. Первый пик связан с уносом расплава через верхнюю границу твэла, второй – с тем, что при постепенном увеличении толщины пленки из-за плавления гравитационные силы начинают превышать силу трения с потоком газа. В результате происходит обращение направления движения расплава, т.е. расплав начинает стекать через нижнюю границу.

Рис. 4.

Зависимости скорости потери массы стали 316 при ламинарном режиме стекания расплава (а), числа Рейнольдса (б) и толщины пленки расплава (в) от времени. U_g, м/с: 1 – 0; 2 – 50; 3 – 100; 4 – 150; 5 – баланс тепла

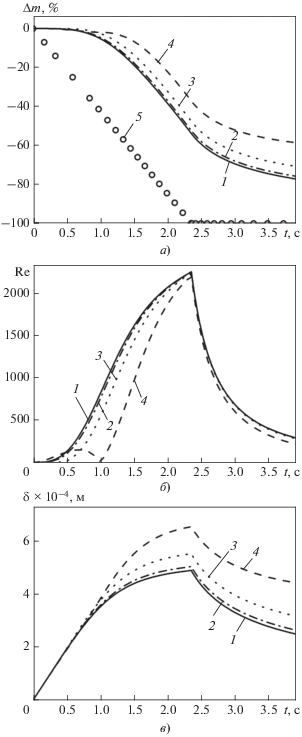
При этом из рис. 4, в можно заключить, что толщина пленки расплава не превышает 0.8 мм, что говорит о возможности рассматривать пленку для твэла диаметром 8 мм как относительно тонкую. В этом случае выражение для скорости течения расплава можно записать в виде

(2)

$U = \frac{{{{{\tau }}_{{\text{c}}}}\delta }}{{2{\mu }}} - \frac{{\rho g{{\delta }^{2}}}}{{3{\mu }}}.$

Возможность использования данного допущения была проверена независимо путем сравнения результатов расчетов по формулам (1) и (2). Известно, что формула (2) справедлива при небольших скоростях газа, по крайней мере, до захлебывания. Возможность переноса формулы на более высокие диапазоны будет представлена далее путем сравнения результатов расчета по ней с доступными экспериментальными данными и известными эмпирическими формулами.

Из рис. 4, б следует также, что даже для номинального энерговыделения число Рейнольдса для расплава немного больше критического значения при переходе от ламинарного режима течения к турбулентному (Re = 2000). Таким образом, для аварий с потерей расхода теплоносителя ULOF, когда энерговыделение близко к номиналу, или аварий типа LOF (loss of flow) при работе реактора на уровне остаточного энерговыделения можно предполагать, что будет реализовываться ламинарный режим стекания пленки. Для аварии с набросом мощности типа UTOP (unprotected transient over power), когда мощность может быть больше номинальной в несколько раз, упрощенная модель ламинарного стекания будет некорректной. По этой причине требуется развитие упрощенных подходов к расчету движения расплава в ламинарной и турбулентной областях.

УСОВЕРШЕНСТВОВАНИЕ МОДЕЛИ

Скорость движения расплава может быть рассчитана исходя из баланса действующих сил

${{{\tau }}_{w}}{{\Pi }_{w}} = {{{\tau }}_{с}}{{\Pi }_{c}} - \rho gS,$

где τ_w – напряжение трения на стенке в ламинарном режиме течения (индекс w от англ. wall); ${{\Pi }_{w}} = 2\pi R$ – смоченный периметр твэла; ${{\Pi }_{c}} = 2\pi \left( {R + \delta } \right)$ – периметр контакта расплава с теплоносителем; $S = \pi {{\left( {R + \delta } \right)}^{2}} - \pi {{R}^{2}}$ – площадь сечения расплава.

В представленном выражении учтено, что расплав вследствие трения движется вверх с потоком газа, под действием гравитации – вниз. Для тонкой пленки выражение для τ_w может быть упрощено:

${{{\tau }}_{w}} = {{{\tau }}_{с}} - \rho g\delta {\text{.}}$

С использованием уравнения баланса скорость течения расплава может быть найдена путем решения нелинейного уравнения

$\xi \left( {\operatorname{Re} } \right){{U}^{2}} = \frac{{8\left| {{{{\tau }}_{с}} - \rho g\delta } \right|}}{\rho }.$

Расчет напряжения трения в ламинарном режиме течения выполняется по формуле [5]

${{{\tau }}_{w}} = \frac{{2\left( {3\alpha - 1} \right){\mu }U}}{{\alpha \delta }},$

где α – коэффициент, учитывающий неравномерность профиля скорости по толщине расплава.

При этом

$\alpha = {{\left( {3 + r} \right)} \mathord{\left/ {\vphantom {{\left( {3 + r} \right)} 6}} \right. \kern-0em} 6},$

где $r = {{\rho g\delta } \mathord{\left/ {\vphantom {{\rho g\delta } {\left[ {2{{{\tau }}_{c}} + \rho g\delta } \right]}}} \right. \kern-0em} {\left[ {2{{{\tau }}_{c}} + \rho g\delta } \right]}}.$

Если профиль расплава описывается степенной функцией с показателем n, то $\alpha = {1 \mathord{\left/ {\vphantom {1 {\left( {n + 1} \right)}}} \right. \kern-0em} {\left( {n + 1} \right)}}.$

Для турбулентного течения в предположении степенного закона распределения скорости (при n = 1/7) [5, 6] может быть получено следующее соотношение:

(3)

${{{\tau }}_{w}} = {{\xi }_{w}}{{\rho {{U}^{2}}} \mathord{\left/ {\vphantom {{\rho {{U}^{2}}} 8}} \right. \kern-0em} 8},$

где ${{\xi }_{w}} = 0.37{{\left( {4U{{\delta \rho } \mathord{\left/ {\vphantom {{\delta \rho } {\mu }}} \right. \kern-0em} {\mu }}} \right)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 4}} \right. \kern-0em} 4}}}}$ = ${{0.37} \mathord{\left/ {\vphantom {{0.37} {{{{\operatorname{Re} }}^{{0.25}}}}}} \right. \kern-0em} {{{{\operatorname{Re} }}^{{0.25}}}}}.$

Следуя методике, предложенной в работе [6], для турбулентного течения в качестве автомодельного профиля скорости можно применить степенной закон распределения по толщине расплава

$u\left( y \right) = {{U}_{s}}{{\left( {{y \mathord{\left/ {\vphantom {y \delta }} \right. \kern-0em} \delta }} \right)}^{{{1 \mathord{\left/ {\vphantom {1 7}} \right. \kern-0em} 7}}}},$

где ${{U}_{s}}$ – скорость на поверхности расплава (индекс s от англ. surface).

Согласно [6] выражение для определения толщины вязкого подслоя δ_v (индекс v от англ. viscous) выглядит следующим образом:

${{\delta }_{{v}}} = {{\alpha }_{{v}}}{{\mu } \mathord{\left/ {\vphantom {{\mu } {(\rho {{U}_{*}})}}} \right. \kern-0em} {(\rho {{U}_{*}})}},$

где ${{\alpha }_{{v}}}$ = 11.5 – параметр модели; ${{U}_{*}} = \sqrt {{{{{{\tau }}_{w}}} \mathord{\left/ {\vphantom {{{{{\tau }}_{w}}} \rho }} \right. \kern-0em} \rho }} $ – пульсационная скорость.

Так как ${{{\tau }}_{w}} = {{\xi }_{w}}{{\rho {{U}^{2}}} \mathord{\left/ {\vphantom {{\rho {{U}^{2}}} 8}} \right. \kern-0em} 8},$ можно записать следующее выражение:

${{{{U}_{*}}} \mathord{\left/ {\vphantom {{{{U}_{*}}} U}} \right. \kern-0em} U} = \sqrt {{{{{\xi }_{w}}} \mathord{\left/ {\vphantom {{{{\xi }_{w}}} 8}} \right. \kern-0em} 8}} .$

В соответствии с [6] формулу для скорости движения расплава на границе вязкого подслоя можно записать в виде

${{u}_{{v}}} = {{\alpha }_{{v}}}{{U}_{*}}.$

В то же время при использовании степенного профиля скорости

${{{{u}_{{v}}}} \mathord{\left/ {\vphantom {{{{u}_{{v}}}} {{{U}_{s}}}}} \right. \kern-0em} {{{U}_{s}}}} = {{\left( {{{{{\delta }_{{v}}}} \mathord{\left/ {\vphantom {{{{\delta }_{{v}}}} \delta }} \right. \kern-0em} \delta }} \right)}^{{{1 \mathord{\left/ {\vphantom {1 7}} \right. \kern-0em} 7}}}},$

откуда ${{{{\alpha }_{{v}}}{{U}_{*}}} \mathord{\left/ {\vphantom {{{{\alpha }_{{v}}}{{U}_{*}}} {{{U}_{s}}}}} \right. \kern-0em} {{{U}_{s}}}}$ = ${{\left[ {{{{{\alpha }_{{v}}}{\mu }} \mathord{\left/ {\vphantom {{{{\alpha }_{{v}}}{\mu }} {\left( {\rho \delta U} \right)}}} \right. \kern-0em} {\left( {\rho \delta U} \right)}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 7}} \right. \kern-0em} 7}}}}.$

Пользуясь выражением (3) и тем, что U/U_s = = $\alpha = \frac{7}{8}$ [6], можно получить

${{\left( {{{{{\xi }_{w}}} \mathord{\left/ {\vphantom {{{{\xi }_{w}}} 8}} \right. \kern-0em} 8}} \right)}^{{{4 \mathord{\left/ {\vphantom {4 7}} \right. \kern-0em} 7}}}} = \frac{8}{7}{{4}^{{{1 \mathord{\left/ {\vphantom {1 7}} \right. \kern-0em} 7}}}}\alpha _{{v}}^{{{{ - 6} \mathord{\left/ {\vphantom {{ - 6} 7}} \right. \kern-0em} 7}}}{{\left( {{{4\rho \delta U} \mathord{\left/ {\vphantom {{4\rho \delta U} {\mu }}} \right. \kern-0em} {\mu }}} \right)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 7}} \right. \kern-0em} 7}}}},$

или

${{\xi }_{w}} = 8{{\left( {{8 \mathord{\left/ {\vphantom {8 7}} \right. \kern-0em} 7}} \right)}^{{{7 \mathord{\left/ {\vphantom {7 {24}}} \right. \kern-0em} {24}}}}}\alpha _{v}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}{{4}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}{{\operatorname{Re} }^{{ - 0.25}}} = {{0.37} \mathord{\left/ {\vphantom {{0.37} {{{{\operatorname{Re} }}^{{0.25}}}}}} \right. \kern-0em} {{{{\operatorname{Re} }}^{{0.25}}}}}.$

Таким образом, для предложенной авторами модели

${{\xi }_{w}} = \max \left[ {{{64{{{\operatorname{Re} }}^{{ - 1}}}\left( {3\alpha - 1} \right)} \mathord{\left/ {\vphantom {{64{{{\operatorname{Re} }}^{{ - 1}}}\left( {3\alpha - 1} \right)} \alpha }} \right. \kern-0em} \alpha },\,\,\,\,{{0.37} \mathord{\left/ {\vphantom {{0.37} {{{{\operatorname{Re} }}^{{0.25}}}}}} \right. \kern-0em} {{{{\operatorname{Re} }}^{{0.25}}}}}} \right].$

ОБОСНОВАНИЕ МОДЕЛИ

Для обоснования представленной модели был проведен анализ экспериментальных [7–9] и теоретических [7, 10–13] работ по стеканию пленки жидкости. В большинстве работ изучалась зависимость безразмерной толщины пленки ${{\delta }^{ + }} = \frac{\delta }{{\nu }}\sqrt {{{{{{\tau }}_{w}}} \mathord{\left/ {\vphantom {{{{{\tau }}_{w}}} \rho }} \right. \kern-0em} \rho }} $ (здесь ${\nu }$ – кинематический коэффициент вязкости) от числа Рейнольдса $\operatorname{Re} = {{4U{\delta }} \mathord{\left/ {\vphantom {{4U{\delta }} \nu }} \right. \kern-0em} \nu },$ для расчета которой рекомендовались различные соотношения:

$\begin{gathered} {{\delta }^{ + }} = {{\left[ {{{{\left( {0.707{{{\operatorname{Re} }}^{{0.5}}}} \right)}}^{{2.5}}} + {{{\left( {0.0379{{{\operatorname{Re} }}^{{0.9}}}} \right)}}^{{2.5}}}} \right]}^{{0.4}}}, \\ \operatorname{Re} = {{4U\delta } \mathord{\left/ {\vphantom {{4U\delta } {{\nu }\,}}} \right. \kern-0em} {{\nu }\,}}\,\,\,[10]; \\ \end{gathered} $

${{\delta }^{ + }} = 0.19{{\operatorname{Re} }^{{0.7}}}\,\,\,\,[7];$

$\begin{gathered} {{\delta }^{ + }} = \left\{ {\frac{{\operatorname{Re} }}{4}\left[ {\frac{{F + {{{\left( {{{\operatorname{Re} } \mathord{\left/ {\vphantom {{\operatorname{Re} } 4}} \right. \kern-0em} 4}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}{{0.5F + 0.333{{{\left( {{{\operatorname{Re} } \mathord{\left/ {\vphantom {{\operatorname{Re} } 4}} \right. \kern-0em} 4}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}} + } \right.} \right. \\ {{\left. { + \,\,\left. {\frac{{{{\operatorname{Re} } \mathord{\left/ {\vphantom {{\operatorname{Re} } {340}}} \right. \kern-0em} {340}}}}{{\sqrt {{{{\left[ {\ln \left( {10 + {{\operatorname{Re} } \mathord{\left/ {\vphantom {{\operatorname{Re} } {680}}} \right. \kern-0em} {680}}} \right)} \right]}}^{2}} + {{680} \mathord{\left/ {\vphantom {{680} {\operatorname{Re} }}} \right. \kern-0em} {\operatorname{Re} }}} }}} \right]} \right\}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}, \\ F = \frac{{{{{\tau }}_{c}}}}{{\rho {{{\left( {g{\nu }} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}\,\,\,\,[11]; \\ \end{gathered} $

$\begin{gathered} {{\delta }^{ + }} = {{\left( {{{\operatorname{Re} } \mathord{\left/ {\vphantom {{\operatorname{Re} } 2}} \right. \kern-0em} 2}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},\,\,\,\,\operatorname{Re} < 1160;\,\,\,\,{{\delta }^{ + }} = 0.0504{{\left( {\operatorname{Re} } \right)}^{{{7 \mathord{\left/ {\vphantom {7 8}} \right. \kern-0em} 8}}}}, \\ \operatorname{Re} \geqslant 1160\,\,\,\,[12]; \\ \end{gathered} $

${{\delta }^{ + }} = 0.095{{\operatorname{Re} }^{{0.8}}}\,\,\,\,[13].$

Для стекающей под действием гравитации пленки жидкости Нуссельтом была получена следующая формула: ${{\delta }^{ - }} = {{\left( {0.75\operatorname{Re} } \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}},$ где ${{\delta }^{ - }} = \delta {{\left( {{g \mathord{\left/ {\vphantom {g {{{{\nu }}^{2}}}}} \right. \kern-0em} {{{{\nu }}^{2}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}},$ которая может быть приведена к стандартному виду

${{\delta }^{ + }} = {{\left( {{{\delta }^{ - }}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} = {{\left( {0.75\operatorname{Re} } \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$

Размерная зависимость коэффициента трения от числа Рейнольдса выглядит следующим образом:

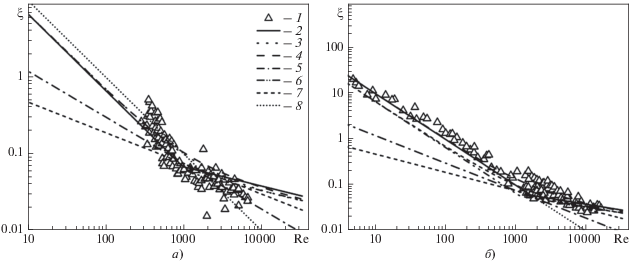
$\begin{gathered} {{{\tau }}_{w}} = {{\left( {{{\delta }^{ + }}} \right)}^{2}}\frac{{\rho {\nu }}}{\delta } = \frac{{128{{{\left( {{{\delta }^{ + }}} \right)}}^{2}}}}{{{{{\left( {4{{\delta U} \mathord{\left/ {\vphantom {{\delta U} \nu }} \right. \kern-0em} \nu }} \right)}}^{2}}}}\frac{{\rho {{U}^{2}}}}{8} = \frac{{128{{{\left( {{{\delta }^{ + }}} \right)}}^{2}}}}{{{{{\operatorname{Re} }}^{2}}}}\frac{{\rho {{U}^{2}}}}{8}; \\ \xi \left( {\operatorname{Re} } \right) = \frac{{128{{{\left( {{{\delta }^{ + }}} \right)}}^{2}}}}{{{{{\operatorname{Re} }}^{2}}}}. \\ \end{gathered} $

Результаты сравнения модели авторов с экспериментальными данными и данными других авторов показаны на рис. 5, из которого следует, что большинство формул применимы только в определенной области чисел Рейнольдса и с вполне приемлемой точностью описывают весь диапазон изменения числа Рейнольдса. Представленная в настоящей работе формула обладает близкой к остальным формулам погрешностью, но имеет более простую форму записи и удовлетворяет всем предельным переходам при больших и малых числах Рейнольдса.

Рис. 5.

Зависимость коэффициента трения для движения расплава под действием напряжения трения с потоком газа (а) и под действием силы тяжести (б) от числа Рейнольдса. 1 – экспериментальные данные: а – [7]; б – [8, 9]; 2 – текущая модель; 3 – формула [10]; 4 – [11]; 5 – [7]; 6 – [12]; 7 – [13]; 8 –формула Нуссельта

РАСЧЕТЫ ПРИ ТУРБУЛЕНТНОМ РЕЖИМЕ ТЕЧЕНИЯ

С использованием разработанной модели и представленной выше формулы были выполнены расчеты при турбулентном режиме движения пленки, характерном для большого энерговыделения. Скорость в этом режиме может быть найдена в явном виде по выражению

$U = {{\left( {\frac{{4\delta }}{{\nu }}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 7}} \right. \kern-0em} 7}}}}{{\left( {\frac{8}{{0.37}}\frac{{\left| {{{{\tau }}_{с}} - \rho g\delta } \right|}}{\rho }} \right)}^{{{4 \mathord{\left/ {\vphantom {4 7}} \right. \kern-0em} 7}}}}.$

Результаты расчетов для больших энерговыделений с учетом изменения режима течения представлены на рис. 6. Расчеты были выполнены для значений энерговыделения в 2, 5, 7 и 10 раз больших номинального (N_ном = 450 МВт/м³), что соответствует гипотетическому сценарию с набросом мощности (авария UTOP). Как видно из рис. 6, даже при энерговыделении в 10 раз большем номинального число Рейнольдса не превышает 6000, а характерное время потери массы вследствие плавления и стекания расплава оболочки твэла составляет несколько секунд. Все это говорит о том, что при высоких мощностях основным видом разрушения будет механическое, которое характеризуется меньшим временем реализации этого процесса.

Рис. 6.

Зависимости расчетного числа Рейнольдса (а) и расчетной скорости потери массы расплава (б) для стали 316 от времени. N: 1 – 2 N_ном; 2 – 5 N_ном; 3 – 7 N_ном; 4 – 10 N_ном

ВЫВОДЫ

1. Разработанные модели позволяют проводить расчет начального этапа аварии, который сопровождается термическим разрушением твэла и перемещением расплава под действием гравитации, вязких сил и трения с потоком теплоносителя.

2. Апробация расчетов с помощью предложенной модели в различных условиях течения показала, что модель достоверно описывает литературные данные, в том числе и с фазовым переходом.

3. В процессе аварии характерные времена потери массы оболочки твэла составляют несколько секунд, а число Рейнольдса для расплава не превышает 6000.

Список литературы

Анализ экспериментальных данных по плавлению и движению расплава металла по цилиндрической поверхности / П.Д. Лобанов, Э.В. Усов, А.И. Светоносов, С.И. Лежнин // Теплофизика и аэромеханика. 2020. Т. 27. № 3. С. 483–490.
Experimental and numerical determination of the rate of mass loss and temperature evolution of the single fuel rod cladding imitator during its melting / P.D. Lobanov, E.V. Usov, V.S. Zhdanov, A.I. Svetonosov, I.A. Klimonov // Nucl. Eng. Des. 2020. V. 363. P. 110681. https://doi.org/10.1016/j.nucengdes.2020.110681
Usov E.V. Analytical investigation of the fuel rod destruction and melt relocation along the surface of the fuel rod // J. Phys. Conf. Series. 1382. 2019. P. 012146. https://doi.org/10.1088/1742-6596/1382/1/012146
Кузнецов И.А., Поплавский В.М. Безопасность АЭС с реакторами на быстрых нейтронах. М.: ИздА-т, 2012.
Алексеенко С.В., Накоряков В.Е., Покусаев Б.Г. Волновое течение пленок жидкости. Новосибирск: Наука, 1992.
Лойцянский Л.Г. Механика жидкости и газа. М.: Дрофа, 2003.
Asali J.C., Hanratty T.J., Andreussi P. Interfacial drag and film height for vertical annular flow // AiChE J. 1985. V. 31. Is. 6. P. 895–902. https://doi.org/10.1002/aic.690310604
Jackson M. Liquid films in viscous flow // AiChE J. 1955. V. 1. Is. 2. P. 231–240. https://doi.org/10.1002/aic.690010217
Karapantsios T., Paras S., Karabelas A. Statistical characteristics of free falling films at high Reynolds number // Int. J. Multiphase Flow. 1989. V. 15. Is. 1. P. 1–21. https://doi.org/10.1016/0301-9322(89)90082-7
Henstock W.H., Hanratty T.J. The interfacial drag and the height of the wall layer in annular flows // AiChE J. 1976. V. 22. Is. 6. P. 990–1000. https://doi.org/10.1002/aic.690220607
Гешев П.И. Простая модель для расчета толщины турбулентной пленки жидкости, увлекаемой силой тяжести и потоком газа // Теплофизика и аэромеханика. 2014. Т. 21. № 5. С. 579–586.
Kosky P.G. Thin-liquid films under simultaneous shear and gravity forces // Int. J. Heat Mass Transfer. 1971. V. 14. Is. 8. P. 1220–1224. https://doi.org/10.1016/0017-9310(71)90216-X
Brauer H. Stoffaustausch beim Rieselfilm // Chem. Ing. Tech. 1958. V. 30. Is. 2. P. 75–84. https://doi.org/10.1002/cite.330300205

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теплоэнергетика

Архивы выпусков Информация о журнале Отправить рукопись в журнал