Теплофизика высоких температур, 2019, T. 57, № 3, стр. 426-430

ВВЕДЕНИЕ

Всякое тело понуждается к движению приложенной силой. В газе и жидкости такой силой является градиент давления. Примером может служить течение, возникающее в одномерной простой волне сжатия Римана. При одномерном изэнтропическом течении в направлении x до образования разрывов распределение скорости U в волне определяется соотношениями

где P – давление, $\rho $ – плотность, с – местная скорость звука, t – время, f(U) – функция, зависящая от начальных граничных условий. В политропном газе (см., например, [1]):

Здесь γ – показатель адиабаты, индекс 0 соответствует покоящемуся газу. Полезная одномерная модель простой волны при распространении в канале не учитывает особенностей возникающего в ней течения и поэтому не отражает ряда реальных процессов. Две из этих особенностей являются следствием ограниченного сечения канала, как то: вязкое трение, возникающее при взаимодействии текущей среды со стенками канала, а также изменение формы фазовой поверхности звуковых волн.

ТРЕНИЕ ПОТОКА О СТЕНКИ КАНАЛА

Рассмотрим роль трения в простом случае ламинарного течения несжимаемой среды в направлении оси х канала, образованного парой параллельных пластин с зазором между ними d. Трение о стенки тормозит движение среды. Компонента i вектора J плотности потока импульса среды через поверхность, перпендикулярную к одной из осей координат в направлении нормали n к ней, выражается через тензор плотности потока импульса П_ik [1]:

В этом выражении первое слагаемое представляет действующую силу давления. Второе слагаемое описывает обратимый перенос импульса, вызванный перемещением элементов среды. Тензор напряжений

в третьем слагаемом в (2) означает необратимый перенос импульса, который связан с трением и зависит от коэффициента динамической вязкости η.

В простой волне сразу за фронтом скорость течения постоянна по сечению. Со временем под действием трения скорость в канале U($U{\text{,}}$ V = 0, W = 0) приобретает параболический профиль, известный как профиль Пуазейля:

Согласно (2), в середине канала при z = d/2 компоненты потока импульса по осям х и z имеют вид

На стенке (z = 0) движение жидкости отсутствует и в переносе импульса не участвует, поэтому

Второе слагаемое компоненты ${{J}_{{z0}}}$ означает дополнительный поток импульса в направлении нормали к поверхности стенки:

В связи с этим заметим, что отношение динамической части продольного потока импульса (4) в средней части течения (3) к поперечному потоку импульса у стенки (5) с точностью до численного множителя равняется числу Рейнольдса:

Следовательно, число Рейнольдса указывает на долю потока импульса, теряемую течением на преодоление вязкого трения. Перенос импульса всегда связан с переносом энергии, так что число Рейнольдса характеризует также потери энергии течением, обусловленные вязкостью. Вид профиля скорости течения с градиентом в направлении от стенки является явным подтверждением влияния диссипации. Согласно [1], зависимость ее удельной величины от поперечного градиента скорости определяется выражением

Градиент ${{\partial U} \mathord{\left/ {\vphantom {{\partial U} {\partial z}}} \right. \kern-0em} {\partial z}}$ быстро растет по мере приближения к стенке, и диссипация локализуется в слое трения, в основном у стенки. Граница этого слоя определяется так называемой толщиной вытеснения δ – расстоянием, на которое потенциальное течение оттесняется от стенки под действием уменьшения скорости, вызванного трением [1]:

Оттеснение потока означает поперечное движения среды, W > 0, и наличие градиента давления по нормали к основному потоку в направлении от стенки. И в соответствии с (6) получим

Изменение параметров среды у стенки и их зависимость от градиента скорости ${{\left. {{{\partial U} \mathord{\left/ {\vphantom {{\partial U} {\partial z}}} \right. \kern-0em} {\partial z}}} \right|}_{w}}$ имеет место и в пограничном слое простой волны, что подтверждают результаты измерений коэффициента теплопередачи α от газа к стенке в процессе при формирующемся профиле скорости течения [2]. По этим данным, сразу за фронтом профиль скорости близок к прямоугольному, и градиент максимален. Соответственно, коэффициент α превышает его значение вдали от фронта почти на порядок.

ОГРАНИЧЕННОСТЬ УРАВНЕНИЙ ПРАНДТЛЯ ДЛЯ ПОГРАНИЧНОГО СЛОЯ

Для описания течения в ламинарном пограничном слое принято использовать уравнения Прандтля. Они получены в предположении малого поперечного движения, W ⪡⪡ $U,$ что предполагает постоянство давления в каждом сечении потока:

Условие (8) дает возможность описать течение в пограничном слое, используя давление в потенциальной части течения, определяемое уравнением Бернулли:

Такой подход сильно упрощает описание пограничного слоя, но на основе совсем другой системы уравнений движения. Действительно, уравнения движения включают уравнение Навье–Стокса. Его компоненты в стационарном двумерном течении имеют вид

В первом уравнении пропадает слагаемое с производной ${{\partial U} \mathord{\left/ {\vphantom {{\partial U} {\partial z}}} \right. \kern-0em} {\partial z}}$ ≠ 0 (W = 0), а второе выражение заменяется равенствами P(z) = P(x) и W = 0, т.е. уравнения Прандтля не учитывают диссипацию. Ее роль можно выяснить, придавая соотношению (9) статус обобщенного уравнения Бернулли [3], что дает возможность проверить корректность допущения (8), оценить профиль давления в пограничном слое и конкретизировать неравенство (7).

КОРРЕКЦИЯ ИСХОДНЫХ ПРЕДПОЛОЖЕНИЙ

В установившемся адиабатическом течении значение const в (9) должно сохраняться во всем объеме течения, иначе оно постоянно только вдоль линии тока. Значение const для линий тока пограничного слоя отличается уровнем диссипации. В этом необратимом процессе часть механической энергии переходит в тепло, поэтому в уравнении Бернулли следует учесть удельные потери энергии на трение ν$\left( {{{\partial U} \mathord{\left/ {\vphantom {{\partial U} {\partial z}}} \right. \kern-0em} {\partial z}}} \right)$ и энергию поперечного движения:

Следуя стандартному методу решения (см., например, [1]), перейдем к безразмерному виду уравнения (10). Для этого выразим компоненты скорости через функцию тока ψ согласно $U(x, z) = {{\partial \psi } \mathord{\left/ {\vphantom {{\partial \psi } {\partial z}}} \right. \kern-0em} {\partial z}},$ $W(x, z) = {{\partial \psi } \mathord{\left/ {\vphantom {{\partial \psi } {\partial x}}} \right. \kern-0em} {\partial x}}$ и введем переменные Блазиуса $\zeta = z\sqrt {{{{{U}_{0}}} \mathord{\left/ {\vphantom {{{{U}_{0}}} {\nu x}}} \right. \kern-0em} {\nu x}}} ,$ $\psi = \sqrt {\nu x{{U}_{0}}} f(\zeta )$. В новых переменных представим (10) зависимостью относительного изменения корректируемого распределения давления у стенки от безразмерной функции тока $f(\zeta )$ и ее производных [4]:

Здесь $\operatorname{Re} = {{x{{U}_{0}}} \mathord{\left/ {\vphantom {{x{{U}_{0}}} \nu }} \right. \kern-0em} \nu },$ производная $f{\kern 1pt} {\text{'}}(\zeta )$ соответствует продольной компоненте скорости течения, разность $\zeta {\kern 1pt} f{\kern 1pt} {\text{'}}(\zeta ) - f(\zeta )$ означает поперечную компоненту скорости, производная $f{\kern 1pt} {\text{''}}(\zeta )$ выражает силу трения. Функция $f(\zeta )$ является решением обыкновенного дифференциального уравнения [1]

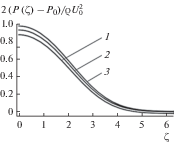
Коррекцию профиля давления дает решение уравнения (11), результаты которого показаны на рис. 1 для чисел Рейнольдса течения Re = 30, 100 и 1000. Таким образом, вязкое трение ведет к перераспределению профиля давления в потоке, которое проявляется в повышении давления на границах течения. Поправка к профилю давления имеет порядок величины ${{\rho {{U}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{\rho {{U}^{{\text{2}}}}} 2}} \right. \kern-0em} 2}.$ Она мала относительно давления Р₀ и при М $ \ll $ 1 составляет всего несколько процентов от Р₀. Например, для воды, движущейся со скоростью 20 см/с, при x = 1 см и числе Рейнольдса потока ${{\operatorname{Re} }_{f}} = {{10}^{4}}$ она равна $\rho {{{{U}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{U}^{{\text{2}}}}} {2{{P}_{0}}}}} \right. \kern-0em} {2{{P}_{0}}}} \approx 0.02.$ При этом отношения пульсаций скорости и давления к их средним значениям – величины одного порядка.

Рост давления у стенки не выглядит неожиданным. Более того, он легко предсказуем. Согласно (9), падение скорости в пограничном слое как раз и означает увеличение давления, которое реализуется в виде локализованных у стенки зон возмущения. Как известно [1], зоны избыточного давления эмитируют акустические волны. Их совокупность создает в объеме канала пространственно-временнóе поле возмущений, которое нарушает струйность течения. Течение, инициируемое поршнем (и иными методами), теряет свойство автомодельности и не отвечает определению “простая волна”.

ТЕЧЕНИЕ В ПРОСТОЙ ВОЛНЕ КАК ВОЛНОВОЙ ПУЧОК

Перейдем теперь к профилю звуковых волн, образующих течение (3), и рассмотрим простую волну сжатия в канале, имеющем вид цилиндрической трубы. Существует три способа возбуждения простой волны сжатия в трубе [5]: созданием перепада давления на открытом конце ресивера, при истечении из большого объема и при перемещении поршня. Возмущения на входе в трубу в первых двух вариантах непредсказуемым образом осложняют анализ свойств течения. Поэтому остановимся на формировании течения перед поршнем.

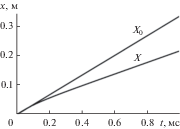
Решение задачи об одномерном движении газа в трубе перед поршнем хорошо известно (см., например, [1]). В момент t = 0 поршень начинает движение из точки x = 0 в сторону x > 0 по закону X '(t). Перемещаясь, поршень создает простую волну. Течение газа в волне простирается от фронта первичной впереди бегущей звуковой волны Х₀ = c₀t до поршня X(t). Скорость течения U(x,t) и зависящее от нее распределение параметров (1) описывают параметрические уравнения

Обычно скорость поршня X '(t) вначале возрастает, а затем стремится к пределу U₀. Для определенности представим ее выражением

Траектории фронта первичной звуковой волны Х₀ и поршня X определяются соотношениями

До появления разрывов их взаимное расположение при движении в воздухе показано на рис. 2 для c₀ = 340 м/с, U₀ = 200 м/с и τ = 0.1 мс.

Простая волна обычно представляется волновым пакетом генерируемых поршнем плоских волн, которые поддерживают течение, компенсируя потери на трение. Но волновой фронт этих волн может быть плоским лишь при условии, что его диаметр не ограничен. В канале он, естественно, конечен, и фактически это не волновой пакет, а волновой пучок, свойства которого хорошо известны из оптики [6]: его распространению сопутствует дифракционная расходимость, как показано на рис. 3.

Волновой фронт пучка принято считать плоским на протяжении релеевской длины L_R, в пределах которой расходимостью можно пренебречь:

За пределами L_R, в дальней зоне, угол расходимости пучка составляет

и фронту волны можно приписать форму сферического сегмента. Закономерности (14) и (15) применимы также и к акустическим волнам, поскольку волновое уравнение не зависит от природы дифрагирующих полей.

КАНАЛ В РОЛИ ВОЛНОВОДА

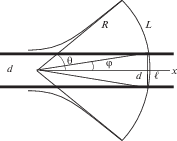
Как следует из (12), (13) и (1), частотные характеристики параметров простой волны ν ≈ 1/τ зависят от постоянной τ, которой соответствует длина волны λ = сτ. Тогда соотношения (14), (15) позволяют оценить релеевскую длину L_R и угол расходимости волнового пучка θ для диаметра трубы d. Так, если d = 3 см, то L_R ≈ 8 см и θ ≈ 67°. Далее фронт волны приобретает форму сферического сегмента растущего радиуса R = ct при соответствующем диаметре его основания, D = 2ct sin θ. Конфигурация сегмента в продольном сечении на фоне контура трубы приведена на рис. 4.

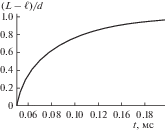
В этом сечении часть большой окружности на поверхности сегмента имеет длину L = 2ctθ. Но в направлении x > 0 по трубе распространяется только центральная часть фронта волны, и в ней длина большой окружности составляет $\ell $ = = 2ctφ (φ < θ). Угол φ задан условием d = 2ct sin φ. Поскольку φ < θ и D = 2ct sin θ > d, распространение сегмента сопровождается отражением от стенок сферического пояса, выходящего за пределы диаметра трубы и имеющего ширину Δ = (D – d)/2. Учитывая симметрию конфигурации, зависимость длины отраженного сферического пояса от времени оценим как

Эта зависимость приведена на рис. 5 и показывает возвращение в объем течения части волны после отражения от стенки.

Объем, занимаемый простой волной, имеет длину X₀(t) – X(t). Он заполнен акустическими волнами с составляющей волнового вектора в направлении нормали к скорости течения. Суперпозиция этих волн и их последующих отражений создает в канале моды колебаний, структура которых зависит от характера движения поршня (12) и от формы сечения канала. На структуру колебаний влияет также затухание волн, которое становится функцией не только коэффициента отражения волны, но и геометрического фактора, связанного с изменением кривизны волнового фронта. В этом отношении канал выполняет функции акустического волновода [8].

ЗАКЛЮЧЕНИЕ

Математический институт Клэя инициировал поиск решений семи величайших нерешенных математических проблем [9]. Нерешенные проблемы существуют и в физике. К ним можно отнести, например, зарождение турбулентности, создание протяженного волнового пучка конечной апертуры и другие. Между тем причина полуторавековой задержки их решения довольно проста. Дело в том, что аппарат фундаментальной теории волны Римана используется для описания простой волны в канале. При этом не учитывается наличие стенок, которые служат причиной возникновения трения и дифракционной расходимости волн конечной апертуры, компенсирующих потери энергии на трение. В результате в канале течение с волновым фронтом теряет струйность и изэнтропичность и не отвечает определению “простая волна”. В то же время трение и расходимость имеют важные следствия. Эти следствия известны и исследуются как отдельные независимые направления.

Торможение течения и вызванная трением диссипация ведут к повышению давления в локальных зонах у стенок. Эти зоны излучают акустические сферические волны. Совокупность волн формирует пространственно-временнóе поле пульсаций параметров течения. Пока скорость течения мала, эти пульсации незаметны на фоне случайных возмущений другого происхождения, и течение называется ламинарным. С ростом скорости пульсации усиливаются. При критическом числе Рейнольдса их энергия становится значительной, и течение называется турбулентным.

Дифракционной расходимости элементарных волн фактически волнового пучка сопутствует отражение волн от стенок, что ведет к образованию мод колебаний в канале. В акустическом волноводе наблюдается именно этот процесс. Систему канал–“простая волна” можно также рассматривать как акустический волновод. Но модовая структура этой системы имеет особенность. Она состоит в том, что к пространственно-когерентной модовой структуре добавляется пространственно-временнóе поле пульсаций. В силу их случайного возникновения они не являются когерентными.

Дифракционная расходимость в принципе неустранима. В канале размер сечения потока удерживают стенки. Но существует возможность компенсировать расходимость, обращая направления векторов (см. рис. 3). Эту операцию выполняет аксикон, а также коническое зеркало или киноформ. В силу аксиальной симметрии фокусировки гауссов профиль волнового пучка аксикон трансформирует в поле с радиальным профилем типа функции Бесселя, т.е. образуется акустический бесселев пучок. Релеевская длина сформированного таким образом волнового пучка на много порядков превосходит длину, свойственную фокусировке волнового пучка сферической линзой. Удержание сечения бесселева пучка осуществляет конфигурация оптических волновых векторов, аналогичная стационарной конфигурации Маха [10]. Указанная особенность бесселева пучка позволяет создать простую волну конечного диаметра в свободном пространстве, не прибегая к помощи ударной трубы [11, 12].