Теплофизика высоких температур, 2021, T. 59, № 1, стр. 69-73

ВВЕДЕНИЕ

Фазовые переходы первого рода предполагают существование метастабильных состояний. Две фазы, метастабильные по отношению к некоторой третьей фазе, могут равновесно сосуществовать друг с другом на плоской межфазной границе [1]. Последнее означает, что в однокомпонентной системе каждая из линий фазового равновесия может быть продолжена за тройную точку. Метастабильное продолжение линии плавления встречается в области отрицательных давлений со спинодалью растянутой жидкости [2, 3]. Точка встречи этих линий является особой для жидкой фазы. В то же время она ничем не выделяется для сосуществующей с ней кристаллической фазы.

Твердые тела по-разному реагируют на бесконечно малые однородные и неоднородные возмущения плотности. Это связано с тем, что при всяком неоднородном изменении плотности в твердом теле возникают сдвиговые деформации, медленно убывающие с расстоянием [4].

Состояние кубического кристалла, находящегося под гидростатическим давлением p, будет устойчивым относительно однородных деформаций, если выполнены условия [5]:

Здесь K – модуль всестороннего сжатия, являющийся мерой сопротивления вещества по отношению к объемной деформации; μ, $\mu {\kern 1pt} '$ – модули простого и тетрагонального сдвигов, характеризующие отклик твердого тела на статические сдвиговые деформации; ${{\tilde {c}}_{{11}}}$, ${{\tilde {c}}_{{12}}}$, ${{\tilde {c}}_{{44}}}$ – эффективные упругие постоянные Бирча, функции температуры и давления.

Неравенства (1) известны как борновские критерии устойчивости [6]. Они нарушаются на границе существенной неустойчивости кристалла по отношению к однородным деформациям, которая определяется первым обратившимся в нуль модулем упругости. Нарушение первого критерия в (1) обычно называется спинодальной неустойчивостью.

Деформации и напряжения в твердых телах, вызываемые тепловым движением, являются, как правило, неоднородными. Неоднородные флуктуации плотности в твердом теле – это тепловые продольные звуковые волны, которые зависят от волнового вектора $\vec {q}$ [4]. Если ось z декартовой системы координат направлена вдоль вектора $\vec {q}$, пространственно неоднородной флуктуации отвечает лишь одна отличная от нуля компонента тензора деформаций ${{u}_{{zz}}} = {{\partial {{u}_{z}}} \mathord{\left/ {\vphantom {{\partial {{u}_{z}}} {\partial z}}} \right. \kern-0em} {\partial z}} \equiv u$. Средний квадрат флуктуаций фурье-компонентa смещения u есть [4]

где k_B – постоянная Больцмана, V – объем кристалла, $\tilde {K}$ – модуль одностороннего сжатия, зависящий от направления деформации.

Для главных направлений ГЦК-кристалла имеем [7]

Таким образом, в анизотропном твердом теле в пределе q → 0 при K = 0, когда $\mu > 0$ и $\mu {\kern 1pt} ' > 0$, пространственно-неоднородные флуктуации плотности конечны.

Здесь анализируются только длинноволновые флуктуации ($q \ll {{\xi }^{{ - 1}}}$, где $\xi $ – корреляционная длина), поэтому член, пропорциональный q², в (2) в явном виде не выписан и далее не рассматривается.

Сохраняя восстановительную реакцию на бесконечно малые изменения параметров состояния, метастабильная система проявляет неустойчивость относительно локальных возмущений определенного масштаба [1, 8]. Потеря устойчивости происходит в отдельных “точках”. Эти “точки роста”, или жизнеспособные зародыши, могут формироваться как на дефектах, неоднородностях в строении твердых тел, так и на порождаемых в процессе теплового движения флуктуациях плотности. Спонтанное зародышеобразование описывается классической теорией зародышеобразования (КТЗ), которая определяет число жизнеспособных зародышей, образующихся в единице объема за единицу времени (частоту зародышеобразования) [8]:

где ρ – плотность кристалла, Z – неравновесный фактор Зельдовича, D – коэффициент диффузии зародышей в пространстве их размеров, ${{W}_{*}}$ – работа образования критического зародыша.

В неограниченной изотропной упругой среде радиус критической полости [9] равен

а работа ее образования Здесь ${{\gamma }_{e}}$ – эффективная поверхностная свободная энергия на межфазной границе жидкость–газ, $\left\langle \mu \right\rangle $ – сдвиговый модуль изотропного твердого тела.

Если определяющим механизмом формирования кавитационных полостей является выход вакансий, для коэффициента диффузии зародышей имеем [10]

где ${{n}_{{{{A}_{*}}}}}$ – число частиц на поверхности критического зародыша, ${{\nu }_{0}}$ – частота колебаний частиц, $E{\kern 1pt} '$ – энергия активации диффузии в кристалле. Частота колебаний ${{\nu }_{0}}$ оценивается по соотношению $h{{\nu }_{0}} \approx {{k}_{{\text{B}}}}T$, где h – постоянная Планка.

В данной работе методом молекулярно-динамического (МД) моделирования исследуется устойчивость леннард-джонсовского (ЛД) ГЦК-кристалла относительно бесконечно малых и конечных изменений параметров состояния при температурах ниже температуры конечной точки линии плавления T_K.

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

Исследуемые системы содержали от 2048 до 108 000 взаимодействующих частиц, которые размещались в кубической ячейке в узлах ГЦК-решетки. На границы ячейки налагались периодические граничные условия.

Свойства кристалла рассчитывались в NVT-ансамбле с использованием классического МД-кода LAMMPS [11]. Процесс зарождения и роста новой фазы протекал в условиях постоянства объема и энергии (NVE-ансамбль).

Устойчивость кристаллической фазы исследовалась при температурах $T < T_{K}^{{}} = 0.529$ [2] по изотермам T = 0.2, 0.3 и 0.4. Здесь и далее рассчитываемые величины приводятся в безразмерном виде. Единицами приведения выступают параметры потенциала $\sigma $, $\varepsilon $, масса частицы m и постоянная Больцмана ${{k}_{{\text{B}}}}$: единица длины $\sigma $, температуры ${\varepsilon \mathord{\left/ {\vphantom {\varepsilon {{{k}_{{\text{B}}}}}}} \right. \kern-0em} {{{k}_{{\text{B}}}}}}$, давления ${\varepsilon \mathord{\left/ {\vphantom {\varepsilon {{{\sigma }^{3}}}}} \right. \kern-0em} {{{\sigma }^{3}}}}$, плотности $\sigma _{{}}^{{ - 3}}$, времени $\sigma {{({m \mathord{\left/ {\vphantom {m \varepsilon }} \right. \kern-0em} \varepsilon })}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$. Парный потенциал ЛД обрезался на расстоянии r_c = 6.58σ от центра взаимодействия.

Заход в метастабильную область осуществлялся пошаговым уменьшением плотности путем увеличения длины ребер ячейки и соответствующего масштабирования координат частиц. Результаты расчета давления в кристаллической фазе представлены на рис. 1. При ${{\left( {{{\partial p} \mathord{\left/ {\vphantom {{\partial p} {\partial \rho }}} \right. \kern-0em} {\partial \rho }}} \right)}_{T}} < 0$ МД-моделирование проводилось до тех пор, пока не происходил фазовый распад кристалла.

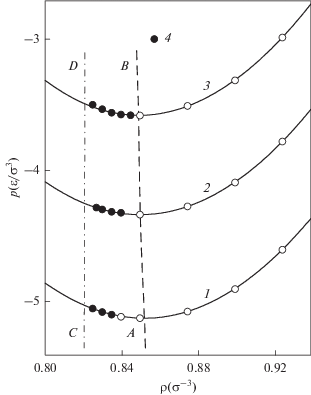
Для определения границы идеальной прочности нагруженного ГЦК-кристалла рассчитывались эффективные упругие постоянные ${{\tilde {c}}_{{\alpha \beta }}}$, которые учитывают как изменение свободной энергии Гельмгольца при деформации вблизи исходного состояния с заданным значением p, так и работу против гидростатического давления силами, обусловленными этой деформацией. Процедура расчета постоянных ${{\tilde {c}}_{{\alpha \beta }}}$ подробно описана в работах [12–14].

Результаты расчета модулей всестороннего сжатия, простого и тетрагонального сдвигов ЛД ГЦК-кристалла при всех температурах свидетельствуют, что первым обращается в нуль объемный модуль. Модули μ и $\mu {\kern 1pt} '$ сохраняют при этом конечные, положительные значения. Это отличает поведение устойчивости кристаллической фазы в области температур $T < {{T}_{K}}$ от области $T > {{T}_{K}}$, где потеря устойчивости ГЦК-кристаллом связана с тетрагональным сдвигом ($\mu {\kern 1pt} ' = 0$) [14].

Экстраполяция результатов расчета модулей одностороннего сжатия для трех главных направлений ГЦК-решетки в ту часть метастабильной области кристаллической фазы, где МД-вычисления проведены быть не могут, свидетельствует, что первым обращается в нуль модуль $\tilde {K}$[100]. Это происходит за спинодалью (K = 0). На спинодали кристаллическая фаза сохраняет восстановительную реакцию на бесконечно малые возмущения плотности.

Кинетика разрушения кристаллического состояния исследовалась при растяжениях, отмеченных на рис. 1 точками 4. Во всех случаях распад кристаллической фазы связан с образованием и ростом локальной неоднородности. Начало разрушения кристалла регистрировалось по скачку давления. Время появления жизнеспособной локальной неоднородности $\tau $ связывалось с моментом, когда давление в кристалле на 2–3% превышало его среднее значение в однородном состоянии.

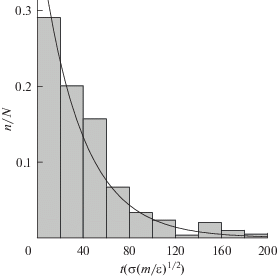
При температурах, близких к T_K, жизнеспособная локальная неоднородность имела вид кавитационной полости. Полость свободна от частиц, а скорость ее роста почти в десять раз выше, чем скорость роста жидкой капли в случае плавления кристалла [14]. Для фиксированных значений температуры и давления распределение времен ожидания появления первой жизнеспособной полости описывается законом Пуассона (рис. 2). Среднее время ожидания полости $\bar {\tau }$ рассчитывалось как среднее арифметическое по числу событий зародышеобразования N. Среднее время связано с частотой зародышеобразования соотношением $J = {{\left( {\bar {\tau }V} \right)}^{{ - 1}}}$.

Частота зародышеобразования как функция давления представлена на рис. 3, где данные МД-моделирования сопоставляются с результатами расчета по КТЗ в рамках модели сферического зародыша в изотропном твердом теле. Сдвиговый модуль изотропного твердого тела $\left\langle \mu \right\rangle $ определялся по данным о модулях μ и $\mu {\kern 1pt} '$ ГЦК-кристалла как $\left\langle \mu \right\rangle = {{\left( {3\mu + 2\mu {\kern 1pt} '} \right)} \mathord{\left/ {\vphantom {{\left( {3\mu + 2\mu {\kern 1pt} '} \right)} 5}} \right. \kern-0em} 5}$ [15]. При нахождении работы образования и радиуса сферического зародыша использовались значения поверхностной свободной энергии на плоской межфазной границе кристалл–газ ${{\gamma }_{{e\,\infty }}}$ [16].

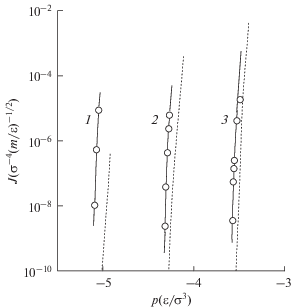
При существенном, до семи порядков по частоте нуклеации (T = 0.2), расхождении данных МД-моделирования и теории (рис. 3) имеет место близость наклонов изотерм J, т.е. производных $\left( {{{d\ln J} \mathord{\left/ {\vphantom {{d\ln J} {dp}}} \right. \kern-0em} {dp}}} \right){{{\kern 1pt} }_{T}}$.

С использованием МД-данных о частоте нуклеации рассчитаны работа образования критического зародыша (уравнение (3)), поверхностная свободная энергия ${{\gamma }_{{e*}}}$ и радиус $R{{{\kern 1pt} }_{*}}$ критического зародыша (уравнения (4), (5)). При T = 0.4 и ρ = 0.845 получены значения $R{{{\kern 1pt} }_{*}}$ = 0.68, ${{\gamma }_{{e*}}}$ = 1.96. Уменьшение плотности кристалла до ρ = 0.825 приводит к уменьшению размера критического зародыша и поверхностной свободной энергии: $R{{{\kern 1pt} }_{*}}$ = 0.20, ${{\gamma }_{{e*}}}$ =  1.14. Поверхностная свободная энергия на плоской межфазной границе кристалл–газ при данной температуре равна ${{\gamma }_{{e\,\infty }}}$ = 2.75 [16].

Результаты МД-моделирования позволяют оценить эффективный радиус полости, с которого начинается ее необратимый рост. При температуре T = 0.4 и плотностях ρ = 0.825 и 0.845 это 0.24 и 0.52 соответственно. КТЗ дает для этих плотностей значения $R{{{\kern 1pt} }_{*}}$ = 0.48, ${{R}_{*}}$ = 0.95. Таким образом, можно предположить, что вблизи температуры конечной точки линии плавления расхождения в частоте зародышеобразования между данными МД-моделирования и КТЗ связаны с размерной зависимостью поверхностной свободной энергии на границе кристалл–полость.

ЗАКЛЮЧЕНИЕ

Молекулярно-динамическое моделирование ЛД ГЦК-кристалла показало, что при $T < {{T}_{K}}$ первым обращается в нуль модуль всестороннего сжатия K, при этом потери восстановительной реакции ГЦК-кристаллом на длинноволновые возмущения плотности не наблюдается. Кристалл сохраняет устойчивость и в состояниях с $K \leqslant 0$. Это отличает поведение ГЦК-кристалла при $T < {{T}_{K}}$ от $T > {{T}_{K}}$, где состояния, в которых происходит зануление какого-либо из модулей упругости, не достигаются, а экстраполяция модулей к их нулевым значениям свидетельствует, что первым обращается в нуль модуль тетрагонального сдвига $\mu {\kern 1pt} '$ [14].

Устойчивость кристалла относительно бесконечно малых неоднородных деформаций определяет модуль одностороннего сжатия $\tilde {K}$. Экстраполяция модуля $\tilde {K}$ к нулевому значению свидетельствует, что потеря устойчивости ГЦК-кристаллом связана с направлением [100].

При $T < {{T}_{K}}$ в состояниях с $K \leqslant 0$ фазовый распад носит активационный характер и начинается с появления первого жизнеспособного зародыша. Времена ожидания жизнеспособных зародышей распределены по закону Пуассона. Это характерно как для распада кристаллической фазы при $T > {{T}_{K}}$, когда образуются зародыши жидкой фазы [14], так и для других метастабильных фаз [1, 2].

Сопоставление результатов МД-расчетов частоты зародышеобразования с данными КТЗ показывает, что при удовлетворительном согласии в барической зависимости J имеют место систематические расхождения в абсолютных значениях частоты, которые достигают шести–семи порядков. Рассчитанные в соответствии с КТЗ по МД-данным о частоте зародышеобразования значения поверхностной свободной энергии критического зародыша меньше, чем на плоской межфазной границе. Меньшее значение имеет при этом и радиус критического зародыша. Для T = 0.4 расхождения в значениях ${{\gamma }_{{e\,\infty }}}$ и ${{\gamma }_{{e*}}}$ составляют 30–60%. Радиусы критических зародышей здесь – 0.20–0.68, что хорошо согласуется с прямыми оценками размеров критических полостей в процессе МД-моделирования.

Работа выполнена при поддержке Российского научного фонда (проект № 18-19-00276).