Теплофизика высоких температур, 2021, T. 59, № 6, стр. 960-963

ВВЕДЕНИЕ

Большинство существующих моделей распространения инфекции моделируют спонтанное развитие эпидемии и описывают все ее стадии. Есть два типа таких моделей: модели SIS и модели SIR и SEIR. Первые относятся к пионерской работе [1] и используют предположение, что выздоровевшие люди могут немедленно снова заразиться. Модели SIR построены на предположении, что выздоровевшие имеют иммунитет и выпадают из эпидемии (см., например, [2]). Модели SIS используются в математической эпидемиологии [3]. Обзор приведен в [4] (см. также приведенные там ссылки). Баланс между восприимчивыми к инфекции и инфицированными членами популяции при различных условиях передачи инфекции является предметом исследования в [5]. В настоящее время эти базовые модели развиваются с учетом процесса вакцинации [6–9].

Модели SIR (“восприимчивый–заразный–удаленный”) и SEIR (“восприимчивый–зараженный–заразный–удаленный”) предполагают иммунитет выздоровевших людей ([10, 11] и ссылки в них), как и в предлагаемой модели. Однако возможность немедленного выздоровления, содержащаяся в моделях типа SIR и SEIR, весьма сомнительна для заболевания COVID-19. Наличие в этих моделях производной числа инфекционных людей по времени dI/dt определяется, в частности, членом –γI (где γ^–1 – средняя продолжительность заболевания). Следовательно, существует вероятность немедленного выздоровления, что противоречит данным о течении COVID-19.

В данной работе учтены некоторые особенности COVID-19, следующие из недавней дискретной модели эпидемии [12]. Важной особенностью используемой модели является запаздывание, учитывающее подтвержденное клиническими данными длительное вирусоносительство. В отличие от запаздывания, рассматриваемого в [13], предлагаемая модель с запаздыванием предполагает, что переболевший является иммунным и в этом отношении соответствует модели SIR, а не SIS. В то же время рассматриваемая модель запаздывания не предполагает выделения отдельной категории скрытых вирусоносителей (см., например, SEIR-модель с запаздыванием в [14]). Скрытые носители вируса могут заражать окружающих без запаздывания и в этом смысле подобны инфицированным, в отличие от модели SEIR. Цель данной работы заключается в получении простой оценки для минимальной величины насыщения эпидемии в условиях модели, приближенной к реальности, где есть лишь носители вируса, способные заражать в течение времени d вне зависимости от своего субъективного состояния, иммунные переболевшие и не иммунные здоровые, способные заразиться. Различие между зараженными и заразными для вируса SARS-CoV-2 и его мутантов в данной модели не предполагается существенным. Вследствие этого, в отличие от моделей типа SIR, рассматриваемая модель для замкнутой популяции имеет три независимых параметра. Один из них – средняя продолжительность заболевания d, понимаемая как продолжительность того времени, в течение которого зараженный заразен. Другой параметр, скорость передачи инфекции p, подобен числу репродуктивности R₀ в моделях SIR. Параметр p есть произведение p = n_ck, где n_c – среднее количество опасных контактов в день для одного инфицированного человека, а k – средняя восприимчивость к вирусу здорового человека.

ОПИСАНИЕ МОДЕЛИ И РЕЗУЛЬТАТЫ РАСЧЕТА

Поскольку уже на ранней стадии эпидемии власти прибегают к изоляции, здесь рассматриваются замкнутые популяции (странa, регион, город и т.д.). При этом необходимо знать исходное состояние популяции, а именно количество инфицированных в начале эпидемии.

Согласно [12], дискретные уравнения, описывающие эпидемию день за днем (как и официальная статистика [8], которая здесь учитывается), имеют при l > d вид

где N_I(l) – количество инфицированных людей (носителей вируса, способных инфицировать окружающих) в день l, N_T(l) – общее количество заразившихся ко дню l с начала эпидемии. При l ≤ d предполагается, что удаленных (выздоровевших или умерших) нет, поэтому N_I(l) = N_T(l). Фактор n_ck[1 – – (N_T(l)/N)] отражает постепенное изменение параметра p = n_ck, поскольку заражение зараженного, а также удаленного (так или иначе переболевшего) предполагается невозможным.

Исключая N_I(l), получаем нелинейное уравнение относительно N_T(l):

На рис. 1 показаны кривые, соответствующие уравнениям (1) для свободно текущей эпидемии в ограниченной популяции, как процент от ее численности. Использованы параметры p = 0.15 (черные кривые), 0.13 (темно-серые), 0.11 (светло-серые) и d = 14 суток. Ось x показывает число суток после первого заражения, ось y – долю затронутых членов популяции. Для расчетов использовалось начальное условие N_I(l = 1) = N_T(l = 1) = 1 + n_ck. Теория (рис. 1) описывает достижение коллективного иммунитета, зависящего от характерных параметров. Можно строго показать, что учет специальных карантинных мероприятий сводится к замене в уравнениях (1), (2) n_ck → n_lk, где фактор n_l отражает снижение среднесуточного числа опасных контактов вследствие принятых карантинных мер.

В уравнении (2) можно перейти от дискретного времени l к непрерывному времени. Для этого обозначим t = Δt(l – 1), где Δt – единица времени, равная одному дню, и положим N_T(l) = x(t)N, N_T(l) – N_T(l – 1) = x'(t)N. Тогда уравнение (2) переписывается как

где θ(t) – ступенчатая функция Хевисайда, а T = d –1. Здесь предполагается, что время по-прежнему измеряется в днях, т.е. Δt = 1, иначе коэффициент p следует перенормировать.

На начальной стадии эпидемии 0 ≤ t ≤ T уравнение (3) имеет вид

а его решение равно где x(0) = $\epsilon $ определяется начальной долей вирусоносителей в популяции, способных инфицировать.

Решение (5) служит начальной функцией для уравнения (3), т.е. x(t) = x₀(t) при 0 ≤ t ≤ T.

Есть два стационарных решения уравнения (4), а именно неустойчивое решение x₀(t) = 0 и устойчивое решение x₀(t) = 1, которое является пределом x₀(t) (5) при t → ∞. Напротив, дифференциальное уравнение с запаздыванием (3) имеет произвольное стационарное решение x(t) = C при t > T (0 ≤ C ≤ 1). Очевидно, что в течение длительного времени любое решение уравнения (3) стремится к некоторому стационарному стабильному значению насыщения, как показано на рис. 1.

Минимальное значение насыщения можно оценить путем линеаризации уравнения (3) вблизи произвольного стационарного решения x(t) = C. Пусть x(t) = C + Δx(t), тогда линеаризованное уравнение Δx'(t) = p (1 – C)[ Δx(t) – Δx(t – T)]. Полагая, что Δx(t) = exp(λt/T), приходим к характеристическому уравнению

Один из корней этого уравнения – λ = 0. Другой действительный корень уравнения (6) отрицательный λ < 0, если Tp(1 – C) < 1. Другими словами, стационарное решение x(t) = C устойчиво, если

Следовательно, значение насыщения x_∞(p) = = $\mathop {\lim }\limits_{t \to \infty } x\left( t \right)$ должно превышать значение, заданное уравнением (7). На рис. 2 показана зависимость асимптотического значения решения уравне-ния (3) от pT, вычисленная для двух значений начального возмущения ϵ = 10^–6 и 5 × 10^–2. Если pT < 1, значительного роста эпидемий нет. Для больших значений pT уровень насыщения всегда больше, чем значение, заданное уравнением (7), и стремится к единице при pT $ \gg $ 1. При достаточно малом значении $\epsilon \ll $ 1 функция x_∞(p) стремится к универсальной кривой, не зависящей от начального возмущения (например, кривая 1 на рис. 2). Однако время, необходимое для достижения значения насыщения, зависит от начального возмущения.

Сравним полученные результаты с предсказаниями модели SIR (см., например, [11]). В рамках этой модели динамика роста доли заразившихся с начала эпидемии может быть записана как dx(t)/dt = F(x(t)), где

Примеры роста эпидемии, рассчитанные с использованием предложенной модели (3) и SIR-модели (8), показаны на рис. 3. Для достаточно малого начального возмущения ϵ модель SIR предсказывает примерно вдвое большее время насыщения.

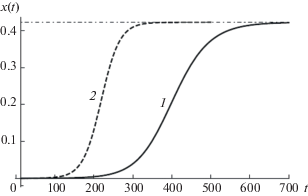
Как уже упоминалось, существует бесконечное количество стационарных состояний уравнения с запаздыванием (3). Напротив, помимо корня x = 1, существует только один корень уравнения F(x₁) = = 0, который можно записать как x₁(ϵ, pT) = 1 + + W(–pTe^{–pT(ϵ + 1)})/(pT), где W(z) – функция Ламберта [15]. Легко проверить, что стационарное состояние устойчиво, т.е. F '(x₁) > 0. Численно установлено, что для наиболее интересного случая малого начального возмущения ε $ \ll $ 1 уровни насыщения, заданные обеими моделями, практически равны.

Реальное течение эпидемии требует учета характерных особенностей COVID-19, что важно для определения стратегии карантинных мероприятий. Вместо модели SIR-типа, основанной на обыкновенных дифференциальных уравнениях, получено дифференциальное уравнение с запаздыванием, вызванным большой продолжительностью COVID-19.

Данная работа ограничена закрытыми популяциями (страна, регион, город и т.д.). Конечно, между рассматриваемыми популяциями существует постоянный обмен. Однако уже на ранней стадии эпидемии власти используют меры изоляции, чтобы свести такие потоки к минимуму. Точно рассчитать трансграничную передачу инфекции до карантина невозможно. Эту первую стадию эпидемии можно условно назвать свободно текущей эпидемией, когда карантинные меры практически отсутствуют. Анализ влияния потока людей между регионами на эпидемию – отдельная задача, которую можно рассмотреть, в том числе на основе предложенной модели.

Существенно, что полученные результаты позволяют изучить влияние карантинных мероприятий в общем виде через зависящую от времени “функцию внешнего воздействия” путем замены p на функцию времени p(t) по аналогии с дискретной моделью [12], где функции n_l(p(l)) находились на основе реальных статистических данных по заболеваемости в ряде стран. Роль различных карантинных мер и количественная оценка их влияния все еще не ясны и обсуждаются. Тем не менее, рассматриваемая модель позволяет найти эту функцию на начальном этапе свободного течения эпидемии обратным расчетом [12] на основе имеющихся дискретных статистических данных [16].

ЗАКЛЮЧЕНИЕ

Результаты таких расчетов с функцией p(t) могут быть использованы для оценки воздействия карантинных мер и вакцинации для отдельных регионов и стран в целом, поскольку известны даты и типы правил административных карантинных ограничений и кампаний вакцинации. Это способ понять эффективность вводимых ограничений. В настоящей работе анализ устойчивости решений ограничен постоянным значением p для оценки того, как насыщение зависит от этой величины.

Также показано и исследовано появление коллективного иммунитета в условиях карантина. Это свойство рассматриваемой детерминированной модели с запаздывающим процессом перехода от подмножества носителей вируса V к подмножеству выздоровевших людей R, которое, как отмечено выше, отличается от известных SIR- и SEIR-моделей, включая и их модификации с запаздыванием [13, 14]. Запаздывание является характерной особенностью COVID-19, хотя в менее выраженной форме может наблюдаться и при иных инфекциях. Показано, как коллективный иммунитет может поддерживаться на низком уровне.

Представленная теория может описать весь эпидемический процесс, в том числе новые волны заражений COVID-19, наблюдаемые в настоящее время, и периодическое изменение баланса между карантинными мерами и снижением карантинных ограничений.