1. На главную
  2. Электронные версии
  3. Теплофизика высоких температур
  4. T. 59, № 6, 2021

Теплофизика высоких температур, 2021, T. 59, № 6, стр. 952-955

Аналитическая аппроксимация для уравнения состояния вырожденного электронного газа

В. П. Коновалов 1, 2, *, Э. Е. Сон 1, 2

1 Объединенный институт высоких температур РАН
Москва, Россия

2 Московский физико-технический институт
Москва, Россия

* E-mail: konovalov.vp@mipt.ru

Поступила в редакцию 22.10.2021
После доработки 16.11.2021
Принята к публикации 23.11.2021

Полный текст (PDF)

Аннотация

Получено уравнение состояния вырожденного электронного газа в явной форме из распределения Ферми–Дирака с помощью аналитических разложений по параметру вырождения. Для подтверждения полученных аналитических аппроксимаций выполнен прямой компьютерный расчет по точным интегральным формулам распределения Ферми–Дирака. Предложены практические уравнения состояния и выражения для химического потенциала вырожденного электронного газа.

ВВЕДЕНИЕ

Помимо хорошо известных примеров вырожденного электронного газа, таких как электронный газ в обыкновенных металлах и в недрах звезд белых карликов, имеются области существования этого газа в плазме при определенных условиях, доступных экспериментально [1, 2]. Квантовое вырождение электронов в достаточно плотной плазме приводит к увеличению давления, при этом уравнение состояния вещества существенно видоизменяется. Монография [3] представляет модель Томаса–Ферми и самосогласованный потенциал для плотного вещества многокомпонентного состава (атомы, электроны, ионы). Запутанность (сцепленность) квантовых состояний в вырожденном электронном газе может трактоваться как термодинамическая величина [4], способная связывать соотносительное межэлектронное расстояние с давлением и температурой. Аналитический метод разложения предложен в работе [5] для оценки уравнения состояния слаборелятивистского, частично вырожденного электронного газа. Однородный вырожденный электронный газ при конечной температуре численно моделировался в работе [6] методом интегрирования по траекториям, исходя из первых принципов, чтобы получить точные термодинамические данные. В исследованиях [7, 8] разрабатывалось уравнение состояния релятивистского электронного газа при его произвольном вырождении и под действием магнитного поля. В настоящее время термодинамические свойства однородного электронного газа могут быть установлены посредством сложного численного интегрирования по траекториям методом Монте-Карло [9] в широком диапазоне плотностей и температур. В то же время желательны возможные простые оценки таких свойств. В настоящей работе учитывается именно электронная компонента плазмы, являющейся основной при эффекте вырождения.

НЕЯВНОЕ УРАВНЕНИЕ СОСТОЯНИЯ ФЕРМИ-ГАЗА

Функция распределения электронов по кинетическим энергиям f(ε), описывающая квантовые свойства, определяется распределением Ферми–Дирака

(1)
$f\left( \varepsilon \right) = \frac{{g{{m}^{{3/2}}}}}{{\sqrt 2 {{\pi }^{{2~}}}{{\hbar }^{3}}}}~\frac{{\sqrt \varepsilon }}{{\left( {{{{\text{e}}}^{{\frac{{\left( {\varepsilon - \mu } \right)}}{T}}}} + 1} \right)}}.$
Здесь m, ε, μ – масса электрона, энергия и химический потенциал соответственно; T – температура, измеренная в энергетических единицах; ħ – постоянная Планка; g – статистический вес электрона (g = 2).

На этом основании концентрация электронов n вместе с внутренней энергией E и давлением p могут быть выражены посредством неявных интегральных формул через химический потенциал µ, температуру T и объем V [10]

(2)
$n = \int\limits_0^\infty {f\left( \varepsilon \right)d\varepsilon } = \frac{{g{{m}^{{3/2}}}}}{{\sqrt 2 {{\pi }^{{2~}}}{{\hbar }^{3}}}}\int\limits_0^\infty {\frac{{\sqrt \varepsilon d\varepsilon }}{{\left( {{{{\text{e}}}^{{\frac{{\left( {\varepsilon - \mu } \right)}}{T}}}} + 1} \right)}}} ~,$
(3)
$E = \int\limits_0^\infty {f\left( \varepsilon \right)} \varepsilon d\varepsilon = \frac{{g{{m}^{{3/2}}}}}{{\sqrt 2 {{\pi }^{{2~}}}{{\hbar }^{3}}}}\int\limits_0^\infty {\frac{{{{\varepsilon }^{{3/2}}}d\varepsilon }}{{\left( {{{{\text{e}}}^{{\frac{{\left( {\varepsilon - \mu } \right)}}{T}}}} + 1} \right)}}} ~,$
(4)
$p = \frac{2}{3}~\frac{E}{V}.$

Формула (4) представляет общее соотношение между давлением, внутренней энергией и объемом любого идеального газа.

Здесь появляется ключевой безразмерный параметр задачи – параметр вырождения A = = n(2πħ2/(mT))3/2. Он имеет ясную физическую интерпретацию, выражая количество частиц (электронов) в кубике размером с тепловую длину волны де Бройля λB= (2πħ2/(mT))1/2. Параметр вырождения определяется только электронной плотностью и температурой A = A(n, T), он передает квантовое отличие от классического больцмановского газа и просто связан с энергией Ферми εF: A = (8/3π1/2)(εF/T)3/2. Можно выделить три типичных случая: идеальный невырожденный классический больцмановский газ, A ≥ 0; слабовырожденный газ, A $ \ll $ 1, и сильновырожденный газ, A $ \gg $ 1.

С помощью параметра вырождения A вместе с безразмерными переменными x = ε/T и z = μ/T формулы (2)–(4) преобразуются в следующую систему двух уравнений:

(5)
$A = \frac{4}{{\sqrt \pi }}\int\limits_0^\infty {\frac{{{{x}^{{1/2}}}dx}}{{\left( {{{{\text{e}}}^{{ - z}}}~{{{\text{e}}}^{x}} + 1} \right)}}} ~,$
(6)
$\left( {\frac{p}{{nT}}} \right)A = \frac{8}{{3\sqrt \pi }}\int\limits_0^\infty {\frac{{{{x}^{{3/2}}}dx}}{{\left( {{{{\text{e}}}^{{ - z}}}~{{{\text{e}}}^{x}} + 1} \right)}}} ~.$
Здесь имеются две неизвестные переменные: безразмерное электронное давление p/(nT) и безразмерный электронный химический потенциал z. Если исключить переменную z, то зависимость безразмерного давления p/(nT) от A проявит себя как уравнение состояния для электронов в явной форме p = p(n, T).

Невырожденный классический газ описывается распределением Максвелла, которое просто следует из распределения Ферми–Дирака (1) при устранении единицы в знаменателе. В этом случае интегралы (5), (6) выражаются через Γ-функцию:

$A = \frac{4}{{\sqrt \pi }}~{{{\text{e}}}^{z}}\int\limits_0^{\infty ~} {{{{\text{e}}}^{{ - x}}}~{{x}^{{1/2}}}dx} ~ = \frac{4}{{\sqrt \pi }}~{{{\text{e}}}^{z}}\Gamma \left( {\frac{3}{2}} \right) = 2{{{\text{e}}}^{z}},$
$\left( {\frac{p}{{nT}}} \right)A = ~\frac{8}{{3\sqrt {{\pi }} }}{{{\text{e}}}^{z}}\int\limits_0^\infty {{{{\text{e}}}^{{ - x}}}{{x}^{{3/2}}}dx} = \frac{8}{{3\sqrt {{\pi }} }}{{{\text{e}}}^{z}}{{\Gamma }}\left( {\frac{5}{2}} \right) = 2{{{\text{e}}}^{z}}.$

Отсюда сразу следуют стандартные соотношения для классического идеального газа: уравнение состояния p/(nT) = 1 и химический потенциал μ/T = ln(A/g), для электронов g = 2. Следует осознавать, что химический потенциал идеального газа равен большому отрицательному значению, так что множитель e–µ/T является чрезвычайно большим и устранение единицы в знаменателе распределения Ферми–Дирака (1) разумно.

АНАЛИТИЧЕСКОЕ ПРИБЛИЖЕНИЕ

В случае слабовырожденного электронного газа A $ \ll $ 1 и параметр z является отрицательной величиной, так что соответствующий член e–zex в интегралах (5), (6) велик. Тогда разложение в ряд по малой величине eze–x $ \ll $ 1 позволяет провести интегрирование и дает следующий результат:

$\frac{1}{{{{{\text{e}}}^{{ - z}}}{{{\text{e}}}^{x}} + 1}} \cong {{{\text{e}}}^{z}}{{{\text{e}}}^{{ - x}}}(1 - {{{\text{e}}}^{z}}{{{\text{e}}}^{{ - x}}}),$
$\begin{gathered} \int\limits_0^\infty {\frac{{{{x}^{s}}dx}}{{{{{\text{e}}}^{{ - z}}}{{{\text{e}}}^{x}} + 1}}} \cong {{{\text{e}}}^{z}}\left( {\mathop \smallint \limits_0^\infty {{x}^{s}}{{{\text{e}}}^{{ - x}}}dx - {{{\text{e}}}^{z}}\mathop \smallint \limits_0^\infty {{x}^{s}}{{{\text{e}}}^{{ - 2x}}}dx} \right) = \\ = {{{\text{e}}}^{z}}{{\Gamma }}\left( {s + 1} \right)\left( {1 - \frac{{{{{\text{e}}}^{z}}}}{{{{2}^{{s + 1}}}}}} \right)~,\,\,\,\,~{{{\text{e}}}^{z}} \ll 1, \\ \end{gathered} $
где s – произвольный действительный показатель степени.

Таким образом, система уравнений (5), (6) принимает форму

(7)
$A = \frac{4}{{\sqrt {{\pi }} }}~{{{\text{e}}}^{z}}{{\Gamma }}\left( {\frac{3}{2}} \right)\left( {1 - \frac{{{{{\text{e}}}^{z}}}}{{{{2}^{{3/2}}}}}} \right)~,$
(8)
$\left( {\frac{p}{{nT}}} \right)A = \frac{8}{{3\sqrt {{\pi }} }}{{{\text{e}}}^{z}}{{\Gamma }}\left( {\frac{5}{2}} \right)\left( {1 - \frac{{{{{\text{e}}}^{z}}}}{{{{2}^{{5/2}}}}}} \right)~$
со значениями Γ-функции, равными ${{\Gamma }}\left( {\frac{3}{2}} \right) = ~\frac{{\sqrt {{\pi }} }}{2}~,~$ ${{\Gamma }}\left( {\frac{5}{2}} \right) = \frac{{3\sqrt {{\pi }} }}{4}$.

Уравнение (7) может быть решено как квадратное уравнение для малого параметра ez $ \ll $ 1, и затем из (7), (8) получаются следующие формулы:

$z \cong \ln \left( {\frac{A}{2}} \right) + \frac{A}{{4\sqrt 2 ~}}~,\,\,\,\,~\frac{p}{{nT}} = \frac{{1 - {{{{{\text{e}}}^{z}}} \mathord{\left/ {\vphantom {{{{{\text{e}}}^{z}}} {{{2}^{{5/2}}}}}} \right. \kern-0em} {{{2}^{{5/2}}}}}}}{{1 - {{{{{\text{e}}}^{z}}} \mathord{\left/ {\vphantom {{{{{\text{e}}}^{z}}} {{{2}^{{3/2}}}}}} \right. \kern-0em} {{{2}^{{3/2}}}}}}} \cong 1 + \frac{{{{{\text{e}}}^{z}}}}{{4\sqrt 2 ~}}~.$

Они ведут непосредственно к уравнению состояния и химическому потенциалу для слабовырожденного электронного газа в явной безразмерной форме

(9)
$\frac{p}{{nT}} \cong 1 + \frac{A}{{8\sqrt 2 ~}}~,\,\,\,\,~A \ll 1;$
(10)
$\frac{{{\mu }}}{T} \cong \ln \left( {\frac{A}{2}} \right) + \frac{A}{{4\sqrt 2 }}~,\,\,\,\,A \ll 1.$

В противном случае – сильно вырожденного электронного газа, A $ \gg $ 1, параметр z оказывается большим, z $ \gg $ 1, e–z $ \ll $ 1, и интегрирование в (5), (6) заметно усложняется. Требуется замена переменной ξ = x – z и последующее разложение числителя в ряд по этой переменной ξ [10]. Подобное интегрирование может быть представлено следующей формулой:

$\mathop \smallint \limits_0^\infty \frac{{{{x}^{s}}dx}}{{{{{\text{e}}}^{{ - z}}}{{{\text{e}}}^{x}} + 1}} \cong \frac{{{{z}^{{s + 1}}}}}{{s + 1}} + \frac{{s{{\pi }^{2}}}}{6}{{z}^{{s - 1}}}~,\,\,\,\,~z \gg 1.$

С учетом данного соотношения система уравнений (5), (6) принимает вид

(11)
$A = \frac{4}{{\sqrt \pi }}~\left( {\frac{2}{3}{{z}^{{3/2}}} + \frac{{{{\pi }^{2}}}}{{12}}{{z}^{{ - 1/2}}}} \right) = \frac{8}{{3\sqrt \pi }}{{z}^{{3/2}}}\left( {1 + \frac{{{{\pi }^{2}}}}{{8{{z}^{2}}}}} \right),$
(12)
$\begin{gathered} \left( {\frac{p}{{nT}}} \right)A = ~\frac{8}{{3\sqrt \pi }}\left( {\frac{2}{5}{{z}^{{5/2}}} + \frac{{{{\pi }^{2}}}}{4}{{z}^{{1/2}}}} \right) = \\ = \frac{{16}}{{15\sqrt \pi }}{{z}^{{5/2}}}~\left( {1 + \frac{{5{{\pi }^{2}}}}{{8{{z}^{2}}}}} \right)~. \\ \end{gathered} $

В рассматриваемом случае с большой величины z $ \gg $ 1 уравнение (11) для переменной z может быть решено последовательными итерациями, и это решение удобно выражается через безразмерную энергию Ферми εF/T следующим образом:

(13)
$z \cong \frac{{{{\varepsilon }_{{\text{F}}}}}}{T} - \frac{{{{\pi }^{2}}}}{{12}}\frac{T}{{{{\varepsilon }_{{\text{F}}}}}}~,\,\,\,\,~\frac{{{{\varepsilon }_{{\text{F}}}}}}{T} = ~{{\left( {\frac{{3\sqrt \pi }}{8}A} \right)}^{{2/3}}}~.$

Безразмерное давление следует из уравнений (11), (12):

$\frac{p}{{nT}} = \frac{2}{5}z\left( {\frac{{1 + \frac{{5{{\pi }^{2}}}}{{8{{z}^{2}}}}}}{{1 + \frac{{{{\pi }^{2}}}}{{8{{z}^{2}}}}}}} \right) \cong \frac{2}{5}z + \frac{{{{\pi }^{2}}}}{{5z}}~,\,\,\,\,~z \gg 1.$

Подстановка решения (13) в последнее соотношение дает значение давления, выраженное через безразмерную энергию Ферми εF/T

(14)
$\frac{p}{{nT}} \cong \frac{2}{5}\frac{{{{\varepsilon }_{{\text{F}}}}}}{T} + \frac{{{{\pi }^{2}}}}{6}~\frac{T}{{{{\varepsilon }_{{\text{F}}}}}}~.$

Как и предсказывает теория [3, 10], в пределе полного вырождения (T ≥ 0) давление электронного газа не зависит от температуры, а его химический потенциал стремится к энергии Ферми. Найденные решения (13), (14) позволяют явно выписать аппроксимации уравнения состояния и химического потенциала для сильно вырожденного электронного газа через безразмерный параметр вырождения A:

(15)
$\frac{p}{{nT}} \cong \left( {\frac{{{{3}^{{2/3}}}{{\pi }^{{1/3}}}}}{{10}}} \right){{A}^{{2/3}}} + 2{{\left( {\frac{\pi }{3}} \right)}^{{5/3}}}\frac{1}{{{{A}^{{2/3}}}}}~,~\,\,\,\,A \gg 1;$
(16)
$\frac{\mu }{T} \cong \left( {\frac{{{{3}^{{2/3}}}{{\pi }^{{1/3}}}}}{4}} \right){{A}^{{2/3}}} - {{\left( {\frac{\pi }{3}} \right)}^{{5/3}}}\frac{1}{{{{A}^{{2/3}}}}}~,\,\,\,\,A \gg 1.$

Следует упомянуть замечательную особенность вырожденного электронного газа как фермиевского газа. По мере вырождения электронов их кинетическая энергия сильно возрастает так, что заметно превосходит энергию потенциального кулоновского взаимодействия. Таким образом, плотный вырожденный электронный газ оказывается идеальным, и эффектом неидеальности можно пренебречь.

ЧИСЛЕННЫЙ РАСЧЕТ

Чтобы проверить и подтвердить полученные аналитические аппроксимации, был проведен прямой численный расчет по точным интегральным формулам распределения Ферми–Дирака (5), (6) в диапазоне параметра вырождения 10–2 < A < 102. По сути, компьютерный код широко варьирует параметр e–z в уравнениях (5), (6) и затем собирает расчетные данные для переменных p/nT и A. Результаты численного расчета показаны на рис. 1 и 2 в сравнении с аналитическими аппроксимациями (9), (10) и (15), (16). Эти аппроксимации оказываются в весьма хорошем соответствии с численным расчетом во всем диапазоне параметра A, включая промежуточную область A ~ 1.

Рис. 1.

Аппроксимация уравнения состояния вырожденного электронного газа: сплошная линия – точный компьютерный расчет, 1 – слабовырожденные электроны (9), 2 – сильновырожденные электроны (15).

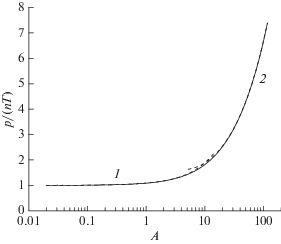
Рис. 2.

Аппроксимация химического потенциала вырожденного электронного газа: сплошная линия – точный компьютерный расчет, 1 – слабовырожденные электроны (10), 2 – сильновырожденные электроны (16).

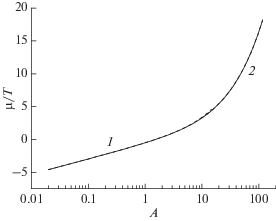
Сочленение двух ветвей полученной аппроксимации происходит при A ~ 10. Более точно, согласно компьютерному анализу, практическое “сглаживание” двух ветвей уравнения состояния (9) и (15) осуществляется при значении A = 9.85, а “сглаживание” двух ветвей химического потенциала (10) и (16) происходит при значении A = 7.15. Ветви аппроксимаций, объединенные подобным образом, по существу представляют собой гладкие функции во всем диапазоне параметра A.

Ниже приведены удобные аппроксимационные формулы для практических расчетов, их относительная ошибка ~2%.

Непрерывная аппроксимация уравнения состояния по формулам (9), (15):

$\frac{p}{{nT}} = 1 + \frac{A}{{11.3}}~,\,\,\,\,A \leqslant 9.85;$
$\frac{p}{{nT}} = 0.305~{{A}^{{2/3}}} + \frac{{2.16}}{{{{A}^{{2/3}}}}},\,\,\,\,~A \geqslant 9.85.$

Непрерывная аппроксимация химического потенциала по формулам (10), (16):

$\frac{\mu }{T} = \ln \left( {\frac{A}{2}} \right) + \frac{A}{{5.66}}~,\,\,\,\,A \leqslant 7.15;$
$\frac{\mu }{T} = 0.762~{{A}^{{2/3}}} - \frac{{1.08}}{{{{A}^{{2/3}}}}}~,\,\,\,\,A \geqslant 7.15.$

Единственный безразмерный параметр в этих формулах – параметр вырождения A, численно равный:

$A = n{{\left( {\frac{{2\pi {{\hbar }^{2}}}}{{mT}}} \right)}^{{3/2}}} = 4.14 \times {{10}^{{ - 16}}}\frac{n}{{T_{{}}^{{3/2}}}}~$
(концентрация электронов n дана в обратных кубических сантиметрах см3, температура T – в К).

ЗАКЛЮЧЕНИЕ

Полученные аппроксимации оказываются в приличном соответствии со строгим численным расчетом во всем диапазоне параметра вырождения A. Поэтому уравнение состояния вырожденного электронного газа принимает ясное аналитическое представление с помощью единственного параметра вырождения A в широком диапазоне концентраций и температур.

Тема исследования была поставлена академиком В.Е. Фортовым. Работа поддержана грантом Российского научного фонда (проект № 21-79-30062).

Список литературы

  1. Энциклопедия низкотемпературной плазмы / Под ред. Фортова В.E. Т. 1. М.: Наука, 2000. С. 6.

  2. Фортов В.Е. Экстремальные состояния вещества. М.: Физматлит, 2009. С. 14.

  3. Nikiforov A.F., Novikov V.G., Uvarov V.B. Quantum-statistical Models of Hot Dense Matter. Basel‒Boston‒Berlin: Birkhauser, 2005. P. 287.

  4. Lunkes C., Brukner Č., Vedral V. Equation of State for Entanglement in a Fermi Gas // Phys. Rev. A. 2007. V. 71. 034309.

  5. Haug E. Simple Equation of State for Partially Degenerate Semirelativistic Electrons // Astron. Astrophys. 2003. V. 407. P. 787.

  6. Schoof T., Groth S., Vorberger J., Bonitz M. Ab initio Thermodynamic Results for the Degenerate Electron Gas at Finite Temperature // Phys. Rev. Lett. 2015. V. 115. P. 130402.

  7. Faussurier G. Equation of State of the Relativistic Free Electron Gas at Arbitrary Degeneracy // Phys. Plasmas. 2016. V. 23. P. 122704.

  8. Faussurier G. Equation of State of the Free Electron Gas in a Magnetic Field at Arbitrary Degeneracy // Phys. Plasmas. 2020. V. 27. 022709.

  9. Filinov V.S., Larkin A.S., Levashov P.R. Uniform Electron Gas at Finite Temperature by Fermionic-path-integral Monte Carlo Simulations // Phys. Rev. E. 2020. V. 102. № 3-1. 033203.

  10. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. 5. Статистическая физика. Ч. 1. М.: Физматлит, 2002. С. 187.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теплофизика высоких температур

Архивы выпусков Информация о журнале Отправить рукопись в журнал