Теплофизика высоких температур, 2021, T. 59, № 6, стр. 817-825
О сдвиге границ термодинамической неустойчивости асимметричной комплексной плазмы с учетом эффекта нелинейного экранирования
И. А. Мартынова 1, 2, *, И. Л. Иосилевский 1, 2
1 Объединенный институт высоких температур РАН
Москва, Россия
2 Московский физико-технический институт (национальный
исследовательский университет)
г. Долгопрудный, Россия
* E-mail: martina1204@yandex.ru
Поступила в редакцию 19.04.2021
После доработки 17.11.2021
Принята к публикации 23.11.2021
Аннотация
В данной работе рассмотрена двухкомпонентная электронейтральная равновесная система макроионов конечных размеров с зарядом Z $ \gg $ 1 и точечных противоположно заряженных микроионов c единичным зарядом. На фазовой диаграмме комплексной плазмы в переменных κ–Γ (κ – безразмерный структурный параметр, Г – параметр кулоновской неидеальности) выявлены области отрицательной сжимаемости и отрицательного давления для широкого диапазона зарядов макроионов. С учетом эффекта нелинейного экранирования макроионов микроионами в приближении Пуассона–Больцмана получена автомодельная зависимость эффективного заряда макроиона Z* от исходного заряда Z, температуры системы и размеров макроионов для фиксированных параметров упаковки. В работе проведена оценка возможности достижения границы термодинамической неустойчивости с учетом полученной автомодельной зависимости. Показано, что граница термодинамической устойчивости по одному из уравнений состояния может оказаться недостижимой при характерных параметрах комплексной плазмы.
ВВЕДЕНИЕ
Данная работа посвящена проблеме термодинамической устойчивости и фазовых переходов в неидеальной асимметричной комплексной плазме. Эта проблема занимает одно из центральных мест в творчестве В.Е. Фортова, что отражено, в частности, в целом ряде монографий ([1, 2] и др.) и подытожено в известной Энциклопедии низкотемпературной плазмы под его редакцией [3]. В своих работах В.Е. Фортов неоднократно обращался к проблеме влияния кулоновской неидеальности на макроскопические свойства низкотемпературной плазмы, и прежде всего, на возможность специфических фазовых переходов в такой плазме. Еще в одной из ранних работ [4] рассмотрена проблема гидродинамических аномалий, обязанных своим происхождением эффектам кулоновской неидеальности. В работе [5] сделана одна из первых попыток единым образом оценить параметры экспериментально труднодостижимых критических точек перехода газ–жидкость в плазме большого числа металлов, рассматриваемых именно как сильно-неидеальная система заряженных частиц. Теоретический подход, ставящий во главу угла именно “кулоновость” межчастичного взаимодействия плазмы металлов в окрестности их критических точек, успешно развивался впоследствии в работах А.А. Ликальтера [6–8] и др.
Специфика фазовых переходов в резко асимметричной (Z $ \gg $ 1) классической плазме изучалась во многих работах [1, 3, 9–23] и др. Так, в [24, 25] на примере модифицированной модели однокомпонентной плазмы (ОСР) на однородно-сжимаемом компенсирующем фоне (ОСР(~)) было показано существование в зоне сильной неидеальности обширных зон термодинамической неустойчивости, приводящей к фазовым переходам первого рода, включая энтальпийный (ван-дер-ваальсов) переход типа газ–жидкость со значительным межфазным скачком плотности. В этих и других работах подчеркивалось (см., например, обзоры [14, 26, 27] и ссылки в них), что суммарный эффект межчастичного притяжения в разнозарядных асимметричных кулоновских системах реализуется в виде двух конкурирующих между собой механизмов: образования конечных ассоциаций (связанных комплексов) и фазовых переходов. В модели ОСР(~) [24], как и в других вариантах семейства “безассоциативных” моделей плазмы [26], связанные комплексы отсутствуют по определению. Соответственно, весь эффект межчастичного притяжения реализуется в виде обширного фазового перехода типа газ–жидкость с верхней критической точкой. Учет же локализации микроионов в виде плотного приповерхностного корреляционного слоя вокруг макроиона, например, описываемой приближением Пуассона–Больцмана [15, 28], должен по теории [26, 27] заметно сократить масштабы возможного фазового расслоения, вплоть до полного исчезновения “плазменного” фазового перехода типа газ–жидкость в специальной высоко асимметричной модели плазмы с так называемым “гладким” потенциалом Глаубермана, имеющим положительный фурье-образ и конечным при r → 0 (см. [26, 27, 29] и ссылки в них)
Понятие “комплексная плазма” традиционно используется для обозначения целого семейства объектов и включает в себя несколько различных видов асимметричной по заряду плазмы. Среди них есть коллоидная плазма [11, 16], термически равновесная плазма с конденсированной дисперсной фазой (КДФ-плазма) [30], газоразрядная пылевая плазма [1, 2, 17, 31, 32], пылевая плазма серебристых облаков [33] и другие. В данной работе все эти виды плазмы будут рассматриваться как электронейтральные системы классических высокозаряженных макроионов конечных размеров (коллоидов, пылинок и пр.) и точечных микроионов, причем заряд макроионов будет во много раз превосходить заряд микроиона. Характерные значения рассматриваемых видов комплексной плазмы: для коллоидной плазмы концентрация макроионов nZ ∼ 105–109 см–3, абсолютное значение зарядового числа (далее – заряд) макроиона Z ~ ~ 102–104, радиус макроиона RZ ∼ 0.01–1 мкм, наиболее характерная температура системы – комнатная, система обычно находится в воде [16]. Для газоразрядной пылевой плазмы: nZ ∼ 103–109 см–3, Z ~ 103–104, RZ ∼ 1–100 мкм, температура макроионов kTZ ≈ 1–2 эВ, температура положительно заряженных микроионов kTi ≈ 0.03 эВ, температура электронов (отрицательно заряженных микроионов) kTe ≈ 1–7 эВ [1, 2, 17]. Для КДФ-плазмы: nZ ~ 108–1014 см–3, Z ∼ 103–104, температура и макроионов, и микроионов kT ≈ 2000–3000 К, RZ ~ 0.01–100 мкм [30]; для пылевой плазмы серебристых облаков максимальное значение заряда Z ~ 102, kT = kTZ = kTi = kTe ≈ 0.03 эВ, nZ ∼ 100–104 см–3, RZ ∼ 1 мкм [33]. Коллоидную плазму, КДФ-плазму и пылевую плазму серебристых облаков можно считать полностью равновесными, в то время как газоразрядная пылевая плазма является в значительной мере неравновесной системой, в которой заряд макроиона переменный и зависит от параметров системы. Тем не менее, по аналогии с работами других авторов, в данной работе представлена полностью равновесная идеализированная модель, где заряд макроиона считается постоянным.
Здесь рассматриваются преимущественно резко асимметричные системы (Z $ \gg $ 1). Однако некоторое время назад очень активно изучались модели электролитов, где соотношение зарядов макроионов и микроионов обычно не превышало 3 : 1 (см., например, [34, 35] и др.). В работе [34] для симметричных (соотношение зарядов макроиона и микроиона – 1 : 1) и асимметричных (2 : 1 и 3 : 1) систем на основе предположения о составе низкотемпературной плазмы при температурах, близких к критическим, предложены параметры фазового перехода газ–жидкость. В [35] для определения поведения системы в области параметров, близких к критическим, применялся метод Монте-Карло в большом каноническом ансамбле для систем с асимметрией зарядов (соотношение заряда макроиона к заряду микроиона – 1 : 1, 2 : 1 и 3 : 1) и асимметрией радиусов макроиона и микроиона.
Многие авторы рассчитывали фазовые переходы для различных систем, описывающих комплексную плазму. Одной из таких работ является статья Хамагучи и др. [10], где фазовая диаграмма была промоделирована методом Монте-Карло для однокомпонентной системы с дебаевским потенциалом
(1)
${{\varphi }_{{\text{D}}}}(r) = \frac{{{{{\left( {Ze} \right)}}^{2}}}}{r}\exp \left( { - \frac{r}{{{{r}_{{\text{D}}}}}}} \right).$В качестве прототипа для своей системы авторы рассматривали пылевую и коллоидную плазмы. На фазовой диаграмме [10] представлено три фазовых состояния: флюид, кристалл с объемно-центрированной решеткой (ОЦК) и кристалл с гранецентрированной решеткой (ГЦК). Фазовая диаграмма построена в переменных κ–Γ (κ – безразмерный структурный параметр, Г – параметр кулоновской неидеальности):
(2)
$\kappa = {{\left( {\frac{3}{{4\pi {{n}_{Z}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}\frac{1}{{{{r}_{{\text{D}}}}}},\,\,\,\,\Gamma = \frac{{{{{\left( {Ze} \right)}}^{2}}}}{{kT}}{{\left( {\frac{{4\pi {{n}_{Z}}}}{3}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}},$Аппроксимация для кривой плавления фазовой диаграммы [10] была получена в работе [20]. Численно кривая плавления рассчитывалась также в других статьях, например в [21–23].
В контексте фазовых переходов в системе Юкавы следует упомянуть и работу [18], где приведена теоретическая оценка границы стеклования переохлажденной жидкой фазы системы Юкавы, которая не является фазовым переходом в строгом смысле, но в то же время представляется важным структурным переходом в рассматриваемой системе.
Принято считать, что в системе с отталкивательным потенциалом и отсутствием притяжения между макроионами невозможен фазовый переход типа газ–жидкость. Но, например, в работе [11] методом Монте-Карло моделируется однокомпонентная система с дебаевским потенциалом. Прямым моделированием в этой системе при достаточно высоких зарядах макроионов зафиксировано фазовое расслоение типа флюид–флюид на две фазы существенно разной плотности, условно называемой авторами [11] газом и жидкостью. Таким образом, в обеих работах [10, 11] моделировались однокомпонентные системы с дебаевским потенциалом, однако термодинамика в [10] рассчитывалась для многокомпонентной системы с одним сортом макроионов и одним или двумя сортами микроионов, а в [11] для однокомпонентной системы с дебаевским радиусом, зависящим от одной компоненты фона (в выражении для внутренней энергии в [10] есть слагаемые с притяжением, а в выражении [11] их нет). По уравнению состояния [10] давление в системе может получиться отрицательным, а по уравнению состояния [11] давление принимает только положительные значения. В работе [10] при моделировании приравнивались плотности макроионов и свободные энергии Гельмгольца, а в работе [11] на границе двух фаз при постоянной температуре системы приравнивались давления и свободные энергии Гиббса, что является более корректным, так как в обеих работах рассматриваются фазовые переходы первого рода, где должен наблюдаться скачок плотности. При этом на фазовой диаграмме [10] есть три фазовых состояния (флюид, ОЦК и ГЦК), а в статье [11] – более плотное (жидкость) и менее плотное (газ) состояния флюида. Более того, в [11] утверждается, что в некотором диапазоне зарядов макроионов может формироваться кристаллическая фаза, но она является неустойчивой в отличие от фазы флюида (более или менее плотного), так как свободная энергия кристаллической фазы по абсолютному значению меньше свободных энергий фаз жидкости и газа.
Еще более важной является работа [12], где моделируется непосредственно уже двухкомпонентная модель – прототип дебаевской модели [11]. Модель состоит из классических макроионов конечных размеров и противоположно заряженных точечных микроионов, где заряд макроиона Z больше и/или много больше заряда микроиона. В [12] в рамках прямого численного моделирования с помощью метода Монте-Карло рассчитываются все три стандартных фазовых перехода – плавление (кристалл–жидкость), испарение (жидкость–газ) и сублимация (кристалл–газ), и видно фазовое расслоение флюида на газ и жидкость. При этом скачок плотности на границе плавления достигает аномально высоких значений (~30%).
Другим важным примером теоретического предсказания возможности фазового перехода флюид–флюид (в принципе отсутствующего на диаграмме [10]) с большой величиной межфазного скачка плотности в асимметричной системе зарядов является работа [13], где в рамках строгого метода функционала плотности зафиксирован даже не один, а два типа таких переходов. В [13] рассматривалась система конечных по размеру положительно заряженных макроионов с зарядом Z в сочетании с микроионами двух сортов, отличающихся знаком заряда. Для упрощенной системы с одним сортом микроионов был зафиксирован фазовый переход типа газ–жидкость с верхней критической точкой, а для более сложной системы с двумя сортами микроионов в некотором интервале значений заряда макроионов был зафиксирован фазовый переход с двумя (!) критическими точками.
В [15] подчеркивалось, что при использовании уравнений состояния [19, 36] на фазовой диаграмме [10] присутствуют обширные области отрицательного давления и отрицательной сжимаемости. В равновесной системе подобная ситуация должна вести к фазовому расслоению на фазы разной плотности [37].
Фазовые переходы в неравновесной пылевой плазме также рассматривались в ряде работ, например в [17, 32].
В данной работе термодинамическая устойчивость в классической равновесной трехмерной двухкомпонентной электронейтральной асимметричной комплексной плазме анализируется с помощью автомодельных зависимостей эффективного заряда макроиона от исходного заряда макроиона, температуры системы, размеров и концентрации макроионов [38, 39]. В ходе расчета автомодельных зависимостей в двухкомпонентной равновесной системе макроионов конечных размеров с зарядом Z $ \gg $ 1 и противоположно заряженных точечных микроионов с единичным зарядом учитывалось нелинейное экранирование макроионов микроионами в рамках приближения Пуассона–Больцмана (ПБ) в средней сферически-симметричной электронейтральной ячейке Вигнера–Зейтца (ВЗ). Рассматривается одна ячейка, однако сама модель ячеек ВЗ позволяет учитывать корреляции между макроионами различных ячеек вне зависимости от силы взаимодействия между макроионами. Приближение ПБ позволит корректно учитывать сильные корреляции между микроионами и макроионом одной ячейки.
ЗОНЫ ОТРИЦАТЕЛЬНОГО ДАВЛЕНИЯ И ОТРИЦАТЕЛЬНОЙ СЖИМАЕМОСТИ НА ФАЗОВОЙ ДИАГРАММЕ КОМПЛЕКСНОЙ ПЛАЗМЫ [10] С УЧЕТОМ УРАВНЕНИЙ СОСТОЯНИЯ [19, 36]
Рассматривается однотемпературная электронейтральная система классических макроионов c зарядом Z и микроионов фона с единичным зарядом. В такой системе параметры κ и Г уже не являются независимыми. С учетом условия электронейтральности ZnZ = ni и уравнения (1) получаем
Таким образом, при фиксированном значении Z все двумерное пространство значений температуры системы kT и концентрации макроионов nZ в координатах κ и Г редуцируются на единую одномерную кривую – параболу.
В данной работе для расчета областей отрицательного давления и отрицательной сжимаемости использовалось два уравнения состояния [19, 36]. В [19, 36] приведены зависимости безразмерной поправки на неидеальность для давления pex = = Pex/(nZ kT) как функции параметра Г при фиксированных значениях параметра κ (Pex – поправка на неидеальность для давления). Примечательно, что на обоих графиках pex(Г) принимает отрицательные значения. Более того, с ростом параметра Г абсолютное значение безразмерной поправки на неидеальность для давления монотонно возрастает.
Анализ работ [19, 36] показывает, что существует неоднозначность в точном определении термодинамической роли фона микроионов, что является принципиальным в процедуре вычисления давления в плазме. Неоднозначность в определении термодинамической роли фона подтверждается тем, что кривые pex(Г) работ [19, 36] при фиксированных значениях κ не только не совпадают друг с другом, но также и с аппроксимацией для однокомпонентной плазмы (κ = 0), рассчитанной с использованием результатов [40] (см. подробнее [15]). Более того, наклон кривых при фиксированных κ [2, 12] при увеличении параметра κ меняется в разные стороны. Это происходит потому, что в работе [36] при выводе зависимости параметра κ от концентрации макроионов nZ фон считается сжимаемым, поскольку вследствие условия электронейтральности дебаевский радиус (2) зависит от nZ. Это дает право дифференцировать дебаевский радиус по nZ и приводит к условию ${{(\partial \kappa } \mathord{\left/ {\vphantom {{(\partial \kappa } {\partial {{n}_{Z}}{{)}_{T}}}}} \right. \kern-0em} {\partial {{n}_{Z}}{{)}_{T}}}} = {\kappa \mathord{\left/ {\vphantom {\kappa {6{{n}_{Z}}}}} \right. \kern-0em} {6{{n}_{Z}}}}.$ Авторы [19] приводят аргументы в пользу того, что указанную выше зависимость параметра κ от nZ не следует учитывать при дифференцировании. Это приводит к условию ${{(\partial \kappa } \mathord{\left/ {\vphantom {{(\partial \kappa } {\partial {{n}_{Z}}{{)}_{T}} = {{ - \kappa } \mathord{\left/ {\vphantom {{ - \kappa } {3{{n}_{Z}}}}} \right. \kern-0em} {3{{n}_{Z}}}}}}} \right. \kern-0em} {\partial {{n}_{Z}}{{)}_{T}} = {{ - \kappa } \mathord{\left/ {\vphantom {{ - \kappa } {3{{n}_{Z}}}}} \right. \kern-0em} {3{{n}_{Z}}}}}}.$
Безразмерное давление в электронейтральной системе макроионов и микроионов p = P/(nZkT) можно записать как
Здесь первые два члена соответствуют идеальногазовому вкладу макроионов и микроионов. Обратную сжимаемость можно записать какДля расчета границ отрицательного давления и сжимаемости с помощью уравнения состояния [36] из этой работы была взята зависимость pex(κ, Г).
Второе уравнение состояния было получено в статье [19]. Обсуждаемая асимметричная плазма макроионов и микроионов рассматривается в этой работе как чисто кулоновская система, подчиняющаяся уравнению Пуассона. По этой причине и ввиду указанной выше неопределенности с учетом сжимаемости фона и необходимости дифференцирования по nZ при вычислении давления и при вычислении границ термодинамической неустойчивости в настоящей работе используется известная связь кулоновских поправок на неидеальность к давлению pex и энергии uex, справедливая для кулоновских систем:
(3)
${{p}_{{{\text{ex}}}}}(\kappa ,\Gamma ) = {{{{u}_{{{\text{ex}}}}}(\kappa ,\Gamma )} \mathord{\left/ {\vphantom {{{{u}_{{{\text{ex}}}}}(\kappa ,\Gamma )} 3}} \right. \kern-0em} 3},$На рис. 1 на фазовую диаграмму [10] (сплошные линии без нумерации – границы фазовых переходов) нанесены параболы (штриховые линии), соответствующие определенным значениям заряда макроиона Z. Справа от линий 1a и 2a находятся области отрицательной сжимаемости, а справа от линий 1b и 2b – области отрицательного давления. При расчете линий 1a и 1b опирались на уравнение состояния [36], при расчете линий 2a и 2b на уравнение состояния [19]. Фон микроионов в обоих случаях считался сжимаемым.
Рис. 1.
Области отрицательной сжимаемости (справа от линий 1a и 1b) и отрицательного давления (справа от линий 2a и 2b) двухкомпонентной электронейтральной однотемпературной системы макроионов и противоположно заряженных микроионов, рассчитанные по уравнениям состояния [19, 36] на фазовой диаграмме [10]; сплошные линии – границы фазовых переходов диаграммы [10], штриховые линии – параболы Г = κ2Z/3; 1a, 1b рассчитаны с помощью уравнения состояния [36]; 2a, 2b ‒ [19]; фон микроионов сжимаемый.
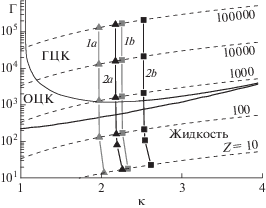
Рис. 1 можно трактовать следующим образом: при движении слева направо вдоль параболы Г ~ κ2, соответствующей некоторому значению заряда макроиона Z, система изохорически охлаждается (или изотермически сжимается), и в некоторый момент ее сжимаемость становится отрицательной. В этом случае некоторые области на фазовой диаграмме становятся недостижимыми. Следует подчеркнуть, что таким образом нельзя достичь, например, тройной точки на исходной фазовой диаграмме для двухкомпонентной равновесной трехмерной системы.
АВТОМОДЕЛЬНОСТЬ ЗАВИСИМОСТИ ЭФФЕКТИВНОГО ЗАРЯДА МАКРОИОНА ОТ ЕГО ИСХОДНОГО ЗАРЯДА, ТЕМПЕРАТУРЫ СИСТЕМЫ И РАЗМЕРОВ МАКРОИОНОВ
Известно, что эффект нелинейности в экранировании заряда проявляется прежде всего при учете вклада интенсивного притяжения макроиона и микроионов в области максимума притяжения вблизи поверхности макроиона, где нарушается условие линеаризации |(eφ(r))/(kT)| $ \ll $ 1 (φ(r) – средний электростатический потенциал, создаваемый макроионом и окружающими его микроионами). Хорошо известным следствием обсуждаемого эффекта (см., например, [30]) является резкий рост в этой зоне концентрации микроионов, локализованных вблизи поверхности макроиона, создающих своеобразную плотную “пленку” и образующих вместе с экранированным макроионом квазичастицу с эффективным (“видимым”) зарядом Z*, который может быть заметно меньше исходного заряда макроиона Z. Такая локализация части микроионов вблизи поверхности макроиона делает обоснованным выделение этой части экранирующего облака микроионов в отдельный сорт связанных микроионов [16] с оставлением в разряде свободных микроионов в зоне, где выполняется упомянутое условие линеаризации.
Поскольку в рамках бескорреляционного приближения ПБ такое разделение микроионов на свободные и связанные является условным, в литературе обсуждаются различные способы этого разделения. Один из них [16] относит к свободным микроионы, расположенные вдали от макроиона – в области, где выполняется условие линеаризации и где параметры экранирования могут описываться линеаризованным дебаевским приближением. Другой способ выделения свободных ионов и определения эффективного заряда Z* рассмотрен в [41]. Согласно этой процедуре к разряду свободных относят все микроионы с положительной полной энергией (т.е. суммой кинетической и потенциальной энергий), а все микроионы с отрицательной полной энергией ‒ к связанным. Более простой вариант определения эффективного заряда с ориентацией на использование модели средней сферической ячейки ВЗ использован в [42]. В рамках этой процедуры свободными считаются микроионы с концентрацией, равной концентрации микроионов на границе ячейки ВЗ (с радиусом R) ni 0, однородно заполняющие все пространство ячейки, а связанными – все микроионы с концентрацией выше ni0:
Этот упрощенный вариант был использован в [43] для учета эффекта нелинейного экранирования и соответствующей “перенормировки” заряда макроиона Z ⇒ Z* и последующей оценки предполагаемого cдвига фазового состояния системы на фазовой диаграмме [10] комплексной плазмы.
Как и в [43], в расчетах настоящей работы рассматривается электронейтральная сферически-симметричная ячейка ВЗ с центральным макроионом с зарядом Z и радиусом RZ. Остальной объем ячейки заполнен противоположно заряженными точечными микроионами с единичным зарядом. Радиус ячейки равен R. Результаты расчета профиля микроионов в приближении ПБ приведены на рис. 2, где изображена зависимость перенормированного (эффективного) заряда Z* от исходного Z в вариации последнего при фиксированных значениях температуры системы и концентрации макроионов (так называемый процесс “зарядки”).
Рис. 2.
Эффективный заряд макроиона как функция исходного заряда макроиона для различных температур в приближении Пуассона–Больцмана при nZ = = 108 см–3, R = 13.34 мкм, RZ = 1 мкм; 1 – kT = 0.135 эВ, 2 – 0.087, 3 – 0.05, 4 – 0.01; левые и правые полые маркеры – Ф(RZ) = 1 и Ф(RZ) = 10 соответственно; 5 – условие ${{Z{{e}^{2}}} \mathord{\left/ {\vphantom {{Z{{e}^{2}}} {({{R}_{Z}}kT)}}} \right. \kern-0em} {({{R}_{Z}}kT)}} = 8.$
Главный результат расчетов, демонстрируемый на рис. 1, состоит в отчетливом распаде всей зависимости Z*(Z) на два режима изменения эффективного заряда Z* – слабого экранирования, когда Z* ≈ Z, и режима сильного экранирования (насыщения), когда Z* ≈ const, с плавным, но отчетливым переходом между ветвями. Характерно, что условия этого перехода между двумя режимами экранирования точно соответствуют этапу нарушения условия линеаризации. На рис. 2 нанесены границы интервала выхода из этого условия: $\Phi ({{R}_{Z}}) \equiv {{e\varphi ({{R}_{Z}})} \mathord{\left/ {\vphantom {{e\varphi ({{R}_{Z}})} {(kT)}}} \right. \kern-0em} {(kT)}} = 1$ и $\Phi ({{R}_{Z}}) = 10,$ где φ(r) – средний электростатический потенциал, создаваемый макроионом и окружающими его микроионами. В дальнейшем в качестве простой условной границы обсуждаемой смены режима экранирования в приближении ПБ можно взять приближенное положение середины участка перехода – точку максимального перегиба, также отмеченную на рис. 3, с простым условием ${{Z{{e}^{2}}} \mathord{\left/ {\vphantom {{Z{{e}^{2}}} {({{R}_{Z}}kT)}}} \right. \kern-0em} {({{R}_{Z}}kT)}} = 8.$
Рис. 3.
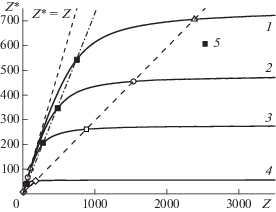
Автомодельные зависимости Z*(Z, kT, RZ) в приближении Пуассона–Больцмана при фиксированных параметрах упаковки: штриховые линии – касательные к кривым 1–4, 1 – ϕ = 4.2 × 10–6 (nZ = = 106 см–3, RZ = 1 мкм), точка пересечения двух касательных q* = 6.2; 2 – 4.2 × 10–5 (nZ = 107 см–3, RZ = = 1 мкм), 7.6; 3 – 4.2 × 10–4 (nZ = 108 см–3, RZ = = 1 мкм), 9.9; 4 – 4.2 × 10–3 (nZ = 109 см–3, RZ = 1 мкм), 12.6; 5, 6 – точки пересечения двух касательных к каждой из кривых 1–4; 7 – условие ${{Z{{e}^{2}}} \mathord{\left/ {\vphantom {{Z{{e}^{2}}} {({{R}_{Z}}kT)}}} \right. \kern-0em} {({{R}_{Z}}kT)}} = 8.$

Еще одно замечательное свойство ПБ-экранирования, которое следует из рис. 2, это своеобразная автомодельность зависимости Z*(Z,kT,RZ). Следует уточнить, что данная автомодельность означает возможность простым и физически понятным масштабированием совместить воедино все зависимости Z*(Z), отвечающие различным температурам макроионов. Это иллюстрируется на рис. 3, где обе величины как исходного заряда Z, так и рассчитанного в приближении ПБ эффективного заряда Z* отнесены к величине температуры плазмы для различных фиксированных параметров упаковки $\phi \equiv {{4\pi {{n}_{Z}}R_{Z}^{3}} \mathord{\left/ {\vphantom {{4\pi {{n}_{Z}}R_{Z}^{3}} 3}} \right. \kern-0em} 3}.$ Для простоты дальнейшего использования введены более краткие обозначения безразмерных комбинаций параметров по горизонтальной и вертикальной осям соответственно
Для каждой из автомодельных кривых рис. 3 проведено две касательных – к участкам, отвечающим за линейное (Z* ≈ Z) и нелинейное (Z* ≈ const) насыщение. Точки пересечения обозначены незаполненными кружками. Именно эти точки используются в качестве условной границы между двумя режимами экранирования для соответствующей фиксированной концентрации макроионов.
В данной работе понятие эффективного заряда макроиона используется для демонстрации автомодельности зависимости этого заряда от различных параметров плазмы и оценки достижимости границы термодинамической устойчивости на основе полученной автомодельной зависимости. Расчет же термодинамических потенциалов с использованием эффективного заряда макроиона в данной работе не проводится.
ОЦЕНКА ВОЗМОЖНОСТИ ДОСТИЖЕНИЯ ГРАНИЦЫ ТЕРМОДИНАМИЧЕСКОЙ УСТОЙЧИВОСТИ
Как известно, реальное фазовое состояние системы зависит от эффективного межчастичного взаимодействия макроионов на средних расстояниях между ними. Предполагается [43], что это определяется эффективным зарядом макроиона Z*, экранируемым только свободными микроионами с концентрацией ni0(r), а не исходным зарядом макроиона Z и концентрацией всех микроионов ni. При этом структура фазовой диаграммы [10] приближенно сохраняется для асимметричной системы-прототипа, состоящей из макроионов конечных размеров и точечных микроионов, но уже в переменных κ*–Г*:
Поскольку Z* < Z и ni 0 < ni, то при учете эффекта нелинейного экранирования реальное положение фазового состояния указанной системы-прототипа на исходной фазовой диаграмме смещается в сторону меньших Г и κ. Вывод, который можно сделать о положении фазовых состояний электронейтральной системы макроионов конечных размеров и точечных микроионов с учетом эффекта нелинейного экранирования, позволяет предположить, что учет нелинейного экранирования в подходе [11] может привести к существенному смещению границ фазовых состояний такой же системы-прототипа относительно их положений для рассматриваемой однокомпонентной системы макроионов на сжимаемом фоне микроионов [11]. Более того, границы отрицательного давления и отрицательной сжимаемости, полученные в настоящей работе, также сохраняются, но не в переменных κ–Г, а в переменных κ*–Г*.
Выражая ni0 из уравнения (3) и подставляя туда радиус ячейки $R = {{\left( {{3 \mathord{\left/ {\vphantom {3 {4\pi {{n}_{Z}}}}} \right. \kern-0em} {4\pi {{n}_{Z}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}},$ находим
Подставим это выражение в уравнения для κ* и Г* (4) и получим соотношение между этими параметрами в двухкомпонентной системе
Так как параметр упаковки в комплексной плазме обычно принимает значения примерно от 10–3 до 10–8 [39], то выражение (5) приобретает вид
В таком случае безразмерный параметр q* можно выразить и через Г*, и через κ*. Запишем первый вариант
На рис. 4 проведены вертикальные оценочные кривые, примерно соответствующие границам отрицательного давления и отрицательной сжимаемости [19] рис. 1. Последние две кривые, как утверждалось в данном разделе выше, с учетом эффекта нелинейного экранирования должны сохраняться в переменных κ*–Г*. Штрихпунктир на рис. 4 соответствуют параметрам упаковки кривых 1–4 рис. 3. Линии 1–4 на рис. 4 соответствуют значениям q* в точкax пересечения двух касательных к кривым 1–4 на рис. 3 соответственно. Для каждой автомодельной кривой на рис. 3 при росте параметра q значение параметра q* в режиме насыщения практически остается постоянным, поэтому можно считать, что значение q* точки пересечения касательных является практически максимальным для соответствующего параметра упаковки. Следовательно, при перемещении вдоль любой штрихпунктирной кривой рис. 4 слева направо значение q* повышается до некоторого максимального значения, которое отмечено черным кружком в точке пересечения кривых ϕ = const и q* = const. Все четыре точки находятся сравнительно далеко от границ отрицательного давления и отрицательной сжимаемости по уравнению состояния [19]. Исходя из этого, можно предположить, что граница термодинамической неустойчивости по уравнению состояния [19] не достигается.
Рис. 4.
Оценка достижимости термодинамической неустойчивости по уравнению состояния [19]: I – граница отрицательной (справа от линии) сжимаемости, II – граница отрицательного (справа) давления по уравнению состояния [19]; штрихпунктирные линии – ϕ = const (снизу вверх: ϕ = 4.2 × 10–6, 4.2 × 10–5, 4.2 × 10–4, 4.2 × 10–3 в соответствии с линиями 1–4); 1 – q* = 12.6, 2 – 9.9, 3 – 7.6, 4 – 6.2, 5 – 3, 6 – 1.

В работе [16] также показано, что учет нелинейного экранирования в двухкомпонентной коллоидной плазме и результирующая перенормировка исходного заряда макроиона ведут к тому, что фазовый переход типа газ–жидкость отсутствует в такой системе. Без учета данного эффекта наблюдается фазовое расслоение. Отличие указанного результата [16] от настоящей работы заключается в использовании другого определения эффективного заряда.
ЗАКЛЮЧЕНИЕ
В работе получены границы областей отрицательного давления и отрицательной сжимаемости, задаваемых уравнениями состояния [19, 36] на фазовой диаграмме асимметричной комплексной плазмы [10]. Значительная часть фазовой диаграммы занята областью отрицательных значений давления и сжимаемости.
С учетом эффекта нелинейного экранирования макроионов микроионами в приближении Пуассона–Больцмана в средней сферической ячейке Вигнера–Зейтца была получена автомодельная зависимость эффективного заряда макроиона Z* от исходного заряда Z, температуры системы kT и радиуса макроиона RZ при фиксированном параметре упаковки.
Проведенная на основе полученной автомодельной зависимости Z*(Z, kT, RZ) оценка возможности достижения границы термодинамической устойчивости по уравнению состояния [19] дает основание полагать, что указанная граница может оказаться недостижимой. В работе получены границы отрицательного давления и отрицательной сжимаемости по уравнениям состояния [19, 36] на фазовой диаграмме [10] комплексной плазмы. Показано, что большая часть данной фазовой диаграммы также лежит в области отрицательных значений давлений и сжимаемости.
Список литературы
Фортов В.Е., Храпак А.Г., Якубов И.Т. Физика неидеальной плазмы. Учеб. пособ. М.: Физматлит, 2004. 528 с.
Фортов В.Е., Морфилл Г.Е. Комплексная и пылевая плазма: из лаборатории в космос / Под ред. Фортова В.Е., Морфилла Г.Е. Пер. с англ. под ред. Храпака А.Г. М.: Физматлит, 2012. 444 с.
Энциклопедия низкотемпературной плазмы. Т. прилож. III-1 / Под ред. Фортова В.Е. М.: Физматлит, 2004. 535 с.
Фортов В.Е. Гидродинамические эффекты в неидеальной плазме // ТВТ. 1972. Т. 10. № 1. С. 168.
Фортов В.Е., Дремин А.Н., Леонтьев А.А. Простые и единые оценки параметров критических точек многих веществ // ТВТ. 1975. Т. 13. № 5. С. 1072.
Ликальтер А.А. Газообразные металлы // УФН. 1992. Т. 162. С. 119.
Ликальтер А.А. О критических параметрах металлов // ТВТ. 1985. Т. 23. № 3. С. 465.
Ликальтер А.А. Плазма металлов и полупроводников в окрестности критической точки конденсации // Энциклопедия низкотемпературной плазмы. Т. прилож. III-1 / Под ред. Старостина А.Н., Иосилевского И.Л. Под общ. ред. Фортова В.Е. М.: Физматлит, 2004. С. 349.
Иосилевский И.Л. Фазовые переходы в кулоновских системах. В сб.: Уравнение состояния в экстремальных условиях / Под ред. Гадияка Г.В. Новосибирск: Изд-во СОАН СССР, 1981. С. 20.
Hamaguchi S., Farouki R., Dubin D. Phase Diagram of Yukawa Systems near the One-component-plasma Limit Revisited // J. Chem. Phys. 1996. V. 105. № 17. P. 7641.
Dijkstra M., van Roij R. Vapour-liquid Coexistence for Purely Repulsive Point-Yukawa Fluids // J. Phys. Condens. Matter. 1998. V. 10. № 6. P. 1219.
Hynninen A.-P., Panagiotopoulos A. Z. Disappearance of the Gas-liquid Phase Transition for Highly Charged Colloids // Phys. Rev. Lett. 2007. V. 98. № 19. P. 198301.
Warren P.B. Phase Separation, Interface Properties, and Charge Density Waves in a Simplified Model for a Macroion Suspension // Phys. Rev. E. 2006. V. 73. № 1. P. 011411.
Иосилевский И.Л., Старостин А.Н. Проблема термодинамической устойчивости и фазовых переходов в низкотемпературной плазме // Энциклопедия низкотемпературной плазмы. Т. прилож. III-1 / Под ред. Фортова В.Е. М.: Наука, 2000. С. 327.
Martynova I., Iosilevskiy I. Features of Phase Transitions in Models of Complex Plasma // Contrib. Plasma Phys. 2016. V. 56. № 5. P. 432.
Diehl A., Barbosa M., Levin Y. Charge Renormalization and Phase Separation in Colloidal Suspensions // EPL. 2001. V. 53. № 1. P. 86.
Фортов В.Е., Храпак А.Г., Храпак С.А., Молотков В.И., Петров О.Ф. Пылевая плазма // УФН. 2004. Т. 174. № 5. С. 495.
Yazdi A., Ivlev A., Khrapak S., Thomas H., Morfill G.E., Löwen H., Wysocki A., Sperl M. Glass-transition Properties from Hard Spheres to Charged Point Particles // Phys. Rev. E. 2014. V. 89. P. 063105.
Khrapak S., Khrapak A., Ivlev A., Morfill G. Simple Estimation of Thermodynamic Properties of Yukawa Systems // Phys. Rev. E. 2014. V. 89. № 2. P. 023102.
Vaulina O., Khrapak A. Scaling Law for the Fluid-solid Phase Transition in Yukawa Systems (Dusty Plasmas) // JETP. 2000. V. 90. № 2. P. 289.
Vaulina O.S., Koss X.G. Solid–Liquid Phase Transitions in 3D Systems with the Inverse-power and Yukawa Potentials // Phys. Lett. A. 2016. V. 380. № 13. P. 1290.
Meijer E.J., Frenkel D. Melting Line of Yukawa System by Computer Simulation // J. Chem. Phys. 1991. V. 94. № 3. P. 2269.
Kremer K., Robbins M.O., Grest G.S. Phase Diagram of Yukawa Systems: Model for Charge-stabilized Colloids // Phys. Rev. Lett. 1986. V. 57. № 21. P. 2694.
Иосилевский И.Л. Фазовый переход в простейшей модели плазмы // ТВТ. 1985. Т. 23. № 6. С. 1041.
Iosilevski I., Chigvintsev A. Phase Transition in Simplest Plasma Models. In: Physics of Non-ideal Plasmas / Eds. Ebeling W., Forster A., Radtke R. Stuttgart–Leipzig: Teubner, 1992. P. 87.
Иосилевский И.Л. Эффекты неидеальности в низкотемпературной плазме // Энциклопедия низкотемпературной плазмы. Т. прилож. III-1 / Под ред. Старостина А.Н., Иосилевского И.Л. Под общ. ред. Фортова В.Е. М.: Физматлит, 2004. С. 349.
Иосилевский И.Л., Красников Ю.Г., Сон Э.Е., Фортов В.Е. Термодинамика и транспорт в неидеальной плазме. М.: Изд-во МФТИ, 2000. 476 с.
Martynova I., Iosilevskiy I., Shagayda A. Macroions Non-linear Screening in Complex Plasma // J. Phys.: Conf. Ser. 2018. V. 946. P. 012147.
Иосилевский И.Л. Физика неидеальных кулоновских систем. Saarbruecken: Lambert Acad. Publ., 2011. 235 с.
Жуховицкий Д.И., Храпак А.Г., Якубов И.Т. Ионизационное равновесие в сильно неидеальной плазме с конденсированной дисперсной фазой // ТВТ. 1984. Т. 22. № 5. С. 833.
Липаев А.М., Молотков В.И., Жуховицкий Д.И., Наумкин В.Н., Усачев А.Д., Зобнин А.В., Петров О.Ф., Фортов В.Е. Исследования пылевой газоразрядной плазмы на космической установке “Плазменный кристалл-3 плюс” (обзор) // ТВТ. 2020. Т. 58. № 4. С. 485.
Khrapak S.A., Klumov B.A., Huber P., Molotkov V.I., Lipaev A.M., Naumkin V.N., Ivlev A.V., Thomas H.M., Schwabe M., Morfill G.E., Petrov O.F., Fortov V.E., Malentschenko Yu., Volkov S. Fluid-solid Phase Transition in Three-dimensional Complex Plasmas under Microgravity Conditions // Phys. Rev. E. 2012. V. 85. P.066407.
Клумов Б., Морфилл Г., Попель С. Формирование структур в запыленной ионосфере // ЖЭТФ. 2005. Т. 127. № 1. С. 171.
Хомкин А.Л., Муленко И.А. Фазовый переход в моделях электролитов, несимметричных по размеру и заряду // ТВТ. 2003. Т. 41. № 5. С. 659.
Kim Y.C., Fisher M.E., Panagiotopoulos A.Z. Universality of Ionic Criticality: Size- and Charge-asymmetric Electrolytes // Phys. Rev. Lett. 2005. V. 95. № 19. P. 195703.
Farouki R.T., Hamaguchi S. Thermodynamics of Strongly-coupled Yukawa Systems near the One-component-plasma Limit. II. Molecular Dynamics Simulations // J. Chem. Phys. 1994. V. 101. № 11. P. 9885.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Учеб. пособ. В 10-ти т. Т. V. Статистическая физика. Ч. I. М.: Физматлит, 2002. 616 с.
Martynova I., Iosilevskiy I. Macroion Effective Charge in Complex Plasmas with Regard to Microions Correlations // Contrib. Plasma Phys. 2021. V. 61. e202000142.
Martynova I., Iosilevskiy I. Self-similarity of Nonlinear Screening in Asymmetric Complex Plasmas // Contrib. Plasma Phys. 2021. V. 61. e202100007.
Chabrier G., Potekhin A.Y. Equation of State of Fully Ionized Electron-ion Plasmas // Phys. Rev. E. 1998. V. 58. № 4. P. 4941.
Szichman H., Eliezer S., Salzmann D. Calculation of the Moments of the Charge State Distribution in Hot and Dense Plasmas Using the Thomas–Fermi Mo-dels // J. Quant. Spectrosc. Radiat. Transfer. 1987. V. 38. № 4. P. 281.
Martynova I., Iosilevskiy I. Effect of Non-linear Screening on Thermodynamic Properties of Complex Plasma // J. Phys.: Conf. Ser. 2019. V. 1147. P. 012107.
Martynova I.A., Iosilevskiy I.L. Non-linear Screening and Phase States of a Complex Plasma // Contrib. Plasma Phys. 2018. V. 58. № 2–3. P. 203.
Дополнительные материалы отсутствуют.
Инструменты
Теплофизика высоких температур


