Теоретические основы химической технологии, 2019, T. 53, № 1, стр. 102-111

Снижение неравномерности распределения толщины гальванического покрытия с использованием отключаемых анодных секций при реверсировании тока

Д. С. Соловьев^{1, 2, *}, А. Ю. Потлов², Ю. В. Литовка²

¹ Тамбовский государственный университет им. Г.Р. Державина
Тамбов, Россия

² Тамбовский государственный технический университет
Тамбов, Россия

^* E-mail: solovjevdenis@mail.ru

Поступила в редакцию 01.05.2016
После доработки 19.07.2018
Принята к публикации 16.05.2018

DOI: 10.1134/S0040357118060155

Полный текст (PDF)

Аннотация

Предложен способ снижения неравномерности гальванического покрытия на основе отключения анодных секций в режиме реверсирования тока, отличающийся относительной простотой технической реализации, что позволяет расширить номенклатуру обрабатываемых изделий для серийного производства. Гальванический процесс в режиме реверсирования тока с отключаемыми анодными секциями формализован посредством постановки задачи оптимального управления и разработки математической модели. Приведены результаты компьютерного моделирования, а также проверки адекватности разработанной математической модели по экспериментальным данным, демонстрирующие эффективность предложенного способа.

Ключевые слова: гальванический процесс, неравномерность толщины покрытия, режим реверсирования тока, многоанодная ванна, математическая модель, оптимальное управление

ВВЕДЕНИЕ

Одной из наиболее сложных проблем, возникающих при нанесении гальванических покрытий, является получение на изделии сложной геометрической конфигурации равномерного слоя покрытия. Неравномерное распределение покрытия влечет за собой дополнительный расход не только металла покрытия, но и электроэнергии, затрачиваемой на гальванический процесс. Соблюдение точности заданной толщины покрытия позволит исключить брак (толщина меньше заданной) и устранить из технологического процесса последующую механическую обработку изделий (при излишней толщине). Изучению проблемы снижения неравномерности гальванического покрытия посвящено значительное количество исследований. Одним из ключевых трудов в этой области является работа [1], согласно которой равномерность распределения толщины слоя гальванического покрытия обусловливается электрохимическими и геометрическими условиями осаждения. При учете электрохимических условий осаждения покрытия решается задача устранения диффузионных ограничений электролиза за счет интенсивного механического перемешивания электролита, покачивания катодных штанг, непрерывной или периодической фильтрации электролита, вибрации, осаждения в ультразвуковом поле, а также применения нестационарных режимов электролиза (реверсивного [2], импульсного [3] и ассиметричного тока [4]), включающих изменение формы и параметров тока с целью замедления роста металлического покрытия на участках с повышенными плотностями тока, предоставляя возможность получать более качественные катодные покрытия, чем при электролизе с прямым током.

Одним из основных геометрических факторов, оказывающих влияние на равномерность распределения толщины гальванического покрытия, является межэлектродное расстояние. Согласно правилам получения равномерного распределения толщины гальванического покрытия, следующим из законов Г.С. Ома и Г. Кирхгофа, протекание наибольшего количества тока происходит в участках электролита с наименьшими межэлектродными расстояниями, и наибольшая толщина покрытия осаждается на углах и ребрах изделия (краевой эффект). В связи с этим при покрытии внешней поверхности изделия аноду придают форму, воспроизводящую очертания поверхности катода [5]. Дополнительно для защиты ребер, острых углов и выступов на покрываемых деталях от избыточного концентрирования на них силовых линий тока применяют защитные экраны [6]. Использование биполярного электрода, имеющего большую электропроводность, чем электролит в межэлектродном пространстве, также позволяет осуществить регулирование распределения тока на поверхности детали [7].

Тем не менее ряд исследователей предлагают различные сочетания электрохимических и геометрических условий нанесения гальванического покрытия. Так, в работе [8] предлагается использовать дополнительные аноды, способные перемещаться в направлении, перпендикулярном своей поверхности, причем их положение подбирается из расчета получения наиболее равномерного гальванического покрытия. Однако существование ограничений, как на число дополнительных анодов, так и на занимаемые ими положения, связанных с технической реализацией конструкции перемещающих устройств, сделало эффективность применения такого способа для нанесения покрытий на детали сложной формы незначительной. В работе [9] рассматривается применение дополнительных анодов, питание которых осуществляется от независимых источников питания с различными значениями подаваемых напряжений. При этом использование более одного источника питания затрудняет не только техническую реализацию данного процесса, но и делает его экономически нецелесообразным.

Целью исследования является снижение неравномерности распределения толщины гальванического покрытия на изделиях сложной формы за счет оригинального сочетания оптимального электрохимического режима с геометрическими конфигурациями используемых электродов, отличающегося относительной простотой технической реализации, а также пригодностью для серийного производства.

Основная идея предлагаемого технологического процесса нанесения гальванического покрытия предусматривает разбиение монолитного анода на систему из прямоугольных анодных секций с возможностью отключения от источника питания требуемых анодных секций во время “прямого” и “обратного” режима реверсирования тока. В свою очередь, требуемые для отключения анодные секции, а также длительность периодов “прямого” и “обратного” режима реверсирования определяются с ориентацией на получение наиболее равномерного покрытия на поверхности изделия.

ТЕОРЕТИЧЕСКИЙ АНАЛИЗ

Для оценки неравномерности распределения покрытия на поверхности катода применяют отношения экстремальных значений толщины на покрываемой поверхности, полученные за длительность процесса Т:

(1)

${{R}_{1}}\left( T \right) = \frac{{\overline \delta }}{{{{\delta }^{{\min }}}}},$

(2)

${{R}_{2}}\left( T \right) = \frac{{{{\delta }^{{\max }}}}}{{{{\delta }^{{\min }}}}},$

где R₁, R₂ – критерии Л.И. Каданера и В.Т. Иванова соответственно; δ^min, δ^max, $\bar {\delta }$ – минимальная, максимальная и средняя толщина покрытия:

(3)

${{\delta }^{{\min }}} = \mathop {\min }\limits_{\delta \in {{S}_{k}}} \left( {\delta \left( {x,y,z,T} \right)} \right),$

(4)

${{\delta }^{{\max }}} = \mathop {\max }\limits_{\delta \in {{S}_{k}}} \left( {\delta \left( {x,y,z,T} \right)} \right),$

(5)

$\bar {\delta } = \frac{1}{{\left\| {{{S}_{k}}} \right\|}}\int\limits_{{{S}_{k}}} {\delta \left( {x,y,z,T} \right)d{{S}_{k}}} ,$

где $\left\| {{{S}^{k}}} \right\|$ – площадь поверхности катода; x, y, z – координаты точки в пространстве гальванической ванны.

Наиболее предпочтительным критерием оценки неравномерности покрытия, по мнению авторов, является суммарная комбинация критериев (1) и (2), что позволяет учесть наросты на незначительной площади изделия-катода, когда неравномерность на остальных участках будет удовлетворительной.

Однако эффективность применения такого технологического процесса невозможна без разработки алгоритмов моделирования и оптимального управления для предлагаемого процесса. В связи с этим постановка задачи оптимального управления рассматриваемым гальваническим процессом будет звучать следующим образом. Найти режимы работы системы анодных секций ${{S}_{{{{a}_{{MxN}}}}}}$ для “прямого” $I_{{MxN}}^{{st*}}\left( {\tau } \right)$ и “обратного” $I_{{MxN}}^{{rv*}}\left( {\tau } \right)$ гальванического процесса реверсирования тока с длительностями ${\tau }{{_{{}}^{{st}}}^{*}}$ и ${\tau }{{_{{}}^{{rv}}}^{*}}$, минимизирующие критерий неравномерности распределения толщины покрытия на поверхности катода S_k:

(6)

$\begin{gathered} R\left( T \right) = \frac{1}{{\left\| {{{S}_{k}}} \right\|}}\frac{{\int\limits_{{{S}_{k}}} {\delta \left( {x,y,z,T} \right) \cdot d{{S}_{k}}} }}{{\min \left( {\delta \left( {x,y,z,T} \right)} \right)}} + \\ + \,\,\frac{{\mathop {\max }\limits_{\delta \in {{S}_{k}}} \left( {\delta \left( {x,y,z,T} \right)} \right)}}{{\mathop {\min }\limits_{\delta \in {{S}_{k}}} \left( {\delta \left( {x,y,z,T} \right)} \right)}} \to \min , \\ \end{gathered} $

при этом должны выполняться следующие ограничения:

(7)

$\mathop {\min }\limits_{\delta \in {{S}_{k}}} \left( {\delta \left( {x,y,z,T} \right)} \right) \geqslant {{\delta }^{{{\text{zad}}}}},$

(8)

$T = \sum\limits_{j = 0}^\upsilon {\left( {\tau _{j}^{{st}} + \tau _{j}^{{rv}}} \right)} \leqslant {{T}^{{\max }}},$

где δ^zad – заданная толщина гальванического покрытия; Т^max – максимальная продолжительность гальванического процесса; τ – момент времени; υ – количество периодов включения “прямого” и “обратного” тока; M, N – число рядов и количество анодных секций в каждом из них.

Матрица, описывающая режим работы системы анодных секций для “прямого” включения, имеет вид

(9)

$I_{{MxN}}^{{st}}\left( \tau \right) = \left( {\begin{array}{*{20}{c}} {I_{{1,1}}^{{st}}\left( \tau \right)...}&{I_{{1,n}}^{{st}}\left( \tau \right)...}&{I_{{1,N}}^{{st}}\left( \tau \right)} \\ {I_{{m,1}}^{{st}}\left( \tau \right)...}&{I_{{m,n}}^{{st}}\left( \tau \right)...}&{I_{{m,N}}^{{st}}\left( \tau \right)} \\ {I_{{M,1}}^{{st}}\left( \tau \right)...}&{I_{{M,n}}^{{st}}\left( \tau \right)...}&{I_{{M,N}}^{{st}}\left( \tau \right)} \end{array}} \right),$

для “обратного” включения:

(10)

$I_{{MxN}}^{{rv}}\left( \tau \right) = \left( {\begin{array}{*{20}{c}} {I_{{1,1}}^{{rv}}\left( \tau \right)...}&{I_{{1,n}}^{{rv}}\left( \tau \right)...}&{I_{{1,N}}^{{rv}}\left( \tau \right)} \\ {I_{{m,1}}^{{rv}}\left( \tau \right)...}&{I_{{m,n}}^{{rv}}\left( \tau \right)...}&{I_{{m,N}}^{{rv}}\left( \tau \right)} \\ {I_{{M,1}}^{{rv}}\left( \tau \right)...}&{I_{{M,n}}^{{rv}}\left( \tau \right)...}&{I_{{M,N}}^{{rv}}\left( \tau \right)} \end{array}} \right),$

где

Для определения связи критерия оценки неравномерности распределения толщины покрытия (6) с работой анодных секций в “прямом” и “обратном” режимах составим математическую модель для рассматриваемого процесса.

Толщина покрытия в результате υ периодов включения “прямого” и “обратного” тока определяется следующей суммой:

(11)

$\begin{gathered} \delta \left( {x,y,z,T} \right) = \\ = \sum\limits_{j = 1}^\upsilon {\left( {\delta _{j}^{ + }\left( {x,y,z,\tau _{j}^{{st}}} \right) + \delta _{j}^{ - }\left( {x,y,z,\tau _{j}^{{rv}}} \right)} \right)} . \\ \end{gathered} $

Прирост слоя покрытия на изделии за длительность j-го “прямого” включения тока, согласно закону Фарадея, описывается выражением

(12)

$\begin{gathered} \delta _{j}^{ + }\left( {x,y,z,\tau _{j}^{{st}}} \right) = \frac{E}{\rho }\int\limits_0^{\tau _{j}^{{st}}} {{{\eta }_{k}}\left( {x,y,z,\tau } \right)} \times \\ \times \,\,i_{k}^{{st}}\left( {x,y,z,\tau } \right)d\tau . \\ \end{gathered} $

Растворение слоя покрытия на изделии за длительность j-го “обратного” включения тока имеет вид

(13)

$\begin{gathered} \delta _{j}^{ - }\left( {x,y,z,\tau _{j}^{{rv}}} \right) = \\ = - \frac{E}{\rho }\int\limits_0^{\tau _{j}^{{rv}}} {{{\eta }_{a}}\left( {x,y,z,\tau } \right)} i_{k}^{{rv}}\left( {x,y,z,\tau } \right)d\tau . \\ \end{gathered} $

В уравнения (12)–(13) входят катодный и анодный выходы по току, которые зависят от температуры (t), катодной плотности тока и концентрации основных компонентов электролита:

(14)

${{\eta }_{a}}\left( {x,y,z,\tau } \right) = {{\eta }_{a}}\left( {t, i_{k}^{{rv}}\left( {x,y,z,\tau } \right),{{C}_{1}},{{C}_{2}},...} \right),$

(15)

${{\eta }_{k}}\left( {x,y,z,\tau } \right) = {{\eta }_{k}}\left( {t, i_{k}^{{st}}\left( {x,y,z,\tau } \right),{{C}_{1}},{{C}_{2}},...} \right).$

Для вычисления плотностей тока на поверхности детали S_k и анода ${{S}_{{{{a}_{{m,n}}}}}}$ в системе M × N секций воспользуемся законом Ома в дифференциальной форме:

(16)

$i_{k}^{{st}}\left( {x,y,z,\tau } \right) = \left. {\chi \nabla {{\varphi }_{{st}}}\left( {x,y,z,\tau } \right)} \right|{{S}_{k}},$

(17)

$i_{k}^{{rv}}\left( {x,y,z,\tau } \right) = \left. { - \chi \nabla {{\varphi }_{{rv}}}\left( {x,y,z,\tau } \right)} \right|{{S}_{k}},$

(18)

$i_{{{{a}_{{m,n}}}}}^{{st}}\left( {x,y,z,\tau } \right) = \left. { - \chi \nabla {{\varphi }_{{st}}}\left( {x,y,z,\tau } \right)} \right|{{S}_{{{{a}_{{m,n}}}}}},$

(19)

$i_{{{{a}_{{m,n}}}}}^{{rv}}\left( {x,y,z,\tau } \right) = \left. {\chi \nabla {{\varphi }_{{rv}}}\left( {x,y,z,\tau } \right)} \right|{{S}_{{{{a}_{{m,n}}}}}},$

где φ_st, φ_rv – распределение потенциала электрического поля в пространстве гальванической ванны при “прямом” и “обратном” реверсивном режиме; χ – электропроводность электролита.

Распределение потенциала электрического поля в пространстве гальванической ванны размерами L_x (длина), L_y (ширина) и L_z (высота) для “прямого” и “обратного” режима описывается дифференциальными уравнениями в частных производных параболического типа:

(20)

$\begin{gathered} \frac{{\partial {{\varphi }_{{st}}}(x,y,z,\tau )}}{{\partial \tau }} = \frac{{{{c}^{2}}}}{{4\pi \chi \mu }} \times \\ \times \,\,\left( {\frac{{{{\partial }^{2}}{{\varphi }_{{st}}}(x,y,z,\tau )}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{{\varphi }_{{st}}}(x,y,z,\tau )}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}{{\varphi }_{{st}}}(x,y,z,\tau )}}{{\partial {{z}^{2}}}}} \right), \\ \end{gathered} $

(21)

$\begin{gathered} \frac{{\partial {{\varphi }_{{rv}}}(x,y,z,\tau )}}{{\partial \tau }} = \frac{{{{c}^{2}}}}{{4\pi \chi \mu }} \times \\ \times \,\,\left( {\frac{{{{\partial }^{2}}{{\varphi }_{{rv}}}(x,y,z,\tau )}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{{\varphi }_{{rv}}}(x,y,z,\tau )}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}{{\varphi }_{{rv}}}(x,y,z,\tau )}}{{\partial {{z}^{2}}}}} \right), \\ \end{gathered} $

где μ – магнитная проницаемость электролита; с – скорость света в вакууме.

Для “прямого” режима включения (20) граничные условия имеют следующий вид:

(22)

$\left. {\frac{{\partial {{\varphi }_{{st}}}\left( {x,y,z,\tau } \right)}}{{\partial{ \vec {n}}}}} \right|{{S}_{{ins}}} = 0,$

(23)

$\begin{gathered} \left. {{{\varphi }_{{st}}}\left( {x,y,z,\tau } \right) + {{F}_{3}}\left( {i_{{{{a}_{{m,n}}}}}^{{st}}\left( {x,y,z,\tau } \right)} \right)} \right|{{S}_{{{{a}_{{m,n}}}}}} = {{U}_{{be}}}, \\ {\text{е с л и }}\,\,\,\,{\text{ }}I_{{m,n}}^{{st}}\left( \tau \right) = 0, \\ \end{gathered} $

(24)

$\begin{gathered} \left. {{{\varphi }_{{st}}}\left( {x,y,z,\tau } \right) + {{F}_{1}}\left( {i_{{{{a}_{{m,n}}}}}^{{st}}\left( {x,y,z,\tau } \right)} \right)} \right|{{S}_{{{{a}_{{m,n}}}}}} = U, \\ {\text{е с л и }}\,\,\,\,{\text{ }}I_{{m,n}}^{{st}}\left( \tau \right) = 1, \\ \end{gathered} $

(25)

$\left. {{{\varphi }_{{st}}}\left( {x,y,z,\tau } \right) - {{F}_{2}}\left( {i_{k}^{{st}}\left( {x,y,z,\tau } \right)} \right)} \right|{{S}_{k}} = 0,$

(26)

${{\varphi }_{{st}}}\left( {x,y,z,0} \right) = {{\varphi }_{{st}}}_{0}\left( {x,y,z} \right),$

где S_ins, $\vec {n}$– поверхность изолятора и нормаль к ней; φ_st0 – начальное распределение потенциала, оставшееся после включения “обратного” режима; F₁, F₂, F₃ – функция поляризации на аноде, катоде и биполярном электроде; U, U_be – напряжение на аноде и биполярном электроде.

Тогда граничные условия для “обратного” режима включения (21) примут вид

(27)

$\left. {\frac{{\partial {{\varphi }_{{rv}}}\left( {x,y,z,\tau } \right)}}{{\partial{ \vec {n}}}}} \right|{{S}_{{ins}}} = 0,$

(28)

$\left. {{{\varphi }_{{rv}}}\left( {x,y,z,\tau } \right) + {{F}_{1}}\left( {i_{k}^{{rv}}\left( {x,y,z,\tau } \right)} \right)} \right|{{S}_{k}} = U,$

(29)

$\begin{gathered} \left. {{{\varphi }_{{rv}}}\left( {x,y,z,\tau } \right) + {{F}_{3}}\left( {i_{{{{a}_{{m,n}}}}}^{{rv}}\left( {x,y,z,\tau } \right)} \right)} \right|{{S}_{{{{a}_{{m,n}}}}}} = {{U}_{{be}}}, \\ {\text{е с л и }}\,\,\,\,I_{{m,n}}^{{rv}}\left( \tau \right) = 0, \\ \end{gathered} $

(30)

$\begin{gathered} \left. {{{\varphi }_{{rv}}}\left( {x,y,z,\tau } \right) - {{F}_{2}}\left( {i_{{{{a}_{{m,n}}}}}^{{rv}}\left( {x,y,z,\tau } \right)} \right)} \right|{{S}_{{{{a}_{{m,n}}}}}} = 0, \\ {\text{е с л и }}\,\,\,\,I_{{m,n}}^{{rv}}\left( \tau \right) = 1, \\ \end{gathered} $

(31)

${{\varphi }_{{rv}}}\left( {x,y,z,0} \right) = {{\varphi }_{{rv}}}_{0}\left( {x,y,z} \right),$

где φ_rv0 – начальное распределение потенциала, оставшееся после включения “прямого” режима.

Наличие уравнений (23) и (29) обусловлено тем, что электрически неподключенные к источнику питания аноды выполняют роли биполярных электродов, которые также оказывают влияние на распределение тока в гальванической ванне, при отключении соответствующих анодных секций в результате решения задачи оптимального управления рассматриваемым гальваническим процессом. Таким образом, уравнения (1)–(31) формируют математическую модель динамики в распределенных координатах для гальванического процесса с отключаемыми анодными секциями при реверсировании тока, позволяющую отыскать режимы работы системы анодных секций, доставляющих минимум критерию неравномерности распределения толщины покрытия на поверхности катода.

В процессе решения полученной системы уравнений наиболее значимыми являются дифференциальные уравнения в частных производных параболического типа (20), (21) с краевыми условиями второго (22), (27) и третьего рода (23)–(25), (28)–(30). В связи с тем, что в правой части параболических уравнения имеется константа с²/(4πχμ) с порядком значений 10¹⁶–10¹⁸, а значения правой части функций анодного и катодного выхода по току (14), (15) находятся в диапазоне 10^–3–10^–2, то для решения полученных уравнений математической модели используется подход, описанный в работе [10], при котором обе части параболического уравнения делятся на константу с²/(4πχμ). При этом параболическое уравнение сводится к набору дифференциальных уравнений эллиптического типа, описывающих работу всех M × N активных анодных секций при “прямом” и “обратном” режимах реверсирования тока. Для решения данных уравнений пространство гальванической ванны аппроксимируется сеткой и вместо производных функции распределения потенциала электролита в объеме гальванической ванны рассматриваются их приближенные неявные разностные формулы в узлах сетки. Полученный набор уравнений в частных производных эллиптического типа заменяется системой алгебраических уравнений, решение которой отыскивается методом простых итераций, в свою очередь метод нижней релаксации используется для уравнений по катодным (16), (17) и анодным (18), (19) плотностям тока [11]. Задача поиска оптимального управления предложенным процессом представляет собой частично целочисленную задачу нелинейного бинарного программирования. В связи с этим предлагается искать режимы работы секций с использованием сочетания комбинаторных методов (для поиска индексов активных анодов) с методами нелинейной оптимизации (для поиска длительностей “прямого” и “обратного” режима включения) [12].

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Для проверки корректности предложенного способа был проведен ряд экспериментов по нанесению цинкового покрытия на уголок V-образной формы в условиях реверсирования тока с использованием двух монолитных анодов и системы из шести анодных секций при следующих условиях. Длина, ширина и высота гальванической ванны составили 320 × 200 × 500 мм. В качестве монолитного анода использовалась цинковая пластина размером 210 × 5 × 400 мм, анодной секции – 70 × 5 × 400 мм. Размеры стального уголка составляли 290 × 3 × 350 мм. Аноды размещены от стенок ванны на расстоянии 15 мм. Ванна заполнена цианистым электролитом на уровень 460 мм. Состав компонентов цианистого электролита, г/л: ZnO – 35–45; NaCN – 80–90, NaOH – 50–100; Na₂S – 0.5–1.5; C₃H₈O₃ – 1–2. В цианистом электролите взаимодействие оксида цинка с цианидом натрия сопровождается образованием комплексных соединений цинка:

$2{\text{ZnO}} + 4{\text{NaCN}} + 2{{{\text{H}}}_{2}}{\text{O}} = {\text{N}}{{{\text{a}}}_{2}}\left[ {{\text{Zn}}{{{\left( {{\text{CN}}} \right)}}_{4}}} \right],$

при этом тетрациано(II) цинкат натрия диссоциирует в растворе на ионы натрия и комплексный ион:

${\text{N}}{{{\text{a}}}_{2}}\left[ {{\text{Zn}}{{{\left( {{\text{CN}}} \right)}}_{4}}} \right] = 2{\text{N}}{{{\text{a}}}^{ + }} + {{\left[ {{\text{Zn}}{{{\left( {{\text{CN}}} \right)}}_{4}}} \right]}^{{2 - }}}.$

В свою очередь, химические процессы на катоде и анодах описываются нижеприведенными уравнениями соответственно:

${{[{\text{Zn(CN}}{{)}_{4}}]}^{{2 - }}} + 2e = {\text{Zn}} + 4{\text{C}}{{{\text{N}}}^{ - }},$

${\text{Zn}}--2e + 4{\text{C}}{{{\text{N}}}^{ - }} = {{[{\text{Zn}}{{({\text{CN}})}_{4}}]}^{{2 - }}}.$

Температура электролита 22°C. Выход по току 0.81. Напряжение питания 5 В. Плотность цинка 7133 кг/м³, электропроводность 0.085 м/Ом, электрохимический эквивалент 3.39 × 10^–7 кг/(А с).

Согласно результатам решения описанной задачи оптимального управления, посредством разработанного авторами программного обеспечения [13], был получен следующий режим работы анодных секций для достижения заданной толщины покрытия в 15 мкм: при “прямом” включении отключаются секции 1,1;1,3;1,5; при “обратном” включении – 1,2;1,4;1,6; длительности “прямого” и “обратного” режима составляют 12 и 2 с. Адресация индексов анодных секций начинается с верхнего левого угла и по направлению часовой стрелки. Для достижения той же заданной толщины покрытия процесс цинкования уголка V-образной формы был проведен с использованием монолитных анодов. Для реализации рассмотренного процесса использовался микроконтроллер Arduino Uno Rev3, управляющий отключением требуемых анодных секций для “прямого” и “обратного” режимов посредством системы однофазных твердотельных реле PSSR и задающий необходимые значения длительностей режимов посредством программирования команд выпрямительного агрегата Flex Kraft с рабочим напряжением 0–12 В и силой тока 0–600 А, поддерживающего реверсирование тока.

Измерение нанесенного цинкового покрытия осуществлялось по ГОСТ 9.302-88 толщиномером List Magnetic Top-Check, обладающим погрешностью измерения ±1 мкм на диапазоне 0–100 мкм с разрешающей способностью 0.1 мкм. Для уменьшения влияния случайных факторов проводилась серия экспериментов с усреднением измеренной в геометрически эквивалентных друг другу точках толщины слоя покрытия на поверхности изделия.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

На рис. 1 и 2 представлены распределения потенциала φ для сечения, проходящего параллельно оси L_x0L_y, при использовании монолитного анода и системы с отключаемыми анодными секциями для “прямого” (а) и “обратного” (б) режима реверсирования тока.

Рис. 1.

Распределение потенциала для “прямого” (а) и “обратного” (б) режима реверсирования тока с монолитными анодами в гальванической ванне для одного из сечений, параллельного дну ванны.

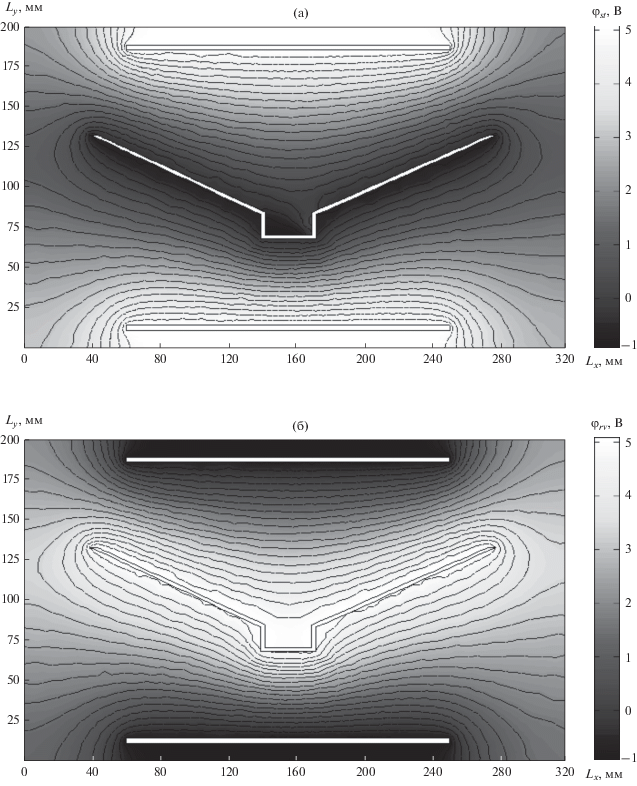
Рис. 2.

Распределение потенциала для “прямого” (а) и “обратного” (б) режима реверсирования тока с отключаемыми анодными секциями в гальванической ванне для одного из сечений, параллельного дну ванны.

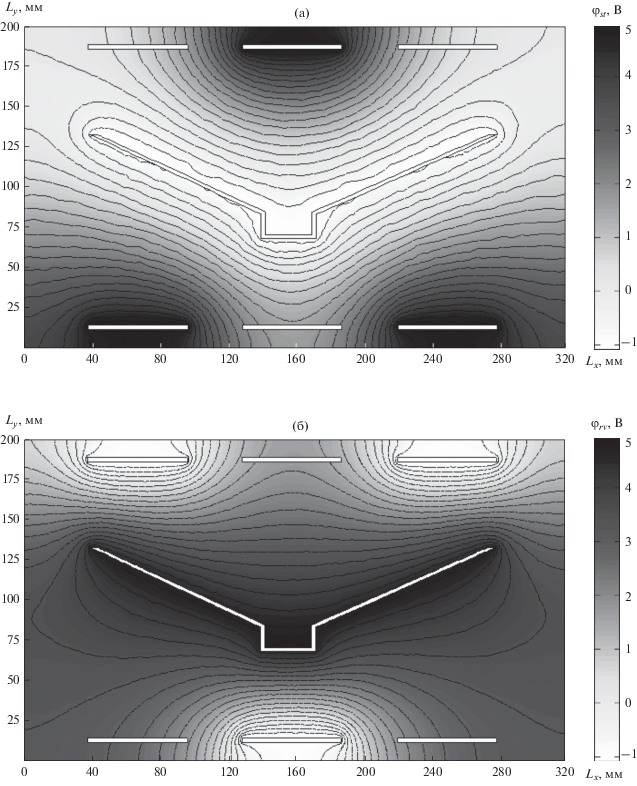
Из данных рисунков видно, что происходит корректировка первичного поля распределения потенциала за счет изменения геометрической конфигурации составного анода посредством отключения соответствующих анодных секций при “прямом” и “обратном” режимах реверсирования тока.

Рис. 3а и 3б демонстрируют численный расчет распределения прироста δ⁺ и уменьшения δ^– толщины цинкового покрытия по поверхности V-образного изделия при использовании монолитного анода и системы отключаемых анодных секций. Отключение анодных секций при “прямом” режиме реверсирования тока оказывает наибольшее влияние на краевой эффект, в то время как “обратный” режим обеспечивает увеличение скорости растворения металла покрытия на более близких к включенным анодным секциями поверхностях катода, чем к отключенным анодам.

Рис. 3.

Развертка распределения толщины покрытия по поверхности изделия для монолитного анода (а), системы анодных секций (б) и их сравнение (в): 1, 2 – прирост и уменьшение толщины покрытия; 3, 4 – толщина покрытия в случаях применения монолитного анода и предлагаемой системы анодных секций.

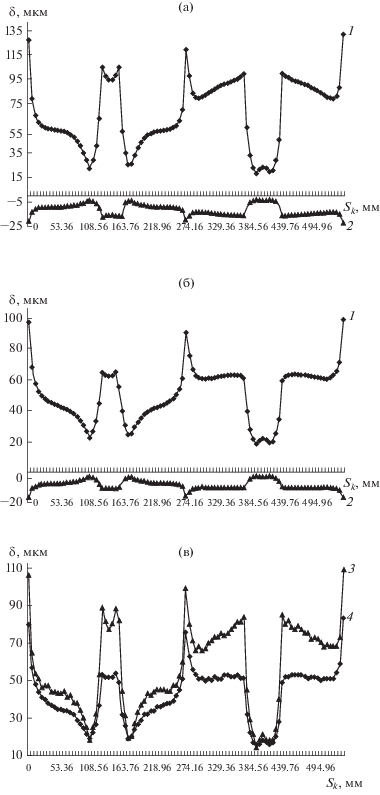
На рис. 3в приводятся экспериментальные распределения толщины покрытия по развернутой поверхности изделия для сечения, параллельного дну ванны, с использованием: монолитного анода (кривая 3); предлагаемого способа (кривая 4). Относительное отклонение критериев неравномерности (6), вычисленных по расчетным и измеренным значениям толщины покрытия, не превышает 8%, что говорит об адекватности разработанной математической модели.

Вычисленные по измеренным значениям распределения толщины покрытия критерии неравномерности составили 9.428 и 6.573 для монолитного анода и системы анодных секций соответственно. В таком случае эффективность применения режима отключения анодных секций при реверсировании тока по сравнению с использованием монолитного анода составила 30.2%.

Таким образом, использование монолитного анода при реверсивном режиме для значительной номенклатуры обрабатываемых изделий не позволяет оказывать влияние на равномерность распределения гальванического покрытия, так как не предусматривает конструктивных изменений используемых анодов, что не способствует эффективному применению данного способа для серийного производства.

ЗАКЛЮЧЕНИЕ

Подходы, реализующие сочетание оптимальных режимов электролиза с геометрическими условиями нанесения покрытия, сложны в технической реализации, и при этом не всегда приносят ожидаемых результатов (в плане равномерности), а значит, плохо подходят для серийного производства. В связи с этим предложен оригинальный способ снижения неравномерности гальванического покрытия с использованием системы независимых анодных секций, отключаемых в процессе нанесения покрытия в режиме реверсирования тока. Для описанного процесса поставлена задача оптимального управления в соответствии с критерием неравномерности покрытия и составлена математическая модель динамики с распределенными координатами, отличающаяся учетом режима реверсирования тока с отключаемыми анодными секциями. Адекватность и эффективность предложенного режима гальванического процесса подтверждается экспериментально.

К числу процессов, в которых применение способа оправдано, следует отнести: цинкование, никелирование, кадмирование, меднение, хромирование, серебрение, латунирование, золочение, железнение. В данных процессах существует возможность варьирования распределением потенциала в пространстве ванны, позволяющая уменьшить плотность тока на более нагруженных участках и увеличить ее на менее нагруженных участках катода, что повлечет за собой снижение неравномерности распределения гальванического покрытия.

Следует также отметить, что важным преимуществом предложенного авторами способа снижения неравномерности гальванического покрытия является низкая стоимость необходимого оборудования. Тот факт, что для нового гальванического процесса или формы покрываемой детали не требуется вносить изменения в конструктивную часть системы секций, а необходимо лишь рассчитать оптимальный режим функционирования системы анодных секций при реверсировании тока, позволяет применять предлагаемый способ снижения неравномерности гальванического покрытия для широкой номенклатуры обрабатываемых гальваническим образом изделий при серийном производстве.

ОБОЗНАЧЕНИЯ

C	концентрация компонента электролита, г/л
с	скорость света, м/с
E	электрохимический эквивалент, кг/(А с)
F₁, F₂, F₃	поляризация на аноде, катоде и биполярном электроде, В
I	режим работы
i	плотность тока, А/м²
L_x, L_y, L_z	длина, ширина и высота гальванической ванны, мм
M, N	число рядов и количество анодных секций в каждом из них
$\vec {n}$	нормаль к поверхности
R	критерий неравномерности
S	поверхность детали, мм²
T	длительность процесса, ч
t	температура, ºC
U	напряжение на электроде, В
x, y, z	координаты точки в пространстве гальванической ванны, мм
δ	толщина покрытия, мкм
η	выход по току
μ	магнитная проницаемость электролита, Гн/м
ρ	плотность металла, кг/м³
τ	момент времени, с
υ	количество периодов включения “прямого” и “обратного” тока
φ	потенциал в гальванической ванне, В
χ	электропроводность, м/Ом

ИНДЕКСЫ

0	начальное значение
a	анод
be	биполярный электрод
ins	изолятор
j	период включения
k	катод
max	максимальное значение
min	минимальное значение
rv	“обратное” включение
st	“прямое” включение
zad	заданное значение
+	прирост
–	растворение

Список литературы

Каданер Л.И. Равномерность гальванических покрытий. Харьков: Изд-во Харьков. гос. ун-та, 1961.
Romanenko A.V. Effect of reversing current parameters on the uniformity of zinc coatings obtained in ammonia electrolyte // Russian J. Applied Chemistry. 1998. V. 71. P. 2020. [Романенко А.В. Изучение влияния параметров реверсивного тока на равномерность цинковых покрытий, полученных в аммонийном электролите // Журн. прикладной химии. 1998. Т. 71. № 11. С. 1900.]
Zemanová M., Krivosudská M., Chovancová M., Jorík V. Pulse current electrodeposition and corrosion properties of Ni–W alloy coatings // J. Applied Electrochemistry. 2011. V. 41. P. 1077.
Dini J.W., Johnson H.R. The properties of gold deposits produced by DC, pulse and asymmetric AC plating // Gold Bulletin. 1980. V. 13. P. 31.
Kronsbein J. The effect of insulating and conducting shields and partly stopped-off electrodes on current distribution in electrolytic cells // Proceedings of the London Mathematical Society. 1947. V. 49. № 4. P. 260.
Lavelaine de Maubeuge H. Calculation of the optimal geometry of electrochemical cells: application to the plating on curved electrodes // Journal of Applied Electrochemistry. 2002. V. 149. № 8. P. 413.
Litovka Yu.V., Mikheev V.V. Numerical calculation of the electric field in an electroplating bath with bipolar electrodes // Theor. Found. Chem. Eng. 2006. V. 40. № 3. P. 305. [Литовка Ю.В., Михеев В.В. Численный расчет электрического поля в гальванической ванне с биполярными электродами // Теорет. основы хим. технологии. 2006. Т. 40. № 3. С. 328.]
Helle H.P.E., Beek G.H.M., Ligtelijn J.Th. Numerical determination of potential distribution and current densities in multi-electrode systems // Corrosion. 1981. V. 37. № 9. P. 522.
Litovka Yu.V., D’yakov I.A. Method to determine the potentials of anodes in a multianode electroplating bath // Theor. Found. Chem. Eng. 1997. V. 31. № 2. P. 191. [Литовка Ю.В., Дьяков И.А. Метод расчета потенциалов анодов в многоанодной гальванической ванне // Теорет. основы хим. технологии. 1997. Т. 31. № 2. С. 218.]
Гольдберг С.М. О некоторых численных методах решения жестких систем обыкновенных дифференциальных уравнений. М.: Препринт ИПМ АН СССР, 1976.
Лионс Ж.-Л. Оптимальное управление системами, описываемыми уравнениями в частных производных. М.: Мир, 1972.
Бояринов А.И., Кафаров В.В. Методы оптимизации в химической технологии. М.: Химия, 1969.
Конкина В.В., Соловьев Д.С. Свидетельство о государственной регистрации программы для ЭВМ ФИПС № 2015613760 RU. Расчет распределения толщины покрытия по поверхности изделия для реверсивного режима в многосекционной гальванической ванне. Дата регистрации 25.03.2015 г.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал